Introduction

Midline shift (MLS, which is the deformation of midline) is the most important quantitative feature for clinicians to evaluate the severity of brain compression caused by space-occupying lesions such as hemorrhage and tumor, for diagnosis and prognosis [1]. Cerebral glioma is one of the most aggressive space-occupying diseases with incidence around five to ten per 100,000 general population [2]. Magnetic resonance imaging (MRI) is commonly used for early diagnosis of gliomas [3]. Researches manifest that the presence of MLS is an important prognostic factor influencing survival [4]. While considerable attentions have been paid on MLS quantification of hemorrhage patients, there is no existing literature on quantification of cerebral gliomas. Tumor and edema are two major pathological factors influencing MLS for patients with cerebral gliomas [5]. Quantification of MLS for hemorrhage patients is based on computed tomography images and thus could not be directly applicable to patients with gliomas. Hence, an efficient method to compute MLS for patients with gliomas from MRI is desirable.

So far, researches on quantification of MLS are concentrated on traumatic brain injury [1, 6–11]. These methods could be classified as: symmetry-based [1], regression model based [6], and anatomical markers based [7–11]. Liao et al. [1] employed a quadratic Bezier curve to approximate the deformed midline (dML) with three segments: the upper and lower line segments of the falces, and the middle curved segment formed by the intervening brain using the traditional local intensity symmetry. Liu et al. [6] measured MLS based on a linear regression model for the relationship between the hemorrhage and the MLS and adjusted according to local intensity symmetry. Anatomical markers based methods assume the existence of feature points on the dML: falx, septum pellucidum (SP), and the center of third ventricle. Xiao et al. [7, 8] approximated MLS from SP by combining multiresolution binary level set segmentation [9] and Hough transform. Chen et al. [10] applied a set of ventricle templates based on which the MLS was estimated to match feature points. Liu et al. [11] estimated the dML as the 3 line segments connecting 4 anatomical markers (the frontal falx, center of the frontal horn of lateral ventricle, center of the third ventricle, and lateral falx).

As noted in [7], symmetry-based methods might fail for cases with symmetry destroyed by pronounced brain compression. The regression model cannot be well suited to individual data due to the complexity of deformation and the nature of regression. Anatomical markers based methods [7–11] will fail when the markers are absent (such as the SP in [7]) or the model to determine the markers is not always valid (such as the model for falces in [11] and SP in [7]).

The maximum MLS is known as most relevant measurement for quantifying pathology severity. In fact, the maximum MLS might not always occur at the axial slice containing SP and third ventricle as did in [1, 6–11]. Thus, to identify the axial slice with maximum MLS is desirable.

Viscoelasticity is a significant measure of the microstructural constitution of soft biological tissue. In viscoelastic theory, the stress–strain relationship is usually modeled by a combination of elastic and viscous elements for characterizing the specific rheological behavior (i.e. viscoelastic deformation) of the material [12]. Numerical studies show that the brain tissue deformation should be approximated by non-linear-viscoelastic model [13–15] rather than simple linear or quadratic curve model [1, 6]. Voigt model is frequently used in the literature [16], which is mainly applied in image registration for surgery plan and intraoperative navigation [17].

In this paper, we investigate approximation of MLS on axial slices by combining mechanics model and features of image symmetry. More specifically, an enhanced Voigt model is proposed to simulate the midline deformation after cerebral gliomas to predict the dML. A new way to define local symmetry based on intensities and intensity gradients is explored for the mechanical model to be tailored to the image features to refine the dML. The issues of finding the appropriate axial slice and robust determination of falces are also addressed. The preliminary results of this study have been presented as an oral lecture at the 29th International Congress and Exhibition on Computer Assisted Radiology and Surgery (2015) in Barcelona, Spain.

Materials and methods

Materials

Thirty subjects from the Virtual Skeleton Database (https://www.virtualskeleton.ch/BRATS/Start2013) are used for this study. All subjects are provided from the Multimodal Brain Tumor Segmentation challenge organized by the MICCAI 2013 conference. The data contain multi-contrast MRI scans of 10 low- and 20 high-grade glioma patients that have been manually annotated with four lesions labels (necrosis, edema, non-enhanced tumor, and enhanced tumor). The ground truths of the tumor and the edema regions were manually delineated by clinical experts of MICCAI conference and could be accessible from the website (http://martinos.org/qtim/miccai2013/index.html). For each subject, the data include T1, T2, FLAIR, and post-Gadolinium T1 magnetic resonance volumes. All volumes have been skull stripped, linearly co-registered to T1 contrast volume, and interpolated to 1 mm isotropic resolution. In this study, only the T2 volume of each subject is used for delineating dML. The ground truths of the MLS were determined by a clinical expert from Linyi People’s Hospital on both the original and interpolated axial slices (with spatial resolution of 1 and 0.33 mm respectively).

Methods

The proposed method consists of three components: preprocessing, prediction and refinement of dML. The preprocessing component is to determine the midsagittal plane (MSP), find the representative axial slice to quantify the MLS, rotate the axial slice and interpolate the representative axial slice. The prediction component is to determine the initial dML using enhanced Voigt model iteratively. The refinement component is to construct the local symmetry metric, refine and smooth the predicted dML. These components are detailed below.

Preprocessing

The axial slice with maximum MLS is manually picked for each data. Its automation is elaborated in Discussion section.

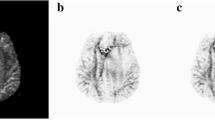
The MSP is extracted based on local symmetry and outlier removal [18] (Fig. 1b, yellow line).The ideal midline (iML) of an axial slice is obtained by connecting two intersections between the MSP and the brain boundary. Each scan is rotated to make iML vertical for facilitating subsequent processing (Fig. 1c, blue line).

Fig. 1
figure 1

An axial slice (a), the brain and the delineated lesions (region enclosed within the red contour) (b), and the rotated brain with the ideal midline (green line segment) being vertical (c)

Full size image

The frontal and lateral falces are the starting and ending points of both iML and dML segments which will not deform due to pathology. It is thus desirable to determine the two falces based on a methodology that can get rid of the influence of pathology. Since the MSP is determined as if there were no pathology due to outlier removal [18], the intersection points between the MSP and the brain boundaries of the axial slice are taken as the two falces (Fig. 1c, the end points of the green line segment).

As the spatial resolution of the axial slice is 1 mm, which is much lower than the spatial resolution of computed tomography axial slice (around 0.30 mm per voxel) for determining MLS, the rotated axial slice is then interpolated 3 × 3 using a bicubic interpolation scheme to have a new spatial resolution of 0.33 mm per voxel in both X and Y directions. The subsequent processing is based on the rotated and interpolated axial slice. The dependency of MLS accuracy on the interpolated spatial resolution is elaborated in the Discussion section.

Prediction of the deformed midline

In this section, the original Voigt model is first introduced, followed by construction of an enhanced model according to the analysis of the viscoelastic properties of brain tissues.

  1. (1)

    The original Voigt model The viscoelasticity of brain tissues can be described intuitively as consisting of an ideal spring (to simulate the ordinary spring deformation whose mechanical properties follow the Hooke’s law) and dashpot (to simulate the viscous deformation which obeys the laws of Newtonian fluid) [19]. The Voigt model is employed to describe the viscoelastic properties of brain tissue due to its good fitting of the property of the deformation of brain tissues corresponding to the creep curve of the Voigt model [20].The relationship between the strain \(\varepsilon\) and stress \(\sigma\)(Pa) could be described by the following equation:

    $$\sigma = K\varepsilon + \mu \frac{{{\text{d}}\varepsilon }}{{{\text{d}}t}}$$
    (1)

    where K (Pa) is the elastic coefficient of the ideal spring, and \(\mu\)(Pa.sec) is the viscosity coefficient of the ideal dashpot. The solution is

    $$\varepsilon \left( t \right) = \frac{\sigma }{K}\left( {1 - e^{{{{ - t} \mathord{\left/ {\vphantom {{ - t} \tau }} \right. \kern-0pt} \tau }}} } \right)$$
    (2)

    where \(\tau = \frac{\mu }{K}\) is the relaxation time (sec).

  2. (2)

    Construction of the enhanced Voigt model The dML can be influenced by at least the following 4 factors: the size of the lesions (larger size will yield greater amount of MLS), the distance between the lesion and the iML (longer distance will yield smaller amount of MLS), the elastic property of midline points (those further apart from the skull are easier to deform), and the rigidity of the skull (points with smaller distance to the skull will deform less).

    To account for these factors, the stress in Eq. (2) is adjusted to construct an enhanced Voigt model. In particular, the gravity \(G\left( {P,Q} \right)\) (N) between voxel Q on the iML and the lesion is used to indirectly represent the pressure of the lesion

    $$G\left( {P,Q} \right) = \frac{{gM_{P} M_{Q} }}{{r^{2} }}$$
    (3)

    where P is the geometric center of the lesion, \(M_{P}\) and \(M_{Q}\)(kg) are respectively the mass of the lesion and Q, r(m) is the Euclidean distance between P and Q, and \(g\)(Nm2/(kg)2) is the gravitation constant (Fig. 2). In addition, a positional harmonic item \(F\left( r \right)\)(1/m2) is introduced to account for the positional constraint with variable rigidity,

    $$F\left( r \right) = A\left( {1 - \frac{1}{{\sqrt {2\pi } \delta }}{ \exp }\left( { - \frac{{\left( {r - r_{0} } \right)^{2} }}{{2\delta^{2} }}} \right)} \right)$$
    (4)

    where \(r_{0}\)(m) is the distance from P to the iML, \(\delta\) is the standard deviation of the distances between P and all voxels on the iML, and A is the modulation factor in the range [5 × 10−5, 4.5 × 10−3]. The stress after adjustment is

    $$\sigma = F\left( r \right) \times G\left( {P,Q} \right)$$
    (5)
    Fig. 2
    figure 2

    The sketch map of the midline shift of the enhanced Voigt model and determination of local neighborhood for dML refinement

    Full size image

    The eventual constitutive equation of the enhanced Voigt model is thus,

    $$\varepsilon \left( {r,t} \right) = \frac{{F\left( r \right)gM_{p} M_{Q} }}{{Kr^{2} }}\left( {1 - e^{{^{{{{ - t} \mathord{\left/ {\vphantom {{ - t} \tau }} \right. \kern-0pt} \tau }}} }} } \right)$$
    (6)
  3. (3)

    Parameters assignment The geometric center P and voxel Q in Eq. (6) correspond to two particles with masses:\(M_{P}\) = the number of the voxels of the lesion and \(M_{Q} = 1\) (kg). The geometric center \(P\) is derived from tumor voxels (see Discussion for justification). The elastic coefficient and the viscosity coefficient of brain tissue are set from literature [21] as follows: \(K = 6.67\; \times \;10^{ - 4}\)(Pa), and \(\mu = 0.0075\)(Pa.sec). The gravity constant g is 1 (Nm2/(kg)2).

    As shown in Eq. (6), the strain changes with time, while the dML to be extracted is a static state at a certain time instant. Thus, we assume that the dML has reached the stable state when the MRI scans are obtained. Experiments with varying t in [1, 1500] (sec) are carried out to find that a value of not smaller than 1000 (sec) is appropriate. The curve of error evolution corresponding to parameter t is shown in Fig. 3.

    Fig. 3
    figure 3

    The curve of error evolution with respect to parameter t

    Full size image
  4. (4)

    Prediction The initial strains of all voxels on the iML are approximated in this step. According to the strong rigidity of the cerebral dura matter, we consider the segments of the first one-twelfth from the top and the last one-fourth of the iML as the falx segment, and the positional harmonic item \(F\left( r \right)\) is set as the minimum of \(F\left( r \right)\), i.e., \(A\left( {1 - \frac{1}{{\sqrt {2\pi } \delta }}} \right)\). For the remaining voxels on the iML, \(F\left( r \right)\) is computed according to Eq. (4). An example of the predicted dML is shown in Fig. 4a (purple curve).

    Fig. 4
    figure 4

    The predicted dML (a), points with maximum composite local symmetry within the neighborhood of predicted dML (b), the eventual dML after curve smoothing (c), and magnified points with maximum local symmetry of (b) (green points) and the corresponding curve after smoothing within the green window of (c) (red curve) (d)

    Full size image

Composite local symmetry

As pointed out by Davidson and Hugdahl [22], the brain exhibits rough local symmetry around the midline. Resorting to local symmetry to refine the predicted dML seems reasonable. Unlike most existing methods which only employ the intensity information to describe the local symmetry, both intensities and intensity gradients are exploited to form the composite local symmetry that intends to enhance the local symmetry contrast of voxels both in the uniform and non-uniform region around dML.

  1. (1)

    Local intensity symmetry Denote the intensity of a voxel at (x,y) as f(x, y), and the coordinates of a voxel P as (x p ,y p ). The traditional expression of local intensity symmetry is the sum of absolute intensity differences for pairs of voxels along the line segment perpendicular to dML. Since the iML has been rotated to be vertical, the initial local intensity symmetry can be approximated along the horizontal direction. All voxel within its neighborhood N p (7 × 7) will be involved to calculate the initial local intensity symmetry of a voxel P. Suppose voxel q is within N p and its mirror voxel with respect to p is q’. The initial local intensity symmetry SD is calculate as

    $$SD(p) = \mathop \sum \limits_{{q \in N_{p} }} \Bigg| {f\left( {x_{q,} y_{p} } \right) - f\left( {x_{{q^{\prime}}} ,y_{p} } \right)} \Bigg|e^{{ - \frac{{(q - p)^{2} }}{2}}}$$
    (7)

    One potential problem of SD in Eq. (7) is that voxels in a region with uniform intensities could also be small, which makes it difficult to differentiate from its neighboring voxels. A Gaussian filtering in vertical direction is employed to enhance the intensity symmetry contrast. The modified SD map could then be detected through edge detection such as a Laplacian-of-Gaussian (LOG) filter [23]. The local intensity symmetry can then be defined as

    $$SS = \left( {SD*Gauss} \right)*LOG$$
    (8)

    where \(*\) is for convolution, and Guass is for Gaussian filter (mean being 0, and standard deviation being 0.5).

    As shown in Fig. 5, SS of the voxels on the symmetry curve in regions with uniform intensities tends to be maximal due to the introduction of Gaussian filtering and LOG (the red curve), which will not be discernable from neighborhood voxels if LOG is not employed (the blue curve).

    Fig. 5
    figure 5

    Illustration of the difference between local symmetry of the voxels in the region (green line) with uniform intensities for SD (blue curve in (d)) and SS (red curve in (d)), where the location of the arrow is the symmetry center. Figure 5b, c are respectively the SD and SS images of Fig. 5a

    Full size image
  2. (2)

    Local intensity gradient symmetry As is pointed out [24], the gradient information is more discriminative than intensity, and more stable to photometric changes [24]. Inspired by SIFT [25], HOG [26], and the method proposed by Hauagge and Noah [27], a histogram of local intensity gradient orientations h(q) at each voxel q is constructed from the intensity gradient magnitude M(x, y) and orientation θ(x, y) (in the range of 0 to π) with a gradient operator such as Sobel operator.

    The orientation of voxels (Dir) within N q (7 × 7) are grouped into an orientation histogram with 8 bins, i.e., [0, π/8)(Dir 0 ), [π/8, π/4)(Dir 1 ), …, and [7π/8, π](Dir 7 ), weighted by the gradient magnitude of voxels within N q . The gradient orientation histogram \(\mathop {h_{q} }\limits^{ \wedge } \left( {Dir_{j} } \right)\) is thus calculated as follow:

    $$\mathop {h_{q} }\limits^{ \wedge } \left( {Dir_{j} } \right) = \mathop \sum \limits_{{\begin{array}{*{20}c} {\theta_{i} \in Dir_{j} } \\ {i \in N_{q} } \\ \end{array} }} M_{i} (\theta_{i})$$
    (9)

    where \(j = 0,1,2, \ldots ,7\), \(\theta_{i}\) and \(M_{i}\) are the gradient orientation and the gradient magnitude of voxel i.

    The histogram \(\mathop {h_{q} }\limits^{ \wedge }\) is normalized to form the final gradient orientation histogram:

    $$h_{q} \left( {Dir_{j} } \right) = \frac{{\mathop {h_{q} }\limits^{ \wedge } \left( {Dir_{j} } \right)}}{{\sum\limits_{j = 0}^{7} {\mathop {h_{q} }\limits^{ \wedge } \left( {Dir_{j} } \right)} + \xi }}$$
    (10)

    where \(\xi\) is a constant (0.05) used to enhance the robustness to noise.

    If voxels \(q\) and \(q^{\prime}\) are symmetrical to dML in terms of both position and local intensity distribution, histogram \(h_{q}\) should be similar to the reflected histogramof \(q^{\prime}\) which is denoted as \(h^{\prime}\left( {q^{\prime}} \right)\). A possible way to quantify the similarity of intensity gradients of two voxels \(q\) and \(q^{\prime}\) is to define the metric as dot product of the two vectors \(h_{q}\) and \(h^{\prime}\left( {q^{\prime}} \right)\). The intensity gradient symmetry \(SG\left( p \right)\) is calculated as:

    $$SG\left( p \right) = \mathop \sum \limits_{{q \in N_{p} }} h\left( q \right) \circ h^{\prime}\left( {q^{\prime}} \right)e^{{ - \frac{{(q - p)^{2} }}{2}}}$$
    (11)

    where \(\circ\) is dot production of vectors.It can be shown clearly that SG will be maximized when \(q\) and \(q^{\prime}\) are a pair of symmetric intensity gradient voxels (Fig. 6).

    Fig. 6
    figure 6

    Two gradient orientation histograms of a voxel-pair being symmetric in terms of both position and local gradient distribution with respect to dML

    Full size image
  3. (3)

    The composite local symmetry The composite local symmetry metric Sym is defined as:

    $$Sym = SS^{'} \times \left( {1 - grad} \right) + grad \times SG^{'}$$
    (12)

    where grad is the normalized gradient magnitude \(M\left( {x,y} \right)\), \(SS^{'}\) and \(SG^{'}\) are respectively the normalized SS and SG with range [0, 1]. It can be shown that the greater the Sym of a voxel p, the bigger the probability of the voxel to be on the dML: the local intensity symmetry will be dominant (\(Sym \approx SS^{'}\)) when the voxels belong to uniform regions with weak edge information (i.e., \(\left( {1 - grad} \right) > > grad\)); the local gradient symmetry will be dominant (\(Sym \approx SG^{'}\)) when the voxels belong to non-uniform regions with strong edge information (i.e., \(grad > > \left( {1 - grad} \right)\)). Figure 7a, b, c show respectively SS, SG and the Sym of Fig. 1a.

    Fig. 7
    figure 7

    Images of the local symmetry (a) SS, (b) SG, and (c) Sym of Fig. 1a

    Full size image

    With different modulation factor A, the sum of composite local symmetry on the dML can be calculated. The eventual dML will be the one with maximum sum of composite local symmetry to be refined.

Refinement based on local symmetry

The deformation of midline is caused by multi-factors besides lesions such as imaging time and inhomogeneity of the viscoelasticity of different brain tissues. Thus, it is necessary to adjust the predicted dML according to image features. The refinement is to include: determination of local neighborhood and refinement of dML within the local neighborhood according to the composite local symmetry.

  1. (1)

    Determination of local neighborhood The local neighborhood of the predicted dML is a rectangle inspired by the pinhole camera model determined in the following way. For any voxel Q on the iML, we connect points \(P\) and Q, and extend the line segment \(PQ\) to get two intersection points (\(B_{1}\) and \(B_{2}\)) on the lesions boundary (Fig. 2). The mirror points \(C_{2}\) and \(C_{1}\) of the points \(B_{1}\) and \(B_{2}\), respectively, are obtained by using the predicted strain \(\varepsilon\) computed from Eq. (6) as the focal length and the point Q as the pinhole.

  2. (2)

    Refinement according to local symmetry and curve smoothing For each voxel P on the predicted dML, the voxel with maximum composite local symmetry Sym within the local rectangular neighborhood of P is searched to replace the predicted voxel P (Fig. 4b). Denote the coordinates of these voxels as \(p_{i} \left( {x_{i} ,y_{i} } \right)\) and the voxels \(p_{i}^{'}\) after smoothing as \(\left( {x_{i}^{'} ,y_{i}^{'} } \right)\) (\(i = 1,2, \ldots ,N\)), where N is the number of voxels of the predicted dML. We fix the first and last points on both the predicted and eventual dMLs to be the intersection points between the MSP and the brain boundaries of the axial slice. The following rules are employed to find voxels \(\left( {x_{i} ,y_{i} } \right)\) with maximum local symmetry to replace the predicted dML:

  1. (a)

    If there is only one voxel \(p_{i}\) with the maximum local symmetry, \(p_{i}\) is chosen to replace the voxel P;

  2. (b)

    If there is more than one voxel with the same maximum local symmetry, the point closest to the last optimal point \(p_{i - 1}\) is chosen to replace the voxel p.

A simple average of p i-2 , p i-1 , p i , p i+1 , and p i+2 is implemented to smooth the coordinates to derive \(p_{i}^{'}\) with coordinates \(\left( {x_{i}^{'} ,y_{i}^{'} } \right)\)(Fig. 4d). Finally, the approximated dML is obtained by connecting voxels \(p_{i}^{'}\) and \(p_{i + 1}^{'}\) (\(i = 1,2, \ldots ,N - 1\)) (Fig. 4c).

The complete procedure to approximate dML is summarized in Table 1.

Table 1 The procedure to approximate dML
Full size table

Results

The dML error of a voxel on the approximated dML is defined as the minimum distance between this voxel and all the voxels on the ground truth dML. To evaluate the performance of the proposed method, the following measures are employed: the mean and standard deviation of the dML errors (denoted respectively as meanE and sdE), and the ratio of the area of the left hemisphere to that of the right hemisphere separated by the dML [11].

For quantifications, the position of P is the geometric center of the tumor, while the mass of P is the sum of voxels of tumor and edema on the axial slice with maximum MLS.

In this section, we show the quantification results of the proposed method, some relevant additional experimental results, and the contributing factors of tumor and edema to dML.

Performance evaluation

The dMLs of ground truth, the proposed method for two typical scans with different extents of edema are shown in Fig. 8.

Fig. 8
figure 8

The ground truth of dML(blue curve) (a), the lesions segmented manually with four labels for different pathologies (from dark to bright): necrosis, edema, non-enhanced tumor and enhanced tumor (b), and the estimated dML by the proposed method of two typical data

Full size image

Comparisons between the approximated and ground truth dMLs are measured as well for quantification. Specifically, the maximum value of the dML errors of the voxels on the approximated dML is adopted to quantify the error of the maximum distance of the proposed method, which is called the maximum distance error of the approximated dML. Similarly, the error of area ratio of the approximated dML is the absolute difference between the ratios calculated by approximated and ground truth dML. The scatter plot of MLS (approximated and ground truth) and the error distribution are shown respectively in Figs. 9 and 10. The distributions of the maximum distance errors, area ratio errors, Mean_sim, and sd_sim of the 30 data are summarized in Table 2.

Fig. 9
figure 9

The scatter plot of MLS: approximated and ground truth

Full size image
Fig. 10
figure 10

The error distribution of 30 subjects

Full size image
Table 2 Statistics of the errors between the approximated and ground truth dMLs
Full size table

Performance comparison using different local symmetry metrics

To see the accuracy dependency on four ways of local symmetry: SD, SS, SG, and Sym, experiments are carried out for all the 30 subjects. The approximated dMLs using SD, SS, SG, and Sym are shown in Fig. 11 for a scan with large MLS, while the statistics of the accuracy are summarized in Table 3.

Fig. 11
figure 11

dML of ground truth (blue curve) (a), dML of the proposed method with composite local symmetry Sym (red curve) (b), SD (green curve) (c), SS (yellow curve) (d), and SG (purple curve) (e) of a subject

Full size image
Table 3 Accuracy dependency of the approximated dMLs on four ways to defined the local symmetry for all the 30 subjects
Full size table

Paired t-tests have been carried out to see if the proposed method with four local symmetries will have significantly different accuracies. The maximum distance error, area ratio error, meanE and sdE with Sym are significantly smaller than those of SD, all with p ≤ 0.002. Compared with SS and SG, the proposed method with Sym has significantly smaller meanE (p = 0.003 and p < 0.001) and sdE (both p = 0.001).

Discussion

A midline, which is the border between the left and right hemispheres, is a feature requiring a large number of voxels to compute regardless of being deformed or not. For the cases without deformation, midlines could be approximated as a plane and attained through exploring local symmetry and outlier removal [18]. However, it becomes challenging to calculate in case of deformation due to the following reasons:

  1. (a)

    The shape of a midline is hard to predict;

  2. (b)

    The grayscales on a midline can change substantially as it may contain cerebrospinal fluid, gray matter, white matter, and voxels with pathology such as tumor and edema, and

  3. (c)

    The symmetry might be destroyed due to the deformation of the lesion.

The axial slice with maximum MLS is most relevant for clinical implications and is picked manually for quantification, which is a tedious procedure to be automated. We checked closely these 30 data sets and summarized the following rule that was applicable to these 30 data sets. The rule may need more investigation to be generalized. Here the pathology-brain ratio of an axial slice is defined as the ratio of the number of pathology voxels to the number of brain voxels within the axial slice, and pathology could be either tumor or edema. For each of the 30 data sets, the axial slice with the maximum tumor-brain ratio could be found, and the axial slice with the maximum edema-brain ratio could also be found; these two maximum pathology-brain ratios are compared to pick the axial slice with the bigger pathology-brain ratio as the representative axial slice.

Extraction of feature points that are supposed to be on the midline such as falces and SP sounds good, but these points are too sparse for an accurate determination of the midline, let alone the difficulty and possible errors to determine these feature points. In this regard, the proposed method has an inherent advantage as it is based on calculating the deformation of all the points on the iML and does not assume the existence of any anatomical markers.

From Fig. 11 and Table 3, it can be seen that: (a) SS performs better than the traditional local intensity symmetry SD as adopted by Liao et al. [1], (b) SG performs better than SS, and (c) Sym performs substantially better than SS and SG, which may mean that SG and SS provide complementary information to locate dML.

An additional experiment has been carried out to see the relationship between the MSL accuracy and the interpolated spatial resolution. Seven interpolated spatial resolutions of a patient are used to compare the accuracy and time consumption. As the result shown (Fig. 12; Table 4), decreasing the voxel size from 1 to 0.2 mm via bicubic interpolation can decrease the maximum distance error (E1) from 2.94 mm to at most 1.45 mm, but E1 will not change much from spatial resolution of 0.4 mm (spatial amplification of 2.5 × 2.5) while the time consumed can increase substantially. The error will not take the minimum value at the highest spatial resolution. It seems that a spatial amplification of 3 × 3 could attain a good trade-off between accuracy and time consumption (with E1 = 1.45 mm and time = 15.42 s).

Fig. 12
figure 12

The accuracy versus the spatial amplification of a patient data

Full size image
Table 4 Accuracy dependence on the interpolated spatial resolution of a patient data with different spatial resolutions via bicubic interpolation
Full size table

A comparative experiment has been carried out to compare the performance of simple curve smoothing and B-spline curve fitting. Simple curve smoothing was preferred as it yielded a smaller average E1 (1.89 mm) than the curve fitting (E1 = 1.91).

Tumor and cerebral edema are the major contributing factors to MLS through mass effect. In our model, these two factors will impact the dML through the geometrical center P and the pathological region (Fig. 2). To see the influence of P, we carry out experiments with the pathological region fixed (to be the whole lesion) while changing the P to be the geometrical center of tumor, edema, and the whole lesion respectively (Fig. 13). Experiments are also carried out to see the influence of pathological region by fixing P (to be the geometric center of tumor) while varying the pathological region to be respectively the tumor, edema, and the whole lesion (Fig. 14). Quantification of these experiments is summarized in Tables 5 and 6.

Fig. 13
figure 13

Estimation of dML based on the proposed method with different geometric center P and fixed pathological region: the ground truth dML (blue curve) (a), the ground truth lesions (from dark to bright: necrosis, edema, non-enhancing tumor and enhanced tumor) (b), dML from P being the geometric center of tumor (c), dML from P being the geometric center of edema (d), and dML from P being the geometric center of the whole lesion (e)

Full size image
Fig. 14
figure 14

Estimation of dML based on proposed method with fixed P but varying pathological regions: ground truth dML (blue curve) (a), dML from the whole lesions (red curve) (b), dML from the tumor (purple curve) (c), dML from the edema (green curve) (d), and (e) dML form the edema plus tumor (yellow curve)

Full size image
Table 5 Quantification of the experiments using different geometric centers
Full size table
Table 6 Quantification of the experiments using different pathological regions
Full size table

The proposed method will yield better accuracy with P being the geometric center of tumor (Fig. 13; Table 5) and the pathological region being the whole lesion (Fig. 14; Table 6). This may imply that the size of the whole lesion and the location of tumor (instead of edema or the sum of edema and tumor) are more appropriate to determine the extent of deformation. The mechanism of deformation will need more investigation.

Below is a summarization of the major contributions of this study.

  1. (a)

    An enhanced Voigt model to relate the deformation of midline to the size and position of lesions for dML prediction to reflect the viscoelasticity of tissues on dML.

  2. (b)

    A new way to calculate the local symmetry in the vicinity of dML has been proposed by combining the local intensity symmetry and local intensity gradient symmetry. In this way, the dML voxels within the uniform regions could be better differentiated than the traditional local intensity symmetry. The new way of quantifying local symmetry around dML makes the dML refinement more accurate (Table 3).

  3. (c)

    For the cases with large deformation, where the traditional local symmetry around dML is destroyed or the anatomical markers are missing (Fig. 8a), the proposed method could still perform well as it is based on mechanical model and composite local symmetry, while existing methods [1, 6–11] based on the existence of anatomical markers will fail.

  4. (d)

    The proposed methodology has been exploited to investigate the contribution of different pathologies after glioma, which may be employed as a methodological tool for deformation study of MRI scans.

The proposed method could not handle well cases when a large portion of dML is occupied by lesions. Figure 15 shows two scans of low- and high-grade gliomas with the maximum error. In these cases, the portion of dML occupied by lesions is even difficult to be manually delineated by experienced radiologists.

Fig. 15
figure 15

Two cases with maximum error of the proposed method: the ground truth and the estimated dMLs for low- (a and b) and high-grade (c and d) gliomas

Full size image

As the proposed method approximates the dML on each voxel, it could be explored for estimating midsagittal surface which could be useful for registration and quantifying the brain.

Conclusion

To the best of our knowledge, for delineation of deformed midline, this is the first report on both quantification of gliomas and delineation from MRI, which hopefully will provide valuable information for diagnosis and therapy. The study suggests that the size of the whole lesion and the location of tumor (instead of edema or the sum of edema and tumor) could be more appropriate to determine the extent of deformation. Composite local symmetry is recommended to represent the local symmetry around the dML. The proposed method could be potentially used to quantify the severity of patients with cerebral gliomas and other brain pathology, as well as to approximate midsagittal surface for brain quantification.