Modeling Flow in Cerebral Aneurysm After Coils Embolization Treatment: A Realistic Patient-Specific Porous Model Approach

Abstract

Purpose

Computational fluid dynamics (CFD) has been used to evaluate the efficiency of endovascular treatment in coiled cerebral aneurysms. The explicit geometry of the coil mass cannot typically be incorporated into CFD simulations since the coil mass cannot be reconstructed from clinical images due to its small size and beam hardening artifacts. The existing methods use imprecise porous medium representations. We propose a new porous model taking into account the porosity heterogeneity of the coils deployed in the aneurysm.

Methods

The porosity heterogeneity of the coil mass deployed inside two patients’ cerebral aneurysm phantoms is first quantified based on 3D X-ray synchrotron images. These images are also used to compute the permeability and the inertial factor arising in porous models. A new homogeneous porous model (porous crowns model), considering the coil’s heterogeneity, is proposed to recreate the flow within the coiled aneurysm. Finally, the validity of the model is assessed through comparisons with coil-resolved simulations.

Results

The strong porosity gradient of the coil measured close to the aneurysmal wall is well captured by the porous crowns model. The permeability and the inertial factor values involved in this model are closed to the ideal homogeneous porous model leading to a mean velocity in the aneurysmal sac similar as in the coil-resolved model.

Conclusion

The porous crowns model allows for an accurate description of the mean flow within the coiled cerebral aneurysm.

Introduction

Endovascular coiling is a common technique to treat cerebral aneurysms before rupture to slow down blood flow in the aneurysm and to promote thrombus formation inside the aneurysmal sac. Subsequently, this relieves the hemodynamics stimuli on the vascular wall and leads to aneurysmal stability or healing.¹¹ There is, however, a risk of recurrence,⁹ and being able to evaluate the efficiency of coil embolization treatment would help in the prediction of outcomes. Hemodynamics in the aneurysm can provide information on the growth and rupture of the aneurysm,¹⁹ in particular when employing patient-specific data.^13,18,24 The study of the hemodynamics of flow in the aneurysmal sac through CFD, and computing metrics linked to thrombus formation have shown the impact of hemodynamics on aneurysm recurrence after treatment.¹⁰

Computational modeling of the blood flow inside an aneurysm treated with coils presents several challenges. First, the geometry of the coil mass cannot be reconstructed from clinical images, due to scatter artifacts of computed tomography (CT) or low resolution of the coil on magnetic resonance imaging (MRI). To approach coil modeling in CFD, we used a high-energy scan of 3D-printed aneurysmal phantoms containing coils. This high-energy narrow-bandwidth scan, such as is available in a Synchrotron, is necessary to reconstruct the coil configuration as deployed inside the aneurysmal sac.¹⁵ These studies that reproduce the exact configuration of the coils can serve as a reference to understand the hemodynamics features in coil-treated aneurysms, but cannot be used in vivo, and therefore are not translatable to patient-care in a clinical setting. Additionally, these coil-resolved basic fluid mechanics studies carry a very high computational cost, an obstacle that also needs to be overcome to translate CFD to clinically relevant time frames for treatment planning or outcome assessment.¹ Modeling the coil configuration in the aneurysmal sac in vivo, rather than obtaining the coil-resolved geometry, can reduce the computational cost and, if it captures the hemodynamics in sufficient level of detail to produce accurate metrics for treatment prediction, bridge the gap between basic and translational studies.

Modeling coils as porous media has shown promise,¹⁵ even if the homogeneous isotropic porous medium assumptions are well known to oversimplify the coil configuration. Early porous models in the literature considered the coil mass as a homogeneous and isotropic medium.^12,15,20 The material parameters involved such as the permeability and the inertial factor were estimated using the mean porosity of the aneurysm after coiling. The geometry of the coils, however, is well known to be heterogeneous and have preferential directionality due to the deployment method and the memory-shape alloys used in the coils. The need for these more complex models, and higher accuracy in simulating the hemodynamics in coil-treated cerebral aneurysms was demonstrated by comparing predictions from homogeneous isotropic porous medium computations, where the permeability is calculated from the mean porosity in the aneurysm, and those from synchrotron coil-resolved simulations.¹⁵ The results of this study showed that the mean velocities and wall shear stresses in the aneurysm are overestimated and not fully representative of blood flow in the aneurysm with coils.

Experimental work has been done to determine the equivalent permeability of the coil mass.^8,21 These have provided evidence of how, at the same packing density, the permeability varies significantly. Therefore, there is a need to consider the heterogeneity of coil distribution to determine the permeability. As the previous study do not consider the complexity of the geometry, the models are not accurate enough. Yafollahi-Farsani et al.²⁶ studied a porous model that considered the heterogeneous distribution of the porosity and permeability. The method consisted of creating a heterogeneous porous media model within a grid and defining for each element the porosity and permeability in that space, and varying the element size. The prediction of hemodynamics metrics improves with a more complex porous model, as it provides a more accurate reconstruction of the blood flow in aneurysmal sac after being treated with coils. However, the heterogeneous models proposed to date need the actual configuration of the coils to compute the heteregenous porosity and permeability, and therefore cannot be used for prediction of treatment outcomes in patient-specific cases.²⁶

There is a well-established need to define the porous parameters (porosity, permeability, and inertial factor) by considering the heterogeneity of the media, but also creating a model that can be used for prediction, therefore not reliant on detailed knowledge of the coil configuration inside the aneurysm. The purpose of this study is to present an accurate porous media model after coil deployment and validate this model against coil-resolved hemodynamics in two in-vitro reproductions of treated aneurysm patients, using patient-specific boundary conditions in the CFD model. This is done in three steps: (i) characterizing the heterogeneity of the porous media (coils in the cerebral aneurysm) through image analysis of the in vitro aneurysmal vasculature models; (ii) formulating a porous model that allows for the description of the flow inside the aneurysm; and (iii) validating this model against the gold standard coil-resolved geometry obtained through synchrotron microtomography.

Method

Image Acquisition

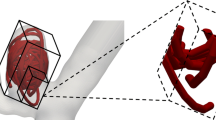
Two patients (A and B) with a cerebral aneurysms treated with endovascular coils (Stryker Endovascular, Kalamazoo, Michigan, USA), with diameters 240–250 μm and lengths 2–30 cm, were enrolled at the University of Washington’s Harborview Medical Center in Seattle, WA, USA. Figure  1 shows the anatomy of both patients and Table  1 presents the volume of the aneurysm and the characteristic length L, with L being the longest inertial axis. Three-dimensional rotational angiography of the carotid artery and aneurysm were obtained before each patient’s aneurysm treatment. After image segmentation of those scans, a 3D model of the aneurysm and parent vessel was created. Briefly, a 1:1 scale positive mold was 3D printed in acrylonitrile butadiene styrene, then, casted in a clear polyester resin (PDMA, Clear-Lite; TAP plastics, San Leandro, California, USA).²³ The same neurosurgeon who performed the endovascular surgery in the patient, treated the in vitro model with the same procedure: the same commercially-available coils were inserted and in the same order. This ensures consistency between the in vivo and in vitro techniques.

Coils cannot be reconstructed from the clinical CT scans, but can be imaged in vitro with synchrotron tomography, with high resolution and without beam hardening artifact. To create the coil geometry reconstructions, the in vitro aneurysmal models were imaged at beamline ID19 of the European Synchrotron Radiation Facility (http://www.esrf.eu) in Grenoble (France), before and after coil placement. The company Novitom in Grenoble (France) performed the tomography on the two models and provided the images segmented. The image resolution was 12.92 and 15.58 $\mu$m for patient A and B respectively. The use of monochromatic radiation avoids artifacts, and beam hardening effects. The scans of the coils were segmented and, to validate the segmentation, the volume of the coils based on the image reconstruction was compared to the volume calculated from the characteristics of the real coils provided by the manufacturer.

The coil geometry was positioned in the 3D model of the aneurysm reconstructed from the patient CT scans. The centerlines from the patient’s parent vessel (from the clinical scan) and from the model (synchrotron microtomography) were extracted using Vascular Modeling Toolkit software (http://www.vmtk.org) and matched by an iterative closest point method.²⁵ This provided the transformation matrices (rotation and translation matrix) that were then applied to the geometry of the coils, using MATLAB (MathWorks, Inc., Natick, Massachusetts, USA), to reposition the coils onto the patient vasculature. This entire process is summarized in Fig. 2.

Figure 1

Aneurysmal anatomy: Patient A (left) and B (right). The arrows present the direction of flow: blue is the inlet and red the outlet. L is a characteristic length, defined as the length of the longest inertial axis (Table 1).

Figure 2

Main steps of the image acquisition: from the angiographic image on the left, to the positioning of the coils in the aneurysm. The results of this process is shown for Patient A.

Table 1 Volume of the aneurysm and characteristic length L for patient A and B.

Porosity Distribution

Definition of the Porous Media

The neck surface was defined as the intersection between the coil mass envelope and the aneurysm’s parent vessel geometry. The envelope was created using MATLAB and the geometry adjustments to create the neck interface were done using StarCCM+ (CD-adapco, Melville, New-York, USA). The volume of the aneurysm with coils was transformed into image format using ImageJ²² and the porosity was calculated by pixel counting (with coils being the solid in white and aneurysmal sac being the pores in grey, see Fig. 3). The mean porosity $\phi _{\rm m}$ of the coil is 0.697 and 0.825 for the patient A and B respectively. Two methods were then developed to analyze the porosity distribution of the coils within the aneurysmal sac : the cubes porosity map and crowns porosity map.

Cubes Porosity Map

The first method to analyze the porosity distribution consisted of creating a porosity map of the aneurysm using a cubic discretization. The volume of the coil and aneurysm was divided into cubes and the porosity of each cube was calculated counting the pixels, as explained above. Only the centered cubes were analyzed to avoid edge effects (Fig. 3). Two cube sizes were defined: small cube with a size of 2d (d been the diameter of the coil, 250 μm), and large cubes with size equal to 4d. In both cases 4d and 2d were very small compared to L, and having two different sizes allows to evaluate the impact of the element size. Figure 3 shows, for example, the cubes porosity map of the patient A. All the image analysis was performed using MATLAB.

Crowns Porosity Map

The objective of the second method is to determine a porosity profile, that is, the porosity gradient along the radius of the aneurysm, induced by the presence of the aneurysm wall. Through image treatment, the crowns were defined by eroding consecutively the cerebral aneurysm with coils defined by a using MATLAB, where the erode region is a crown. The porosity was calculated for each crown. This method allows us to characterize the porosity gradient near the walls and at the neck, represented in the external crowns. This is the key to define the flow in the rest of the aneurysm treated with coils, as will be shown in “Results” section. Four sizes of crowns were defined: 0.25d, 0.5d, 1d, and 2d and a total radial thickness to fill (spherical shells) within the aneurysmal sac of 4d, for all crown sizes. As for the cubes porosity map, these four crowns sizes allow us to evaluate their impact on the results. Figure 3 shows for example a section of the crowns porosity map, sharing the same representation as the cube map, for two different crowns sizes.

Figure 3

Definition of the porous media for patient A: The aneurysm containing the exact coil geometry as obtained from synchrotron microtomography (top left). Cross-section of the aneurysm with coils (top right). Cubes porosity map with the 2 cube sizes: 2d (middle left) and 4d (bottom left), and in red the centered cubes. The crown porosity model, with two different crown sizes 0.25d (middle right) and 1d (bottom right). The colors vary with the porosity, as seen in the color-bar.

Flow Through the Porous Media

Flow in the coil-filled aneurysm is modeled as a porous media, described as a homogeneous and isotropic porous medium by the Darcy–Forchheimer equation (1), as it has been done extensively for cerebral aneurysms in Refs. 12, 15, 20:

$$\begin{aligned} \nabla p=-\frac{\mu }{K}\bar{\mathbf{u }}- \frac{1}{2} \rho C_{2} \mid {\bar{\mathbf{u }}} \mid \bar{\mathbf{u }} \end{aligned}$$

(1)

where $\rho$ is the fluid density (kg/m$^3$), $\nabla$p is the pressure gradient (Pa/m), $\mu$ the fluid viscosity (Pa s), $\bar{\mathbf{u }}$ is the mean fluid velocity (m/s) (i.e. the volume average of the fluid velocity $\mathbf{u}$ at the pore scale) and K (m$^2$) and $C_2$ (1/m) are the permeability and inertial factor coefficient, respectively. These two parameters mainly depend on the porosity at the first order.

Permeability of the Coil

In order to determine the evolution of the permeability of the coil as a function of its porosity, the permeability tensor $\mathbf {K}$ of the 4d centered cubes used in “Cubes Porosity Map” section was computed using Geodict2019 (Math2Market) by solving a specific boundary value problem arising from the homogenization.³ In the following, the non-diagonal terms of the tensor $\mathbf {K}$, about 50 times lower than diagonal terms ($K_x$, $K_y$ and $K_z$), are not presented. These non-zero permeability components were then compared with the self-consistent estimates (SCE) established by Boutin⁵ for parallel ($K_{\rm L}$) and perpendicular ($K_{\rm T}$) flow through cylindrical bundles, given by Eqs. (3) and (4) respectively, with $a=d/2$.

$$ K_{{\text{T}}} = \frac{{a^{2} }}{{8 \times (1 - \phi )}} \times \left( { - \ln (1 - \phi ) - \frac{{(1 - (1 - \phi )^{2} )}}{{(1 + (1 - \phi )^{2} )}}} \right) $$

(2)

$$ K_{{\text{L}}} = \frac{{a^{2} }}{{4 \times (1 - \phi )}} \times \left( { - \ln (1 - \phi ) - \frac{{(1 - (1 - \phi )) \times (3 - (1 - \phi ))}}{2}} \right) $$

(3)

$$ K_{{\text{T}}} = \frac{{a^{2} }}{{8 \times (1 - \phi )}} \times \left( { - \ln (1 - \phi ) - \frac{{(1 - (1 - \phi )^{2} )}}{{(1 + (1 - \phi )^{2} )}}} \right) $$

(4)

Inertial Factor

The inertial factor of the 4d centered cubes was calculated using Geodict2019 (Math2Market) by solving a specific boundary value problem arising from the homogenization.³ More precisely, Navier–Stokes equations were solved in the x, y, and z direction with periodic boundary conditions, the flow was induced by an imposed pressure drop (Pa) which varies to have pore Reynolds numbers (using d the characteristic length) between 0.001 and 100. Let us remark that according to Barbour ⁴ the pore Reynolds number of the flow in the coil-treated aneurysm is around 10 at peak systole. The inertial factor was calculated based on Eq. (1) for the highest pressure drop imposed, with the permeability value calculated with the previous study. The calculations were done using water as the working fluid (density=1000 kg/m$^3$, viscosity = 0.001 Pa s) but the value of the form factor is not affected by whether the working fluid is water or blood. The inertial factor results were then fitted by the following equation,

$$\begin{aligned} C_2(\phi )=\frac{2}{\sqrt{K_{\rm T}(\phi )}}\times 3(1-\phi )^2 \end{aligned}$$

(5)

where $K_{\rm T}$ is the permeability given by Eq. (4).

CFD Validation

Reference Model (Coil Resolved)

To be able to determine the success or failure of treatment through CFD, it is necessary to have patient-specific models with realistic boundary conditions used as a reference. This reference model uses the 3D model of aneurysm with coils described in “Image Acquisition” section.¹⁵ The meshing of the model was done using StarCCM+, using a tetrahedral grid. The size of the mesh was $200~\mu$m for the parent vessel and 20–40 μm at the surface of the coils.¹⁵ Finite volume fluid simulations were performed using Fluent (ANSYS, Release 17.1; ANSYS, Canonsburg, Pennsylvania, USA). Blood flow was modeled as Newtonian and incompressible, with a viscosity of 0.0035 Pa s and a density of 1050 kg/m$^3$, consistent with previous studies in the literature¹⁷. The Navier–Stokes equations were solved:

$$\begin{aligned} \rho \left( \frac{\partial \mathbf{u} }{\partial t} + \mathbf{u} \nabla \mathbf{u} \right) = -\nabla p + \mu {\nabla }^2\mathbf{u} \quad \text {and}\quad \nabla .\mathbf{u} =0 \end{aligned}$$

(6)

Patient-specific boundary conditions were obtained by using a dual-sensor Doppler guidewire (ComboWire and ComboMap; Volcano Corp, San Diego, California, USA), with the measurements obtained during the surgical procedure.¹⁴ These measurements were converted into a pulsatile Womersley velocity inlet profile, and a Resistance Capacitance (RC) condition was used at the outlets for patient A to match mean and peak flow rate splits (see Fig. 1). Since Patient B has only one outlet (see Fig. 1), the boundary condition at the outlet was constant pressure. The artery wall was considered rigid, with a non-slip boundary condition. The simulation ran for three cardiac cycles and the values of the hemodynamics parameters were taken from the last cycle, discarding the first two as influenced by transient effects from the simulation initialization. Multiple parameters such as mean velocity in the aneurysmal sac and at the neck, wall shear stress along the aneurysmal wall (WSS), oscillatory shear index (OSI), etc. can be used to describe blood flow in the aneurysm.

This “coil-resolved model” provides data that could be used to understand the hemodynamics factors that play a role in the efficacy of the endovascular treatment. However, it cannot be used for prediction in the clinical setting. A porous model that reproduces the flow in the coil-resolved simulation but without requiring the exact coil configuration after deployment is sought. This technique would allow the prediction of the treatment outcome in a patient-specific manner, just based on the clinical imaging (rather than the creation of 3D printed models and subsequent mdezaphy), with low computational requirements and time delay.

Porous Models

This paper shows the methodology to create patient-specific CFD simulations where porous media have replaced the exact coil mass geometry, and the flow can be described by Darcy–Forchheimer’s equation (1). Modeling coils as a homogeneous and isotropic porous media (see Eq. 1) can potentially take into account the heterogeneity of the coil mass, without adding the complexity of the fully homogeneized anisotropic and inhomogeneous volumes filling the aneurysmal sac. In order to evaluate the improvement of the proposed modelling, three different cases have been considered:

• Case 1—Porous model based on the mean porosity—$K_{\rm m}$ and $C_{2{\rm m}}$: As the first porous model analyzed in the literature,¹⁵ a homogeneous isotropic porous media based on the mean porosity $\phi _{\rm m}$ of the aneurysm with coils, is studied for reference. The variables defining the porous media, $K_{\rm m}$ and $C_{2{\rm m}}$, were calculated with Eq. (4) for the permeability and (5) for the inertial factor, where $\phi =\phi _{\rm m}$ as the mean porosity in the aneurysm with coils for each patient.

• Case 2—Optimal porous model—$K_{\rm op}$ and $C_{2{\rm op}}$: The second model is created with the purpose of defining the optimal permeability and inertial factor ($K_{\rm op}$ and $C_{2{\rm op}}$), to obtain the same mean velocities in the aneurysm as for the coil-resolved model (where the percentage of error was below 1%, see Table 5). The optimal parameters have been determined by first running Stokes flow simulations varying the permeability value to determine $K_{\rm op}$, and then complete model simulations varying the inertial term only, to determine $C_{2{\rm op}}$.

• Case 3—Porous crowns model—$K_{\rm p}$ and $C_{2{\rm p}}$: The porous crowns model developed in “Crowns Porosity Map” section is used at this stage to define a homogeneous isotropic porous model that would match the optimal porous model (case 2). Modeling the flow using the crown model, there are two main possible directions in which the flow propagates in the aneurysm: predominantly tangential to the crowns as shown by the red arrow on Fig. 4, or perpendicular to the crowns as shown by the blue arrow. The model for permeability and inertial factor in the crown model is defined in Eqs. (7) and (8), based on published data from a model arising from homogenization.² The permeability and inertial factor for the parallel model (the flow along the crowns) are expressed in Eq. (7) and in Eq. (8) for the serial model (flow perpendicular to the crowns):

  $$\begin{aligned}&K_{\rm p}=\sum _1^{N} f_{i} K_{i} + f_{\rm b} K_{\rm b} \\&\quad C_{2{\rm p}}=\left( \sum _1^{N} \frac{f_i}{\sqrt{C_{2i}}}+ \frac{f_{\rm b}}{\sqrt{C_{2{\rm b}}}} \right) ^{-2} \end{aligned}$$

  (7)
  $$\begin{aligned}&K_{\rm s}=\left( \sum _1^{N} \frac{f_i}{K_i} + \frac{f_{\rm b}}{K_{\rm b}} \right) ^{-1} \\&\quad C_{2{\rm s}}=\sum _1^{N} f_{i} C_{2i} + f_{\rm b} C_{2{\rm b}} \end{aligned}$$

  (8)

  where $K_i$, $C_{2i}$ and $f_i$ are the permeability, the inertial factor and the volume fraction for the ith crown and N is the number of crowns. $K_{\rm b}$, $C_{2{\rm b}}$ and $f_{\rm b}$ are the permeability, the inertial factor and the volume fraction for the homogeneous center (bulk). Permeabilities $K_i$ and $K_{\rm b}$ are calculated based on the self-consistent estimate concerning the transversal flow (4), inertial factors $C_{2i}$ and $C_{2{\rm b}}$ are computed from Eq. (5). The values of $K_{\rm p}$, $K_{\rm s}$, $C_{2{\rm p}}$ for patients A and B for a crown size of 0.25d are in Tables 3 and 4. This crown size was chosen because the smallest crown better reflects the heterogeneity of the porosity distribution close to the aneurysm’s wall, i.e. where the porosity and consequently the permeability are very large. The number of layers $N$ was defined as 16 crowns (Fig. 4). The parallel model seems to represent better the flow model propagation since the values of $K_{\rm p}$ and $C_{2{\rm p}}$ are very close to $K_{\rm op}$ and $C_{\rm op}$. This hypothesis was also validated numerically.

To analyze the accuracy of each porous model, we compared it with the coil-resolved CFD simulations, which used the synchrotron microtomographic scans of the coil mass as the ground truth. The fluid properties and the meshing were defined above (“Reference Model (Coil Resolved)” section). Fluid flow in the porous medium was described by following Navier Stokes–Brinkman equations:

$$\begin{aligned}&-\rho \left( \frac{\partial \bar{\mathbf{u }}}{\partial t} + \bar{\mathbf{u }}\nabla \bar{\mathbf{u }} \right) - \nabla p + \mu _{\rm e} \nabla ^2 \bar{\mathbf{u }}\\&\quad = \frac{\mu }{K}\bar{\mathbf{u }}+C_2 \frac{1}{2} \rho \mid \bar{\mathbf{u }}\mid \bar{\mathbf{u }} \quad \text {and}\quad \nabla .\bar{\mathbf{u }}=0 \end{aligned}$$

(9)

where $\nabla p$ is the pressure gradient ($Pa/m$), $\bar{\mathbf{u }}$ is the mean velocity, $K$ ($m^2$) the permeability, $C_2$ (1/m) is the inertial factor and $\mu _{\rm e}$ is an effective viscosity given by $\mu _{\rm e} = \mu _{\rm r}\mu$, where $\mu _{\rm r}$ is the relative viscosity and $\mu$ is the blood’s viscosity. Equation (9) can be simply viewed as a superposition of Navier–Stokes (6) and Darcy–Forchheimer (1) equations. The term $\mu _{\rm e} \nabla ^2 \bar{\mathbf{u }}$ is often referred as the Brinkman term. If we neglect inertial effects $(C_2=0)$, Eq. (9) reduces to Darcy’s law for low values of the permeability K and to the Navier–Stokes equation for high values of K. The transition between these two regimes occurs when the Brinkman’s term $\mu _{\rm e} \nabla ^2 \bar{\mathbf{u }}$ is of the same order of magnitude as $\mu \bar{\mathbf{u }}/K$ ⁶. The value of the relative viscosity is not well known and several values can be found in the literature. In our case, the relative viscosity was taken as 1, as has been determined by comparing 2D numerical simulations and analytical solutions recently proposed by Ref. 27 for simple configurations.

The values of the permeability and the inertial coefficient used in the three porous models are summarized in Tables 3 and 4. The accuracy of each porous model has been evaluated in two steps. First a Stokes flow simulation has been performed to assess the accuracy of the linear part of Eq. (9), i.e. assuming that $C_2=0$. In that case, the flow was steady with an inlet velocity equal to 0.001 m/s (Stokes flow) and the pressure outlets equal to 0 Pa. Second, to validate the non-linear part of the Darcy–Forchheimer equation, the Navier–Stokes–Brinkman equations were solved. The boundary conditions were the same as described in “Reference Model (Coil Resolved)” section. The summary of these two sets of simulations is given in Table 2 and are noted S0$_{\alpha }$, and S1$_{\alpha \beta }$ respectively. For both patients A and B, the accuracy of each porous model has been evaluated by comparing the mean velocity values in the aneurysm with the corresponding coil-resolved model (Tables 3 and 4).

Figure 4

Modeling aneurysms with coils as a homogeneous porous media, demonstrating blood flow through the crown model: red arrow shows flow moving along the crowns and the blue arrow shows the blood flow perpendicular to the crowns.

Table 2 Summary of the simulations for patients A and B.

Table 3 Summary of the permeability values for patients A and B for the porous media models, used in Stokes (and pulsatile) flow simulations.

Table 4 Summary of the inertial factor values for patients A and B for the porous media models, used in pulsatile flow simulations.

Results

Porosity Distribution

Cubes Porosity Map

The results for the analysis of the porosity distribution with the cube method are presented in Fig. 5 for patient A. The bar size represents the number of cubes having the same porosity for the two cube sizes: 2d (a) and 4d (b). Patient A and B show similar results: for a cube edge equal to 2d the porosity varies between 0.52 and 1. This latter value suggests that the size of some pores are larger than 2d, and this cube size is too small to be representative of a porous medium. For a cube edge equal to 4d, the porosity varies between 0.72 and 0.9. This cube size seems more appropriate to capture the heterogeneity of the porous medium and has been then used to compute the permeability and the inertial factor.

Figure 5

Histogram of the porosity of the cubes for two sizes of cube’s side: 2d (left) and 4d (right) for patient A.

Crowns Porosity Map

Figure 6 shows the porosity profile along the radius of the aneurysm for patients A and B, where each curve reflects the porosity for each crown size (from 0.25 d to 2d). The x-axis reflects the radial center of the crown and $x=0$ mm is the wall of the aneurysm. The two patients show similar distribution: the porosity near the walls is close to 1 and decreases until a plateau around the mean porosity for $x>0.75$ or 1 mm, i.e. for $x> 3d$ or 4d. The homogeneous center part (the bulk) represents for both patients around 50$\%$ of the total volume of aneurysms. Even if the different crown’s size give similar results, the smallest one (0.25d) seems most appropriate to capture the strong variations of the porosity close to the aneurysm’s wall, which have a strong impact on the modelling since the porosity, and consequently the permeability, are very large.

Figure 6

Porosity along the crowns for the two patients studied (patient A in the left and patient B in the right). The x-axis represents the center point of the crown, with $x=0$ mm being the aneurysm’s wall.

Permeability and Inertial Factor

Permeability

The results of the permeability study for patient A and B are presented in Fig. 7. The black circles, the yellow squares, and the green triangles represent respectively the dimensionless permeability along the x, y, and z axis of the cubes. These directions are arbitrary. The large circle represents the mean permeability and porosity for the largest volume that fit in the aneurysm geometry. The blue line and the red line represent the estimates (SCE) given by Eqs. (3) and (4) respectively. This figure shows that (i) numerical results of the permeability for 4d cubes and the largest volume are consistent with these estimates and (ii) the permeability anisotropy of each cube is small in comparison with permeability variation (around two decades) within the porosity range 0.6–1 of the coils (Fig. 6). In this first approximation, this anisotropy is neglected in the following. Overall, Fig. 7 shows that the permeability of the coils can be well fitted by the transverse estimate (4) with a coefficient of determination ($R^2=0.75$).

Figure 7

Dimensionless permeability results versus porosity on each cube for a 4d cube size for patient A and B. The blue line and the red line represent the estimates (SCE) given by Eqs. (3) and (4) respectively.

Inertial Factor

Figure 8a presents, for the patient A (patient B showed similar results) the evolution of the ratio between the mean velocity in each cube and pressure gradient between inlet and outlet along x, depending on the value of the Reynolds number at the pore scale. The Reynolds number at the pore scale is calculated using the coil diameter as the characteristic length. Non-linear effects appear when the pore Reynolds number is larger than 1. According to Barbour,⁴ the Reynolds number of the flow in the coil-treated aneurysm is around 10 at peak systole, therefore non-linear effects need to be considered. Numerical results on each cube (symbols) have been adjusted by the Darcy–Forchheimer (dashed line) equation in order to determine the inertial factor. Figure 8b presents the evolution of the inertial factor with the porosity. Each symbol is the value of the inertial factor in one direction (x, y or z) for each cube and both patients, and the line represents the expression (5) adjusted on the numerical data. As for the permeability, the anisotropy is neglected in first approximation.

Figure 8

The figure (a) shows the evolution of the ratio between the mean velocity in the x direction and the gradient of pressure for each cube with the pore Reynolds number for patient A. Dashed lines represent the Darcy–Forchheimer equation (1) adjusted on the numerical results (symbols). Figure (b) shows, for patients A and B, the evolution of the inertial factor with the porosity deduced from the computations on each cube. The continuous line represents the adjusted Eq. (5).

Permeability and Inertial Factor Profile

Figure 9 shows the permeability and inertial factor profile along the crowns for patients A and B. These profiles were computed from the crown porosity profiles (crown’s size is 0.25d) using Eqs. (4) and (5). This figure shows that for both patient the permeability and inertial factor are strongly heterogeneous: the permeability typically varies over almost three decades, and the inertial factor from 0 to 30,000 (1/m). The horizontal dashed lines represent the permeability values $K_{\rm m}$, $K_{\rm op}$ and $K_{\rm p}$ ; and the inertial factor values $C_{2{\rm m}}$, $C_{2{\rm op}}$, $C_{2{\rm p}}$ of the three different porous models. As already mentioned, the classical porous model defined by $K_{\rm m}$ and $C_{2{\rm m}}$ based on the mean porosity is very far from the optimal values $K_{\rm op}$ and $C_{2{\rm op}}$. The permeability is underestimated whereas the inertial factor is overestimated. By contrast, the values predicted by the crown porous model, $K_{\rm p}$ and $C_{2{\rm p}}$ are very close to the optimal values, therefore this model seems to be very accurate to represent the porosity heterogeneity of the coil mass in the aneurysm.

Figure 9

(a, b): Porosity profiles for the two patients (Number of crowns = 16, crown’s size = 0.25d), corresponding permeability (c, d) and inertial factor (e, f) profiles given by Eqs. (4) and (5) respectively. The bulk is separated from the crowns by a grey vertical dashed line. The horizontal dashed lines represent the permeability values $K_{\rm m}$, $K_{\rm op}$ and $K_{\rm p}$ ; and the inertial factor values $C_{2{\rm m}}$, $C_{2{\rm op}}$, $C_{2{\rm p}}$ of the three different porous models.

CFD Simulations

Table 5 presents the results of the CFD simulations for patients A and B: the percentage of error of the mean velocity in the aneurysm, with the coil-resolved values being the reference.

• Case 1—Porous model based on the mean porosity—$K_{\rm m}$ and $C_{2{\rm m}}$: The results of the simulations for the porous media based on the mean porosity are S0$_{\rm m}$ and S1$_{\rm mm}$ in Table 5. Both patients show similar results: the results of the Stokes flow simulations show 65$\%$ difference, and for the complete models for patient A and B, the errors are 46 and 58$\%$ respectively. These results are consistent with the uncertainty reported in the literature¹⁵ and confirm that the permeability and inertial factor based on the mean porosity are not sufficient to reproduce the mean blood velocity within coiled aneurysms.

• Case 2—Optimal porous model—$K_{\rm op}$ and $C_{2{\rm op}}$: The results for the optimal porous model simulations are S0$_{\rm op}$ and S1$_{\rm opop}$ in Table 5. The values of $K_{\rm op}$ and $C_{2{\rm op}}$ allow to reproduce the mean blood velocity within coiled aneurysms with an error below 1%. Therefore, they can be considered as reference values.

• Case 3—Porous crowns model—$K_{\rm p}$ and $C_{2{\rm p}}$: Focusing on the Stokes flow simulation (simulations S0$_{\rm p}$), the porous crowns model for the permeability shows errors below $3\%$ for both patients. From these results, we can validate the accuracy of the porous crowns model to define the permeability. These results are also supported by the complete model simulations (simulations S1$_{\rm pm}$), as they show that when modifying only the permeability value, the mean velocity values in the aneurysm approximate the coil-resolved gold standard, decreasing the errors from $\approx 65\%$ to $\approx 30\%$ for both patients. However this error is still significant, therefore it is also important to consider the heterogeneity of the porous media when defining the inertial factor. When the porous crowns model is also used to defined the inertial factor (simulations S1$_{\rm pp}$), the error decreases to $6\%$ and $16\%$ for patients A and B respectively. Overall, these results clearly show that the porous crowns model allows to reproduce with accuracy the mean blood velocity within coiled aneurysms, even if it might need improvement to define the non-linear effects.

Table 5 Summary of CFD results for patients A and B: Mean velocities in the aneurysm and percentage of change of the mean velocity.

Discussion

A new porous model (the porous crowns model) is proposed to describe the flow in cerebral aneurysms treated with embolic coils. We have shown, starting from 3D X-ray synchrotron images of coiled aneurysms to CFD simulations, that this model allows to capture the porosity heterogeneity of the coil within the aneurysmal sac and to predict with accuracy the mean blood velocity in the treated cerebral aneurysms.

This study is based on the combination between in vivo and in vitro models to have the realistic coiled aneurysm from two patients. The error that is created during the 3D model creation process (clinical image segmentation, model making, etc.) has no impact on the results presented in this study,⁷ since we are comparing results from in silico models (coils resolved versus porous models) based on the same geometry. However, it would be interesting to validate the coil-resolved flow simulations against measurements in the in vitro coiled-treated aneurysm.

One limitation concerning this part of the project, is the repeatability of the coil deployment in the aneurysm (inter-operator variability). The coil deployment may vary even for the same coils placed in the same order, and this variability would result in certain variations in the heterogeneous porosity distribution. For both patients A and B, the same neurosurgeon performed the endovascular procedure. The inter-operator variability, between surgeons, is expected to be negligible as long as the treatment strategy is standardized in terms of how many coils are placed and which sizes. Thus, inter-operator variability is not expected to affect the outcome of this study. However, it is important to ensure that the same number of coils are deployed in the same order and that they occupy the volume inside the aneurysmal sac in the same way, to ensure that the porosity distribution does not fundamentally change among patients.

As it has been already underlined in previous studies,^21,26 the present work confirms that the heterogeneous distribution of the porosity must be included in porous models. As it is not possible to characterize the coils used in treatment of cerebral aneurysms from the clinical imaging scans, our method is based on 3D X-ray synchrotron images. This presents a significant step towards understanding blood flow inside treated aneurysms as we have a realistic coil explicit geometry.

Kakalis and Mitsos studies modeled the coiled aneurysm as a homogeneous porous medium where the permeability was calculated only based in the mean porosity using the Kozeny-Carman model. This porous model has become the state of the art but was never validated. There is no experimental or numerical data in the literature that could be used for rigorous validation of the porous model, which require the actual flow in a coiled aneurysm experiment or the flow field in a coil-resolved computational model. Levitt et al. used the same Kozeny Carman model to calculate the permeability based on the mean porosity, and then they compared the hemodynamics computed with the homogenous porous medium model against the computations with the coil-resolved geometry, a comparison we also performed in this study. They compared two patients (porous vs. coil-resolved model) and found errors of 28.68% and 89.56% between the mean flow at the neck in the porous model and the coil-resolved simulations (taking the coil-resolved simulations as the gold standard in the absence of intra-aneurysm hemodynamics from experiments). Based on these comparisons, they reach the conclusion that we reproduce as a secondary result in our study: the mean hemodynamic velocities are systematically underestimated by the simple homogeneous porous model.

Using the crown’s method, we have shown that the porosity gradient is very high in the first millimeter (equivalent to 3 or 4 coils diameters) near the wall and the neck, and the porosity is homogeneous in the rest of the aneurysm (bulk) for both patients. The bulk part represents around 50$\%$ of the total volume of the aneurysm. As in Refs. 12,15,20, the homogeneous isotropic porous media model based on the mean porosity leads to large error (around $50\%$) in terms of mean velocity in comparison with the coils resolved (Table 5). Indeed, the blood flow within the aneurysm is highly impacted by the porosity heterogeneity near the wall and at the neck, i.e where the porosity and the permeability are large, and the inertial factor is small. At the neck, this heterogeneity plays an important role on the fluid velocity at the inlet of the aneurysm, and consequently in the whole aneurysmal sac. The permeability and inertial factor defined in the porous crowns model assume that the flow predominantly moves along the crown (parallel model). From the physical point of view, the blood penetrates in the aneurysmal sac through the neck, maintaining the same direction it had in the parent artery, and moves predominantly along crowns (tangentially, not normally), where the porosity is higher.

The evolution of the permeability and the inertial factor as function of the porosity have been determined numerically on representative elementary volumes of 4d size extracted from the 3D X-ray images. The obtained results showed that the permeability of the coils, and thus of each crown, can be well estimated by the self consistent estimate (4),⁵ when the anisotropy is neglected in first approximation. It has been confirm by the CFD simulations (Stokes flow) which led to error bellow 3$\%$ for both patients, instead of 60$\%$ in previous modelings¹⁵). The inertial factor expression of each crown have been estimated using the proposed relation (5). CFD simulations (pulsatile flow) have shown that the results are also improved when considering the heterogeneity of the porous media, leading to an error lower than 16$\%$ (Table 5).

In the CFD simulations, the only hemodynamics metric used in the comparison between models was the mean velocity within the aneurysm. In porous models, it can be shown using upscaling methods³ that this mean velocity is by definition equal to the volume average of the fluid velocity at the pore scale, i.e. the fluid velocity computed in coil-resolved simulations. This metric, also used in Ref. 26, is thus relevant to validate porous models. This metric is also relevant to assess coil treatment outcome, and more precisely to predict the thrombus formation (blood coagulation) which is linked to the blood velocity.¹⁶ Other hemodynamics metrics, such as residence time, shear integrated over the entire trajectory of platelets in the domain, and other hemodynamics quantities linked with thrombosis are necessary to validate advanced porous models.

Overall the proposed porous crowns model represents a step forward towards clinical prediction of treatment outcomes, but only the results for two patients are presented in this work. More patients must be considered to further evaluate and analyze its robustness.

Conclusion

This study presents a novel homogeneous isotropic porous media model to recreate coil-treated aneurysms, by defining the permeability and inertial factor based on a porous crowns map. By considering the heterogeneity of the porosity distribution in these crowns, and the patient-specific boundary conditions, the mean velocity of the blood in the porous model is predicted with high accuracy, when compared with the gold-standard coil-resolved simulations. This model could eventually be employed in future CFD studies of coiled cerebral aneurysms for treatment planning and outcome prediction.