1 Introduction

In reality, human decision-making often deviates from perfect rationality, with a tendency to imitate strategies from our neighbors. Research by [30] and [15] illustrates this through the gradual adoption of more productive hybrid corn in the U.S., following a distinct spatial pattern. This adoption process, characterized by an S-curve, exemplifies the diffusion of superior strategies via imitation within social networks.

Social networks possess intriguing characteristics that have prompted extensive research. Classic studies [20, 24, 33] reveal the ’small world’ phenomenon, where individuals in social networks are connected through a surprisingly small number of intermediaries. Contrary to previous assumptions of randomness, many social networks differ significantly from regular and random networks.

Scale-free social networks, typifying heterogeneous networks, include diverse real-world examples such as mathematical collaboration networks [16], citation networks [29], communication networks [6, 10, 13], and so forth. These networks often exhibit small-world properties, characterized by short path lengths and high clustering coefficients, a measure of local link density.

The relationship between network structure and the game highlights the importance of spatial or social structure of populations, represented as graphs, in shaping the evolution of cooperation and other strategies within evolutionary games. A comprehensive review can be found in the review by [3]. Population structure is modeled as a graph, where vertices represent individuals, and edges indicate interactions for game payoffs and competition for reproduction. This structural representation fundamentally influences evolutionary outcomes by determining the interactions and competitive dynamics among individuals. The conditions under which a strategy, such as cooperation, is evolutionarily successful are derived from the benefit-to-cost ratio of cooperative behavior and the degree of the graph, which represents the number of connections per individual. Different update rules, which govern the mechanisms by which individuals reproduce and replace others, can lead to different evolutionary outcomes on the same graph structure, highlighting the complexity of the dynamics. Furthermore, considering separate graphs for interactions and replacements reveals intricate dynamics where the evolution of cooperation can depend on both the structure of interactions (who plays the game with whom) and the structure of competition (who competes with whom for reproduction). The network structure plays a crucial role in evolutionary games by shaping the interaction and competition patterns among individuals, which, in turn, influence the evolutionary viability of different strategies. The specific outcomes depend on the network’s characteristics, the rules governing strategy update and the nature of the game itself. Comprehensive reviews on complex networks are available in [2, 8, 9, 12, 14, 17, 26, 34], and others. Studies [1, 5, 21, 25] have explored social learning processes. Our work adds a new dimension by considering complex network structures like degree distribution and network heterogeneity.

The structure of underlying networks significantly influences outcomes in network models. Scale-free networks, in particular, have substantial effects due to their heterogeneous nature. This paper focuses on how network heterogeneity impacts outcomes by studying scale-free networks.

We address key questions about the influence of social network structures on learning processes from neighbors and the role of network heterogeneity. Our study involves a game on a social network where each player interacts only with adjacent players. Our model, based on imitation, is social learning through social networks.

2 Scale-Free Networks Enhance Social Learning Process

2.1 The Model of Social Learning

We explore a learning process based on imitation within social networks, focusing on how different network structures influence the spread of effective strategies. We analyze a simple game where consistently choosing one strategy is more advantageous than the other. This choice is a result of the social learning process. In our game model, each player, located at a network vertex, interacts only with adjacent players. The payoff matrix for this game is:

(1)

assuming \(a+c> b\) and \(a\ge b\). All parameters are not necessarily positive. Here, choosing strategy H is always more beneficial than E by a constant c. Players earn their total payoff G from these games, and the overall payoff T combines a baseline payoff and the game-derived payoff, scaled by a factor w.

The strategy update follows an imitation dynamic, where players are likely to adopt the majority strategy of their neighbors or a strategy yielding a better payoff. This dynamic ensures that the more effective strategy gradually but consistently spreads over time.

2.2 The Update Rule of the Strategies

Initially, a fraction r of players adopt strategy H, while the rest choose E. Strategy updates occur at each time step, where a randomly selected player imitates the strategy of adjacent players based on their total payoffs. Figure 1 illustrates this update rule, demonstrating how the strategy spread can be viewed as a learning process through local social interactions.

We aim to understand how the speed of strategy spread varies with different network structures.

Fig. 1
figure 1

Update rule of the game: the shaded circle represents a randomly chosen player who will adopt the strategy of adjacent players (H or E) based on a probability proportional to their total payoffs

Full size image

2.3 Notations Used

We define the network size as N, the mean degree as \(\langle k \rangle \), and the mean degree of nearest neighbors as \(\langle k_\text {nn}\rangle \). The latter is crucial for network dynamics and differs from the mean degree in non-regular networks. We apply the mean-field approximation from our previous studies [18, 19], where the degree of a randomly chosen vertex is approximated by \(\langle k\rangle \), and that of its nearest neighbor by \(\langle k_\text {nn}\rangle \). Let \(q_{X|Y}(k_1,k_2)\) denote the conditional probability of finding an X-player, given that the adjacent vertex is occupied by a Y-player, and that the degrees of the X-player and the Y-player are \(k_1\) and \(k_2\), respectively. We define \(q_{X|Y}^\text {nn}:=q_{X|Y}(\langle k_\text {nn}\rangle ,\langle k_\text {nn}\rangle )\). Figure 2 schematically represents this approximation. We also introduce various probabilities and conditional probabilities to describe the network’s strategy distribution, using the pair approximation method [22]. Our approach extends the method developed in [18] to analyze the spread of strategies in general uncorrelated networks, leading to Eq. (38).

Fig. 2
figure 2

Mean-field approximation scheme: a shows a randomly chosen vertex with mean degree \(\langle k\rangle \), surrounded by vertices with degree \(\langle k_\text {nn}\rangle \). b depicts neighboring vertices with degree \(\langle k_\text {nn}\rangle \), also surrounded by vertices with the same degree in the mean-field model

Full size image

2.4 The Case of a General Payoff Matrix

While our primary interest lies in the specific payoff matrix outlined in Eq. (1), we extend our analysis to a general payoff matrix involving strategies A and B, represented as:

(2)

2.5 The Change in the Probability of Strategy A

Following the approach in our previous work [18], we examine the scenario where a randomly chosen player, initially adopting strategy B, switches to strategy A. This change results in an increase in the probability of strategy A, denoted as \(p_A\), by 1/N. In the mean-field approximation, where the degrees of nearest neighbors are represented by \(\langle k_\text {nn}\rangle \), the payoffs \(f_A\) and \(f_B\) for neighboring A and B players are calculated as follows:

$$\begin{aligned} f_A&=1-w+w\left[ (\langle k_\text {nn}\rangle -1)q_{A|A}^\text {nn} x+((\langle k_\text {nn}\rangle -1)q_{B|A}^\text {nn}+1)y\right] ,\end{aligned}$$
(3)
$$\begin{aligned} f_B&=1-w+w\left[ (\langle k_\text {nn}\rangle -1)q_{A|B}^\text {nn} z+((\langle k_\text {nn}\rangle -1)q_{B|B}^\text {nn}+1) s\right] . \end{aligned}$$
(4)

The probability of a configuration where a randomly chosen B-player is surrounded by \(k_A\) A-neighbors and \(k_B\) B-neighbors is given by:

$$\begin{aligned} (q_{A|B})^{k_A}(q_{B|B})^{k_B}\frac{\langle k\rangle !}{k_A!k_B!}. \end{aligned}$$
(5)

In this configuration, the probability of the B-player switching to strategy A is:

$$\begin{aligned} \frac{k_A f_A}{k_A f_A+k_B f_B}. \end{aligned}$$
(6)

Thus, the probability that a B-player is randomly chosen and updates their strategy from B to A, resulting in an increase in \(p_A\) by 1/N, is:

$$\begin{aligned} p_B\sum _{k_A+k_B=\langle k \rangle } (q_{A|B})^{k_A}(q_{B|B})^{k_B}\frac{\langle k\rangle !}{k_A!k_B!}\frac{k_A f_A}{k_A f_A+k_Bf_B}. \end{aligned}$$
(7)

Conversely, when an A-player is randomly chosen and switches to strategy B, \(p_A\) decreases by 1/N. The payoffs \(g_A\) and \(g_B\) for neighboring A and B players in this case are:

$$\begin{aligned} g_A&=1-w+w\left[ ((\langle k_\text {nn}\rangle -1)q_{A|A}^\text {nn}+1) x+(\langle k_\text {nn}\rangle -1)q_{B|A}^\text {nn} y\right] ,\end{aligned}$$
(8)
$$\begin{aligned} g_B&=1-w+w\left[ ((\langle k_\text {nn}\rangle -1)q_{A|B}^\text {nn}+1)z+(\langle k_\text {nn}\rangle -1)q_{B|B}^\text {nn}s\right] . \end{aligned}$$
(9)

The probability of a configuration where the randomly chosen A-player is surrounded by \(k_A\) A-neighbors and \(k_B\) B-neighbors is:

$$\begin{aligned} (q_{A|A})^{k_A}(q_{B|A})^{k_B}\frac{\langle k\rangle !}{k_A!k_B!}. \end{aligned}$$
(10)

In this configuration, the probability of the A-player switching to strategy B is:

$$\begin{aligned} \frac{k_B g_B}{k_A g_A+k_B g_B}. \end{aligned}$$
(11)

Therefore, the expected change in \(p_A\) per time step in the mean-field approximation is given by:

$$\begin{aligned} E[\triangle p_A]&=\frac{1}{N} p_B\sum _{k_A+k_B=\langle k \rangle } (q_{A|B})^{k_A}(q_{B|B})^{k_B}\frac{\langle k\rangle !}{k_A!k_B!}\frac{k_A f_A}{k_A f_A+k_Bf_B}\nonumber \\&\quad -\frac{1}{N}p_A \sum _{k_A+k_B=\langle k\rangle }(q_{A|A})^{k_A}(q_{B|A})^{k_B}\frac{\langle k\rangle !}{k_A!k_B!}\frac{k_B g_B}{k_A g_A+k_B g_B} . \end{aligned}$$
(12)

Similarly, considering the scenario where a player with degree \(\langle k_\text {nn}\rangle \) is randomly chosen to change their strategy, we derive the change in \(p_A^\text {nn}\) per time step in the mean-field approximation as:

$$\begin{aligned} E[\triangle p_A^\text {nn}] =&\frac{1}{N} p_B^\text {nn} \sum _{k_A+k_B=\langle k_\text {nn} \rangle } (q^\text {nn}_{A|B})^{k_A} (q^\text {nn}_{B|B})^{k_B} \frac{\langle k_\text {nn}\rangle !}{k_A!k_B!} \frac{k_A f_A}{k_A f_A + k_B f_B} \nonumber \\&- \frac{1}{N} p_A^\text {nn} \sum _{k_A+k_B=\langle k_\text {nn}\rangle } (q_{A|A}^\text {nn})^{k_A} (q_{B|A}^\text {nn})^{k_B} \frac{\langle k_\text {nn}\rangle !}{k_A!k_B!} \frac{k_B g_B}{k_A g_A + k_B g_B} . \end{aligned}$$
(13)

2.6 The Change in Conditional Probabilities

The dynamics of the probabilities \(p_A\) and \(p_A^\text {nn}\), as outlined in Eqs. (12) and (13), are influenced by the conditional probabilities \(q_{A|A}\) and \(q_{A|A}^\text {nn}\). We explore the dynamics of these conditional probabilities.

First, we consider the scenario where \(q_{A|A}\) increases. This occurs when a B-player, chosen randomly with probability \(p_{B}\), updates their strategy to A. Let \(k_A\) and \(k_B\) represent the number of neighboring A-players and B-players to the chosen B-player, respectively, satisfying \(k_A+k_B=\langle k\rangle \). The likelihood of this configuration is:

$$\begin{aligned} \frac{\langle k\rangle !}{k_A!k_B!}(q_{A|B})^{k_A}(q_{B|B})^{k_B}. \end{aligned}$$
(14)

The probability of the B-player switching to A is:

$$\begin{aligned} \frac{k_A f_A}{k_A f_A+k_B f_B}. \end{aligned}$$
(15)

Thus, the increase in \(q_{A|A}\) is:

$$\begin{aligned} \triangle ^+=\frac{k_A}{p_A N\langle k\rangle }+O(w). \end{aligned}$$
(16)

The expected increase in \(q_{A|A}\) per time step in the mean-field approximation is:

$$\begin{aligned} \sum _{k_A+k_B=\langle k\rangle }\frac{k_A}{p_A \langle k \rangle N}p_B \frac{\langle k\rangle !}{k_A!k_B!}(q_{A|B})^{k_A}(q_{B|B})^{k_B}\frac{k_A f_A}{k_A f_A +k_B f_B}. \end{aligned}$$
(17)

Conversely, when an A-player is randomly chosen (probability \(p_{A}\)) and switches to B, \(q_{A|A}\) decreases. The probability of this configuration is:

$$\begin{aligned} \frac{\langle k\rangle !}{k_A!k_B!}(q_{A|A})^{k_A}(q_{B|A})^{k_B}. \end{aligned}$$
(18)

The probability of the A-player switching to B is:

$$\begin{aligned} \frac{k_B g_B}{k_A g_A+k_B g_B}. \end{aligned}$$
(19)

Thus, the decrease in \(q_{A|A}\) is:

$$\begin{aligned} \triangle ^-=\frac{k_A}{p_A N\langle k\rangle }+O(w). \end{aligned}$$
(20)

The expected decrease in \(q_{A|A}\) per time step in the mean-field approximation is:

$$\begin{aligned} \sum _{k_A+k_B=\langle k\rangle }\frac{k_A}{p_A \langle k \rangle N}p_A \frac{\langle k\rangle !}{k_A!k_B!}(q_{A|A})^{k_A}(q_{B|A})^{k_B}\frac{k_B g_B}{k_A g_A +k_B g_B}. \end{aligned}$$
(21)

Combining these cases, the expected change in \(q_{A|A}\) per time step in the mean-field approximation is:

$$\begin{aligned} E[\triangle q_{A|A}]&=\sum _{k_A+k_B=\langle k\rangle }\frac{k_A}{p_A \langle k \rangle N}p_B \frac{\langle k\rangle !}{k_A!k_B!}(q_{A|B})^{k_A}(q_{B|B})^{k_B}\frac{k_A f_A}{k_A f_A +k_B f_B} \nonumber \\&\quad -\sum _{k_A+k_B=\langle k\rangle }\frac{k_A}{p_A \langle k \rangle N}p_A \frac{\langle k\rangle !}{k_A!k_B!}(q_{A|A})^{k_A}(q_{B|A})^{k_B}\frac{k_B g_B}{k_A g_A +k_B g_B} . \end{aligned}$$
(22)

For \(q_{A|A}^\text {nn}\), we consider the case where the degree of the randomly chosen vertex is \(\langle k_\text {nn}\rangle \). The expected change in \(q_{A|A}^\text {nn}\) per time step in the mean-field approximation is:

$$\begin{aligned} E[\triangle q_{A|A}^\text {nn}] =&\sum _{k_A+k_B=\langle k_\text {nn}\rangle } \frac{2k_A}{p_A^\text {nn} \langle k_\text {nn} \rangle N} p_B^\text {nn} \frac{\langle k_\text {nn}\rangle !}{k_A!k_B!} (q_{A|B}^\text {nn})^{k_A} (q_{B|B}^\text {nn})^{k_B} \frac{k_A f_A}{k_A f_A + k_B f_B} \nonumber \\&- \sum _{k_A+k_B=\langle k_\text {nn}\rangle } \frac{2k_A}{p_A^\text {nn} \langle k_\text {nn} \rangle N} p_A^\text {nn} \frac{\langle k_\text {nn}\rangle !}{k_A!k_B!} (q_{A|A}^\text {nn})^{k_A} (q_{B|A}^\text {nn})^{k_B} \frac{k_B g_B}{k_A g_A + k_B g_B}. \end{aligned}$$
(23)

This analysis provides insights into the dynamics of conditional probabilities within the network, crucial for understanding the spread of strategies in social learning processes.

2.7 The Speed of the Spread of General Strategy A

Through detailed calculations and expansion of Eqs. (12), (13), (22) and (23), and considering the continuous time limit, we arrive at the following equations:

$$\begin{aligned} \frac{d}{dt}{p}_{A}&=\frac{\langle k\rangle -1}{\langle k\rangle N}p{AB} \left( I_x x + I_y y - I_z z-I_s s\right) w +O(w^2) ,\end{aligned}$$
(24)
$$\begin{aligned} \frac{d}{dt}{p}_{A}^\text {nn}&=\frac{\langle k\text {nn}\rangle -1}{\langle k_\text {nn}\rangle N}p_{AB} \left( I_x^\text {nn} x + I_y^\text {nn} y - I_z^\text {nn} z-I_s^\text {nn} s\right) w +O(w^2) ,\end{aligned}$$
(25)
$$\begin{aligned} \frac{d}{dt}{q}_{A|A}&=\frac{1}{\langle k\rangle N p_A}p{AB}\left[ 1+(\langle k\rangle -1){q_{A|B}-q_{A|A}} \right] +O(w) ,\end{aligned}$$
(26)
$$\begin{aligned} \frac{d}{dt}{q}_{A|A}^\text {nn}&=\frac{2}{\langle k\text {nn}\rangle N p_A^\text {nn}}p_{AB} \left[ 1+(\langle k_\text {nn}\rangle -1){q_{A|B}^\text {nn}-q_{A|A}^\text {nn}} \right] +O(w) , \end{aligned}$$
(27)

where

$$\begin{aligned} \begin{aligned} I_x:&=(\langle k_\text {nn}\rangle -1) q_{A|A}^\text {nn} (q_{A|A}+q_{B|B})+q_{A|A},\\ I_y:&=(\langle k_\text {nn}\rangle -1) q_{B|A}^\text {nn} (q_{A|A}+q_{B|B})+q_{B|B},\\ I_z:&=(\langle k_\text {nn}\rangle -1) q_{A|B}^\text {nn} (q_{A|A}+q_{B|B})+q_{A|A},\\ I_s:&=(\langle k_\text {nn}\rangle -1) q_{B|B}^\text {nn} (q_{A|A}+q_{B|B})+q_{B|B}, \end{aligned} \end{aligned}$$
(28)
$$\begin{aligned} \begin{aligned} I_x^\text {nn}:&=(\langle k_\text {nn}\rangle -1) q_{A|A}^\text {nn} (q_{A|A}^\text {nn}+q_{B|B}^\text {nn})+q_{A|A}^\text {nn},\\ I_y^\text {nn}:&=(\langle k_\text {nn}\rangle -1) q_{B|A}^\text {nn} (q_{A|A}^\text {nn}+q_{B|B}^\text {nn})+q_{B|B}^\text {nn},\\ I_z^\text {nn}:&=(\langle k_\text {nn}\rangle -1) q_{A|B}^\text {nn} (q_{A|A}^\text {nn}+q_{B|B}^\text {nn})+q_{A|A}^\text {nn},\\ I_s^\text {nn}:&=(\langle k_\text {nn}\rangle -1) q_{B|B}^\text {nn} (q_{A|A}^\text {nn}+q_{B|B}^\text {nn})+q_{B|B}^\text {nn}. \end{aligned} \end{aligned}$$
(29)

We confirm that \(E[\triangle p_A]\) is of the order O(w), while \(E[\triangle q_{A|A}]\) is of the order \(O(w^0)\).

To derive Eq. (24), we employed the mean-field relation \(q_{X|Y}p_Y=p_{XY}=p_{YX}=q_{Y|X}p_X\). This relation is justified as follows: In the mean-field approximation, the pair probability \(p_{XY}\) is given by:

$$\begin{aligned} p_{XY}&=\frac{\sum _{k_\text {nn},k}q_{X|Y}(k_\text {nn},k)P(k_\text {nn},k)p(k)p_Y(k) k N }{N\langle k\rangle }\end{aligned}$$
(30)
$$\begin{aligned}&=\frac{q_{X|Y}p_Y N\langle k\rangle }{N\langle k \rangle }=q_{X|Y}p_Y , \end{aligned}$$
(31)

where \(P(k_\text {nn},k)\) is the probability of a vertex pair having degrees k and \(k_\text {nn}\), p(k) is the probability of a vertex having degree k, \(p_Y(k)\) is the probability of a vertex with strategy Y and degree k, and \(q_{X|Y}(k_\text {nn},k)\) is the conditional probability of a vertex with strategy X and degree \(k_\text {nn}\) given a neighboring vertex with strategy Y and degree k.

Thus, \(p_{XY}=q_{X|Y}p_Y\) holds in the mean-field approximation, and similarly, \(p_{YX}=q_{Y|X}p_X\) holds. Therefore, the mean-field relation \(q_{Y|X}p_X=p_{YX}=p_{XY}=q_{X|Y}p_Y\) is valid.

Due to this relation, the \(O(w^0)\) term in Eq. (24) vanishes.

We now have the following system of equations from Eqs. (24)–(27):

$$\begin{aligned} \begin{aligned} {\dot{p}}_A&=F_1(p_A,q{A|A},q_{A|A}^\text {nn})w+O(w^2),\\ {\dot{p}}_A^\text {nn}&=F_2(p^\text {nn}A,q{A|A}^\text {nn})w+O(w^2),\\ {\dot{q}}_{A|A}&=F_3(p_A,q_{A|A},q_{A|A}^\text {nn})+O(w),\\ {\dot{q}}_{A|A}^\text {nn}&=F_4(p^\text {nn}A,q{A|A}^\text {nn})+O(w). \end{aligned} \end{aligned}$$
(32)

Since \({\dot{p}}_A\) and \({\dot{p}}_A^\text {nn}\) are of order O(w), while \({\dot{q}}_{A|A}\) and \({\dot{q}}_{A|A}^\text {nn}\) are of order \(O(w^0)\), the conditional probabilities \(q_{A|A}\) and \(q_{A|A}^\text {nn}\) converge much faster than \(p_{A}\) and \(p_{A}^\text {nn}\). Thus, we can assume that \({\dot{q}}_{A|A}=0\) and \({\dot{q}}_{A|A}^\text {nn}=0\) always hold. In other words, the system converges to the slow manifold given by \(F_{3}=0\) and \(F_{4}=0\). From \(F_{3}=0\) and \(F_{4}=0\), we have:

$$\begin{aligned} \begin{aligned} 1+(\langle k\rangle -1)&{q_{A|B}-q_{A|A}}=0,\\ 1+(\langle k_\text {nn}\rangle -1)&{q_{A|B}^\text {nn}-q_{A|A}^\text {nn}}=0. \end{aligned} \end{aligned}$$
(33)

Using the mean-field relations and Eqs. (33), the probabilities of strategies \(p_A\), \(p_B\), \(p_A^\text {nn}\), \(p_B^\text {nn}\), and the conditional probabilities \(q_{A|A}\), \(q_{B|A}\), \(q_{B|B}\), \(q_{A|B}\), \(q_{A|A}^\text {nn}\), \(q_{B|A}^\text {nn}\), \(q_{B|B}^\text {nn}\), and \(q_{A|B}^\text {nn}\) can be expressed in terms of only \(p_A\) and \(p_A^\text {nn}\) as follows:

$$\begin{aligned} (\langle k\rangle -1)q_{A|A}&=(\langle k\rangle -1)p_A+p_B, \end{aligned}$$
(34)
$$\begin{aligned} (\langle k\rangle -1)q_{B|B}&=(\langle k\rangle -1)p_B+p_A,\end{aligned}$$
(35)
$$\begin{aligned} (\langle k_\text {nn}\rangle -1)q_{A|A}^\text {nn}&=(\langle k_\text {nn}\rangle -1)p_A^\text {nn}+p_B^\text {nn},\end{aligned}$$
(36)
$$\begin{aligned} (\langle k_\text {nn}\rangle -1)q_{B|B}^\text {nn}&=(\langle k_\text {nn}\rangle -1)p_B^\text {nn}+p_A^\text {nn}. \end{aligned}$$
(37)

Proposition 1

The expected change of the probability \(p_A\) for the general payoff matrix in a unit time step \(\triangle t\) is derived using Eq. (24), (34)–(37):

$$\begin{aligned} E[\triangle p_A]&=\frac{1}{N} \Pr \left( \triangle p_A=\frac{1}{N}\right) -\frac{1}{N} \Pr \left( \triangle p_A=-\frac{1}{N}\right) \nonumber \\&\simeq \frac{\langle k\rangle -2}{\langle k\rangle (\langle k\rangle -1)N}p_A(1-p_A)\left[ \alpha p_A +\beta p_A^\text {nn}+ \gamma \right] w\triangle t , \end{aligned}$$
(38)

where

$$\begin{aligned} \alpha&:=(x-y-z+s) (\langle k\rangle -2),\end{aligned}$$
(39)
$$\begin{aligned} \beta&:=(x-y-z+s) \langle k\rangle (\langle k_\text {nn}\rangle -2) ,\end{aligned}$$
(40)
$$\begin{aligned} \gamma&:= (x-y-z+s)+(x-y)\langle k \rangle +\langle k\rangle \langle k_\text {nn}\rangle (y-s). \end{aligned}$$
(41)

This proposition outlines the speed \(E[\triangle p_A]\) of the spread of strategy A with the general payoff matrix given by Eq. (2).

2.8 The Speed of the Spread of the Better Strategy H

We have already derived the expected change \(E[\triangle p_A]\) in \(p_A\) per unit time step as Eq. (38) for a general payoff matrix. Now, we apply this to the specific payoff matrix of social learning in Eq. (1). Let \(p_H\) denote the probability that a randomly chosen player adopts strategy H. The expected change \(E[\triangle p_H]\) in the probability \(p_H\) per unit time step \(\triangle t\) is given by:

$$\begin{aligned} E[\triangle p_H]&\simeq \frac{\langle k\rangle -2}{(\langle k\rangle -1)N}p_H(1-p_H)\left[ a-b+\langle k_\text {nn}\rangle c\right] w\triangle t\nonumber \\&=:m^\text {sl}(p_H,\langle k\rangle , \langle k_\text {nn}\rangle )\triangle wt. \end{aligned}$$
(42)

Here, \(m^\text {sl}(p_H,\langle k\rangle , \langle k_\text {nn}\rangle )\) represents the speed of spread of the better strategy H. The superscript sl in \(m^\text {sl}\) stands for social learning. This speed satisfies the following conditions:

$$\begin{aligned}&\frac{\partial m^{\text {sl}}}{\partial \langle k\rangle }>0, \end{aligned}$$
(43)
$$\begin{aligned}&\frac{\partial ^{2} m^{\text {sl}}}{\partial \langle k\rangle ^{2}}<0, \end{aligned}$$
(44)
$$\begin{aligned}&\frac{\partial m^\text {sl}}{\partial \langle k_\text {nn}\rangle }>0 . \end{aligned}$$
(45)

Based on these conditions, we propose the following:

Proposition 2

The expected speed \(E[\triangle p_{H}]\) of the spread of the better strategy H increases with the mean degree \(\langle k\rangle \) and the mean degree of nearest neighbors \(\langle k_\text {nn}\rangle \) in the mean-field approximation.

Comparing two networks, network 1 and 2, with the same network size N, number of links L, and initial probability of strategy H, but different mean degrees of nearest neighbors \(\langle k_\text {nn}\rangle \), we find that the network with a greater \(\langle k_\text {nn}\rangle \) enhances social learning more effectively. This is captured by the difference in the speed of spread of strategy H between the two networks, denoted as \(\triangle m^\text {sl}_{12}\):

$$\begin{aligned} \triangle m^\text {sl}_{12}:&= m^\text {sl}(p_H,\langle k\rangle , \langle k_\text {nn}^1\rangle )-m^\text {sl}(p_H,\langle k\rangle ,\langle k_\text {nn}^2\rangle )\nonumber \\&=\frac{\langle k\rangle -2}{\langle k\rangle -1}\frac{1}{N} p_H(1-p_H)\left[ \langle k_\text {nn}^1\rangle -\langle k_\text {nn}^2\rangle \right] c . \end{aligned}$$
(46)

Given that \(\langle k_\text {nn}\rangle =\frac{\sigma ^2+\langle k\rangle ^2}{\langle k\rangle }\) in uncorrelated networks, where \(\sigma ^2\) is the variance of the degree distribution, we have:

$$\begin{aligned} \frac{\partial m^\text {sl}}{\partial (\sigma ^2)}=\frac{\partial \langle k_\text {nn}\rangle }{\partial (\sigma ^2)}\frac{\partial m^\text {sl}}{\partial \langle k_\text {nn}\rangle }>0. \end{aligned}$$
(47)

Thus, we conclude with the following proposition:

Proposition 3

The more heterogeneous the network is, the more it enhances the speed of the social learning process in the mean-field approximation.

Considering three representative networks-a regular network, a random network, and a scale-free network-with the same mean degree, we find that scale-free networks enhance social learning the most, while regular networks do the least. This is summarized in the following lemma:

Lemma 1

Among three representative networks with the same mean degree, scale-free networks enhance social learning the most, and regular networks the least, in the mean-field approximation.

Furthermore, if the mean degree \(\langle k\rangle \) is large enough such that \((\langle k\rangle -2)/(\langle k\rangle -1)\approx 1\), the speed of the spread of the better strategy is primarily influenced by the mean degree of nearest neighbors \(\langle k_\text {nn}\rangle \), as stated in the following proposition:

Proposition 4

If the mean degree \(\langle k\rangle \) is sufficiently large, the speed \(m^\text {sl}\) of the spread of the better strategy H is approximately given by:

$$\begin{aligned} m^\text {sl} \approx&\frac{1}{N}p_H(1-p_H)\left[ a-b+\langle k_\text {nn}\rangle c\right] . \end{aligned}$$
(48)

Therefore, in networks with a large mean degree \(\langle k\rangle \), the mean degree of nearest neighbors \(\langle k_\text {nn}\rangle \) becomes the critical factor influencing the speed of the spread of the better strategy in the mean-field approximation.

2.9 Numerical Simulation for Social Learning in Scale-Free Networks

To validate the theory that network heterogeneity enhances social learning, we conducted numerical simulations on scale-free networks. These networks were constructed using a preferential attachment mechanism, known as the Barabási–Albert (BA) model [7, 11]. The construction process is as follows:

1. We start with a complete network of K vertices, where every vertex is connected to every other vertex. 2. A new vertex with m links is added to the existing network. The probability of this new vertex connecting to an existing vertex i is proportional to \((k_i+A)/\sum _j( k_j +A)\), where \(k_i\) is the degree of vertex i. 3. This process is repeated until the network reaches the desired size.

For our simulations, we used \(m=5\), \(K=m+1\), and a network size of \(N=3000\). The mean degree across all networks was \(\langle k\rangle =10\). We varied the exponent \(\gamma \) of the scale-free network to be 2.1, 2.2, 2.4, and 3, respectively. Initially, 750 players were randomly assigned as H players, and the remaining 2250 were E players. Each player’s strategy was updated according to the rule described in Sect. 2.2. Each simulation ran for 15, 000 time steps, after which we recorded the number of H players. This process was repeated 100 times for each network to calculate the average number of H players and the average mean degree of nearest neighbors \(\langle k_\text {nn}\rangle \). The game’s payoff parameters were set as \(a=1.5\), \(b=1\), and \(c=10\), with \(w=5\times 10^{-4}\).

The results, illustrated in Fig. 3, confirm that network heterogeneity significantly enhances social learning, aligning with our theoretical predictions.

Fig. 3
figure 3

The spread of the better strategy: the graph demonstrates that a more heterogeneous network facilitates the spread of the better strategy. These numerical experiments also support Proposition 4 and Eq. (47). The network size is \(N=3000\), the mean degree is \(\langle k\rangle =10\), w=\(5\times 10^{-4}\), and the payoff parameters are \((a,b,c)=(1.5,1,10)\). The y-axis represents the number of H players at the end of the simulation, while the x-axis shows the mean degree of nearest neighbors \(\langle k_{nn}\rangle \), indicating the extent of network heterogeneity. Note that while \(\langle k_{nn}\rangle \) varies, the connection density \(\langle k \rangle \) remains constant across different networks

Full size image

3 Understanding the Enhancement of Social Learning in Scale-Free Networks

In Sect. 2, we established that scale-free networks significantly enhance social learning. This section delves into the reasons behind this phenomenon, focusing on the role of hub players in these networks.

3.1 Model Overview

To elucidate this, we examine a model where players’ payoffs are independent of their neighbors’ strategies, yet a learning network exists to indicate who learns from whom. This scenario, essentially not a game in the traditional sense, represents a specific case of the general payoff matrix [Eq. (2)]. We consider two strategies, U and V, with U yielding a higher payoff (u) than V (v), assuming \(u>v\). If we express the payoff using the payoff matrix, it is

(49)

The strategy update rule remains the same as previously described, with players likely to adopt the majority strategy among neighbors or the one with a better payoff.

Initially, a fraction r of players adopt strategy U, while the rest opt for V. The network in this model lacks degree-degree correlation, similar to our earlier discussions.

3.2 Strategy Update Example

An example of strategy updating is depicted in Fig. 4. Here, the total payoff for players adopting strategy U around a randomly chosen player is denoted as \(T_U=2(1-w+w u)\), and similarly, \(T_V=2(1-w+w v)\) for strategy V. The probability of the randomly chosen player switching from V to U in the next step is \(T_U/(T_U+T_V)\).

Fig. 4
figure 4

Strategy update example: this figure illustrates how a player’s strategy is updated. The shaded circle represents a randomly chosen player, whose strategy change is influenced by the total payoffs of adjacent players adopting strategies U and V

Full size image

3.3 Speed of Strategy Spread

Let \(p_U\) and \(p_V\) represent the probabilities of a randomly chosen player adopting strategies U and V, respectively. The speed of strategy U’s spread, denoted as \(E[\triangle p_U]\), is approximately given by Eq. (A.20) in the appendix as:

$$\begin{aligned} E[\triangle p_U]&\approx \frac{u-v}{N} \frac{\langle k \rangle -2}{\langle k \rangle -1}p_U(1-p_U)w\triangle t. \end{aligned}$$
(50)

This equation indicates that the speed of social learning is independent of the mean degree of nearest neighbors \(\langle k_\text {nn}\rangle \) in this model, where only the learning network exists and payoffs depend solely on individual strategies. Conversely, when both the learning network and the game network exist, the speed of social learning is influenced by \(\langle k_\text {nn}\rangle \).

3.4 Proposition and Implications

We propose the following:

Proposition 5

  In a learning network where payoffs depend only on individual strategies, the speed of spreading a superior strategy increases with the network’s mean degree \(\langle k\rangle \). However, this speed is not influenced by the mean degree of nearest neighbors \(\langle k_\text {nn}\rangle \) in the mean-field approximation.

This finding suggests that the enhancement of social learning in scale-free networks is not due to the learning network’s scale-free nature per se, but rather because the game network is scale-free. In such networks, hub players, who have a significant payoff difference between strategies, are more inclined to adopt the superior strategy. Consequently, their neighboring players are likely to follow suit, leading to a rapid spread of the better strategy through these influential hub players.

3.5 Numerical Validation of Proposition 5

To verify whether network heterogeneity impacts the social learning process, particularly when the learning network exists and payoffs depend solely on individual strategies, we conducted numerical simulations on scale-free networks.

3.5.1 Simulation Setup

The construction of scale-free networks and the parameters used are identical to those in Sect. 2.9. Specifically, we utilized networks with a mean degree of \(\langle k\rangle =10\) and a size of \(N=3000\). Four distinct networks were simulated, each characterized by different values of the exponent \(\gamma \): 2.1, 2.2, 2.4, and 3. Initially, 750 players were designated as U strategists, with the remaining 2250 adopting strategy V. Strategy updates followed the previously outlined rule, with simulations running for 15,000 time steps.

3.5.2 Simulation Parameters and Procedure

The payoff parameters were set at \(u=10\) and \(v=-10\), with \(w=5\times 10^{-3}\). Each simulation was repeated 100 times for every network to ensure reliability. The primary focus was on the final count of U players and the average mean degree of nearest neighbors \(\langle k_{nn}\rangle \) across these repetitions.

3.5.3 Results and Implications

The results, depicted in Fig. 5, demonstrate that network heterogeneity does not significantly influence the social learning process under the given conditions. This finding aligns with the expectations set forth in Proposition 5.

Fig. 5
figure 5

Impact of network heterogeneity on strategy spread: this figure illustrates the results of numerical simulations, supporting Proposition 5. It shows that the spread speed of the superior strategy is not significantly influenced by network heterogeneity. The scale-free networks used in the simulation have a consistent network size (\(N=3000\)) and mean degree (\(\langle k\rangle =10\)), with varying mean degrees of nearest neighbors \(\langle k_{nn}\rangle \). The y-axis represents the final count of U players, and the x-axis reflects the mean degree of nearest neighbors, indicating network heterogeneity

Full size image

4 Coordination Game: Threshold Probability for Strategy Spread in Networks

In exploring a coordination game with imitation dynamics on networks, we first analyze the game with a general payoff matrix to determine the conditions under which a particular strategy, denoted as A, proliferates across the network.

Threshold Initial Probability for Strategy Spread.

We denote \(p_A^\text {nn}\) as the probability that a player adjacent to a randomly chosen player adopts strategy A. In the mean-field approximation, the degree of such a neighboring player is represented by \(\langle k_\text {nn}\rangle \). The expected change in the probability \(p_A^\text {nn}\) over a unit time step \(\triangle t\) is derived using Eqs. (25), (34)–(37). The detailed calculation, akin to Eq. (38), yields:

$$\begin{aligned} E[\triangle p_A^\text {nn}]&\approx \frac{\langle k_\text {nn}\rangle -2}{\langle k_\text {nn}\rangle (\langle k_\text {nn}\rangle -1)N(\langle k_\text {nn}\rangle )}p_A^\text {nn}(1-p_A^\text {nn})\left[ (\alpha _\text {nn} +\beta _\text {nn}) p_A^\textrm{nn}+ \gamma _\textrm{nn}\right] w\triangle t, \end{aligned}$$
(51)

where \(\alpha _\textrm{nn}\), \(\beta _\textrm{nn}\), and \(\gamma _\textrm{nn}\) are defined based on the payoff matrix elements and \(\langle k_\textrm{nn}\rangle \).

Threshold Conditions for Strategy Spread.

We define \(r:=p_A(t=0)\) as the initial probability of adopting strategy A. The condition for strategy A to spread over the network is determined by whether \(m(r,r^\textrm{nn})>0\). The threshold conditions, depending on the payoff matrix elements, are as follows:

  • If \(x-y-z+s>0\), the threshold condition is:

    $$\begin{aligned} r>\frac{-(x-y-z+s)-\langle k\rangle (x-y+(y-s)\langle k_\text {nn}\rangle )}{(x-y-z+s)[\langle k\rangle (\langle k_\text {nn}\rangle -1)-2]} , \end{aligned}$$
    (52)
    $$\begin{aligned} \langle k_\text {nn}\rangle (y-s)>y-x. \end{aligned}$$
    (53)

  • If \(x-y-z+s=0\), the condition becomes:

  • If \(x-y-z+s<0\), the threshold condition is:

    $$\begin{aligned} r<\frac{-(x-y-z+s)-\langle k\rangle (x-y+(y-s)\langle k_\text {nn}\rangle )}{(x-y-z+s)[\langle k\rangle (\langle k_\text {nn}\rangle -1)-2]}. \end{aligned}$$
    (54)

Proposition on Strategy Spread.

We propose that a strategy spreads over the network as time progresses if the initial probability of a player adopting the strategy exceeds (or does not exceed) the threshold probabilities as outlined in Eqs. (52)–(54), within the framework of the mean-field approximation. Additionally, we explore the impact of network heterogeneity on these thresholds, particularly in the limit as \(\langle k_\text {nn}\rangle \rightarrow \infty \).

4.1 Coordination Game: Payoff Matrix and Strategy Spread Dynamics

In this section, we delve into a coordination game characterized by a specific payoff matrix and analyze the dynamics of strategy spread within network structures.

4.1.1 Payoff Matrix of the Coordination Game

The coordination game under consideration is defined by the following payoff matrix:

(55)

Players choose between strategies R and P, with the payoff parameters satisfying \(d+e>f\) and \(f>d>e>0\). This scenario corresponds to the case where \(x-y-z+s>0\). The optimal strategy pair is (P, P), with Nash equilibriums at (R, R) and (P, P). Strategy R is risk-dominant over P.

4.1.2 Threshold Initial Probability for Strategy Spread

The initial probability r for a player to adopt strategy R plays a crucial role. If r satisfies the following condition:

$$\begin{aligned} r>\frac{-(d-e+f)-(e-f)\langle k\rangle \langle k_\text {nn}\rangle -(d-e)\langle k\rangle }{(d-e+f)[\langle k\rangle \langle k_\text {nn}\rangle -\langle k\rangle -2]} (=: r_\text {th}) , \end{aligned}$$
(56)

then strategy R proliferates over time. Conversely, if r is below this threshold, the Pareto optimal strategy P becomes dominant.

In the context of significant network heterogeneity (i.e., \(\langle k_\text {nn}\rangle \rightarrow \infty \)), the threshold condition simplifies to:

$$\begin{aligned} r>\frac{f-e}{d-e+f}. \end{aligned}$$
(57)

This implies that the expected payoffs for adopting strategies R and P become equivalent.

4.1.3 Impact of Network Heterogeneity on Strategy Spread

The relationship between network heterogeneity and the spread of the Pareto optimal strategy is influenced by the sign of \(e+(d-f)(1+\langle k\rangle )\). Specifically:

  1. 1.

    If \(e+(d-f)(1+\langle k\rangle )>0\), increasing network heterogeneity lowers the threshold initial probability, favoring the spread of the Pareto optimal strategy.

  2. 2.

    Conversely, if \(e+(d-f)(1+\langle k\rangle )<0\), the result is reversed, favoring the risk-dominant strategy.

Additionally, as the mean degree \(\langle k\rangle \) rises, the threshold for the Pareto optimal strategy’s spread decreases, regardless of the sign.

4.1.4 Proposition on Strategy Spread in Networks

We propose that the network’s heterogeneity plays a significant role in determining the spread of strategies. In networks with a sufficiently large mean degree \(\langle k \rangle \), the mean degree of nearest neighbors \(\langle k_{nn}\rangle \) predominantly influences the spread of the risk-dominant strategy R.

4.1.5 Scenario Where Risk Dominant Strategy is Also Pareto Optimal

In our previous discussions, we considered scenarios where the risk dominant strategy differed from the Pareto optimal strategy. We now turn our attention to a scenario where the risk dominant strategy is also the Pareto optimal. This situation arises under the conditions \(d+e>f\), \(d>f\), and \(d>e>0\), where strategy R is both risk dominant and Pareto optimal.

Threshold Initial Probability for Strategy Spread. In this unique scenario, the threshold initial probability for the spread of strategy R is governed by the same equation as before [Eq. (56)]. However, the condition \(e+(d-f)(1+\langle k\rangle )>0\) is always satisfied, leading to an interesting outcome: as network heterogeneity increases, the threshold initial probability for strategy R also rises. This indicates that network heterogeneity, in this case, acts as a barrier to the spread of strategy R, despite its dual status as both the risk dominant and Pareto optimal.

Impact of Mean Degree and Network Heterogeneity. The role of the mean degree \(\langle k\rangle \) is also noteworthy. Since \(\frac{\partial r_\text {th}}{\partial \langle k\rangle }>0\), an increase in the mean degree similarly raises the threshold initial probability for strategy R. This contrasts with scenarios where the risk dominant and Pareto optimal strategies are distinct, where the influence of the mean degree and the mean degree of nearest neighbors can diverge. In this unique case, however, both factors align in their impact on strategy spread.

In summary, when the risk dominant strategy also represents the Pareto optimal choice, both network heterogeneity and the mean degree of the network play a reinforcing role in determining the threshold for strategy proliferation. This highlights the nuanced interplay between network characteristics and strategy dynamics in coordination games.

4.2 Numerical Validation of the Theoretical Threshold in the Mean-Field Approximation

To validate the theoretical threshold derived in the mean-field approximation, we conducted numerical simulations of a coordination game. The game’s payoff matrix is defined as follows:

(58)

Simulation Setup. The simulations were executed on both a random network and a scale-free network, as illustrated in Figs. 6 and 7. The scale-free networks were constructed using the BA model, similar to the approach in Sect. 2.9. In each simulation step, a player is selected at random to update their strategy based on the defined rules. The simulation concludes after 40,000 time steps, at which point we record the proportion of players adopting strategy P.

Simulation Repetition and Averaging. Each simulation was repeated 100 times, and the results were averaged. A data point above the 45-degree line in the figures indicates that strategy P has successfully spread across the network over time. The simulations demonstrate that when the initial probability surpasses the theoretical threshold, the prevalence of strategy P is higher at the end of the simulation than at the beginning, confirming the validity of the mean-field approximation threshold.

Fig. 6
figure 6

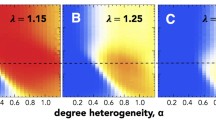
Coordination game simulation on a random network: this figure validates the theoretical threshold [Eq. (56)] through numerical experiments on a random network. The network parameters are \(N=1000\), \(\langle k\rangle =10\), and \(w=5\times 10^{-4}\). The payoff matrix is as per Eq. (58). The y-axis represents the final probability of P players, while the x-axis shows the initial probability of adopting the Pareto optimal strategy P. The dashed line marks the theoretical threshold

Full size image
Fig. 7
figure 7

Coordination game simulation on a scale-free network: this figure confirms the theoretical threshold [Eq. (56)] for a scale-free network. Parameters include \(N=1500\), \(\langle k\rangle =10\), \(w=5\times 10^{-4}\), and \(\gamma =3\). The payoff matrix follows Eq. (58). The y-axis shows the final probability of P players, and the x-axis represents the initial probability of adopting strategy P. The dashed line indicates the theoretical threshold

Full size image

Figures and Interpretation These simulations corroborate the theoretical findings, demonstrating that the mean-field approximation provides an accurate prediction of the threshold for strategy spread in coordination games on both random and scale-free networks.

4.3 Facilitating the Spread of Pareto Optimal Strategy

Previously, we analyzed scenarios where the initial probability of adopting a strategy was independent of a player’s network degree. We now explore how the strategic positioning of players, particularly on hub vertices, can influence the spread of the Pareto optimal strategy. Specifically, we examine the impact when hub vertices are more likely to adopt strategy P initially.

Threshold Derivation for Differing Probabilities. To illustrate this, we derive the threshold condition for the case where \(r \ne r^\text {nn}\). Following a similar approach as before, we consider the general payoff matrix and establish the threshold r for different probabilities r and \(r^\text {nn}\), representing the likelihood of strategy R being adopted by vertices of varying degrees.

Threshold Conditions.

  • Positive Case: If \(x-y-z+s>0\), the threshold is defined as:

    $$\begin{aligned} r&> \frac{-(x-y-z+s)\langle k\rangle (\langle k_\text {nn}\rangle )r^\text {nn}-(x-y-z+s)-(x-y)\langle k\rangle -(y-s)\langle k\rangle \langle k_\text {nn}\rangle }{(x-y-z+s)(\langle k\rangle -2)}\nonumber \\&=: r^\text {th}. \end{aligned}$$
    (59)

  • Neutral Case: If \(x-y-z+s=0\), the condition becomes:

    $$\begin{aligned} \langle k_\text {nn}\rangle (y-s) > y-x. \end{aligned}$$
    (60)

  • Negative Case: If \(x-y-z+s<0\), the threshold is:

    $$\begin{aligned} r < \frac{-(x-y-z+s)\langle k\rangle (\langle k_\text {nn}\rangle )r^\text {nn}-(x-y-z+s)-(x-y)\langle k\rangle -(y-s)\langle k\rangle \langle k_\text {nn}\rangle }{(x-y-z+s)(\langle k\rangle -2)}. \end{aligned}$$
    (61)

Impact of Hub Vertices. In scenarios where \(x-y-z+s>0\), a key relationship emerges:

$$\begin{aligned} \frac{\partial r^\text {th}}{\partial r^\text {nn}} = -\frac{\langle k\rangle (\langle k_\text {nn}\rangle -2)}{\langle k\rangle -2} < 0. \end{aligned}$$
(62)

This relationship implies that as the initial probability of hub vertices adopting strategy P increases, the overall threshold probability for strategy P to spread across the network decreases.

Proposition for Strategy Spread.

Proposition 6

In a coordination game, increasing the initial probability of hub vertices adopting the Pareto optimal strategy P leads to a lower threshold probability for the widespread adoption of strategy P across the network, as per the mean-field approximation.

This proposition suggests that strategically positioning players on hub vertices to adopt the Pareto optimal strategy can significantly enhance its spread across the network.

4.4 Numerical Validation of Proposition 6

To validate Proposition 6, we conducted a numerical simulation on a scale-free network, using the payoff matrix detailed in Eq. (58). The simulation results are depicted in Fig. 8. Initially, players adopting strategy P were strategically placed on vertices in descending order of their degree, until the ratio of P players to the total network size N matched the initial probability \(1-r\). The strategy updates continued for 40, 000 time steps.

Simulation Results. The outcomes of this simulation are represented by crosses in Fig. 8. For comparison, we also present results from a previous simulation (illustrated in Fig. 7) where the initial probability of adopting a strategy was not influenced by the players’ network degree. These results are indicated by dots in the figure.

Interpreting the Results. The crosses consistently appear above the dots, signifying that the simulation supports Proposition 6. This outcome suggests that when players on hub vertices initially adopt the Pareto optimal strategy, it significantly enhances the strategy’s spread across the network.

Fig. 8
figure 8

Comparison and confirmation of Proposition 6: the proposition is substantiated by the numerical simulations. The proposition implies that the spread of the Pareto optimal strategy is facilitated when players on hub vertices initially adopt this strategy. The dots represent the simulation results from Fig. 7, where the initial probability of adopting a strategy was independent of the players’ network degree. The crosses represent the simulation where hub players are more likely to be P players initially. The network parameters include a scale-free network with a size of \(N=1500\), a mean degree of \(\langle k\rangle =10\), \(w=5\times 10^{-4}\), and an exponent \(\gamma =3\). The payoff matrix follows Eq. (58). The y-axis shows the probability of players adopting strategy P at the end of the simulation, while the x-axis represents the initial probability of adopting strategy P. The 45-degree line is also included for reference

Full size image

5 Understanding How a Large Mean Degree of Nearest Neighbors Facilitates Strategy Spread in Networks

This section aims to provide an intuitive understanding, using a mean-field perspective, of why networks with a large mean degree of nearest neighbors (\(\langle k_{\text {nn}}\rangle \)) are conducive to the spread of a strategy. This understanding is crucial for comprehending various phenomena observed in highly heterogeneous networks, such as scale-free networks.

Fig. 9
figure 9

Intuitive understanding and mean-field perspective: a Illustrates a randomly chosen vertex (representing ordinary vertices) and its nearest neighbors. The degree of the randomly chosen vertex is the mean degree \(\langle k\rangle \), while the degrees of the nearest neighbors are the mean degree \(\langle k_{\text {nn}}\rangle \). b Depicts neighboring vertices with degree \(\langle k_{\text {nn}}\rangle \), each surrounded by vertices also having a degree of \(\langle k_{\text {nn}}\rangle \), in the mean-field model

Full size image

Understanding Ordinary Vertices. To comprehend network-wide phenomena, it is essential to first understand what occurs at ordinary vertices. The state of these vertices is influenced by their surrounding vertices. As shown in Fig. 9a, in the mean-field model, the degrees of vertices surrounding an ordinary vertex are represented by the mean degree of nearest neighbors, \(\langle k_{\text {nn}}\rangle \).

Regular Network of \(\langle k_{\text {nn}}\rangle \). In Fig. 9b, the vertices with a degree of \(\langle k_{\text {nn}}\rangle \) are also encircled by vertices of the same degree, forming a regular network. This setup allows for the resolution of states on vertices with degree \(\langle k_{\text {nn}}\rangle \), under the assumption that the expected values, such as the probability of adopting a certain strategy, are determined by the degree of the vertices in the mean-field model.

Strategy Spread Dynamics. Consider a scenario with two strategies, A and B. If it is determined that strategy A dominates in the regular network of degree \(\langle k_{\text {nn}}\rangle \) (as in Fig. 9b), then the vertices with degree \(\langle k_{\text {nn}}\rangle \) in Fig. 9a will likely adopt strategy A. Consequently, the strategy of ordinary vertices with degree \(\langle k\rangle \) is influenced by the strategies of their surrounding vertices with degree \(\langle k_{\text {nn}}\rangle \). Thus, the prevailing strategy in the entire network is essentially dictated by the dynamics within the regular network of degree \(\langle k_{\text {nn}}\rangle \).

Impact of \(\langle k_{\text {nn}}\rangle \). The larger the degree \(\langle k_{\text {nn}}\rangle \) of this regular network, the more effectively a strategy propagates across the network. This insight explains why networks with a substantial mean degree of nearest neighbors, \(\langle k_{\text {nn}}\rangle \), are particularly effective in facilitating the spread of a strategy.

6 Conclusion

6.1 Summary

This paper has demonstrated that networks with heterogeneous degree distributions, particularly scale-free networks, significantly enhance social learning processes. The study focused on how network structures, perceived as social local interactions, influence social learning.

The model investigated players located at network vertices, engaging in games only with their immediate neighbors and deriving payoffs from these interactions. Players adopted strategies based on weak selection rules, leading to a gradual spread of more advantageous strategies across the network. This process, akin to the well-known S-curve, was analytically examined using the mean-field approximation of network structures, as introduced in previous works [18, 19].

Key findings include:

  • Networks with a larger mean degree of nearest neighbors (\(\langle k_{\text {nn}}\rangle \)) accelerate the spread of superior strategies, a phenomenon termed ’social learning’.

  • The mean degree (\(\langle k \rangle \)) also influences social learning, but its impact diminishes in networks with sufficiently high mean degrees.

  • Among various network types, scale-free networks most effectively enhance social learning, attributed to their high network heterogeneity.

The study also explored a coordination game on networks, deriving the threshold initial probability for the spread of Pareto optimal strategies. It was shown that networks with a high probability of hub vertices initially adopting Pareto optimal strategies are more conducive to the spread of these strategies.

6.2 More Discussion

We demonstrate how a scale-free network structure enhances social learning. Evolutionary games are viewed as social learning processes, where effective strategies spread through imitation dynamics. Foundational works like Maynard Smith and Price [23] show that spatial structures in these games can foster cooperative behavior. Studies [4, 28, 31, 32, 35] explore the interplay between evolutionary games, coevolution, and networks.

This paper mathematically derives the speed of strategy diffusion in evolutionary games with general payoff matrices and mean-field approximations of heterogeneous networks. We show that network heterogeneity facilitates the spread of effective strategies. We also examine coordination games, revealing the relationship between network heterogeneity, network structures, and the spread of Pareto optimal strategies. These findings are validated through numerical simulations.

We conclude that scale-free networks significantly enhance social learning. Additionally, we investigate coordination games on networks, examining how network structure influences outcomes. We identify the threshold initial probability for the spread of Pareto optimal strategies and demonstrate how network heterogeneity determines this threshold. Our analysis also shows that Pareto optimal strategies spread more effectively when players on hub vertices initially adopt these strategies. We employ mean-field approximations for networks, a crucial tool for approximate computations in complex network models.

The mean degree of nearest neighbors (\(\langle k_{\text {nn}}\rangle \)) emerges as a critical factor in network-based models, often overshadowing the influence of the mean degree. This paper emphasizes that \(\langle k_{\text {nn}}\rangle \) is a more significant determinant of network behavior than the mean degree. The concept of ’determining networks’ - virtual networks surrounding vertices with degree \(\langle k_{\text {nn}}\rangle \) - is introduced to illustrate this point. In the mean-field model, these determining networks, conceptualized as regular networks with degree \(\langle k_{\text {nn}}\rangle \), are pivotal in influencing network-wide phenomena.

6.3 Future Research Directions

While the mean-field approximation offers valuable insights, it does not account for degree-degree correlations known to exist in real networks. Future research should aim to incorporate these correlations into the mean-field model and extend the analysis to include pair approximations of game strategies. This advancement would provide a more comprehensive understanding of complex network dynamics and their implications for social learning and other network-based phenomena.