Abstract
In an interconnected society, social networks grow through formation of strategic connections based on the hierarchy within the social network. Often, the hierarchy becomes self-reinforcing and the observed valuations of the individuals in the hierarchy become disconnected from the corresponding fundamentals. We propose a network model to characterize the disconnect between the observed and fundamental valuations of entities, where the difference is a function of the linkages across the entities. In a growing social network, new entrants come at every point of time and offer connections to the incumbents based on the observed valuations. Individuals care only about their ranks in the hierarchy of observed valuation. With myopic individuals, network grows in equilibrium, but the associated hierarchy becomes unstable. However, with farsighted individuals, the network growth process is hierarchy-preserving and depending on the structure of seed network, the process may be completely halted by individuals who have incentives to preserve hierarchy. These two mechanisms taken together provide a comprehensive characterization of valuation in a growing inter-connected, hierarchical society. We illustrate an application of the model by analyzing the Indian board interlocking network. Our model enables us to find the hierarchy of the board members’ network and to identify the dispersion in magnitude of network externalities across directors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the current global economy and society, many entities are interdependent and possess intertwined structures. Corporate networks, political networks, and scientific collaboration networks are some of the most prominent examples of interdependence. These networks have two important features. One, there is an internal hierarchy of the nodes in the network based on the ordering of observable influences of the nodes. Typically, not all nodes are equally important in the network. Two, linkages across nodes are often strategic in nature, which in turn, frequently makes the hierarchy self-reinforcing. Once a hierarchy appears, it is often preserved even with regular addition of newer individuals to the network.
In this paper, we focus on two questions. First, how does a network grow with strategic individuals who decide about whom to connect to by using an observable metric of influence of the existing individuals? Second, under what conditions the hierarchy is preserved during the growth process? We propose that the individuals derive values from linkages with other influential entities apart from their fundamental valuations. Thus, the observed valuation of individuals in the network becomes disconnected from the corresponding fundamentals, leading to a wedge between the two. Since the new entrants considers only the observed valuation, the hierarchy itself becomes disconnected from the fundamentals and influential individuals retain influence solely by being connected to other influential individuals.
Economically, there are many quantifiable examples of such interdependence across entities and separation from fundamentals. Consider a neighborhood where houses can be rented. When rent of a house goes up, it pulls the housing rent in the same neighborhood.Footnote 1 Peer effects are very significant in corporate decision-making process. Acharya and Pedraza [2] showed that excess trading due to peer benchmarking of the institutional investors occurs to a significant extent. Interdependence can be clearly seen in case of corporate executive compensation. One well-established observation is that the compensation is a function of the hierarchy and hence, it does not necessarily reflect marginal productivity.Footnote 2 Before 1980s, the companies used to fix the salaries of the top executives with respect to the salary distribution within the companies. A major change occurred in the subsequent period and the companies started moving from internal equity to external equity. Faulkender and Yang [21] summarized the finding that “After controlling for industry, size, visibility, CEO responsibility, and talent flows, we find that firms appear to select highly paid peers to justify their CEO compensation and this effect is stronger in firms where the compensation peer group is smaller ...”. Liu and Sun [33] stated that the prevailing attitude is that in presence of relative wealth concern, executives’ pays should not fall behind the peers. Hochberg et al. [28] showed in the same vein that the social networks of the executives matter for compensation and in particular, along with the number of connections, identities of the connections also matter. DeMarzo and Kaniel [16] analyzed such keeping up with the Joneses behavior to formulate contracts on relative compensation for the corporate executives. Additionally, Horton et al. [29] showed that compensation is positively associated with how central is the individual in the corporate network. Thus the empirical literature suggests that interdependence, notably size and the nature of connections, plays a substantial role in determining valuation of the economic entities in a non-trivial way.
We propose a model of valuation in an interdependent economy where valuation can be derived from fundamentals as well as the interdependence (peer effect or network effect). This model helps us to analyze the relative contribution of fundamentals and the network effect. In particular, the model provides a clean characterization of how the architecture of a given network affect the valuation of the individuals. Consequently, we can uniquely pin down the network externalities in the form of one individual’s indirect impact on another individual.
To suitably model the network effect, we need an index of influence which can accurately capture the network externality. We propose that eigenvector centrality is an appropriate measure to do that. Consider panel (a) in Fig. 1. It shows a symmetric network with seven nodes (\(A,~\ldots ,~G\)). We note that C and E are equally central.Footnote 3 Suppose now, node D and F connects with each other. It can be shown that E now becomes more central than C in terms of eigenvector centrality, while neither of them participate in the network growth process. Thus, the measure of eigenvector centrality can efficiently capture the network externality where evolution in one part of the network can non-trivially affect the rest of the network.
Following the literature, we adopt a linear framework to analytically model interdependence. Brioschi et al. [12] introduced a static, linear model of firm-to-firm connections, which has been used in the recent times by several authors. Notably, Elliott et al. [20] used that framework to study contagion in financial networks. The fact that such interdependence leads to the separation of book value from market value is a well-known phenomenon. Brioschi et al. [12] as well as Fedenia et al. [22] emphasize such inflation (see also [20]).
We treat the linear dependence model as a building block to study the dynamic network growth process. We show that the eigenvector centrality provides a unique way to characterize the hierarchy of the individuals in the network and we can rank individuals in terms of their relative influence due to their position in the hierarchy, with the aid of centrality measure. Given that individuals are rank-conscious, we show that a new entrant would like to connect to the individual with the highest centrality as it gives the maximum centrality to the entrant, and then work downwards according to relative centrality. With a sequence of entrants entering the economy and making connections, the network grows. Strategically, the individuals can be backward-looking as well as forward-looking. We show that they would not be backward-looking in the sense that they would not retrospectively analyze whether an earlier decision was wrong and alter that decision. There is no incentive to do this in equilibrium as it can only worsen the relative ranking in the hierarchy of individuals.
The key question is whether the network growth process preserves the hierarchy or not? Our model readily delivers the result that with myopic individuals (only one attempt to form links), the hierarchy changes very frequently. However, with farsighted individuals who can make multiple attempts, we show that the network growth process can be halted. The network architecture plays a big role in determining the growth process (or lack thereof) with farsighted individuals.
The intuition is that in the first case, the entrant makes only one offer to the incumbents and it is hit-or-miss for the incumbents. Myopic individuals would think that by forming linkages they can increase their relative ranking unequivocally. But when everyone does that, the new entrant emerges as the new winner and dismantles the existing hierarchy. In this case, the network grows in size maximally fast as every potential entrant becomes part of the network and the hierarchy becomes extremely unstable as the incumbents do not cooperate with each other. However, when we introduce farsightedness, the incumbents take into account the possibility that even though a link formation can provide higher payoffs temporarily, eventually it might lead to loss in rank as other players also respond; in such a scenario, they can maintain status quo and the hierarchy becomes stable. We show that architecture of the network affects growth process with farsighted individuals. If there are multiple identically ranked individuals in the top or middle of the hierarchy, typically they block the network growth process in equilibrium.
A corollary of the model is that higher density of connections reduces the inequality of influence across individuals. The intuition is as follows. Here valuation depends on the nature of influential connections and hence, if the density of connections in the network increases, then the individuals lose uniqueness of having access to influential connections. Thus with higher density of connections (an extreme example is a complete graph) the individuals’ influences are equalized whereas with sparseness (an extreme example is star network) inequality increases.
Since the whole idea is based on analyzing hierarchy in a network, we need an unique and unambiguous definition of centrality, which is useful to extract hierarchy from a given network. In the paper, we use eigenvector centrality to constitute a hierarchy in the network. Our choice is based on a very influential result derived in Ballester et al. [5], which showed that in the context of linear-quadratic games, the pure strategy Nash equilibrium profile is proportional to the corresponding Bonacich centrality,Footnote 4 which is related to eigenvector centrality. They indicated that their framework can be extended to a two-level game (with an intra-period and an inter-period game), where the intra-period game is defined by their main result that Nash equilibrium is identical to the centralities in a given network, and the inter-period game can deal with the network formation mechanism due to players deciding to stay in or drop out of the network. In this paper, we are precisely doing that by defining a network formation game where the players follow their equilibrium solution in the intra-period game (the first stage) and based on the hierarchy thus created, they play a network formation game where every period there is a new entrant. Since the result linking Nash equilibrium with Bonacich centrality of a given network is already well established, we keep the result only in the background and describe it in “Appendix”. Our main focus is on the inter-period game of network formation and growth.
After describing the network growth process, we analyze impact of the evolved network on the valuation of individuals. Because of the interdependence in valuation, we show that a wedge emerges between the fundamental valuation and the market valuation. This leads to two kinds of network effect. One, it generates a network multiplier in valuation over and above the fundamentals. Two, this gives rise to spill-over effects where one individual contributing more in real terms causes his neighbors to benefit because of the interdependence in valuation, without any actual contributions on their parts.
Finally, we illustrate the mechanics of our model by analyzing Indian board interlocking network. Board interlocking network is a bipartite network where there are two sets of nodes, directors and companies. We create a one-sided projection to get the directors’ network, where they are connected if they sit on at least one common board. Empirically, the formation of such interlocking board membership network has been analyzed in details (see for example [26]).Footnote 5 The model easily delivers the hierarchy or the pecking order from the directors’ network and characterizes the spillover effects of a shock to any director in the network.
The literature analyzing games on network is extensive. There are multiple definitions and concepts of equilibrium in network formation games [9]. Starting with the paper by Ballester et al. [5], there is now a sizeable literature that has emphasized the connection between centrality and Nash equilibrium (Bloch et al. [10] provides a comprehensive summary of different types of centrality measures). We note that there is also a complementary literature that connects the concept of centrality with competitive equilibrium.Footnote 6 Below we discuss some features of our model in the context of relevant literature.
First, our model is deterministic and we introduce a payoff function that is a function of ranks in the hierarchy and relative influence within the network. The deterministic nature of the game differentiates our paper from literature on stochastic network formation games (see Pin and Rogers [39] for a review). On the other hand, Bala and Goyal [4] presented one of the key models in the literature on deterministic network formation. They introduced costly link formation in a potentially directed network game and analyzed the corresponding stability, growth and efficiency. This structure has been followed in the later literature as well (see, e.g., [24]). A typical description of this kind of models would include an utility function of the agents which depend on local effects, e.g., the cost and benefit of a link between two nodes will directly affect only the concerned nodes. In contrast, our model explicitly features a payoff function that is dependent on the structure of the whole network. Referring to Fig. 1, the payoffs of nodes might drastically change due to a link formation, even if they do not participate in that. This network externality is reminiscent of general equilibrium effects in networks (seen for example in R&D games where the effects of investment into link formation by a pair of firms is not contained only to that firm and its neighbors; see, e.g., [25]). Also, the payoff function in our case is step-wise linear in the rank of players in the hierarchy, a property which becomes very useful in defining the equilibrium. We are not aware of any other paper that uses a similar payoff function.
Second, this paper proposes the possibility that with farsighted players, the network growth process might completely stop. Therefore, it provides an explanation of why it may be difficult to change hierarchy in an organization. The result that farsighted players may completely stop the network growth process, relates to interest groups, club goods and entry barrier [45]. The literature on farsighted individuals’ behavior in network games is quite large (see e.g. [18, 19, 27, 30, 35]). There are two differentiating features of our definition of farsightedness: Players in our model consider the future evolution of not creating a link as well in his future payoff (as opposed to considering only the effects due to creating a link), and the stability here is defined in terms of incorporating the new entrant in the network with incumbents (as opposed to only within the network of incumbents).
Third, we do not assume a cost of link formation. The reason is that with a cost of link formation, the network growth might be halted whenever the cost of growth becomes larger than the benefit. Therefore, we consider the extreme case and show that even when the cost of link formation is zero, the network growth might be halted. At this stage, it is important to point out a paper which is very closely related to the core idea of our modeling approach. In Neligh [37], the author investigated how timing of entry in a network might influence the evolution of centralities of the nodes in the network. This paper is experimental in nature, which in turn builds on a theoretical model where the agents face a cost of link formation and derives benefit out of closeness centrality. The paper characterizes a behavioral trait of players who exhibit ‘vie for dominance’. Our theoretical model explicitly differs in the zero cost setting along with eigenvector centrality driven payoffs and rank-ordering-based utility.
Fourth, we relate our model to macroeconomic fluctuations and characterize the network multiplier as a function of business cycles. There are models of networks that relate to macroeconomic phenomena (see Goyal [24] for a detailed review of such models). A series of models in this stream of the literature are non-strategic in nature (a canonical example is Acemoglu et al. [1] which also utilizes the link between network topology of production linkages and market structure) whereas players in our model are strategic. There are models with strategic players engaging in transactions with macroeconomic implications: e.g., in labor markets (e.g. [13]), in financial markets (e.g., [14]) and goods market (e.g., [23]). Our model complements this literature by linking the effects of business cycles on the disconnect between fundamental valuation and observed valuation. Elliott et al. [20] used a very similar framework of book valuation and market valuation, and studied effects of financial shock propagation on a static and fixed network. Although we have borrowed the decomposition of final valuation into own effects and peer effects following their work, our model involves strategic individuals utilizing the network structure to play games and thereby changing the network structure itself. Finally, we apply our theoretical model to a real world dataset on directors’ network to demonstrate its applicability. Although studies are abound on corporate networks, they are almost exclusively empirical in nature (see Borgatti and Foster [11] for a comprehensive review of the associated sociological theories), whereas our paper provides a link to the strategic behavior of the players and corresponding macroeconomic consequences.
Structure of the paper is as follows. In Sect. 2, we introduce the basic model and analyze the connection between network structure and valuation. We introduce the network growth process in Sect. 3. A network growth process with myopic agents leads to a complete graph. Section 4 describes the growth process with farsighted individuals. We show that depending on the network structure, the growth process might be completely halted or there might be scope for partial growth. Given the network structure, we quantify the network effects in the form of network multiplier as well as spillover effects in Sect. 5. Then we analyze the implications of the model in the context of Indian elite corporate network in Sect. 6. Section 7 concludes.
2 Interdependence in Observed Valuation
First, we define a network of individuals as follows.
Definition 1
(Network) A static network \({\mathbb {N}}\) is defined as a collection of nodes or vertices and edges connecting them,  . The edges are binary: \(\gamma _{ij}\in \{0,~1\}\). If there exists at least one path i.e. sequence of edges in the network across all pairs of nodes, then we call such a network connected. The degree sequence of \({\mathbb {N}}\) is given as
. The edges are binary: \(\gamma _{ij}\in \{0,~1\}\). If there exists at least one path i.e. sequence of edges in the network across all pairs of nodes, then we call such a network connected. The degree sequence of \({\mathbb {N}}\) is given as  and the set of edges is denoted by
and the set of edges is denoted by  . We denote the corresponding adjacency matrix by \(\varGamma \).
. We denote the corresponding adjacency matrix by \(\varGamma \).
Time is discrete, \(t=0,1,2,\ldots \). A dynamic network is given by  ; in short,
; in short,  where the network’s connectivity structure at time t is given by
where the network’s connectivity structure at time t is given by  where \(\gamma _{ijt}\in \{0,~1\}\).Footnote 7 We consider a symmetric network, i.e.,
where \(\gamma _{ijt}\in \{0,~1\}\).Footnote 7 We consider a symmetric network, i.e.,

We imagine that there are \(n_t\) granular strategic individuals in the economy at a generic time point t. Each individual is indexed by  .Footnote 8
.Footnote 8
The starting point of our analysis is that the observed valuations are interdependent:Footnote 9

where \(\omega _t\) denotes the network coefficient and  is the set of entities at time t. In Eq. 2, the fundamentals
is the set of entities at time t. In Eq. 2, the fundamentals  are exogenously given. Given the relative weight \(\omega \), the valuation
are exogenously given. Given the relative weight \(\omega \), the valuation  can be expressed as a function of the network structure and the fundamentals. We can rewrite Eq. 2 without the time subscript as
can be expressed as a function of the network structure and the fundamentals. We can rewrite Eq. 2 without the time subscript as
where \(\beta \) is a column vector and captures the fundamentals.
Before proceeding further, we need some definitions that will be used throughout the paper.
Definition 2
(Eigenvector centrality) Eigenvector centrality \(\{e\}\) is defined as the dominant right eigenvector of the adjacency matrix \(\varGamma \). Since the eigenvector is not unique due to scale factors, we normalize the elements of the vector \(\{e\}\) so that sum of the elements is 1. We will denote the dominant eigenvalue by \(\lambda _\mathrm{max}\).
Definition 3
(Katz–Bonacich centrality) Katz–Bonacich centrality for a given network with a symmetric adjacency matrix \(\varGamma \), is defined as a vector \(e^{KB}\) such that
where \(\omega \) is an exogenous constant, \(\beta \) is a column vector and I is an identity matrix. Under the condition that \(\omega < 1/\lambda _\mathrm{max}\) (\(\lambda _\mathrm{max}\) being the highest eigenvalue of \(\varGamma \)), the centrality measure is well-defined.
In other words, the Katz–Bonancich centrality is exactly the same as V solving Eq. 2. Next, we define hierarchy over the centrality vector V.
Definition 4
(Hierarchy) Given a network \({\mathbb {N}}\), hierarchy \({\mathcal {H}}_{\varGamma }\) is an ordered vector \(\{h_i\}_{i=1,\ldots ,n}\) where \(h_i \in \{1,\ldots ,n\}\) such that \(V_{h_i}> V_{h_j}\) if \(h_i<h_j\) for all \(i,j\in \{1,~2,~\ldots ,n\}\). The ordered vector h denotes ranking of the nodes, which produces the hierarchy in the network. Additionally, we will assume that in case of a tie between s nodes (with \(n_s\) number of nodes having higher centralities), then all of the s nodes will have the same rank (\(n_s\)+1) and the next node in term of ranking will have a rank of \(n_s+1+s\).
It is important to note the specific scheme of ranking used in this is paper. We assume in the hierarchical ordering that the number of players above a given player matters for ranking. Therefore, the ranking is not purely ordinal. For example, in a three players’ world, if the centralities are 0.4, 0.3, 0.3, then the ranking would be 1, 2, 2; but if the centralities are 0.4, 0.4, 0.3, then the ranking would be 1, 1, 3. The specific mode of the ranking scheme is important for the result stated afterward in this paper. In “Appendix 8.5”, we provide an example where a purely ordinal ranking scheme would lead to different network growth process. Briefly, the chief reason for adopting this ranking scheme is that a ranking scheme which takes into account how many players are above a given player, stops the network growth in certain cases whereas a purely ordinal ranking does not lead to a complete halt in the process. Since in this paper we want to analyze the cases where the network growth might be completely halted, we focus on the relevant ranking scheme.
2.1 Network Coefficient \(\omega \)
From Eq. 2, we note that the unspecified parameter is \(\omega \). The first question we address is how to endogenize the weight \(\omega \) for a connected network? In general, we can choose arbitrary weights for \(\omega \in [0,~1]\). However, we make two assumptions about \(\omega \).
Assumption 1
The relative weight \(\omega \) is a function of the architecture of the network  .
.
From the empirical literature discussed earlier, we note that the network effect is the strongest for small number of competitors (see e.g. [21]). This observation leads to the following assumption.
Assumption 2
Relative weight \(\omega \) should endogenously decrease as the network size n increases.
We claim that one good candidate for \(\omega \) is the inverse of the dominant eigenvalue \(\lambda _\mathrm{max}\) of the adjacency matrix of \(\varGamma \). More formally, we state the following proposition.
Proposition 1
Given a connected network \({\mathbb {N}}\), the relative weight \(\omega \) proportional to the inverse of the dominant eigenvalue of the network \({\mathbb {N}}\) satisfies Assumptions 1 and 2 if the proportionality constant \(\theta <1\).
Proof
See “Appendix 8.2”. \(\square \)
We need to make one more assumption to uniquely pin down the hierarchy \({\mathcal {H}}\) based on network \({\mathbb {N}}\).
Assumption 3
\(\beta _i={\bar{\beta }}\) for all  where \({\bar{\beta }}\) is a constant.
where \({\bar{\beta }}\) is a constant.
Under Assumption 3 and if \(\theta ~\rightarrow ~ 1\) from below, \(\omega =\theta /\lambda _\mathrm{max}~\rightarrow ~1/\lambda _\mathrm{max}\). Now, we state a proposition that uniquely pins down a hierarchy. We show that the hierarchies implied by valuation and eigenvector centrality, are identical in the limit.
Proposition 2
Consider a network \({\mathbb {N}}\). Let nodes i and j (for all i and j) have valuation \(V_i\) and \(V_j\) following Eq. 2, and eigenvector centrality of \(e_i\) and \(e_j\). Then under Assumption 3 and if \(\theta ~\rightarrow ~ 1\) from below, \(V_i\ge V_j\) implies \(e_i\ge e_j\) and vice versa. Hence, the implied hierarchies are identical.
Proof
This result is a straightforward application of Corrollary 1 of Theorem 5.1 from Benzi and Klymko [8] which states that as \(\omega \rightarrow \frac{1}{\lambda _\mathrm{max}}\) (converges from below), the ranking produced by \(e^{KB}(\omega )\) converges to that produced by e. \(\square \)
In the rest of the paper, we assume that \(\omega =\frac{\theta }{\lambda _\mathrm{max}}\).
2.2 Valuation on a Static Network
Let us assume a connected graph \({\mathbb {N}}\) with n nodes. The first result deals with the interpolation between the duopoly and competitive limits.
Theorem 1
The valuation (V) through network effect is the maximum for \(n=2\). As the number of the individuals (n) increases, the network effect decreases monotonically. In a fully connected network of n individuals, asymptotically (\(n\rightarrow \infty \)) valuation depends only on fundamentals (\(\pi \)).
Proof
As per Eq. 2, the valuation of the ith individual can be written as

without the time subscript.
There are three claims in the theorem, which we prove in three parts. First, we note that for a complete graph (all elements of the adjacency matrix = 1 except the diagonal) of size n, the dominant eigenvalue is \(n-1\). Thus the first claim of the theorem follows from Proposition 1. In proof of Proposition 1, we have noted that if the network expands, then \(\lambda _\mathrm{max}\) monotonically increase, implying that \(\omega \) correspondingly decreases. Thus the second claim is proved. Finally, we observe that for a complete graph
This completes the proof. \(\square \)
3 Strategic Network Formation
So far we have characterized the valuations on a static network. Now we introduce a scheme for dynamic network formation. Time t is discrete. At every point of time t, the network is defined as  , and there is a potential entrant who can make at most \(n_t\) number of connections (one with each incumbent). Thus the number of potential connections will change over time (as opposed to a fixed number of connections; see e.g. [36]). Given a certain network \({\mathbb {N}}_t\), the entrant wants to enter the network by forming links with the incumbents. The entrant’s goal is to maximize his ranking in the social hierarchy. Accordingly, he would choose who to connect to and make offers for connection. If the receiver of an offer agrees to connect, then they form a link, else the entrant moves to the next best choice.Footnote 10
, and there is a potential entrant who can make at most \(n_t\) number of connections (one with each incumbent). Thus the number of potential connections will change over time (as opposed to a fixed number of connections; see e.g. [36]). Given a certain network \({\mathbb {N}}_t\), the entrant wants to enter the network by forming links with the incumbents. The entrant’s goal is to maximize his ranking in the social hierarchy. Accordingly, he would choose who to connect to and make offers for connection. If the receiver of an offer agrees to connect, then they form a link, else the entrant moves to the next best choice.Footnote 10
We make an assumption that reservation values for the individuals are zero, i.e., individuals derive zero values from outside opportunities (by not participating in the network growth process).
Assumption 4
The reservation values for all individuals are zeros. Only the seed network can grow (e.g., seed network might have endowments of complementary assets).
Example 1
As an illustrative example, the seed network may represent incumbent members in a club. All other players want to enter the club, but in our model, they cannot create a new club on their own.
The interpretation of the assumption in real world production process can be envisaged in the context of labor and capital. Let us assume that capital is held by only the players in the seed network. If we consider that for generating the values \(\{V\}\), workers need access to physical capital stock (we can think of white-collar workers in a financial firm where the physical infra-structure is important for most kinds of operations) which they would lose if they do not become a part of the organization. Technically, this assumption is important as it allows us to study the network growth process exclusively without considering possibilities that some groups of individuals might form a coalition and leave the parent network.
Here we define the game in the following way. There are \(n_t\) individuals in \({\mathbb {N}}_t\) at a generic time point t. The individuals’ payoffs are defined as a function of their rank in the hierarchy defined by the eigenvector centralityFootnote 11 obtained from \({\mathbb {N}}_t\). The entrant’s strategy is to offer connections to the incumbents. The incumbents’ strategies are to either accept or reject after evaluating the offer. Formally, we make the following the assumption which provides a lexicographic preference of the players over hierarchy and centrality.
Assumption 5
(Rank-consciousness) Payoff of a player is an increasing function of the relative ranks in the hierarchy \({\mathcal {H}}\) and conditional on being in the same rank, payoff increases in centrality (sum of centralities of all incumbents is normalized to 1). In the following, we will use eigenvector centrality for rank-ordering.
Individuals are rank-conscious, and hence, they are interested in their rank (ordinality) in terms of centrality. This assumption is natural as people may care about whether they are more influential than their competitors or not, rather than computing exactly how much more influence do they yield over their competitors. Therefore, a connection is formed only when ranks improve of both the entrant and the incumbent in the hierarchy. But conditional on being in the same rank, if creating a new link gives them higher centrality compared to the previous scenario, then they will create the link (even if that does not increase the rank). This assumption is required for tie-breaking scenarios. Without making this assumption, we get into situations where the players can potentially create links without affecting their ranks and the network can grow, but the players would not do that if their payoffs are solely dependent on the ranking. By making this assumption, we can avoid such scenarios.
Given that there is only one possible entrant every point of time t, we can denote the existing network by \({\mathbb {N}}_t\) and the entrant by index t. Since the entrant makes a series of offers to the existing nodes in \({\mathbb {N}}_t\), the network structure evolves if any connection is formed within each t. To keep track of that, we use a notation \({\mathbb {N}}_{ti}\) where \(i~=~1,\ldots ,n_t\) where \(n_t\) is the number of incumbents at time t.
The network growth process is defined as follows:
- Step 1:
-
Start from a seed network \({\mathbb {N}}_t={\mathbb {N}}_{t,0}\) at time point t.
- Step 2:
-
A new individual comes in who attempts to sequentially make connections with incumbents starting with the most influential incumbent. The process continues across all existing incumbents in \({\mathbb {N}}_t\) in the sequence of the associated hierarchy \({\mathcal {H}}_{\varGamma _t}\). The associated network can be denoted by \({\mathbb {N}}_{t,i}\) where \(i~=~1,\ldots ,n_t\).
- Step 3:
-
After all decisions are made about formation of the links,Footnote 12 the entrant becomes either an incumbent (if at least one link is formed) or remains an outsider and drops off from the system (if no links are formed). Time proceeds by one unit and a new entrant appears. Then we go back to the first step above at time point \(t+1\) with network \({\mathbb {N}}_{t+1}={\mathbb {N}}_{t+1,0}\).
3.1 Myopia and Instability in Hierarchy
Before getting to the farsighted network formation, we first discuss briefly the network growth process with myopia and the corresponding instability of the associated hierarchy. Intuitively, here the players always want to connect to more agents if possible, since higher number of connections increases payoff of the players. At the same time, the players would also like to increase their relative ranks by connecting to the central players. Therefore, this system has a direct parallel to the model studied by Ballester et al. [5] and the same result can be derived here that the network will eventually tend towards a complete graph. Note that since a complete graph has no non-trivial hierarchy, the present model will display disappearance of hierarchy. Clearly this is an unrealistic scenario. König et al. [31] avoid this scenario by introducing stochastic decay in links with variable rates and random choice of players who can update their links, resulting in stochastically stable graph that generates nested split graphs. Here we pursue a different goal and show that if the players are farsighted, then the network growth process might halt. Thus our framework provides a theory of stability of hierarchy and stasis in network growth process, as opposed to the literature on dynamic process leading to growth in the network.
Although the following results are very similar to the results discussed in Ballester et al. [5] and König et al. [31], we formally present the case with myopic players so that it becomes easier to compare with the farsighted case. All proofs of the results with myopic players are in “Appendix 8.3”. Let us first define myopia in terms of players evaluating their ranks in a ceteris paribus condition, i.e., they do not consider future evolution of the network which can potentially affect their rank.
Assumption 6
(Myopia) Individuals evaluate each offer myopically in the sense that if rank (weakly) increases immediately after an offer to form a link is accepted, then the individuals accept it. In other words, the individual evaluates the offer in a ceteris paribus condition.
Given the above mechanism and the assumption that the individuals’ payoffs are defined over their relative ranks, we can show that all new entrants will be accommodated in the network.
Theorem 2
All new entrants will be accepted in the existing network with at least one connection.
Proof
See “Appendix 8.3”. \(\square \)
Theorem 3
Consider a network \({\mathbb {N}}\) with monotonic ranking of centralities \(V_1 \ge V_2 \ge V_3\ldots \ge V_n\) (without loss of generality). A new node m would connect to the existing n nodes in sequence \(1,2,\ldots ,n\) given by their hierarchy \({\mathcal {H}}\) and eventually would become weakly more central than the earlier most central node, under the condition that when node i connects to node m with lesser centrality (without loss of generality), the relative ranking between i and m does not change.
Proof
See “Appendix 8.3”. \(\square \)
The intuition for the above result is simply that creating a link will not reduce centrality (Ballester et al. [5]; see the discussion in p. 702, König et al. [31]). Clearly, the assumption of myopia is extreme in that the players are not taking into account that their competing players in the network might respond to their actions if the actions hurt the rankings of the competitors. The way they can respond is simply by connecting to the entrant in an attempt to increase their own ranks. We see from Theorem 3 that such cases might lead to worse outcome for every incumbent. In the next section, we relax the assumption of myopia and show that if the players recognize this reaction from the competitors, then the network growth might completely stop and the hierarchy would be preserved.
4 Farsighted Network: Stability of Hierarchy
We assume that the entrant can repeatedly make offers to the incumbents, and stops only when no new edges are formed. Imagine that the network is denoted by \({\mathbb {N}}_{t0}\) with \(n_t\) nodes. The entrant makes a series of offers from node 1 to \(n_t\). If any offer is accepted and an edge is formed, then the entrant again starts making a series of offers from node 1 to \(n_t\). This process stops when during one round of making offers, no edges are formed.
By introducing the repeated structure, we show that a fear of punishment can be supported in equilibrium, which would lead to cases where the fear of losing rank in the next round, would induce the individuals to not exploit the myopic gain arising out of making connections. Thus, such a mechanism might even lead to complete halt of the growth process where no edges are formed at all.
Let us use the notation \({\mathbb {N}}_{ti \rho }\) to denote the network at time t (with entrant indexed by t) making offers of incumbent  in round \(\rho \).
in round \(\rho \).
Assumption 7
(Farsightedness) Individuals are farsighted in the sense that the ith incumbent evaluates the offer made by entrant t in round \(\rho \) (\(\rho =1,~2,~3\dots \)) knowing that if any edge has been formed in round \(\rho \), then the other incumbents (if they have not made a link with the entrant yet) can consider creating a link with the entrant and game advances to round \(\rho +1\). After all decisions have been made by the incumbents regarding forming the links with entrant t, then a new entrant appears in time \(t+1\).
Here we note that farsightedness of incumbents in period t is defined to be applicable only within period t’s offers of link formation (\(\rho =1,~2,~3\dots \)) Period t’s incumbents do not think about entrants the future period (\(t+1\), \(t+2\) and so forth). We will first define the concept of equilibrium with farsighted individuals.
Definition 5
The network reaches a pure strategy Nash equilibrium for entrant t when  , i.e., no willing incumbent is left to create a new link after all possible offers and counter-offers.
, i.e., no willing incumbent is left to create a new link after all possible offers and counter-offers.
The main insight is that with farsightedness, individuals would be unwilling to break status quo when there are multiple individuals in the same rank and with the formation of new edges the entrant can be more influential than them. Let the existing centrality of nodes in \(\varGamma _t\) be given by (without loss of generalization) \(V_1\ge V_2\ge \cdots \ge V_n\) such that the individuals can be partitioned into k groups (\(k\le n\)) with ranking \(r_1\ge r_2\ge \cdots \ge r_k\). As an example, consider individuals i and j with identical rank \(k>1\). Also assume that if the entrant can make connections to both of them, then they would be pushed to rank \(k+1\). Then there is no incentive for them to unilaterally deviate to form a link. Say individual i deviates. The formation of a link gives individual i a temporary gain in ranking over j in round \(\rho \), but then the game is extended to round \(\rho +1\) and the individual j forms a connection which is relatively beneficial for j given that i has already deviated. But this pushes both individuals i and j to rank \(k+1\).
Then we have the following result.
Proposition 3
A sufficient condition for the farsighted network growth would be that the ranking of the nodes in the seed graph is weakly preserved in the new graph.
Proof
If the network hierarchy does not change due to the new connections, then players do not have any incentive to halt the growth process. \(\square \)
Figures 2 and 3 provides two examples of growth with farsighted players. A star-shaped networks grows into another star-shaped network which reinforces the hierarchy and a complete network grows into another complete network which preserves the absence of hierarchy (everyone is equally central). Below, we explain these two cases in details.
Example 2
Figure 2 considers a possible growth process for a star network. Panel (a) shows that a new entrant appears and connects with the central node (panel (b)). We will show that this is a stable graph (panel (b)). Say one of the peripheral nodes breaks status quo and makes a connection which temporarily improves its rank. But then all peripheral nodes will make connections, making the entrant more central than all of the peripheral nodes. Thus none of the peripheral nodes connect.
Example 3
In the other extreme, consider a complete graph where all nodes are equally influential. We see that the entrant can connect to all nodes and lead to another complete graph where no individual is losing rank in the hierarchy.
However, the main result we derive with farsighted players is that such a network may not grow at all. The players can simply preserve the existing hierarchy and never accept a new entrant. Below we give two examples of that (Figs. 4, 5).
Example 4
The most interesting case is that this process can lead to a complete stop of the growth process. The entrant can make offers to either the central nodes (there are two of them) or the peripheral nodes (there are four of them). We will show that no connections will be made here. Table 1 provides the eigenvector centralities along with ranks in the hierarchy under different possible scenarios.
Initially, both the core nodes are ranked 1 while all the peripheral nodes are ranked 3. Since there are only two types of nodes in the given seed network on the basis of hierarchy, we only need to consider two cases to exhaust all possible cases of network evolution. The new node would make its first edge with either a core node or a periphery node. Below we analyze both the cases:
-
Core nodes: In the initial configuration, the centralities and the corresponding rank is given in Table 1, column titled Original. If one core node (say, node 1) makes an edge with the new node. This will not change the hierarchy of node 1. But it changes the rank of node 2 from 1 to 2. Thus, node 2 would also form an edge with the new node. This puts back node 2 at the same hierarchy with node 1 i.e. rank 1 (column Core connects in Table 1). The new node is now ranked 2 as it is connected with two core nodes but has no peripheral nodes connected with it, pushing peripheral nodes to rank 4. For peripheral nodes it’s weakly dominating to connect with the new node as it would increase the centrality (but not the rank; see column All nodes connect in Table 1). This would put the new node at rank 1 while pulling the two core nodes down to rank 2. Hence, a farsighted core node takes this into account and will not connect with the new node to begin with.
-
Peripheral nodes: Again we start from the initial configuration with the centralities and the corresponding rank as given in Table 1, column titled Original. Without loss of generalization, suppose periphery node 3 connects with the new node. It can be checked that this will not change the rank of core nodes but all other periphery nodes will have a rank of 4 (nodes 1, 2 and 3 will dominate them). This would lead to the new node forming edges with all of the peripheral nodes (column Periphery connects in Table 1). This pushes all the peripheral nodes down to rank 4, while the new node goes to rank 1. No matter whatever edges are formed with the core nodes after this, the periphery nodes rank would still be 4 which is worse than their original rank 3 (column Original in Table 1). A farsighted periphery node would take this into account and will not form an edge with the new node.
This leads to no edges being formed with the new node in Fig. 4.
Example 5
An extension of the above example shows that in asymmetric networks, growth might occur partially. The network will grow till symmetry is attained and then stops. A detailed explanation is as follows.
In Table 2, we have provided the centralities along with the rankings under alternate scenarios. Note that the initial ranking of nodes: Node 1 has rank 1, node 2 has rank 2, nodes 4 and 5 have rank 3 and node 3 has rank 5 (column Original in Table 2). Since there are four types of nodes in the given seed network on the basis of hierarchy, we need to consider four cases to exhaust all possible cases of network evolution.
-
Node 1: Let’s assume node 1 connects with the new node (column Node 1 connects in Table 2). This would lead to two changes in the hierarchy. Rank of node 1 does not change and rank of node 3 is pushed down to 6 and nodes 4, 5 and 6 have the same centrality. But the fall in rank of node 3 would provide incentive to node 3 to connect to the new node. This leads to a fall in rank of node 4 and 5 as new node becomes more central than them by gaining a new link. This would lead to 4 and 5 connecting with node 6 leading to fall in rank of node 2. As node 2 also now connects with the new node. Thus we arrive at column All nodes connect in Table 2. This leads to loss of rank for node 1. A farsighted node 1 will take this into account and will not form an edge with the new node.
-
Node 2: Suppose node 2 connects with the new node (column Node 2 connects in Table 2). Node 1 stays at rank 1. Rank of node 2 improves to 1. Rank of node 3 improves to 3 while 4 and 5 still have rank 3. Now let us consider the following cases:
-
Suppose node 1 connects with the new node, this would result in fall of rank for nodes 3, 4 and 5. Therefore, they would also connect with the new node to increase their centralities, resulting in column All nodes connect in Table 2. This reduces node 1’s rank. Therefore, a farsighted node 1 will not connect with the new node after node 2 has made a connection with the new node.
-
Nodes 4 or 5 will not form an edge with the new node. If either of them makes a connection, then the other one will also do it. Then node 3 loses rank and therefore it would also make a connection. But then node 1 would lose its rank. In order to increase centrality, then it makes a connection to the new node leading to column All nodes connect in Table 2, where all incumbents are worse off.
-
Suppose node 3 connects with the new node. This would result in node 2 becoming rank 1 and ranks of node 4 and 5 fall to 5. Thus, nodes 1, 4 and 5 would form edges with node 6, resulting in a fall of rank for node 3 to 6 (All nodes connect in Table 2). A farsighted node 3 will take this into account and not form an edge with node 6.
Thus, no edges are formed with the new node after node 2 forms an edge with it. Resulting in panel (b) of Fig. 5.
-
-
Node 3: Suppose node 3 forms an edge with the new node. This would result in two cases:
-
No other node connects with the new node: In that case the new node is only connected with node 3, which results in a rank of new node is 6. While in the previous case when the new node makes its first connection with node 2 it has rank 3 and that is an equilibrium. A farsighted new node would take this into account and form its first edge with node 2.
-
At least one other node connects with the new node (other than node 2, we have shown above that if node 2 connects, then 3 would not connect): In that case, all remaining nodes have incentive to form a link and given that node 2 would form a link, forming no other links would be beneficial. Therefore, node 3 would not connect.
-
-
Nodes 4 and 5 (symmetric): Suppose node 5 connects with the new node. This would lead to fall in rank of node 4 which will result in node 4 connecting with the new node. This step leads to fall in rank of node 3 (initially it has rank 5 in column Original in Table 2), which leads to forming an edge with the new node. Then nodes 1 and 6 become symmetric. Thus to increase centrality 1 will form a link with 6. Then node 2 will increase centrality by connecting with node 6 leading to column All nodes connect in Table 2. A farsighted node 5 will take this into account and will not form an edge with the new node.
This leads to new node only connecting with node 2.
5 Valuation in Network Organizations
In this section, we analyze the model of valuation in a hierarchical organization. To fix ideas, we consider a network \({\mathbb {N}}\) of fixed size n. The observed valuation depends on two components, fundamental valuation and the network effect. In this context, one can call the first term profit alignment and the second term, peer effect. Let us consider the valuation equation for a given network \({\mathbb {N}}\):
In matrix form, it can be rewritten as
where \({\mathbf {I}}\) is a column vector unit all elements equal to 1. Therefore, the valuation can be solved as
Valuation V is also known as Katz centralityFootnote 13 if \(\pi _i=\pi \) for all \(i~\in ~n\) (see, for example [46]). Note that if the individuals have different fundamentals \(\pi _i\), then it is not particularly surprising that the valuations would also differ across individuals. Our basic point is that even with the same fundamentals, there can be spread in valuation and the spread is a function of the difference in the hierarchical positions.
Equation 9 also provides an explanation for the requirement of \(\theta <1\) while defining the relative weight \(\omega =\frac{\theta }{\lambda _\mathrm{max}}\). Note that given the solution to the valuation equation (Eq. 9),we have \(\mathrm{det}(I-\omega \varGamma )=0\). To have \(V<\infty \), we need \(\omega <\frac{1}{\lambda _\mathrm{max}}\). We will also show that the assumption \(\theta <1\) will also allow the network multiplier to be greater than one in magnitude.
Before analyzing the network effects, here we provide a lower bound for the valuation in a network organization. Note that Assumption 4 already provides a bound of zero. However, we can provide tighter and more intuitive bound.
Proposition 4
If the valuation is determined by Eq. 7, then for every individual  , the valuation has a lower bound of \((1-\omega )\pi _i\), i.e.,
, the valuation has a lower bound of \((1-\omega )\pi _i\), i.e.,

Proof
We have to show that the additive second term in Eq. 7 is weakly positive. Suppose not. In that case, there would be at least one \(i\in n\) such that
For this to hold true, there has to be at least one individual \(j\in n\) such that \(V_j<0\). Recall from the Eq. 9 that
According to Proposition 1, the weight \(\omega <\frac{1}{\lambda _\mathrm{max}}\). We can apply Theorem \(I^*\) and \(III^*\) by Debreu and Hernstein [15] to show that \((I-\omega \varGamma )^{-1}\) is well-defined and all elements of the resultant matrix are weakly positive.Footnote 14 Given \(\pi >0\), it follows that
This provides a contradiction to the statement that \(V_j<0\). Hence proved that \(V_i\ge (1-\omega )\pi _i\) for all \(i\in n\). \(\square \)
5.1 Quantifying the Disconnect
Given the above framework, we can find the total observed value \(V=\sum _i V_i\) and the fundamental value \(\Pi =\sum _j \pi _j\) of all individuals \(i\in n\) in a network \({\mathbb {N}}\).
Definition 6
(Network multiplier) The network multiplier is defined as \({\mathcal {M}}=\frac{V}{\Pi }\).
Next, we define spill-over effects that arise due to linkages.
Definition 7
(Spill-over effect) We define the spill-over effect as the indirect impact on valuation of j due to change in fundamental valuation of i: \(s_{ij}=\frac{\delta V_i}{\delta \pi _j}\).
The key message that we are utilizing from Elliott et al. [20] (which in turn builds on Brioschi et al. [12] and Fedenia et al. [22]) is that the book value of an entity can be decomposed into its primitives (what we call fundamentals) and the network effects on the valuation. As Elliott et al. [20] described, the market valuations become a multiplier of the primitives, where the multiplier depends on the structure of the network linkages. Therefore, the book value (what we have termed as observed value) is more that the primitive value (what we have termed as fundamental value). The interpretation of the multiplier is that it quantifies the wedge between total observed value and the total fundamental value. It is an aggregate measure of the wedge between the two sets of valuation.
We note that the disconnect of \(\sum _i V_i\) from \(\sum _j \pi _j\) is captured by the network multiplier \({\mathcal {M}}\). Given a network \(\varGamma \), if \({\mathcal {M}}>1\) then we can infer that the observed value is inflated. From Proposition 4, we can readily infer that \(\sum _i V_i\ge (1-\omega ) \sum _i \pi _i\). However having the multiplier \({\mathcal {M}}>1\) is a stronger result. Below, we provide proofs that \({\mathcal {M}}>1\) for three basic types of networks.
5.1.1 Complete Graph
Consider a complete graph \(\varGamma \) of n nodes. The valuation equation is given by

The network multiplier is given by (see “Appendix 8.4” for complete calculation)
5.1.2 Star Graph
Consider a star graph with \(n-1\) peripheral nodes. The valuation equation is given by

The network multiplier is given by (see “Appendix 8.4” for complete calculation)
5.1.3 Linear Graph
Consider a linear graph with n nodes. The valuation equation is given by

The network multiplier is given by (see “Appendix 8.4” for complete calculation; for a closed form solution, we assume \(n\rightarrow \infty \))
6 Application: Hierarchy in the Indian Board Network
In this section, we present an empirical application of the model and its consequences. We have gathered data on the Indian board interlock for the year 2016. The company-director network is a bipartite network between companies and its board of directors. Each of the companies has a board of directors. A pair of companies can have a director interlock if they share one director, i.e., one director serves both the companies. Similarly, a pair of directors are connected if they sit on the board of the same company. The directors’ network is an unweighted and undirected network, making it appropriate for our analysis.
Figure 6 shows part of the the giant componentFootnote 15 of the directors’ network in India in 2016. There were total around 9000 directors. We extract the giant component for our analysis, which has 6453 directors. Panel (a) shows a small part (142 directors) of the giant component for visualization purpose. Panel (b) shows a larger connected component (subset of the full giant component) with 1544 directors. We have not shown the full giant component as the nodes becomes visually inseparable.
Figure 7 (Panel (a)) shows the imputed valuation V by applying Eq. 7 with \(\pi _i=1\) and \(\theta =0.99\) (\(\varGamma \) is matched to the actual interlocking network). Clearly, there is a large number of directors who are very close to each other in the hierarchy whereas there are a few who are significantly more important than the rest (indicated by the spikes). We conduct the following counterfactual experiments to explain the mechanism.
Effects of Business Cycles The first experiment is that all individuals have a boost in their corresponding fundamentals \(\pi _i\) by the same multiplier \(f>1\). As the solution to the valuation equation shows (Eq. 9), valuation of all individuals would be exactly multiplied by f.
Spill-Over Effects We have already defined spillover effect of the ith individual’s fundamentals on the jth individual’s valuation, \(s_{ij}=\frac{\delta V_j}{\delta \pi _i}\). Here we consider a summary measure of aggregate spill-over effect of the individual i as \(s_{i}=\sum _j s_{ij}\). The aggregate response is measured as \({\tilde{s}}_i=\left( \frac{\sum _j V_{j,\mathrm{spillover}}-\sum _j V_{j}}{N}\right) \) which approximates \(s_i\), across all directors. Numerically, we see that \({\tilde{s}}_i/{\tilde{s}}_j\) for all pairs (i, j) very closely mimics the ratio \(V_i/V_j\) of the corresponding pair.
Network Multiplier We compute the network multiplier (following Eq. 9) over three sets of data for a given \(\theta \).Footnote 16 We consider connected subgraphs of the giant component of the director network (first two are shown in Fig. 6, panels (a) and (b)). With 142 nodes (Fig. 6, panel (a)), the network multiplier is 6.35. With 1544 nodes (Fig. 6, panel (a)), the network multiplier is 2.65. For the giant component (6453 nodes; not shown in this paper), the network multiplier \(\approx \) 1.89. The results clearly show that the network multiplier decays as the size of the network grows. This is reconcilable with Theorem 1 which states that as the network grows in size, the network effect diminishes.
Finally, we also show that high degree centrality is not a necessary condition for superstar effect. Figure 7 (Panel (b)) shows that the directors with the highest valuation do not necessarily have high degree. This simple observation demonstrates that the number of connections may not matter much, what matters is the identity of the neighbors. On a related note, the correlation coefficient between the valuation \(V_i\) implied by Eq. 9 and the number of board directorships held, is 0.25 (based on the giant component of the Indian corporate network in 2016). Such a low value of the estimate shows that number of connections is not a very robust indicator of true influences of the nodes in a network.
7 Summary and Conclusion
In this paper, we present a model of strategic growth in an interconnected society. The network of individuals creates a hierarchy based on observed valuation where new entrants want to maximize their own position in the hierarchy by strategically linking with incumbents with higher values. In our model, individuals’ utility is dependent on hierarchy and going higher in the hierarchy gives more utility. Individuals being strategic, respond to incentive of letting newcomers in only when it is in their incentive to do so, i.e., only when their own ranking will improve. We show that the hierarchy induces a disconnect between observed valuation of individuals and their corresponding fundamentals. Thus along with the mechanism to capture the dispersion in hierarchy, the network growth process provides a detailed characterization of the static as well as the dynamic nature of the network effects. In this context, it is useful to note that there has been empirical research on how status differential across a hierarchy might influence creation of negative ties [42]. It would be interesting to generalize the hierarchy game presented in this paper further to incorporate such features.
We use a linear interaction model with strategic individuals and use its property that eigenvector centrality provides a very useful way to model hierarchy in the linear model as it mathematically relates to the architecture of the network. Based on existing results in the spectral graph theory, we have comprehensively characterized the network growth process as an outcome of a game between entrants and incumbents, based on the observed valuation. Through the valuation mechanism, we quantify the disconnect between the observed valuation and the fundamentals as a function of the network architecture.
Our model provides important insights into organizational dynamics. With myopic individuals, network grows very fast and the hierarchies are quite unstable. On the other hand, results are exactly the opposite with farsighted individuals. The hierarchy is maintained and the network growth process can be halted depending on the topological characteristics of the pre-existing network. This has important consequences for the associated network effects. We focus on two phenomena. One, the divergence between observed valuation and fundamentals. Two, the spill-over effects from one node to its neighbors, both directly and indirectly. Both of them quantitatively depend on the architecture of the network.
We illustrate the framework with an application to a large-scale network-based organizational structure, namely the Indian board interlocking network. This is a bipartite network between two sets of entities: companies and directors. We take a one-dimensional projection of the network to create a interlocking network of directors where an edge between two directors indicate that they sit on common boards of at least one company. This kind of social networks undergoes a strategic growth process and a large literature indicates that such interlocks do have substantial economic and financial consequences across companies. By applying our model, we find out the full hierarchy in the interlocking network and identify which directors hold the key positions. Then we conduct a series of numerical experiments to analyze the effects of shocks (common as well as idiosyncratic) to their fundamentals on the valuation of the network.
We note that there is a defining feature of our model and its conclusions. The whole mechanism depends on the idea that players make attempts to enter in a hierarchy by making connections based on perceived influence of the incumbents. In real-world interactions, it is difficult to keep track of individual meetings and interactions to justify the mechanism. However, there are business card companies with machine-readable business cards that keep track of business card exchanges.Footnote 17 A future direction of this work would be to extend and validate (or modify) our theory based on empirical data on such pairwise meetings.
Finally, the valuation framework has significant policy implications. As the model embeds network growth process in the valuation mechanism, we can analyze the static as well as the dynamic responses of rupture or growth in the network. We can comprehensively characterize direct as well as indirect spill-over effects. This is important for evaluating effect of organizational structure on economic and financial variables, and vice versa.
Notes
Autor et al. [3] for example, shows that the unanticipated elimination of rent controls in Cambridge, MA in 1995, led to a sharp price appreciation in the decontrolled housing units. Interestingly, the effect also spilled over to never-controlled units as well, which were in geographic proximity. In fact, the authors had shown that a larger portion of the total property valuation appreciation comes from the indirect effect on the never-controlled units and the appreciation was far more than can be explained by the observed increase in residential investment.
A simple example is that presidents are chosen from pools of vice presidents in corporate board rooms. In such cases, compensation increases by a significant margin overnight, but productivity does not. There is a large literature on efficiency of the relevant compensation schemes, starting with a very influential paper by Lazear and Rosen [32].
In Sect. 2 we will provide a formal definition of centrality. Here, we can imagine centrality to represent the degree of influence of nodes in the network.
In this paper, we utilize the term Katz–Bonacich centrality to denote the same, following the textbook definition given in Newman [38].
There is a vast literature on the statistical analysis of such large-scale social network (see for example an analysis of the US and Italian firms by Battiston and Catanzaro [7], exclusively Italian firms by Bargigli and Giannetti [6], German firms by Raddant et al. [40]) and their interplay with financial decision-making (see, for example,, [43]).
We do not pursue the link with market equilibrium here. Ghiglino and Goyal [23] for example provides a link between centrality and equilibrium prices and consumption in an exchange economy. Interested readers can refer to Goyal [24] for a review on the network description various economic (both micro and macro) and financial phenomena.
Therefore, this network is unweighted. A connection either exists or not. Also, there is no self-loop, i.e., \(\gamma _{iit}=0\) for all
 and t. Finally, one can have an alternative representation of the edges in terms of pairs of nodes it connects. However, here we will explicitly utilize the description through adjacency matrix as that will help us to economize on notations.
and t. Finally, one can have an alternative representation of the edges in terms of pairs of nodes it connects. However, here we will explicitly utilize the description through adjacency matrix as that will help us to economize on notations.We will denote the cardinality of set
 by \(n_t\).
by \(n_t\).In “Appendix 8.1” we provide a standard game with linear quadratic payoff functions that give rise to such interdependent valuation [5, 31]. This framework constitutes the stage game and we use it to motivate the intra-period actions where given the network structure, players optimize their action profiles. The main influential result from Ballester et al. [5] is that given a network structure, the action profile in the Nash equilibrium in a linear quadratic setup is the same as the Katz–Bonacich centrality. Our focus in the main text of the paper is on the inter-period game where the players decide on their connectivities, which leads to network formation.
If no one in \({\mathbb {N}}_{t}\) accepts the offers, then no connections are made and the potential entrant cannot enter.
We note from Proposition 2 that asymptotically the observed valuation and eigenvector centrality give rise to the same hierarchy.
We discuss in Sect. 4 what kind of connections can be formed in equilibrium. As we will see, not all possible connections will materialize if the players are farsighted.
The weight parameter \(\omega \) works as attenuation factor in case of Katz centrality.
The giant component refers to the largest connected component in the network.
We have assumed \(\theta =0.99\) for numerical calculations; the estimates will change for different values of the parameter. The goal of the exercise is to show how the network multiplier changes as the size of the network changes for a given \(\theta \).
In a personal communication with social networks researchers from a Japanese business card company, we came to know that indeed there is a large number of meetings with two participants with extreme differences in eigenvector centrality. However, the data is not available in the public domain.
Elliott et al. [20] have used a static variant of the linear valuation equations to describe firm to firm connections via cross-holding in assets.
References
Acemoglu D, Carvalho V, Ozdaglar A, Tahbaz-Salehi A (2012) The network origin of economic fluctuations. Econometrica 80:1977–2016
Acharya S, Pedraza A (2015) Asset price effects of peer benchmarking: evidence from a natural experiment. Federal Reserve Bank of New York Staff Reports, No. 727
Autor DH, Palmer CJ, Pathak PA (2014) Housing market spillovers: evidence from the end of rent control in Cambridge, Massachusetts. J Polit Econ 122(3):661–717
Bala V, Goyal S (2000) A noncooperative model of network formation. Econometrica 68(5):1181–1229
Ballester C, Calvo-Armengol A, Zenou Y (2006) Who’s who in networks. Wanted: the key player. Econometrica 74:1403–1417
Bargigli L, Giannetti R (2017) The Italian corporate system in a network perspective (1952–1983). Physica A 494:367–379
Battiston S, Catanzaro M (2004) Statistical properties of corporate board and director networks. Eur Phys J B 38(2):345–352
Benzi M, Klymko C (2015) On the limiting behavior of parameter-dependent network centrality measures. arXiv preprint arXiv:1312.6722
Bloch F, Jackson M (2006) Definitions of equilibrium in network formation games. Int J Game Theory 34(3):305–318
Bloch F, Jackson M, Tebaldi P (2017) Centrality measures in networks. Working paper
Borgatti SP, Foster PC (2003) The network paradigm in organizational research: a review and typology. J Manag 29(6):991–1013
Brioschi F, Buzzacchi L, Colombo MG (1989) Risk capital financing and the separation of ownership and control in business groups. J Bank Finance 13:747–772
Calvo-Armengol A, Jackson MO (2004) The effects of social networks on employment and inequality. Am Econ Rev 94(3):426–454
Colla P, Mele A (2009) Information linkages and correlated trading. Rev Financ Stud 23(1):203–246
Debreu G, Hernstein IN (1953) Nonnegative square matrices. Econometrica 21(4):597–607
DeMarzo P, Kaniel R (2016) Relative pay for non-relative performance: keeping up with the Joneses with optimal contracts. Working paper
Dequiedt V, Zenou Y (2017) Local and consistent centrality measures in parameterized networks. Math Soc Sci 88:28–36
Dutta B, Ghosal S, Ray D (2005) Farsighted network formation. J Econ Theory 122:143–164
Dutta B, Jackson M (2003) On the formation of networks and groups. In: Dutta B, Jackson MO (eds) Networks and groups: models of strategic formation. Springer, Heidelberg
Elliott M, Golub B, Jackson M (2014) Financial networks and contagion. Am Econ Rev 104(10):3115–3153
Faulkender M, Yang J (2010) Inside the black box: the role and competition of compensation peer groups. J Financ Econ 96:257–270
Fedenia M, Hodder JE, Triantis AJ (1994) Cross-holdings: estimation issues, biases, and distortions. Rev Financ Studi 7:61–96
Ghiglino C, Goyal S (2010) Keeping up with the neighbors: social interaction in a market economy. J Eur Econ Assoc 8(1):90–119
Goyal S (2017) Networks and markets. In: Honore B, Pakes A, Piazzesi M, Samuelson L (eds) Advances in economics: eleventh world Congress of the econometric society. CUP
Goyal S, Joshi S (2003) Networks of collaboration in oligopoly. Games Econ Behav 43:57–85
Hallock KF (1999) Dual agency: corporate boards with reciprocally interlocking relationships. In: Yermack D (ed) Executive compensation and shareholder value, vol 4. Springer, Berlin, pp 55–75
Herings PJ, Mauleon A, Vannetelbosch V (2009) Farsightedly stable networks. Games Econ Behav 67(2):526–541
Hochberg Y, Ljungqvist A, Lu Y (2007) Whom you know matters: venture capital networks and investment performance. J Finance 62(1):251–301
Horton J, Millo Y, Serafeim G (2012) Resources or power? Implications of social networks on compensation and firm performance. J Bus Finance Acc 39(3–4):399–426
Jackson M (2005) A survey of models of network formation: stability and efficiency. In: Demange G, Wooders M (eds) Chapter 1 in Group formation in economics; networks, clubs and coalitions. Cambridge University Press, Cambridge
König MD, Tessone CJ, Zenou Y (2014) Nestedness in networks: a theoretical model and some applications. Theor Econ 9(3):695–752
Lazear EP, Rosen S (1981) Rank-order tournaments as optimum labor contracts. J Polit Economy 89(5):841–864
Liu Q, Sun B (2016) Relative wealth concerns, executive compensation, and systemic risk-taking. International Finance Discussion Papers (1164)
Lovasz L (2007) Eigenvalues of graphs. http://web.cs.elte.hu/~lovasz/eigenvals-x.pdf. Accessed 10 Jan 2017
Mauleon A, Vannetelbosch V (2016) Network formation games. In: Galeotti A, Bramoullé Y, Rogers B (eds) The Oxford handbook of the economics of networks. Oxford University Press, Oxford
Mele A (2017) A structural model of dense network formation. Econometrica 85(3):825–850
Neligh N (2020) Vying for dominance: an experiment in dynamic network formation. J Econ Behav Organ 178:719–739
Newman MEJ (2010) Networks: an introduction. Oxford University Press, Oxford
Pin P, Rogers B (2016) Stochastic network formation and homophily. In: Galeotti A, Bramoullé Y, Rogers B (eds) The Oxford handbook of the economics of networks. Oxford University Press, Oxford
Raddant M, Milakovic M, Berg L (2017) Persistence in corporate networks. J Econ Interact Coord 12(2):249–276
Roy S, Saberi A, Wan Y (2008) Majorizations for the dominant eigenvector of a nonnegative matrix. In: American control conference. https://doi.org/10.1109/ACC.2008.4586780
Rubineau B, Lim Y, Neblo M (2019) Low status rejection: how status hierarchies influence negative tie formation. Soc Netw 56:33–44
Shropshire C (2010) The role of the interlocking director and board receptivity in the diffusion of practices. Acad Manag J 35(2):246–264
Spielman D (2012) The adjacency matrix and the nth eigenvalue. Spectral Graph Theory. http://www.cs.cmu.edu/~15859n/RelatedWork/Spielman-SpectralClass/lect03-12.pdf. Accessed 10 Jan 2017
Stevens JB (2018) The economics of collective choice. Routledge, London
Zafarani R, Abbasi M, Liu H (2014) Social media mining: an introduction. Cambridge University Press, Cambridge
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We are grateful to seminar and conference participants at IIM Ahmedabad, JNU New Delhi, IIM Udaipur, University of Kiel, WEHIA’18 and Centre for Studies in Social Sciences, Kolkata for a number of useful feedback. We are also grateful to a reviewer for helping us to significantly improve the manuscript. We thank Mayank Aggarwal for helping us with the data that was used for empirical purpose. This research was partially supported by Institute Grant, IIM Ahmedabad. All remaining errors are ours.
Appendix
Appendix
1.1 Intra-period Setup: Linear-Quadratic Payoff Functions
To model the stage game or the intra-period game, we posit a standard linear-quadratic game. The ith individual has a fundamental valuation \(\pi _i\) and they have strategic complementarities. The utility function is given by [5, 31]

where  is the action profile of the agents. Solving the problem in equilibrium (maximizing with respect to \(V_{it}\)) given the connections \(\{\gamma _{ijt}\}\), we get a linear network modelFootnote 18 of observed valuation V:
is the action profile of the agents. Solving the problem in equilibrium (maximizing with respect to \(V_{it}\)) given the connections \(\{\gamma _{ijt}\}\), we get a linear network modelFootnote 18 of observed valuation V:

where \(\omega \) denotes the network coefficient and  is the set of entities at time t. Following Ballester et al. [5], we can substitute the first order conditions back in the utility functions to show that at the equilibrium,
is the set of entities at time t. Following Ballester et al. [5], we can substitute the first order conditions back in the utility functions to show that at the equilibrium,
Therefore, in equilibrium utility is monotonically increasing in the action profile. This is a very useful result for us because given this result, the hierarchy defined over the equilibrium action profile \(V^*\) is the same as the one defined over utility \(U^*\) in equilibrium.
1.2 Proof of Proposition 1
Proof
Consider a static network \({\mathbb {N}}\). From the spectral theory of graphs, we know that (see, e.g., [34])
where \(\lambda _\mathrm{max}\) is the dominant eigenvalue, E(d) is the average degree and \(d_\mathrm{max}\) is the maximum degree. Note that for a connected network, \(E(d) \ge 1\). Assuming \(\theta \) is the constant of proportionality and \(\theta \in (0,1)\), we get
Thus for a generic network \({\mathbb {N}}\), \(\omega \in [0,1]\) and its value depends on the adjacency matrix \(\varGamma \) of \({\mathbb {N}}\). Therefore, it satisfies Assumption 1.
Next, we show that this choice of \(\omega \) also satisfies Assumption 2. We have to analyze how \(\omega \) changes as the network size increases. We use a result from spectral graph theory [44]. \(\square \)
Theorem 4
Let A be a symmetric matrix with largest eigenvalue \(A_{\lambda _\mathrm{max}}\). Let B be the matrix obtained by removing the last row and column from A, and let \(B_{\lambda _\mathrm{max}}\) be the largest eigenvalue of B. Then,
Therefore by increasing size of the graph with symmetric connections, \(\lambda _\mathrm{max}\) monotonically (weakly) increases. This implies \(\omega \) decreases as n increases. Therefore, it satisfies Assumption 2 as well. \(\square \)
1.3 Proofs of Sect. 3.1
1.3.1 Proof of Theorem 2
Proof
The adjacency matrix for a graph of n nodes be \(\varGamma _{0}~= ~[\gamma _{ij}]_{i,j\in n}\). Let us assume that a new node m comes up and offers an edge to the top node in hierarchy. Let us denote that node by node 1. The entrant has no outside option and hence, formation of an edge is always rank-improving. Interestingly, we will show that node 1 always accepts that edge as it can never decrease node 1’s rank. Note that the new adjacency matrix is
Therefore, the new eigenvector centrality \(V'\) solves the equation
where \(V'=[V'_1,~V_2',\ldots ,~V'_n,~V'_m]^\mathrm{Tr}\) is a column vector. Therefore, Eq. 26 gives us \(V^{'}_{1}=\lambda ^{'}_\mathrm{max}V^{'}_{m}\). Note that
for a graph which has average degree more than 1 [34]; we have also used the same argument in Proposition 1). Therefore, we conclude
i.e., node 1 does not lose its rank with respect to the new entrant m. Node 1 cannot lose its rank with respect to any of the other incumbents by having a new connection. Therefore, node 1 will connect to node m. \(\square \)
1.3.2 Proof of Theorem 3
Proof
We know from Theorem 2 that node 1 accepts the incoming individual m. We have to show that after forming that connection, m would like to connect to 2 and 2 would also like to connect to him. By induction, everyone forms connections with the new individual m. Intuitively, Ballester et al. [5] showed that V is increasing in the number of links. Thus all individuals have incentives to accept offers to form links. But we have to also show that their ranks are not negatively impacted by the link formation mechanism.
First, we prove that forming a connection between a pair of nodes cannot reduce ranks of that pair of nodes. We note that by forming an edge between any generic pair \(\{i,j\}\), the edge weights \(\gamma _{ij}\) and \(\gamma _{ji}\) increases from 0 to 1. Now we appeal to the Theorem 1 in Roy et al. [41] (in particular, see corollary 1) which shows that by adding a row vector \(\{a_{i}\}_{i\in n}\) (where \(a(i)>0\) and \(a(j)=0\) for \(j\in n{\setminus } i\)) to an \(n\times n\) real irreducible nonnegative matrix \(\varGamma \), the element \(v_i\) of the dominant eigenvector strictly increases in ratio with respect to the rest of the elements \(\{v_j\}_{j\in n{\setminus } i}\). Note that forming an edge between the pair \(\{i,j\}\) in a symmetric matrix leads to \(\varGamma _{ij}\) and \(\varGamma _{ji}\) to be converted into 1 from 0. This operation can be interpreted as adding a row vector of zeros with 1 in the jth entry (0, 0, 0, \(\dots \), 1 ,\(\ldots \), 0) to the ith row of matrix \(\varGamma \) and adding a row vector of zeros with 1 in the ith entry (\(0, 0, 0, \dots , 1, \ldots , 0\)) to the jth row of matrix \(\varGamma \). Formally, the first row is \(\{a_{j}\}_{j\in n}\) (where \(a(j)>0\) and \(a(k)=0\) for \(k\in n{\setminus }k\)) and \(\{a_{i}\}_{i\in n}\) (where \(a(i)>0\) and \(a(k)=0\) for \(k\in n{\setminus }i\)). Thus by applying Theorem 1 in Roy et al. [41], both the nodes \(\{i,j\}\) are better off in terms of centrality with respect to all other nodes k such that \(k\in n{\setminus }{\{i,j\}}\). Therefore, forming a connection between nodes i and j will not reduce rank for i and j with respect to the rest of the nodes \(n{\setminus }\{i,j\}\).
This step leaves out one scenario where node i connects to a lesser central node j (for a generic pair of nodes i and j) and the relative ranking between i and j is not preserved. We incorporate it as a condition and as stated in the theorem, if such a case appears, then the link would not be formed as node i would not form a link where it loses rank. However, in numerical experimentations we could not find a case where that happens and in all cases, ranking is preserved after formation of the link.
Next, we have to show that the new entrant (after connecting to all incumbents), would now weakly dominate all the pre-existing incumbents. In order to do that we first write down the eigenvector centrality of the entrant m as

Since the entrant m forms a connection with all incumbents  , \(\gamma _{im}=1\) for all
, \(\gamma _{im}=1\) for all  . For any incumbent
. For any incumbent  , the valuation would be
, the valuation would be

where the neighborhood of the jth node  (since some links may be non-existent). Therefore, \(V_m\ge V_j\) for all
(since some links may be non-existent). Therefore, \(V_m\ge V_j\) for all  .
.
This completes the proof. \(\square \)
1.4 Proofs of Sect. 5.1
1.4.1 Complete Graph
Here we compute the network multiplier for a complete graph \({\mathbb {N}}\) of n nodes. The valuation equation is given by

Therefore the total valuation is
Solving for the total valuation, we get
Therefore, the network multiplier is given by
1.4.2 Star Graph
We compute the network multiplier for a star graph with \(n-1\) peripheral nodes. The valuation equation is given by

If node 1 is at the center, then (for \(i \ne 1\))
Combining the above two equations, we get
Therefore, the total valuation is given by
Note that for a star graph, \(\lambda _\mathrm{max}=\sqrt{n-1}\). Hence, the network multiplier is given by
1.4.3 Linear Graph
We compute the network multiplier for a linear graph with n nodes. The valuation equation is given by

To simplify the calculation, we solve the model in the limit. If \(n~\rightarrow ~\infty \),
Summing over all i and using symmetry across all nodes, we get the total valuation as
Hence, the network multiplier is given by
1.5 Ranking Scheme Matters for Network Growth
Here we show the usefulness of the ranking scheme we assumed. To give an example, if we have three nodes with centralities 0.4, 0.4 and 0.2, then our ranking scheme would assign ranks 1, 1, 3 to the three nodes. One can possibly imagine a closely related ranking scheme that will assign 1, 1, 2. The difference between our preferred ranking scheme and the alternate one is that our ranking scheme is not purely ordinal, how many players are more influential than a given player matters for the rank of that given player. Below we show that the two ranking schemes can lead to very different types of network growth. In Table 3, we consider a linear network of three nodes (numbered as 2, 1, 3 from left to right for a horizontal linear network of 3 nodes) and the 4th node is the entrant. In Table 4, we consider a linear network of three nodes (numbered as 4, 2, 1, 3, 5 from left to right for a horizontal linear network of 5 nodes) and the 6th node is the entrant. The key take away is that the growth processes would be quite different under two schemes. See the captions for a complete description of the resulting growth process.
Rights and permissions
About this article
Cite this article
Chakrabarti, A.S., Moorjani, S. Strategic Connections in a Hierarchical Society: Wedge Between Observed and Fundamental Valuations. Dyn Games Appl 11, 433–462 (2021). https://doi.org/10.1007/s13235-020-00374-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13235-020-00374-9


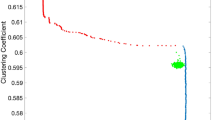
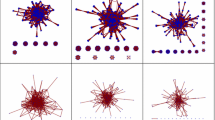







 and t. Finally, one can have an alternative representation of the edges in terms of pairs of nodes it connects. However, here we will explicitly utilize the description through adjacency matrix as that will help us to economize on notations.
and t. Finally, one can have an alternative representation of the edges in terms of pairs of nodes it connects. However, here we will explicitly utilize the description through adjacency matrix as that will help us to economize on notations.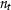 by
by