1 Introduction

Evolutionary game theory is the suitable mathematical framework whenever there is frequency-dependent selection—the fitness of an individual does not only depend on its strategy, but also on the composition of the population in relation with (multiple) other strategies [17, 27, 28]. The payoff from the games is interpreted as individual fitness, naturally leading to a dynamical approach. As in classical game theory with the Nash equilibrium [25, 26], the analysis of properties of equilibrium points in evolutionary game theory has been of special interest [5, 10, 27]. Herein, equilibrium points of a dynamical system predict the composition of strategy frequencies, where all the strategies have the same average fitness. Biologically, these points can predict a coexistence of different types in a population and the maintenance of polymorphism.

Recently, some attention has been paid to both numerical and analytical studies of equilibrium points and their stability in random evolutionary games [10, 18]. The focus was on analyzing the probability of observing a certain number of equilibria (whether counting all equilibria or only the stable ones) if the payoff entries are randomly drawn. This probability allows one to predict the complexity of the interactions as the number of strategies and the number of players in the game increase, especially when the environments are unknown or changing rapidly over time [8, 9]. Furthermore, these studies have paid substantial attention to the maximal number of equilibrium points and the attainability of the patterns of evolutionarily stable strategies, as knowing them is insightful, and historically, they have been studied extensively, not only in classical and evolutionary game theory, but also in other fields such as population genetics [2–6, 10, 12, 18–20, 27, 37–39]. However, as the studies deal with the concrete numbers of equilibrium points, they need to take a direct approach that consists of solving a system of polynomial equations, the degree of which increases with the number of players in a game. As such, the mathematical analysis was mostly restricted to evolutionary games with a small number of players, due to the impossibility of solving general polynomial equations of a high degree [1, 18].

In this paper, we ask instead the question: what is the mean or expected number of equilibria that one can observe if the payoff matrix entries of the game are randomly drawn? Knowing the mean number of equilibria not only gives important insights into the overall complexity of the interactions as the number of participating players in the game and the potential strategies that the players can adopt are magnified. It also enables us to predict the boundaries of the concrete numbers of (stable) equilibrium points such as the maximal one as we show later on in the paper. By connecting to the theory of random polynomials [7], we first provide an exact, computationally implementable formula for the expected number of equilibria in a general multi-player multi-strategy random game when the payoff entries are normally distributed. Secondly, we derive lower and upper bounds of such a formula for the case of two-player games and provide an explicit formula for the case of two-strategy games. As a consequence, we can derive similar bounds when considering only equilibrium points that are stable. Finally, numerical results are provided and discussed when there are more players and strategies.

The rest of the paper is structured as follows. In Sect. 2, we introduce the models and methods: The replicator equations in evolution game theory and the random polynomial theory are summarized in Sects. 2.1 and 2.2, respectively. The link between them, which is a major aspect of our method, is described in Sect. 2.3. The main results of this paper are presented in Sect. 3, starting with two-strategy games in Sect. 3.1, then with two-player games in Sect. 3.2, and lastly, with the general case of games with arbitrary numbers of players and strategies in Sect. 3.3. We compare our results with related ones in the literature and discuss some future directions in Sect. 4. Finally, some detailed computations are given in the “Appendix.”

2 Models and Methods

2.1 Evolutionary Game Theory and Replicator Dynamics

The classical approach to evolutionary games is replicator dynamics [17, 28, 32, 35, 41], describing that whenever a strategy has a fitness larger than the average fitness of the population, it is expected to spread. Formally, let us consider an infinitely large population with \(n\) strategies, numerated from 1 to \(n\). They have frequencies \(x_i\), \(1 \le i \le n\), respectively, satisfying that \(0 \le x_i \le 1\) and \(\sum _{i = 1}^{n} x_i = 1\). The interaction of the individuals in the population is in randomly selected groups of \(d\) participants, that is, they play and obtain their fitness from \(d\)-player games. We consider here symmetric games (e.g., the public goods games and their generalizations [13–15, 30, 33]) in which the order of the participants is irrelevant. Let \(\alpha ^{i_0}_{i_1,\ldots ,i_{d-1}}\) be the payoff of the focal player, where \(i_0\) (\(1 \le i_0 \le n\)) is the strategy of the focal player, and let \(i_k\) (with \(1 \le i_k \le n\) and \(1 \le k \le d-1\)) be the strategy of the player in position \(k\). These payoffs form a \((d-1)\)-dimensional payoff matrix [10], which satisfies (because of the game symmetry)

$$\begin{aligned} \alpha ^{i_0}_{i_1,\ldots ,i_{d-1}} = \alpha ^{i_0}_{i_1',\ldots ,i_{d-1}'}, \end{aligned}$$
(1)

whenever \(\{i_1'\ldots ,i_{d-1}'\}\) is a permutation of \(\{i_1\ldots ,i_{d-1}\}\). This means that only the fraction of each strategy in the game matters.

The average payoff or fitness of the focal player is given by

$$\begin{aligned} \pi _{i_0} = \sum \limits _{i_1,\ldots ,i_{d-1}=1}^{n}\alpha ^{i_0}_{i_1,\ldots ,i_{d-1}} \prod \limits _{k=1}^{d-1}x_{i_k}. \end{aligned}$$
(2)

By abuse of notation, let us denote \(\alpha ^{i_0}_{k_{1}, ..., k_{n} } := \alpha ^{i_0}_{i_1,\ldots ,i_{d-1}}\), where \(k_i\), \(1 \le i \le n\), with \(\sum ^{n}_{i = 1}k_i = d-1\), is the number of players using strategy \(i\) in \(\{i_1,\ldots ,i_{d-1}\}\). Hence, from Eq.  (1), the fitness of strategy \(i_0\) can be rewritten as follows

$$\begin{aligned} \pi _{i_0} = \sum \limits _{\begin{array}{c} 0\le k_{1}, ..., k_{n}\le d-1,\\ \sum \nolimits ^{n}_{i = 1}k_i = d-1 \end{array}}\alpha ^{i_0}_{k_{1}, ..., k_{n} }\begin{pmatrix} d-1\\ k_{1}, ..., k_n \end{pmatrix} \prod \limits _{i=1}^{n}x_{i}^{k_i} \quad \text { for } i_0 = 1, \dots , n, \end{aligned}$$
(3)

where \(\begin{pmatrix} d-1\\ k_{1}, \dots , k_{n} \end{pmatrix} = \frac{(d-1)!}{\prod \nolimits _{k=1}^n k_i! }\) are the multinomial coefficients.

Now the replicator equations for games with \(n\) strategies can be written as follows [17, 31]

$$\begin{aligned} \dot{x_i} = x_i \left( \pi _i - \langle \pi \rangle \right) \quad \quad \text { for } i = 1,\dots ,n-1, \end{aligned}$$
(4)

where \(\langle \pi \rangle = \sum ^n_{k = 1} x_k \, \pi _k\) is the average payoff of the population. The equilibrium points of the system are given by the points \((x_1, \dots , x_n)\), satisfying the condition that the fitness of all strategies are the same. That is, they are represented by solutions of the system of equations

$$\begin{aligned} \pi _i = \pi _n \quad \text{ for } \text{ all } 1 \le i \le n-1. \end{aligned}$$
(5)

Subtracting from each of the equations the term \(\pi _n\), we obtain a system of \(n-1\) polynomials of degree \(d-1\)

$$\begin{aligned} \sum _{\begin{array}{c} 0\le k_{1}, ..., k_{n}\le d-1,\\ \sum \nolimits ^{n}_{i = 1}k_i = d-1 \end{array}}\beta ^i_{k_{1}, ...,k_{n-1} }\begin{pmatrix} d-1\\ k_{1}, ..., k_n \end{pmatrix} \prod _{i=1}^{n}x_{i}^{k_i} = 0\quad \text { for } i = 1, \dots , n-1, \end{aligned}$$
(6)

where \(\beta ^{i}_{k_{1}, ..., k_{n-1} } := \alpha ^{i}_{k_{1}, ..., k_{n} } -\alpha ^{n}_{k_{1}, ..., k_{n} } \). Assuming that all the payoff entries have the same probability distribution, then all \(\beta ^{i}_{k_{1}, ..., k_{n-1} }\), \(i = 1, \dots , n-1\), have symmetric distributions, i.e., with mean 0 (see also the proof in [18]).

In the following analysis, we focus on internal equilibrium points [10, 18], i.e., \(0 < x_i < 1\) for all \(1 \le i \le n-1\). Hence, by using the transformation \(y_i = \frac{x_i}{x_n}\), with \(0< y_i < +\infty \) and \(1 \le i \le n-1\), dividing the left hand side of the above equation by \(x_n^{d-1}\), we obtain the following equation in terms of \((y_1,\ldots ,y_{n-1})\) that is equivalent to (6)

$$\begin{aligned} \sum \limits _{\begin{array}{c} 0\le k_{1}, ..., k_{n-1}\le d-1,\\ \sum \nolimits ^{n-1}_{i = 1}k_i \le d-1 \end{array}}\beta ^i_{k_{1}, ..., k_{n-1} }\begin{pmatrix} d-1\\ k_{1}, ..., k_{n} \end{pmatrix} \prod \limits _{i=1}^{n-1}y_{i}^{k_i} = 0\quad \quad \text { for } i = 1, \dots , n-1. \end{aligned}$$
(7)

As stated, one of the main goals of this article was to compute the expected number of (internal) equilibria in a general \(n\)-strategy \(d\)-player random evolutionary game. That consists in computing the expected number of solutions \((y_1, \dots , y_{n-1}) \in {{{\mathbb {R}}}_+}^{n-1}\) of the system of \((n-1)\) polynomials of degree \((d-1)\) in (7). Furthermore, herein our analysis focuses on payoff matrices with normally distributed entries. It is known that, even for \(n=2\), it is impossible to analytically solve the system whenever \(d > 5\) [1], as seen in [18]. Hence, it is not feasible to use this direct approach of analytically solving the system if one wants to deal with games with a large number of players and with multiple strategies. In this work, we address this issue by connecting to the theory of random polynomials described in the following section.

2.2 Random Polynomial Theory

Keeping the form of Eq. (7) in mind, we consider a system of \(n-1\) random polynomials of degree \(d-1\),

$$\begin{aligned} \sum \limits _{\begin{array}{c} 0\le k_{1}, ..., k_{n-1}\le d-1,\\ \sum ^{n-1}_{i = 1}k_i \le d-1 \end{array}}a^i_{k_{1}, ..., k_{n-1} }\prod \limits _{i=1}^{n-1}y_{i}^{k_i} = 0\quad \quad \text { for } i = 1, \dots , n-1, \end{aligned}$$
(8)

where \(a^i_{k_{1}, ..., k_{n-1} }\) are independent and identically distributed (i.i.d.) multivariate normal random vectors with mean zero and covariance matrix \(C\). Denote by \(v(y)\) the vector whose components are all the monomials \(\big \{\prod \nolimits _{i=1}^{n-1}y_i^{k_i}\big \}\) where \(0\le k_i\le d-1\) and \(\sum \nolimits _{i=1}^{n-1}k_i\le d-1\). Let \(A\) denote the random matrix whose \(i-\)th row contains all coefficients \(a^i_{k_1,\ldots , k_{n-1}}\). Then (8) can be rewritten as

$$\begin{aligned} A v(y)=0. \end{aligned}$$
(9)

The following theorem is the starting point of the analysis of this paper.

Theorem 1

[7, Theorem 7.1] Let \(U\) be any measurable subset of \({{\mathbb {R}}}^{n-1}\). Assume that the rows of \(A\) are i.i.d. multivariate normal random vectors with mean zero and covariance matrix \(C\). The expected number of real roots of the system of Eqs. (9) that lie in the set \(U\) is given by

$$\begin{aligned} \pi ^{-\frac{n}{2}}\varGamma \left( \frac{n}{2}\right) \int _U\left( \det \left[ \frac{\partial ^2}{\partial x_i\partial y_j}(\log v(x)^T C v(y))\big |_{y=x=t}\right] _{ij}\right) ^\frac{1}{2}\, \mathrm{d}t. \end{aligned}$$

2.3 From Random Polynomial Theory to Evolutionary Game Theory

Let \(E(n,d)\) be the number of internal equilibria in a \(d\)-player random game with \(n\) strategies. As has been shown in Sect. 2.1, \(E(n,d)\) is the same as the number of positive solutions of Eq. (7). We will apply Theorem 1 with \(a^i_{k_{1}, ..., k_{n-1} }=\beta ^i_{k_{1}, ..., k_{n-1} }\begin{pmatrix} d-1\\ k_{1}, ..., k_{n} \end{pmatrix}\) and \(U=[0,\infty )^{n-1}\subset {{\mathbb {R}}}^{n-1}\).

Suppose that all \(\beta ^{i}_{k_{1}, ..., k_{n-1} }\) are Gaussian distributions with mean \(0\) and variance \(1\), then for each \(i\) (\(1 \le i \le n-1\)), \(A^i=\left\{ \beta ^i_{k_{1}, ..., k_{n-1} }\begin{pmatrix} d-1\\ k_{1}, ..., k_{n} \end{pmatrix}\right\} \) is a multivariate normal random vector with mean zero and covariance matrix \(C\) given by

$$\begin{aligned} C=\mathrm {diag} \left( \begin{pmatrix} d-1\\ k_{1}, ..., k_{n} \end{pmatrix}^2\right) _{0\le k_i\le d-1,~\sum \nolimits _{i=1}^{n-1}k_i\le d-1}. \end{aligned}$$
(10)

We obtain the following lemma, which is a direct application of Theorem 1.

Lemma 1

Assume that \(\{A^i\}_{1\le i\le n-1}\) are independent normal random vectors with mean zero and covariance matrix \(C\) as in (10). The expected number of internal equilibria in a d-player n-strategy random game is given by

$$\begin{aligned} E(n,d)=\pi ^{-\frac{n}{2}}\varGamma \left( \frac{n}{2}\right) \underbrace{\int _0^\infty \ldots \int _0^\infty }_{n-1\,\text {times}}\left( \det \left[ \frac{\partial ^2}{\partial x_iy_j}(\log v(x)^T C v(y))\big |_{y=x=t} \right] _{ij}\right) ^\frac{1}{2}\,\mathrm{d}t, \end{aligned}$$
(11)

where

$$\begin{aligned} v(x)^T C v(y)=\sum \limits _{\begin{array}{c} 0\le k_{1}, ..., k_{n-1}\le d-1,\\ \sum \nolimits ^{n-1}_{i = 1}k_i\le d-1 \end{array}}\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\prod \limits _{i=1}^nx_i^{k_i}y_i^{k_i}. \end{aligned}$$
(12)

Denote by \(L\) the matrix with entries

$$\begin{aligned} L_{ij}&=\frac{\partial ^2}{\partial x_iy_j}(\log v(x)^T C v(y))\big |_{y=x=t}, \end{aligned}$$

then \(E(n,d)\) can be written as

$$\begin{aligned} E(n,d)=\pi ^{-\frac{n}{2}}\varGamma \left( \frac{n}{2}\right) \underbrace{\int _0^\infty \ldots \int _0^\infty }_{n-1\,\text {times}}\left( \det L\right) ^\frac{1}{2}\mathrm{d}t. \end{aligned}$$
(13)

It has been shown that a \(d\)-player \(n\)-strategy game has at most \((d-1)^{n-1}\) isolated internal equilibria (and this bound is sharp) [18]. We denote by \(p_i\), \(1 \le i \le (d-1)^{n-1}\), the probability that the game has exactly \(i\) such equilibria. Then \(E(n,d)\) can also be defined through \(p_i\) as follows

$$\begin{aligned} E(n,d)=\sum _{i=1}^{(d-1)^{n-1}}i \cdot p_i. \end{aligned}$$
(14)

3 Results

We start with the case where there are two strategies \((n = 2)\), analytically deriving the upper and lower bounds for \(E(2, d)\). Next we derive exact results for games with two players \((d = 2)\). Finally, we provide numerical results and discussion for the general case with an arbitrary number of players and strategies. For ease of representation, we start by assuming that the coefficients \(\beta ^i_{k_1,\ldots ,k_{n-1}}\) are standard normal distributions. We then show that the results do not change if they have arbitrary identical normal distributions.

3.1 Multi-player Two-Strategy Games

We first consider games with an arbitrary number of players, but having only two strategies, i.e., \(n = 2\). In this case, Eq. (7) is simplified to the following univariate polynomial equation of degree \(d-1\) with \(y \in {{\mathbb {R}}}_+\)

$$\begin{aligned} \sum \limits _{k=0}^{d-1}\beta _k\begin{pmatrix} d-1\\ k \end{pmatrix}y^k=0. \end{aligned}$$
(15)

The following lemma describes a closed form of \(E(2,d)\).

Lemma 2

Assume that \(\beta _k\) are independent Gaussian distributions with variance \(1\) and mean \(0\). Then the number of internal equilibria, \(E(2,d)\), in a \(d\)-player random game with two strategies is given by

$$\begin{aligned} E(2,d)=\int _0^\infty f(t)\,\mathrm{d}t, \end{aligned}$$
(16)

where

$$\begin{aligned} f(t)=\frac{1}{\pi }\left[ \frac{\sum \nolimits _{k=1}^{d-1}k^2\begin{pmatrix} d-1\\ k \end{pmatrix}^2t^{2(k-1)}}{\sum \nolimits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2t^{2k}}-\left( \frac{\sum \nolimits _{k=1}^{d-1}k\begin{pmatrix} d-1\\ k \end{pmatrix}^2t^{2k-1}}{\sum \nolimits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2t^{2k}}\right) ^2\right] ^{\frac{1}{2}}. \end{aligned}$$
(17)

Proof

Since \(\beta _k\) has Gaussian distribution with variance \(1\) and mean \(0\), \(\beta _k\begin{pmatrix} d-1\\ k \end{pmatrix}\) has Gaussian distribution with variance \(\begin{pmatrix} d-1\\ k \end{pmatrix}^2\) and mean \(0\). According to Lemma 1, the equality (16) holds with

$$\begin{aligned} f(t)=\frac{1}{\pi }\left[ \frac{\partial ^2}{\partial x\partial y}\left( \log v(x)^T C v(y)\right) \Big |_{y=x=t}\right] ^\frac{1}{2}, \end{aligned}$$
(18)

where the vector \(v\) and the matrix \(C\) (covariance matrix) are given by

$$\begin{aligned} v(x)=\begin{pmatrix} 1\\ x\\ \vdots \\ x^{d-1} \end{pmatrix}, \quad C=(C_{ij})_{i,j=1,\ldots ,d-1}\quad \text {with}~~ C_{ij}=\delta _{ij}\begin{pmatrix} d-1\\ i \end{pmatrix}\begin{pmatrix} d-1\\ j \end{pmatrix}, \end{aligned}$$
(19)

where \(\delta _{ij}\) is the Kronecker notation,

$$\begin{aligned} \delta _{ij}={\left\{ \begin{array}{ll} 1\quad \text {if}\quad i=j,\\ 0\quad \text {if}\quad i\ne j. \end{array}\right. } \end{aligned}$$

A straightforward calculation gives

$$\begin{aligned} v(x)^T C v(y)=\sum \limits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2x^ky^k, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2}{\partial x\partial y}\left( \log v(x)^T C v(y)\right)&=\frac{\sum \nolimits _{k=1}^{d-1}k^2\begin{pmatrix} d-1\\ k \end{pmatrix}^2x^{k-1}y^{k-1}}{\sum \nolimits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2x^{k}y^{k}}\\&\ \ - \frac{\left( \sum \nolimits _{k=1}^{d-1}k\begin{pmatrix} d-1\\ k \end{pmatrix}^2x^ky^{k-1}\right) \left( \sum \nolimits _{k=1} ^{d-1}k\begin{pmatrix} d-1\\ k \end{pmatrix}^2x^{k-1}y^{k}\right) }{\left( \sum \nolimits _{k=0} ^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2x^{k}y^{k}\right) ^2}. \end{aligned}$$

Substituting this expression into (18), we obtain (17).\(\square \)

Example 1

For the cases \(d=2\) and \(d=3\), we have

$$\begin{aligned}&E(2,2)=\frac{1}{\pi }\int _0^\infty \frac{1}{1+t^2}\,\mathrm{d}t = \frac{1}{\pi } \lim _{t \rightarrow +\infty } \tan ^{-1}(t) = 0.5,\\&E(2,3)=\frac{2}{\pi }\int _0^\infty \frac{\sqrt{t^4+t^2+1}}{t^4+4t^2+1}\,\mathrm{d}t\approx 0.77. \end{aligned}$$

The following proposition presents some properties of the density function \(f(t)\), which will be used later for estimating the asymptotic behavior of \(E(2,d)\).

Proposition 1

The following properties hold

  1. 1.
    $$\begin{aligned} f(t)=\frac{d-1}{\pi }\frac{\sqrt{\sum \nolimits _{k=0}^{2d-4} a_k\,t^{2k}}}{{\sum \nolimits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k\end{pmatrix}^2t^{2k}}}, \end{aligned}$$
    (20)

    where

    $$\begin{aligned} a_k=&\sum \limits _{\begin{array}{c} 1\le i\le d-1\\ 1\le j\le d-2\\ i+j=k \end{array}}\begin{pmatrix} d-1\\ i\end{pmatrix}^2\begin{pmatrix} d-2\\ j \end{pmatrix}^2-\sum \limits _{\begin{array}{c} 1\le i'\le d-2\\ 1\le j'\le d-2\\ i'+j'=k \end{array}}\begin{pmatrix} d-2\\ i'\end{pmatrix}\begin{pmatrix}d-1\\ i'+1 \end{pmatrix}\begin{pmatrix}d-2\\ j' \end{pmatrix}\begin{pmatrix}d-1\\ j'+1 \end{pmatrix}\!, \end{aligned}$$
    (21)
    $$\begin{aligned} a_{k}=&a_{2d-4-k}, \quad \text {for all}~~0\le k\le 2d-4, \quad a_{0}=a_{2d-4}=1, \quad a_k\ge 1. \end{aligned}$$
    (22)
  2. 2.

    \(f(0)=\frac{d-1}{\pi },\quad f(1)=\frac{d-1}{2\pi }\frac{1}{\sqrt{2d-3}}\).

  3. 3.

    \(f(t)=\frac{1}{2\pi }\left[ \frac{1}{t}G'(t)\right] ^\frac{1}{2}\), where

    $$\begin{aligned} G(t)=t\frac{\frac{\mathrm{d}}{\mathrm{d}t}M_d(t)}{M_d(t)}=t\frac{\mathrm{d}}{\mathrm{d}t}\log M_d(t). \end{aligned}$$
  4. 4.

    \(t\mapsto f(t)\) is a decreasing function.

  5. 5.

    \(f\left( \frac{1}{t}\right) =t^2 f(t)\).

  6. 6.
    $$\begin{aligned} E(2,d)=2\int _0^1\, f(t)\mathrm{d}t=2\int _1^\infty f(t)\,\mathrm{d}t. \end{aligned}$$
    (23)

Proof

  1. 1.

    Set

    $$\begin{aligned}&M_d(t)=\sum \limits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2t^{2k},\quad A_d(t)=\sum \limits _{k=1}^{d-1}k^2\begin{pmatrix} d-1\\ k \end{pmatrix}^2t^{2(k-1)}, \end{aligned}$$
    (24)
    $$\begin{aligned}&B_d(t)=\sum \limits _{k=1}^{d-1}k\begin{pmatrix} d-1\\ k \end{pmatrix}^2t^{2k-1}. \end{aligned}$$
    (25)

    Then

    $$\begin{aligned} f(t)=\frac{1}{\pi }\frac{\sqrt{A_d(t)M_d(t)-B_d(t)^2}}{M_d(t)}. \end{aligned}$$

    Using

    $$\begin{aligned} k\begin{pmatrix} d-1\\ k \end{pmatrix}=(d-1)\begin{pmatrix} d-2\\ k-1 \end{pmatrix}, \end{aligned}$$

    we can transform

    $$\begin{aligned}&A_d(t)=(d-1)^2\sum \limits _{k=1}^{d-1}\begin{pmatrix} d-2\\ k-1 \end{pmatrix}^2t^{2(k-1)}=(d-1)^2\sum \limits _{k=0}^{d-2}\begin{pmatrix} d-2\\ k \end{pmatrix}^2t^{2k}=(d-1)^2M_{d-1}(t),\\&B_d(t)=(d-1)\sum \limits _{k=1}^{d-1}\begin{pmatrix} d-2\\ k-1 \end{pmatrix}\begin{pmatrix} d-1\\ k \end{pmatrix}t^{2k-1}=(d-1)t\sum \limits _{k=0}^{d-2}\begin{pmatrix} d-2\\ k \end{pmatrix}\begin{pmatrix} d-1\\ k+1 \end{pmatrix}t^{2k}. \end{aligned}$$

    Therefore,

    $$\begin{aligned}&A_d(t)M_d(t)-B_d(t)^2\\&\quad =(d-1)^2\left[ \left( \sum \limits _{k=0}^{d-2}\begin{pmatrix} d-2\\ k \end{pmatrix}^2t^{2k}\right) \left( \sum \limits _{k=0}^{d-1}\begin{pmatrix} d-1\\ k \end{pmatrix}^2t^{2k}\right) \right. \\&\left. \qquad \qquad \qquad \qquad -t^2\left( \sum \limits _{k=0}^{d-2}\begin{pmatrix} d-2\\ k \end{pmatrix}\begin{pmatrix} d-1\\ k+1 \end{pmatrix}t^{2k}\right) ^2\right] \\&\quad =(d-1)^2\sum \limits _{k=0}^{2d-4}a_k\,t^{2k}, \end{aligned}$$

    where

    $$\begin{aligned} a_k =\sum \limits _{\begin{array}{c} 0\le i\le d-1\\ 0\le j\le d-2\\ i+j=k \end{array}}\begin{pmatrix} d-1\\ i \end{pmatrix}^2\begin{pmatrix} d-2\\ j \end{pmatrix}^2-\sum \limits _{\begin{array}{c} 0\le i'\le d-2\\ 0\le j'\le d-2\\ i'+j'=k-1 \end{array}}\begin{pmatrix} d-2\\ i' \end{pmatrix}\begin{pmatrix} d-1\\ i'+1 \end{pmatrix}\begin{pmatrix} d-2\\ j' \end{pmatrix}\begin{pmatrix} d-1\\ j'+1 \end{pmatrix}\!. \end{aligned}$$

    For the detailed computations of \(a_k\) and the proof of (22), see “Appendix.”

  2. 2.

    The value of \(f(0)\) is found directly from (20). For the detailed computations of \(f(1)\), see “Appendix.”

  3. 3.

    It follows from (24)–(25) that

    $$\begin{aligned} B_d(t)=\frac{1}{2}M_d'(t),\quad A_d(t)=\frac{1}{4 t}(tM_d'(t))', \end{aligned}$$
    (26)

    where \('\) is derivative with respect to \(t\). Hence,

    $$\begin{aligned} f(t)&=\frac{1}{2\pi }\left( \frac{\frac{1}{t}(tM_d'(t))'M_d(t)- M_d'(t)^2}{M_d(t)^2}\right) ^\frac{1}{2}\\&=\frac{1}{2\pi }\left( \frac{(tM_d'(t))'M_d(t)-tM_d'(t)^2}{tM_d(t)^2}\right) ^\frac{1}{2}\\&=\frac{1}{2\pi }\left( \frac{1}{t}G'(t)\right) ^\frac{1}{2}, \end{aligned}$$

    where \(G(t)=t\frac{M_d'(t)}{M_d(t)}\).

  4. 4.

    Since \(M_d(t)\) contains only even powers of \(t\) with positive coefficients, all of its roots are purely imaginary. Suppose that

    $$\begin{aligned} M_d(t)=\prod _{i=1}^{d-1} (t^2+r_i), \end{aligned}$$

    where \(r_i>0\) for all \(1\le i\le d-1\). It follows that

    $$\begin{aligned} G(t)=t\frac{M_d'(t)}{M_d(t)}=\sum \limits _{i=1}^{d-1}\frac{2t^2}{t^2+r_i}, \end{aligned}$$

    and hence,

    $$\begin{aligned} (2\pi f(t))^2=\frac{1}{t}G'(t)=\sum \limits _{i=1}^{d-1}\frac{4r_i}{(t^2+r_i)^2}. \end{aligned}$$
    (27)

    Since \(r_i>0\) for all \(i=1,\ldots ,d-1\), the above equality implies that \(f(t)\) is decreasing in \(t\in [0,\infty )\).

  5. 5.

    Set

    $$\begin{aligned} g(t):=\sqrt{A_d(t)M_d(t)-B_d(t)^2}, \end{aligned}$$

    Then

    $$\begin{aligned} f(t)=\frac{1}{\pi }\frac{g(t)}{M_d(t)}. \end{aligned}$$
    (28)

    It follows from the symmetric properties of the binomial coefficients that

    $$\begin{aligned} M_d\left( \frac{1}{t}\right) =\frac{1}{t^{2(d-1)}}M_d(t). \end{aligned}$$

    Similarly, from (22), we have

    $$\begin{aligned} g\left( \frac{1}{t}\right) =\frac{1}{t^{2(d-2)}}g(t). \end{aligned}$$

    Therefore,

    $$\begin{aligned} f\left( \frac{1}{t}\right) =\frac{1}{\pi }\frac{g(1/t)}{M_d(1/t)}=\frac{1}{\pi } t^2\frac{g(t)}{M_d(t)}=t^2 f(t). \end{aligned}$$
  6. 6.

    By change of variable, \(s=\frac{1}{t}\), and from (5), we have

    $$\begin{aligned} \int _1^\infty f(t)\,\mathrm{d}t=\int _1^0 f\left( \frac{1}{s}\right) \frac{-1}{s^2}\,ds=\int _0^1 f(s)\, ds. \end{aligned}$$

    Therefore,

    $$\begin{aligned} E(2,d)=\int _0^\infty f(t)\,\mathrm{d}t=\int _0^1 f(t)\,\mathrm{d}t+\int _1^\infty f(t)\,\mathrm{d}t=2\int _0^1 f(t)\,\mathrm{d}t. \end{aligned}$$

\(\square \)

Remark 1

We provide an alternative proof of the fifth property in the above lemma in “Appendix.”

Remark 2

Besides enabling a significantly less complex numerical computation of \(E(2,d)\) (see already our numerical results using this formula in Table 1), the equality (23) reveals an interesting property: The expected number of zeros of the polynomial \(P(y)\) in two intervals \((0,1)\) and \((1,\infty ]\) are the same. Equivalently, the expected numbers of internal equilibria in two intervals \((0,\frac{1}{2}]\) and \((\frac{1}{2},1)\) are equal since \(y=\frac{x}{1-x}\). Indeed, this result also confirms the observation that by swapping indices between the two strategies \((n = 2)\), we move equilibrium from \(x\) to \(1 -x\), thereby not resulting in change in the number of equilibria.

Based on the analytical formula of \(E(2,d)\), we now provide upper and lower bounds for the mean number of equilibria as the payoff entries of the game are randomly drawn.

Theorem 2

\(E(2,d)\) satisfies the following estimate

$$\begin{aligned} \frac{d-1}{\pi \sqrt{2d-3}}\le E(2,d)\le \frac{1}{\pi }\sqrt{d-1}\sqrt{1+\frac{\pi }{2}\sqrt{d-1}}. \end{aligned}$$
(29)

Proof

Since \(f(t)\) is decreasing, we have \(f(0)\ge f(t)\ge f(1)\) for \(t\in [0,1]\). As a consequence,

$$\begin{aligned} E(2,d)\ge 2\int _0^1 f(1)\,\mathrm{d}t=2f(1)=\frac{d-1}{\pi \sqrt{2d-3}}. \end{aligned}$$

To obtain the upper bound, we proceed as follows.

$$\begin{aligned} E(2,d)^2&=4\left( \int _0^1 f(t)\,\mathrm{d}t\right) ^2\nonumber \\&\le 4\int _0^1 f(t)^2\,\mathrm{d}t \quad \text {(by Jensen's inequality)}\nonumber \\&=\frac{1}{\pi ^2}\int _0^1\frac{1}{t}G'(t)\,\mathrm{d}t\nonumber \\&\mathop {=}\limits ^{(27)}\frac{1}{\pi ^2}\int _0^1 \sum \limits _{i=1}^{d-1}\frac{4r_i}{(t^2+r_i)^2}\,\mathrm{d}t\nonumber \\&=\frac{1}{\pi ^2}\sum \limits _{i=1}^{d-1}\int _0^1\frac{4r_i}{(t^2+r_i)^2}\,\mathrm{d}t\nonumber \\&=\frac{1}{\pi ^2}\sum \limits _{i=1}^{d-1}\left( \frac{2}{r_i+1}+ \frac{\cot ^{-1}(\sqrt{r_i})}{\sqrt{r_i}}\right) . \end{aligned}$$
(30)

Note that if \(ab=1\), then

$$\begin{aligned} \frac{1}{a+1}+\frac{1}{b+1}=1. \end{aligned}$$
(31)

We observe that if \(z\) is a zero of \(M_d(t)\), then \(\frac{1}{z}\) is also a zero because \(M_d(t)=t^{2(d-1)}M_d(1/t)\). This implies that the sequence \(\{r_i, i=1,\ldots ,d-1\}\) can be grouped into \(\frac{d-1}{2}\) pairs of the form \(\left( a,\frac{1}{a}\right) \). Using (31), we obtain

$$\begin{aligned} \frac{1}{\pi ^2}\sum \limits _{i=1}^{d-1}\frac{2}{r_i+1}= \frac{1}{\pi ^2}(d-1). \end{aligned}$$
(32)

For the second term, since \(\cot ^{-1}(z)\le \frac{\pi }{2}~~ \text {for all}~~ z\ge 0\), we have

$$\begin{aligned} \sum \limits _{i=1}^{d-1}\frac{\cot ^{-1}(\sqrt{r_i})}{\sqrt{r_i}}&\le \frac{\pi }{2}\sum \limits _{i=1}^{d-1}\frac{1}{\sqrt{r_i}}\nonumber \\&=\frac{\pi }{2}\frac{\sum \nolimits _{i=1}^{d-1}\prod \nolimits _{j\ne i} \sqrt{r_j}}{\prod \nolimits _{i=1}^{d-1}\sqrt{r_i}}\nonumber \\&=\frac{\pi }{2}\sum \limits _{i=1}^{d-1}\prod \limits _{j\ne i}\sqrt{r_j}\nonumber \\&\le \frac{\pi }{2}\sqrt{(d-1)\sum \limits _{i=1}^{d-1} \prod \limits _{j\ne i}r_j}\nonumber \\&=\frac{\pi }{2}(d-1)^\frac{3}{2}, \end{aligned}$$
(33)

where we have used the Cauchy-Schwartz inequality

$$\begin{aligned} \left( \sum \limits _{i=1}^nb_i\right) ^2\le n\sum \limits _{i=1}^nb_i^2, \end{aligned}$$

and the fact that \(\prod \nolimits _{i=1}^{d-1}r_i=1 \) and \(\sum \nolimits _{i=1}^{d-1}\prod \nolimits _{j\ne i}r_j=(d-1)^2\) according to Vieta’s theorem for the roots \(\{r_i\}\) of \(M_d\).

From (30), (32) and (33), we have

$$\begin{aligned} E(2,d)^2\le \frac{1}{\pi ^2}\left( (d-1)+\frac{\pi }{2}(d-1) ^\frac{3}{2}\right) =\frac{1}{\pi ^2}(d-1)(1+\frac{\pi }{2}\sqrt{d-1}), \end{aligned}$$

or equivalently

$$\begin{aligned} E(2,d)\le \frac{1}{\pi }\sqrt{d-1}\sqrt{1+\frac{\pi }{2}\sqrt{d-1}}. \end{aligned}$$

\(\square \)

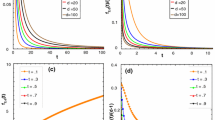
In Fig. 1a, we show the numerical results for \(E(2,d)\) in comparison with the obtained upper and lower bounds.

Corollary 1

  1. 1.

    The expected number of equilibria increases unboundedly when \(d\) tends to infinity

    $$\begin{aligned} \lim _{d\rightarrow \infty }E(2,d)=+\infty . \end{aligned}$$
    (34)
  2. 2.

    The probability \(p_m\) of observing \(m\) equilibria, \(1\le m\le d-1\), is bounded by

    $$\begin{aligned} p_m\le \frac{E(2,d)}{m}\le \frac{1}{\pi m}\sqrt{d-1}\sqrt{1+\frac{\pi }{2}\sqrt{d-1}}. \end{aligned}$$
    (35)

    In particular,

    $$\begin{aligned} p_{d-1}\le \frac{1}{\pi }\frac{\sqrt{1+\frac{\pi }{2}\sqrt{d-1}}}{\sqrt{d-1}},\quad \text {and}\quad \lim _{d\rightarrow \infty }p_{d-1}=0. \end{aligned}$$

Proof

  1. 1.

    This is a direct consequence of (29), as the lower bound of \(E(2,d)\) tends to infinity when \(d\) tends to infinity.

  2. 2.

    This is again a direct consequence of (29) and definition of \(E(2,d)\). For any \(1\le m\le d-1\), we have

    $$\begin{aligned} E(2,d)=\sum _{i=1}^{d-1}p_i\cdot i\ge p_m\cdot m. \end{aligned}$$

    In particular,

    $$\begin{aligned} p_{d-1}\le \frac{E(2,d)}{d-1}\le \frac{1}{\pi }\frac{\sqrt{1+\frac{\pi }{2}\sqrt{d-1}}}{\sqrt{d-1}}. \end{aligned}$$

    As a consequence, \(\lim \limits _{d\rightarrow \infty } p_{d-1}=0\). More generally, we can see that this limit is true for \(p_{k}\) for any \(k=O(d)\) as \(d\rightarrow \infty \).

\(\square \)

From this corollary, we can see that, interestingly, although the mean number of equilibria tends to infinity when the number of players \(d\) increases, the probability to see the maximal number of equilibria in a \(d\)-player system converges to 0. There has been extensive research studying the maximal number of equilibrium points of a dynamical system [2, 3, 5, 19, 20, 27, 37–39]. Our results suggest that the possibility to reach such a maximal number is very small when \(d\) is sufficiently large.

Corollary 2

The expected number of stable equilibrium points in a random game with \(d\) players and two strategies is equal to \( \frac{E(2,d)}{2}\) and is thus bounded within to the following interval

$$\begin{aligned} \left[ \frac{d-1}{2\pi \sqrt{2d-3}}, \ \frac{1}{2\pi }\sqrt{d-1}\sqrt{1+\frac{\pi }{2}\sqrt{d-1}}\right] . \end{aligned}$$

Proof

From [18, Theorem 3], it is known that an equilibrium in a random game with two strategies and an arbitrary number of players is stable with probability \(1/2\). Hence, the corollary is a direct consequence of Theorem 2.\(\square \)

3.2 Two-player Multi-strategy Games

In this section, we consider games with two players, i.e., \(d=2\), and arbitrary strategies. In this case, (7) is simplified to a linear system

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum _{j}\beta ^i_j \,y_j=0, \quad \text {for}~~i=1,\ldots ,n-1,\\ \sum _j y_j=1, \end{array}\right. } \end{aligned}$$
(36)

where \(\beta _j^i\) have Gaussian distributions with mean 0 and variance 1. The main result of this section is the following explicit formula for \(E(n,2)\).

Theorem 3

We have

$$\begin{aligned} E(n,2)= \frac{1}{2^{n-1}}. \end{aligned}$$
(37)

This theorem can be seen as a direct application of [18, Theorem 1] and the definition of \(E(n,d)\) in Eq. (14). Indeed, according to [18, Theorem 1], the probability that Eq. (36) has a (unique) isolated solution is \(p_1=2^{1-n}\), and the probability of having no solution is 0. By (14), \(E(n,2)=p_1\), and hence, \(E(n,2)=2^{1-n}\).

To demonstrate further the usefulness of our approach using the random polynomial theory, we present here an alternative proof that can directly obtain \(E(n,2)\), i.e., without computing the probability of observing concrete numbers of equilibria. Our proof requires an assumption that \(\{A^i=(\beta _j^i)_{j=1,\ldots ,n-1}; i=1,\ldots , n-1\}\) are independent random vectors. We will elaborate and discuss this assumption in Remark 4. The main ingredient of our proof is the following lemma, whose proof is given in “Appendix.”

Lemma 3

Let \(t_1,\dots ,t_{n-1}\) be real numbers, and let \(L\) be the matrix with entries

$$\begin{aligned}&L_{ii}=\frac{1}{1+\sum \nolimits _{k=1}^{n-1} t_k^2}-\frac{t_i^2}{\left( 1+\sum \nolimits _{k=1}^{n-1} t_k^2\right) ^2},\\&L_{ij}=\frac{-t_i t_j}{\left( 1+\sum \nolimits _{k=1}^{n-1} t_k^2\right) ^2}\quad \forall i \ne j. \end{aligned}$$

It holds that

$$\begin{aligned} \det L = \frac{1}{\left( 1+\sum \nolimits _{k=1}^{n-1} t_k^2\right) ^n}. \end{aligned}$$
(38)

Proof

(Proof of Theorem 3 under the assumption that \(\{A^i=(\beta _j^i)_{j=1,\ldots ,n-1}; i=1,\ldots , n-1\}\) are independent random vectors.)

Let \(L\) be the matrix in Lemma 3. According to Lemma 1 and Lemma 3, we have

$$\begin{aligned} E(n,2)&=\pi ^{-\frac{n}{2}}\varGamma \left( \frac{n}{2}\right) \underbrace{\int _0^\infty \ldots \int _0^\infty }_{n-1\,\text {times}} \left( \det L \right) ^{1/2} \,\mathrm{d}t_1\ldots \mathrm{d}t_{n-1}\\&=\pi ^{-\frac{n}{2}}\varGamma \left( \frac{n}{2}\right) \underbrace{\int _0^\infty \ldots \int _0^\infty }_{n-1\,\text {times}} \left( 1+\sum _{k=1}^{n-1} t_k^2\right) ^{-n/2} \,\mathrm{d}t_1\ldots \mathrm{d}t_{n-1} \\&=\frac{1}{2}\pi ^{-\frac{n-1}{2}}\varGamma \left( \frac{n-1}{2}\right) \underbrace{\int _0^\infty \ldots \int _0^\infty }_{n-2\,\text {times}} \left( 1+\sum _{k=1}^{n-2} t_k^2\right) ^{-(n-1)/2} \,\mathrm{d}t_1\ldots \mathrm{d}t_{n-2} \\&\ldots \\&=\frac{1}{2^{n-1}}\pi ^{-\frac{1}{2}}\varGamma \left( \frac{1}{2}\right) \\&=\frac{1}{2^{n-1}}, \end{aligned}$$

where we have repeatedly used the equality (with \(a > 0\) and \(p > 1\))

$$\begin{aligned} \int _0^\infty (a + t^2)^{-p} \mathrm{d}t = \frac{\sqrt{\pi } \ \varGamma {(p-\frac{1}{2})}}{2 \ \varGamma (p)}a^{\frac{1}{2}-p}. \end{aligned}$$

\(\square \)

Remark 3

Note that, as in [18, Theorem 2], it is known that the probability that a two-player \(n\)-strategy random game has a stable (internal) equilibrium is at most \(2^{-n}\). Hence, the expected number of stable equilibrium points in this case is at most \(2^{-n}\). From [18, Theorem 2], we also can show that this bound is sharp only when \(n = 2\).

Remark 4

Let \(M\) be the number of sequences \((k_1,\ldots , k_{n-1})\) such that \(\sum _{j=1}^{n-1}k_j\le d-1\). For each \(i=1,\ldots , n-1\), we define a random vector \(A^i=(\beta ^i_{k_1,\ldots ,k_{n-1}})\in {{\mathbb {R}}}^M\). Recalling from Sect. 2 that \(\beta ^{i}_{k_{1}, ..., k_{n-1} }= \alpha ^{i}_{k_{1}, ..., k_{n} } -\alpha ^{n}_{k_{1}, ..., k_{n} } \), where \(\alpha ^{i}_{i_1,\ldots ,i_{d-1}}\) is the payoff of the focal player, with \(i\) (\(1 \le i \le n\)) being the strategy of the focal player, and \(i_k\) (with \(1 \le i_k \le n\) and \(1 \le k \le d-1\)) is the strategy of the player in position \(k\). The assumption in Lemma 1 is that \(A^1,\ldots , A^{n-1}\) are independent random vectors, and each of them has mean \(0\) and covariance matrix \(C\). This assumption clearly holds for \(n = 2\). For \(n>2\), the assumption holds only under quite restrictive conditions such as \(\alpha ^{n}_{k_{1}, ..., k_{n} }\) is deterministic or \(\alpha ^{i}_{k_{1}, ..., k_{n} }\) are essentially identical. Nevertheless, from a purely mathematical point of view (see for instance [21, 22] and Sect. 4 for further discussion), it is important to investigate the number of real zeros of the system (7) under the assumption of independence of \(\{A^i\}\) since this system has not been studied in the literature. As such, the investigation provides new insights into the theory of zeros of systems of random polynomials. In addition, it also gives important hint on the complexity of the game theoretical question, i.e., the number of expected number of equilibria. Indeed, for \(d = 2\) and arbitrary \(n\), the assumption does not affect the final result as shown in Theorem 3. We recall that [7, Theorem 7.1] also required that the rows \(\{A^i\}\) are independent random vectors. Hence, to treat the general case, one would need to generalize [7, Theorem 7.1] and this is a difficult problem as demonstrated in [21, 22]. With this motivation, in the next section, we keep the assumption of independence of \(\{A^i\}\) and leave the general case for future research. We numerically compute the number of zeros of the system (7) for \(n\in \{2,3,4\}\). Again, as we shall see, the numerical results under the given assumption lead to outcomes closely corroborated by previous works in [10, 18].

3.3 Multi-player Multi-strategy Games

We now move to the general case of multi-player games with multiple strategies. We provide numerical results for this case. For simplicity of notation in this section, we write \(\sum \limits _{k_1,\ldots ,k_{n-1}}\) instead of \(\sum \limits _{\begin{array}{c} 0\le k_{1}, ..., k_{n-1}\le d-1,\\ \sum \nolimits ^{n-1}_{i = 1}k_i\le d-1 \end{array}}\) and \(\sum \limits _{k_1,\ldots ,k_{n-1} | k_{i_1}, .., k_{i_m} }\) instead of \(\sum \limits _{\begin{array}{c} 0\le k_{i}\le d-1 \ \forall i \in S \setminus R, \\ 1\le k_j\le d-1 \ \forall j \in R , \\ \sum \nolimits ^{n-1}_{i = 1}k_i\le d-1 \end{array}}\) where \(S= \{1, \ldots , n-1\}\) and \(R = \{i_1, \ldots , i_m\} \subseteq S\).

According to Lemma 1, the expected number of internal equilibria in a \(d\)-player random game with \(n\) strategies is given by

$$\begin{aligned} E(n,d)&=\pi ^{-\frac{n}{2}}\varGamma \left( \frac{n}{2}\right) \int _U \left( \det \left[ \frac{\partial ^2}{\partial x_iy_j}(\log v(x)^T C v(y))\big |_{y=x=t} \right] _{ij}\right) ^\frac{1}{2}\mathrm{d}t\\&=\pi ^{-\frac{n}{2}}\varGamma \left( \frac{n}{2}\right) \int _U\left( \det L\right) ^\frac{1}{2}\mathrm{d}t, \end{aligned}$$

where \(\varGamma \) is the Gamma function, and \(L\) denotes the matrix with entries

$$\begin{aligned} L_{ij}&=\frac{\partial ^2}{\partial x_iy_j}(\log v(x)^T C v(y))\big |_{y=x=t}. \end{aligned}$$

We have

$$\begin{aligned} v(x)^T C v(y)=\sum \limits _{k_1,\ldots ,k_{n-1}}\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\prod \limits _{i=1}^nx_i^{k_i}y_i^{k_i}. \end{aligned}$$

Set \(\varPi (x,y):=\prod \limits _{l=1}^{n-1}x_{l}^{k_l}y_{l}^{k_l}\). Then

$$\begin{aligned}&\frac{\partial ^2}{\partial x_iy_j}(\log v(x)^T C v(y)) =\frac{\frac{1}{x_iy_j}\sum \nolimits _{k_{1}, ..., k_{n-1} | k_i, k_j}k_ik_j\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n-1} \end{pmatrix}^2\varPi (x,y)}{\sum \nolimits _{k_1,\ldots ,k_{n-1}}\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n-1} \end{pmatrix}^2\varPi (x,y)}\\&\qquad -\frac{\left( \frac{1}{x_i}\sum \nolimits _{k_{1},\ldots , k_{n-1} | k_i}k_i\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\varPi (x,y)\right) \left( \frac{1}{y_j}\sum \nolimits _{k_{1}, ..., k_{n} |k_j}k_j\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\varPi (x,y)\right) }{ \left( \sum \nolimits _{k_1,\ldots ,k_{n-1}}\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\varPi (x,y)\right) ^2}. \end{aligned}$$

Therefore,

$$\begin{aligned} L_{ij}&=\frac{\frac{1}{t_it_j}\sum \nolimits _{k_1,\ldots ,k_{n-1} | k_i, k_j}k_ik_j\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\prod \nolimits _lt_l^{2k_l}}{\sum \nolimits _{k_1,\ldots ,k_{n-1}}\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\prod \nolimits _lt_l^{2k_l}}\end{aligned}$$
(39)
$$\begin{aligned}&\qquad -\frac{\left( \frac{1}{t_i}\sum \nolimits _{k_{1}, ..., k_{n-1} | k_i}k_i\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\prod \nolimits _lt_l^{2k_l}\right) \left( \frac{1}{t_j}\sum \nolimits _{k_{1}, ..., k_{n-1} | k_j}k_j\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\prod \nolimits _lt_l^{2k_l}\right) }{ \left( \sum \nolimits _{k_1,\ldots ,k_{n-1}}\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\prod \nolimits _lt_l^{2k_l}\right) ^2}. \end{aligned}$$
(40)

So far in the paper, we have assumed that all the \(\beta ^i_{k_{1}, ..., k_{n-1} }\) in Eq. (7) are standard normal distributions. The following lemma shows, as a consequence of the above described formula, that all the results obtained so far remain valid if they have a normal distribution with mean zero and arbitrary variance (i.e., the entries of the game payoff matrix have the same, arbitrary normal distribution).

Lemma 4

Suppose \(\beta ^i_{k_{1}, ..., k_{n-1} }\) have normal distributions with mean 0 and arbitrary variance \(\sigma ^2\). Then, \(L_{ij}\) as defined in (39) does not depend on \(\sigma ^2\).

Proof

In this case, \(\beta ^i_{k_{1}, ..., k_{n-1} }\begin{pmatrix} d-1\\ k \end{pmatrix}\) has a Gaussian distribution with variance \(\sigma ^2\begin{pmatrix} d-1\\ k \end{pmatrix}^2\) and mean \(0\). Hence,

$$\begin{aligned} v(x)^T C v(y)=\sum \limits _{k_1,\ldots ,k_{n-1}}\sigma ^2\begin{pmatrix} d-1\\ k_1,\ldots ,k_{n} \end{pmatrix}^2\prod \limits _{i=1}^nx_i^{k_i}y_i^{k_i}. \end{aligned}$$

Repeating the same calculation, we obtain the same \(L_{ij}\) as in (39), which is independent of \(\sigma \).\(\square \)

This result suggests that when dealing with random games as in this article, it is sufficient to consider that payoff entries are from the interval [0, 1] instead of from an arbitrary one, as done numerically in [10]. A similar behavior has been observed in [18] for the analysis and computation with small \(d\) or \(n\), showing that results are not dependent on the interval where the payoff entries are drawn. Furthermore, it is noteworthy that this result confirms the observation that multiplying a payoff matrix by a constant does not change the equilibria [17], provided a one-to-one mapping from [0,1] to the arbitrary interval.

Example 2

(d-players with \(n=3\) strategies)

$$\begin{aligned} L_{11}&=\frac{\frac{1}{t_1^2}\sum \nolimits _{k_1=1,k_2=0}k_1^2\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}}{\sum \nolimits _{k_1,k_2}\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}}-\frac{\left( \frac{1}{t_1} \sum \nolimits _{k_{1}=1, k_2=0}k_1\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}\right) ^2}{ \left( \sum \nolimits _{k_1,k_2}\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}\right) ^2},\\ L_{12}&=\frac{\frac{1}{t_1t_2}\sum \nolimits _{k_1=1,k_2=1}k_1k_2\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}}{\sum \nolimits _{k_1,k_2}\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}}\\&\qquad -\frac{\left( \frac{1}{t_1}\sum \nolimits _{k_{1}=1, k_2=0}k_1\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}\right) \left( \frac{1}{t_2} \sum \nolimits _{k_{1}=0, k_2=1}k_2\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}\right) }{ \left( \sum \nolimits _{k_1,k_2}\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}\right) ^2},\\ L_{21}=&L_{12},\\ L_{22}=&\frac{\frac{1}{t_2^2}\sum \nolimits _{k_1=0,k_2=1}k_2^2\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}}{\sum \nolimits _{k_1,k_2}\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}}-\frac{\left( \frac{1}{t_2} \sum \nolimits _{k_{1}=0, k_2=1}k_2\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}\right) ^2}{ \left( \sum \nolimits _{k_1,k_2}\begin{pmatrix} d-1\\ k_1,k_2 \end{pmatrix}^2t_1^{2k_1}t_2^{2k_2}\right) ^2}. \end{aligned}$$

Therefore,

$$\begin{aligned} E(3,d)=\pi ^{-\frac{3}{2}}\varGamma \left( \frac{3}{2}\right) \int _0^\infty \int _0^\infty \sqrt{L_{11}L_{22}-L_{12}L_{21}}\,\mathrm{d}t_1\mathrm{d}t_2. \end{aligned}$$

Next we provide some numerical results. We numerically compute \(E(n,d)\) for \(n\in \{2,3,4\}\) and show them in Table 1 (for \(d\le 10\)) and Figs.  1b (for \(d\le 20\)). We also plot the lower and upper bounds for \(E(2,d)\) obtained in Theorem 2 and compare them with its numerical computation, see Fig. 1a. We note that for small \(n\) and \(d\) (namely, \(n\le 5\) and \(d\le 4\)), \(E(n,d)\) can also be computed numerically via the probabilities \(p_i\) of observing exactly \(i\) equilibria using (14). This direct approach has been used in [18] and [10], which our results are compatible with. Furthermore, as a consequence of Corollary 2, we can derive the exact expected number of stable equilibria for \(n = 2\), which is equal to half of the expected number of equilibria given in the first row of Table 1.

Table 1 Expected number of internal equilibria for some values of \(d\) and \(n\)
Full size table
Fig. 1
figure 1

a Expected number of equilibria, \(E(2,d)\), for varying the number of players in the game, and the upper and lower bounds obtained in Theorem 2. b Expected number of equilibria, \(E(n,d)\), for varying the number of players and strategies in the game. We plot for different number of strategies: \(n = 2\), 3 and 4. The payoff entries of the d-player n-strategy game are randomly drawn from the normal distribution. In general, the larger the number of players in the game, the higher the number of equilibria one can expect if the payoff entries of the game are randomly chosen. We observe that for small \(d\), \(E(n,d)\) increases with \(n\), while it decreases for large \(d\) (namely, \(d \ge 5\), see also Table 1). The results were obtained numerically using Mathematica

Full size image

4 Discussion

In the evolutionary game literature, mathematical results have been mostly provided for two-player games [17, 28], despite the abundance of multi-player game examples in nature [5, 10]. The mathematical study for multi-player games has only attracted more attention recently, apparently because the resulting complexity and dynamics from the games are significantly magnified with the number of the game participants [5, 18, 40]. As seen from our analysis, multi-player games introduce nonlinearity into the inducing equations, because the fitness functions are polynomial instead of linear as in the pairwise interactions [10, 17, 40]. It is even more so if we consider scenarios in which the payoff matrix is nonlinear naturally, such as for public goods games with nonlinear returns [30], as observed in animal hunting [29, 34]. In addition, as the number of strategies increases, one needs to deal with systems of multivariate polynomials. This seemingly complexity of the general multi-player multi-strategy games makes the analysis of the equilibrium points extremely difficult. For instance, in [18], as the analysis was based on an explicit calculation of the zeros of systems of polynomials, it cannot go beyond games with a small number of players (namely, \(d \le 5\)), even for the simplest case of \(n = 2\). Here we have taken a different approach based on the well-established theory of random polynomials. We have derived a computationally implementable formula, \(E(n,d)\), of the mean number of equilibria in a general random \(d\)-player game with \(n\) strategies. For \(n = 2\) and with an arbitrary \(d\), we have derived asymptotic upper and lower bounds of \(E(2,d)\). An interesting implication of these results is that although the expected number of equilibria tends to infinity when \(d\) increases, the probability of seeing the maximal possible number of equilibria tends to 0. This is a notable observation since knowing the maximal number of equilibrium points in an evolutionary process is insightful and has been of special focus in biological contexts [10, 24]. Furthermore, for \(d = 2\) with an arbitrary \(n\), we have derived the exact value \(E(n,2) = 2^{1 - n}\), recovering results obtained in [18]. In the general case, based on the formula that we have derived, we have been able to numerically calculate \(E(n,d)\), thereby going beyond the analytical and numerical computations from previous work that made use of the direct approach. As a consequence of the results obtained for the extreme cases, we could also derive the boundaries for the expected number of equilibrium points when counting only the stable ones. Note that some studies have been carried out to study the stable equilibrium points or evolutionary stable strategies (ESS) [27] in a random evolutionary game, but it has been mostly done for two-player games, see for example [11, 16, 23]. As such, we have provided further understanding with respect to the asymptotic behavior of the expected number of stable equilibria for multi-player random games, though with only two strategies, leaving the more general case for future study.

On the other hand, in the random polynomial literature, the study of distribution of zeros of system of random polynomials as described in (8), especially in the univariate case, has been carried out by many authors, see for instance [7] for a nice exposition and [36] for the most recent results. The most well-known classes of polynomials are flat polynomials or Weyl polynomials for \(a_i:=\frac{1}{i!}\), elliptic polynomials or binomial polynomials for \(a_i:=\sqrt{\begin{pmatrix} d-1\\ i \end{pmatrix}}\) and Kac polynomials for \(a_i:= 1\). We emphasize the difference between the polynomial studied in this paper with the elliptic case: \(a_i=\begin{pmatrix} d-1\\ i \end{pmatrix}\) are binomial coefficients, not their square root. In the elliptic case, \(v(x)^TCv(y)=\sum _{i=1}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}x^iy^i=(1+xy)^{d-1}\), and as a result \(E=E(2,d)=\sqrt{d-1}\). While in our case, because of the square in the coefficients, \(v(x)^TCv(y)=\sum _{i=1}^{d-1}\begin{pmatrix} d-1\\ i \end{pmatrix}^2x^iy^i\) is no longer a generating function. Whether one can find an exact formula for \(E(2,d)\) is unclear. For the multivariate situation, the exact formula for \(E(n,2)\) is interesting by itself and we could not be able to find it in the literature. Due to the complexity in the general case \(d,n\ge 3\), further research is required.

In short, we have described a novel approach to calculating and analyzing the expected number of (stable) equilibrium points in a general random evolutionary game, giving insights into the overall complexity of such dynamical systems as the players and the strategies in the game increase. Since the theory of random polynomials is rich, we envisage that our method could be extended to obtain results for other more complex scenarios such as games having a payoff matrix with dependent entries and/or with general distributions.