A comprehensive analysis of transient rate and rate derivative data of an oil well intercepted by infinite-conductivity hydraulic fracture in closed systems

Abstract

This paper presents a method for analyzing constant-pressure drawdown test of infinite-conductivity fractured wells in bounded reservoirs. The presented method is based on the Tiab direct synthesis approach. The fracture and reservoir parameters are directly determined from the rate and rate derivative of the well test data. New equations describing the elliptical flow regime and the transition from the pseudoradial regime to the boundary-dominated regime of different rectangular reservoirs are also presented. The various flow regimes occurring during the well test are easily identified based on the shape of the plotted data and the slope of each flow regime. The unique features of the slopes of the various regimes and their intersection points are utilized to determine the fracture half-length, formation permeability, skin factor, well drainage area, and reservoir shape factor. Moreover, new equations defining the intersection points of the straight lines corresponding to different flow regimes are presented. These equations are very important for confirming the precision of the calculated results. A systematic process demonstrating the application of the proposed method to linear, elliptical, pseudoradial, and boundary-dominated regimes is well delineated. Comprehensive examples are presented to validate the efficiency of the proposed technique. The examples show that even if some of the flow regimes are not fully developed, the method can still be used to determine the formation and fracture properties using information obtained from the remaining flow regimes. This is one of several advantages of the proposed technique over conventional techniques.

Introduction

Massive hydraulic fracturing is a stimulation process that is typically implemented in tight oil and gas reservoirs to improve well productivity. Appropriate liquids are injected into the reservoir zone for stimulation, creating a vertical fracture. Massive hydraulic fracturing has recently received considerable attention and has been widely and successfully applied in shale gas reservoirs in the US and worldwide (King 2020; Jiang et al. 2021; Ibrahim 2022; Temizel et al. 2022). Efficient evaluation of reservoirs and fracture properties is essential for assessing stimulation treatments, forecasting well performance, and developing optimal reservoirs.

Several semianalytical methods, asymptotic analytical approaches, numerical models, and type curves describing the pressure or rate variations with time of finite- and infinite-conductivity vertically fractured wells have been presented in the literature. Prats (1961) and Prats et al. (1962) investigated the impacts of massive hydraulic fracturing on the productivity and behavior of liquid and gas wells and proposed analysis techniques for both constant-rate and constant-pressure producing wells. Russel and Truitt (1964) developed a mathematical model with synthetic buildup test plots to forecast the pseudoradial flow regime performance of hydraulically fractured (HF) wells. They presented their results in terms of the dimensionless pressure versus the time and fracture penetration. In 1977, Cinco-Ley and Samaniego-V (1977) investigated the impact of wellbore storage and fracture impairment on well performance. They considered the skin as a very thin layer covering the fracture face and noted that the skin effect or fracture face damage must be considered to efficiently assess the pressure transient behavior of HF wells. Cinco-Ley et al. (1978) revised the mathematical model of Russell and Truitt (1964) and developed analytical and type curve methods for well test analysis of HF wells in infinite systems.

Hanley and Bandyopadhyay (1979) presented an analytical solution for wells intercepted by a uniform-flux infinite-conductivity fractures that penetrate the pay zones of square reservoirs. They examined the impacts of wellbore storage, fracture penetration and capacity, and reservoir properties on well performance and concluded that the wellbore storage effects must be considered to understand the transient pressure behavior of HF wells in low-permeability reservoirs. More recently, Guo et al. (2015) investigated the various factors affecting the flow regimes in finite-conductivity HF wells producing from shale gas reservoirs. They presented pressure transient and rate decline models that describe gas flow behavior in HF wells.

Type-curve matching has also been utilized to characterize HF wells. Well test analysts have proposed type-curves as effective diagnostic tools that cover the full spectrum of flow regimes and incorporate the overlapping transition periods occurring during the well test. Nevertheless, since type curves yield nonunique matching results, these models must be interpreted carefully.

In 1989, Tiab (1989) developed the Tiab direct synthesis (TDS) approach for interpreting the transient pressure behavior of infinite-conductivity HF wells. The TDS method does not require type-curve matching. It enables accurate calculation of various reservoir and well parameters such as the formation permeability, well damage/improvement, and fracture penetration, based directly on the characteristic plots of the pressure derivative versus time. In another paper, Tiab (1994) successfully applied his technique to HF wells with constant flux produced from closed systems under constant flow rate conditions. In 1999, Tiab et al. (1999) applied the TDS method to wells intersected by finite-conductivity hydraulic fracture. The TDS technique has been demonstrated to be highly effective in calculating different reservoir and fracture properties. The strength of the technique is that the developed equations are based on exact analytical solutions. However, similar to other conventional constant-rate methods, the TDS method is limited by time delays caused by wellbore storage phenomena. Moreover, researchers in the well test community have suggested that the wellbore storage effect distorts the critical early well test data mainly in low-permeability and/or low-pressure reservoirs and in some circumstances masks the presence of natural fractures in the area surrounding the wellbore, leading to uninterpretable fracture flow data. On the other hand, many authors have demonstrated that constant-bottomhole pressure techniques are not influenced by the wellbore storage effect, allowing the fracture and reservoir area near the tested well to be well characterized using early test data (Earlougher 1977; Samaniego-V and Cinco-Ley 1980; Thompson 1981; Guppy et al. 1981, 1988; Lio and Lee 1994; Berumen et al. 1997; Nashawi 2006; Malallah et al. 2007). More recently, Escobar et al. (2015) applied the TDS technique to analyze the production rate of HF horizontal wells in naturally fractured shale gas reservoirs. Their results were in excellent agreement with the actual reservoir and fracture parameters.

This paper presents an efficient and straightforward technique to analyze well test data of infinite-conductivity HF wells produced at constant-bottomhole pressure from bounded systems. The proposed method uses rate and rate derivative plots to determine the various reservoir and fracture properties. The presented procedure covers the linear, elliptical, pseudoradial, and boundary-dominated flow regimes. New equations describing the elliptical flow regime and the flow behavior during the transition time from the pseudoradial regime to the fully developed boundary-dominated regime are presented. Moreover, new equations for calculating the fracture and formation properties are developed. Two examples are utilized to demonstrate the implementation of the method and its efficiency in reducing the wellbore storage effect and providing accurate well test results.

Reservoir and fractured well modeling

The investigated reservoir has a single layer with constant thickness and uniform and invariant formation properties. A massive vertical hydraulic fracture penetrates the entire producing zone. The tested well produces single-phase oil at a constant bottomhole pressure.

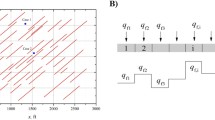
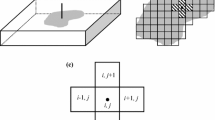
The reservoir model is divided into four identical quadrants and the well is in the center of the reservoir. The gridding network used in the simulation is identical to the networks used by Morse and Von Gonten (1972), Agarwal et al. (1979), and Nashawi (2008). Figure 1 shows a schematic illustration of the gridding mesh surrounding the vertical fracture in the bounded square reservoir (Nashawi 2008). The fine grid cells near the fracture and parallel to the fracture face enable precise prediction of the flow regime performance. Furthermore, the small grids perpendicular to the fracture near the well and fracture tips allow accurate description of the fluid flow behavior in these vital locations, with high pressure gradients occurring in the reservoir near the fracture. The grid size parallel to the fracture face increases exponentially toward the outer reservoir boundary.

Fig. 1

Schematic of the gridding mesh near a vertical fracture in a bounded square reservoir

The numerical simulator used in this work is a two-dimensional finite-difference single-phase model for simulating fluid flow behavior reservoirs. The simulation can be performed with either x–y or r–z geometries (Lee and Wattenbarger 1996). Although this simulator was initially developed to simulate real gas flow behavior in reservoirs, Rattu (2002) presented numerous detailed examples to demonstrate that the model could be easily modified to accurately simulate black oil in homogenous, fractured, layered reservoirs, and HF wells.

Reservoir and fracture properties

The following reservoir and fracture properties were adopted in the simulation:

• 1. The producing formation is bounded by upper and lower impermeable layers. It has a constant thickness, h, porosity, ϕ, and permeability, k.

• 2. The well is intercepted by a massive infinite-conductivity vertical fracture that fully penetrates the pay zone.

• 3. The fracture is modeled by a rectangular slab with constant fracture length, 2x_f, width, w_f, and permeability, k_f.

• 4. The fracture half-length, x_f, is less than the reservoir drainage radius, x_e. This ensures that the pseudoradial flow regime occurs during the well test.

• 5. The fractured well produces single-phase oil under constant bottomhole pressure conditions.

Theoretical and mathematical considerations

Fluid flow behavior near a hydraulically fractured well and the surrounding formation highly depends on the type of created fracture, which could have finite or infinite conductivity. For infinite-conductivity fractures in closed systems, the major flow regimes that may evolve include fracture and formation linear flow regimes, elliptical flow regimes, and pseudoradial flow regimes; moreover, for sufficiently long tests, boundary-dominated flow regimes may also appear.

The fracture linear flow regime diminishes quickly and is often dominated by wellbore storage effects. Nevertheless, when this regime prevails, the equations describing its flow behavior and data analysis methodology are exactly the same as those used for the formation linear flow regime. The elliptical flow regime and the transition to the pseudoradial flow regime were well described by Kucuk and Brigham (1979).

The subsequent sections present the mathematical formulation of the working equations corresponding to the linear, elliptical, pseudoradial, and boundary-dominated flow regimes and the methodology required to determine the different reservoir and fracture properties.

Dimensionless equations

Dimensionless equations are often used in well test analysis to represent the various analytical solutions in precise and concise forms. The subsequent dimensionless equations are vital to this study.

Dimensionless time

Many forms of dimensionless time are used in well test analysis. The differences among the various forms are dictated by the specific application goal. The following equations are used in this investigation.

Dimensionless time, t _D

The dimensionless time t_D is defined as:

$$t_{D} = \frac{0.0002637\,k\,t}{{\phi \mu \,c_{t} r_{w}^{2} }}$$

(1)

This form is based on the wellbore radius, r_w. It is the most commonly used form in reservoir characterization.

Dimensionless time, t _DA

t_DA is related to the drainage area, A, of the well. It is defined as:

$$t_{{{\text{DA}}}} = \frac{0.0002637\,k\,t}{{\phi \mu \,c_{t} A}}$$

(2)

Dimensionless time, t _Dxf

t_Dxf is related to the fracture half-length, x_f. It is defined as:

$$t_{{{\text{Dxf}}}} = \frac{0.0002637\,k\,t}{{\phi \mu \,c_{t} x_{f}^{2} }}$$

(3)

This form is frequently used in well test analysis of HF wells.

Dimensionless fracture conductivity

The dimensionless fracture conductivity, F_CD, is defined as:

$$F_{{{\text{CD}}}} = \frac{{k_{f} w_{f} }}{{k\,x_{f} }}$$

(4)

F_CD is used to specify the type of fracture created by the hydraulic fracturing in the stimulation. For infinite-conductivity fractures, F_CD is greater than or equal to 100π (F_CD ≥ 100π).

Dimensionless production rate

The dimensionless rate, q_D, is defined as:

$$q_{D} = \frac{141.2\,\,qB\mu }{{kh(p_{i} - p_{wf} )}}$$

(5)

q_D is used for constant-pressure well test analyzes and decline curve analyzes.

Analysis of the fracture and formation linear flow regimes

Two distinct linear flow regimes occur during well test of infinite-conductivity HF wells. The first linear flow regime occurs in the fracture itself, while the other linear flow regime occurs in the area adjacent to the fracture, as shown in Fig. 2. Both regimes are modeled by the same analytical equation; consequently, identical analysis techniques are used to investigate both flow regime periods.

Fig. 2

a Fracture and b formation linear flow regimes

In the linear flow regime, the dimensionless reciprocal rate is defined as (Earlougher 1977):

$$\frac{1}{{q_{D} }} = \frac{\pi }{2}\sqrt {\pi \,t_{Dxf} }$$

(6)

Substituting Eqs. (3) and (5) into Eq. (6) and solving for 1/q yields:

$$\frac{1}{q} = \frac{6.3838\,B}{{\,h(p_{i} - p_{wf} )}}\sqrt {\frac{\mu }{{\phi \,c_{t} x_{f}^{2} k}}t}$$

(7)

Define:

$$\,m_{L} = \frac{6.3838\,B}{{h\left( {p_{i} - p_{wf} } \right)}}\sqrt {\frac{\mu }{{\phi \,c_{t} x_{f}^{2} k}}}$$

(8)

Then, Eq. (7) can be rewritten as:

$$\frac{1}{q} = m_{L} \sqrt t$$

(9)

The subscript L designates linear flow.

For the constant bottomhole pressure test, a log–log plot of 1/q versus t should yield a half-slope straight line during the linear flow period. Similarly, a Cartesian plot of 1/q versus t^1/2 should also yield a straight line. The slopes of the log–log plot and the Cartesian plot are both equal to m_L, which is defined in Eq. (8). The Cartesian plot is normally used in conventional constant-pressure analyzes of infinite-conductivity HF wells.

In conventional analyzes, the fracture half-length, x_f, is determined based on the slope of the Cartesian plot as:

$$x_{f} = \frac{6.3838\,B}{{h\left( {p_{i} - p_{wf} } \right)m_{L} }}\sqrt {\frac{\mu }{{\phi \,c_{t} k}}}$$

(10)

Equation (9) can be rewritten as:

$$\log \left( \frac{1}{q} \right) = 0.5\log (t) + \log (m_{L} )$$

(11)

For t = 1 h, Eq. (11) becomes:

$$m_{L} = \left( \frac{1}{q} \right)_{{{\text{L1hour}}}}$$

(12)

Combining Eqs. (8) and (12) and solving explicitly for x_f yields:

$$x_{f} = \frac{6.3838\,B}{{\left( \frac{1}{q} \right)_{{{\text{L1hour}}}} h\left( {p_{i} - p_{wf} } \right)}}\sqrt {\frac{\mu }{{\phi \,c_{t} k}}}$$

(13)

Moreover, x_f can be determined based on the reciprocal rate derivative curve. Differentiating Eq. (9) with respect to time yields:

$$- t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}} = 0.5m_{L} \sqrt t$$

(14)

Equation (14) can be rewritten as:

$$\log \left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right) = 0.5\log (t) + \log (0.5m_{L} )$$

(15)

Equation (15) indicates that a log–log plot of –t(1/q²)dq/dt versus t should also yield a half-slope straight line during the linear flow period, similar to the log–log plot of the reciprocal rate (Eq. 11).

Substituting t = 1 h in Eq. (15) and solving for m_L yields:

$$m_{L} = 2\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{L1{\text{hour}}}}$$

(16)

Solving Eqs. (8) and (16) for x_f yields:

$$x_{f} = \frac{3.1919B}{{\left( { - t\frac{1}{{q^{2} }}\frac{dq}{{dt}}} \right)_{{L1{\text{hour}}}} h(p_{i} - p_{wf} )}}\sqrt {\frac{\mu }{{\phi \,c_{t} k}}}$$

(17)

Hydraulically fractured wells in bounded systems

The dimensionless reciprocal rate equation describing the linear flow behavior of infinite-conductivity HF wells in bounded systems is defined as:

$$\frac{1}{{q_{D} }} = \frac{\pi }{2}\sqrt {\pi \left( {\frac{A}{{x_{f}^{2} }}} \right)t_{{{\text{DA}}}} }$$

(18)

Equation (18) indicates that during the linear flow period, a log–log plot of 1/q_D versus t_DA should produce a half-slope line.

Differentiating Eq. (18) with respect to t_DA yields:

$$- t_{DA} \frac{1}{{q_{D}^{2} }}\frac{{{\text{d}}q_{D} }}{{t_{DA} }} = \frac{\pi }{4}\sqrt {\pi \left( {\frac{A}{{x_{f}^{2} }}} \right)t_{{{\text{DA}}}} }$$

(19)

Similar to the cases of the reciprocal rate (Eq. 9) and the reciprocal rate derivative (Eq. 14), a log–log plot of the dimensionless rate derivative of HF wells in bounded systems should also produce a half-slope straight line during the linear flow regime period.

Equation (19) is applicable to HF wells in bounded cylindrical reservoirs. For square systems, Eq. (19) can be written as:

$$- t_{DA} \frac{1}{{q_{D}^{2} }}\frac{{{\text{d}}q_{D} }}{{{\text{d}}t_{{{\text{DA}}}} }} = \frac{\pi }{2}\left( {\frac{{x_{e} }}{{x_{f} }}} \right)\sqrt {\pi \,t_{{{\text{DA}}}} }$$

(20)

Analysis of the elliptical flow regime

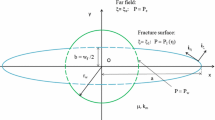
Fluid flow in homogeneous systems is usually radial. However, when areal anisotropy is present in the reservoir, the radial flow geometry is distorted. The inner geometry of the well can also alter the radial flow geometry and change the flow pattern from radial to an elliptical flow regime. One of the many cases in which elliptical flows are encountered is near an infinite-conductivity fractured well (Kucuk and Brigham 1979). Figure 3 shows a schematic illustration of elliptical flow lines around a fractured well.

Fig. 3

Elliptical flow regime

For an infinite-conductivity fractured well producing from a bounded system under constant bottomhole pressure conditions, a log–log plot of the reciprocal rate derivative exhibits a straight line immediately after the end of the linear flow period, indicating the presence of an elliptical flow regime. Tiab (1994) and Escobar et al. (2014) noted the presence of the elliptical flow regime and called it biradial flow. Extensive simulations with various bounded systems and fracture parameters were conducted in this study to derive an analytical equation that best describes the elliptical flow behavior. Regression analyzes of the simulation data illustrate that the elliptical flow regime is best described by a straight line with a slope of 0.3345. Analytical analyzes of the various cases proved that this slope provides a good match between the simulated input parameters and the calculated parameters, as illustrated in the presented examples. The following equation efficiently describes the elliptical flow regime in square systems:

$$- t_{{{\text{DA}}}} \frac{1}{{q_{D}^{2} }}\frac{{dq_{D} }}{{dt_{{{\text{DA}}}} }} = 0.89214\left( {\frac{{x_{e} }}{{x_{f} }}} \right)^{0.66899} t_{{{\text{DA}}}}^{0.3345}$$

(21)

Using Eqs. (3) and (5), Eq. (21) can be written for a real rate and time as:

$$- t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}} = 5.03199\left[ {\frac{B}{{h\left( {p_{i} - p_{wf} } \right)}}} \right]\left( {\frac{\mu }{k}} \right)^{0.6655} \left( {\frac{1}{{\phi \,c_{t} x_{f}^{2} }}} \right)^{0.3345} t^{0.3345}$$

(22)

Let:

$$m_{E} = 5.03199\left[ {\frac{B}{{h(p_{i} - p_{wf} )}}} \right]\left( {\frac{\mu }{k}} \right)^{0.6655} \left( {\frac{1}{{\phi \,c_{t} x_{f}^{2} }}} \right)^{0.3345}$$

(23)

Then, Eq. (22) can be written as:

$$- t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}} = m_{E} \,t^{0.3345}$$

(24)

where the subscript E designates elliptical flow.

Equation (24) can be written as:

$$\log \left( { - t\frac{1}{{q^{2} }}\frac{dq}{{dt}}} \right) = 0.3345\log (t) + \log (m_{E} )$$

(25)

A log–log plot of –t(1/q²)dq/dt versus t should yield a straight line with a slope of 0.3345 during the elliptical period.

For t = 1 h, Eq. (25) becomes:

$$m_{E} = \left( { - t\frac{1}{{q^{2} }}\frac{dq}{{dt}}} \right)_{{E1{\text{hour}}}}$$

(26)

Solving Eqs. (23) and (26) for x_f yields:

$$x_{f} = 11.1932\left[ {\frac{B\,}{{\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{E1{\text{hour}}}} h\left( {p_{i} - p_{wf} } \right)}}} \right]^{1.4948} \left( {\frac{\mu }{k}} \right)^{0.9948} \left( {\frac{1}{{\phi \,c_{t} }}} \right)^{0.5}$$

(27)

The elliptical flow behavior is often not easily recognized on reciprocal rate plot. However, for the cases in which the elliptical flow regime is well defined, the behavior can be described by the following equation:

$$\frac{1}{q} = 15.04332\left[ {\frac{B}{{h\left( {p_{i} - p_{wf} } \right)}}} \right]\left( {\frac{\mu }{k}} \right)^{0.6655} \left( {\frac{1}{{\phi \,c_{t} x_{f}^{2} }}} \right)^{0.3345} t^{0.3345}$$

(28)

Substituting Eq. (23) into Eq. (28) yields:

$$\frac{1}{q} = 2.98954\,m_{E} \,t^{0.3345}$$

(29)

Equation (29) can be written as:

$$\log \left( \frac{1}{q} \right) = 0.3345\,\log (t) + \log (2.98954\,m_{E} )$$

(30)

A log–log plot of 1/q versus t should yield a straight line with a slope of 0.3345 during the elliptical flow period.

For t = 1 h, Eq. (30) becomes:

$$m_{E} = 0.3345\left( \frac{1}{q} \right)_{{E1{\text{hour}}}}$$

(31)

Solving Eqs. (23) and (31) for x_f yields:

$$x_{f} \, = 57.5249\left[ {\frac{B}{{\left( \frac{1}{q} \right)_{{E1{\text{hour}}}} h(p_{i} - p_{wf} )}}} \right]^{1.4948} \left( {\frac{\mu }{k}} \right)^{0.9948} \left( {\frac{1}{{\phi \,c_{t} }}} \right)^{0.5}$$

(32)

Thus, the technique presented in this paper provides four different options for calculating x_f. Two options use the log–log plot of the reciprocal rate data: the first option is based on the slope of the linear flow regime (Eq. 13), and the second option is based on the slope of the elliptical flow regime (Eq. 32). The other two options use the log–log plot of the reciprocal rate derivative: the first option is based on the slope of the linear flow regime (Eq. 17), and the second option is based on the slope of the elliptical flow regime (Eq. 27). Moreover, x_f can be calculated based on the conventional Cartesian graph of the linear flow regime (Eq. 10). These alternative methods are a major advantage of the proposed method over other conventional methods.

Analysis of the pseudoradial flow regime

During the pseudoradial period, the dimensionless reciprocal rate of a well producing from a cylindrical system under constant pressure conditions is defined as:

$$\frac{1}{{q_{D} }} = 0.5 \, \left[ {\ln (t_{D} ) + 0.80907 + 2\,s} \right]$$

(33)

Substituting Eqs. (1) and (5) into Eq. (33) yields:

$$\frac{1}{q} = \frac{162.6\,B\mu }{{k\,h\left( {p_{i} - p_{wf} } \right)}}\left[ {\log (t) + \log \left( {\frac{k}{{\phi \mu c_{t} r_{w}^{2} }}} \right) - 3.23 + 0.869\,s} \right]$$

(34)

Equation (34) is utilized in constant pressure analyzes to calculate the reservoir permeability and skin factor using a conventional semilog plot of 1/q versus t during the pseudoradial period.

Differentiating Eq. (34) with respect to time yields:

$$\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{R} = \frac{70.6\,B\mu }{{kh\left( {p_{i} - p_{wf} } \right)}}$$

(35)

where the subscript R designates pseudoradial flow.

If the pseudoradial regime occurs during the well test, a log–log plot of –t(1/q²)dq/dt versus t should yield a horizontal line. In this case, Eq. (35) can be used to calculate the formation permeability, k, as follows:

$$k = \frac{70.6\,B\mu }{{h\left( {p_{i} - p_{wf} } \right)\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{R} }}$$

(36)

where [–t(1/q²)dq/dt]_R is any convenient point selected on the horizontal straight line passing through the pseudoradial flow points.

For the cases in which the pseudoradial flow regime does not appear in the log–log plot of the well test data, the technique presented in this work provides an alternative method to calculate k based on the straight lines passing through the linear and elliptical flow regimes. Equations (17) and (27) can be equated to develop a new equation to calculate k that is independent of the pseudoradial regime data as follows:

$$k = 12.6259\left[ {\frac{B\mu }{{h\left( {p_{i} - p_{wf} } \right)}}} \right]\frac{{\left[ {\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{L1{\text{hour}}}} } \right]^{2.021} }}{{\left[ {\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{E1{\text{hour}}}} } \right]^{3.021} }}$$

(37)

The mechanical skin factor, s, can also be calculated based on the pseudoradial flow regime. Taking the ratio of Eqs. (34) and (35) and solving for s yields:

$$s = 1.1513\left[ {0.4343\frac{{\left( \frac{1}{q} \right)_{R} }}{{\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{R} }} - \log \left( {\frac{{k\,t_{R} }}{{\phi \mu c_{t} r_{w}^{2} }}} \right) + 3.23} \right]$$

(38)

Equation (38) can also be expressed in natural logarithm form as:

$$s = 0.5\left[ {\frac{{\left( \frac{1}{q} \right)_{R} }}{{\left( { - t\frac{1}{{q^{2} }}\frac{dq}{{dt}}} \right)_{R} }} - \ln \left( {\frac{{k\,t_{R} }}{{\phi \mu c_{t} r_{w}^{2} }}} \right) + 7.437} \right]$$

(39)

where t_R in Eqs. (38) and (39) is any convenient time during the pseudoradial period. [–t(1/q²)dq/dt]_R and (1/q)_R are selected based on the reciprocal rate derivative and reciprocal rate plots at t_R, respectively.

Well test analysis of a well in a bounded reservoir

The dimensionless reciprocal rate equation describing the flow behavior during the pseudoradial period for a well in a bounded reservoir is defined as:

$$\frac{1}{{q_{D} }} = 0.5 \, \left[ {\ln (t_{{{\text{DA}}}} ) + \ln \left( {\frac{A}{{r_{w}^{2} }}} \right) + 0.80907 + 2\,s} \right]$$

(40)

Differentiating Eq. (40) with respect to t_DA yields:

$$- t_{{{\text{DA}}}} \frac{1}{{q_{D}^{2} }}\frac{{dq_{D} }}{{dt_{{{\text{DA}}}} }} = 0.5$$

(41)

Equation (41) indicates that a horizontal line should be produced in the log–log plot of −t_DA(1/q_D)²dq_D/dt_DA versus t_DA in the pseudoradial flow regime.

Analysis of the boundary-dominated flow regime

When the production effects spread to all external reservoir boundaries, the boundary-dominated flow regime prevails. Under constant bottomhole pressure conditions, the log–log plots of the reciprocal rate and reciprocal rate derivative of the well test data divert from the behavior observed in the horizontal pseudoradial flow regime and exhibit an exponential trend as a function of time.

The dimensionless rate behavior in the boundary-dominated flow regime was presented by Raghavan (1993) as:

$$\frac{1}{{q_{D} }} = a\,{\text{Exp}}\left( {\frac{{2\,\pi \,t_{{{\text{DA}}}} }}{a}} \right)$$

(42)

where a is defined as:

$$a = \frac{1}{2}\ln \left( {\frac{4\,A}{{e^{\gamma \,} C_{A} r_{w}^{2} }}} \right) + s$$

(43)

Differentiating Eq. (42) with respect to t_DA yields:

$$- t_{{{\text{DA}}}} \frac{1}{{q_{D}^{2} }}\frac{{{\text{d}}q_{D} }}{{{\text{d}}t_{{{\text{DA}}}} }} = 2\,\pi \,t_{{{\text{DA}}}} {\text{Exp}}\left( {\frac{{2\,\pi \,t_{{{\text{DA}}}} }}{a}} \right)$$

(44)

Equating Eqs. (41) and (44) yields:

$$t_{{{\text{DA}}}} {\text{Exp}}\left( {\frac{{2\,\pi \,t_{{{\text{DA}}}} }}{a}} \right) = \frac{1}{4\pi }$$

(45)

Equation (45) includes many unknown well and reservoir properties such as the reservoir shape factor, skin factor, and well drainage area. Nashawi and Malallah (2007) conducted comprehensive simulation work for different reservoir geometries, formation properties, and fracture half-lengths to find an accurate t_DA value that fits Eq. (45). Their work showed that a t_DA value of 0.0625 in Eq. (45) is remarkably accurate under various reservoir conditions.

Equation (2) can be utilized to determine the well drainage area, A, during the boundary-dominated flow as follows:

$$A = \frac{0.0002637k\,t}{{\phi \mu \,c_{t} t_{{{\text{DA}}}} }}$$

(46)

Using t_DA = 0.0625, Eq. (46) can be written as:

$$A = \frac{{k\,t_{{{\text{RBD}}}} }}{{237\,\phi \mu \,c_{t} }}$$

(47)

where t_RBD is the intersection time between the reciprocal rate derivative curves in the pseudoradial and boundary-dominated regimes.

Wattenbarger et al. (1998) and El-Banbi and Wattenbarger (1998) demonstrated that the boundary-dominated flow regime begins at a t_DA value of 0.25 on the log–log plot of 1/q_D versus t_DA. Using t_DA = 0.25, Eq. (46) can be written as:

$$A = \frac{{k\,t_{{{\text{bBD}}}} }}{{948\,\phi \mu \,c_{t} }}$$

(48)

where t_bBD denotes the time at which the boundary-dominated period starts on the log–log plot of 1/q versus t.

As previously stated, the boundary-dominated period begins at a t_DA value of 0.0625 on the log–log plot of the reciprocal rate derivative. This time value is four times less than the value proposed by Wattenbarger et al. (1998) and El-Banbi and Wattenbarger (1998) for the reciprocal rate plot. This is a remarkable advantage when calculating the drainage area using Eq. (47) instead of Eq. (48). This is also another advantage of the reciprocal rate derivative plot presented in this study over the conventional reciprocal rate plot.

The boundary-dominated period can also be utilized to determine the reservoir shape factor, C_A. Solving Eq. (43) for C_A yields:

$$C_{A} = \frac{4A}{{e^{\gamma } r_{w}^{2} }}{\text{Exp}}\left( {2s - 2a} \right)$$

(49)

The reciprocal rate derivative during the boundary-dominated period (Eq. 44) can be formulated with real parameters as follows:

$$\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{BD} = 2\pi \,t_{{{\text{DA}}}} \left[ {\frac{141.2\,B\mu }{{kh\left( {p_{i} - p_{wf} } \right)}}} \right]{\text{Exp}}\left( {\frac{{2\pi \,t_{{{\text{DA}}}} }}{a}} \right)$$

(50)

Using Eqs. (35) and (50) and solving for parameter a gives:

$$a = \frac{{2\pi \,t_{{{\text{DA}}}} }}{{\ln \left[ {\frac{{\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{BD} }}{{4\pi \,t_{{{\text{DA}}}} \left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{R} }}} \right]}}$$

(51)

Substituting Eq. (51) into Eq. (49) yields:

$$C_{A} = 2.2459\left( {\frac{A}{{r_{w}^{2} }}} \right){\text{Exp}}\left\{ {2s - \frac{{4\pi \,t_{{{\text{DABD}}}} }}{{\ln \left[ {\frac{{\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{{\text{BD}}}} }}{{\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{R} }}} \right] - \ln \left( {4\pi \,t_{{{\text{DABD}}}} } \right)}}} \right\}$$

(52)

where the subscript BD denotes the boundary-dominated regime. t_DABD can be calculated at any time t_BD in the boundary-dominated period.

For the cases in which the fracture extends to the outer reservoir boundary, the pseudoradial regime does not appear on the reciprocal rate derivative plot. For these cases, C_A can be calculated as follows:

$$C_{A} = 2.2459\left( {\frac{A}{{r_{w}^{2} }}} \right){\text{Exp}}\left[ {2s - (4\pi \,t_{{{\text{DABD}}}} )\frac{{\left( \frac{1}{q} \right)_{BD} }}{{\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{{\text{BD}}}} }}} \right]$$

(53)

where (1/q)_BD and [−t(1/q²)(dq/dt)]_BD can be obtained based on the reciprocal rate and the reciprocal rate derivative curves, respectively, at any time t_BD during the boundary-dominated flow regime.

Furthermore, if the reciprocal rate and the reciprocal rate derivative plots of the well test data intersect during the boundary-dominated flow period, Eq. (53) can be further simplified as follows:

$$C_{A} = 2.2459\left( {\frac{A}{{r_{w}^{2} }}} \right){\text{Exp}}\left( {2s - 4\pi \,t_{{{\text{DABDi}}}} } \right)$$

(54)

where t_DABDi is the dimensionless time corresponding to the intersection of the two curves.

The real-time expression of Eq. (54) can be written as:

$$C_{A} = 2.2459\left( {\frac{A}{{r_{w}^{2} }}} \right){\text{Exp}}\left( {2s - \frac{{0.0033138k\,t_{{{\text{BDi}}}} }}{{\phi \mu c_{t} A}}} \right)$$

(55)

where t_BDi is the intersection time of the two curves during the boundary-dominated flow regime period.

Since the C_A values calculated in Eqs. (52–55) are valid under constant pressure conditions, it is vital to mention that these values should not be compared to the Dietz (1965) shape factor, which is calculated under constant rate conditions. Helmy and Wattenbarger (1998) demonstrated that when Dietz shape factors are applied to constant bottomhole pressure well tests, the production forecasting and oil recovery calculations can have errors as high as 10%.

Well test analysis of rectangular reservoirs

For rectangular systems, the reciprocal rate derivative plot shows a straight line trend during the transition from the pseudoradial regime to the fully developed boundary-dominated regime, indicating the presence of two boundaries parallel to the fracture face. The equation for the straight line is defined as (Malallah et al. 2007):

$$- t_{{{\text{DA}}}} \frac{1}{{q_{D}^{2} }}\frac{{{\text{d}}q_{D} }}{{{\text{d}}t_{{{\text{DA}}}} }} = C\,t_{{{\text{DA}}}}^{0.65}$$

(56)

where the constant C is a function of the reservoir dimensions. Figure 4 displays the behavior of the well test data for several rectangular reservoirs during the transition period.

Fig. 4

Flow behavior of the reciprocal rate derivatives of different rectangular systems in various regimes

For a four-to-one reservoir, Eq. (56) can be represented with a real time and rate as follows:

$$- t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}} = 4.663\left[ {\frac{B}{{h\left( {p_{i} - p_{wf} } \right)}}} \right]\left( {\frac{\mu }{k}} \right)^{0.35} \left( {\frac{1}{{\phi \,c_{t} A}}} \right)^{0.65} t^{0.65}$$

(57)

let:

$$m_{{{\text{CB}}}} = 4.663\left[ {\frac{B}{{h\left( {p_{i} - p_{wf} } \right)}}} \right]\left( {\frac{\mu }{k}} \right)^{0.35} \left( {\frac{1}{{\phi \,c_{t} A}}} \right)^{0.65}$$

(58)

Then, Eq. (57) can be rearranged as:

$$- t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}} = m_{CB} \,t^{0.65}$$

(59)

where the subscript CB designates the nearby boundary parallel to the fracture face.

Equation (59) can be written as:

$$\log \left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right) = 0.65\log (t) + \log (m_{CB} )$$

(60)

For t = 1 h, Eq. (60) becomes:

$$\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{CB1{\text{hour}}}} = m_{CB}$$

(61)

Thus far, in this work, two equations, Eq. (47) and Eq. (48), have been presented to calculate A based on the boundary-dominated flow regime. In this section, another equation is derived based on the straight line passing through the data at the closest parallel boundary. Using Eqs. (58) and (61) and solving for A yields:

$$A = 10.683\left( {\frac{1}{{\phi \,c_{t} }}} \right)\left( {\frac{\mu }{k}} \right)^{\frac{7}{13}} \left[ {\frac{B}{{h\left( {p_{i} - p_{wf} } \right)\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{CB1{\text{hour}}}} }}} \right]^{{\frac{20}{{13}}}}$$

(62)

Moreover, two equations, Eqs. (36) and (37), have been proposed to calculate k. Equation (36) was derived based on the pseudoradial flow regime, while Eq. (37) was derived based on the straight lines observed in the linear and elliptical flow regimes. Here, a third equation is derived based on Eqs. (58) and (61) as follows:

$$k = 81.366\mu \left( {\frac{1}{{\phi \,c_{t} A}}} \right)^{\frac{13}{7}} \left[ {\frac{B}{{h\left( {p_{i} - p_{wf} } \right)\left( { - t\frac{1}{{q^{2} }}\frac{{{\text{d}}q}}{{{\text{d}}t}}} \right)_{{CB1{\text{hour}}}} }}} \right]^{\frac{20}{7}}$$

(63)

The importance of this equation is that it does not require pseudoradial flow data, which is needed in conventional analysis. Thus, it can be used to calculate k even when the pseudoradial flow regime does not occur during the well test.

Intersection points on the straight lines in the various flow regimes

The straight lines drawn through the data points in the various flow regimes in the reciprocal rate derivative plot intersect at distinct and very useful points in the analysis of the well test data. These intersection points are important indicators for confirming the precision of the k, A, and x_f values calculated based on the various flow regimes. Moreover, the intersection points can be applied to calculate these properties when the required flow regimes do not occur in the log–log plot. Figure 5 displays the intersection points among the linear, elliptical, and pseudoradial straight lines for a bounded square system. The subsequent sections present the equations of the intersection points and their important role in the analysis procedure.

Fig. 5

Intersection points of the various flow regimes in the reciprocal rate derivative plot–closed square system

Intersection time between the straight lines in the linear and elliptical flow regimes

The intersection time between the straight lines passing through the linear and the elliptical flow regimes in the reciprocal rate derivative plot (Fig. 5) can be obtained from Eqs. (20) and (21) in dimensionless form as:

$$t_{DA} = 0.0010265\left( {\frac{{x_{f} }}{{x_{e} }}} \right)^{2}$$

(64)

The real-time expression of Eq. (64) can be written as:

$$t_{{{\text{LE}}}} = 15.57027\left( {\frac{{\phi \mu \,c_{t} x_{f}^{2} }}{k}} \right)$$

(65)

Equation (65) can be utilized to confirm the precision of the k value calculated from Eq. (37) and the x_f value calculated from the linear period using Eq. (17) or the elliptical period using Eq. (27).

Intersection time between the straight lines in the linear and pseudoradial flow regimes

The intersection time between the straight lines passing through the linear and pseudoradial flow regimes in the reciprocal rate derivative plot (Fig. 5) can be obtained from Eqs. (19) and (41) in dimensionless form as:

$$t_{{{\text{DA}}}} = \left( {\frac{2}{\pi }} \right)^{2} \left( {\frac{{x_{f}^{2} }}{\pi \,A}} \right)$$

(66)

The real-time expression of Eq. (66) can be written as:

$$t_{{{\text{LR}}}} = 489.2155\left( {\frac{{\phi \mu \,c_{t} x_{f}^{2} }}{k}} \right)$$

(67)

Equation (67) can be utilized to confirm the precision of the x_f and k values calculated from Eqs. (17) and (36), respectively.

Intersection time between the straight lines in the elliptical and pseudoradial flow regimes

The intersection time between the straight lines passing through the elliptical and pseudoradial flow regimes in the reciprocal rate derivative plot (Fig. 5) can be obtained from Eqs. (21) and (41) in dimensionless form as:

$$t_{{{\text{DA}}}} = 0.1771\left( {\frac{{x_{f} }}{{x_{e} }}} \right)^{2}$$

(68)

The real-time expression of Eq. (68) can be written as:

$$t_{{{\text{ER}}}} = 2686.5318\left( {\frac{{\phi \mu \,c_{t} x_{f}^{2} }}{k}} \right)$$

(69)

Equation (69) can be used to confirm the precision of the x_f and k values calculated from Eqs. (27), (36) and (37), respectively, by comparing the value of t_ER obtained from Eq. (69) and the graphically determined value based on the log–log plot of the test data.

Intersection between the straight lines in the linear flow regime and the closest parallel boundary

Figure 6 illustrates the intersection points on the straight lines passing through the various flow regimes for a four-to-one rectangular system. The reciprocal dimensionless rate derivative of a four-to-one rectangular system during the transition period is defined as (Malallah et al. 2007):

$$- t_{{{\text{DA}}}} \frac{1}{{q_{{\text{D}}}^{2} }}\frac{{{\text{d}}q_{{\text{D}}} }}{{{\text{d}}t_{{{\text{DA}}}} }} = 7t_{{{\text{DA}}}}^{0.65}$$

(70)

Fig. 6

Intersection points of the various flow regimes in the reciprocal rate derivative plot–4-to-1 closed rectangular system

The dimensionless time corresponding to the intersection point between the straight line in the linear flow regime and the closest boundary can be determined based on Eqs. (19) and (70) as:

$$t_{{{\text{DA}}}} = \left( {\frac{\pi }{28}} \right)^{\frac{20}{3}} \left( {\frac{\pi \,A}{{x_{f}^{2} }}} \right)^{\frac{10}{3}}$$

(71)

The real-time expression of Eq. (71) can be written as:

$$t_{LCB} = \frac{{\phi \mu \,c_{t} A}}{12.512\,k}\left( {\frac{A}{{x_{f}^{2} }}} \right)^{\frac{10}{3}}$$

(72)

Equation (72) can be utilized to confirm the precision of the x_f, k, and A values calculated based on Eqs. (17), (36) or (37), and (47) or (62), respectively, by comparing the t_LCB value calculated from Eq. (72) with the value determined based on the log–log plot of the test data.

Intersection time between the straight lines in the pseudoradial flow regime and the closest parallel boundary

For four-to-one rectangular systems (Fig. 6), the intersection time between the straight lines passing through the pseudoradial flow regime and the closest parallel boundary can be obtained from Eqs. (41) and (70) as follows:

$$7t_{{{\text{DA}}}}^{0.65} = 0.5$$

(73)

Solving Eq. (73) for t_DA yields:

$$t_{{{\text{DA}}}} = \left( \frac{1}{14} \right)^{{\frac{20}{{13}}}}$$

(74)

Equation (74) can be expressed in real time as:

$$t_{{{\text{RCB}}}} = 65.406\left( {\frac{{\phi \mu \,c_{t} A}}{k}} \right)$$

(75)

Equation (75) has many important applications. This equation can be used to calculate k provided that A is known or to calculate A provided that k is known. Moreover, once the values of k and A are available, Eq. (75) can be used to confirm their accuracies by comparing the t_RCB value computed based on Eq. (75) with the value determined graphically based on the log–log plot of the test data.

Intersection between the straight lines in the elliptical flow regime and the closest parallel boundary

For four-to-one rectangular systems (Fig. 6), the intersection time between the straight lines passing through the elliptical flow regime and the closest parallel boundary can be obtained from Eqs. (21) and (70) as follows:

$$t_{{{\text{DA}}}} = 0.0014598\left( {\frac{{x_{e} }}{{x_{f} }}} \right)^{2}$$

(76)

Equation (76) can be expressed in real time as:

$$t_{{{\text{ECB}}}} = 5.5359\left( {\frac{{\phi \mu \,c_{t} A}}{k}} \right)\left( {\frac{{x_{e} }}{{x_{f} }}} \right)^{2.1204}$$

(77)

Similar to the other intersection time equations presented in this work, Eq. (77) has several applications for the well test analysts. This equation can be used to calculate k provided that A and x_f are known; calculate A provided that k and x_f are known; calculate x_f provided that k and A are known; or confirm the accuracy of these parameters by comparing the t_ECB value calculated from Eq. (77) with the value obtained graphically based on the log–log plot.

The constant values associated with Eqs. (56), (62), (63), (72), (75) and (77) for rectangular reservoirs of different dimensions are presented in Table 1. The intersection points are applied in the analysis of the example well test data.

Table 1 Constants associated with the equations for rectangular reservoirs

Characteristics of the infinite-conductivity vertical fracture

Figures 7 and 8 illustrate the behavior of the reciprocal rate and the reciprocal rate derivative, respectively, of the well test data for infinite-conductivity HF wells in the center of square reservoirs of various dimensions. The two figures clearly show the distinctive behaviors of the linear and boundary-dominated flow regimes. However, the reciprocal rate derivative plot (Fig. 8) is more advantageous than the reciprocal rate plot (Fig. 7) since the unique features of the different flow regimes that may be observed during the well test are clearly visualized. These features are very important for calculating the formation and fracture parameters. The straight lines passing through the linear and elliptical flow regimes can be utilized to compute x_f with either Eq. (13) and Fig. 7 or Eqs. (17) and (27) and Fig. 8. They can also be used to calculate k with Eq. (37). The horizontal line drawn through the pseudoradial flow regime displayed in Fig. 8 can also be utilized to determine k based on Eq. (36) and s based on Eqs. (38) or (39).

Fig. 7

Reciprocal dimensionless rate behavior as a function of dimensionless time

Fig. 8

Reciprocal dimensionless rate derivative behavior as a function of dimensionless time

The exponential trends shown in Figs. 7 and 8 are consistent with the analytical solutions presented in Eqs. (42) and (44) for the reciprocal rate and reciprocal rate derivative, respectively. This graphical behavior is a characteristic feature of the boundary-dominated regime. The well test measurements collected during this period can be utilized to determine A based on either Eq. (47) and Fig. 8 or Eq. (48) and Fig. 7. Moreover, C_A can be calculated using either the reciprocal rate derivative plot alone or the reciprocal rate and reciprocal rate derivative plots, as formulated in Eqs. (52–55). Furthermore, the intersection time t_LR (Eq. (67)) between the straight lines in the linear and pseudoradial flow regimes is critical in the proposed methodology. This intersection time can be utilized to confirm the precision of the x_f and k values calculated based on Eqs. (17) and (36), respectively. The intersection time t_ER (Eq. 69) between the straight lines in the elliptical and pseudoradial flow regimes is also important, and t_ER can be used to validate the accuracy of the x_f and k values calculated based on Eqs. (27) and (36), respectively.

The straight line drawn through the transition data points on the reciprocal rate derivative plot (Fig. 8) can be utilized to either calculate k with Eq. (63) provided that A is known or calculate A based on Eq. (62) provided that k is known during the pseudoradial period (Eq. (36)) or the linear and elliptical flow periods (Eq. 37). Moreover, the transition straight line intersects the straight line in the linear, elliptical, and pseudoradial flow regimes at three distinctive times (Fig. 6). The first intersection time, t_LCB, defined by Eq. 72, can be utilized to validate the results obtained from the straight lines in the linear and transition periods. The second intersection time, t_ECB, defined by Eq. (77), can be used to confirm the results obtained from the straight lines in the elliptical and transition periods. Moreover, t_LCB and t_ECB can both be used to calculate the fracture and reservoir parameters. Finally, the third intersection time, t_RCB, defined by Eq. (75), has multiple advantages in the analysis methodology. This value can be used to either calculate A provided that k is known or calculate k provided that A is known. Moreover, this value can be used to confirm the accuracy of the two calculated values.

Therefore, our proposed method provides well test analysts with several alternatives for calculating x_f based on Eq. (13), (17), or (27), k based on Eq. (36), (37), or (63), C_A based on Eq. (52–55), and A based on Eq. (47), (48), or (62). These multiple options demonstrate the great advantage of the proposed method over conventional schemes. Furthermore, it is worth mentioning that the time required to determine A using the equation presented in this work (Eq. 47) is four times shorter than the time required to calculate A using Eq. (48) proposed by Wattenbarger et al. (1998) and El-Banbi and Wattenbarger (1998).

Applications

Two synthetic cases are analyzed to illustrate the applicability and effectiveness of the proposed technique with HF wells in the center of bounded systems. The first case represents a well producing from a square reservoir, while the second case represents a well producing from a four-to-one rectangular reservoir. The main oil, reservoir, and fracture properties of the two examples are listed in Table 2.

Table 2 Fluids, fracture, well, and reservoir properties

Synthetic case no. 1

This case represents an oil well produced at a constant bottomhole pressure of 2900 psi. A vertical infinite-conductivity hydraulic fracture with an x_f value of 125 ft intercepts the well and penetrates the entire 150 ft thick pay zone. The reservoir has a permeability of 1 mD.

The reciprocal rate and reciprocal rate derivative data for this well test are displayed in Fig. 9. The reciprocal rate derivative plot shows that the data are influenced by the reservoir outer boundary starting at 584 h during the well test. The reciprocal rate derivative plot exhibits a half-slope straight line, a 0.3345 slope straight line, a horizontal straight line, and exponential behavior, indicating the existence of all four flow regimes: linear, elliptical, pseudoradial, and boundary-dominated. Moreover, the reciprocal rate plot displays a half-slope straight line at the beginning of the test and exponential behavior at the end of the test, reflecting the presence of linear and boundary-dominated flow regimes; however, the elliptical and pseudoradial flow regimes are not clearly visible in this plot.

Fig. 9

Reciprocal rate and reciprocal rate derivative behavior as a function of time–synthetic case no. 1

Two points at one hour during the well test, (1/q)_L1hour = 0.00513 (STB/D)⁻¹ and [−t(1/q²)dq/dt]_L1hour = 0.002565(STB/D)⁻¹, were selected from the straight lines in the linear flow regime in the reciprocal rate and reciprocal rate derivative plots, respectively. These values are used to calculate x_f with Eqs. (13) and (17). Both equations yield an x_f value of 125 ft. This value is exactly the same as the input value for the simulation. A third point at 1 h was also selected from the straight line in the elliptical flow regime in the reciprocal rate derivative plot, [-t(1/q²)dq/dt]_E1hour = 0.001809 (STB/D)⁻¹. Substituting this value into Eq. (27), x_f was calculated to be 125.05 ft. To calculate k based on the reciprocal rate derivative data in the linear and elliptical flow regimes, the same values that were previously selected in these flow regimes at 1 h were substituted into Eq. (37). The calculation yielded a k value of 1 mD, which is identical to the input value for the simulation. As previously discussed, k can also be calculated based on the reciprocal rate derivative data in the pseudoradial flow regime. Any convenient point on the horizontal line drawn through the pseudoradial flow regime can be used to calculate this value. In this study, the intersection point between the horizontal line and the y-axis, [-t(1/q²)dq/dt]_R = 0.0049 (STB/D)⁻¹, was selected. Using Eq. (36), k was calculated to be 1.02 mD.

To determine s, two points in the pseudoradial flow period at t = 100 h in Fig. 9 were selected. One point was selected from the reciprocal rate plot, (1/q)_R = 0.02 (STB/D)⁻¹, while the other point was selected from the reciprocal rate derivative plot, [-t(1/q²)dq/dt]_R = 0.0049 (STB/D)⁻¹; then, s was calculated to be -4.504 and -4.507 using Eqs. (38) and (39), respectively.

A close inspection of Fig. 9 indicates that the boundary-dominated period starts at t_RBD = 584 h in the reciprocal rate derivative plot and at t_bBD = 2350 h in the reciprocal rate plot. Using these values, A was calculated to be 5,059,214 ft² and 5,089,535 ft² using Eqs. (47) and (48), respectively. The first calculated area is very similar to the actual input area, with a relative error of 0.06%, while the latter value has a relative error of 0.5%.

To complete the analysis, C_A was calculated using Eqs. (52–55). To use Eq. (52), two readings at arbitrary times t_BD in the boundary-dominated flow regime on the reciprocal rate derivative plot are needed. Therefore, [−t(1/q²)dq/dt]_BD = 0.065562 (STB/D)⁻¹ and [−t(1/q²)dq/dt]_R = 0.0049 (STB/D)⁻¹ were selected at t_BD = 3550 h from the exponential curve and the horizontal line, respectively. Using these values, C_A was determined to be 44.8. To calculate C_A with Eq. (53), (1/q)_BD = 0.065985 (STB/D)⁻¹ was chosen from the reciprocal rate plot at the same t_BD value used for Eq. (52). Substituting this value along with the value previously selected on the horizontal line (0.0049 (STB/D)⁻¹) into Eq. (53), C_A was calculated to be 45.03. Finally, to calculate C_A with Eq. (55), the intersection time t_BDi between the reciprocal rate and reciprocal rate derivative curves was determined to be 3574 h based on Fig. 9. Substituting t_BDi into Eq. (55) yields a C_A value of 44.96. The various calculations demonstrate that all computed values of C_A are consistent. Thus, the proposed method allows well test analysts to select the equation that best suits their need. However, Eq. (55) is the simplest equation to use to calculate this value.

As shown in Fig. 9, the horizontal straight line drawn through the pseudoradial flow data intersects the straight lines in the linear and elliptical flow regimes at t_LR = 3.65 h and t_ER = 19.69 h, respectively. These inputs were used to confirm the accuracy of the fracture and reservoir parameters calculated based on these flow regimes by comparing the graphically obtained results with the values calculated using the proposed equations. For instance, using x_f = 125 ft and k = 1.02 mD, which were calculated with Eqs. (17) and (36), respectively, t_LR was calculated to be 3.72 h based on Eq. (67). Similarly, a t_ER value of 20.44 h was calculated using Eq. (69). The computed values of t_LR and t_ER are consistent with the values determined graphically from Fig. 9. This agreement between the graphical and calculated values demonstrates that the computed values of x_f and k are accurate. Similarly, Fig. 9 indicates that the straight lines in the linear and elliptical flow regimes intersect at t_LE = 0.12 h. Using the values of x_f = 125 ft and k = 1 mD calculated based on the linear and elliptical flow regimes, a t_LE value of 0.12 h was calculated based on Eq. (65). This consistency between the graphical and analytical values of t_LE proves that the calculated values of x_f and k are accurate.

The calculated reservoir and fracture properties for this example are summarized in Table 3. The reported results clearly show that the properties calculated using the different equations are consistent with each other and the simulation parameters.

Table 3 Results of synthetic case no. 1

Synthetic case no. 2

The objective of this example is to illustrate the application of the proposed method to a rectangular system. For this purpose, a bounded four-to-one reservoir with a formation permeability of 3 mD and a pay zone thickness of 150 ft is used. The well, which is in the center of the reservoir, is intercepted by a massive infinite-conductivity vertical hydraulic fracture with a fracture half-length of 250 ft. The tested well produces oil at a constant bottomhole pressure of 2900 psi.

The reciprocal rate and reciprocal rate derivative plots based on the well test data are illustrated in Fig. 10. In addition to the linear, elliptical, pseudoradial, and boundary-dominated flow periods, the reciprocal rate derivative plot indicates the presence of a no-flow boundary parallel to the direction of the fracture. This no-flow barrier is identified by a well-defined straight line during the transition period from the pseudoradial flow regime to the fully developed boundary-dominated flow regime.

Fig. 10

Reciprocal rate and reciprocal rate derivative behavior as a function of time–synthetic case no. 2

To compute x_f based on Eqs. (13) and (17), two points at 1 h of the test were selected from the straight lines passing through the linear flow data. One point was selected from the reciprocal rate plot, (1/q)_L1hour = 0.0014808 (STB/D)⁻¹, while the other point was selected from the reciprocal rate derivative plot, [−t(1/q²)dq/dt]_L1hour = 0.0007404 (STB/D)⁻¹. Substituting these values into Eqs. (13) and (17), both equations yield x_f values of 250.01 ft. Similarly, [-t(1/q²)dq/dt]_E1hour = 0.0005478 (STB/D)⁻¹ was selected from the straight line passing through the elliptical flow data in the reciprocal rate derivative plot. Using this value, x_f was computed to be 250.01 ft based on Eq. (27). This value is exactly the same as those computed based on the linear flow regimes. The relative errors between the calculated values of x_f and the actual input value are all less than 0.006%. The same values previously selected from the linear and elliptical flow regimes at 1 h were used to compute k based on Eq. (37). The calculation showed that k = 3 mD. This value is consistent with the input value for the simulation. The straight line passing through the pseudoradial flow data was also used to calculate k using Eq. (36). For this purpose, [-t(1/q²)dq/dt]_R = 0.001575 (STB/D)⁻¹ was selected from the pseudoradial straight line and substituted in Eq. (36). The calculation yielded k = 3.17 mD. The pseudoradial period was also used in conjunction with the linear period to calculate s. (1/q)_R = 0.005389 (STB/D)⁻¹ was selected from the reciprocal rate plot at t = 54 h; then, s was computed with Eqs. (38) and (39). Both equations yielded identical values of −5.786.

To calculate the drainage area, A, [−t(1/q²)dq/dt]_CB1hour = 0.0000765 (STB/D)⁻¹ was selected from the straight line drawn through the data points in the transition period. Substituting this value into Eq. (62), A was calculated to be 10,255,925 ft². This value is very similar to the actual value, with a relative error of less than 0.16%. Importantly, the fully developed boundary-dominated flow regime for this type of reservoir requires a long production time to appear on the test plot; hence, it is impractical to calculate the drainage area with the conventional methods. Thus, Eq. (62) presented herein is another advantage of the proposed method over conventional techniques.

Finally, C_A can be computed using Eqs. (52), (53), or (55). To use Eq. (52), two points were selected from Fig. 10 at 9950 h of the well test. [-t(1/q²)dq/dt]_R = 0.001575 (STB/D)⁻¹ and [-t(1/q²)dq/dt]_BD = 0.69895 (STB/D)⁻¹ were selected from the pseudoradial and boundary-dominated periods, respectively. Using these points, C_A was calculated to be 4.36. Equation (53) also requires two readings from Fig. 10. Both readings were taken from the boundary-dominated flow period at 3500 h. One point was selected from the reciprocal rate curve, (1/q)_BD = 0.035697 (STB/D)⁻¹, and the other point was selected from the reciprocal rate derivative curve, [-t(1/q²)dq/dt]_BD = 0.038557(STB/D)⁻¹. Using these points, C_A was calculated to be 4.32 based on Eq. (53). Equation (55) is the simplest equation to calculate C_A. This equation requires only the intersection time, t_BDi, between the reciprocal rate and reciprocal rate derivative curves. A close inspection of Fig. 10 reveals that t_BDi = 3225 h. Using this time value, C_A was computed to be 4.49 based on Eq. (55). Thus, the technique presented in this work not only provides good results but is also efficient since it is impractical to run very long well tests to reach the fully developed boundary-dominated regime, which is needed for this type of reservoir to calculate the drainage area of the well and the reservoir shape factor.

To further prove the accuracy of the fracture and reservoir parameters calculated with the various equations, the intersection points of the straight lines passing through the various flow regimes were computed by substituting the calculated parameters into the appropriate equations; then, the results were compared with the graphically obtained values. Using x_f = 250.01 ft and k = 3 mD, t_LE = 0.16 h was calculated based on Eq. (65). This value is exactly the same as the graphically determined value based on Fig. 10. Similarly, using x_f = 250.01 ft and k = 3.17 mD, t_LR = 4.79 h and t_ER = 26.31 h were computed with Eqs. (67) and (69), respectively. These values are in good agreement with t_LR = 4.52 h and t_ER = 23.50 h obtained from Fig. 10. Finally, t_RCB = 105.12 h was calculated with Eq. (75) using the k and A values calculated with Eqs. (36) and (62), respectively. This value is consistent with t_RCB = 104.94 h obtained from Fig. 10. Consequently, the good match between the analytically obtained intersection times using the x_f, k, and A values calculated based on the various flow regimes and the graphically obtained values from Fig. 10 confirms the precision of the calculated parameters.

All results obtained from this case are presented in Table 4. The calculated reservoir and fracture properties displayed in the table illustrate the effectiveness and excellent results of the proposed technique.

Table 4 Results of synthetic case no. 2

Conclusions

The important conclusions of this study can be summarized as follows:

• 1. The presented technique is straightforward and simple. No type curves or regression analyzes are needed, which guarantees the uniqueness of the calculated parameters.

• 2. The fracture and reservoir properties, such as the fracture half-length, x_f, permeability, k, skin factor, s, well drainage area, A, and reservoir shape factor, C_A, are computed directly using the log–log plots of the reciprocal rate and reciprocal rate derivative of the well test data.

• 3. Equations describing the behavior of the different flow regimes observed during well tests of infinite-conductivity HF wells are established and utilized to accurately determine the various fracture and reservoir properties.

• 4. Since the proposed method is based on a constant bottomhole pressure approach, wellbore effects are diminished, allowing the interpretation of early well test measurements and good characterization of the reservoir near the wellbore.

• 5. The intersection points of the characteristic straight lines offer an exceptional opportunity to confirm the precision of the calculated parameters and to compute some of the unknown fracture and/or reservoir properties for the cases in which the required flow regime is not observed in the test plots.