1 Introduction

Mixture experiments involve mixing of different ingredients to form end products. In these experiments, the response depends on the proportions of the ingredients present in the mixture and not on the total amount of the mixture. For example, the cleaning power of a detergent which is formed by mixing Alcohol Ethoxylate, Alkyl Ethoxy Sulphate, Amine Oxide, Carboxymethyl Cellulose (CMC), Citric Acid, Cyclodextrin, Diethyl Ester Dimethyl Ammonium Chloride, Ethanol, Hydrogen Peroxide, Percarbonate, Sodium carbonate, Sodium Hypochlorite, Zinc Phthalocyanine Sulphonate (ZPS) depends on the proportions of these ingredients in the detergent.

Quenouille (1953) led the foundation of a mixture experiments. For a mixture with s components or ingredients, if \({\text{x}}_{{\text{i}}}\) represents the proportion of the \({\text{ith}}\) component in the mixture, then

$$0 \le {\text{x}}_{{\text{i}}} \le 1{ },{\text{ i}} = 1,2,{ } \ldots { },{\text{s}}$$
(1)

with \(\mathop \sum \nolimits_{{{\text{i}} = 1}}^{{\text{s}}} {\text{x}}_{{\text{i}}} = {\text{x}}_{1} + {\text{x}}_{2} + \ldots + {\text{x}}_{{\text{s}}} = 1\)

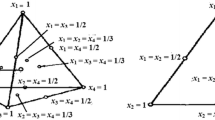
The factor space for the s component mixture is the \(\left( {s - 1} \right)\) dimensional simplex \(S_{s - 1}\) given by

$$S_{s - 1} = \left\{ {x = \left( {x_{1} ,x_{2} , \ldots ,x_{s} } \right):\mathop \sum \nolimits_{i = 1}^{s} x_{i} = 1, x_{i} \ge 0} \right\}.$$

The term simplex design was first used by Claringbold (1955) during his study on joint action of hormones. Scheffé (1958, 1963) introduced simplex lattice and simplex centroid designs with corresponding associated models. Mixture experiments have wide applications in different fields. Bezerra et al. (2020) used mixture design in chemometric for optimization of any stage of an analytical method. Zhou et al. (2007) used mixture designs to design the formulation of pure cultures in Tibetan Kefir. Bahram Parvar et al. (2015) discussed application of simplex centroid design to optimize stabilizer combinations for ice cream manufacture. For more details on mixture experiments see Cornell (2011).

In many pharmaceuticals and petrochemicals industries there is a need of large number of design points that are scattered uniformly over the experimental region. Fang (1980) and Wang and Fang (1981) were the first to introduce uniform design based on Quasi Monte Carlo method and Number-Theoretic net (NT-net) method. Uniform design is obtained by using the concept of U-type design based on NT-net design. The NT-net design is obtained by using good lattice point (glp) generator. There are several other methods defined in literature for obtaining NT-net design. However, glp method is used because of its economic computation and good performance (Hua and Wang (1981) and Shaw (1988)). Zhou and Xu (2015) have also mentioned that the design obtained by using the glp generator possesses low discrepancy. The glp method was proposed by Korobov (1959a, 1959b) and was further discussed by Hua and Wang (1981), Fang and Wang (1994). Fang and Wang (1994) and Borkowski and Piepel (2009) introduced distance-based criteria to measure the uniformity of a design. Ning et. al. (2011) gave \({\text{DM}}_{2}\)-discrepancy to measure the uniformity of a mixture design.

Often experimenter is not interested in mixture combinations in entire simplex rather, the interest lies in a smaller subregion inside the simplex (see Cornell 2011, pp 108). One such region can be spherical region. In response surface methodology, extensive research exists for designs in spherical regions. In Box-Behnken designs (Box and Behnken (1960)) and hybrid designs of Roquemore (1976) spherical region is considered. Talke and Borkowski (2016) proposed a method for the generation of the uniform design in 2-and 3-dimensional spherical regions. Lai et al. (2021) used coordinate descent method to construct uniform designs over continuous domain in computer experiments. Uniform mixture designs can be useful for dealing with multi response problem (see Menchaca-Mendez et al. (2022)).

Now question arises, is it possible to construct uniform mixture designs in higher dimensional space using the designs in lower dimensional spherical region. In this paper, a method is proposed for obtaining the uniform designs in s-dimensional spherical region using the design in 2-dimensional spherical region given by Talke and Borkowski (2016). The discrepancy of the constructed designs is measured using three distance-based criteria. The constructed designs are then transformed into mixture designs using the transformation proposed for this purpose. The uniformity of the mixture designs is computed by D \({\text{M}}_{2}\)-discrepancy and the design with minimum value is selected.

The paper is organized as follows. In Sect. 2, various measures of uniformity are described. In Sect. 3, a method is proposed for obtaining the design in s- dimensional spherical region from the designs in 2-dimensional spherical region. Section 4 proposes a transformation to obtain mixture designs from the designs in spherical region. Section 5 outlines the conclusion of the paper.

2 Uniformity criteria

Fang (1980) and Wang and Fang (1981) were the first to apply the idea of Number-theoretic methods (NTM) to experimental designs. Number-theoretic method or Quasi Monte Carlo method is a combination of number-theory and numerical analysis and has a variety of applications in statistics. Discrepancy is a measure of uniformity which provides a way of construction of uniform design. Fang and Wang (1994) introduced the root mean square distance (RMSD) to measure the uniformity of mixtures designs. Borkowski and Piepel (2009) introduced criteria based on average distance (AD) and maximum distance (MD).

Generally Monte Carlo sampling method is used to compute these values. In this method two sets a training set and a sampling set are taken and the design points of these sets are obtained using Number-Theoretic net (NT-net). From the given training set, a sampling set with smaller number of runs is obtained and the value of uniformity measure of the sampling set is evaluated based on the training set. However, in this article, different sampling sets are generated based on different glp generator and the training set is separately generated by an appropriate glp generator which is selected arbitrarily. The criteria values of different sampling sets are evaluated using the training set. For higher dimensional spherical region, there is no discrepancy measures are available in the literature. Therefore, the distance-based approach is preferred for measuring uniformity.

Suppose \({\text{D}} = \left\{ {x_{j} = \left( {x_{j1} ,x_{j2} , \ldots ,x_{js} } \right); j = 1,2, \ldots ,n} \right\}\) represents a sampling set i.e. a design with s components and n runs for which the distance based uniformity measures are to be computed and \({\text{T}} = \left\{ {t_{k} = \left( {t_{k1} ,t_{k2} , \ldots ,t_{ks} } \right),k = 1,2, \ldots ,N} \right\}\) represent a training set consisting of N \(( > n)\) runs and s components. Then D and T matrices of order \({\text{n}} \times {\text{s}}\) and \({\text{N}} \times {\text{s}}\) respectively, where

$${\text{D}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{11} } \\ {x_{21} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . \\ . \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . \\ \end{array} } \\ {x_{n1} } \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{12} } & \ldots & \ldots \\ \end{array} } \\ {\begin{array}{*{20}c} {x_{22} } & \ldots & \ldots \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . & . & . \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . & . & . \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . & . & . \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {x_{n2} } & \ldots & \ldots \\ \end{array} } \\ \end{array} \ldots } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{1s} } \\ {x_{2s} } \\ \end{array} } \\ . \\ \end{array} } \\ {\begin{array}{*{20}c} . \\ {\begin{array}{*{20}c} . \\ \end{array} } \\ \end{array} } \\ {x_{ns} } \\ \end{array} } \\ \end{array} } \right],{\text{T }} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {t_{11} } \\ {t_{21} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . \\ . \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . \\ \end{array} } \\ {t_{N1} } \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {t_{12} } & \ldots & \ldots \\ \end{array} } \\ {\begin{array}{*{20}c} {t_{22} } & \ldots & \ldots \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . & . & . \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . & . & . \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} . & . & . \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {t_{N2} } & \ldots & \ldots \\ \end{array} } \\ \end{array} \ldots } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {t_{1s} } \\ {t_{2s} } \\ \end{array} } \\ . \\ \end{array} } \\ {\begin{array}{*{20}c} . \\ {\begin{array}{*{20}c} . \\ \end{array} } \\ \end{array} } \\ {t_{Ns} } \\ \end{array} } \\ \end{array} } \right]$$

Let \(d_{s}^{2} \left( {x_{j} ,t_{k} } \right)\) denote the Euclidean distance between the points \(x_{j}\) and \(t_{k}\) scaled between 0 and 1, then

$$d_{s}^{2} \left( {x_{j} ,t_{k} } \right) = \mathop \sum \nolimits_{i = 1}^{s} \left( {x_{ji} - t_{ki} } \right)^{2}$$

and the three distance-based criteria are defined as follows:

  1. 1)

    \({\text{RMSD}}\left( {\text{D}} \right) = \sqrt {\frac{{\sum\nolimits_{{k = 1}}^{N} m in_{{1 \le \,j\, \le n}} d_{s}^{2} \left( {x_{j} ,t_{k} } \right)}}{N}}\)

  2. 2)

    \({\text{AD}}\left( {\text{D}} \right) = \frac{1}{N}\sum\nolimits_{{k = 1}}^{N} m in_{{1\, \le \,j\, \le \,n}} d_{s} \left( {x_{j} ,t_{k} } \right)\)

  3. 3)

    \({\text{MD}}\left( {\text{D}} \right) = max_{{1\, \le \,k\, \le \,N}} \left( {min_{{1\, \le \,j\, \le \,n}} d_{s} \left( {x_{j} ,t_{k} } \right)} \right)\)

The above mentioned distance-based measures can also be applied for mixture experiments where \(\mathop \sum \nolimits_{i = 1}^{s} x_{ji} = 1\) and \(\mathop \sum \nolimits_{i = 1}^{s} t_{ki} = 1\) to measure the uniformity of the design.

When the number of runs is small, the uniformity of a mixture design can be measured using the \({\text{DM}}_{2}\)-discrepancy which is generalization of star discrepancy (Ning et al. 2011). Star discrepancy given by Weyl (1916) is a basic and simplest measure of uniformity. Ning et al. (2011) gave the following analytical expression to compute the \({\text{DM}}_{2}\)-discrepancy value of a design \({\text{P}}_{{\text{n}}}\) with n runs defined over the s-dimensional simplex \(T^{s}\).

$${\text{DM}}_{2} \left( {{\text{P}}_{{\text{n}}} } \right) = \left( {\frac{\sqrt s }{{\left( {s - 1} \right)!}}} \right)^{1/2} \left\{ {C_{n,s} - \frac{{2\left( {s - 1} \right)!}}{n}\mathop \sum \limits_{i = 1}^{n} \mathop \sum \limits_{{\left( {\tau_{2 } , \ldots ,\tau_{s} } \right)\varepsilon \left[ {0,1} \right]^{s - 1} }} a_{\tau } .\left( {x_{i1} } \right)^{{\tau_{1} }} .\mathop \prod \limits_{j = 2}^{s} x_{ij}^{{\tau_{j} }} + \frac{1}{{n^{2} }}\mathop \sum \limits_{i = 1.k = 1}^{n} \left( {max\left( {1 - \mathop \sum \limits_{j = 2}^{s} \max \left( {x_{ij} ,x_{kj} } \right) ,0} \right)} \right)^{s - 1} } \right\}^{1/2} .$$

where \(\left\{ {0,1} \right\}^{s - 1} = \left\{ {\left( {t_{1} ,t_{2} , \ldots ,t_{s - 1} } \right):t_{i} = 0~ {\text{or }} 1} \right\}.\)

$$C_{n,s} = \left( {\left( {s - 1} \right)!} \right)^{3} 2^{s - 1} /\left( {2\left( {s - 1} \right)!} \right)\;\mathop \prod \nolimits_{k = 0}^{s - 2} \left( {2s + k - 1} \right),$$
$$a_{\tau } = \left( {s - 1} \right)!/\left( {2\left( {s - 1} \right) - \sum \tau_{i} } \right)!\; {\text{and}}\;\tau_{1} = 2\left( {s - 1} \right) - \mathop \sum \nolimits_{2}^{s} \tau_{j}$$

Xiao et al. (2023) applied wighted centered \(L_{2}\)-discrepancy for obtaining the sequentially weighted uniform design.

3 Uniform design in the s-dimensional spherical region.

An s-dimensional spherical region of radius \(r\) centred at \(y_{0} = \left( {y_{01} , y_{02} , \ldots , y_{0s} } \right)\) is given by

$$S_{n}^{s} \left( {y_{0} } \right) = \left\{ {\left( {y_{1} ,y_{2} , \ldots ,y_{s} } \right):\left( {y_{1} - y_{01} } \right)^{2} + \left( {y_{2} - y_{02} } \right)^{2} + \ldots + \left( {y_{s} - y_{0s} } \right)^{2} \le r^{2} } \right\}$$
(2)

If \(y_{0} = \left( {0,0, \ldots ,0} \right)\) and \(r = 1\), then it represents the standard spherical region and is given by

$$S_{n}^{s} = \left\{ {\left( {y_{1} ,y_{2} , \ldots ,y_{s} } \right):\left( {y_{1} } \right)^{2} + \left( {y_{2} } \right)^{2} + \ldots + \left( {y_{s} } \right)^{2} \le 1} \right\}$$

Design in s-dimensional spherical region is the set of points which lie inside or on the spherical region (2).

Talke and Borkowski (2016) proposed a method to obtain uniform design in 2-dimensional spherical region. The design points are first obtained in \(C^{2} = \left[ {0, 1} \right]^{2}\). Suppose \(\left\{ {\left( {r_{i} , \theta_{i} } \right);i = 1,2, \ldots ,n.} \right\}\) is the design in \(C^{2}\), then the design in two-dimensional spherical region is given by \(\{ (z_{{i1}} ,z_{{i2}} );\;i = 1,2, \ldots ,n\}\) with

$$z_{i1} = \sqrt {r_{i} } Cos\left( {2\pi \theta_{i} } \right), z_{i2} = \sqrt {r_{i} } Sin\left( {2\pi \theta_{i} } \right)$$
(3)

which are uniformly scattered in \(B^{2} = \left\{ {\left( {z_{i1} , z_{i2} } \right):z_{i1}^{2} + z_{i2}^{2} \le 1;i = 1,2, 3, \ldots ,n} \right\}\).

Theorem 1.1:

Let \(\left\{ {\left( {z_{i1} , z_{i2} } \right);i = 1,2, \ldots ,n} \right\}\) be an n-point design in 2-dimensional spherical region \(B^{2}\). For the s-dimensional spherical region, the design \({\text{D}} = \left\{ {\left( {y_{i1} , y_{i2} , \ldots ,y_{is} } \right);i = 1,2, \ldots ,n} \right\}\) can be obtained by using the transformation given below:

$$y_{i1} = \sqrt {\frac{{z_{i1}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}} , y_{i2} = \sqrt {\frac{{2z_{i1}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}} + \frac{{z_{i2}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}} , \ldots ,\;y_{{i\left( {s - 1} \right)}} = \sqrt {\frac{{\left( {s - 1} \right)z_{i1}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}} + \frac{{\left( {s - 2} \right)z_{i2}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}} ,$$
$$y_{is} = \sqrt {\frac{{\left( {s - 1} \right)z_{i1}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}} ;i = 1,2, \ldots ,n.$$

The number of design points n is to be taken more than the parameters in the model to be fitted. For example, for the Scheffé (1958) quadratic model with s component n should be more than \(s + \left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)\).

Proof:

Consider the design \(z = \left\{ {\left( {z_{i1} , z_{i2} } \right);i = 1,2, \ldots ,n} \right\}\) in 2-dimensional spherical region as.

$$z_{i1} = \sqrt {r_{i} } \cos \left( {\theta_{i} } \right), z_{i2} = \sqrt {r_{i} } \sin \left( {\theta_{i} } \right)$$

so that \(z_{i1}^{2} + z_{i2}^{2} = r_{i} .\)

where \(\left\{ {\left( {r_{i} , \theta_{i} } \right);i = 1,2, \ldots ,n} \right\}\) is an NT-net design in unit hypercube dimensions obtained by a generator \(\left( {1, h_{1} } \right)\).

Consider the following vector of dimension \(\left( {1 \times s} \right)\), given by

$$\underline {C} = \frac{1}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}\left( {1, 2, \ldots , s - 1, 0} \right) \;{\text{and}}\;\underline {d} = \frac{1}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}\left( {0, 1, 2, \ldots , s - 1} \right).$$

Define \(y_{ij} = \sqrt {C_{j} z_{i1}^{2} + d_{j} z_{i2}^{2} } ;j = 1, 2, \ldots ,s ; i = 1,2, \ldots , n.\)with \(y_{i1} = \sqrt {\frac{{z_{i1}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}} , y_{i2} = \sqrt {\frac{{2z_{i1}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}} + \frac{{z_{i2}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}} , \ldots ,\)

$$y_{{i\left( {s - 1} \right)}} = \sqrt {\frac{{\left( {s - 1} \right)z_{i1}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}} + \frac{{\left( {s - 2} \right)z_{i2}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}} , y_{is} = \sqrt {\frac{{\left( {s - 1} \right)z_{i2}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}}} ;i = 1,2, \ldots ,n.$$

Then

$$\begin{aligned} \left( {y_{i1} } \right)^{2} + \left( {y_{i2} } \right)^{2} + \ldots + \left( {y_{{i\left( {s - 1} \right)}} } \right)^{2} + \left( {y_{is} } \right)^{2} = & \frac{{z_{i1}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}} + \frac{{2z_{i1}^{2} + z_{i2}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}} + \ldots + + \frac{{\left( {s - 1} \right)z_{i1}^{2} + \left( {s - 2} \right)z_{i2}^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}} + \frac{{\left( {s - 1} \right)z_{i2 }^{2} }}{{\left( {\begin{array}{*{20}c} s \\ 2 \\ \end{array} } \right)}} \\ = & \;z_{i1}^{2} + z_{i2}^{2} = r_{i} ; i = 1,2,3, \ldots ,n. \\ \end{aligned}$$

D is the required n-point design in s-dimensional spherical region given in (2). The particular cases for \(s = 3, 4,\) and \(5\) are given in the following theorems.

Theorem 1.2:

Let \(\left\{ {\left( {z_{i1} , z_{i2} } \right);i = 1,2, \ldots ,n} \right\}\) be the n-point design in 2-dimensional spherical region \(B^{2}\), then for the 3-dimensional spherical region, the design \({\text{D}} = \left\{ {\left( {y_{i1} , y_{i2} , y_{i3} } \right);i = 1,2, \ldots ,n} \right\}\) can be obtained by using the transformation given below:

$$y_{i1} = \sqrt {\frac{{z_{i1}^{2} }}{3}} , y_{i2} = \sqrt {\frac{{2z_{i1}^{2} }}{3} + \frac{{z_{i2}^{2} }}{3}} , y_{i3} = \sqrt {\frac{{2z_{i2}^{2} }}{3}} ;i = 1,2, \ldots ,n.$$

Theorem 1.3:

Let \(\left\{ {\left( {z_{i1} , z_{i2} } \right);i = 1,2, \ldots ,n} \right\}\) be the n-point design in 2-dimensional spherical region \(B^{2}\), then for the 4-dimensional spherical region, the design \({\text{D}} = \left\{ {\left( {y_{i1} , y_{i2} , y_{i3} ,y_{i4} } \right);i = 1,2, \ldots ,n} \right\}\) can be obtained by using the transformation given below:

$$y_{i1} = \sqrt {\frac{{z_{i1}^{2} }}{6}} , y_{i2} = \sqrt {\frac{{2z_{i1}^{2} }}{6} + \frac{{z_{i2}^{2} }}{6}} , y_{i3} = \sqrt {\frac{{3z_{i1}^{2} }}{6} + \frac{{2z_{i2}^{2} }}{6}} , y_{i4} = \sqrt {\frac{{3z_{i2}^{2} }}{6}} ; i = 1,2, \ldots ,n.$$

Theorem 1.4:

Let \(\left\{ {\left( {z_{i1} , z_{i2} } \right);i = 1,2, \ldots ,n} \right\}\) be the n-point design in 2-dimensional spherical region \(B^{2}\), then for the 5-dimensional spherical region, the design \({\text{D}} = \left\{ {\left( {y_{i1} , y_{i2} , y_{i3} ,y_{i4} , y_{i5} } \right);i = 1,2, \ldots ,n} \right\}\) can be obtained by using the transformation given below:

$$y_{i1} = \sqrt {\frac{{z_{i1}^{2} }}{10}} , y_{i2} = \sqrt {\frac{{2z_{i1}^{2} }}{10} + \frac{{z_{i2}^{2} }}{10}} , y_{i3} = \sqrt {\frac{{3z_{i1}^{2} }}{10} + \frac{{2z_{i2}^{2} }}{10}} , y_{i4} = \sqrt {\frac{{4z_{i1}^{2} }}{10} + \frac{{3z_{i2}^{2} }}{10}}$$
$$,y_{i5} = \sqrt {\frac{{4z_{i2}^{2} }}{10}} ;i = 1,2, \ldots ,n.$$

3.1 Illustrations:

Let us consider the case of 3-, 4-, and 5-dimensional spherical regions.

3.1.1 Case 1: 3-dimensional spherical region

Consider a design in 2-dimensional spherical region with 11 design points.

For \(n = 11\), the initial candidate generating vector is \(H_{11} = \left\{ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} \right\}\) and the list of generators are given in Table 1.

Table 1 List of glp generators of design in \({\left[0, 1\right]}^{2}\)
Full size table

From the list of all the possible generators given in Table 1, the designs in 2- dimensional spherical regions are obtained and are transformed into the designs in 3-dimensional spherical region using Theorem 1.2. The values of three distance-based measures are computed for all the constructed designs which are given in Table 2. These values are computed on the basis of 8000 evaluation points by using the generator \(\left( {1, 7} \right).\)

Table 2 RMSD, AD, and MD values of the designs in 3-dimensional spherical region with 11 design points
Full size table

From the Table 2, it can be observed that the criteria values of the designs obtained by generators \(\left( {1, 4} \right), \left( {2, 8} \right), \left( {4, 5} \right), \left( {5, 9} \right)\) and \(\left( {8, 10} \right)\) are same and lowest among all possible design.

3.1.2 Case 2: 4-dimensional spherical region

Consider a design in 2-dimensional spherical region with 18 design points.

For \(n = 18\), the initial candidate generating vector \(H_{18}\) is given by

$$H_{18} = \left\{ {1, 5, 7, 11, 13, 17} \right\}$$

Different generating vectors for constructing uniform designs in 4-dimensional spherical region are given in Table 3.

Table 3 List of glp generators of the design in \({\left[0, 1\right]}^{2}\) with \(18\) design points
Full size table

From the list of all the possible generators given in Table 3, the designs in 2- dimensional spherical regions are obtained and the designs are transformed into the design in 4-dimensional spherical region using the Theorem 1.3. The criteria value of the design in 4-dimensional spherical region is obtained and is given in Table 4. For computing the criteria values a design obtained by using the generator \(\left( {1, 13} \right)\) is considered and the criteria values are computed on the basis of 10,000 evaluation points.

Table 4 RMSD, AD, and MD values of the designs in 4-dimensional spherical region with 18 design points
Full size table

From the Table 4, it can be observed that the designs obtained using the generators \(\left( {1, 7} \right), \left( {5, 17} \right), \left( {7, 13} \right)\) have lowest RMSD and AD value and the designs with generators \(\left( {1, 11} \right), \left( {11, 13} \right), \left( {13, 17} \right)\) have lowest MD value.

3.1.3 Case 3: 5-dimensional spherical region

Consider the design in 5-dimensional spherical regions using the design in 2- dimensional spherical region with \(n = 21\) design points.

For \(n = 21\), the initial candidate generating vector \(H_{21}\) is given by

$$H_{21} = \left\{ {1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20} \right\}$$

Different generating vectors for constructing uniform designs in 5-dimensional spherical region are given in Table 5. For computing the criteria values a design obtained by using the generator \(\left( {7, 13} \right)\) is considered and the criteria values are computed on the basis of 12,000 evaluation points.

Table 5 List of glp generator of the design in \({\left[0, 1\right]}^{2}\) with 21 design points
Full size table

From the list of all possible generators, the designs in 2-dimensional spherical regions are obtained and the designs are transformed into the design in 5-dimensional spherical region using the Theorem 1.4. The criteria value of the design in 5- dimensional spherical region is given in Table 6.

Table 6 RMSD, AD, and MD values of the designs in 5-dimensional spherical region with 21 design points
Full size table

From the Table 6, it can be observed that the designs obtained using the generators \(\left( {1, 17} \right), \left( {2, 13} \right), \left( {4, 5} \right), \left( {8, 10} \right), \left( {11, 19} \right), \left( {16, 20} \right)\) have the lowest RMSD and AD values and the design with generator \(\left( {1, 2} \right), \left( {2, 4} \right), \left( {5, 10} \right), \left( {8, 16} \right), \left( {10, 20} \right)\) have the same lowest MD value.

If the generator giving minimum value of RMSD and AD is different from the generator giving minimum value of MD, then this generator may be considered as optimal generator whereas if the generator giving the smallest value of AD is also different from the generator giving minimum value of RMSD, then the generator for RMSD is considered as optimal generator as RMSD is least affected by variation of points near the boundary. However, in mixture space this might not be true. Therefore, the designs in mixture space are generated by considering all the generators chosen on the basis of RMSD, AD, and MD values. The method for obtaining mixture design from the designs in s-dimensional spherical region is described in the next section.

4 Method of obtaining mixture design using the design in the spherical region

Suppose that \(\left\{ {\left( {y_{i1} , y_{i2} , \ldots , y_{is} } \right);i = 1,2, \ldots ,n} \right\}\) represents a design in the s-dimensional spherical region. Then the mixture design \(\left\{ {\left( {x_{i1} , x_{i2} , \ldots , x_{is} } \right);i = 1,2, \ldots ,n} \right\}\) which satisfies Eq. (1) can be obtained by using the following transformation

$$x_{ij} = \frac{{t_{ij} }}{{\mathop \sum \nolimits_{j = 1}^{s} t_{ij} }};i = 1,2,3, \ldots ,n;j = 1,2, \ldots s.$$
(4)

where \(t_{i1} = y_{i1}\),\(t_{ij} = \left| {y_{ij} - \mathop \sum \nolimits_{k = 1}^{j} \frac{{y_{ik} }}{j}} \right|;j = 2, 3, \ldots ,s.\)

In this case, the design is constructed by considering the absolute deviation of the design points from the central points. From all the possible designs, the design with minimum value of \({\text{DM}}_{2}\)-discrepancy is chosen.

Example 1:

Consider 11 run designs in 3-dimensional spherical region obtained in Sect. 3. It is observed that the designs obtained by using the generator \(\left( {1, 4} \right), \left( {2, 8} \right), \left( {4, 5} \right), \left( {5, 9} \right)\) and \(\left( {8, 10} \right)\) are best in terms of uniformity. Using these designs, the mixture designs are obtained by using the transformation (5). The \({\text{DM}}_{2}\) value of the mixture designs is computed and is given in Table 7 with corresponding generators.

Table 7 \({\mathrm{DM}}_{2}\) values of the 3 component mixture design with 11 design points
Full size table

From the Table 7, it can be observed that the \({\text{DM}}_{2}\) value of the design obtained by using the generator \(\left( {8, 10} \right)\) is lowest. The uniform mixture design and corresponding uniform design in 3-dimensional spherical region based on generator (8, 10) are given in Table 8.

Table 8 Design in 3-dimensional spherical region with corresponding uniform mixture design obtained using generator \((\mathrm{8,10})\)
Full size table

Example 2:

Consider 18 run designs in 4-dimensional spherical region obtained in Sect. 3. The designs obtained by using the generator \(\left( {1, 7} \right), \left( {5, 17} \right),\) and \(\left( {7, 13} \right)\) are best in terms of uniformity. Using these designs, the mixture designs are obtained by using the transformation (5). The \({\text{DM}}_{2}\) value of the mixture designs is computed and is given in Table 9 with corresponding generator.

Table 9 \({\mathrm{DM}}_{2}\) values of the 4 component mixture design with 18 design points
Full size table

From the Table 9, it can be observed that the \({\text{DM}}_{2}\) value of the design obtained by using the generator \(\left( {11, 13} \right)\) is lowest. The uniform mixture design and the corresponding uniform design in the 4-dimensional spherical region based on generator \(\left( {11, 13} \right)\) are given in Table 10.

Table 10 Design in 4-dimensional spherical region with corresponding uniform mixture design obtained using generator \((11, 13)\)
Full size table

Example 3:

Consider 21 run designs in 5-dimensional spherical region obtained in Sect. 3. The designs obtained by using the generator \(\left( {1, 17} \right), \left( {2, 13} \right), \left( {4, 5} \right), \left( {8, 10} \right), \left( {11, 19} \right),\) and \(\left( {16, 20} \right)\) are best in terms of uniformity. Using these designs, the mixture designs are obtained by using the transformation (5). The \({\text{DM}}_{2}\) value of the mixture designs is computed and is given in Table 11 along with corresponding generators.

Table 11 \({\mathrm{DM}}_{2}\) values of the 5 component mixture design with 21 design points
Full size table

From the Table 11, it can be observed that the \({\text{DM}}_{2}\) value of the design obtained by using the generator \(\left( {1, 17} \right)\) is lowest. The uniform mixture design and the corresponding uniform design in 5-dimensional spherical region based on generator \(\left( {1, 17} \right)\) are given in Table 12.

Table 12 Uniform design in 5-dimensional spherical region and the corresponding uniform mixture design with generator \((1, 17)\)
Full size table

5 Conclusion

Mixture experimental design is a powerful tool that can be used in quality control and product formulation. The space filling property of the uniform design makes it suitable for generating uniformly scattered design points for the mixture experiments. In present scenario, the uniform mixture design has come up as a useful statistical tool that can improve the overall performance and quality of the product by generating the design points that are uniformly scattered in the experimental region. Different experimental region can produce different mixture combinations, resulting in different final product. In this paper, spherical region is considered and the design in s-dimensional spherical region is obtained by considering the existing design in 2-dimensional spherical region. A transformation to construct uniform mixture design is also proposed in this paper. The proposed method is useful in the sense that it only need the design in 2-dimensional spherical regions to construct the desired mixture designs in higher dimensional region. Designs for 3, 4, and 5 component mixtures are constructed and the value of \({\text{DM}}_{2}\)-discrepancy is calculated. It is observed that the mixture designs based on the designs in spherical region with lowest ‘MD’ value possess maximum uniformity in the simplex region. Thus, the uniformity is preserved when proposed transformation is used for obtaining the mixture design from the design in spherical region.