1 Introduction

Fault-tolerant control for sensors in wind energy systems has grown in importance during the past few years. Despite its unpredictable nature and lack of control over failure, wind energy has become one of the most successful renewable energy technologies (Sloth et al. 2010). For improved performance and dependability, the high capacity wind energy systems need to be thoroughly explored.

A sensor failure that results in false feedback lowers the effectiveness of wind energy control systems. It could result in subsequent defects in other parts. The sensitivity of the control system to the inaccurate measurement determines the fault severity (Kim and Lee 2019). Even in the presence of a problem, fault-tolerant control systems continue to function properly. Additionally, it shields the system against breakdown. A physical or analytical alternative measurement is possible. Rather than duplicating every sensitive component, analytical measurement is more cost-effective.

A fault-tolerant control system for sensors and actuators has been discovered (Pourmohammad and Fekih 2011). For the estimation of wind speed, rotor speed, and aerodynamic torque, observer-based techniques are provided in a few studies (Oestergaard et al. 2007). The drive train’s mathematical model is utilized in these works. An extended Kalman filter is used to estimate system states and different failure parameters in the literature. By applying the residual generation method, these estimations have been used to identify sensor failures (Kavaz 2018). A more precise two mass drive train model was used for observer-based estimate of unknown input. A fault-tolerant control strategy using a bank of unknown input observers is suggested based on these estimations (Mazare and Taghizadeh 2021). It is made to be resistant to wind speed uncertainty. The design of the unknown input observer uses the measurements of the healthy sensors. It is made sure that, despite the possibility that the healthy sensor measurement employed may have an offset, it won’t push the generator speed over its upper limit.

Mechanical issues with gearboxes and bearings in drive trains of wind energy systems result in frictional losses that reduce torque in the system. In this study, the robustness of the system is examined, and the fault-tolerant observer is constructed by taking these losses into account. Additionally, using a constructed observer, the rotor speed and generator torque are estimated (Alwi et al. 2011). A state observer can be used to estimate the status and predict the sensor’s recovery when a catastrophic failure is determined. Robustness against uncertainty and self-recovery are two characteristics that are combined to create fault-tolerant robust control (Odgaard et al. 2009).

2 Literature review

Active fault-tolerant control (AFTC) methods have been applied to Takagi–Sugeno fuzzy systems, stochastic systems, singly perturbed systems (SPS), nonlinear systems, and inter-connected systems (Kharrat et al. 2015). Fuzzy system faults are analyzed with an adaptive observer and controller. Liu et al. (2019) created an unknown input observer with sliding mode terms considering Brownian parameter perturbations, process uncertainties, and failures in TS fuzzy systems. Authors proposed employing feedback gain and sensor compensation output to stabilize condition and reduce faults. Sun et al. (2017) developed an anti-disturbance FTC for the stochastic systems. Abdelkrim et al. (2012) recommended an SPS controller using State-feedback and Luenberger-observer global controllers.

Li et al. (2019) devised fuzzy fault-tolerant optimal nonlinear control and created a control strategy for the fault-tolerance using a fault diagnostic observer and interconnected separation ideas. Compared to PFTC, AFTC is flexible. For a wind service provider, a trustworthy wind farms and turbines are needed. The three phase system’s positive, negative, and zero sequence are included in the reduced model, which allows it to account for asymmetrical electrical failures in wind power plants. Fault tolerance rebuilds the faulty actuators.

The Fuzzy logic diagnose an open phase and inter-turn short circuit faults. Successful fault diagnostic approaches go beyond current, voltage, torque, and power signal analysis and incorporate model-based methodologies. In difficult conditions, observers estimate the system outputs. Sliding-mode observers can find a robot, car, or motor fault (Bechkaoui et al. 2015).

Consider a linear system with two cascaded SMOs and an estimating system state variables with flawed sliding mode observers. Wind turbine FDI employs Kalman filters. Apply the same approach to detect sensor and actuator faults and estimate blade root moment sensor and pitch actuator stuck problems. Kamal et al. (2012) enables observer-based stator inter-turn short circuit fault detection.

This research proposes observer-based generator speed sensor control and protects the equipment’s operation.

3 Wind energy system modeling and controlling

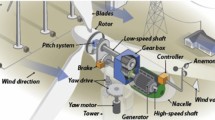
This examination covers a 2-MW, 3-blade horizontal turbine, anemometer, tower, rotor, nacelle, yaw mechanism, generator, low-speed shaft, gearbox, and brakes. Wind turbine brakes are electric, hydraulic, or pneumatic incorporating low-speed rotor-to-gearbox shaft. Shaft connects the generator and its output is provided to grid. An anemometer measures wind speed to start or stop a wind turbine. The nacelle is rotated by wind vanes.

Figure 1 shows the wind system structure for mathematical model forming. It has sub-models as the drive train, generator and converter, wind, aerodynamics, pitch actuator, etc. Vr represents wind speed of rotor(m/s), Ta represents the aerodynamic torque (N), wr represents rotor speed (rad/s), \(\beta\) represents the pitch angle (degrees), wg represents speed of generator (rad/s), \(\beta\) refrepresents the reference pitch angle (degrees), Tg represents the generator torque (N).

Fig. 1
figure 1

Wind energy model structure with a feedback system

Full size image

3.1 Wind model

Local factors like wind shear, wind turbulence, and the wind shadow effect all have an impact on the wind. A wind model with turbulence, mean wind, tower shadow and wind shear provide the effective wind for each blade.

3.2 Aerodynamic model

The rotor rotates as a result of effective speed of wind. It causes the rotor’s aerodynamic torque and is represented as Eq. (1):

$${T}_{a}=\frac{1}{2}{\rho }_{wind}{A}_{wind}\frac{{R}^{3}}{{\lambda }_{wind}^{3}}{{w}_{r}}^{2}{C}_{pwind}\left(\beta ,{\lambda }_{wind}\right)$$
(1)

In which \({\rho }_{wind}\) representsdensity of air [kg/m3], \(A\) represents swept areas of rotor [m2],\({w}_{r}\) represents the rotor speed [rad/s], \({C}_{pwind}(\beta ,\lambda )\) represents power coefficient depicting the power available in wind. It is based on tip speed ratio (\({\lambda }_{wind}\)) as well as blade pitch angle in degrees. The formula for tip speed ratio:

$${\lambda }_{wind}=\frac{{w}_{r}R}{Vr}= \frac{2\pi {N}_{wind}R}{Vr}$$
(2)

In which \(\lambda\) represents tip speed ratio, whereas \({N}_{wind}\) representsno. of revsper min.

3.3 Pitch actuator

This is utilized to modify blade pitch angle in order to keep the rotor whirling at the desired speed. Equation (3) is used to model it as system of second order.

$$\beta \left(t\right)=-2{\zeta }_{wind}{\omega }_{wind}\dot{\beta }\left(t\right)-{\omega }_{wind}^{2}\beta \left(t\right)+ {\omega }_{wind}^{2}\beta \left(t\right)ref$$
(3)

In which \({\omega }_{wind}\) representsnatural frequency,\({\zeta }_{wind}\) represents damping ratio for model for pitch actuator.

3.4 Drive train

Aerodynamic torque speeds up the drive train shafts. The wind and aerodynamic torque are variable. The Drivetrain oscillations change the dynamics and Torque-shifting. Dynamic drive train models can assess this modified torque.

There are one, two, three, and six-mass models of drive train. Inertia of the rotor and generator are considered in modelling. Two-mass model includes rotor and generator inertia, not the gearbox as it negligible. Accurate two-mass drivetrain models- the aerodynamic and electrical torques affect the driving train from opposite direction. Drivetrain equations are given as:

$${J}_{ref}{\dot{\mathrm{w}}}_{ref}={T}_{a}-{K}_{drive}{\theta }_{{\delta }_{wind}}-{B}_{drive}{\dot{\uptheta }}_{{\delta }_{wind}}$$
(4)
$${J}_{gen}{N}_{gen}{\dot{\mathrm{w}}}_{gen}=-{T}_{gen}{N}_{gen}-{T}_{losses}{N}_{gen}+{K}_{drive}{\theta }_{{\delta }_{wind}}+{B}_{drive}{\dot{\uptheta }}_{{\delta }_{wind}}$$
(5)
$${\dot{\uptheta }}_{{\delta }_{wind}}={w}_{ref}-\frac{{w}_{gen}}{{N}_{gen}}$$
(6)

In which Ng represents the gear ratio, Jg represents the high-speed shaft inertia[Kgm2], Bdt represents the viscous damping parameter, Tlosses represents the friction loss. Provides the drive train model.

The drive train is complex structure. Mechanical difficulties stem from misalignment, broken bearings and the misalignment disrupts rotation. Incorrect lubrication and maintenance harm the bearings, increasing the friction. Torque and rotational speed affect the losses dramatically. Partial load affects rotational speed. Tlosses is an additional element considered in the model above but not in earlier research articles.

3.5 Generator

It is a crucial part of the system for producing electricity from wind energy. It must operate with variable wind and adjust to changes in wind speed. The first-order model with time delay can be approximated by combining the generator and converter. It can be found in Eq. (7).

$$\dot{{T}_{g}}\left(t\right)=-\frac{1}{{\tau }_{wind}}{T}_{g}+\frac{1}{{\tau }_{wind}}{T}_{gref}$$
(7)

In which \({\tau }_{wind}\) represents the system’s time constant.

A combined state space model for drive train and generator serves as a representation of the wind energy system which is shown in Eq. (8)

$$\dot{\mathrm{A}}=\mathrm{ XA}+\mathrm{Y}1\mathrm{u}+\mathrm{Y}2\mathrm{v}$$
$$B=\mathrm{ZA}$$
(8)

where: \(X\; = \;\left[ {\begin{array}{*{20}l} {\frac{{ - B_{dt} }}{{J_{r} }}} \hfill & {\frac{{B_{dt} }}{{J_{r} N_{g} }}} \hfill & {\frac{{ - K_{dt} }}{Jr}} \hfill & 0 \hfill \\ {\frac{{B_{dt} }}{{J_{r} Ng}}} \hfill & {\frac{{ - B_{dt} }}{{J_{g} N_{g}^{2} }}} \hfill & {\frac{{K_{dt} }}{{J_{g} Ng}}} \hfill & {\frac{ - 1}{{J_{g} }}} \hfill \\ 1 \hfill & {\frac{ - 1}{{N_{g} }}} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\frac{ - 1}{\tau }} \hfill \\ \end{array} } \right]\),

$$Y1 = \left[ {\begin{array}{*{20}l} {\frac{1}{{J_{r} }}} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill \\ 0 \hfill & {\frac{1}{\tau }} \hfill \\ \end{array} } \right],\;Y2 = \left[ {\begin{array}{*{20}c} { 0} \\ {\frac{ - 1}{{J_{g} }}} \\ { 0} \\ { 0} \\ \end{array} } \right],\;Z = \left[ {\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} } \right]$$

With, \(A = \left[ {\begin{array}{*{20}c} {w_{r} } \\ {w_{g} } \\ {\theta_{\delta } } \\ {T_{g} } \\ \end{array} } \right]\), \(u = \left[ {\begin{array}{*{20}c} {T_{a} } \\ {T_{gref} } \\ \end{array} } \right]\), \(v = \left[ {T_{loss} } \right]\), \(B = \left[ {\begin{array}{*{20}c} {w_{r} } \\ {w_{g} } \\ {\theta_{\delta } } \\ {T_{g} } \\ \end{array} } \right]\).

A denotes state vector, B denotes output vector, u denotes input vector, v denotes constant disturbance vector. Aerodynamic torque as well as the Reference torque are considered as the inputs. Generator speed, Rotor speed, torque of generator and torsion angleare model states.

3.6 Control system

The system of wind energy has two modes: partial load for low wind and full load for high wind. Two controllers are used in these zones. In partial load, pitch angle is maintained and torque is changed to maximize power. Pitch angle and generator torque adjust speed and power to attain full-load rated power.

4 Fault-tolerant observer design for wind energy system

System maintenance prevents breakdowns and reduce unexpected off shore costs. Stochastic wind affects offshore wind energy systems. Planned maintenance can’t prevent the gearbox and bearing failures. Damaged bearings induce unpredictable drive train rotation, as shown by torque spectrum with and without gearbox crack.

When wind speed is moderate, variable-speed wind turbines reduce friction. Full-load wind speeds are higher than rated. Partial load control enhances output power. It increases the productivity and ultimately the economy boosts. Model-based methods diagnose the control system failures. Signal-based methods detect the plant problems (component faults). The fault-tolerant observer designed in this work considers the generator and drive train faults.

Failures in rotor, generator speed, and torque sensors are tolerated, passively handling the sensor failures. The controller calculates feedback variables using healthy sensors in this fault-tolerant observer technique. Assuming steady-state speed, generator torque regulates speed. i.e.,\({\dot{\mathrm{w}}}_{r}=0; {\dot{\mathrm{w}}}_{g}=0\) and \({{w}_{g}={N}_{g}w}_{r}\), the \({T}_{gref}\) is calculated as (9),

$${T}_{gref}=0.5\rho A\frac{{R}^{3}}{{{{{N}_{g}}^{3}\lambda }_{opt}}^{3}}{C}_{p,max}{{w}_{g}}^{2}$$
(9)

Because it depends on the generator or rotor speed, only one of those speeds needs to be observed. Figure 2 depicts the wind energy control system.

Fig. 2
figure 2

Control system of partial load wind energy system

Full size image

Over the partial load zone, Tgref retains closed-loop behavior, feedback F is mentioned later. The torque controller of generator regulates the speed of generator speed in this system. The Rotor/generator speed is critical if these sensors breakdown. The generator or the rotor speed can be predicted (Yan and Edwards 2008).

4.1 Model of the design

For creating fault-tolerant observers for generator speed & rotor speed, Sect. 3.4-discussed the mathematical formalism of the drive train with generator. It is given as,

$${J}_{ref}{\dot{\mathrm{w}}}_{r}={T}_{a}-{K}_{drive}{\theta }_{{\delta }_{wind}}-{B}_{drive}{w}_{r}+{B}_{drive}\frac{{w}_{g}}{{N}_{gen.}}$$
(10)
$${J}_{gen.}{N}_{gen.}{\dot{\mathrm{w}}}_{gen.}=-{T}_{gen.}{N}_{gen.}-{T}_{losses}{N}_{gen.}+{K}_{drive}{\theta }_{{\delta }_{wind}}+{B}_{drive}{w}_{r}-{B}_{drive}\frac{{w}_{gen}}{{N}_{gen.}}$$
(11)
$${\dot{\uptheta }}_{{\delta }_{wind}}={w}_{r}-\frac{{w}_{gen.}}{{N}_{gen.}}$$
(12)
$$\dot{{T}_{gen}}\left(t\right)=-\frac{1}{{\tau }_{wind}}{T}_{gen}+\frac{1}{{\tau }_{wind}}{T}_{gref}$$
(13)

This system has four states and two inputs.

$${\dot{\mathrm{w}}}_{ref.}={f}_{1}\left({w}_{ref},{w}_{gen},{\theta }_{{\delta }_{wind}}, {T}_{a}\right)$$
$${\dot{\mathrm{w}}}_{gen}={f}_{2}\left({w}_{ref},{w}_{gen},{\theta }_{{\delta }_{wind}}, {T}_{gen}\right)$$
$${\dot{\uptheta }}_{{\delta }_{wind}}={f}_{3}\left({w}_{ref},{w}_{gen}\right)$$
$$\dot{{T}_{gen}}\left(t\right)={f}_{4}({T}_{gen,}{T}_{gref})$$

where:

$${\mathrm{B}=\mathrm{ g}(w}_{ref},{w}_{gen},{\theta }_{{\delta }_{wind}}, {T}_{gen}$$
(14)

The generator and drive train’s mechanical (incipient) defects were the cause of the Tlosses. These losses are taken to be constant in this instance. It is what leads to the mathematical model’s nonlinearity. Around the steady—state operating point, a Taylor series approximation progressively linearizes the model.

When a steady state deviates from its steady-state point of operation,

$$\overline{{w_{ref} }} = w_{ref} - w_{rs} ,\;\overline{{w_{gen} }} = w_{gen} - w_{gen.s} ,\;\overline{{\theta_{{\delta_{wind} }} }} = \theta_{{\delta_{wind} }} - \theta_{\delta s} , \overline{{T_{gen} }} = T_{gen} - T_{gen.s}$$
(15)

State-space model can be expressed as,

$$\left[ {\begin{array}{*{20}c} {\mathop {\overline{{w_{ref} }} }\limits^{.} } \\ {\mathop {\overline{{w_{gen} }} }\limits^{.} } \\ {\mathop {\overline{{\theta_{{\delta_{wind} }} }} }\limits^{.} } \\ {\mathop {\overline{{T_{gen} }} }\limits^{.} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\frac{{\delta f_{1} }}{{\delta w_{ref} }}} \hfill & {\frac{{\delta f_{1} }}{{\delta w_{gen} }}} \hfill & {\frac{{\delta f_{1} }}{{\delta \theta_{\delta } }}} \hfill & {\frac{{\delta f_{1} }}{{\delta T_{g} }}} \hfill \\ {\frac{{\delta f_{2} }}{{\delta w_{ref} }}} \hfill & {\frac{{\delta f_{2} }}{{\delta w_{gen} }}} \hfill & {\frac{{\delta f_{2} }}{{\delta \theta_{\delta } }}} \hfill & {\frac{{\delta f_{2} }}{{\delta T_{gen} }}} \hfill \\ {\frac{{\delta f_{3} }}{{\delta w_{ref} }}} \hfill & {\frac{{\delta f_{3} }}{{\delta w_{gen} }}} \hfill & {\frac{{\delta f_{3} }}{{\delta \theta_{\delta } }}} \hfill & {\frac{{\delta f_{3} }}{{\delta T_{gen} }}} \hfill \\ {\frac{{\delta f_{4} }}{{\delta w_{ref} }}} \hfill & {\frac{{\delta f_{4} }}{{\delta w_{gen} }}} \hfill & {\frac{{\delta f_{4} }}{{\delta \theta_{\delta } }}} \hfill & {\frac{{\delta f_{4} }}{{\delta T_{gen} }}} \hfill \\ \end{array} } \right]\;\;\left[ {\begin{array}{*{20}c} {\overline{{w_{ref} }} } \\ {\overline{{w_{gen} }} } \\ {\overline{{\theta_{{\delta_{wind} }} }} } \\ {\overline{{T_{gen} }} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {\frac{{\delta f_{1 } }}{{\delta T_{a} }}} \hfill & {\frac{{\delta f_{1} }}{{\delta T_{gref} }}} \hfill \\ {\frac{{\delta f_{2} }}{{\delta T_{a} }}} \hfill & {\frac{{\delta f_{2} }}{{\delta T_{gref} }}} \hfill \\ {\frac{{\delta f_{3} }}{{\delta T_{a} }}} \hfill & {\frac{{\delta f_{3} }}{{\delta T_{gref} }}} \hfill \\ {\frac{{\delta f_{4} }}{{\delta T_{a} }}} \hfill & {\frac{{\delta f_{4} }}{{\delta T_{gref} }}} \hfill \\ \end{array} } \right]\;\;\left[ {\begin{array}{*{20}c} {\overline{{T_{a} }} } \\ {\overline{{T_{gref} }} } \\ \end{array} } \right],$$
$$\overline{B} = \left[ {\begin{array}{*{20}l} {\frac{{\delta g_{en1} }}{{\delta w_{ref} }}} \hfill & {\frac{{\delta gen_{1} }}{{\delta w_{gen} }}} \hfill & {\frac{{\delta gen_{1} }}{{\delta \theta_{\delta } }}} \hfill & {\frac{{\delta g_{en1} }}{{\delta T_{gen} }}} \hfill \\ {\frac{{\delta gen_{2} }}{{\delta w_{ref} }}} \hfill & {\frac{{\delta gen_{2} }}{{\delta w_{gen} }}} \hfill & {\frac{{\delta g_{en2} }}{{\delta \theta_{\delta } }}} \hfill & {\frac{{\delta gen_{2} }}{{\delta T_{gen} }}} \hfill \\ {\frac{{\delta gen_{3} }}{{\delta w_{ref} }}} \hfill & {\frac{{\delta g_{en3} }}{{\delta w_{gen} }}} \hfill & {\frac{{\delta gen_{3} }}{{\delta \theta_{\delta } }}} \hfill & {\frac{{\delta gen_{3} }}{{\delta T_{gen} }}} \hfill \\ {\frac{{\delta gen_{4} }}{{\delta w_{ref} }}} \hfill & {\frac{{\delta gen_{4} }}{{\delta w_{gen} }}} \hfill & {\frac{{\delta gen_{4} }}{{\delta \theta_{\delta } }}} \hfill & {\frac{{\delta gen_{4} }}{{\delta T_{gen} }}} \hfill \\ \end{array} } \right]\;\left[ {\begin{array}{*{20}c} {\overline{{w_{ref} }} } \\ {\overline{{w_{gen} }} } \\ {\overline{{\theta_{{\delta_{wind} }} }} } \\ {\overline{{T_{gen} }} } \\ \end{array} } \right]$$

i.e.,

$$\dot{\overline{A}} = X\overline{A} + Y\overline{u}$$
$$\overline{B} = Z\overline{A}$$
(16)

In which \(X\) representssystem matrix, \(Z\mathrm{ represents output matrix}, Y\) represents input matrix, \(\overline{A }\) represents state vector, \(\overline{B }\) represents output vector, \(\overline{u }\) represents input vector. The generator torque and aerodynamic torque are considered as inputs.The generator speed, rotor speed, torque of generator and torsion angle are states for the model of wind energy system.

Using the provided state observer mechanism, an observer is created.

$$\dot{\hat{\overline{A}}} = X\hat{\overline{A}} + {\text{Yu}} + {\text{K}}\left( {{\text{B}} - \hat{\overline{B}}} \right)$$
$$\hat{\overline{B}} = Z\hat{\overline{A}}$$
(17)

The equation might be arranged as:

$$\dot{\hat{\overline{A}}} = X\hat{\overline{A}} + {\text{Yu}} + {\text{K}}\left( {{\text{Z}}\overline{A} - {\text{Z}}\hat{\overline{A}}} \right)$$
(18)
$${\text{i}}.{\text{e}}.,\dot{A} = \left( {X - KZ} \right)\hat{\overline{A}} + {\text{Yu}} + K{\text{Z}}\overline{A}$$
$${\text{i}}.{\text{e}}.,\;\dot{\hat{\overline{A}}} = \left( {X - KZ} \right)\hat{\overline{A}} + \left[ {{\text{Y }}K} \right]\left[ {\begin{array}{*{20}c} {\text{u}} \\ {\text{B}} \\ \end{array} } \right]$$
(19)

Equation (17) provides the observer’s state equation. The observed states are corrected using the discrepancy between the measured states and the observed states, A. By positioning Eigenvalues of the matrix (X-KZ) to induce observer dynamic faster to that of the actual system, the gain matrix (K) as well as the observer’s error dynamics are defined.

5 Result and discussion

Figure 3 represents the block diagram of the observer configuration. In MATLAB and MATLAB Simulink, the observer is actually implemented.

Fig. 3
figure 3

Block diagram of system observer configuration

Full size image

Observer poles affect the system response in this case. Observer gain matrices K are developed based on desired characteristic equations, and simulation tests are undertaken to assess system performance (Pourmohammad and Fekih 2011). MATLAB Simulink replicates the generator, rotor, and torque observer. Simulation results indicate that observed data can be utilized in the event of sensor malfunctions.

The Fig. 4 shows how the discrepancy between the observed and actual generator speed gets smaller over time. Two observed and real generator speed differ slightly, with the latter producing better outcomes.

Fig. 4
figure 4

Actual and observed speed of generator wg at a varying input

Full size image

In Fig. 5, a simulation is performed with a constant mean wind speed to assess the observer’s performance. It demonstrates that the highest deviation among the observed value and the actual value is 6 units. Thus, in the event of a fault, the predicted value might be used instead of the actual measurement of the generator speed sensor (Basak et al. 2016).

Fig. 5
figure 5

Actual and observed speed of generator wg at a constant input

Full size image

Figure 6 indicates that the disparity between the actual and observed speed of rotor diminishing over time.

Fig. 6
figure 6

Actual and observed speed of generator \({w}_{r}\) at a variable input

Full size image

As shown in Fig. 7, the difference of the estimated and real values for constant mean wind speed is 0.06 units at most. In the event of a failure, the predicted value can take the place of the real measurement of the rotor speed sensor (Chen et al. 2011).

Fig. 7
figure 7

Actual and Observed speed ofrotor \({w}_{r}\) forconstant input

Full size image

Figure 8 shows that the estimated and real generator torque is close. In Fig. 9, an observer’s performance is simulated using a constant mean wind speed. The perceived and true values differ by 10 units. In an issue, the anticipated value can replace the generator torque sensor measurement.

Fig. 8
figure 8

Actual and Observed torque of generator \({T}_{g}\) forvariable input

Full size image
Fig. 9
figure 9

Actual and Observed torque of generator \({T}_{g}\) for constant input

Full size image

Passive fault-tolerant based control systems don’t change when a breakdown occurs. Calculated parameter replaces an incorrect sensor reading to evaluate fault-free, no-fault and the fault-tolerant based system of control & fault-tolerant and fault control system, Fig. 10. The difference in output speed of the generator between fault-tolerant and fault-free and fault control is 5.5 units. It advises using a designed observer. Depending on the failure type, generators with fault-tolerant controllers may run faster than those without (Wang et al. 2021) (Fig. 11).

Fig. 10
figure 10

Fault-free generator speed, faulty generator speed with fault-tolerant control and without fault-tolerant control

Full size image
Fig. 11
figure 11

Faulty generator speed, Fault-free generator speed along fault-tolerant control as well as without the fault-tolerant control

Full size image

Any disturbance in the system of drive train input causes an error in the system’s output in the wind energy system.

Fault-tolerant observers are constructed and validated in this study (Raveendran et al. 2013).

6 Conclusion

In the study, a fault-tolerant based control algorithm for wind energy systems is proposed. A model for the fault tolerant based system of control is developed. Using the model, an observer can estimate rotor, generator, and torque speeds. The simulated results show that the predicted parameters can be applied in the fault-tolerant based system of control. MATLAB produces simulation results. It depicts how the fault-tolerant based system of control can improve wind energy system reliability. The robustness and frictional losses are also examined. Later studies will simulate asymmetric short circuits and grid events such sudden load changes or unbalanced effects in conjunction with active fault compensation.