Keywords

1 Introduction

The last decades have witnessed an increasing growth in the contribution of renewable energy over fossil fuel energy resources. However, installation and maintenance costs are the main challenges in the green energy sector (Karimi 2018; Luo et al. 2014). Recent publications have introduced several methods to tackle these challenges (Bergami and Poulsen 2015; Dunne and Pao 2016; Lio 2018; Wang et al. 2014). For instance, research in controlling wind turbines has led to enhancing the conversion efficiency of wind energy to electrical energy. In this regard, fault-tolerant control (FTC) methods have led to a significant reduction of plant downtime through avoiding unscheduled maintenance (Lan et al. 2018; Lio 2018; Schulte and Gauterin 2016; Simani 2015a; Simani 2015b).

Badihi et al. (2014) combines a model-based fault estimation (FE) observer and a PI fuzzy controller to guarantee closed-loop control robustness to sensor faults. Sami and Patton (2012c) and Shaker and Patton (2014a) proposed an active sensor FTC using the Takagi-Sugeno (TS) fuzzy multiple-model approach for 5 MW wind turbines. In the latter, estimation and compensation of generator and rotor sensor faults were achieved. FE and FTC methods for systems with model uncertainty and disturbance have attracted several researchers. Schulte and Gauterin (2015) used the TS sliding mode observer to attain robust actuator fault estimation for uncertain wind turbine systems. Additionally, the robustness of sliding mode controllers (SMC) has motivated several researchers to operate wind turbine systems (Azizi et al. 2019). An SMC is used by Benbouzid et al. (2014) to maintain optimal conversion efficiency by tolerating scale fault in generator subsystem. Further, Lan et al. (2018) have developed a sliding mode observer-based FTC tolerating blade pitch actuator faults.

An approach combining virtual sensor/actuator with set membership is proposed by Rotondo et al. (2012) to achieve active FTC for wind turbine system. However, the proposal does not consider the case of simultaneous actuator and sensor faults. Further, the parametric defect in blade pitching system influences the performance of the developed FTC strategy. Various studies have attempted fixing the estimation of fault in blade pitching system. In this regard, it is worth remarking that the interval observer in Blesa et al. (2014) was unable to tackle the limitation of Rotondo et al. (2012). Simani and Castaldi (2012) proposed adaptive PI controllers with an online estimation module for the full load region. The PI method cannot tolerate the faults of the blade pitch system (Odgaard and Stoustrup 2014). Results have examined the usefulness of TS-based model inverse control for wind turbines (Simani and Castaldi 2013). However, the controller has tackled model uncertainty without considering the effects of actuator and sensor faults.

Authors (Sami and Patton 2012a; Shaker and Patton 2014a) have suggested the TS fuzzy approach to model and design an FTC for a wind turbine in the partial load region. Considering one operation region, the actuator and sensor faults in the full load region influence the FTC response. The above literature highlights the reason for the recent interest in tolerating simultaneous actuator and sensor faults (Han et al. 2016; Li and Zhu 2016; Shaker 2019).

The main contributions of this chapter are (i) the proposal of FTC architecture for simultaneous system and sensor faults in blade pitching systems in full range of operation and (ii) setting the nominal reference pitch controller against generator speed sensor fault via the use of a robust proportional-proportional-integral-observer (PPIO)-based sensor fault estimation/compensation methodology.

2 Wind Turbine Projects: Current Situation and Challenges

Renewable energy projects have shown significant growth as an alternative to fossil fuels and nuclear systems. The aim of deploying renewable projects is to transfer various nonrenewable energy supply systems into one based on renewables. The interest in such projects aims to reduce global carbon emission, secure energy production, and increase access to electricity worldwide. In recent years, the expenses for renewable projects were higher than for conventional energy sources (Fig. 11.1). Nowadays, renewable power dominates other power sources worldwide and contributes 30% of the global power capacity (REN21 2019).

Fig. 11.1
figure 1

World energy investment 2019 (IEA 2019)

Full size image

Wind power is the leading form of renewables. Compared with conventional power plants, wind projects have been approved as the most cost-competitive form of renewables. The average price of wind power in the USA has dropped to 2 cents per kilowatt-h in 2017 compared with 7 cents per kilowatt-h in 2009. Hence, the global gigawatt of wind power shows an annual increase worldwide as a mean of diversification of national energy sources, creates new jobs, and reduces carbon emissions, thus stabilizing the cost of electricity against price and supply disruptions.

The World Wind Energy Association (WWEA 2019) site, https://wwindea.org/information-2/information/ (accessed 21 May 2021), highlights the growth in wind power generation. The overall capacity of all wind turbines installed worldwide reached 597 gigawatt in 2018. In Table 11.1, about 9.1% growth was achieved by addition of 50 gigawatts. All wind turbines installed by the end of 2018 cover 6% of the overall electricity demand. Furthermore, the continuous increase in wind power installation will play an essential role in the global energy transition towards renewables. Nowadays, 91 countries worldwide take part in total wind energy production. Figure 11.2 shows the leading countries developing wind turbine projects.

Table 11.1 Total installed capacity by the end of 2018 (WWEA 2019)
Full size table
Fig. 11.2
figure 2

Shares of total installed wind power capacity in megawatt (by the end of 2018)

Full size image

The new wind energy investments focus on large-scale multi-megawatt onshore/offshore wind farm projects. Installation of these farms worldwide has made wind power more cost-competitive than the conventional power generation. Although onshore wind farms are the cheapest, the stochastic nature of wind as well as population resistance to onshore sites has lessened deployment. Interest in offshore wind farm projects has been recognized worldwide. Offshore sites offer faster and steadier wind speeds and thus permit more wind energy. Thus, the industry has exploited offshore sites to build large-scale wind farms and install large turbine size thereby offering large wind power capacity. However, installation, operation, and maintenance (IOM) cost of offshore projects are higher than for onshore and vary depending on the site, water depth and distance to shore, and wind variation. IOM consumes around 25–30% of the life span costs of projects (Shafiee and Dinmohammadi 2014). Further, maintenance in projects is expensive and incorporates safety-critical work. Figure 11.3 shows the number of recorded accidents in wind turbine projects up to 2018. This chart confirms that as more turbines are built, more accidents occur (Forum 2019).

Fig. 11.3
figure 3

Numbers of recorded accidents (Forum 2019)

Full size image

Wind power projects need to operate sustainably and minimize the IOM cost. To fulfill needs, turbine downtime may be reduced, harvesting more wind energy. The benefit enhances the cost-competitiveness of wind power above conventional fossil fuel and nuclear power. Fault diagnosis (FD) and FTC strategies sustain operation of wind turbines. Research in FD and control strategies has been led by “kk-electronic” and “MathWorks” in 2009. Since which, an emerging research trend in FD and FTC has been established to ensure reliable and sustainable wind turbine systems. This chapter focuses on employing model-based FD and FTC methods for sustainable operation of wind turbines.

3 Wind Turbine Model, Operation, and Control

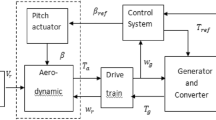
Wind turbine systems convert wind energy into mechanical energy to drive an electrical generator. The working principle of such systems has been extensively explained (Bianchi et al. 2007; Carriveau 2011; Hansen 2015; Shaker and Patton 2014b).

As given in (11.1), three variables affect the amount of power captured by the rotor: the effective wind speed (vEWS), the blade pitch angles (β), and the rotor speed (ωr):

$$ {P}_{\mathrm{cap}}=\frac{1}{2}\rho \pi {R}^3{C}_p\left(\lambda, \beta \right){v}_{\mathrm{EWS}}^3 $$
(11.1)

where ρ, R, and Cp are air density, rotor radius, and power coefficient, respectively. Cp depends on the blade pitch angle (β) and the tip speed ratio (λ) (TSR). The λ is given by

$$ \lambda =\frac{\omega_rR}{v_{\mathrm{EWS}}} $$
(11.2)

In an ideal case, the TSR should be kept optimal by controlling the rotor speed and blade pitch angle. Sustaining optimality of TSR ensures maximum wind energy conversion efficiency. In this regard, one should note the following:

  • Each turbine has its own optimal TSR value, determined by the manufacturer.

  • In low wind speed, setting the pitch angle at a value (β = 0) ensures harvesting maximum wind energy, while the generator torque control is used to track the optimal rotor speed. The generator will load the aerodynamic subsystem leading to deceleration or release of rotor rotation. Precise tracking of the optimal speed will oscillate the output power and load the drive train shafts though reduce its lifetime.

  • In high wind speeds, the pitch angle maybe controlled to prevent the turbine from surpassing the rated power. Further, inertia of large-scale wind turbines limits the rate of blade rotation. Generator torque control technique is used in this range to improve regulation.

Since wind turbines are driven by a natural force, the operation range may be divided into four regions depending on wind speed. In region one, the wind speed is not adequate to overcome the wind turbine inertia, and hence there is no rotation and no electrical power generation. Region two covers the range between the cut-in and the rated wind speed; wind force is adequate to drive the turbine and initiate rotation; the objective is to maintain the harvested power from the available wind at the optimal value. In region three, there is a high enough wind speed to achieve rotational speed equal or above the rated speed, and below the cut-out speed, an objective is to achieve rated electrical power using regulation. Region four corresponds to the case when the wind speed is above the upper predefined limit.

It is important to ensure reliable operation of wind turbine systems due to their great contribution electrical power, as stated in Sect. 11.2. However, faults and failures decrease system sustainability leading to higher IOM costs (Artigao et al. 2018; Liu et al. 2019; Ozturk et al. 2018). Figure 11.4 shows failures in different parts of the wind turbine system (Ozturk et al. 2018).

Fig. 11.4
figure 4

Wind turbines for geared drive 500 kW: (a) percentage of annual failure rate; (b) downtime per failure

Full size image

It should be clear by now that the stochastic nature of wind, the probability of different types of faults, and the nonlinearly of the aerodynamic subsystem should be considered by the controller designer to meet required control objectives. Consequently, there is increased interest in robust control, fault diagnosis, and fault-tolerant control of wind turbines. Recent studies have attended to development of control strategies to relax these challenges (Corradini et al. 2017; Jabbari Asl and Yoon 2016; Kinnaert and Rakoto 2016; Liu et al. 2017; Miguel et al. 2017; Yang and Chai 2016). In context, the use of FTC and FD methods offers significant reduction of plant downtime and avoids unscheduled maintenance costs (Lan et al. 2018; Liu et al. 2017; Sami and Patton 2012c; Shaker and Kraidi 2017; Shaker and Patton 2014a; Shaker and Patton 2014b). Most proposed designs tolerate either sensor or actuator faults; the real challenge is to develop an FTC design strategy which tolerates simultaneous system and sensor faults.

4 Wind Turbine Nominal Control: FTC

Wind turbine operation is governed by two distinct regions, namely, partial and full load regions. Maximizing the amount of power harvested from wind is the control objective at low wind speed. Conversely, regulating the generated electrical power to its rated value is the objective at high wind speed (Carriveau 2011; Hansen 2015; Luo et al. 2014). Whenever wind speed is below the rated value, the reference controller maintains turbine operation via the optimal tip speed ratio. Above the rated wind speed, controllers produce the reference pitch angle required to regulate the output power constant at its rated value. Further, inner controllers are designed to ensure robust tracking performance of the reference signals that are produced by the reference controller.

From the viewpoint of system reliability, faults potentially affect any subsystem of wind turbines, and hence the objective of robust control is to tolerate consequent effects to sustain nominal closed-loop performance (Odgaard et al. 2013; Odgaard and Johnson 2013). This work concerns the blade pitch actuator system since it has a high failure rate (Ozturk et al. 2018). The hydraulic pitch system consists of three identical pitch actuators. Such actuators are modeled in state space relating the measured pitch angle and its reference, written as

$$ \left.\begin{array}{c}{\dot{x}}_p={A}_p{x}_p+{B}_p{\beta}_r+{D}_p{\varphi}_p\left({x}_p,{\beta}_r\right)\\ {}{y}_p={C}_p{x}_p\end{array}\right\} $$
(11.3)

where \( {\dot{x}}_p=\left[\begin{array}{c}\beta \\ {}\dot{\beta}\end{array}\right],{A}_p=\left[\begin{array}{cc}0& 1\\ {}-{\omega}_n^2& -2\zeta {\omega}_n\end{array}\right],{B}_p=\left[\begin{array}{c}0\\ {}{\omega}_n^2\end{array}\right],{D}_p=\left[\begin{array}{c}0\\ {}1\end{array}\right],{C}_p=\left[1\kern0.5em 0\right] \), and φp(xp, βr) represents system fault or actuator fault, ζ is the damping ratio, and ωn is the natural undamped frequency. The nominal values of the parameters are ζ = 0:6 and ωn = 11:11 rad = s.

Remark One

  • In the blade pitch scale and stuck sensor fault scenarios, the inner-loop blade pitch controller alleviates the difference between the βr and the faulty measured β and causes improper blade orientation (see Fig. 11.5). Clearly, this situation induces structural loads of the wind turbine system due to the unevenness in the wind force on the rotor area.

  • The system fault of pitch actuators is attributed to the drop of oil pressure or the increase in air content of the pitch actuator. This fault will directly affect the tracking performance of the pitch system.

  • Variations in the nominal values of the parameters ζ and ωn may represent a drop of oil pressure fault or increase in air content fault (Corradini et al. 2017; Odgaard and Stoustrup 2015; Shaker and Kraidi 2017). Thus, the model parameters of (11.3) have the following generalized form:

Fig. 11.5
figure 5

Possible faults that affect blade pitch system

Full size image
$$ {\omega}_n^2={\omega}_{no}^2+\Delta \left({\omega}_{nf}^2-{\omega}_{no}^2\right)\ \mathrm{and}\ \zeta {\omega}_n={\zeta}_{\mathrm{o}}{\omega}_{no}++\Delta \left({\zeta}_f{\omega}_{nf}-{\zeta}_o{\omega}_{no}\right) $$
(11.4)

where Δ ∈ [0 1] is the fault severity parameter, Δ = 0 and Δ = 1 corresponds to fault free and complete faulty system, respectively. The parameters ζoωno, ζωn, and ζfωnf refer to nominal, generalized, and faulty model parameters. Hence, the parameters of (11.3) become

$$ {A}_p=\left[\begin{array}{cc}0& 1\\ {}-{\omega}_{no}^2& -2\zeta {\omega}_{no}\end{array}\right],{B}_p=\left[\begin{array}{c}0\\ {}{\omega}_{no}^2\end{array}\right],{D}_p=\left[\begin{array}{c}0\\ {}1\end{array}\right],{C}_p=\left[1\kern0.5em 0\right] $$
(11.5)
$$ {\varphi}_p\left({\mathrm{x}}_p,{\beta}_r\right)=\Delta \left(2{\zeta}_o{\omega}_{no}-2{\zeta}_f{\omega}_{nf}\right)\dot{\beta}+\Delta \left({\omega}_{no}^2-{\omega}_{nf}^2\right)\beta -\Delta \left({\omega}_{no}^2-{\omega}_{nf}^2\right){\beta}_r $$

Assumption One

The function φp(xp, βr) satisfies the condition φp(xp, βr) ≤ ϑ, where ϑ represents the known upper bound of φp(xp, βr). This assumption is acceptable in practical terms since xp and βr are bounded.

It is important to maintain the nominal closed-loop performance of the pitch system without changes being imposed in both faulty and fault-free operating conditions. Figure 11.5 shows the faults that directly affect the pitch system are the generator speed sensor fault, the pitch angle sensor fault, and the pitch actuator system fault.

Employing the inherent robustness of incremental sliding mode controllers (ISMC) against matched uncertainty and the fault estimation capability of PPIO develops FTC of the pitch actuator system against the simultaneous system and sensor faults (see Fig. 11.6). The ISMC is used as passive FTC to maintain the nominal closed-loop performance of the pitch actuator system during parametric pitch actuator fault; two PPIOs are used to provide online estimation and compensation of the faults of generator speed sensor and pitch position sensor from the inputs of reference and inner controllers.

Fig. 11.6
figure 6

The proposed control structure

Full size image

5 Sliding Mode Controller (SMC) Design

The use of robust SMCs against matched disturbances has been widely approved. Robustness affects SMC as the dominant candidate for passive fault-tolerant controller design against actuator and system faults. To attain the robustness of SMC, the sliding motion must occur within a finite time – the reaching time (treach). Additionally, the states should remain within the sliding vicinity for all time greater than the reaching time (t > treach). Basically, the SMC law has a linear control term and a discontinuous term (Shtessel et al. 2014). While the linear control term enables the reachability condition, the discontinuous control term ensures the sliding condition.

Remark Two

  • While the generator speed sensor faults force the reference controller to produce incorrect reference pitch angle (βr), the inner controller is directly affected by the pitch position sensor faults. The consequence is that the overall system performance deviates from the rated operating conditions.

  • The sliding mode controller is considered as a passive fault-tolerant controller responsible for tolerating the effects of parametric pitch system faults, thereby ensuring acceptable reference tracking of the pitching system.

The objective of the controller is to stabilize the error e = β − βr regardless of the effect of parametric pitch system faults. The error dynamic of the pitch actuator system combined with the supplementary controller is given as

$$ \left.\begin{array}{c}\dot{e}=\dot{\beta}-\dot{\beta_r}\\ {}\ddot{e}=-2\varsigma {w}_{no}\dot{\beta}-{w}_{no}^2\beta -{\ddot{\beta}}_r+{w}_{no}^2{\beta}_r+{w}_{no}^2{u}_{\mathrm{ftc}}^{\mathrm{smc}}+{\psi}_p\left({x}_p,{\beta}_r\right)\end{array}\right\} $$
(11.6)

Initially, a sliding surface capable of achieving control objectives whenever the system attains this surface is to be designed. In this concern, Wang et al. (2015) and Shaker and Kraidi (2019) solved the pitch actuator system of (11.3) by proposition of the following integral surface shown in Eq. (11.7):

$$ S=\dot{e}+{k}_1e+{k}_2\int e\ \mathrm{dt} $$
(11.7)

where the tuning variables k1 and k2 are used to set the performance of the pitch system during the sliding phase. This begets the further setting of a control action that satisfies the reachability condition and the sliding condition. To achieve this, the control signal must satisfy the following inequality:

$$ S\dot{S}\le -\varepsilon \left|S\right| $$
(11.8)

where ε is a positive constant. Using (11.6) gives the following expression for \( \dot{S} \):

$$ \dot{S}=\ddot{e}+{k}_1\dot{e}+{k}_2e=-2\zeta {\omega}_{no}\dot{\beta}-{\omega}_{no}^2\beta -{\ddot{\beta}}_r+{\omega}_{no}^2{\beta}_r+{\omega}_{no}^2{u}_{\mathrm{ftc}}^{\mathrm{smc}}+{\psi}_p\left( xp,{\beta}_r\right)+{k}_1\dot{e}+{k}_2e $$
(11.9)

Once the system reaches the sliding region (\( S=\dot{S}=0 \)), the equivalent control signal becomes

$$ {u}_{\mathrm{eq}}=\frac{1}{\omega_{no}^2}\ \Big[2\zeta {\omega}_{no}\dot{\beta}+{\omega}_{no}^2\beta +{\ddot{\beta}}_r-{\omega}_{no}^2{\beta}_r-{\psi}_p\left({x}_p,{\beta}_r\right)-{k}_1\dot{e}-{k}_2e $$
(11.10)

A more practical expression for the equivalent control (11.10) is

$$ {u}_{\mathrm{eq}}=\frac{1}{\omega_{no}^2}\ \Big[2\zeta {\omega}_{no}\dot{\beta}+{\omega}_{no}^2\beta +{\ddot{\beta}}_r-{\omega}_{no}^2{\beta}_r-{\psi}_p\left({x}_p,{\beta}_r\right)-{k}_1\dot{e}-{k}_2e-\eta \operatorname{sgn}\ (S) $$
(11.11)

where η = φ + ε. By substituting (11.10) into (11.9), one can obtain

$$ \dot{S}={\psi}_{\mathrm{p}}\left({x}_{\mathrm{p}},{\beta}_{\mathrm{r}}\right)-\left(\varphi +\varepsilon \right)\operatorname{sgn}\ (S) $$
(11.12)

Multiplying both sides of (11.12) by (S) gives reachability condition as for region four of Sect. 11.2. Therefore, regardless of the effects of low-pressure faults or increase in air content fault, the SMC ensures accurate tracking of the reference pitch angle.

Remark Three

Although the controller in (11.11) provides robust closed-loop tracking performance against parametric system faults, the sensor fault directly affects the sliding surface in (11.7) and hence cannot be tolerated using the controller (11.11). Additionally, the terms that contain unmeasurable signals can be considered as matched uncertainty.

The robustness of the SMC is remarked upon for various faults in the remainder of this section.

5.1 The Effect of System Fault ψp(xp, βr)

With reference to (11.6), this fault affects the system in the direction of the input channel (11.7). Hence, with an appropriate choice of the discontinuous control component gain (φ + ε), the system reaches the sliding surface at finite time (tr) and remains within the sliding manifold for all time (t < tr). While sliding, the tracking error dynamics will be governed by the design parameters (k1, k2) of the second-order homogeneous equation \( \left(S=0=\dot{e}+{k}_1e+{k}_2\int edt\right). \) The non-homogeneous part \( \left(\mathrm{i}.\mathrm{e}.,-{\dot{f}}_{\beta }-{k}_1{f}_{\beta }-{k}_2\int {f}_{\beta } dt\right) \) corresponds to a forcing term that prevents the SMC from achieving the objective (e = 0).

5.2 The Effect of the Generator Speed Sensor ωgf = ωg + fg (Where ωgf Is the Faulty Measurement and fs Is the Additive Sensor Fault)

Figure 11.6 illustrates that this fault directly affects the reference controller (i.e., the outer loop controller) and thereby generates incorrect reference pitch angle βrf which can be written as βrf = βr + fr, where fr represents additive fault signal. Therefore, while sliding, the tracking error dynamics will be governed by the second-order non-homogeneous equation \( \left(S=0=\dot{e}+{k}_1e+{k}_2e+{k}_2\int e\ \mathrm{dt}+{\dot{f}}_{\mathrm{r}}+{k}_1{f}_r+{k}_2\int {f}_r dt\right). \) The non-homogeneous part (i.e., \( {\dot{f}}_{\mathrm{r}}+{k}_1{f}_r+{k}_2\int {f}_r dt \)) corresponds to a forcing term that prevents the SMC from achieving the objective (e = 0).

Consequently, the controller in (11.11) provides robust closed-loop tracking performance against parametric system fault; the sensor fault directly affects the sliding surface in (11.7) and hence cannot be tolerated using the controller in (11.11). Therefore, a combination of SMC with PPIO-based sensor fault estimation/compensation has been proposed in this chapter (see Fig. 11.6) to enhance the overall robustness of the closed-loop system against simultaneous system and sensor faults.

6 PPIO-Based Generator Speed Sensor Fault Estimation

This section presents the proposed FTC approach to correct a faulty generator speed sensor reading. A proportional-proportional-integral augmented fault estimation observer is proposed to provide accurate estimations of various sensor fault scenarios. The model of the drive train system affected by generator speed sensor fault is given as

$$ \left.\begin{array}{c}\dot{x}= Ax+B{T}_{a,g}+D{\psi}_D\\ {}y= Cx+{D}_s{f}_s\end{array}\right\} $$
(11.13)
$$ \dot{x}=\left[\begin{array}{c}{\dot{\omega}}_r\\ {}{\dot{\omega}}_g\\ {}{\dot{\theta}}_{\delta}\end{array}\right],A=\left[\begin{array}{ccc}{a}_{11}& {a}_{12}& {a}_{13}\\ {}{a}_{21}& {a}_{22}& {a}_{23}\\ {}{a}_{31}& {a}_{32}& {a}_{33}\end{array}\right],B=\left[\begin{array}{cc}{b}_{11}& 0\\ {}0& {b}_{22}\\ {}0& 0\end{array}\right],D=\left[\begin{array}{c}1\\ {}1\\ {}0\end{array}\right], $$
$$ \kern0.5em {T}_{a,g}=\left[\begin{array}{c}{T}_a\\ {}{T}_g\end{array}\right],C=\left[0\kern0.5em 1\kern0.5em 0\right],{D}_s={\left[\begin{array}{ccc}0& 1& 0\end{array}\right]}^T $$
$$ {a}_{11}=\frac{-\left({B}_{dt}+{B}_r\right)}{J_r},{a}_{12}=\frac{B_{dt}}{n_g{J}_r},{a}_{13}=\frac{-{K}_{dt}}{J_r},{a}_{21}=\frac{B_{dt}}{n_g{J}_g}, $$
$$ {a}_{22}=\frac{-\left({B}_{dt}+{n}_g{B}_g\right)}{n_g^2{J}_g},{a}_{23}=\frac{K_{dt}}{n_g{J}_g},{a}_{31}=1,{a}_{32}=\frac{-1}{n_g},{a}_{33}=0,{b}_{11}=\frac{1}{J_r},{b}_{22}=\frac{-1}{J_g}, $$

where Jr, Βr, Jg, ωg, Tg, Bg, ng, Kdt, Bdt, θΔ, Ta, and fs are the rotor inertia, the rotor external damping, the generator inertia, the generator speed, the generator torque, generator, external damping, the gearbox ratio, the torsion stiffness, the torsion damping coefficient, the torsion angle, represents bounded uncertainty, and the aerodynamic torque and fs is the sensor fault.

Remark Four

The aerodynamic and generator torques of (11.11) are not directly measured. Instead, these two input signals are obtained via soft sensors (Sloth et al. 2011). In (11.11), the term ψD represents the expected error between the actual and the soft sensed Ta, g. Consequently, the PPIO should guarantee robust fault estimation regardless of the effect of ψD.

To estimate sensor fault using an extended state observer framework (Klinkhieo 2009), an augmented system accumulates the model in (11.13), and an output filter (11.14) is developed in (11.15) (Sami and Patton 2012b).

$$ \overset{.}{x_s}=-{A}_s{x}_s+{A}_s{C}_x+{A}_s{D}_s{f}_s $$
(11.14)
$$ \dot{x}=\overline{A}\overline{x}+\overline{B}{T}_{a,g}+{D}_{\psi D}+{\overline{D}}_s{f}_s,\overline{y}=\overline{C}\overline{x} $$
(11.15)
$$ {A}_s=\left[\begin{array}{cc}A& 0\\ {}{A}_{\mathrm{s}}C& -{A}_{\mathrm{s}}\end{array}\right],\overline{B}=\left[\begin{array}{c}B\\ {}0\end{array}\right],\overline{D}=\left[\begin{array}{c}D\\ {}0\end{array}\right],{\overline{D}}_{\mathrm{s}}=\left[\begin{array}{c}0\\ {}{D}_{\mathrm{s}}{A}_{\mathrm{s}}\end{array}\right],{\overline{C}}_s=\left[0\kern0.5em {I}_{\mathrm{l}}\right] $$

where −As ∈ Rl ∗ l is a stable filter matrix. As illustrated in remark three, the proposed control strategy employs compensation of the sensor faults affecting the system. The PPIO for the system (11.15) is given as

$$ \left.\begin{array}{c}\dot{\hat{x}}=\overline{A}\hat{x}+\overline{B}{T}_{a,g}+{\overline{D}}_s{\hat{f}}_s+L\overline{C}{e}_x\\ {}\hat{y}=\overline{C}\hat{x}\\ {}{\dot{\hat{f}}}_s=\rho\ \left[{K}_1\overline{C}{\dot{e}}_x+{K}_2\overline{C}{e}_x\right]\ \end{array}\right\} $$
(11.16)

where \( \hat{x}\ \mathrm{and}\ \hat{y}\kern0.50em \mathrm{and}\ {e}_y=\overline{y}-\hat{y}=\overline{C}{e}_x \) are the estimated state, estimated output, and output estimation error, respectively, and K1 and K2 are the proportional and integral gains, respectively, and are a symmetric positive definite matrix. Subtracting the observer in (11.16) from the system (11.15), the state estimation error will be defined as

$$ \left.\begin{array}{c}{\dot{e}}_{\mathrm{x}}=\left(\overline{A}-L\overline{C}\right){e}_x+{\overline{D}}_s{e}_{fs}+{\overline{D}}_{\psi D}\\ {}{e}_y=\overline{C}{e}_x\end{array}\right\} $$
(11.17)

where \( {e}_{fs}={f}_s-{\hat{f}}_s \). Using (11.13), the efs dynamics will become

$$ \left.\begin{array}{c}{\dot{e}}_{fs}={\dot{f}}_s-{\dot{\hat{f}}}_s\\ {}{\dot{e}}_{fs}={\dot{f}}_s-\rho {K}_1\overline{C}\overline{A}{e}_x+\rho {K}_1\overline{C}L\overline{C}{e}_x-\rho {K}_2\overline{C}{e}_x-\rho {K}_1\overline{C}{\overline{D}}_{\mathrm{s}}{e}_{fs}-\rho {K}_1\overline{C}{\overline{D}}_{s\psi D}\end{array}\right\} $$
(11.18)

By combining (11.17) and (11.18), the augmented error dynamics can be assembled as in (11.19)

$$ {\dot\tilde{e}}_a=\overset{\sim }{A}\tilde{e}_a+\overset{\check{} }{N}\overset{\sim }{z} $$
(11.19)
$$ {\overset{\sim }{A}}_{\mathrm{s}}=\left[\begin{array}{cc}\overline{A}-L\overline{C}& {\overline{D}}_s\\ {}\rho {K}_1\overline{C}\overline{A}+\rho {K}_1\overline{C}L\overline{C}-\rho {K}_2\overline{C}& -\rho {K}_1\overline{C}{\overline{D}}_s\end{array}\right],\tilde{e}_a=\left[\begin{array}{c}{e}_x\\ {}{e}_{fs}\end{array}\right],{\overset{\sim }{N}}_a=\left[\begin{array}{cc}\overline{D}& 0\\ {}-\rho {K}_1\overline{C}\overline{D}& I\end{array}\right],\overset{\sim }{z}=\left[\begin{array}{c}\psi (D)\\ {}{\dot{f}}_{\mathrm{s}}\end{array}\right] $$

Now, the goals are to compute the gains L, K2, and K3 as well as attenuate the effects of the input \( \overset{\sim }{z} \) on the estimation error via minimizing the L2 norm, which should stay below a desired level.

Remark Five

Based on the available information of \( \overline{D}\ \mathrm{and}\ {\overline{D}}_s \), the following theorem guarantees an attenuation of disturbance effects \( \overset{\sim }{z\ } \) on fault estimation signal via L2 norm minimization.

Theorem 1

The \( {\dot\tilde{e}}_a \) in (11.19) is stable, and the performance is guaranteed with an attenuation level if there exists a symmetric positive definite matrices P1, ρ−1, and G; matrices H, K1, and K2; and a scalar μ satisfying the following LMI constraint, provided that the signals (\( {\psi}_D,{\dot{f}}_s \)) are bounded, rank\( \overline{C}{\overline{D}}_{\mathrm{s}} \), and the pair (\( \overline{A},\overline{C} \)) is observable:

Minimize \( \overline{\gamma} \) such that

$$ \left[\begin{array}{ccccccc}{\varphi}_{11}& {\varphi}_{12}& {\varphi}_{13}& 0& 0& {\varphi}_{16}& 0\\ {}\ast & {\varphi}_{22}& {\varphi}_{23}& {\rho}^{-1}& {\varphi}_{25}& 0& 0\\ {}\ast & \ast & -\gamma I& 0& 0& 0& 0\\ {}\ast & \ast & \ast & -\gamma I& 0& 0& 0\\ {}\ast & \ast & \ast & \ast & -{G}^{-1}& 0& 0\\ {}\ast & \ast & \ast & \ast & \ast & -2\mu {P}_1& \mu I\\ {}\ast & \ast & \ast & \ast & \ast & \ast & {G}^{-1}\end{array}\right]<0 $$
(11.20)
$$ {\varphi}_{11}={P}_1\overline{A}+{\left({P}_1\overline{A}\right)}^T-H\overline{C}-{\left(H\overline{C}\right)}^T+{\omega}_1,{\varphi}_{12}={P}_1{\overline{D}}_{\mathrm{s}}+{\left({K}_1\overline{C}\overline{A}\right)}^T-{\left({K}_2C\overline{A}\right)}^T,{\varphi}_{13}={P}_1{\overline{D}}_s,{\varphi}_{16}={\left(H\overline{C}\right)}^T,{\varphi}_{22} $$
$$ =-\rho {K}_1\overline{C}{\overline{D}}_{\mathrm{s}}-{\left(\rho {K}_1\overline{C}{\overline{D}}_{\mathrm{s}}\right)}^T+{\omega}_2,{\varphi}_{23}=-{K}_1\overline{C}\overline{D},{\varphi}_{25}={K}_1\overline{C},L={P}_1^{-1}H,\gamma =\sqrt{\overline{\gamma}}, $$

where ω1 and ω2 are weighting matrices.

Proof

The PPIO-based sensor fault estimation presented in (11.16) and Theorem 1 represents extension to the PPIO-based actuator fault estimation presented in Shaker (2015); hence the proof is omitted here.

Remark Six

Using (11.3) and the design procedure presented in Sect. 11.3, it is easy to design PPIO for pitch position sensor fault estimation.

7 Simulation Results

This section investigates the response of the benchmark model given in Odgaard et al. (2009) and Odgaard and Stoustrup (2015) to verify the usefulness of the proposed hybrid control strategy in Fig. 11.7. Determining the gain η of (11.11) is an essential step to achieve sliding motion governed by the second-order sliding dynamics:

Fig. 11.7
figure 7

The tracking performance of pitch actuator system: (a) ζ = 0:25, ωn= 5:73 rad/s; (b) ζ= 0:9, ωn= 3:42 rad/s

Full size image
$$ \ddot{e}+{k}_1\dot{e}+{k}_2e=0 $$
(11.21)

Clearly, the performance parameters during sliding phase, governed by k1 and k2, are nominated to maintain the nominal values of the pitch actuator system parameters (i.e., ζ and ωn) as closely as possible.

Remark Seven

The sliding surface parameters (k1, k2) should be chosen such that the error dynamics remain within specific bound on transient responses such as the settling time (Ts) and the peak time (Tp):

$$ {T}_p^2=\left[\frac{\pi^2}{\omega_{\mathrm{n}}^2\left(1-{\zeta}^2\right)}=\frac{\pi^2}{k_2\left(1-{\zeta}^2\right)}\right],{T}_s=\left[\begin{array}{c}\frac{4}{\zeta \omega}=\frac{8}{k_1}\end{array}\right] $$
(11.22)

Additionally, the design parameter η = 50 is selected to satisfy the reachability condition.

7.1 The Performance of ISMC as a Passive FTC Against Pitch Actuator System Fault

For two sets of faulty system parameters, Fig. 11.7 shows the response of the fault free and faulty pitch actuator to a multilevel reference pitch angle.

The function of ISMC is to steer the faulty system to track the nominal desired response. Figure 11.8 shows the effectiveness of the proposed ISMC. The advantage of the proposal is that once the ISMC is designed, there is no need to readjust controller parameters during faults.

Fig. 11.8
figure 8

The ISMC performance of pitch actuator system: (a) ζ= 0:25, ωn= 5:73 rad/s; (b) ζ= 0:9, ωn= 5:73 rad/s

Full size image

Additionally, the ISMC tolerates system faults without needing for fault diagnosis block. Hence, using such controller will result in a simple structure that makes the ISMC a proper candidate for reliable pitch control.

7.2 The Performance of Integrated ISMC and PPIO Against Simultaneous System and Generator Speed Sensor Faults

Regarding Fig. 11.5, the reference controller is directly affected by the generator speed sensor fault. The consequence is that this controller will produce incorrect βr. The ISMC has unable to tolerate the effects of this scenario since it directly affects the sliding surface. Such scenarios have stimulated the integration of ISMC with PPIO. In the integrated system, the PPIO is responsible for providing online sensor fault estimation. Then, the estimated signals compensate for the faulty readings that feed the input of the reference controller. Thus, the integrated ISMC and PPIO is capable of tolerating simultaneous system and sensor faults. Now, solving the LMI constraints of the PPIO in inequality (11.20) gives the following values: \( \rho =0.1,{A}_s=10,\gamma =0.0198,{K}_1=0.6451,{K}_2=5969,L={\left[0.00003-0.0585\kern0.5em 0.000002\kern0.5em 1.5068\right]}^T \). Figure 11.9 shows the tracking performance of the ISMC when 1.5βr scale fault affects the input of the inner controller. Such a scenario occurs when the reference controller receives faulty generator speed measurement. Hence, while sliding, the error signal becomes e = 0 = β − 1.5βr, and hence the actual pitch position is β = 1.5βr.

Fig. 11.9
figure 9

ISMC performance against simultaneous system fault ζ = 0:25, ωn = 5:73 rad/s and faulty ωg

Full size image

7.3 The Performance of Integrated ISMC and PPIO Against Simultaneous System and Pitch Angle Sensor Fault

In this scenario, the ISMC-based inner controller minimizes the error e = (β + fs) − βr, and hence, when e = (β + fs) − βr = 0, the actual pitch position becomes β = βr − fs. Figure 11.10 demonstrates the performance of the proposed integrated ISMC and PPIO. It should be noted that the sensor fault (Dsfs = 0.5β) has been tolerated using an estimation and compensation approach to FTC.

Fig. 11.10
figure 10

The integrated SMC and PPIO for simultaneous actuator system fault ζ = 0.25, ωn = 5.73 rad/s and sensor fault fs = 0.5β

Full size image

Remark Eight

In this subsection, for comparison purposes, the fault tolerance capability of the proposal (Sami and Patton 2012a) has been tested against actuator system fault and sensor fault. Figures 11.11 and 11.12 show inability (Sami and Patton 2012a) to tolerate these faults as also stated in 11.1.

Fig. 11.11
figure 11

The performance of Sami and Patton (2012a) against pitch system fault

Full size image
Fig. 11.12
figure 12

The performance of Sami and Patton (2012a) against pitch sensor fault

Full size image

The effectiveness of the proposal has been verified by realistic faults and wind data of the 5 MW wind turbine FTC benchmark model. Figure 11.13 demonstrates the effects of parametric fault as well as the tolerance capability of the ISMC. Figure 11.14 shows the nominal generator speed and faulty generator speed measurement. In Fig. 11.15, the PPIO has been used to estimate generator speed sensor fault. Moreover, the advantages of using the combining ISMC and PPIO to tolerate simultaneous system and generator speed sensor faults have been demonstrated in Fig. 11.16. Finally, in Fig. 11.17, the PPIO has been exploited to estimate stuck sensor fault of blade-1. Besides, the advantages of combining ISMC and PPIO to tolerate simultaneous system and pitch position sensor faults have been demonstrated in Fig. 11.18.

Fig. 11.13
figure 13

The tracking performance of the ISMC for faulty pitch actuator system ζ = 0.9, ωn = 3.42 rad/s using realistic wind data

Full size image
Fig. 11.14
figure 14

Nominal speed and faulty speed sensor

Full size image
Fig. 11.15
figure 15

Speed sensor fault and its estimation using PPIO

Full size image
Fig. 11.16
figure 16

The performance of integrated ISMC+PPIO

Full size image
Fig. 11.17
figure 17

Blade stuck fault estimation using PPIO

Full size image
Fig. 11.18
figure 18

The performance of integrated SMC + PPIO against simultaneous actuator system fault ζ = 0.25, ωn = 5.73 rad/s and blade-1 stuck sensor fault

Full size image

8 Conclusions

This chapter proposes an integrated PPIO and ISMC design methodology to solve the robustness problem of control systems affected by simultaneous system and sensor faults. The ISMC has been employed to passively tolerate system faults; two PPIOs have been used to estimate and compensate the effects of sensor faults. The effectiveness of the proposal has been presented using a 5 MW wind turbine benchmark model in which the pitch system is affected by system and sensor faults. Based on simulation results, the ISMC can inherently tolerate faults that achieve the matching condition without the need for a fault diagnosis system. However, sensor faults have direct effects on the sliding variable, and hence the ISMC signal steers the system to follow incorrect measurements. The observer-based fault estimation/compensation approach to FTC shows powerful capability to tolerate sensor faults of control systems. Therefore, combining ISMC with PPIO presents robust closed-loop tracking performance against simultaneous system and sensor faults. Finally, for further improvement, minimizing structural loads induced by wind force and/or faults is an interesting objective for fault-tolerant individual pitch control. Moreover, model uncertainty due to system aging and blade deformation and the uncertainty in the measured wind speed represent real challenges to wind turbine control problems. Robust estimation of these variables ensures good system performance and hence integrity in wind renewable energy ensuring sustainability value in energy mixes.