1 Introduction

Moment distributions have found their applications in many studies of practical interest including bio-assay, clinical, income and life testing experiments. Hasnain (2013) studied an exponentiated moment exponential (EME) distribution and developed various distributional properties of it. He showed that this distribution is more flexible than Dara (2012) moment exponential distribution and Gupta and Kundu (2001) exponentiated exponential distribution. He discussed unbiasedness and sufficiency of the parameters of EME distribution. He also discussed different properties of nth order statistic and obtained dual generalized order statistics for this distribution. The moment distributions have applicability in numerous situations. For example, in the field of physics, Krumbein and Pettijohn (1938) and Gy (1982) studied moment distributions to examine the relation between particle diameter and its frequency. Preston (1962) applied canonical distributions in ecology. Zelen (1974) analyzed cell cycle and pulse labeling on length biased data. Zelen (1976) also used length biased sample for the screening of disease and scheduling of examinations of patients. Brown (1972) studied various aspects of the traffic streams. Warren (1975) examined different case studies to observe the role of statistical distributions in forest and forestry products research. Taillie et al. (1979) modeled populations of fish stocks using weighted distributions. Temkin (1976) studied length biased survival models to analyze the cardiac transplantation situations and so on. In these and other application areas, it is pertinent that one has accurate estimation and prediction procedures based on records and moments of record values.

The probability density function (PDF) of an exponentiated moment exponential (EME) distribution is given by

$$\begin{aligned} f(x;\alpha , \beta )=\frac{\alpha x}{\beta ^2}\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\alpha -1}e^{-\frac{x}{\beta }}, \quad x>0, \alpha>0, \beta >0, \end{aligned}$$
(1.1)

and the corresponding cumulative distribution function (CDF) is

$$\begin{aligned} F(x;\alpha ,\beta )=\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\alpha }, \quad x>0, \alpha>0, \beta >0. \end{aligned}$$
(1.2)

The survival function is of the form

$$\begin{aligned} S(x;\alpha , \beta )=1-\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\alpha }, \quad x>0, \alpha>0, \beta >0, \end{aligned}$$
(1.3)

and the hazard function is

$$\begin{aligned} h(x;\alpha , \beta )=\frac{\alpha x}{\beta ^2}\frac{1-\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\alpha -1}e^{-\frac{x}{\beta }}}{1-\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\alpha }}. \end{aligned}$$
(1.4)

Here the parameters α controls the shape of the distribution and β controls the scale of the distribution. We assume that β is known except for real data analysis. In this paper, we estimate the PDF and the CDF of the model under the assumption that the shape parameter α is unknown. For this purpose, we employ various methods of estimation which includes maximum likelihood estimation (MLE), uniformly minimum variance unbiased (UMVU) estimation, percentile (PC) estimation, least-square estimation (LSE), weighted least-square estimation (WLSE), maximum product spacings (MPS) method of estimation, Cramér–von-Mises method of estimation and Anderson–Darling method of estimation. Several researchers have carried out similar kind of studies for various lifetime models. For example, Dixit and Jabbari Nooghabi (2010) obtained efficient estimates for the PDF and the CDF of a Pareto distribution. They showed that MLEs are more efficient than UMVUEs of the PDF and the CDF. In a subsequent work, Dixit and Jabbari Nooghabi (2011) derived efficient estimators of the PDF and the CDF of a four-parameter Pareto distribution under the assumption that its shape parameter is unknown and other parameters are known quantities. Bagheri et al. (2013) considered efficient estimation of the PDF and the CDF of a three-parameter generalized exponential-Poisson distribution with unknown shape parameter. Recently, Bagheri et al. (2016) estimated the CDF and the PDF of an exponentiated Gumbel distribution using different methods of estimation. They compared the performance of the proposed estimators using a simulation study and analyzed a real data set for illustrative purpose.

The main difference between our work with the existing work is that we have considered eight methods of estimation for estimating the pdf and the cdf whereas in existing literature only five methods of estimation is considered to the best of our knowledge.

We organize the contents of this paper as follows. In Sect. 2 maximum likelihood estimators of the PDF and the CDF are derived. Mean squared errors (MSEs) of both the estimators are presented as well. The uniformly minimum variance unbiased (UMVU) estimators and their MSEs are discussed in Sect. 3. We present least squares estimators (LSEs) and the weighted LSEs (WLSEs) in Sect. 4 and in Sect. 5 percentile estimators (PCEs) are obtained. The maximum product spacings estimators are obtained in Sect. 6. We derive Cramér–von-Mises estimators of PDF and CDF in Sect. 7 and in Sect. 8 Anderson–Darling estimators are discussed. In Sect. 9 performance of suggested estimators is studied using a Monte Carlo simulation study. We analyze a real data set in Sect. 10 for illustration purpose. Finally, the paper ends with a conclusion in Sect. 11.

2 Maximum likelihood estimation

Let \(X_1,X_2, \ldots ,X_n\) be a random sample of size n drawn from a EME(\(\alpha , \beta \)) distribution with known scale β. The maximum likelihood estimator (MLE) α is then obtained as

$$ \hat{\alpha }=-\frac{n}{\sum _{i=1}^n \log \left[ 1-\left( 1+\frac{x_i}{\beta }\right) e^{-\frac{x_i}{\beta }}\right] }=\frac{n}{T_1} $$
(2.1)

where \(T_1=-\sum _{i=1}^n \log \left[ 1-\left( 1+\frac{x_i}{\beta }\right) e^{-\frac{x_i}{\beta }}\right] \). Now if X follows EME(\(\alpha , \beta \)) distribution then \(T=-\log \left[ 1-\left( 1+\frac{X}{\beta }\right) e^{-\frac{X}{\beta }}\right] \) has an exponential distribution with rate α. Thus \(T_1\) being sum of n independent such exponential distributions, it follows that \(T_1\) is distributed as gamma \(G(n,\alpha )\) distribution with density function given by

$$ f_{T_1}(t_1)=\frac{\alpha ^n}{\Gamma n} t_1^{n-1} e^{-\alpha t_1}, \quad t_1>0, \alpha >0. $$
(2.2)

Also observe that \(\frac{1}{T_1}\) has inverse gamma distribution and then the distribution of MLE \(\hat{\alpha }=\frac{n}{T_1}=S\) is given by

$$ f_{S}(s)=\frac{n^n \alpha ^n}{\Gamma n} \, s^{-n-1}\, e^{-\frac{n\alpha }{s}},\, s>0. $$

Next we observe that MLEs of the PDF and the CDF are respectively given by

$$\begin{aligned} \hat{f}(x)=\frac{\hat{\alpha }x}{\beta ^2}\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\hat{\alpha } -1}e^{-\frac{x}{\beta }} \end{aligned}$$
(2.3)

and

$$\hat{F}(x)=\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\hat{\alpha }}. $$
(2.4)

In the theorem presented below we show that the estimators \(\hat{f}(x)\) and \(\hat{F}(x)\) are biased for estimating f(x) and F(x) respectively. Before we proceed further we rewrite these estimators as \(\hat{f}(x)=\hat{\alpha } b(x)(a(x))^{\hat{\alpha }-1}\) and \(\hat{F}(x)=(a(x))^{\hat{\alpha }}\) where \(b(x)=\frac{xe^{-\frac{x}{\beta }}}{\beta ^2},\,a(x)=\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] \).

Theorem 2.1

We have

$$\begin{aligned} E[\hat{f}(x)]^m= 2\left[ \frac{b(x)}{a(x)}\right] ^m \frac{(n\alpha )^{\frac{m+n}{2}}}{\Gamma n}\left[ -\frac{1}{m\ln a(x)}\right] ^{\frac{m-n}{2}} K_{m-n}\left( 2\sqrt{-n\alpha m\ln a(x)}\right) \end{aligned}$$

and

$$\begin{aligned} E[\hat{F}(x)]^m= 2 \frac{(n\alpha )^{\frac{n}{2}}}{\Gamma n} \left[ -\frac{1}{m\ln a(x)}\right] ^{-\frac{n}{2}} K_{-n}\left( 2\sqrt{-n \alpha m \ln a(x)}\right) . \end{aligned}$$

Proof

We can write

$$\begin{aligned} E[\hat{f}(x)]^m&= \int _0^{\infty } \left[ sb(x)(a(x))^{s-1}\right] ^m \frac{(n\alpha )^n}{\Gamma n} \frac{1}{s^{n+1}}e^{-\frac{n\alpha }{s}} ds\\&= \frac{(n\alpha )^n}{\Gamma n} (b(x))^m \int _0^{\infty } s^m (a(x))^{sm-m}\frac{1}{s^{n+1}}e^{-\frac{n\alpha }{s}} ds\\&= \frac{(n\alpha )^n}{\Gamma n} (b(x))^m \int _0^{\infty } e^{(sm-m)\ln a(x)} s^{m-n-1} e^{-\frac{n\alpha }{s}} ds\\&= 2\left[ \frac{b(x)}{a(x)}\right] ^m \frac{(n\alpha )^{\frac{m+n}{2}}}{\Gamma n}\left[ -\frac{1}{m\ln a(x)}\right] ^{\frac{m-n}{2}} K_{m-n}\left( 2\sqrt{-n\alpha m\ln a(x)}\right) , \end{aligned}$$

where \(K_{\nu }\) denotes the modified Bessel function of second kind of order \(\nu \). Also

$$\begin{aligned} E[\hat{F}(x)]^m&= \int _0^{\infty } (a(x))^{sm} \frac{(n\alpha )^n}{\Gamma n} \frac{1}{s^{n+1}} e^{-\frac{-n\alpha }{s}} ds\\&= \frac{(n\alpha )^n}{\Gamma n} \int _0^{\infty } e^{sm \ln a(x)} \frac{e^{-\frac{n\alpha }{s}}}{s^{n+1}} ds\\&= 2 \frac{(n\alpha )^{\frac{n}{2}}}{\Gamma n} \left[ -\frac{1}{m\ln a(x)}\right] ^{-\frac{n}{2}} K_{-n}\left( 2\sqrt{-n \alpha m \ln a(x)}\right) \end{aligned}$$

\(\square \)

Theorem 2.2

The mean squared error of estimates \(\hat{f}(x)\) and \(\hat{F}(x)\) are given by respectively

$$\begin{aligned} { MSE}(\hat{f}(x))&= 2 \left( \frac{a(x)}{b(x)}\right) ^2 \frac{(n\alpha )^{\frac{n+2}{2}}}{\Gamma n}\left[ -\frac{1}{2\ln a(x)}\right] ^{\frac{2-n}{2}}K_{2-n}\left( 2\sqrt{-2\alpha n \ln a(x)}\right) \\&\quad -4f(x)\frac{a(x)}{b(x)} \frac{(n\alpha )^{\frac{n+1}{2}}}{\Gamma n} \left[ -\frac{1}{\ln a(x)}\right] ^{\frac{1-n}{2}} K_{1-n}\left( 2\sqrt{-n\alpha \ln a(x)}\right) +(f(x))^2 \end{aligned}$$

and

$$\begin{aligned} { MSE}(\hat{F}(x))&= 2 \frac{(n\alpha )^{\frac{n}{2}}}{\Gamma n}\left[ -\frac{1}{2\ln a(x)}\right] ^{-\frac{n}{2}}K_{-n}\left( 2\sqrt{-2n\alpha \ln a(x)}\right) \\&\quad -4F(x)\frac{(n\alpha )^{\frac{n}{2}}}{\Gamma n} K_{-n} \left( 2\sqrt{-n\alpha \ln a(x)}\right) +(F(x))^2 \end{aligned}$$

Proof

The proof follows by proceeding in a manner similar to the proof of the previous theorem. \(\square \)

3 Uniformly minimum variance unbiased estimation

This section deals with finding uniformly minimum variance unbiased (UMVU) estimators of the PDF and the CDF of an EME distribution. The mean square errors (MSE) of these estimators are also obtained. Suppose \(X_1,X_2, \ldots , X_n\) denotes a random sample of size n drawn from the EME distribution as defined in (1.1). We consider estimation of f(x) and F(x) under the assumption that the scale parameter β is known. For this problem \(T_1=\sum _{i=1}^n \log \left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{-1}\) is a complete and sufficient statistic for α and it has a gamma \(G(n,\alpha )\) distribution. Following Lehmann–Scheffe theorem if \(g_{X_1 \mid {T_1}}(x_1 \mid T_1=t) = h^* (t)\) is the conditional pdf of \(X_1\) given \(T_1 = t\) then we have

$$ E\left[ h^*(T_1)\right] =\int g_{X_1 \mid {T_1}}(x_1\mid t) g_{T_1}(t) dt= \int g(x_1,t) dt=f(x_1) $$

where \(g(x_1,t)\) is the joint pdf of \((X_1,T_1)\). Thus \(h^*(T_1)\) is the UMVU estimator of f(x).

Lemma 3.1

The conditional distribution of \(Z_1\) given \(T_1=t_1\) is obtained as

$$\begin{aligned} f_{Z_1\mid T_1}(z_1 \mid t_1)&= \frac{(n-1)\left[ t_1-\log \left( 1-\left( 1+\frac{x_1}{\beta }\right) e^{-\frac{x_1}{\beta }}\right) \right] ^{n-2}}{t^{n-1}_1},\\&\quad -\log \left[ 1-\left( 1+\frac{x_1}{\beta }\right) e^{-\frac{x_1}{\beta }}\right]< t_1 <\infty \end{aligned}$$

where \(z_1=\log \left[ 1-\left( 1+\frac{x_1}{\beta }\right) e^{-\frac{x_1}{\beta }}\right] ^{-1}\).

Proof

We can write the joint pdf of \((Z_1,T_1)\) as

$$ f_{Z_1,T_1}(z_1,t_1)=f(t_1)f(z_1\mid t_1). $$

We now have

$$\begin{aligned} f_{Z_1\mid T_1}(z_1\mid t_1)&= \frac{f(Z_1=z_1,T_1=t_1)}{f_{T_1}(t_1)}\\&= \frac{f(Z_1=z_1,\sum _{i=2}^n\left[ 1-\left( 1+\frac{x_i}{\beta }\right) e^{-\frac{x_i}{\beta }}\right] ^{-1}=t_1-z_1)}{f_{T_1}(t_1)}\\&= \frac{\alpha e^{-\alpha z_1} \frac{\alpha ^{n-1}}{\Gamma (n-1)}(t_1-z_1)^{n-2}e^{-\alpha (t_1-z_1)}}{\frac{\alpha ^n}{\Gamma n}t^{n-1}_1e^{-\alpha t_1}}\\&= (n-1)\frac{(t_1-z_1)^{n-2}}{t^{n-1}_1}\\= & {} (n-1)\frac{\left[ t_1+\log \left( 1-\left( 1+\frac{x_1}{\beta }\right) e^{-\frac{x_1}{\beta }}\right) \right] ^{n-2}}{t^{n-1}_1},\\&\quad -\log \left( 1-\left( 1+\frac{x_1}{\beta }\right) e^{-\frac{x_1}{\beta }}\right)<t_1<\infty . \end{aligned}$$

In the following theorem we provide UMVU estimators of f(x) and F(x). \(\square \)

Theorem 3.1

For a given \(T=t\), the estimator \(\tilde{f}(x)\) with

$$\begin{aligned} \tilde{f}(x)=\frac{x}{\beta ^2}\frac{e^{-\frac{x}{\beta }}(n-1)}{\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] }\frac{\left[ t_1+\log \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) \right] ^{n-2}}{t^{n-1}_1} \end{aligned}$$

is the UMVUE of f(x) and the estimator \(\tilde{F}(x)\) with

$$\begin{aligned} \tilde{F}(x)= \left[ 1+\frac{\log \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) }{t_1}\right] ^{n-1} \end{aligned}$$

is the UMVUE of F(x) where

$$ -\log \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right)<t_1<\infty $$

Proof

We observe that

$$\begin{aligned} E[\tilde{f}(x)]&= \left[ \frac{x}{\beta ^2} \frac{e^{-\frac{x}{\beta }}(n-1)}{\left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) }\right] \int _{-\log {a(x)}}^{\infty } \frac{(t_1 + \log {a(x)})^{n-2}}{t^{n-1}_1}\frac{\alpha ^n t^{n-1}_1 e^{-\alpha t}}{\Gamma n} dt\\&= \frac{x}{\beta ^2} \frac{e^{\frac{x}{\beta }}(n-1)}{\left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) }\frac{\alpha e^{\alpha \log \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) }}{n-1}\\&= \frac{\alpha x}{\beta ^2} e^{-\frac{x}{\beta }}\left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) ^{\alpha -1}= f(x) \end{aligned}$$

Thus the estimator \(\tilde{f}(x)\) is UMVU estimator of f(x). In order to prove that \(\tilde{F}(x)\) is UMVU estimator of F(x) we show that \(\frac{d}{dx}\tilde{F}(x)=\tilde{f}(x)\).

Now

$$\begin{aligned} \frac{d}{dx}\tilde{F}(x)&= \frac{d}{dx} \left[ 1+\frac{\log \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) }{t_1}\right] ^{n-1}\\&= \frac{e^{-\frac{x}{\beta }}x}{\beta ^2}(n-1)\frac{\left[ t_1+\log \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) \right] ^{n-2}}{t^{n-1}_1\left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) }= \tilde{f}(x). \end{aligned}$$

This completes the proof of the theorem. \(\square \)

Theorem 3.2

The mean squared errors of \(\tilde{f}(x)\) and \(\tilde{F}(x)\) are respectively given by

$$\begin{aligned} MSE(\tilde{f}(x))=((n-1)a^*(x))^2\sum _{i=0}^{(2(n-2))}{2(n-2)\atopwithdelims ()i}(a(x))^i\Gamma (n-2-i,a(x)\alpha )-f^2(x) \end{aligned}$$

and

$$\begin{aligned} MSE(\tilde{F}(x))=\frac{\alpha ^n}{\Gamma n}\sum _{j=0}^{(n-1)2}{(n-1)2 \atopwithdelims ()j}(\log (a(x)))^j\Gamma (n-j, -\log {a(x)}\alpha )-F^2(x). \end{aligned}$$

Proof

Note that

$$ \tilde{f}(x)=a^*(x)(n-1)\frac{(t_1 + \log {a(x)})^{n-2}}{t^{n-1}_1},$$

with \(a^*(x)=\frac{x}{\beta ^2}\frac{e^{-\frac{x}{\beta }}}{1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}}\) and \(\tilde{F}(x)=\left[ 1+\frac{\log {a(x)}}{t_1}\right] ^{n-1}\). We calculate the following expectations

$$\begin{aligned} E[\tilde{f}(x)]^p&= (a^*(x))^p(n-1)^p\int _{-\log {a(x)}}^{\infty }\frac{(t_1 + \log {a(x)})^{(n-2)p}}{t^{(n-1)p}_1}\frac{\alpha ^n}{\Gamma n}t^{n-1}_1e^{\alpha t_1} dt_1\\&= ((n-1)a^*(x)^p)\frac{\alpha ^n}{\Gamma n}\int _{-\log {a(x)}}^{\infty } \left( 1+\frac{\log {a(x)}}{t_1}\right) ^{(n-2)p}t^{n-p-1}_1e^{-\alpha t_1} dt_1\\&= ((n-1)a^*(x))^p \frac{\alpha ^n}{\Gamma n}\int _{-\log {a(x)}}^{\infty } \sum _{i=0}^{(n-2)p}{(n-2)p \atopwithdelims ()i}(\log {a(x)})^i t^{n-p-i-1}_1e^{-\alpha t_1} dt_1\\&= ((n-1)a^*(x))^p\sum _{i=0}^{(n-2)p} {(n-2)p \atopwithdelims ()i}(\log {a(x)})^i\Gamma (n-p-i,\log {a(x)}\alpha ) \end{aligned}$$

and

$$\begin{aligned} E[\tilde{F}(x)]^p&= \int _{-\log {a(x)}}^{\infty } \left[ \left( 1+\frac{\log {a(x)}}{t_1}\right) ^{n-1}\right] ^p\frac{\alpha ^n}{\Gamma n} t^{n-1}_1 e^{-\alpha t_1} dt_1\\&= \frac{\alpha ^n }{\Gamma n}\int _{-\log {a(x)}}^{\infty } \sum _{j=0}^{(n-1)p}{(n-1)p \atopwithdelims ()j}\left( \frac{\log {a(x)}}{t_1}\right) ^jt^{n-1}_1e^{-\alpha t_1} dt_1\\&= \frac{\alpha ^n }{\Gamma n}\sum _{j=0}^{(n-1)p}{(n-1)p \atopwithdelims ()j} (\log {a(x)})^j\Gamma (n-j, -\log {a(x)}\alpha ). \end{aligned}$$

We further observe that \(MSE(\tilde{f}(x)) = E [\tilde{f}(x)]^2 - (f(x))^2\) and the corresponding expectation can be obtained using the above calculations. Similarly we can obtain mean squared error of the estimator \(\tilde{F}(x)\). \(\square \)

4 Least squares and weighted least squares estimators

This section deals with regression based estimators for the unknown shape parameter α. This method has been introduced in literature by Swain et al. (1988) for estimating the unknown parameters of a beta distribution. Let \(F(X_{(j:n)})\) denotes the distribution function of the order random variables \((X_{1:n}, X_{2:n}, \ldots , X_{n:n})\) with \(X_1,X_2, \ldots , X_n\) being a random sample drawn from the distribution as defined in (1). Observe that for a sample of size n we have \(E(F(X_{(j:n)}))=\frac{1}{n+1}, V(F(X_{(j:n)}))=\frac{j(n-j+1)}{(n+1)^2(n+2)}\) and \(cov(F(X_{(j:n)}),F(X_{(k:n)}))=\frac{j(n-k+1)}{(n+1)^2(n+2)}, j<k\) (see, Johnson et al. 1994) we provide two different least square estimators for the unknown parameter α which can be used to estimate the PDF and the CDF of the considered model.

4.1 Least square estimators (LSEs)

In this method we minimize the expression \(\sum _{j=1}^n \left[ F(X_{j:n}-\frac{j}{n+1}\right] ^2\) with respect to the unknown parameter. For the considered model the desired estimator \(\alpha _{ls}\) of α (with known β) is the value minimizing \(\sum _{j=1}^n \left[ \left( 1-\left( 1+\frac{X_{(j:n)}}{\beta }\right) e^{-\frac{X_{(j:n)}}{\beta }}\right) ^{\alpha }-\frac{j}{n+1}\right] ^2\). Thus the least square estimators of the PDF and the CDF are given by

$$\begin{aligned} f_{ls}(x)=\frac{\tilde{\alpha }_{ls}}{\beta ^2}\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\tilde{\alpha }_{ls}-1}e^{-\frac{x}{\beta }} \end{aligned}$$
(4.1)

and

$$\begin{aligned} F_{ls}(x)=\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\tilde{\alpha }_{ls}}. \end{aligned}$$
(4.2)

The expected values and mean square errors of these estimators are computed using simulations as it is difficult to evaluate these quantities analytically.

4.2 Weighted least square estimators

In this set up we minimize the expression \(\sum _{j=1}^n w_j \left[ F(X_{(j:n)}-\frac{j}{n+1})\right] ^2\) with respect to the unknown quantity α where the weight function is \(w_j=\frac{(n+1)^2(n+2)}{j(n-j+1)}\). For the EME distribution the weighted LSE \(\tilde{\alpha }_{wls}\) of α is obtained by minimizing the expression

$$\begin{aligned} \sum _{j=1}^n \frac{(n+1)^2(n+2)}{j(n-j+1)}\left[ \left( 1-\left( 1+\frac{x_{(j:n)}}{\beta }\right) e^{-\frac{x_{(j:n)}}{\beta }}\right) ^{\alpha }-\frac{j}{n+1}\right] ^2. \end{aligned}$$

Thus the weighted LS estimators of f(x) and (F(x)) are obtained as

$$\begin{aligned} \tilde{f}_{wls}(x)=\tilde{\alpha }_{wls}\frac{x}{\beta ^2}\left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) ^{\tilde{\alpha }_{wls}-1}e^{-\frac{x}{\beta }} \end{aligned}$$
(4.3)

and

$$\begin{aligned} \tilde{F}_{wls}(x)= \left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\tilde{\alpha }_{ls}} \end{aligned}$$
(4.4)

The bias and MSE values of these estimators are calculated using simulation.

5 Estimators based on percentiles

In this section we consider estimation of the pdf and the cdf based percentile estimators. This method is originally discussed in Kao (1958), however, one may also refer to Mann et al. (1974) and Johnson et al. (1994) for some further results on this method of estimation. This method has found easy applications in estimation problems where distribution function has a closed form expression. Since the considered model has a closed form distribution function we can estimate its parameters using this technique.

Let \(F(X_{(j:n)})\) be the CDF of the ordered random sample \((X_{1:n},X_{2:n}, \ldots ,X_{(n:n)})\) with \((X_1, X_2, \ldots , X_n)\) taken from an EME distribution. For further consideration let \(p_i=\frac{i}{n+1}\) then percentile estimator \(\tilde{\alpha }_{pe}\) of α minimizes the expression

$$\begin{aligned} \sum _{i=1}^n \left[ \ln p_i -\alpha \ln \left( 1-\left( 1+\frac{x_{i:n}}{\beta }\right) e^{-\frac{x_{i:n}}{\beta }}\right) \right] ^2. \end{aligned}$$
(5.1)

The desired estimator \(\tilde{\alpha }_{pe}\) is the solution to equation

$$\begin{aligned} \sum _{i=1}^n \left[ \ln p_i -\alpha \ln \left( 1-\left( 1+\frac{x_{i:n}}{\beta }\right) e^{-\frac{x_{i:n}}{\beta }}\right) \right] \ln \left( 1-\left( 1+\frac{x_{i:n}}{\beta }\right) e^{-\frac{x_{i:n}}{\beta }}\right) =0 \end{aligned}$$
(5.2)

This implies that

$$\begin{aligned} \tilde{\alpha }_{pe}=\frac{ \sum _{i=1}^n\left[ (\ln p_i) \ln \left( 1-\left( 1+\frac{x_{i:n}}{\beta }\right) e^{-\frac{x_{i:n}}{\beta }}\right) \right] }{\sum _{i=1}^n\left[ \ln \left( 1-\left( 1+\frac{x_{i:n}}{\beta }\right) e^{-\frac{x_{i:n}}{\beta }}\right) \right] ^2}. \end{aligned}$$
(5.3)

So the percentile estimator of the PDF and the CDF are now given by

$$\begin{aligned} \tilde{f}_{pe}(x)=\frac{\tilde{\alpha }_{pe}x}{\beta ^2}\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\tilde{\alpha }_{pe}-1}e^{-\frac{x}{\beta }} \end{aligned}$$
(5.4)

and

$$\begin{aligned} \tilde{F}_{pe}(x)=\left[ 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right] ^{\tilde{\alpha }_{pe}}. \end{aligned}$$
(5.5)

6 Method of maximum product spacing

This method was introduced by Cheng and Amin (1979) as an alternative method to the maximum likelihood estimation method. For a given sample of size of n taken from an EME distribution, the corresponding uniform spacing is given by

$$\begin{aligned} \Delta _i(\alpha ,\beta )=F(x_{i:n}\mid \alpha , \beta )-F(x_{i-1:n}\mid \alpha ,\beta ) \end{aligned}$$
(6.1)

for i = 1, 2, …, n with \(F(x_{0:n}\mid \alpha , \beta )=0,F(x_{n+1:n}\mid \alpha , \beta )=1\) and \(\sum _{i=1}^n\Delta _i(\alpha ,\beta )=1\).

The maximum product spacing estimator \(\tilde{\alpha }_{mps}\) of α is computed by maximizing the expression

$$\Delta (\alpha ,\beta )=\left[ \prod _{i=1}^{n+1}\Delta _i(\alpha ,\beta )\right] ^{\frac{1}{n+1}}$$
(6.2)

with respect to α. Equivalently we maximize the function

$$ \Delta ^*(\alpha ,\beta )=\frac{1}{n+1}\sum _{i=1}^{n+1}\ln \Delta _i(\alpha ,\beta ), $$

and observe that \(\tilde{\alpha }_{mps}\) can be computed from the equation

$$\begin{aligned} \frac{\partial \Delta ^*(\alpha ,\beta )}{\partial \alpha }=\frac{1}{n+1}\sum _{i=1}^{n+1}\frac{1}{\Delta _i(\alpha ,\beta )}\left[ \Delta _0(x_{i:n)}\mid \alpha ,\beta )- \Delta _0(x_{i-1:n)}\mid \alpha ,\beta )\right] \end{aligned}$$
(6.3)

where \(\Delta _0(x_{i:n)}\mid \alpha ,\beta )=\left[ 1-\left( 1+\frac{x_{i:n}}{\beta }\right) e^{-\frac{x_{i:n}}{\beta }}\right] ^{\alpha }\ln \left[ 1-\left( 1+\frac{x_{i:n}}{\beta }\right) e^{-\frac{x_{i:n}}{\beta }}\right] \). Cheng and Amin (1983) observed that maximizing \(\Delta ^*(\alpha , \beta )\) as a method of parameter estimation is as efficient as the MLEs. The MPS estimator of the PDF and the CDF are, respectively,

$$\begin{aligned} \tilde{f}_{mps}(x)=\left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) ^{\tilde{\alpha }_{mps}-1} \frac{\tilde{\alpha }_{mps} x}{\beta } e^{-\frac{x}{\beta }} \end{aligned}$$
(6.4)

and

$$\begin{aligned} \tilde{F}_{mps}(x)= \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) ^{\tilde{\alpha }_{mps}}. \end{aligned}$$
(6.5)

7 Method of Cramér–von-Mises

Macdonald (1971) gave empirical evidence that bias values of the Cramér–von-Mises type estimators are smaller than the other minimum distance estimators. The Cramér–von-Mises estimates \(\tilde{\alpha }_{cvm}\) of the parameter α is computed by minimizing, with respect to α, the function

$$\begin{aligned} V(\alpha ,\beta )=\frac{1}{12n}+\sum _{i=1}^n \left( F(x_{(i:n)}\mid \alpha ,\beta )-\frac{2i-1}{2n}\right) ^2. \end{aligned}$$
(7.1)

The estimator \(\tilde{\alpha }_{cvm}\) can also be derived from the following non-linear equation

$$\begin{aligned} \sum _{i=1}^n \left( F(x_{(i:n)}\mid \alpha ,\beta )-\frac{2i-1}{2n}\right) \Delta _0(x_{i:n}\mid \alpha ,\beta )=0 \end{aligned}$$
(7.2)

where \(\Delta _0(x_{i:n}\mid \alpha ,\beta )=0\) is defined in the previous section. Now the CVM estimators of the PDF and the CDF are given by

$$\begin{aligned} \tilde{f}_{cvm}(x)=\left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) ^{\tilde{\alpha }_{cvm}-1} e^{-\frac{x}{\beta }} \end{aligned}$$
(7.3)

and

$$\begin{aligned} \tilde{F}_{cvm}(x)= \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) ^{\tilde{\alpha }_{cvm}}. \end{aligned}$$
(7.4)

The bias and MSE values of these estimators are computed using simulations.

8 Method of Anderson–Darling

Anderson and Darling (1952) developed a test to detect normality distribution of various data. The Anderson–Darling estimator \(\tilde{\alpha }_{ad}\) of α is derived by minimizing the function

$$\begin{aligned} AD(\alpha ,\beta )=-n-\frac{1}{n}\sum _{i=1}^n (2i-1) \left[ \ln F(x_{i:n}\mid \alpha ,\beta )+\ln \bar{F}(x_{n+1-i:n}\mid \alpha ,\beta )\right] . \end{aligned}$$
(8.1)

The estimator \(\tilde{\alpha }_{ad}\) can also be obtained by solving the following non-linear equations

$$\begin{aligned} \sum _{i=1}^n(2i-1)\left[ \frac{\Delta _0(x_{(i:n)}\mid \alpha ,\beta )}{F(x_{(i:n)}\mid \alpha ,\beta )}-\frac{\Delta (x_{(i:n)}\mid \alpha ,\beta )}{\bar{F}(x_{(i:n)}\mid \alpha ,\beta )}\right] =0 \end{aligned}$$
(8.2)

where \(\Delta _0(.\mid \alpha ,\beta )\) is defined previously.

The Anderson–Darling estimators of the PDF and the CDF are now given by

$$\begin{aligned} \tilde{f}_{ad}(x)=\left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) ^{\tilde{\alpha }_{ad}}\frac{\tilde{\alpha }_{ad} x}{\beta ^2} e^{-\frac{x}{\beta ^2}} \end{aligned}$$
(8.3)

and

$$\begin{aligned} \tilde{F}_{ad}(x)= \left( 1-\left( 1+\frac{x}{\beta }\right) e^{-\frac{x}{\beta }}\right) ^{\tilde{\alpha }_{ad}}. \end{aligned}$$
(8.4)

9 Simulation study

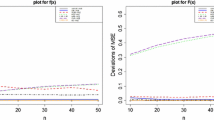
In this section, we study the behavior of the suggested methods of estimation using a simulation study in terms of their mean squared error values. Here, we compute the deviation of MSEs which represent difference between MSE of an estimator from the MSE of maximum likelihood estimator. These values are computed based on 1000 simulated samples from the EME distribution with different sample sizes n = 10, 15, 20, 25, 30, 35, 40, 45, 50 and for arbitrarily assigned values of parameters α and β. We compute MSEs for different values of x as x = 0.75, 1 and 1.5. Figures 1, 2, 3 and 4 represent deviation of MSEs at x = 0.75. Similarly, Figs. 5, 6, 7, 8, 9, 10, 11 and 12 represent deviation of MSEs at x = 1 and x = 1.5 respectively. Note that, left hand side figures are for the PDF estimation and right hand side figures are for the CDF estimation. It is observed from these figures that maximum likelihood estimators of the PDF and the CDF perform better than other proposed estimators and their efficiency improve with the increase in sample sizes. In general, the performance of UMVU estimators is good as far as its MSE is concerned. With moderate increase in α, we get better estimates of the PDF and the CDF for a given β.

Fig. 1
figure 1

\(\alpha =1.5, \beta =0.5\)

Full size image
Fig. 2
figure 2

\(\alpha =1.5, \beta =0.75\)

Full size image
Fig. 3
figure 3

\(\alpha =2, \beta =0.5\)

Full size image
Fig. 4
figure 4

\(\alpha =2, \beta =0.75\)

Full size image
Fig. 5
figure 5

\(\alpha =1.5, \beta =0.5\)

Full size image
Fig. 6
figure 6

\(\alpha =1.5, \beta =0.75\)

Full size image
Fig. 7
figure 7

\(\alpha =2, \beta =0.5\)

Full size image
Fig. 8
figure 8

\(\alpha =2, \beta =0.75\)

Full size image
Fig. 9
figure 9

\(\alpha =1.5, \beta =0.5\)

Full size image
Fig. 10
figure 10

\(\alpha =1.5, \beta =0.75\)

Full size image
Fig. 11
figure 11

\(\alpha =2, \beta =0.5\)

Full size image
Fig. 12
figure 12

\(\alpha =2, \beta =0.75\)

Full size image

10 Data analysis

Here we analyze a real data set to illustrate the use of proposed estimators in practice. This data set as reported in Lawless (1982) represents the survival times for the control group laboratory mice that were exposed to a fixed dose of radiation for a duration of 5–6 weeks and the mice died due to tymic lymphoma. The data set is listed below as

figure a

We first examine whether an EME distribution can be used to draw inference from this data set. For this purpose we fitted this data set using EME and Weibull distributions. Since for real data the unknown parameters α and β of EME distribution are treated as unknown and so they need to be estimated using some estimation method for further analysis. Here we use maximum likelihood estimation method to estimate α and β. To proceed further we assume that \(X_1, X_2, \ldots , X_n\) denote a random sample from a EME distribution. Below we derive MLE of \(\alpha , \beta \) based on the given data set. The likelihood equation of \((\alpha ,\beta )\) is

$$\begin{aligned} L(\alpha ,\beta )=\prod _{i=1}^n \left[ 1-\left( 1+\frac{x_i}{\beta }\right) e^{-\frac{x_i}{\beta }}\right] \frac{\alpha x_i}{\beta ^2} e^{-\frac{x_i}{\beta }} \end{aligned}$$

and the corresponding log likelihood function is obtained

$$\begin{aligned} l=\ln L=\alpha \sum _{i=1}^n \ln \left( 1-\left( 1+\frac{x_i}{\beta }\right) e^{-\frac{x_i}{\beta }}\right) +n \ln \alpha +\sum _{i=1}^n x_i-\frac{\sum _{i=1}^n}{\beta }-2n \ln \beta . \end{aligned}$$

Now the likelihood equations of α and β are

$$\begin{aligned} \frac{\partial l}{\partial \alpha }= & {} \sum _{i=1}^n \ln \left( 1-\left( 1+\frac{x_i}{\beta }\right) e^{-\frac{x_i}{\beta }}\right) +\frac{n}{\alpha }=0\\ \frac{\partial l}{\partial \beta }= & {} \alpha \sum _{i=1}^n \frac{x_i e^{-\frac{x_i}{\beta }}}{\left( 1-\left( 1+\frac{x_i}{\beta }\right) e^{-\frac{x_i}{\beta }}\right) }+\sum _{i=1}^n x_i -2n\beta =0. \end{aligned}$$

The desired estimates of α and β can now be obtained by simultaneously solving the above system of equations. Similarly unknown parameters of the Weibull distribution can be estimated. We report MLEs of unknown parameters of these two distributions along with the values of K-S test and the corresponding p values in Table 1. For computational simplification, we divided each data points by 100. The reported results suggest that the EME distribution fits the data set reasonably good. Further, we also fit the EME distribution to the given data set using the suggested procedures for model selection purpose. In Table 2 we have reported different estimates of α and β obtained using MLE, LSE, WLSE, PCE, CVE, MPS and AD methods of estimation. The corresponding values of different model selection criteria such as maximum likelihood (ML) criterion, Akaike information criterion (AIC), corrected Akaike information criterion (AICc), Bayes information criterion (BIC), Hannan-Quinn criterion (HQC) are also displayed in this table. Results suggest that, the percentile estimators provide better fit among different model selection criteria which is reasonably in line with the simulation study as well. In Fig. 13, we provide Q–Q plots (ovserved versus expected quantiles) for all the suggested estimation methods. Displayed figures indicate that the percentile estimator (fourth in list) provides the better fit. Figure 14 displays the P–P plots (observed versus expected probabilities) for all the suggested methods of estimation. Figure 15 shows the density plots (fitted density functions versus empirical histogram) for all the estimation methods. We may conclude from the figures that percentile estimator provides reasonably good fit.

Table 1 Goodness of fit tests for the real data set
Full size table
Table 2 Different estimates of the parameters of EME distribution and values of model selection criteria for the real data set
Full size table
Fig. 13
figure 13

Q–Q plots for the different estimation methods

Full size image
Fig. 14
figure 14

P–P plots for the different estimation methods

Full size image
Fig. 15
figure 15

Fitted PDFs and the histogram for the seven different estimation methods

Full size image

11 Conclusion

In this article, we have considered eight methods of estimation of the probability density function and the cumulative distribution function for the EME distribution and comparisons are performed. Such comparisons can be useful to find the best estimators for the PDF and the CDF which can be used to estimate functionals like differential entropy, Rényi entropy, Kullback–Leibler divergence, Fisher information, cumulative residual entropy, the quantile function, Bonferroni curve, Lorenz curve, probability weighted moments, hazard rate function, mean deviation about mean etc. From both simulation study and real data analysis, we observe that both ML and UMVU estimators along with percentiles estimator perform better than their counter part. We hope our results and methods of estimation might attract wider sets of applications in the above mentioned functionals. It will be interesting to study the methods of estimation of the PDF and the CDF based on censoring data like progressive censoring and group censoring data. The work is in progress and it will be reported later.