Keywords

1 Introduction

Atanassov [1] generalized the fuzzy sets to intuitionistic fuzzy sets to deal with imprecision, vagueness, and uncertainty for a class of problems in a better way. In fuzzy sets, we consider only belonging of an element to a set, whereas in intuitionistic fuzzy set theory, we consider both the belonging and the non-belonging as membership and non-membership functions. Intuitionistic fuzzy set, with this property, emerged as more powerful tool in dealing with vagueness and uncertainty than fuzzy set. Angelov [3] proposed a method for solving multi-objective programming problems in intuitionistic fuzzy environment. Further, Atanassov and Gargov in [2] generalized intuitionistic fuzzy sets and proposed several new properties to intuitionistic fuzzy sets which made IFS suitable to deal with problems of optimizations. De et al. [4], Mondal and Samanta [12] proposed some properties of intuitionistic fuzzy sets to make it more suitable for various applications. For dealing with multi-objective programming, goal programming emerged as more powerful to provide its solutions, and Mohamed [11] studied relationship in goal programming and fuzzy programming. Etoh et al. [8] considered a probabilistic problem in fuzzy environment for its solution, and this problem was further studied by Garg and Singh [7] for suitability of fuzzy solution of a probabilistic problem. Jana and Roy [9] considered a multi-objective intuitionistic fuzzy linear programming approach for solution of transportation problem, and Mahapatra et al. [13] studied intuitionistic fuzzy mathematical programming on reliability optimization model. Another direction in optimization under interval-valued intuitionistic fuzzy emerged with the work of Li [10] who considered linear programming method for MADM with interval-valued intuitionistic fuzzy sets. Dubey et al. [5, 6] considered the linear programming problems with triangular intuitionistic fuzzy number interval uncertainty in intuitionistic fuzzy set (IFS). Recently Nachammai and Thangaraj [14], Nagoorgani, Ponnalagu and Shahrokhi et al. [16] have also studied the solutions of linear programming problems in intuitionistic fuzzy environment. Here, we construct the membership and non-membership functions and have applied the developed algorithm for solution of an probabilistic problem by intuitionistic fuzzy approach.

2 Preliminaries

Since Zadeh [17] generalized the set theory as fuzzy set theory to deal with information available in imprecise form, many new properties have been developed for fuzzy set and numerous applications have been developed. It was Zimmermann [18] who considered a fuzzy programming with several objectives. As Atanassov [1, 2] theories are considered the generalization of fuzzy set to intuitionistic fuzzy set, it is needed to study the basics of intuitionistic fuzzy to develop an application of this IFS. Thus, here we reproduce some of its fundamentals to make the study self-sufficient.

Definition 1

An intuitionistic fuzzy set \(\tilde{A}\) assigns to each element \(x\) of the universe \(X\) a membership degree \(\mu _{\tilde{A}} (x) \in [0, 1]\) and non-membership degree \(\nu _{\tilde{A}} (x)\in [0, 1]\) such that \(\mu _{\tilde{A}} (x)+\nu _{\tilde{A}} (x)\le 1.\) A IFS is mathematically represented as \(\left\{ \left\langle {x, \mu _{\tilde{A}} (x), \nu _{\tilde{A}} (x)}\right\rangle | x\in X \right\} \) where \(1-\mu _{\tilde{A}} (x)-\nu _{\tilde{A}} (x)\) is called hesitancy margin.

Example

Let \(A\) be set of countries with elected government, and let \(x\) be a member of \(A\). Let \(M(x)\) be the percentage of the electorate that voted for the government, \(N(x)\) the percentage that voted against. If we take \(\mu _{\tilde{A}} (x)=\frac{M(x)}{100},\nu _{\tilde{A}} (x)=\frac{N(x)}{100}\) then \(\mu _{\tilde{A}} (x)\) gives the degree of support, \(\nu _{\tilde{A}} (x)\) the degree of opposition and \(h_{\tilde{A}} (x)=1-\mu _{\tilde{A}} (x)-\nu _{\tilde{A}} (x)\) stand for indeterminacy which is the portion that cast bad votes: invalid votes, abstinent.

2.1 Intuitionistic Fuzzy Number

An IFS \(\tilde{A}=(\mu _{\tilde{A}} ,\nu _{\tilde{A}} )\) of real numbers is said to be an intuitionistic fuzzy number if \(\mu _{\tilde{A}} \) and \(\nu _{\tilde{A}} \) are fuzzy numbers. Hence, \(A=(\mu _{\tilde{A}} ,\nu _{\tilde{A}} )\) denotes an intuitionistic fuzzy number if \(\mu _{\tilde{A}} \), and \(\nu _{\tilde{A}} \) are fuzzy numbers with \(\nu _{\tilde{A}} \le \mu _{\tilde{A}}^{C}\), where \(\mu _{\tilde{A}}^C \) denotes the complement of \(\mu _{\tilde{A}} \).

Some operations on intuitionistic fuzzy sets are as follows:

$$\begin{aligned} \tilde{A}\cap \tilde{B}&=\{\left\langle {x, \min (\mu _{\tilde{A}} (x), \mu _{\tilde{B}} (x) ), \max (\nu _{\tilde{A}} (x), \nu _{\tilde{B}} (x) )}\right\rangle | x\in X \} \\ \tilde{A}\cup \tilde{B}&=\{\left\langle {x, \max (\mu _{\tilde{A}} (x),\mu _{\tilde{B}} (x) ), \min (\nu _{\tilde{A}} (x), \nu _{\tilde{B}} (x) )}\right\rangle | x\in X \} \end{aligned}$$

3 Optimization in Intuitionistic Fuzzy Set

Various studies of optimization problems in fuzzy environment showed the suitability of considering optimization problems in fuzzy environment. The reason for the success was quite obvious that a small violation in constraints leads to more efficient solution. Further studies revealed that fuzzy optimization formulations are more flexible and allow better range of solutions especially when boundaries are not sharp. As a matter of fact in case of multi-objective programming problem, we search an optimal compromise solution rather than optimal solution. This idea of getting compromise solution in intuitionistic fuzzy environment needs to maximize the degree of acceptance to objective functions and constraints and to minimize the rejection of objective functions and constraints.

Consider the intuitionistic fuzzy optimization problem as generalization of fuzzy optimization problem under taken by Angelov [3] and is given as

$$\begin{aligned} \min \ f_i (x),\quad i=1, 2, \ldots m \\ \end{aligned}$$

Such that

$$\begin{aligned} {g_{j}}(x) \le 0,\quad j=1, 2, \ldots n \end{aligned}$$

where \(x\) is decision variables, \(f_i (x)\) denotes objective functions, and \(g_j (x)\) denotes the constraint functions. \(m\) and \(n\) denote the number of objective(s) and constraints, respectively.

Theorem 1 For objective function of maximization problem, the upper bound for non-membership function is always less than that of the upper bound of membership function.

Proof

From definition of IFS, sum of the degree of rejection and acceptance is less than unity.

If, \(U_k^\mu \) and \(L_k^\mu \) are upper and lower bound, respectively, for the membership function and similarly \(U_k^\nu \) and \(L_k^\nu \) are upper and lower bound, respectively, for the non-membership function, then

$$\begin{aligned} \mu _k (f_k (x))+\nu _k (f_k (x))<1\quad \text {for all}\quad k=1,2,\ldots , K \end{aligned}$$

or

$$\begin{aligned} \frac{f_i (x)-L_k^\mu }{U_k^\mu -L_k^\mu }+\frac{U_k^\nu -f_k (x)}{U_k^\nu -L_k^\nu }<1 \end{aligned}$$

Case 1

If possible, let \(U_k^\nu =U_k^\mu \), then we have

$$\begin{aligned} \frac{f_k (x)-L_k^\mu }{U_k^\mu -L_k^\mu }+\frac{U_k^\nu -f_k (x)}{U_k^\mu -L_k^\nu }<1 \end{aligned}$$

this gives \(L_k^\nu <L_k^\mu \) which is contradicting the fact that lower bound of the membership and non-membership is equal; hence, \(U_{k}^{\nu } \ne U_{k}^{\mu }\).

Case 2

Let us consider \(L_k^\nu =L_k^\mu \), then we have

$$\begin{aligned} \frac{f_k (x)-L_k^\mu }{U_k^\mu -L_k^\mu }+\frac{U_k^\nu -f_k (x)}{U_k^\nu -L_k^\mu }<1 \end{aligned}$$

Which imply that \(U_k^\nu <U_k^\mu \).

Case 3

Let us consider \(L_k^\nu =L_k^\mu +\varepsilon _k , \varepsilon _k >0\) for all \(k=1, 2, \ldots , K\).

$$\begin{aligned}&\frac{f_k (x)-L_k^\mu }{U_k^\mu -L_k^\mu }+\frac{U_k^\nu -f_k (x)}{U_k^\nu -L_k^\mu }<1 \\&U_k^\mu >U_k^\nu +\varepsilon _k \frac{U_k^\nu -f_k (x)}{f_k (x)-L_k^\mu -\varepsilon _k } \end{aligned}$$

i.e., \(U_k^\mu >U_k^\nu \) hence \(U_k^\mu >U_k^\nu \).

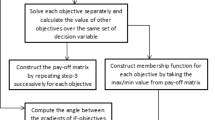
3.1 Computational Algorithm

Using the above-mentioned theorem and with the method by Anglev [3], we develop the following algorithm for getting solution of a multi-objective programming problem in intuitionistic fuzzy environment:

  1. Step 1:

    Take one objective function out of given k objectives and solve it as a single objective subject to the given constraints. From obtained solution vectors, find the values of remaining (\(k-1\)) objective functions.

  2. Step 2:

    Continue the step 1 for remaining (\(k-1\)) objective functions. If all the solutions are same, then one of them is the optimal compromise solution.

  3. Step 3:

    Tabulate the solutions thus obtained in step 1 and step 2 to construct the positive ideal solution (PIS) as given in Table 1.

Table 1 Positive ideal solution
Full size table
  1. Step 4:

    From PIS, obtain the lower bounds and upper bounds for each objective functions, where \(f_{k}^{*}\) and \(f_{k}^{\prime }\) are the maximum and minimum values, respectively.

  2. Step 5:

    Set upper and lower bounds for each objective for degree of acceptance and degree of rejection corresponding to the set of solutions obtained in step 4.

For membership functions:

$$\begin{aligned} U_k^\mu =\max (Z_k (X_r )) \quad \text {and}\quad L_k^\mu =\min (Z_k (X_r )),\quad 1\le r\le k. \end{aligned}$$

For non-membership functions:

$$\begin{aligned} U_k^\nu =U_k^\mu -\lambda (U_k^\mu -L_k^\mu )\quad \text {and}\quad L_k^\nu =L_k^\mu \quad 0<\lambda <1. \end{aligned}$$
  1. Step6:

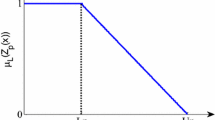
    Consider the membership function \(\mu _k (f_k (x))\) and non-membership function \(\nu _k (f_k (x))\) as following linear functions:

$$\begin{aligned} \begin{aligned} \mu _k (f_k (x))=\left\{ \begin{array}{lll} 0 &{} \mathrm{if} &{} f_k (x)\le L_k^\mu \\ \frac{f_k (x)-L_k^\mu }{U_k^\mu -L_k^\mu } &{} \mathrm{if} &{} L_k^\mu \le f_k (x)\le U_k^\mu \\ 1 &{} \mathrm{if} &{} f_k (x)\ge U_k^\mu \\ \end{array}\right. \end{aligned} \end{aligned}$$
$$\begin{aligned} \begin{aligned} \nu _k (f_k (x))=\left\{ \begin{array}{lll} 0 &{} \mathrm{if} &{} f_k (x)\ge U_k^\nu \\ \frac{U_k^\nu -f_k (x)}{U_k^\nu -L_k^\nu } &{} \mathrm{if} &{} L_k^\nu \le f_k (x)\le U_k^\nu \\ 1 &{} \mathrm{if} &{} f_k (x)\le L_k^\mu \\ \end{array}\right. \end{aligned} \end{aligned}$$

Figure of the membership function and non-membership function for maximization type objective function are shown in Fig. 1.

Fig. 1
figure 1

Membership and non-membership functions

Full size image
  1. Step 7:

    An intuitionistic fuzzy optimization technique for MOLP problem as taken in this section with such membership and non-membership functions can be written as

$$\begin{aligned} \text {Maximize}\quad&\mu _k (f_k (x)) \\ \text {Minimize} \quad&\nu _k (f_k (x)) \\ \text {Subject to} \quad&\mu _k (f_k (x))+\nu _k (f_k (x))\le 1, \\&\mu _k (f_k (x))\ge \nu _k (f_k (x)), \\&\nu _k (f_k (x))\ge 0, \\&g_j (x)\le b_{j}, \quad x\ge 0, \\ \text {for}\quad&k=1,2,\ldots , K;\quad j=1,2,\ldots , m. \end{aligned}$$

Now the above problem may be equivalently written in a linear programming problem as

$$\begin{aligned} \text {Maximize}\quad&(\alpha -\beta ) \\ \text {Subject to}\quad&\alpha \le \mu _k (f_k (x)), \\&\beta \ge \nu _k (f_k (x)), \\&\alpha +\beta \le 1, \\&\alpha \ge \beta , \\&\beta \ge 0, \\&g_j (x)\le b_j, x\ge 0,\quad k=1,2,\ldots K;\quad j=1,2,\ldots , m. \end{aligned}$$

This linear programming problem can be easily solved by a simple method.

4 Numerical Illustration

In this section, the developed algorithm is implemented by a numerical example. We consider the problem as undertaken by Garg and Singh [7], Itoh [8] in which a farmer has to grow carrot, radish, cabbage, and Chinese cabbage in a season under areas \(x_1 ,x_2 ,x_3\), and \(x_4\ (\text {unit}\ 10\, \text {acres}=1000\,\text {m}^{2})\), respectively. The farmer has a total land of 10 acres and a max labor work time available to him is 260 h. The profit coefficients (unit 10,000 Japanese Yen) and work time for the crops are given in the Table 2 .

Table 2 Values of various parameters available to the problem
Full size table

The complete mathematical formulation of the above problem is as follows:

$$\begin{aligned}&\text {Maximize}\ z_1 =29.8x_1 +10.4x_2 +13.8x_3 +19.8x_4 \nonumber \\&\text {Maximize}\ z_2 =23.9x_1 +21.4x_2 +49.2x_3 +32.8x_4 \nonumber \\&\text {Maximize}\ z_3 =37x_1 +16x_2 +3.6x_3 +9.7x_4 \nonumber \\&\text {Maximize}\ z_4 =19.3x_1 +26.6x_2 +48.4x_3 +75.6x_4 \end{aligned}$$
(1)

Subject to the constraints

$$\begin{aligned}&x_1 +x_2 +x_3 +x_4 \le 10 \\&6.9x_1 +71x_2 +2x_3 +33x_4 \le 260, \\&x_1 , x_2 , x_3 , x_4 \ge 0. \end{aligned}$$

The solution procedure of the above problem involves the following steps:

  1. Step 1:

    The solution choosing one by one objective as single objective function programming problem Maximize \(z_1 =29.8x_1 +10.4x_2 +13.8x_3 +19.8x_4\) Subject to the constraints

    $$\begin{aligned}&x_1 +x_2 +x_3 +x_4 \le 10 \\&6.9x_1 +71x_2 +2x_3 +33x_4 \le 260 \\&x_1, x_2, x_3, x_4 \ge 0. \end{aligned}$$

    The optimal solution to this linear programming problem is

    $$\begin{aligned} x_1 =10, x_2 =0, x_3 =0\,x_4 =0, (z_1 )_1 =298. \end{aligned}$$

    And with this solution vectors, the value of other objective functions are as

    $$\begin{aligned} (z_2 )_1 =239,\quad (z_3 )_1 =370\quad \text {and}\quad (z_4 )_1 =193. \end{aligned}$$
  2. Step 2:

    Solve linear programming problem for \(z_{2}, z_{3}, z_{4}\) subject to constraints and find values of remaining objective functions.

  3. Step 3:

    Tabulate the values as given below to form PIS as given in Table 3.

    Table 3 Positive ideal solution
    Full size table
  4. Step 4:

    Find lower and upper bounds for each case of max z\(_{1}\), max z\(_{2}\), max z\(_{3}\), max z\(_{4}\) which are

    $$\begin{aligned} \begin{aligned} U_1^\mu =298, L_1^\mu =138;&U_2^\mu =492, L_2^\mu =239; U_3^\mu =370, L_3^\mu =36; \\&\ U_4^\mu =694.58,\ L_4^\mu =193. \end{aligned} \end{aligned}$$
  5. Step 5:

    Set the upper and lower bounds of each objective for degree of rejections as

    $$\begin{aligned} L_k^\mu&=L_k^\nu \\ U_k^\nu&=U_k^\mu +\lambda (U_k^\mu -L_k^\mu )=(1-\lambda ) U_k^\mu +\lambda L_k^\mu ,\quad k=1, 2, 3, 4. \end{aligned}$$

    Which for \(\lambda =0.6\) becomes

    $$\begin{aligned} U_k^\nu&=(1-0.6)U_k^\mu +0.6L_k^\mu =0.4U_k^\mu +0.6L_k^\mu \\ U_1^\nu&=202,\ L_1^\nu =138,\ U_2^\nu =340.2,\ L_2^\nu =239,&U_3^\nu =169.6,\ L_3^\nu =36, \\&U_4^\nu =393.63,\ L_4^\nu =193. \end{aligned}$$
  6. Step 6:

    Construction of membership functions:

    $$\begin{aligned} \mu _1 (x)&=\frac{29.8 x_1 +10.4x_2 +13.8x_3 +19.8x_4 -138}{(298-138)}, \\ \mu _2 (x)&=\frac{23.9x_1 +21.4x_2 +49.2x_3 +32.8x_4 -239}{(492-239)}, \\ \mu _3 (x)&=\frac{37x_1 +16x_2 +3.6x_3 +9.7x_4 -36}{(370-36)}, \\ \mu _4 (x)&=\frac{19.3x_1 +26.6x_2 +48.4x_3 +75.6x_4 -139}{(694.58-193)}. \end{aligned}$$

    Construction of non-membership functions:

    $$\begin{aligned} \nu _1 (x)&=\frac{202-29.8x_1 -10.4x_2 -13.8x_3 -19.8x_4 }{(202-138)}, \\ \nu _2 (x)&=\frac{340.2-23.9x_1 -21.4x_2 -49.2x_3 -32.8x_4 }{(340.2-239)}, \\ \nu _3 (x)&=\frac{169.6-37x_1 -16x_2 -3.6x_3 -9.7x_4 }{(169.6-36)}, \\ \nu _4 (x)&=\frac{393.63-19.3x_1 -26.6x_2 -48.4x_3 -75.6x_4 }{(393.63-193)}. \end{aligned}$$
  7. Step 7:

    The above problem (1) is now equivalently written to a linear programming problem as

    $$\begin{aligned} \text {Maximize}\quad&(\alpha -\beta ), \nonumber \\ \text {Subject to}\quad&29.8x_1 +10.4x_2 +13.8x_3 +19.8x_4 -138\ge 160\alpha , \nonumber \\&23.9x_1 +21.4x_2 +49.2x_3 +32.8x_4 -239\ge 253\alpha , \nonumber \\&37x_1 +16x_2 +3.6x_3 +9.7x_4 -36\ge 334\alpha , \nonumber \\&19.3x_1 +26.6x_2 +48.4x_2 +75.6x_4 -193\ge 501.58\alpha , \nonumber \\&202-29.8x_1 -10.4x_2 -13.8x_3 -19.8x_4 \le 64\beta , \nonumber \\&340.2-23.9x_1 -21.4x_2 -49.2x_3 -32.8x_4 \le 101.2\beta , \nonumber \\&169.6-37x_1 -16x_2 -3.6x_3 -9.7x_4 \le 133.6\beta , \nonumber \\&393.63-19.3x_1 -26.6x_2 -48.4x_3 -75.6x_4 \le 200.63\beta ,\\&x_1 +x_2 +x_3 +x_4 \le 10, \nonumber \\&6.9x_1 +71x_2 +2x_3 +33x_4 \le 260, \nonumber \\&\alpha +\beta \le 1, \nonumber \\&\alpha \ge \beta ,\quad \beta , x_1, x_{2}, x_3, x_4 \ge 0\nonumber \end{aligned}$$
    (2)

    The above problem (2), a linear programming problem is solved by MATLAB and the solutions obtained are

    $$\begin{aligned} x_1&=4.14\\ x_2&=0.00\\ x_3&=3.79\\ x_4&=2.06\\ \alpha&=0.45\\ \beta&=0.00 \end{aligned}$$
    Table 4 Profit in different probabilistic cases
    Full size table

Putting these values in the problem, the profit obtained are as in (Table 4).

5 Conclusion

The objective of this paper was to develop a method to solve a probabilistic programming problem in an intuitionistic fuzzy optimization environment. Here, the developed method first considers the conversion of the probabilistic programming problem into a multi-objective programming problem. This is done by considering the objective function corresponding to probabilistic cases as one objective function of the said multi-objective programming. Thus, such converted multi-objective programming problem is solved with one objective at a time to construct the PIS. Thus, in order to obtain a best compromise solution of the situation, we construct the membership function and non-membership functions for the solutions, and thus, we introduce intuitionistic fuzzy parameters. Using the intuitionistic fuzzy optimization approach, the problem is transformed into an equivalent linear programming problem. The linear programming problem thus obtained has been solved by using MATLAB. The result thus obtained has been compared with the existing solution, and clearly, the proposed method gives a better solution than existing solutions.