Structure-preserving model reduction for dynamical systems with a first integral

Abstract

Since the expense of the numerical integration of large scale dynamical systems is often computationally prohibitive, model reduction methods, which approximate such systems by simpler and much lower order ones, are often employed to reduce the computational effort. In this paper, we focus on dynamical systems with a first integral, which can always be written as skew-gradient systems. By focusing on and making use of the skew-gradient structure, we present structure-preserving model reduction approaches that yield efficient reduced-order systems while preserving the first integral.

1 Introduction

Since the expense of the numerical integration of large scale dynamical systems is often computationally prohibitive, model reduction methods, which approximate high dimensional systems by simpler and much lower order ones, are often employed to reduce the computational effort [3]. The proper orthogonal decomposition (POD) method with Galerkin projection, which was first introduced by Moore [23], is one of standard data-driven model reduction methods. This method extracts a few basis vectors that fit the empirical solution data with good accuracy and projects the high dimensional system to the subspace spanned by the basis vectors. The POD-Galerkin approach often provides an efficient surrogate system and has found applications in a wide range of areas such as structural dynamics [2], fluid mechanics [16, 17, 28], and time-dependent partial differential equations [20, 29]. However, when the vector field of the original system is nonlinear, the complexity of evaluating the nonlinear term of the reduced-order system remains as expensive as that of the original problem. To resolve this issue, Chaturantabut and Sorensen proposed the discrete empirical interpolation method (DEIM) based on the POD-Galerkin method and an interpolatory projection [6, 7].

Though the aforementioned data-driven approaches work well for many applications, they rarely inherit underlying mathematical structures of the original system, such as symmetry, symplecticity and energy-preservation. For dynamical systems with some mathematical structures, numerical integrators that inherit such properties, referred to as geometric numerical integrators or structure-preserving integrators, are often preferred, since they usually produce qualitatively better numerical solutions than standard general-purpose integrators such as the famous fourth-order explicit Runge–Kutta method (see, e.g. [15]). Therefore, model reduction while preserving such properties would be preferred: for example, if the reduced-order system inherits the mathematical structures, one could easily choose an appropriate numerical integrator for the reduced-order system. Structure-preserving model reduction methods have received attention in recent years (see [1, 5, 12, 24] and references therein).

In this paper, we are concerned with a dynamical system with a first integral, i.e. a dynamical system with a conservation law. Such a system can always be formulated as a skew-gradient system of the form

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\varvec{y}}= S({\varvec{y}}) \nabla _{\varvec{y}}H({\varvec{y}}), \quad {\varvec{y}}(0) = {\varvec{y}}_0 \in {\mathbb {R}}^n, \end{aligned}$$

(1)

where $S({\varvec{y}})\in {\mathbb {R}}^{n\times n}$ is a skew-symmetric matrix, and the function $H:{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ is assumed to be sufficiently differentiable [25]. Indeed, the function H is constant along the solution:

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}H({\varvec{y}}) = \nabla _{\varvec{y}}H({\varvec{y}})^\top {\dot{{\varvec{y}}}} = \nabla _{\varvec{y}}H({\varvec{y}}) ^\top S({\varvec{y}}) \nabla _{\varvec{y}}H({\varvec{y}}) = 0 \end{aligned}$$

due to the skew-symmetry of $S({\varvec{y}})$, where the dot stands for the differentiation with respect to t.

When $S({\varvec{y}})$ is a constant skew-symmetric matrix, that is, it is independent of ${\varvec{y}}$, several structure-preserving model reduction methods have been studied. If S is of the form

$$\begin{aligned} S = J_{2{{\tilde{n}}}}^{-1} = \begin{bmatrix} 0_{{\tilde{n}}}&\quad I_{{\tilde{n}}}\\ -I_{{\tilde{n}}}&\quad 0_{{\tilde{n}}}\end{bmatrix}, \quad n = 2{{\tilde{n}}}, \end{aligned}$$

(2)

where $0_{{\tilde{n}}}, I_{{\tilde{n}}}\in {\mathbb {R}}^{{{\tilde{n}}}\times {{\tilde{n}}}}$ denote the zero and identity matrices, respectively, the corresponding system is called a Hamiltonian system. Peng and Mohseni [24] proposed model reduction techniques that find a lower-order Hamiltonian system. Any structure-preserving integrators, which have been developed for Hamiltonian systems, can be applied to the lower-order Hamiltonian system. For the case $S({\varvec{y}})$ is a constant skew-symmetric matrix but is not necessarily of the form (2), Gong et al. [12] proposed a model reduction approach that yields a lower-order skew-gradient system with a constant skew-symmetric matrix. For other structure-preserving model reduction methods, see, for example [1, 5, 18, 19] and references therein.

In the line of these research, we are concerned with the case $S({\varvec{y}})$ depends on ${\varvec{y}}$. This situation often arises, for example, as a Hamiltonian system with some constraints or from discretizing a Hamiltonian partial differential equation (PDE). The approach by Gong et al. [12] is applicable to such cases straightforwardly to find a lower-order skew-gradient system; however, the computational complexity for evaluating the vector field may still depend on n (the size of the original problem) due to the dependence of $S({\varvec{y}})$ on ${\varvec{y}}$. In this paper, we study structure-preserving model reduction techniques so that the vector field of the reduced-order system can be evaluated efficiently. We classify target systems into two types. First, we consider the case $S({\varvec{y}})$ depends linearly on ${\varvec{y}}$ and has a specific structure such as $S({\varvec{y}}) = YD+DY$, where $D\in {\mathbb {R}}^{n\times n}$ is a constant skew-symmetric matrix and $Y = {{\,\mathrm{diag}\,}}({\varvec{y}}) \in {\mathbb {R}}^{n\times n}$. In this case, we show that the computational complexity for the reduced-order system based on the approach [12] is already independent of n, with the help of the Kronecker product and a vectorization operator. As an example, we employ the KdV equation, which is a nonlinear PDE. We note that the approach [12] does not use the DEIM or other techniques to reduce the complexity for nonlinear terms. Therefore, our discussion indicates that, by focusing on the underlying structure, an efficient surrogate model could be constructed even if the original problem is nonlinear. Next, we develop a new approach for more general cases based on the approach [12] and DEIM, where the key idea is to apply the idea of DEIM to the skew-symmetric matrix $S({\varvec{y}})$.

This paper is organized as follows. In Sect. 2, the proper orthogonal decomposition method with Galerkin-projection, the discrete empirical interpolation method and the existing structure-preserving model reduction method proposed by Gong et al. [12] are briefly reviewed. Structure-preserving model reduction methods for (1) are discussed in Sects. 3 and  4. Section 3 considers the specific case and Sect. 4 treats more general cases. In Sect. 5, we test the methods numerically taking the KdV and modified KdV equations as our toy problems. Finally, concluding remarks are given in Sect. 6.

2 Preliminaries: POD, DEIM and structure-preserving model reduction

In this section, we briefly review the proper orthogonal decomposition (POD) method with Galerkin-projection, the discrete empirical interpolation method (DEIM) and the structure-preserving model reduction method proposed by Gong et al. [12].

2.1 Model reduction with Galerkin-projection

Model reduction methods considered in this paper are based on the Galerkin projection. The basic procedure to construct a reduced-order system is summarized below.

Let us consider a system of ordinary differential equations of the form

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} {\varvec{y}}= \varvec{f}({\varvec{y}}), \quad {\varvec{y}}(0) = {\varvec{y}}_0\in {\mathbb {R}}^n, \end{aligned}$$

(3)

as a full-order model, where $\varvec{f}:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$ is supposed to be sufficiently smooth. A standard way of constructing a reduced-order system is to project the solution of (3) onto an appropriate subspace of ${\mathbb {R}}^n$. Assume that the flow ${\varvec{y}}(t)$ can be well approximated in a lower dimensional subspace, i.e. a linear combination of some basis vectors $\varvec{v}_i\in {\mathbb {R}}^n$ ($i=1,\dots ,r$):

$$\begin{aligned} {\varvec{y}}(t) \approx \sum _{i=1}^r z_i(t) \varvec{v}_i, \end{aligned}$$

(4)

where $r\ll n$. Without loss of generality, the basis vectors are chosen such that they are orthonormal. Let $V := [\varvec{v}_1,\dots ,\varvec{v}_r]\in {\mathbb {R}}^{n\times r}$. Then, $V^\top V = I_r$. By using this notation and ${\varvec{z}}(t) := [z_1(t),\dots ,z_r(t)]^\top$, the relation (4) can be written as ${\varvec{y}}(t) \approx V {\varvec{z}}(t)$. Substituting $V {\varvec{z}}$ into ${\varvec{y}}$ in (3) yields the overdetermined system $V{\dot{{\varvec{z}}}} = \varvec{f}(V{\varvec{z}})$. Applying the Galerkin method by multiplying $V^\top$ from the left leads to the reduced-order system

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\varvec{z}}= V^\top \varvec{f}(V{\varvec{z}}), \quad {\varvec{z}}(0) = V^\top {\varvec{y}}_0. \end{aligned}$$

(5)

2.2 The proper orthogonal decomposition method

The proper orthogonal decomposition (POD) method is a popular approach of finding an appropriate matrix V based on empirical solution data [23].

The POD method seeks to extract important information from empirical solution data, called snapshots, of the full-order system. A snapshot matrix Y consists of either numerical solutions or observed data at some time instances $t=t_1,t_2,\dots ,t_s$. Let $Y := [{\varvec{y}}_1,\dots , {\varvec{y}}_s]\in {\mathbb {R}}^{n\times s}$, where ${\varvec{y}}_i \approx {\varvec{y}}(t_i)$. We then consider the following optimization problem

$$\begin{aligned} \min _{{{\,\mathrm{rank}\,}}(V) = r} \sum _{j=1}^s \Vert {\varvec{y}}_j - VV^\top {\varvec{y}}_j \Vert ^2 \quad \text {such that} \; V^\top V = I_r, \end{aligned}$$

(6)

where $\Vert \cdot \Vert$ denotes the 2-norm in the Euclidean space. The optimal solution to this problem is given by the singular value decomposition (SVD) for Y. Let $\varvec{v}_1,\dots ,\varvec{v}_r$ be the left singular vectors of Y corresponding to the first r leading nonzero singular values. Then the POD matrix $V := [\varvec{v}_1,\dots , \varvec{v}_r]$ solves the above optimization problem (6). If ${{\,\mathrm{rank}\,}}(Y) = d$ and $\sigma _1 \ge \sigma _2\ge \cdots \ge \sigma _d > 0$, it follows that

$$\begin{aligned} \sum _{j=1}^s \Vert {\varvec{y}}_j - VV^\top {\varvec{y}}_j \Vert ^2 = \sum _{j=r+1}^d \sigma _j^2. \end{aligned}$$

If the vector field $\varvec{f}$ is linear, that is, $\varvec{f}({\varvec{y}}) = A {\varvec{y}}$ for some constant matrix $A\in {\mathbb {R}}^{n\times n}$, the reduced-order system (5) becomes ${\dot{{\varvec{z}}}} = {\hat{A}}{\varvec{z}}$, where ${\hat{A}} = V^\top A V \in {\mathbb {R}}^{r\times r}$. Since the matrix ${\hat{A}}$ can be computed in the off-line stage, the computational complexity of evaluating the vector field ${\hat{A}}{\varvec{z}}$ depends only on r and is independent of n (the size of the original problem).

2.3 The discrete empirical interpolation method

In general, the vector field $\varvec{f}$ is often nonlinear. Let $\varvec{f}({\varvec{y}}) = A {\varvec{y}}+ \varvec{g}({\varvec{y}})$, where $A\in {\mathbb {R}}^{n\times n}$ is a constant matrix and $\varvec{g}:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$ denotes a nonlinear part. In this case, the reduced-order system (5) becomes

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\varvec{z}}= {\hat{A}}{\varvec{z}}+ V^\top \varvec{g}( V{\varvec{z}}), \end{aligned}$$

and notice that the computational complexity for the second term $V^\top \varvec{g}( V{\varvec{z}})$ may still depend on n due to the nonlinearity: one first needs to compute the state variable ${\varvec{y}}:= V{\varvec{z}}$ in the original coordinate system, next evaluate the nonlinear vector field $\varvec{g}({\varvec{y}})$, and then project $\varvec{g}({\varvec{y}})$ back onto the column space of V. This could make solving the reduced-order system more expensive than solving the original full-order system.

The discrete empirical interpolation method (DEIM) was proposed by Chaturantabut and Sorensen [6] to reduce the computational complexity of evaluating the nonlinear term. Let $\varvec{g}(t) := \varvec{g}(V{\varvec{z}}(t))$ to simplify the notation. We consider the approximation to $\varvec{g}(t)$ by means of a constant matrix $U \in {\mathbb {R}}^{n\times m}$ ($m\ll n$) and a time-dependent vector $\varvec{c}(t) \in {\mathbb {R}}^m$: $\varvec{g}(t) \approx U \varvec{c}(t)$. The DEIM tells us how to construct appropriate U and $\varvec{c}(t)$. We first explain the construction of $\varvec{c}(t)$ assuming we already have U. We require that $\varvec{g}(t)$ and $U\varvec{c}(t)$ are equal for m variables out of n variables, i.e.

$$\begin{aligned} \varvec{g}_{\rho _i} (t) = U_{\rho _i} \varvec{c}(t), \quad i = 1,\dots , m, \end{aligned}$$

(7)

where $U_{\rho _i}$ denotes the $\rho _i$th row of U. By using $P := [\varvec{e}_{\rho _1},\dots ,\varvec{e}_{\rho _m}]\in {\mathbb {R}}^{n\times m}$ where $\varvec{e}_{\rho _i}$ denotes the $\rho _i$th column of the identity matrix of size n-by-n, the condition (7) can be rewritten as $P^\top \varvec{g}(t) = P^\top U \varvec{c}(t)$. Now, let us assume that $P^\top U \in {\mathbb {R}}^{m\times m}$ is nonsingular. Then, $\varvec{c}(t)$ is given by $\varvec{c}(t) = (P^\top U)^{-1} P^\top \varvec{g}(t)$, and thus $V^\top \varvec{g}(t)$ can be approximated by

$$\begin{aligned} V^\top \varvec{g}(t) \approx \underbrace{V^\top U (P^\top U)^{-1}}_{r\times m} \underbrace{P^\top \varvec{g}(t)}_{m\times 1}. \end{aligned}$$

Note that $V^\top U (P^\top U)^{-1}\in {\mathbb {R}}^{r\times m}$ can be computed in the off-line stage, and thus if the computational complexity for $P^\top \varvec{g}(t)$ is independent of n, the complexity for the approximation of $V^\top \varvec{g}(t)$ is also independent of n. Note that the computational complexity for $P^\top \varvec{g}(t)$ varies from problem to problem. It is independent of n for many applications, though there are some exceptions (see [6] for more details).

The procedure for constructing the matrices U and P is summarized in Algorithm 1, where $[|\rho |, \rho ] = {{\,\mathrm{\textsf {max}}\,}}\{ | \varvec{g}| \}$ implies that $|\rho | = \max \{ | \varvec{g}| \}$ and $\rho$ is the first index of the maximum value(s). Let $\varvec{g}_1, \varvec{g}_2, \dots , \varvec{g}_s$ be snapshot data for $\varvec{g}({\varvec{y}})$ at some time instances and $G := [\varvec{g}_1, \varvec{g}_2, \dots , \varvec{g}_s]$. Applying the SVD to this matrix gives the POD basis vectors $\varvec{u}_1,\varvec{u}_2,\dots ,\varvec{u}_m$. The matrix P can be constructed by a greedy algorithm. Initially, the first interpolation index $\rho _1\in \{1,2,\dots ,n\}$ is selected such that it is corresponding to the largest magnitude of the first basis function $\varvec{u}_1$. The remaining indices $\rho _i$ ($i=2,3,\dots ,m$) are selected such that they correspond to the largest magnitude of the residual (defined in line 5). Note that $P^\top U$ is nonsingular if $\rho \ne 0$ [6].

2.4 Structure-preserving model reduction by Gong et al.

We here review the structure-preserving model reduction proposed by Gong et al. [12].

If S in (1) is of the form (2), the original system is a Hamiltonian system and the approach proposed by Peng and Mohseni [24] is applicable to find a lower-order Hamiltonian system. However, if S is a constant skew-symmetric matrix, but not of the form (2), their approach, which makes use of the structure of $J_{2{{\tilde{n}}}}^{-1}$, is not applicable to (1) .

The reduced-order system to (1) based on the standard Galerkin projection is

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\varvec{z}}= V^\top S \nabla _{\varvec{y}}H(V{\varvec{z}}). \end{aligned}$$

(8)

The key of the approach by Gong et al. [12] is that formally inserting $VV^\top \in {\mathbb {R}}^{n\times n}$ between S and $\nabla H(V{\varvec{z}})$ in (8) yields a small skew-gradient system

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\varvec{z}}= V^\top S V V^\top \nabla _{\varvec{y}}H(V{\varvec{z}}) = S_r \nabla _{{\varvec{z}}} {\tilde{H}}({\varvec{z}}), \end{aligned}$$

(9)

where $S_r = V^\top S V$ and ${\tilde{H}}({\varvec{z}}) := H(V{\varvec{z}})$. Since $VV^\top \ne I_n$ in general, the system (9) differs from (8), and thus we need to carefully consider in what sense $V{\varvec{z}}(t)$ is an approximation to ${\varvec{y}}(t)$. The authors proposed to device the snapshot matrix Y:

$$\begin{aligned} Y = [{\varvec{y}}_1,\dots , {\varvec{y}}_s, \mu \nabla _{\varvec{y}}H ({\varvec{y}}_1) ,\dots , \mu \nabla _{\varvec{y}}H ({\varvec{y}}_s)]\in {\mathbb {R}}^{n\times s} \end{aligned}$$

(10)

for some constant $\mu >0$. The left singular vectors corresponding to the leading nonzero singular values extract the information of the gradient $\nabla _{\varvec{y}}H({\varvec{y}})$ as well as ${\varvec{y}}$. Thus, for the POD matrix for this snapshot matrix, $VV^\top \nabla _{\varvec{y}}H({\varvec{y}})$ could be a good approximation to $\nabla _{\varvec{y}}H({\varvec{y}})$. In this case, the vector fields of (8) and (9) are similar, and the solution to (9) well approximates to that to (8). The error analysis was also given in [12].

3 Structure-preserving model reduction for particular skew-gradient systems

We consider the case that $S({\varvec{y}})$ in (1) may depend in ${\varvec{y}}$. The approach by Gong et al. [12], which was summarized in Sect. 2.4, is also applicable to the general cases to find the reduced-order skew-gradient system

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}{\varvec{z}}= V^\top S(V{\varvec{z}}) V V^\top \nabla _{\varvec{y}}H(V{\varvec{z}}) =S_r ({\varvec{z}}) \nabla _{{\varvec{z}}} {\tilde{H}}({\varvec{z}}), \end{aligned}$$

where $S_r({\varvec{z}}) = V^\top S(V{\varvec{z}}) V$ and ${\tilde{H}}({\varvec{z}}) := H(V{\varvec{z}})$. But the computational complexity of evaluating the matrix $S_r({\varvec{z}})$ is not always independent of the size of the full-order system. In this section, we show that if $S({\varvec{y}})$ is of the form

$$\begin{aligned} S({\varvec{y}}) = YD + DY, \end{aligned}$$

where $D\in {\mathbb {R}}^{n\times n}$ is a skew-symmetric constant matrix and $Y = {{\,\mathrm{diag}\,}}({\varvec{y}}) \in {\mathbb {R}}^{n\times n}$, the computational complexity of evaluating $S_r({\varvec{z}})$ is already independent of n.

To discuss the computational complexity of evaluating $S_r({\varvec{z}})$, we use the Kronecker product, which is defined by

$$\begin{aligned} A \otimes B := \begin{bmatrix} a_{11} B&\quad a_{12}B&\quad \cdots&\quad a_{1n} B \\ a_{21} B&\quad a_{22}B&\quad \cdots&\quad a_{2n} B \\ \vdots&\quad \vdots&\quad \ddots&\quad \vdots \\ a_{m1} B&\quad a_{m2}B&\quad \cdots&\quad a_{mn} B \end{bmatrix} \in {\mathbb {R}}^{mp \times nq} \end{aligned}$$

for $A = [a_{ij}] \in {\mathbb {R}}^{m\times n}$ and $B \in {\mathbb {R}}^{p\times q}$. To simplify the notation, we shall consider the computational complexity for $S_r ({\varvec{z}})$ after vectorizing it. For this aim, for $A=[\varvec{a}_1, \varvec{a}_2, \dots , \varvec{a}_n]\in {\mathbb {R}}^{m\times n}$, we define the vectorization operator, ${{\,\mathrm{vec}\,}}: {\mathbb {R}}^{m\times n} \rightarrow {\mathbb {R}}^{mn}$, by ${{\,\mathrm{vec}\,}}(A) :=[ \varvec{a}_1^\top , \varvec{a}_2^\top , \dots , \varvec{a}_n^\top ]^\top$, and its inverse, ${{\,\mathrm{vec}\,}}^{-1}: {\mathbb {R}}^{mn} \rightarrow {\mathbb {R}}^{m\times n}$, by ${{\,\mathrm{vec}\,}}^{-1} ({{\,\mathrm{vec}\,}}(A)) = A$. We frequently use the following property: for $A\in {\mathbb {R}}^{m\times n}$ and $B\in {\mathbb {R}}^{n\times p}$, it follows that

$$\begin{aligned} {{\,\mathrm{vec}\,}}(AB) =( I_p \otimes A) {{\,\mathrm{vec}\,}}(B) = (B^\top \otimes I_m) {{\,\mathrm{vec}\,}}(A), \end{aligned}$$

(11)

where $I_n\in {\mathbb {R}}^{n\times n}$ is the identity matrix (see e.g. [9, p. 275]).

Let us consider the computational complexity for ${{\,\mathrm{vec}\,}}(V^\top S(V{\varvec{z}}) V)$, which is equivalent to discuss the complexity for $V^\top S(V{\varvec{z}}) V$. By using (11), it follows that

Note that ${{\,\mathrm{vec}\,}}(Y) = [y_1, 0,\dots , 0 ,y_2, 0,\dots , y_n]^\top \in {\mathbb {R}}^{n^2 \times 1}$, where only $(nk+1)$th elements ($k=0,\dots ,n-1$) are nonzero. We define ${\tilde{D}}\in {\mathbb {R}}^{n^2\times n}$ by collecting the $(nk+1)$th columns ($k=0,\dots ,n-1$) of the matrix . Note that ${\tilde{D}}$ is explicitly given by

$$\begin{aligned} {\tilde{D}} = - \begin{bmatrix} {{\,\mathrm{diag}\,}}(d_{11},\dots ,d_{1n} ) \\ {{\,\mathrm{diag}\,}}(d_{21},\dots ,d_{2n} ) \\ \vdots \\ {{\,\mathrm{diag}\,}}(d_{n1},\dots ,d_{nn} ) \end{bmatrix} + \begin{bmatrix} \varvec{d}_1&\quad 0&\quad \cdots&\quad 0 \\ 0&\quad \varvec{d}_2&\quad \cdots&\quad 0 \\ \vdots&\quad \vdots&\quad \ddots&\quad \vdots \\ 0&\quad \cdots&\quad 0&\quad \varvec{d}_n \end{bmatrix}, \end{aligned}$$

where $D = [\varvec{d}_1, \varvec{d}_2, \dots , \varvec{d}_n]$. By using this notation, ${{\,\mathrm{vec}\,}}(V^\top S({\varvec{y}}) V)$ can be simplified as follows:

$$\begin{aligned} {{\,\mathrm{vec}\,}}(V^\top S({\varvec{y}})V)&= \underbrace{(V\otimes V)^\top }_{r^2 \times n^2} \underbrace{{\tilde{D}}}_{n^2 \times n} \underbrace{{\varvec{y}}}_{n\times 1}. \end{aligned}$$

Then, substituting $V{\varvec{z}}$ into ${\varvec{y}}$ in ${{\,\mathrm{vec}\,}}(V^\top S({\varvec{y}})V)$ yields

$$\begin{aligned} {{\,\mathrm{vec}\,}}(V^\top S(V{\varvec{z}})V)&= \underbrace{(V\otimes V)^\top }_{r^2 \times n^2} \underbrace{{\tilde{D}}V}_{n^2 \times r} \underbrace{{\varvec{z}}}_{r\times 1}, \end{aligned}$$

and thus

Since $(V\otimes V)^\top {\tilde{D}}V \in {\mathbb {R}}^{r^2 \times r}$ can be computed in the off-line stage, the computational complexity of evaluating $S_r({\varvec{z}})$ is independent of n.

Remark 1

The above discussion is applicable to a bit more general cases. For example, the approach applies, in a similar manner, to $S({\varvec{y}}) = YD+DY + D_\text {c}$, where $D_\text {c}$ is a constant skew-symmetric matrix, and to $S({\varvec{y}})$ with a different ordering of Y such as $Y ={{\,\mathrm{diag}\,}}(y_n, y_1,y_2,\dots ,y_{n-1})$.

4 Structure-preserving model reduction for general skew-gradient systems

We consider general cases, such as the case that $S({\varvec{y}})$ nonlinearly depends on ${\varvec{y}}$. In such cases, the computational complexity of evaluating $S_r ({\varvec{z}}) = V^\top S(V{\varvec{z}}) V$ may depend on n unless $S({\varvec{y}})$ has a specific structure. In this section, we show that the complexity can be reduced by utilizing the idea of the DEIM while keeping the skew-gradient structure.

Let $S(t) := S(V{\varvec{z}}(t))$ to simplify the notation. Using constant skew-symmetric matrices $U_j \in {\mathbb {R}}^{n\times n}$ ($j=1,\dots , m$), and a time-dependent vector $\varvec{c}(t) \in {\mathbb {R}}^m$, we approximate S(t) by $S(t) \approx \sum _{j=1}^m U_j c_j (t)$. This relation can be written as $\varvec{s}(t) \approx U \varvec{c}(t)$, where $\varvec{s}(t) = {{\,\mathrm{vec}\,}}(S(t))$ and $U = [{{\,\mathrm{vec}\,}}(U_1), {{\,\mathrm{vec}\,}}(U_2), \dots , {{\,\mathrm{vec}\,}}(U_m)] \in {\mathbb {R}}^{n^2 \times m}$.

Following the discussion in Sect. 2.3, we require that $\varvec{s}(t)$ and $U\varvec{c}(t)$ are equal for m variables out of $n^2$ variables, i.e. we require that $P^\top \varvec{s}(t) = P^\top U \varvec{c}(t)$ with $P = [\varvec{e}_{\rho _1},\dots ,\varvec{e}_{\rho _m}]\in {\mathbb {R}}^{n^2\times m}$. Let us assume that $P^\top U \in {\mathbb {R}}^{m\times m}$ is nonsingular. Then, $\varvec{c}(t)$ is given by

$$\begin{aligned} \varvec{c}(t) = (P^\top U)^{-1} P^\top \varvec{s}(t), \end{aligned}$$

and thus $V^\top S(t) V$ can be approximated by

(12)

Since $(V\otimes V )^\top U (P^\top U)^{-1}$ can be computed in the off-line stage, the computational complexity of evaluating the right hand side of (12) is independent of n if the complexity for $P^\top \varvec{s}(t)$ is independent of n.

The matrices U and P are constructed as follows. Let $S_1,\dots ,S_s$ and $\varvec{s}_1={{\,\mathrm{vec}\,}}(S_1),\dots ,\varvec{s}_s ={{\,\mathrm{vec}\,}}(S_s)$ be snapshot data for S(t). Applying the SVD to the matrix $[\varvec{s}_1,\dots , \varvec{s}_s]$ yields the POD basis vectors $\varvec{u}_1,\dots ,\varvec{u}_m$, and then the construction of U and P follows the DEIM procedure summarized in Algorithm 1.

We need to show that if the snapshot matrices $S_1,\dots S_s$ are skew-symmetric, the approximation is also skew-symmetric.

Proposition 1

If $S_1,\dots ,S_s$ are skew-symmetric. Then is also skew-symmetric.

Proof

Since each $U_i$ is a linear combination of the snapshot matrices $S_i$, all of which are skew-symmetric, it follows that if $S_1,\dots ,S_s$ are skew-symmetric, $U_1,\dots ,U_m$ are also skew-symmetric. Further, since S(t) is approximated by a linear combination of is also skew-symmetric. $\square$

5 Numerical experiments

In this section, we check the performance of the structure-preserving model reduction methods presented in Sects. 3 and 4 . The main aim of this section is to check the preservation of a first integral and the stability for the reduced-order system. We employ the KdV equation and the modified KdV equation as our toy problems. For both equations, an appropriate finite difference semi-discretization yields skew-gradient systems.

All the computations are performed in a computation environment: 3.5 GHz Intel Core i5, 8GB memory, OS X 10.1035. We use MATLAB (R2015a). Nonlinear equations are solved by the matlab function ${\mathsf {fsolve}}$ with tolerance $10^{-16}$. The singular value decomposition is performed by ${\mathsf {svd}}$. Note that this function computes all singular values and the corresponding singular vectors, which is not always necessary for practical applications. We employ this function just to observe the distribution of singular values for the test problems.

5.1 KdV equation

As an illustrative example, we consider the KdV equation

$$\begin{aligned} y_t + 6yy_x + y_{xxx} = 0, \quad y(t_0,\cdot ) = y_0, \quad x \in {\mathbb {T}}, \end{aligned}$$

(13)

where ${\mathbb {T}}$ denotes the torus of length L. This equation is completely integrable, and thus has infinitely many conservation laws. Among them, we here consider the $L^2$-norm preservation:

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} {\mathcal {H}}[y] = 0, \quad {\mathcal {H}}[y] = \int _{\mathbb {T}}\frac{y^2}{2}\,\mathrm {d}x . \end{aligned}$$

(14)

We shall call this quantity and its discrete version the energy. The KdV equation can be formulated as

(15)

where the variational derivative of ${\mathcal {H}}$ is given by $\delta {\mathcal {H}}/ \delta y = y$.

We here discretize the KdV Eq. (13) in space as follows. Let ${\varvec{y}}(t) := [ y_1(t),\dots , y_n(t)]^\top$, where $\varDelta x = L / n$ and $y_i (t)$ denotes the approximation to $y(t, i\varDelta x )$. We use the central difference operators in a matrix form:

$$\begin{aligned} D_1&:= \frac{1}{2\varDelta x } \begin{bmatrix} 0&\quad 1&\quad&\quad&\quad -1 \\ -1&\quad 0&\quad 1&\quad&\quad \\ \quad&\ddots&\quad \ddots&\quad \ddots&\\ 1&\quad&\quad&\quad -1&\quad 0 \end{bmatrix} \in {\mathbb {R}}^{n\times n}, \\ D_2&:= \frac{1}{(\varDelta x)^2 } \begin{bmatrix} -2&\quad 1&\quad&\quad&\quad 1 \\ 1&\quad -2&\quad 1&\quad&\quad \\ \quad&\ddots&\quad \ddots&\quad \ddots&\\ 1&\quad&\quad&\quad 1&\quad -2 \end{bmatrix} \in {\mathbb {R}}^{n\times n} \end{aligned}$$

and $D_3:=D_1 D_2\in {\mathbb {R}}^{n\times n}$. An appropriate discretization of the variational form (15) yields the skew-gradient system

$$\begin{aligned} {\dot{{\varvec{y}}}} = S({\varvec{y}}) \nabla _{\varvec{y}}H({\varvec{y}}), \quad H({\varvec{y}}):= \frac{1}{2}{\varvec{y}}^\top {\varvec{y}}\end{aligned}$$

(16)

with

(17)

where $Y = {{\,\mathrm{diag}\,}}({\varvec{y}})$. Note that $\nabla H({\varvec{y}}) = {\varvec{y}}$ is linear. Due to the structure of (17), the approach discussed in Sect. 3 is applicable. For additional details on the spatial discretization based on variational structure, see, e.g. [4, 10, 11] and references therein.

For the temporal discretization, applying the mid-point rule to (16) yields an energy-preserving integrator: for the solution to

where $\varDelta t$ denotes the time stepsize and ${\varvec{y}}_{n} \approx {\varvec{y}}(n\varDelta t)$ ($n=0,1,2,\dots$), it follows that $H({\varvec{y}}_{n+1}) = H({\varvec{y}}_{n})$. Note that any Runge–Kutta methods with the property $b_i a_{ij} + b_j a_{ji} = b_i b_j$ ($i,j=1,\dots ,s$), where $a_{ij}$ and $b_i$ are Runge–Kutta coefficients and s denotes the number of stages, preserve any linear and quadratic invariants [15]. The simplest example is the mid-point rule, which is the second order method.

Remark 2

Runge–Kutta methods cannot be energy-preserving in general. For more general forms of the energy function, applying the discrete gradient method yields an energy-preserving integrator [8, 13, 14, 21, 22, 27].

In the full order simulation, we set $L=20$, $n=500$, $\varDelta x = L/n = 0.04$. The initial vale is set to $u(0,x) = 4.5 {{\,\mathrm{sech}\,}}^2(3x/2)$. The corresponding solution is a solitary wave if the spatial domain is $(-\infty ,\infty )$, but in the bounded domain, the solution behaves almost periodically if L is sufficiently large. We set $T = 3$ and $\varDelta t =T/600$, which means we collect 601 snapshot data: $Y = [{\varvec{y}}_0, {\varvec{y}}_1, \dots , {\varvec{y}}_{600}]\in {\mathbb {R}}^{500 \times 601}$ (note that $\nabla _{\varvec{y}}H({\varvec{y}}) = {\varvec{y}}$ in this case, cf. (10)).

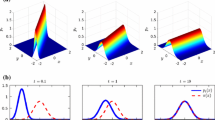
Figure 1 plots the singular values of the snapshot matrix Y. Fast decay of the singular values indicates that a few modes can express the data with reasonable accuracy. Figure 2 shows the error growth of the energy $H(V{\varvec{z}})$. The energy is well preserved with considerable accuracy. We plot the solution in Fig. 3. Due to the structure-preservation, the numerical solution seems stable even for small r. We observe that the solution becomes smooth as r gets large, and note that the solution of the full-order model, which is not displayed, is almost identical to the result for $r=60$. Global errors measured by the discrete version of the $L^2$-norm are plotted in Fig. 4, where the solution to the reduced-order system is compared with that to the full-order system ${\varvec{y}}^{\text {full}}$. We observe that the error gets small as r gets large. When $r=60$, the error remains small for $t>T=3$.

Fig. 1

Singular values corresponding to the POD modes for the matrix Y for the KdV equation

Fig. 2

Error of the energy for the case $r=20$ for the KdV equation: $|H(V{\varvec{z}}_n) - H(V{\varvec{z}}_0)|$ are plotted

Fig. 3

Numerical solutions $V{\varvec{z}}$ at $t=3$ for $r=20,40,60$ for the KdV equation

Fig. 4

Global errors measured by the discrete $L^2$-norm: $\sqrt{\varDelta x\sum _{i=1}^n \left( y_i^{\text {full}} - (V{\varvec{z}})_i\right) ^2}$ are plotted for the KdV equation

In this example, it should be noted that the DEIM (or other techniques to reduce the complexity for nonlinear terms) was not used, and that only the standard POD matrix was used to find the efficient reduced-order system despite the fact that the KdV is a nonlinear PDE. The idea of inheriting the skew-gradient structure made this possible.

5.2 Modified KdV equation

We next consider the modified KdV (mKdV) equation

$$\begin{aligned} y_t + 6y^2y_x + y_{xxx} = 0, \quad y(t_0,\cdot ) = y_0, \quad x \in {\mathbb {T}}. \end{aligned}$$

The $L^2$-norm preservation (14) also holds for this equation, which can be easily checked based on the variational structure

(18)

As is the case with the previous subsection, we discretize the variational form (18) as

$$\begin{aligned} {\dot{{\varvec{y}}}} = S({\varvec{y}}) \nabla H({\varvec{y}}), \quad H({\varvec{y}}):= \frac{1}{2}{\varvec{y}}^\top {\varvec{y}}\end{aligned}$$

with

where $Y = {{\,\mathrm{diag}\,}}({\varvec{y}})$. In this case, since $S({\varvec{y}})$ depends nonlinearly on ${\varvec{y}}$, we apply the approach presented in Sect. 4.

We note that the direct application of the SVD to the snapshot matrix $[{{\,\mathrm{vec}\,}}(S({\varvec{y}}_1)),$${{\,\mathrm{vec}\,}}(S({\varvec{y}}_2)),\dots ,$${{\,\mathrm{vec}\,}}(S({\varvec{y}}_s))]\in {\mathbb {R}}^{n^2\times s}$ can be quite time-consuming. Since the matrix $S({\varvec{y}})\in {\mathbb {R}}^{n\times n}$ has only 4n nonzero entries and their positions are independent of ${\varvec{y}}$, only 4n row vectors in the snapshot matrix are nonzero vectors and other $(n^2-4n)$ row vectors are zero vectors. Hence, the application of the SVD to a 4n-by-s matrix that consists of the 4n nonzero row vectors significantly reduces the computational cost.

In the full-order simulation, we set $L=10$, $n=500$, $\varDelta x = L/n = 0.02$. The initial vale is set to $u(0,x) =\sqrt{c} {{\,\mathrm{sech}\,}}(\sqrt{c}x)$ with $c=4$. The corresponding solution is a solitary wave in the unbounded spatial domain $(-\infty ,\infty )$, but in the bounded domain, the solution behaves almost periodically if L is sufficiently large. We set $T = 3$ and $\varDelta t =T/750$, which means we collect 751 snapshot data: $Y = [{\varvec{y}}_0, {\varvec{y}}_1, \dots , {\varvec{y}}_{750}]\in {\mathbb {R}}^{500 \times 751}$.

Figure 5 plots the singular values of the snapshot matrices Y and $[{{\,\mathrm{vec}\,}}(S({\varvec{y}}_0)),$${{\,\mathrm{vec}\,}}(S({\varvec{y}}_1)),\dots ,$${{\,\mathrm{vec}\,}}(S({\varvec{y}}_{750}))]$. Fast decay of the singular values is observed, which indicates that a few modes can express the solution ${\varvec{y}}$ and the skew-symmetric matrix $S({\varvec{y}})$ with good accuracy. Figure 6 shows the error growth of the energy $H(V{\varvec{z}})$. The energy is well preserved with considerable accuracy. We plot the solution in Fig. 7. The result with $r=50$ is almost identical to the solution of the full-order model, which is not displayed here. But the solution differs substantially when $r=40$, which indicates the number of basis matrices for the skew-symmetric matrix is sensitive to the qualitative behaviour. Global errors measured by the discrete version of the $L^2$-norm are plotted in Fig. 8. For $r=50$, the global error remains small even for $t>T=3$.

Fig. 5

Singular values corresponding to the POD modes for the matrices (left) Y and (right) $[{{\,\mathrm{vec}\,}}(S({\varvec{y}}_0)), {{\,\mathrm{vec}\,}}(S({\varvec{y}}_1)),\dots ,{{\,\mathrm{vec}\,}}(S({\varvec{y}}_{750}))]$ for the mKdV equation

Fig. 6

Error of the energy for the case $r=m=50$ for the mKdV equation: $|H(V{\varvec{z}}_n) - H(V{\varvec{z}}_0)|$ are plotted

Fig. 7

Numerical solutions $V{\varvec{z}}$ at $t=3$ for $r=m=40,50$ for the mKdV equation

Fig. 8

Global errors measured by the discrete $L^2$-norm: $\sqrt{\varDelta x\sum _{i=1}^n \left( y_i^{\text {full}} - (V{\varvec{z}})_i\right) ^2}$ are plotted for the mKdV equation

6 Concluding remarks

In this paper, structure-preserving model reduction methods for skew-gradient systems of the form (1) have been studied. We have shown that if $S({\varvec{y}})$ has a specific structure, the previous approach proposed by Gong et al. [12] can efficiently reduce the size of the full-order system, and also proposed a new approach for general cases that is based on the approach by Gong et al. [12] and the discrete empirical interpolation method (DEIM). Since the reduced-order systems keep the skew-gradient structure and thus have the energy-preservation law, energy-preserving integrators can be easily applied and one could expect the good qualitative behaviour.

The example for the KdV equation indicates that, by focusing on the underlying structure, an efficient surrogate model could be constructed even if the original problem is nonlinear. As an example of the second (general) case, we employed the modified KdV equation. While the skew-symmetric matrix $S({\varvec{y}})$ appearing in the semi-discrete scheme depends nonlinearly on ${\varvec{y}}$, its sparsity is the same as that for the KdV equation. Therefore, one might expect that an efficient structure-preserving reduced-order system could somehow be obtained without employing the idea of DEIM. We are now trying to figure out the class of nonlinear problems for which an efficient energy-preserving surrogate model can be obtained without using DEIM or other techniques to reduce the complexity for nonlinear terms.

We note that extending the proposed method to preserve multiple first integrals might contribute to enhance the quality of the solution to reduced-order models. Although the extension is possible in principle, spacial care must be taken for the computational costs because we need to treat a skew-symmetric tensor, instead of a skew-symmetric matrix, and such a tensor is usually dense [26]. We are now working on this issue as well.