Modelling and optimal control of a nonlinear switched system in microbial continuous fermentation

Abstract

Considering both extracellular and intracellular environments, we propose a nonlinear switched system composed of 16 modes based on the different metabolic mechanism to model the microbial continuous fermentation process of glycerol to 1,3-propanediol (1,3-PD). The existence and continuity of sensitivities of the system states with respect to the decision variables and unknown parameters are discussed. Taking the dilution rate and the feeding glycerol concentration as control variables, the sensitivity functions as constraints, an optimal control problem is presented with the concentration of 1,3-PD at the terminal time as performance index. According to sensitivity analysis, we obtain the gradient formulas of performance index and constraints with respect to the decision variables and the parameters to be identified. The sequential quadratic programming algorithm is adopted to seek a numerical solution. Numerical results indicate that under the obtained optimal dilution rate and feeding glycerol concentration, the productivity of 1,3-PD at the terminal time is increased significantly.

1 Introduction

As an important chemical raw material, 1,3-Propanediol (1,3-PD) is widely applied in polymers, cosmetics, lubricants and so on. Compared with chemical synthesis, the microbial conversion of glycerol to 1,3-PD has been given much attention due to its low cost and less pollution. Among all kinds of microbial conversions, the bioconversion of glycerol to 1,3-PD by Klebsiella pneumoniae (K. pneumoniae) is particularly attractive on account of its high productivity [1].

In recent years, some mathematical models have been proposed to describe the bioconversion process of glycerol to 1,3-PD [1–3]. On the basis of [1–3], Xiu et al. altered the model in [3] by leading in an excess term to describe the continuous culture and bath fermentation [4]. According to the literature [4], Gao et al. [5] studied the parameter identification; Li et al. [6] and Gao et al. [7] discussed the optimal control in continuous culture; Ma et al. [8] established a model to research Hopf bifurcation and chaos analysis; Ye et al. [9] analyzed the stability of the nonlinear dynamical system in microbial continuous cultures; Lian et al. [10] considered the oscillatory behavior in microbial continuous cultures with discrete time delay.

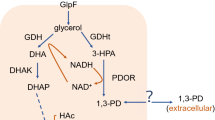
However, all the above works do not deal with the intracellular dynamics behavior. In fact, the fermentation of glycerol bioconversion to 1,3-PD covers both extracellular and intracellular environments in which some important intracellular intermediate metabolites and enzymes such as 3-hydroxypropional (3-HPA), glycerol dehydratase (GDHt) and 1,3-PD oxydoreductase (PDOR) play important roles. In 2008, taking the concentration of both extracellular and intracellular substances into account, Sun et al. [11] proposed a mathematical model for the continuous fermentation under the assumptions that glycerol passes the membrane by active transport coupled with passive diffusion and 1,3-PD passes the membrane by passive diffusion. On the basis of Sun’s model, Zhai et al. [12] established a pathway and parameter identification model and inferred that it is most possible that both glycerol and 1,3-PD pass the cell membrane by active transport coupled with passive diffusion and there exists an inhibition of 3-HPA to the cell growth. Wang et al. [13, 14] presented a nonlinear switched system to describe the fed-batch process with pH feedback control and the parameter optimization of continuous culture via sensitivity, respectively. On the other hand, based on the parameter identification in [12], Zhai et al. [15] further studied the optimal control in continuous fermentation, which regarded the dilution rate and the feeding glycerol concentration as decision variables and took the concentration of 1,3-PD at the terminal time as performance index, respectively. However, in the works [12, 15], the values of some system parameters are changed with the change of the decision variables. The reason is that the fermentation environment may be changed due to the alteration of the decision variables. Therefore, it will be difficult to optimize the continuous culture process directly.

In this paper, a novel nonlinear switched system model is proposed by taking the evolution of concentration of the intracellular and extracellular substances into account. According to the different values of indicator function in the model, the continuous fermentation process is divided into 16 switching modes. Since some system parameters depend on the decision variables, the sensitivities of the system states with respect to the parameters and the decision variables are discussed, and the gradient formulas containing switches are obtained. Based on the sensitivity functions, a switched optimal control model is formulated, in which the dilution rate and the feeding glycerol concentration are taken as decision variables, and the concentration of 1,3-PD at the terminal time is taken as performance index, respectively. The sequential quadratic programming (SQP) algorithm is applied for seeking a numerical solution. The optimal inputs, unknown parameters, switching instants and mode sequence are obtained by implementing the proposed algorithm. Numerical results show that, by employing the optimal control strategies, the concentration of 1,3-PD at the terminal time can be increased considerably.

The rest of this paper is organized as follows. Section 2 introduces the nonlinear dynamical system in continuous fermentation. In Sect. 3, we propose a novel nonlinear switched system model and discuss some important properties of the system. In Sect. 4 , the existence and continuity of parametric sensitivity functions of the switched system are proved and an optimal control model based on the sensitivity functions is constructed. Section 5 constructs a sequential quadratic programming algorithm to solve the optimal problem. And Sect. 6 illustrates the numerical calculations. Conclusions are presented at the end of this paper.

2 Nonlinear dynamical system in continuous fermentation

In continuous fermentation, glycerol is added to the reactor continuously, the broth in reactor pours out at the same rate and the volume of the fermentation broth keeps constant. So the cultivation process is continuous. According to the factual experiments, we assume that

(H1) :

During the process of continuous fermentation, the substrate added to the reactor only includes glycerol.

(H2) :

The concentrations of substrate are uniform, while time delay and nonuniform space distribution are ignored.

(H3) :

The transport mechanisms of both glycerol and 1,3-PD are active transport coupled with passive diffusion. 3-HPA has inhibition to the cell growth and will restrain the activities of enzymes when its concentration reaches a certain critical value [12].

Let ${x}(t): = ({x}_{1}(t), {x}_{2}(t), \ldots , {x}_{8}(t))^{\top }\in \mathbb {R}_{+}^{8}$ ($t\in [0,T]$) be the state vector, where ${x}_{1}(t), {x}_{2}(t), \ldots , {x}_{8}(t)$ represent the concentrations of biomass, extracellular glycerol, extracellular 1,3-PD, acetate, ethanol, intracellular glycerol, intracellular 3-HPA and intracellular 1,3-PD, respectively. And T is the terminal time of continuous fermentation.

Under the assumptions (H1)–(H3), the vector field of reaction in a continuous fermentation can be formulated as follows [12].

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_{1}(t)=(\mu -D)x_{1},\\ \dot{x}_{2}(t)=D(C_{s0}-x_{2})-q_{2}x_{1},\\ \dot{x}_{3}(t)=q_{3}x_{1}-Dx_{3},\\ \dot{x}_{4}(t)=q_{4}x_{1}-Dx_{4},\\ \dot{x}_{5}(t)=q_{5}x_{1}-Dx_{5},\\ \dot{x}_{6}(t)=\frac{1}{u_{3}}\left( u_{4}\frac{x_{2}}{x_{2}+u_{5}}+u_{6}(x_{2}-x_{6})I_{\mathbb {R}_{+}}(x_{2}-x_{6})-q_{2}\right) -\mu x_{6},\\ \dot{x}_{7}(t)=\frac{u_{7}x_{6}}{K^{G}_{m}(1+\frac{x_{7}-u_{9}}{u_{8}}I_{\mathbb {R}_{+}}(x_{7}-u_{9}))+x_{6}}\\ ~~~~~~~~~~-\frac{u_{10}x_{7}}{K_{m}^{P}+x_{7}+\frac{(x_{7}-u_{12})^{2}}{u_{11}}I_{\mathbb {R}_{+}}(x_{7}-u_{12})}-\mu x_{7},\\ \dot{x}_{8}(t)=\frac{u_{10}x_{7}}{K^{P}_{m}+x_{7}+\frac{(x_{7}-u_{12})^{2}}{u_{11}}I_{\mathbb {R}_{+}}(x_{7}-u_{12})}-u_{13}\frac{x_{8}}{x_{8}+u_{14}}\\ ~~~~~~~~~~-u_{15}(x_{8}-x_{3})I_{\mathbb {R}_{+}}(x_{8}-x_{3})-\mu x_{8}. \end{array} \right. \end{aligned}$$

(1)

Here D and $C_{s0}$ represent the dilution rate and the feeding glycerol concentration; $K_{m}^{G}=0.53$ mmol/L and $K_{m}^{P}=0.14$ mmol/L are Michaelis–Menten constants for GDHt and PDOR, respectively. The specific substrate consumption rates and the specific product formation rates can be respectively expressed as follows.

$$\begin{aligned} q_{2}= & {} m_{2}+\frac{\mu }{Y_{2}}+\varDelta q_{2}\frac{x_{2}}{x_{2}+K_{2}^{*}}+u_{1}(x_{2}-x_{6})I_{\mathbb {R}_{+}}(x_{2}-x_{6}),\\ q_{3}= & {} m_{3}+\mu Y_{3}+\varDelta q_{3}\frac{x_{2}}{x_{2}+K_{3}^{*}}+u_{2}(x_{8}-x_{3})I_{\mathbb {R}_{+}}(x_{8}-x_{3}),\\ q_{4}= & {} m_{4}+\mu Y_{4}+\varDelta q_{4}\frac{x_{2}}{x_{2}+K_{4}^{*}},\\ q_{5}= & {} m_{5}+\mu Y_{5}. \end{aligned}$$

$I_{\mathbb {R}_{+}}$ is the indicator function defined as

$$\begin{aligned} I_{\mathbb {R}_{+}}(x)=\left\{ \begin{array}{ll} 1, \ &{} x>0, \\ 0,\ &{} x\le 0. \end{array} \right. \end{aligned}$$

The specific cell growth rate $\mu$ is expressed by

$$\begin{aligned} \mu =\left( 1-\frac{x_{7}}{x_{7}^{*}}\right) \mu _{m}\frac{x_{2}}{x_{2}+K_{s}}\prod _{i=2}^{5}\left( 1-\frac{x_{i}}{x_{i}^{*}}\right) . \end{aligned}$$

Under anaerobic conditions at 37 $^{\circ }$C and pH 7.0, the maximum specific growth rate $\mu _{m}$ and Monod saturation constant $K_{s}$ are 0.67/h and 0.28 mmol/L, respectively. $m_{i}$, $Y_{i}$, $\varDelta q_{i}$ and $K^{*}_{i} (i=2,3,4,5)$ are parameters whose values can be referred to the literature [4] as shown in Table 1.

Table 1 The values of parameters

Let $D_c:=[0.08,0.5]\times [110.96,1883]\in \mathbb {R}_{+}^{2}$ be the value range of the dilution rate and glycerol concentration in feed medium.

Define

$$\begin{aligned} W_{ad}:=\prod _{i=1}^{8}[x_{i*},x_{i}^{*}] \subset \mathbb { R}_{+}^{8}. \end{aligned}$$

From literature [11], the critical concentrations $x_{1}^{*}, x_{2}^{*}, \ldots , x_{8}^{*}$ are 15 g/L, 2039 mmol/L, 2000 mmol/L, 1026 mmol/L, 360.9 mmol/L, 2039 mmol/L, 300 mmol/L, 2000 mmol/L, respectively. And the lower bound of the state vector is given as $x_{*}=(0.01,0,0,0,0,0,0,0)^{\top }$. A function x from [0, T] into $\mathbb {R}_{+}^8$ is called an admissible state if $x(t)\in W_{ad}$ for all $t\in [0,T]$. Let $\mathcal {W}_{ad}$ be the class of all such admissible states.

Let

$$\begin{aligned} U_{ad}:=\prod _{j=1}^{15}[u_{j*},u_{j}^{*}]\subset \mathbb {R}^{15} \end{aligned}$$

be the value range of parameter vector u, where $u_{j*}$, $u_{j}^{*}$ are the lower and upper bounds of $u_{j}$, respectively. For detail, refer to Table 2. It should be noted that the value of system parameter vector u is uncertain and difficult to determine exactly.

Table 2 The value ranges of the undetermined parameters

3 Nonlinear switched system model

Since each indicator function has two different values in Eq. (1), vector field of the dynamical system becomes non-differentiable at the null point of indicator function. To solve this problem, we will regard the system (1) as a switched system.

Define $\sigma _{i}(\cdot ):[0,T]\rightarrow \{0,1\} (i=0,1,2,3)$ as

$$\begin{aligned} \sigma _{0}(t):= & {} I_{\mathbb {R}_{+}}(x_{2}(t)-x_{6}(t)),\\ \sigma _{1}(t):= & {} I_{\mathbb {R}_{+}}(x_{7}(t)-u_{9}),\\ \sigma _{2}(t):= & {} I_{\mathbb {R}_{+}}(x_{7}(t)-u_{12}),\\ \sigma _{3}(t):= & {} I_{\mathbb {R}_{+}}(x_{8}(t)-x_{3}(t)), \end{aligned}$$

and $\sigma (\cdot ):[0,T]\rightarrow \Sigma =\{0,1,2,\ldots ,15\}$ as

$$\begin{aligned} \sigma (t):=\sigma _{0}(t)+2\sigma _{1}(t)+2^{2}\sigma _{2}(t)+2^{3}\sigma _{3}(t),\ t\in [0,T]. \end{aligned}$$

It means that the Eq. (1) can switch between 16 modes. According to the factual process, we assume that

(H4) :

During the whole continuous fermentation process, the total number of switching times is limited.

To simplify expression, let $I_{n}:=\{1, 2, \ldots , n\}$, $\bar{I}_{n}:=\{0, 1, \ldots , n\}$ ($n\in \mathbb {Z}_+)$, $x:=x(t)$, $x_{i}:=x_{i}(t)$ ($i\in I_{8}$), $\sigma :=\sigma (t)$, $z:=(D, C_{s0}, u)\in \mathbb {R}^{17}_{+}$. Let $N~(<\infty )$ be the total number of switching times. $\tau _{1},\tau _{2},\ldots ,\tau _{N}$ are switching instants which satisfy $0<\tau _{1}<\tau _{2}<\cdots<\tau _{N}<T$. For the convenience of discussion, we set $\tau _{0}:=0$ and $\tau _{N+1}:=T$. Let $\varGamma :=\{\tau _{1},\tau _{2},\ldots ,\tau _{n}\}$ be the set of switching instants. Then we define the switching surfaces as follows.

$$\begin{aligned} \varPhi _{0}:= & {} \{ t\in \varGamma \ | \ h_{0}(x(t),z)=x_{2}(t)-x_{6}(t)=0 \},\\ \varPhi _{1}:= & {} \{ t\in \varGamma \ | \ h_{1}(x(t),z)=x_{7}(t)-u_{9}=0 \},\\ \varPhi _{2}:= & {} \{ t\in \varGamma \ | \ h_{2}(x(t),z)=x_{7}(t)-u_{12}=0 \},\\ \varPhi _{3}:= & {} \{ t\in \varGamma \ | \ h_{3}(x(t),z)=x_{8}(t)-x_{3}(t)=0\} \end{aligned}$$

Let $F^{\sigma }(x,z):=(f^{\sigma }_{1}(x,z), f^{\sigma }_{2}(x,z), \ldots , f^{\sigma }_{8}(x,z))^{\top }$ denote the right-hand side of the Eq. (1).

From the above, the continuous fermentation process can be described by the following nonlinear switched system.

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}(t)=F^{\sigma (t)}(x(t),z),~~t\in [0,T]\setminus \varGamma ,\\ \sigma (t)=\sigma _{0}(t)+2\sigma _{1}(t)+2^{2}\sigma _{2}(t)+2^{3}\sigma _{3}(t),~~t\in [0,T],\\ x(t)=x(t^{-}),~~t\in \varGamma ,\\ \sigma _{0}(t)=(\sigma _{0}(t^{-})+1)~\hbox {mod}~2,~~~t\in \varPhi _{0},\\ \sigma _{1}(t)=(\sigma _{1}(t^{-})+1)~\hbox {mod}~2,~~~t\in \varPhi _{1},\\ \sigma _{2}(t)=(\sigma _{2}(t^{-})+1)~\hbox {mod}~2,~~~t\in \varPhi _{2},\\ \sigma _{3}(t)=(\sigma _{3}(t^{-})+1)~\hbox {mod}~2,~~~t\in \varPhi _{3},\\ x(0)=x^{0},\\ \sigma (0)=\sigma ^{0}. \end{array} \right. \end{aligned}$$

(2)

Here $x(t^{-})$ and $\sigma _{i}(t^{-})$ are the left limit of x(t) and $\sigma _{i}(t)~(i=0,1,2,3)$ at time t, respectively. $x^0$ and $\sigma ^{0}$ are the initial values.

Under the assumptions (H1)–(H4), we can easily obtain the following property.

Property 1

For given $\sigma \in \Sigma$, $\forall (x,z)\in \mathcal {W}_{ad}\times D_{c}\times U_{ad}$, the vector field $F^{\sigma }(x,z)$ satisfies

• (1) $F^{\sigma }(x,z)$ is second-order continuous differentiable with respect to (x, z) in $\mathcal {W}_{ad}\times D_{c}\times U_{ad}$;

• (2) $F^{\sigma }(x,z)$ satisfies the linear growth condition, i.e., there exists two positive constants a, b such that

  $$\begin{aligned} \parallel F^{\sigma }(x,z) \parallel \le a \parallel x \parallel +b, \end{aligned}$$

  where $\parallel \cdot \parallel$ is the Euclidean norm.

For fixed $\sigma ^{0}\in \Sigma$ and given $(x^0,z)\in \ W_{ad}\times D_c\times U_{ad}$, let $\tau _k~(k\in I_N)$ be the switching instant and $x(\tau _k)$, $\sigma (\tau _k)$ be the initial values of the Eq. (2), respectively. Then we can formulate the following subsystem on the time interval $[\tau _{k},\tau _{k+1}]$.

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}(t)=F^{\sigma (\tau _{k})}(x(t),z), \\ \sigma (\tau _{k})=\sigma _{0}(\tau _{k})+2\sigma _{1}(\tau _{k})+2^{2}\sigma _{2}(\tau _{k})+2^{3}\sigma _{3}(\tau _{k}),\\ x(\tau _{k})=x(\tau _{k}^{-}),~~~~k\in I_N,\\ \sigma _{0}(\tau _{k})=(\sigma _{0}(\tau _{k}^{-})+1)~\hbox {mod}~2,~~~\tau _{k}\in \varPhi _{0},\\ \sigma _{1}(\tau _{k})=(\sigma _{1}(\tau _{k}^{-})+1)~\hbox {mod}~2,~~~\tau _{k}\in \varPhi _{1},\\ \sigma _{2}(\tau _{k})=(\sigma _{2}(\tau _{k}^{-})+1)~\hbox {mod}~2,~~~\tau _{k}\in \varPhi _{2},\\ \sigma _{3}(\tau _{k})=(\sigma _{3}(\tau _{k}^{-})+1)~\hbox {mod}~2,~~~\tau _{k}\in \varPhi _{3}. \end{array} \right. \end{aligned}$$

(3)

From the Property 1, for fixed initial values $x(\tau _k)$, $\sigma (\tau _k)$ and any $z\in D_c\times U_{ad}$, Eq. (3) has a unique solution $x^{(k)}(\cdot ;x(\tau _{k}),z)$. Based on the assumptions (H1)–(H4), we can obtain a property as follows.

Property 2

For given $\sigma ^{0}\in \Sigma$ and $(x^0,z)\in W_{ad}\times D_{c}\times U_{ad}$, there exists a unique solution to Eq. (2) denoted by $x(\cdot ;x^0,z)$, and the solution can be formulated as a piecewise solution

$$\begin{aligned} x(\cdot ;x^{0},z)=\left\{ \begin{array}{ll} x^{(0)}(t;x(\tau _{0}),z),~~t\in [\tau _{0},\tau _{1}], \\ x^{(1)}(t;x(\tau _{1}),z),~~t\in [\tau _{1},\tau _{2}], \\ \vdots \\ x^{(N)}(t;x(\tau _{N}),z),~~t\in [\tau _{N},\tau _{N+1}]. \end{array} \right. \end{aligned}$$

On the basis of the actual fermentation courses, we can assume that

$\mathbf (H5)$ For $\forall (x,z)\in \mathcal {W}_{ad}\times D_{c}\times U_{ad}$, $\nabla h_{i}(x,u)F^{\sigma }(x,z)\ne 0~(i\in \bar{I}_{3},~\sigma \in \Sigma )$.

By literature [13] and the assumptions (H1)–(H5), we can obtain the following properties.

Property 3

For fixed $\sigma ^{0}\in \Sigma$ and $(x^0,z)\in W_{ad}\times D_{c}\times U_{ad}$, let $x^{(k)}(\cdot ;x(\tau _{k}),z) (k\in \bar{I}_{N})$ be a solution of the subsystem (3), then the switching instant $\tau _{k+1}$ $(k\in I_{N-1})$ is continuous with respect to $(x(\tau _{k}),z)$.

Property 4

For given $\sigma ^{0}\in \Sigma$ and $(x^0,z)\in W_{ad}\times D_{c}\times U_{ad}$, let $x(\cdot ;x^0,z)$ be the unique solution to Eq. (2), then $x(\cdot ;x^0,z)$ is continuous with respect to z in $D_{c}\times U_{ad}$.

Now, we define the following sets of the solutions and admissible solutions to system (2).

$$\begin{aligned}&E:=\{\ x(\cdot ;x^{0},z)\ |\ x(\cdot ;x^{0},z)~\textit{ is a solution to system }(2)\,{ with}~x^{0}\in W_{ad}, \nonumber \\&\quad \quad \quad z\in D_{c}\times U_{ad}.\ \}, \end{aligned}$$

(4)

$$\begin{aligned}&\varLambda :=\{\ x(\cdot ;x^{0},z)\ |\ x(\cdot ;x^{0},z)\in \mathcal {W}_{ad}\cap E\ \}. \end{aligned}$$

(5)

Next, the set of feasible parameter vectors is written as

$$\begin{aligned} \varOmega :=\{\ z\in D_{c}\times U_{ad}\ |\ x(\cdot ;x^{0},z)\in \varLambda \ \}. \end{aligned}$$

(6)

From the compactness of $W_{ad}$ and $D_{c}\times U_{ad}$, and the continuity of the solutions with respect to z, we have the following conclusion.

Property 5

For given $x^{0}\in W_{ad}$, the sets E, $\varLambda$ and $\varOmega$ are compact.

4 Optimal control problem

In this section, an optimal control model will be established to maximize the product concentration by optimizing the dilution rate D and feeding glycerol concentration $C_{s0}$. Since parts of the system parameters depend on the decision variables, the sensitivities of the system states with respect to the parameters and the decision variables will be discussed. Sensitivity functions refer to the partial derivatives of the state variables with respect to the parameters. Thus, we can determine the influence of the parameters to the system from sensitivity analysis. Furthermore, sensitivity functions can provide the necessary gradient information for designing an optimization algorithm as well [16] .

According to [14, 17], we will use $\varphi ^{(k)}_{k+1}$ and $T^{(k)}_{k+1}$, respectively, to designate the discontinuity function and the transition function, where the superscript (k) and the subscript $k+1$ are used to indicate the subsystem when the event considered happened and the subsequent subsystem determined by the switching condition, respectively. The system (2) will switch when $h_{i}=0~(i\in \bar{I}_{3})$, then the switching rule can be expressed as

$$\begin{aligned} \varphi ^{(k)}_{k+1}(x^{(k)},z)= & {} [x_{2}^{(k)}(t;x(\tau _{k}),z)-x_{6}^{(k)}(t;x(\tau _{k}),z)]\cdot [x_{7}^{(k)}(t;x(\tau _{k}),z)-u_{9}]\nonumber \\&\cdot [x_{7}^{(k)}(t;x(\tau _{k}),z)-u_{12}]\cdot [x_{8}^{(k)}(t;x(\tau _{k}),z)-x_{3}^{(k)}(t;x(\tau _{k}),z)]\nonumber \\= & {} 0. \end{aligned}$$

(7)

The transition function $T^{(k)}_{k+1}$ satisfies that

$$\begin{aligned} T^{(k)}_{k+1}(x^{(k+1)},x^{(k)})|_{t=\tau _{k+1}}=x^{(k+1)}(\tau _{k+1};z)-x^{(k)}(\tau _{k+1}^{-};z)=0. \end{aligned}$$

(8)

We can simply obtain the following results by the conclusions in [17, 18].

Property 6

For $\forall t\in (\tau _{k},\tau _{k+1})$, the partial derivatives $\frac{\partial F^{\sigma (\tau _{k})}}{\partial x^{(k)}}$ and $\frac{\partial F^{\sigma (\tau _{k})}}{\partial z}$ exist, and they are continuous in a neighborhood of the solution $x^{(k)}(\cdot ;x(\tau _{k}),z)$.

Property 7

Let $s>\tau _{k}$ be the first switching instant satisfying Eq. (7). There exists an open set $E\subset \mathbb {R}^{17}$ with $z\in E$ and a continuous differential function $\tau (\cdot )$ such that $\tau (z)=s$ and

$$\begin{aligned} \varphi ^{(k)}_{k+1}(x^{(k)}(\tau (z^{\prime });x(\tau _{k}),z^{\prime }),z^{\prime })=0,\qquad \forall z^{\prime }\in E. \end{aligned}$$

Theorem 1

Given $x^{0}\in W_{ad}$, for any $z\in D_{c}\times U_{ad}$, $l,s\in I_{17}$, $\{\tau _{k}\}_{k=1}^{N}$ is the sequence of switching instants. Under the assumptions ${\mathbf {(H1)}}{-}{\mathbf {(H5)}}$, the sensitivity function $\frac{\partial x}{\partial z_{l}}$ exists and is continuous; the second-order partial derivative $\frac{\partial ^{2}x}{\partial z_{l}\partial z_{s}}$ exists. And they satisfy the differential equations

$$\begin{aligned} \frac{\partial }{\partial t}\left( \frac{\partial x}{\partial z_{l}}\right)= & {} \frac{\partial F^{\sigma }}{\partial x}\frac{\partial x}{\partial z_{l}}+\frac{\partial F^{\sigma }}{\partial z_{l}},\end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial }{\partial t}\left( \frac{\partial ^{2}x}{\partial z_{l}\partial z_{s}}\right)= & {} \frac{\partial F^{\sigma }}{\partial x}\left( \frac{\partial ^{2}x}{{\partial z_{l}\partial z_{s}}}\right) +\frac{\partial }{\partial z_{s}}\left( \frac{\partial F^{\sigma }}{\partial x}\right) \frac{\partial x}{\partial z_{l}}+\frac{\partial ^{2}F^{\sigma }}{\partial z_{l}\partial z_{s}}, \end{aligned}$$

(10)

in [0, T] with initial sensitivity

$$\begin{aligned}&\frac{\partial x}{\partial z_{l}}|_{t=0}=0, \end{aligned}$$

(11)

$$\begin{aligned}&\frac{\partial ^{2} x}{\partial z_{l}\partial z_{s}}|_{t=0}=0. \end{aligned}$$

(12)

Furthermore, both $\frac{\partial x}{\partial z_{l}}$ and $\frac{\partial ^{2}x}{\partial z_{l}\partial z_{s}}$ satisfy the following conditions at switching points

$$\begin{aligned} \frac{\partial x^{(k+1)}}{\partial z_{l}}= & {} \frac{\partial x^{(k)}}{\partial z_{l}}, \end{aligned}$$

(13)

$$\begin{aligned} \frac{\partial ^{2}x^{(k+1)}}{\partial z_{l}\partial z_{s}}= & {} -\left( \frac{\partial F^{\sigma (\tau _{k+1})}}{\partial z_{s}}-\frac{\partial F^{\sigma (\tau _{k})}}{\partial z_{s}}\right) \frac{d t}{d z_{l}}+\frac{\partial ^{2}x^{(k)}}{\partial z_{l}\partial z_{s}}, \end{aligned}$$

(14)

where,

$$\begin{aligned} \frac{d t}{d z_{l}}=-\frac{\frac{\partial \varphi ^{(k)}_{k+1}}{\partial x^{(k)}}\frac{\partial x^{(k)}}{\partial z_{l}}+\frac{\partial \varphi ^{(k)}_{k+1}}{\partial z_{l}}}{\frac{\partial \varphi ^{(k)}_{k+1}}{\partial x^{(k)}}F^{\sigma (\tau _{k})}}. \end{aligned}$$

(15)

Proof

For any $k\in I_{N},~l,s\in I_{17}$, on the open interval $(\tau _{k},\tau _{k+1})$, it follows from Properties 6 and 7 that

$$\begin{aligned} \frac{\partial }{\partial t}\left( \frac{\partial x^{(k)}}{\partial z_{l}}\right) =\frac{\partial F^{\sigma (\tau _{k})}}{\partial x^{(k)}}\frac{\partial x^{(k)}}{\partial z_{l}}+\frac{\partial F^{\sigma (\tau _{k})}}{\partial z_{l}}. \end{aligned}$$

(16)

We further calculate the partial derivative of the Eq. (16) with respect to z based on the chain rule as follows.

$$\begin{aligned} \frac{\partial }{\partial t}\left( \frac{\partial ^{2}x^{(k)}}{\partial z_{l}\partial z_{s}}\right)= & {} \frac{\partial F^{\sigma (\tau _{k})}}{\partial x^{(k)}}\left( \frac{\partial ^{2}x^{(k)}}{\partial z_{l}\partial z_{s}}\right) +\frac{\partial }{\partial z_{s}}\left( \frac{\partial F^{\sigma (\tau _{k})}}{\partial x^{(k)}}\right) \frac{\partial x^{(k)}}{\partial z_{l}}\nonumber \\&+\frac{\partial ^{2}F^{\sigma (\tau _{k})}}{\partial z_{l}\partial z_{s}}. \end{aligned}$$

(17)

At the switching instant $\tau _{k+1}$, from the Eq. (8), we have $T^{(k)}_{k+1}=x^{(k+1)}-x^{(k)}=0$. Substituting $T^{(k)}_{k+1}$ into Eq. (49) in [17], we can obtain that

$$\begin{aligned} \frac{\partial x^{(k+1)}}{\partial z_{l}}=-\left( F^{\sigma (\tau _{k+1})}-F^{\sigma (\tau _{k})}\right) \frac{d t}{d z_{l}}+\frac{\partial x^{(k)}}{\partial z_{l}}. \end{aligned}$$

(18)

From the continuity of $F^{\sigma }$, we have

$$\begin{aligned} \frac{\partial x^{(k+1)}}{\partial z_{l}}=\frac{\partial x^{(k)}}{\partial z_{l}}. \end{aligned}$$

(19)

It means that the sensitivity function $\frac{\partial x^{(k)}}{\partial z_{l}}$ exists and is continuous. Then, we calculate the partial derivative of the Eq. (18) with respect to z as follows.

$$\begin{aligned} \frac{\partial ^{2}x^{(k+1)}}{\partial z_{l}\partial z_{s}}= & {} -\left( \frac{\partial F^{\sigma (\tau _{k+1})}}{\partial z_{s}}-\frac{\partial F^{\sigma (\tau _{k})}}{\partial z_{s}}\right) \frac{d t}{d z_{l}}\nonumber \\&-\left( F^{\sigma (\tau _{k+1})}-F^{\sigma (\tau _{k})}\right) \frac{d^{2}t}{d z_{l}d z_{s}}+\frac{\partial ^{2}x^{(k)}}{\partial z_{l}\partial z_{s}}.~~~ \end{aligned}$$

(20)

Since $F^{\sigma }$ is continuous, Eq. (20) is simplified into

$$\begin{aligned} \frac{\partial ^{2}x^{(k+1)}}{\partial z_{l}\partial z_{s}}=-\left( \frac{\partial F^{\sigma (\tau _{k+1})}}{\partial z_{s}}-\frac{\partial F^{\sigma (\tau _{k})}}{\partial z_{s}}\right) \frac{d t}{d z_{l}}+\frac{\partial ^{2}x^{(k)}}{\partial z_{l}\partial z_{s}}. \end{aligned}$$

(21)

Substituting Eq. (7) into Eq. (37) in [17], we can readily get Eq. (15). In addition, Eq. (11) and Eq. (12) can be easily obtained due to the independence of $x^{0}$ with respect to z. $\square$

For given $x^{0}\in W_{ad}$ and any $(D,C_{s0})\in D_{c}$, our purpose is to find an optimal value $(D^{*},C_{s0}^{*})\in D_{c}$ so that we can obtain a higher product concentration of 1,3-PD at the terminal time subject to the corresponding constraint conditions. On the basis of the definitions in Eqs. (4)–(6), we establish the following optimal control model.

$$\begin{aligned}&OCM:~~~\min ~~~J(D,C_{s0},u)=-x_{3}(T;x^{0},D,C_{s0},u)\\&\qquad s.~t.~~~~\frac{\partial x_{i}(T;x^{0},D,C_{s0},u)}{\partial u_{j}}\le \varepsilon , ~~i\in I_{8},~j\in I_{15},\\&\quad \qquad (D,C_{s0},u)\in \varOmega , \end{aligned}$$

where $\varepsilon$ is a given sufficiently small constant.

For the optimization problem OCM, we can obtain the following result.

Theorem 2

The problem OCM has at least one optimal solution for given $x_{0}\in W_{ad}$, i.e., there exist an optimal solution $(D^{*},C_{s0}^{*})\in D_{c}$ and an appropriate parameter $\bar{u}\in U_{ad}$, such that

$$\begin{aligned} J(D^{*},C_{s0}^{*},\bar{u})\le J(D,C_{s0},u),\ \forall (D,C_{s0})\in \ D_{c},\ u\in U_{ad}. \end{aligned}$$

Proof

It is clear that $J(D,C_{s0},u)$ is continuous with respect to $(D,C_{s0},u)$. From the Property 5, the sets $D_{c}$, $U_{ad}$ and $\varOmega$ are compact. Thus, there exist an optimal solution $(D^{*},C_{s0}^{*})\in D_{c}$ and an appropriate parameter $\bar{u}\in U_{ad}$ satisfying constraint conditions such that the conclusion of theorem holds. $\square$

5 Optimization algorithm

The purpose of this section is to solve the problem OCM by SQP algorithm [19]. For the application of the algorithm, we need to provide the necessary gradient information of performance index and constraint conditions.

From the definition of the set $\varLambda$ in Eq. (5), for $\forall t\in [0,T],~z\in D _{c}\times U_{ad},~i\in I_{8}$, the state variable x satisfies the following constraint.

$$\begin{aligned} x_{i*}\le x_{i}(t;z)\le x_{i}^{*}. \end{aligned}$$

(22)

Let

$$\begin{aligned} g_{i}(x(t;z))= & {} x_{i}(t;z)-x_{i*},~~~t\in [0,T]. \end{aligned}$$

(23)

$$\begin{aligned} g_{i+8}(x(t;z))= & {} x_{i}^{*}-x_{i}(t;z),~~~i=1,2,\ldots ,8. \end{aligned}$$

(24)

Then the Eq. (22) is equivalent to

$$\begin{aligned} G(z)=\sum _{i=1}^{16} \int _{0}^{T}\min \{g_{i}(x(t;z)),0\}dt=0. \end{aligned}$$

(25)

However, it should be noted that the equality constraint (25) is non-smooth. To handle the non-smooth equality constraint (25), we define

$$\begin{aligned} \tilde{G}_{\theta }(z)=\sum _{i=1}^{16} \int _{0}^{T}\tilde{g}_{i,\theta }(x(t;z))dt=0, \end{aligned}$$

(26)

where

$$\begin{aligned}&\tilde{g}_{i,\theta }(x(t;z))=\left\{ \begin{array}{ll} g_{i}(x(t;z)) ,\ &{} g_{i}(x(t;z))<-\theta \\ -(g_{i}(x(t;z))-\theta )^{2}/4\theta ,\ &{} -\theta \le g_{i}(x(t;z))\le \theta \\ 0,\ &{} g_{i}(x(t;z))>\theta \end{array} \right. \end{aligned}$$

and $\theta$ is a parameter of approximation quality satisfied $\theta >0$.

Therefore, the problem OCM can be restated as follows.

$$\begin{aligned}&\min ~~~J(z)=-x_{3}(T;x^{0},z)\nonumber \\&s.~t.~~~~W_{ij}(z)=\varepsilon -\frac{\partial x_{i}(T;x^{0},z)}{\partial u_{j}}\ge 0,~~i\in I_{8},~j\in I_{15},\nonumber \\&\quad \tilde{G}_{\theta }(z)=0. \end{aligned}$$

(27)

Define the following Lagrange function as

$$\begin{aligned} L(z,\lambda ,\mu )=J(z)-\sum _{i,j} \lambda _{ij}W_{ij}(z)-\mu \tilde{G}_{\theta }(z), \end{aligned}$$

where $\lambda _{ij}$ $(i\in I_{8}, j\in I_{15})$ and $\mu$ are Lagrange multipliers. Then we will structure a quadratic programming subproblem QP using linear approximation method [20].

$$\begin{aligned}&\min ~~~QP(d)=[\nabla J(z^{(r)})]^{\top }d+\frac{1}{2}d^{\top }H^{(r)}d \nonumber \\&s.t.~~~~~W_{ij}(z^{(r)})+[\nabla W_{ij}(z^{(r)}) ]^{\top }d\ge 0,\nonumber \\&\quad \tilde{G}_{\theta }(z^{(r)})+[\nabla \tilde{G}_{\theta }(z^{(r)})]^{\top }d=0. \end{aligned}$$

(28)

If $d^{(r)}=z^{(r+1)}-z^{(r)}$ is an optimal solution of the problem QP, $d^{(r)}$ is a search direction of the problem OCM. $[\nabla J(z^{(r)})]^{\top }$, $[\nabla W_{ij}(z^{(r)}) ]^{\top }$ and $[\nabla \tilde{G}_{\theta }(z^{(r)})]^{\top }$ are the first-order gradients of performance index and constraint conditions, respectively. $H^{(r)}$ is the second-order Hessian Matrix of Lagrange function L with respect to $z^{(r)}$. All of them can be formulated as follows.

$$\begin{aligned} \frac{\partial J(z)}{\partial z_{l}}= & {} \frac{\partial (-x_{3}(T;x^{0},z))}{\partial z_{l}},~~~l\in I_{17}, \end{aligned}$$

(29)

$$\begin{aligned} \frac{\partial W_{ij}(z)}{\partial z_{l}}= & {} -\frac{\partial }{\partial z_{l}}\left( \frac{\partial x_{i}(T;x^{0},z)}{\partial u_{j}}\right) ,~~i\in I_{8},~j\in I_{15}, \end{aligned}$$

(30)

$$\begin{aligned} \frac{\partial \tilde{G}_{\theta }(z)}{\partial z_{l}}= & {} \sum ^{N}_{k=0}\sum ^{16}_{i=1}\Bigg \{\int ^{\tau _{k+1}}_{\tau _{k}}\frac{\partial \tilde{g}_{i,\theta }(x^{(k)}(t;z))}{\partial x^{(k)}}\frac{\partial x^{(k)}(t;z)}{\partial z_{l}}dt\nonumber \\&+\,\tilde{g}_{i,\theta }(x^{(k)}(\tau _{k+1}(z);z))\frac{\partial \tau _{k+1}}{\partial z_{l}}-\tilde{g}_{i,\theta }(x^{(k)}(\tau _{k}(z);z))\frac{\partial \tau _{k}}{\partial z_{l}}\Bigg \}, \end{aligned}$$

(31)

$$\begin{aligned} H^{(r)}= & {} \nabla ^{2}_{z}L(z,\lambda ,\mu )\nonumber \\= & {} \nabla ^{2}J(z^{(r)})-\sum _{i,j}\lambda ^{(r)}_{ij}\nabla ^{2} W_{ij}(z^{(r)})-\mu ^{(r)}\nabla ^{2}\tilde{G}_{\theta }(z^{(r)}). \end{aligned}$$

(32)

Since $H^{(r)}$ includes the second-order gradient information of performance index and constraint conditions, it would be hard to calculate directly. For overcome the difficulty, our method is to construct a positive definite matrix $A^{(r)}$ instead of $H^{(r)}$ with constantly improving until $A^{(r)}$ approaches to $H^{(r)}$. $A^{(r)}$ can be formed by BFGS method [21] as follows.

$$\begin{aligned} A^{(r+1)}=A^{(r)}-\frac{A^{(r)}\delta \delta ^{\top }A^{(r)}}{\delta ^{\top }A^{(r)}\delta }+\frac{\eta \delta ^{\top }}{\delta ^{\top } \eta }, \end{aligned}$$

(33)

where

$$\begin{aligned} \delta= & {} z^{(r+1)}-z^{(r)},\\ \eta= & {} \nabla _{z} L(z^{(r+1)})-\nabla _{z}L(z^{(r)}), \end{aligned}$$

and $A^{(0)}$ is a unit matrix.

Table 3 The values of the identified parameters

Fig. 1

The computational values of state trajectories. a The concentration of biomass. b The concentration of extracellular glycerol. c The concentration of extracellular 1,3-PD. d The concentration of acetic acid. e The concentration of ethanol. f The concentration of intracellular glycerol. g The concentration of intracellular 3-HPA. h The concentration of intracellular 1,3-PD

With the SQP method, we construct an algorithm, which is given below.

Step 1 :

Give initial values $x^{0}, \sigma ^{0}, z^{(0)}, A^{(0)}, \varepsilon =10^{-2}, \theta =10^{-2}, \zeta =10^{-3}$, and set $r=0$.

Step 2 :

Calculate the solution of Eq. (2). Compute $\frac{\partial x}{\partial z_{l}}$ and $\frac{\partial ^2 x}{\partial z_{l}\partial z_{s}}$ based on the Eqs. (9)–(14) by improved Euler method. Substitute the results into Eqs. (29)-(31) to calculate the first-order gradient information of performance index and constraint conditions, where the integral of Eq. (31) is solved by Newton–Cotes method. After that, calculate the values of performance index and constraint functions, and structure the quadratic programming subproblem (28).

Step 3 :

Solve the quadratic programming subproblem (28) by Active Set method, then we obtain Lagrange multiplier vectors $\lambda ^{(r+1)},~\mu ^{(r+1)}$ and search direction $d^{(r)}$.

Step 4 :

Let $z^{(r+1)}=z^{(r)}+\alpha ^{(r)}d^{(r)}$, where $\alpha ^{(r)}$ is the step-size chosen by Armijo line search.

$\mathbf Step~5$ :

If $\parallel \nabla _{z}L(z^{(r+1)},\lambda ^{(r+1)},\mu ^{(r+1)})\parallel \le \zeta$, substitute $z^{(r+1)}$ into the system (2). Recompute the solution of Eq. (2) by improved Euler method, and substitute the result into Eq. (27) to compute the value of performance index. Then output the optimal value and stop. Otherwise, goto step 6.

Step 6 :

Modify the approximate Hessian Matrix $A^{(r)}$ with Eq. (33), then we obtain $A^{(r+1)}$. Let $r:=r+1$, goto step 2.

6 Numerical results

The whole continuous fermentation was implemented with enough substrate. The total fermentation time is taken as 40h. We take the initial state $x^{0}=(0.155,434.783,0,0,0,0,0,0)^{\top }$ and $\sigma ^{0}=1$. And the value of $z^{(0)}$ is taken from literature [12]. Then we use the proposed algorithm to solve the problem OCM, in which the step size of the Euler method is 1/3600 h. All the computations are performed in Visual C++ 2010. In order to approximate the factual experiments, we have proceeded 10 times calculation for the whole fermentation procedure which spent 8.65 h.

The best result is selected from the ten computational results. The optimal dilution rate and feeding glycerol concentration are 0.08/h and 1805.38 mmol/L, respectively, and the values of the identified parameters are listed in Table 3. The switching instants and the mode sequence are (2.1, 2.4, 3.3, 4, 4.5, 11.5, 14.4, 17, 18.5, 20.7) (unit: h) and (1, 3, 11, 15, 14, 6, 14, 6, 14, 6, 7), respectively. Under the gained optimal dilution rate, feeding glycerol concentration, switching instants and mode sequence, the concentration of 1,3-PD at the terminal time is 906.469 mmol/L, which is increased obviously in comparison with 710.1 mmol/L presented in [15]. Moreover, it is superior to the optimal experimental value 638.16 mmol/L with the dilution rate 0.1h and the feeding glycerol concentration 1568 mmol/L. The trajectories of concentration with all reactants and products are shown in Fig. 1a–h.

7 Conclusions

In this work, we proposed a novel nonlinear switched system model to describe the microbial continuous culture of glycerol bio-dissimilation to 1,3-PD. Then we discussed some properties of the switched system and sensitivity functions, respectively. On that basis, we obtained gradient formulas based on the sensitivity functions of the state variables with respect to parameters. In order to achieve the higher products, we formulated an optimal control model, which is constrained by the sensitivity function of parameters. By employing the proposed algorithm, we obtained the optimal input strategies, which not only play an important role in improving the production of 1,3-PD but also provided a reference for biochemical experiments.