A self-similar solution for transient Darcy–Forchheimer flow in an aquifer

Abstract

In this study we examine the classical problem of fluid flow in an aquifer, obeying the transient Darcy–Forchheimer law. This problem is solved by using the symmetry properties of the governing equations (e.g. the mass balance equation and the transient Darcy–Forchheimer momentum equation) which enable us to transform the time and the space coordinates into one independent coordinate. According to our study the flow in the aquifer may be divided into two main components. One component is the steady part of the flow discharge and the other one is the transient part of the flow discharge. The obtained solution shows that the reduction in the above-mentioned transient part leads to the creation of three zones: (1) the “near zone” located near the inlet face to the aquifer and is characterized by a positive flow; (2) the “far zone” in the aquifer lying at an infinite distance from the inlet face where the flow is also positive and (3) the “intermediate backflow zone”, which is lying among the above-mentioned zones and is characterized by reverse flow. The results obtained in this study may be useful for understanding the transient flow process in the aquifer, stemming from the Darcy–Forchheimer flow, and for the prediction of the discharge and head distribution in the aquifer.

1 Introduction

Fluid flow through porous media with a high penetration rate starts to deviate from the linear relationship between flow rate and hydraulic gradient. At this time, the traditional Darcy law is no longer applicable to the complex flow state of fluid in the porous medium. At such flow conditions, Darcy’s law for laminar flow can no longer be assumed and nonlinear relationships are required (Lopik et al. 2020). Many attempts have been made to correct the Darcy equation by adding a second order of the velocity term to represent the microscopic inertial effect, and corrected the Darcy equation into the Forchheimer equation (Zeng and Grigg 2006). Irmay (1958) starts from the Navier–Stokes hydrodynamic equations of viscous flow, and using statistical methods shows that at low values of Reynolds numbers, Darcy's law is obtained in the Kozeny-Carman form. At larger values of Reynolds number, the Forchheimer formula is obtained, with a coefficient depending on the soil grain diameter and porosity. Wodie and Levy (1991) derived this law analytically for homogeneous isotropic and spatially periodic porous media by double scale homogenization. The existence of a weak inertia regime was confirmed experimentally by Skjetne and Auriault (1999) and they proposed the quadratic Forchheimer equation in order to describe this non-linear behavior. The above description is widely used to describe the inertial flow behavior in porous media (Tosco et al 2013; Zolotukhin and Gayubov 2021).

In the studies reviewed so far (as well as in other studies that we didn't mention), no closed-form analytical solution was found to a problem that contains the mass conservation equation in a porous medium together with the Darcy Forchheimer equation. In this study (as will be shown later), the scale symmetry of the transient Darcy–Forchheimer equations allows us to combine the two independent variables (space $x$ and time $t$) into a new independent variable $x/t$ and the governing partial differential equations are reduced to a single ordinary differential equation. With the use of dimensional analysis and the scaling laws concept (Barenblatt 1979), a closed-form analytical solution for the governing equations is derived for several transient situations.

2 Problem presentation and mathematical formulation

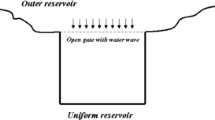
Consider a homogeneous and isotropic aquifer on a regional scale, that is, with a planar horizontal extent much larger than its thickness. The continuity equation, describing transient incompressible water flow in a confined aquifer, is given by Bear (1988)

$$ S\frac{\partial H}{{\partial t}} + \frac{\partial Q}{{\partial x}} = 0, \, $$

(1)

where $S$, is the specific mass storativity of the aquifer [m⁻¹], $Q(x,t)$ is specific water discharge[m·s⁻¹], $t$ and $x$ are respectively the time [s] and space [m] coordinates and $H(x,t)$ is the hydraulic head [m] in the aquifer.

In terms of the Dupuit approximation, the transient Darcy–Forchheimer equation is given by Wang et al. (2016) and Zhu et al. (2014),

$$ c\frac{\partial Q}{{\partial t}} + \frac{\partial H}{{\partial x}} + aQ + bQ\left| Q \right| = 0, \, $$

(2)

where the coefficients a[s/m] and b [s²/m²] represent the linear and quadratic parts of the interaction force and the inertia term due to flow acceleration; c[s²/m] is a coefficient representing the transient part of Eq. (2) (e.g., note that we are writing $Q\left| Q \right|$ to allow for reverse flow).

We will assume that in our model the discharge $Q(x,t)$, composed from a time dependent transient part $Q_{t} (x,t)$ and a time independent constant part $q_{0}$ is as follows

$$ Q(x,t) = Q_{t} (x,t) - q_{0} . \, $$

(3)

where the value of $q_{0}$ is given by

$$ q_{0} = \frac{a}{2b} $$

(3a)

Introducing of (3) and (3a) into (1) and (2) we obtain the continuity and the momentum equation with respect to the transient discharge $Q_{t} (x,t)$ as follows

$$ \frac{\partial H}{{\partial t}} + \frac{1}{S}\frac{{\partial Q_{t} }}{\partial x} = 0, \, $$

(4)

and

$$ c\frac{{\partial Q_{t} }}{\partial t} + \frac{\partial H}{{\partial x}} + bQ_{t} \left| {Q_{t} } \right| - \frac{{a^{2} }}{4b} = 0. \, $$

(5)

Differentiating both sides of Eq. (4) with respect to $x$ we obtain

$$ \frac{\partial }{\partial t}\left( {\frac{\partial H}{{\partial x}}} \right) + \frac{1}{S}\frac{{\partial^{2} Q_{t} }}{{\partial x^{2} }} = 0 \, . \, $$

(6)

We now express Eq. (5) as follows

$$ \frac{\partial H}{{\partial x}} = - \left( {c\frac{{\partial Q_{t} }}{\partial t} + bQ_{t} \left| {Q_{t} } \right| - \frac{{a^{2} }}{4b}} \right) $$

(7)

Introducing (7) into (6), we obtain

$$ \frac{\partial }{\partial t}\left( { - c\frac{{\partial Q_{t} }}{\partial t} - bQ_{t} \left| {Q_{t} } \right|} \right) + \frac{1}{S}\frac{{\partial^{2} Q_{t} }}{{\partial x^{2} }} = 0 \, {. } $$

(8)

We now introduce the dimensionless variables $\hat{x}$ and $\hat{t}$, related to their cartesian counterparts, as follows

$$ \hat{x} = \frac{x}{L} $$

(9a)

$$ \hat{t} = \frac{t}{T} $$

(9b)

where $L$ is a characteristic length of the aquifer and $T$ is a characteristic time to be determined hereafter. We will also define the dimensionless discharge $\hat{Q}_{t}$ and head $\hat{H}$ as follows

$$ \hat{Q}_{t} = \frac{{Q_{t} }}{{Q_{t\;c} }} $$

(9c)

$$ \hat{H} = \frac{H}{{H_{c} }} $$

(9d)

where $Q_{t\;c}$ and $H_{c}$ are respectively the characteristics of transient discharge and head parameters which will be further used in the calibration procedure of this model. With the introduction of (9a)–(9d) into (8), we obtain

$$ \frac{\partial }{{\partial \hat{t}}}\left( {\frac{{ScL^{2} }}{{T^{2} }}\frac{{\partial \hat{Q}_{t} }}{{\partial \hat{t}}} + \frac{{bSL^{2} Q_{t\;c} \hat{Q}_{t} \left| {\hat{Q}_{t} } \right|}}{T}} \right) = \frac{{\partial^{2} \hat{Q}_{t} }}{{\partial \hat{x}^{2} }} \, {. } $$

(10)

We now determine the characteristic length of the aquifer $L$ and the characteristic time $T$ as follows

$$ L = \frac{1}{{\sqrt {Sc} }}T $$

(11)

where

$$ T = \frac{{c^{3/2} }}{{bS^{1/2} H_{c} }} $$

(11a)

$$ L = \frac{c}{{bSH_{c} }} $$

(11b)

and

$$ H_{c} = Q_{t\;c} \sqrt{\frac{c}{S}} . \, $$

(11c)

Substituting (11), (11a), (11b) and (11c) into (10) and (4), we obtain

$$ \frac{\partial }{{\partial \hat{t}}}\left( {\frac{{\partial \hat{Q}_{t} }}{{\partial \hat{t}}} + \hat{Q}_{t} \left| {\hat{Q}_{t} } \right|} \right) = \frac{{\partial^{2} \hat{Q}_{t} }}{{\partial \hat{x}^{2} }}, \, $$

(12a)

and

$$ \frac{{\partial \hat{H}}}{{\partial \hat{t}}} + \frac{{\partial \hat{Q}_{t} }}{{\partial \hat{x}}} = 0, \, $$

(12b)

We assume that the discharge $\hat{Q}{(}\hat{x}{,}\hat{t}{) }$ and the fluid head $\hat{H}{(}\hat{x}{,}\hat{t}{) }$ are functions defined in the region $0 \le \hat{x} \le \infty \,$. Consider a situation in which initially (i.e., at time $\hat{t} < 0 \,$) water flows in the aquifer with constant discharge. We will refer to a situation at which the water level in the reservoir (i.e., at $\hat{x} = - 0$) suddenly drops and in response to this, the dimensionless discharge $\hat{Q}{(}\hat{x}{,}\hat{t}{) }$ at $\hat{x} = 0$ is given by

$$ \hat{Q}(0,\hat{t}) = \hat{Q}_{t} {(}0{,}\hat{t}{)} + \hat{q}_{0} \, $$

(13)

where the transient dimensionless discharge and the dimensionless head at $\hat{x} = 0$ are changing according to the following laws

$$ \hat{Q}_{t} {(}0{,}\hat{t}{)} = \hat{Q}_{t\;0} \, \hat{t}^{ - 1} $$

(13a)

and

$$ \hat{H}{(}0{,}\hat{t}{)} = \hat{H}_{0} \, \hat{t}^{ - 1} $$

(13b)

where $\hat{H}_{0}$ and $\hat{Q}_{t\;0}$ are scaling parameters, depending on the properties of the aquifer. In addition to this, the dimensionless variables $\hat{Q}(\hat{x},\hat{t})$ and the dimensionless parameter $\hat{q}_{0}$ are given by $Q(x,t) = Q_{tc} \hat{Q}(\hat{x},\hat{t})$ and $q_{0} = Q_{tc} \hat{q}_{0}$.

We will assume that the component of the transient dimensionless discharge $\hat{Q}_{t} (\hat{x},\hat{t}) \,$ vanishes at an infinite distance from the inlet face and hence

$$ \hat{Q}_{t} {(}\hat{x}{,}\hat{t}{)} \to {0}\quad {\text{as}}\quad \hat{x} \to \infty $$

(14)

In general, the problem must be solved for specified initial conditions imposed upon $\hat{Q}_{t} {(}\hat{x}{,}\hat{t}{) }$. However, as it is shown below, the long-time profiles of $\hat{Q}_{t} {(}\hat{x}{,}\hat{t}{) }$ are independent of the precise form of the initial conditions $\hat{Q}_{t} {(}\hat{x}{,}0{) }$ that govern the dimensionless transient discharge at early stages only. In accordance with the above, the long-time dimensionless transient discharge profile will prove to be independent of the precise form of the initial conditions existing in the aquifer. Hence, the detail of the initial distribution of the dimensionless transient discharge within the aquifer is irrelevant and the obtained solution is suitable for long periods only.

In the next section, we treat this problem by a self-similar approach and outline special cases for which several analytical solutions are obtained.

3 Self-similar model

We will further refer to the circumstances in which the dimensionless transient discharge function $\hat{Q}_{t} (\hat{x},\hat{t})$ in the aquifer achieves a certain profile at asymptotically long times, which is derived from universal behavior, and described by a single independent self-similar variable $\xi$ (Barenblatt 1979)

$$ \hat{Q}_{t} = \frac{f(\xi )}{{\hat{t}}} $$

(15a)

where

$$ \hat{x} = \xi \hat{t} \, $$

(15b)

and $f(\xi )$ is the discharge self-similar profile.

We rewrite Eq. (12a) as follows

$$ \frac{\partial G}{{\partial \hat{t}}} = \frac{{\partial^{2} \hat{Q}_{t} }}{{\partial \hat{x}^{2} }}, \, $$

(16)

where

$$ G = \frac{{\partial \hat{Q}_{t} }}{{\partial \hat{t}}} + \hat{Q}_{t} \left| {\hat{Q}_{t} } \right| $$

(16a)

We now define $G(\hat{x},\hat{t})$, appearing in (16a) and together with (15a) and (15b) we obtain

$$ G = \hat{t}^{ - 2} g(\xi ) $$

(17)

_where

$$ g(\xi ) = - f - f^{^{\prime}} \xi - f^{2} $$

(17a)

(i.e., $f^{\prime} \equiv \frac{{{\text{d}}f}}{{{\text{d}}\xi }}$).

(e.g., the sign of the absolute value, appearing in Eq. (16a), was deleted). Introducing (17) into (16) together with (15b) we obtain

$$ \left( {f^{\prime} + g\xi } \right)^{\prime} = - g $$

(18)

We express Eq. (18) as follows

$$ w = f^{\prime} + g\xi $$

(19a)

and

$$ w^{\prime } = - g $$

(19b)

Multiplying both sides of Eq. (19b) with $\xi$ and combining it with Eq. (19a), we obtain

$$ \left( {w\xi } \right)^{\prime } = f^{\prime } $$

(20)

which automatically gives

$$ \left( {w\xi - f} \right)^{\prime } = 0 $$

(20a)

Integrating (20a), we obtain

$$ w\xi - f = \lambda $$

(21)

where $\lambda$ is a constant of integration. Introducing (19a) into (21) and using (17a) we obtain

$$ \xi \left[ {f^{\prime } + \xi \left( { - f - f^{\prime } \xi - f^{2} } \right)} \right] - f = \lambda $$

(21a)

After simple arithmetic, we obtain from (21a) the following expression

$$ f^{\prime} = \frac{\xi }{{1 - \xi^{2} }}f^{2} + \frac{{1 + \xi^{2} }}{{\xi \left( {1 - \xi^{2} } \right)}}f + \frac{\lambda }{{\xi (1 - \xi^{2} )}} $$

(22)

where

$$ f(0) = - \lambda $$

(22a)

4 The analytical solution for $f{(}\xi {) }$

In order to solve (22), we apply the Riccati transformation (Polyanin and Zaitsev 2003)

$$ f = - \frac{{1 - \xi^{2} }}{\xi }\frac{1}{u}\frac{{{\text{d}}u}}{{{\text{d}}\xi }} $$

(23)

where $u(\xi )$ is a yet unknown function of $\xi$. Substituting (23) into (22) we obtain the following linear ODE

$$ \frac{{{\text{d}}^{{2}} u}}{{{\text{d}}^{{2}} \xi }} - 2\frac{{1 + \xi^{2} }}{{\xi (1 - \xi^{2} )}}\frac{{{\text{d}}u}}{{{\text{d}}\xi }} + \frac{\lambda }{{\left( {1 - \xi^{2} } \right)^{2} }}u = 0 $$

(24)

The solutions for $f(\xi )$ within the range of $0 \le \xi \le 1$ is given in Appendix A (see equations A18, A18a)) and the solutions for $f(\xi )$ within the range $1 \le \xi \le \infty$ is given in Appendix B (see equation (B9)). The united solution for $f(\xi )$, in the whole range $0 < \xi < \infty$, can be obtained by equating the term $\frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}$, appearing in (A18a) with the constant $K$ appearing in (B9). In addition to this, the term $(\xi - 1)$ appearing in (B9) should be written in its absolute value. As a result the solution for $f(\xi )$ in the domain $0 < \xi < \infty$ is given by

$$ f(\xi ) = \frac{ - \lambda }{{1 + \xi \sqrt {1 - \lambda } \coth \left( {\frac{{\sqrt {1 - \lambda } }}{2}\ln \left[ {\frac{{(1 + \xi_{d} )\left| {\xi - 1} \right|}}{{(1 - \xi_{d} )(\xi + 1)}}} \right]} \right)}},\quad 0 < \xi < \infty $$

(25)

where $\xi_{d}$ is the downstream moving boundary parameter (see Appendix A) and.

$f(\xi ) \to 0$ as $\xi \to \infty$ that assures the boundary condition (14).

The solution $f(1)$ can be obtained from (25) as follows

$$ f(1) = \frac{ - \lambda }{{1 - \sqrt {1 - \lambda } }} $$

(26)

which is always negative for $\lambda < 0$. On the other hand, the solution $f(0)$ is always positive for $\lambda < 0$. This indicates the existence of the first pole $f(\xi_{d} ) = 0$ that is lying in the range $0 < \xi_{d} < 1$. The second pole $\xi = \xi_{u}$ (i.e., the upstream boundary parameter at which $f(\xi_{u} ) = 0$, is lying in the range $1 < \xi_{u} < \infty$) and it can be obtained by equalizing the argument in the “ln” term (i.e., appearing in (25)) to 1 as follows

$$ \frac{{(1 + \xi_{d} )(\xi_{u} - 1)}}{{(1 - \xi_{d} )(\xi_{u} + 1)}} = 1 $$

(27)

Since $\coth (0) = \pm \infty$, we obtain the position of the second pole $\xi = \xi_{u}$ by solving (27) to obtain

$$ \xi_{u} = \frac{1}{{\xi_{d} }} $$

(27a)

5 Discussion on the conditions of the moving boundaries

We will now define the downstream moving boundaries $\hat{X}{}_{d}(\hat{t})$ and an upstream moving boundary $\hat{X}{}_{u}(\hat{t})$ via the boundary parameters $\xi_{d}$, $\xi_{u}$ and together with (15b) as follows

$$ \hat{X}{}_{d}(\hat{t}) = \xi_{d} \hat{t} $$

(28a)

and

$$ \hat{X}{}_{u}(\hat{t}) = \xi_{u} \hat{t} $$

(28b)

Since $f(\xi_{d} ) = 0$ (see A16) and $f(\xi_{u} ) = 0$ (as was explained in the previous section), we obtain conditions on both moving boundaries of the dimensionless transient discharge as follows

$$ \hat{Q}_{t} {(}\hat{x}{,}\hat{t}{)} = 0\quad {\text{on}}\quad \hat{x} = \hat{X}_{d} (\hat{t}) $$

(29a)

and

$$ \hat{Q}_{t} {(}\hat{x}{,}\hat{t}{)} = 0\quad {\text{on}}\quad \hat{x} = \hat{X}_{u} (\hat{t}) $$

(29b)

It is thus assumed that (29a) and (29b) serves as conditions that represent continuity across the moving fronts and both are part of the obtained solution.

The boundary conditions (29a) and (29b) indicate that the function $\hat{Q}_{t} {(}\hat{x}{,}\hat{t}{) }$ can be divided into three main regions. The first region will be defined in this study as the “near zone”. This region is lying in the range $0 < \hat{x} < \hat{X}_{d} (\hat{t})$, where $\hat{X}_{d} (\hat{t})$ is the downstream moving boundary of the dimensionless transient discharge function $\hat{Q}_{t} {(}\hat{x}{,}\hat{t}{) }$. In this zone, the dimensionless transient discharge function is directed toward the $+ \hat{x}$ direction. The "intermediate backflow zone" is confined between two moving boundaries, namely an upstream front $\hat{X}_{u} (\hat{t})$ and the previously mentioned downstream front, e.g., $\hat{X}_{d} (\hat{t}) < \hat{x} < \hat{X}_{u} (\hat{t})$. The flow in this zone is directed to the $- \hat{x}$ direction (i.e., against the propagation of the upstream front $\hat{X}_{u} (\hat{t})$). The third region is the "far zone" located in the range $\hat{X}_{u} (\hat{t}) < \hat{x} < \infty$. In this zone, the flow is directed toward the $+ \hat{x}$ direction. This situation is schematically described in Fig. 1.

Fig. 1

A schematic description of the boundary conditions imposed on the transient flow discharge fraction $Q_{t} (x,t)$ in a porous layer

6 Determination of $\hat{H}{(}\hat{x}{,}\hat{t}{) }$

In the previous section, a closed-form analytical solution for $f(\xi )$ had been derived (which enabled us to obtain the dimensionless transient discharge function $\hat{Q}_{t} {(}\hat{x}{,}\hat{t}{) }$). Now our goal is directed toward obtaining the dimensionless head function $\hat{H}{(}\hat{x}{,}\hat{t}{) }$ existing in the aquifer.

Introducing (9a)–(9d) together with (11a), (11b) and (11c) into (5), we obtain

$$ \frac{{\partial \hat{H}}}{{\partial \hat{x}}} = - \left( {\frac{{\partial \hat{Q}_{t} }}{{\partial \hat{t}}} + \hat{Q}_{t} \left| {\hat{Q}_{t} } \right| - \left( {\frac{a}{{2bQ_{t\;c} }}} \right)^{2} } \right) $$

(30)

where the integration result is given by

$$ \hat{H} = - \int_{0}^{{\hat{X}(\hat{t})}} {\left( {\frac{{\partial \hat{Q}_{t} }}{{\partial \hat{t}}} + \hat{Q}_{t} \left| {\hat{Q}_{t} } \right| - \left( {\frac{a}{{2bQ_{t\;c} }}} \right)^{2} } \right){\text{d}}\hat{x}} $$

(30a)

Introducing (15a) and (15b) into (30a) we obtain

$$ \hat{H} = - \hat{t}^{ - 1} \int_{0}^{\xi } {\left( { - \left[ {f\xi } \right]^{\prime } + f^{2} } \right){\text{d}}\xi } + \left( {\frac{a}{{2bQ_{t\;c} }}} \right)^{2} \hat{x} $$

(31)

We now represent Eq. (22) as follows

$$ f^{2} = \left[ {\frac{{f(1 - \xi^{2} )}}{\xi } + \frac{\lambda }{\xi }} \right]^{\prime } $$

(32)

Substituting (32) into (31) and integrating the latter, we obtain

$$ \hat{H}(\hat{x},\hat{t}) = \hat{H}_{t} (\hat{x},\hat{t}) + \left( {\frac{a}{{2bQ_{t\;c} }}} \right)^{2} \hat{x} $$

(33)

where

$$ \hat{H}_{t} (\hat{x},\hat{t}) = - \hat{t}^{ - 1} h(\xi ) $$

(33a)

is the transient dimensionless head function and $h(\xi )$ is the head self-similar function obtained after solving (31) as follows

$$ h(\xi ) = - 2f\xi + \frac{f + \lambda }{\xi } + C_{\infty } $$

(33b)

where $C_{\infty }$ is a constant of integration to be determined hereafter.

We assume that the transient dimensionless head $\hat{H}_{t}$ decrease to zero, together with $\hat{Q}_{t}$(see (14)), at an infinite distance, i.e.,

$$ h(\xi ) \to 0\quad {\text{as}}\quad \xi \to \infty $$

(34)

In accordance with the above we obtain from (25), (33b) and (34) the following

$$ \frac{2\lambda }{{\sqrt {1 - \lambda } \coth \left( {\frac{{\sqrt {1 - \lambda } }}{2}\ln \frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}} \right)}} + C_{\infty } \to 0\quad {\text{as}}\quad \xi \to \infty $$

(35)

and hence $C_{\infty }$ is given by

$$ C_{\infty } \approx \frac{ - 2\lambda }{{\sqrt {1 - \lambda } \coth \left( {\frac{{\sqrt {1 - \lambda } }}{2}\ln \frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}} \right)}} $$

(35a)

Finally, we obtain the exact expression for $h(\xi )$ from (33b) and (35a) as follows

$$ h(\xi ) = - 2f\xi + \frac{f + \lambda }{\xi } - \frac{2\lambda }{{\sqrt {1 - \lambda } \coth \left( {\frac{{\sqrt {1 - \lambda } }}{2}\ln \frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}} \right)}} $$

(36)

In order to obtain the value of $h(\xi )$ as $\xi \to 0$, we will investigate the behavior of the transient discharge profile in the aquifer, after a sufficiently long time.

(i.e., $\xi \to 0$, $\hat{x} \,$ finite). Toward this goal, we will calculate an approximate expression for $f(\xi )$, by using (25), in the case where $\xi \to 0$ as follows

$$ f \approx - \lambda + \lambda \sqrt {1 - \lambda } {\text{ctgh}}\left( {\frac{{\sqrt {1 - \lambda } }}{2}\ln \frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}} \right)\xi , \, \xi \to 0 $$

(37)

Introducing (37) into (36), we obtain an expression for $h(\xi )$ as $\xi \to 0$ as follows

$$ h(0) = \frac{{\lambda \left[ {(1 - \lambda )\coth^{2} \left( {\frac{{\sqrt {1 - \lambda } }}{2}\ln \frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}} \right) - 2} \right]}}{{\sqrt {1 - \lambda } \coth \left( {\frac{{\sqrt {1 - \lambda } }}{2}\ln \frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}} \right)}}, \, $$

(38)

In order to calculate the value of $\hat{H}_{0}$, as appears in (13b), we obtain from (33) and (33a)

$$ \hat{H}_{0} = - h_{0} $$

(39)

where

$$ h_{0} \equiv h(0) $$

(39a)

Introducing of (13a), (13b), (22a) and (33a) into (38), we obtain the dependence $\hat{H}_{0} (\hat{Q}_{t0} )$, characterizing the parameters of the inlet face

$$ \hat{H}_{0} = \frac{{ - \hat{Q}_{t0} \left[ {(1 + \hat{Q}_{t0} )\coth^{2} \left( {\frac{{\sqrt {1 + \hat{Q}_{t0} } }}{2}\ln \frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}} \right) - 2} \right]}}{{\sqrt {1 + \hat{Q}_{t0} } \coth \left( {\frac{{\sqrt {1 + \hat{Q}_{t0} } }}{2}\ln \frac{{1 + \xi_{d} }}{{1 - \xi_{d} }}} \right)}}, \, $$

(39b)

7 Presentation of the preliminary results

Figures 2a, b and  3a, b exhibit respectively the effects of the main parameters on the distribution of the discharge self-similar profiles $f(\xi )$ and the head self-similar profiles $- h(\xi )$ in the aquifer, resulting from the time-decreasing head at the inlet face at $\hat{x} = 0$, for three discharge parameters $\lambda$ (e.g., $\lambda = - 2, \, - 4$ and $- 6$).

Fig. 2

a Distribution of the discharge self-similar profiles for three discharge parameters $\lambda$ (with $\xi_{d} = 2/5,\xi_{u} = 5/2$). b Distribution of the head self-similar profiles for three discharge parameters $\lambda$ (with $\xi_{d} = 2/5,\xi_{u} = 5/2$)

Fig. 3

a Distribution of the discharge self-similar profiles for three discharge parameters $\lambda$ (with $\xi_{d} = 9/10,\xi_{u} = 10/9$). b Distribution of the head self-similar profiles for three discharge parameters $\lambda$ (with $\xi_{d} = 9/10,\xi_{u} = 10/9$)

In Figs. 2a and b, we used a small value of the downstream boundary arameter $\xi_{d}$ together with a relatively high value of the upstream boundary parameter $\xi_{u}$ (e.g.,$\xi_{d} = \frac{2}{5}$, $\xi_{u} = \frac{5}{2}$, see (27a)). On the contrary, in Fig. 3a and b, we used a high value of the downstream boundary parameter $\xi_{d}$ together with a relatively small value of the upstream boundary parameter $\xi_{u}$ (e.g.,$\xi_{d} = \frac{9}{10}$, $\xi_{u} = \frac{10}{9}$). Comparing both pairs of figures, it can be observed that the self-similar profiles in Fig. 2a and b possess more moderate shapes compared with the figures shown in Fig. 3a and b.This result means that as the values of $\xi_{d}$ and $\xi_{u}$ are close to each other, the intermediate backflow zone becomes very small and hence, the near and the far zones tend to be almost one unit (e.g., with a positive flow direction).

Figures 4 and 5 exhibit the discharge distributions for 3 time steps obtained with the discharge parameter $\lambda = - 2$ and two values of the $\xi_{d}$. Increasing $\xi_{d}$ from 2/5 to 9/10 leads to a less uniformly distributed discharge, characterized by a smoother front and with a smaller intermediate backflow zone. Accordingly, Fig. 4 depicts the situation where the propagation of the upstream front is much larger compared with the propagation of the downstream front. On the contrary, Fig. 5 depicts a situation where the difference in the speed propagation of both the upstream and the downstream fronts is relatively small. Comparing the discharge profiles in Fig. 4 (which was obtained with a relatively large difference between $\xi_{d}$ and $\xi_{u}$) with Fig. 5 (which was obtained with a relatively small difference between $\xi_{d}$ and $\xi_{u}$) shows that the intermediate backflow zone in Fig. 4 is larger compared with this zone shown in Fig. 5, as was expected.

Fig. 4

Distribution of the discharge profiles for three time intervals (with $\lambda = - 2$ $\xi_{d} = 2/5,\xi_{u} = 5/2$)

Fig. 5

Distribution of the discharge profiles for three time intervals (with $\lambda = - 2$ $\xi_{d} = 9/10,\xi_{u} = 10/9$)

8 The calibration procedure

We will now show how our model reduces to the well-known steady state Darcy–Forchheimer equation. Toward this end Eq. (30) can be rewritten, after using (15a) and (15b), as follows

$$ \frac{{\partial \hat{H}}}{{\partial \hat{x}}} = - \left( {\frac{{1 - 2\xi^{2} }}{{1 - \xi^{2} }}\hat{Q}_{t}^{2} - \frac{2}{{1 - \xi^{2} }}\hat{t}^{ - 1} \hat{Q}_{t} - \frac{\lambda }{{1 - \xi^{2} }}\hat{t}^{ - 2} } \right) + \left( {\frac{a}{{2bQ_{t\;c} }}} \right)^{2} $$

(40)

Introducing (9a)–(9d), together with (11a), (11b), and (11c) we obtain $\frac{\partial H}{{\partial x}}$ in its dimension form as follows

$$ \frac{\partial H}{{\partial x}} = - \left( {\frac{{1 - 2\xi^{2} }}{{1 - \xi^{2} }}bQ_{t}^{2} - \frac{2}{{1 - \xi^{2} }}ct^{ - 1} Q_{t} - \frac{\lambda }{{1 - \xi^{2} }}\hat{t}^{ - 2} } \right) + \frac{{a^{2} }}{4b} $$

(41)

Under the assumption that as $\, t \to \infty$ (i.e., $\, \xi \to 0$), we may neglect terms that contain $\, \hat{t}^{ - 2}$ compared with terms that contain $\, \hat{t}^{ - 1}$ in Eq. (41) as follows

$$ \frac{\partial H}{{\partial x}} \approx - \left( {bQ_{t}^{2} - 2ct^{ - 1} Q_{t} } \right) + \frac{{a^{2} }}{4b} \qquad t \to \infty. $$

(42)

Neglecting terms that contain $\, \hat{t}^{ - 1}$ and using (3) and (3a), we obtain $\frac{\partial H}{{\partial x}}$ in its standard form

$$ \frac{\partial H}{{\partial x}} \to - bQ^{2} - aQ \qquad t \to \infty $$

(43)

This result can be directly obtained from (2) under the assumption that the term $\frac{\partial Q}{{\partial t}} \to 0$ for $t \to \infty$.

We will now explain how to calibrate our model by matching the obtained solution for $\hat{H}(\hat{x},\hat{t})$ with field data that enable us to determine the parameters $S$ and $c$, appearing in (1) and (2), which govern the transient behavior of $Q(x,t)$ and $H(x,t)$. Such calibration is necessary in order to predict the temporal distribution of the discharge and head profiles along the aquifer.

We now use (15b), (33), (33a) together with (9a)–(9d), (11), (11a), and (11b) to obtain the following pair of equations

$$ \log t = \log \xi^{ - 1} + \log x\sqrt {Sc} $$

(44a)

$$ \left( {H - \frac{{a^{2} }}{4b}x} \right)t = - h(\xi )H_{c} T $$

(44b)

Equations (44a, 44b) are used to construct type curves (e.g., $- h$ versus $\log \xi^{ - 1}$) as shown in Fig. 6 and Fig. 7 for several values of $\lambda$ and $\xi_{d}$ (i.e., $\xi_{u} = \xi_{d}^{ - 1}$, see (27a)). We will further use the fact that the function $- h(\xi )$ tends to a constant value $- h(0)$(see (38)) at asymptotic long times (e.g., as $\xi^{ - 1} \to \infty$).

Fig. 6

Type curves for three discharge parameters $\lambda$ (with $\xi_{d} = 2/5,\xi_{u} = 5/2$)

Fig. 7

Type curves for three discharge parameters $\lambda$ (with $\xi_{d} = 9/10,\xi_{u} = 10/9$)

Based on the above, we now explain how our model can be calibrated in accordance to the following steps-

• 1. Draw many types of curves $- h(\xi )$ versus $\log \xi^{ - 1}$ as is explained after (44a) and (44b) (For example, see Fig. 6 and Fig. 7).

• 2. Determine the position $x_{0}$ (i.e., with respect to $x = 0$) of a manometer that is used to collect subsequent measurements of heads data $H(x_{0} )$ in the aquifer/porous medium.

• 3. Collect $N$ head measurements $H(x_{0} ,t_{1,2,3 \ldots N} )$ at $N$ time intervals, relatively to the beginning of the experiment.

• 4. For each time step $t_{i}$ (e.g., $i = 1 \ldots N$), calculate the value of $\left( {H(x_{0} ,t_{i} ) - \frac{{a^{2} }}{4b}x_{0} } \right) \times t_{i}$ (see Eq. (44b).¹

• 5. Plot the $N$ results obtained in the previous step as follows: $\left( {H(x_{0} ,t_{i} ) - \frac{{a^{2} }}{4b}x_{0} } \right) \times t_{i}$ versus $\log t$ (note that as $\log t$ becomes large, the values of $\left( {H(x_{0} ,t_{i} ) - \frac{{a^{2} }}{4b}x_{0} } \right) \times t_{i}$ approach a constant value (i.e., note that as $t \to \infty$ the LHS of (44b) approaches a constant value).

• 6. Try to match the figure obtained in step 5 with one of the figures $- h(\xi )$ versus $\log \xi^{ - 1}$ made in step 1. For this purpose it is recommended to upload the measurement results, made in step 5, and to use a traditional visual or automatic curve matching methods.

• 7. Based on the best matching result obtained in step 6, determine the values of $\lambda$, $\xi_{d}$ and $\xi_{u}$.

• 8. Use one matching point $\left. {\xi^{ - 1} } \right|_{{{\text{matching}}}} \, \Leftrightarrow \left. t \right|_{{{\text{matching}}}}$ obtained in step 7 together with the value of $x_{0} \,$ as follows

  • Calculate the value of $\, \frac{1}{{\sqrt {Sc} }}$ by using Eq. (9a)–(9d), (11a), (11b), and (11c) i.e., $\, \frac{1}{{\sqrt {Sc} }} = x_{0} \frac{{\left. {\xi^{ - 1} } \right|_{{{\text{matching}}}} }}{{\left. t \right|_{{{\text{matching}}}} }}$

  • Following Eq. (44b), use the asymptotic value $\left. {\left( {H(x_{0} ,t_{N} ) - \frac{{a^{2} }}{4b}x_{0} } \right) \times t_{N} } \right|_{{{\text{large }}t_{N} }}$ and $h(0)$ from Eq. (38) (e.g., with the use of the obtained values of $\lambda$ and $\xi_{d}$ derived in step 7 to obtain $\, H_{c} T = \frac{{\left. {\left( {H(x_{0} ,t_{N} ) - \frac{{a^{2} }}{4b}x_{0} } \right) \times t_{N} } \right|_{{{\text{large }}t_{N} }} }}{ - h(0)}$.

• 9. Using the results obtained in step 8 and (11a), we will now define two parameters

  $A \equiv H_{c} T = \frac{{c^{3/2} }}{{bS^{1/2} }}$ and $B \equiv \frac{1}{{\left( {Sc} \right)^{1/2} }}$. By making use of both parameters we obtain

  $c = \left( {\frac{A}{B}b} \right)^{1/2}$ and $S = \frac{1}{{A^{1/2} B^{3/2} b^{1/2} }}$.

• 10. Substituting the value of $H_{c} T$ in (44b) we obtain

• (1) $H(x,t) = \left( { - \frac{{c^{3/2} }}{{bS^{1/2} }}\left. {h(\xi )} \right|_{{\lambda ,\xi_{d} }} t^{ - 1} \, + \frac{{a^{2} }}{4b}x} \right){\text{ m}}$,

  Substituting (3a), (11), (11a)-(11c), (15a) and (15b) into (3) we obtain

• (2) $Q(x,t) = \left( {\left. {f(\xi )} \right|_{{\lambda ,\xi_{d} }} t^{ - 1} \frac{c}{b} \, - \frac{a}{2b}} \right){\text{ ms}}^{{ - {1}}}$, where $\xi = \frac{{x\sqrt {Sc} }}{t}$.

9 Summary and conclusions

In this study the combined effects of fluid discharge and head loss had been used to solve the classical equations of transient fluid flow in an aquifer by using the Darcy–Forchheimer law. The symmetry properties of these equations were used to develop self-similar solutions to the above mentioned equations according to which, both coordinates of time and place are transformed into one coordinate. The governing nonlinear continuity and the Darcy–Forchheimer equations had been coupled to form a single equation and solved by using a self-similar technique.

According to our study, the flow discharge in the aquifer may be divided into two main components. One component is the steady part and the other one is the transient part of the flow. The obtained analytical solutions show that the transient part of the flow in the aquifer is characterized by three zones, namely, the "near zone" located near the inlet face of the aquifer and is characterized by positive flow, the "far zone" in the aquifer lying at an infinite distance where the flow is positive and the "intermediate backflow zone", which lies among the above-mentioned zones and is characterized by a reverse flow.

The obtained analytical solutions had been used to construct several types of curves, which can be used to match serial measurements of head data with the obtained model. As such, the implementation of the model, for finding the governed parameters and to predict the actual transient head profile along the aquifer, has been explained.

In general, self-similar solutions are an effective tool for describing transient phenomena in various flow fields, where the problem lacks a characteristic length or time scale. The development of self-similar solutions simplifies the physical problem and changes the partial differential equations to the level of ordinary differential equations. However, the main disadvantage of these solutions is that they are limited to special language conditions. It is not possible to place language terms in finite sections but only in infinite and semi-infinite sections or to place them on moving boundaries, as was done in this study.

The solution developed in this study can be extended to a transient case, with radial symmetry. A similarity solution for a radial case can be helpful for determining aquifer parameters following pumping tests.

Appendices

Appendix A

A new variable $z(\xi )$ is defined now as follows

$$ z = \xi^{2} $$

(A1)

Substituting (A1) into (24) then gives the following equation

$$ z(1 - z)^{2} \frac{{{\text{d}}^{{2}} u}}{{{\text{d}}z^{2} }} + \frac{1}{2}(1 - z)( - 1 - 3z)\frac{{{\text{d}}u}}{{{\text{d}}z}} + \frac{\lambda }{4}u = 0 $$

(A2)

We now define a new function $w(z)$ as follows

$$ u = w(1 - z)^{\kappa } $$

(A3)

where $\kappa (\lambda )$ is given by

$$ \kappa = - \frac{1}{2} \pm \frac{{\sqrt {1 - \lambda } }}{2} $$

(A4)

Introducing (A3), (A4) into (A2) we obtain the following hypergeometric equation as follows

$$ z(1 - z)\frac{{{\text{d}}^{{2}} w}}{{{\text{d}}z^{2} }} + \left( {z( - 2\kappa - \frac{3}{2}) - \frac{1}{2}} \right)\frac{{{\text{d}}w}}{{{\text{d}}z}} - \left( {\kappa^{2} + \frac{\kappa }{2}} \right)w = 0 $$

(A5)

which possesses the following solution

$$ w(z) = C_{1} \left( {2CF_{1} (z) + z^{3/2} F_{2} (z)} \right) $$

(A6)

where the functions

$$ F_{1} \left( z \right) = F\left( {\kappa ,\kappa + \frac{1}{2}, - \frac{1}{2};z} \right) $$

(A6a)

and

$$ F_{2} \left( z \right) = F\left( {\kappa + \frac{3}{2},\kappa + 2,\frac{5}{2};z} \right) $$

(A6b)

are expressed via hypergeometric functions (Polyanin and Zaitsev, 2003) subjected to the limitation

$$ \left| z \right| < 1 $$

(A6c)

and therefore this solution is valid in the range of

$$ - 1 < \xi < 1 $$

(A6d)

where $C$ and $C_{1}$ are constants to be determined below. Using the website https://www.wolframalpha.com/, we obtain a simple form to the above hypergeometric functions

$$ F_{1} \left( z \right) = \frac{1}{2}\left( {S_{1} (z) - S_{2} (z)} \right) $$

(A7a)

$$ F_{2} \left( z \right) = \frac{A}{{z^{3/2} }}\left( {S_{1} (z) + S_{2} (z)} \right) $$

(A7b)

where

$$ S_{1} \left( z \right) = \left( {(2\kappa + 1)\sqrt z + 1} \right)\left( {\sqrt z + 1} \right)^{ - 2\kappa - 1} $$

(A8a)

$$ S_{2} \left( z \right) = \left( {(2\kappa + 1)\sqrt z - 1} \right)\left( {1 - \sqrt z } \right)^{ - 2\kappa - 1} $$

(A8b)

and the constant $A$ is given by

$$ A = \frac{3}{8\kappa (\kappa + 1)(2\kappa + 1)} $$

(A8c)

Introducing (A7a), (A7b), (A8a) and (A8b) into (A6), (A6a) and (A6b), we obtain

$$ w(z) = C_{1} \left( {CS_{1} (z) - CS_{2} (z) + AS_{1} (z) + AS_{2} (z)} \right) $$

(A9)

which can be rewritten in a more simple form as follows

$$ w(z) = C_{1} \left( {(C + A)S_{1} (z) + (A - C)S_{2} (z)} \right) $$

(A9a)

Using the notation $w^{\prime}(z)$ for $\frac{{{\text{d}}w(z)}}{{{\text{d}}z}}$, the derivative of (A9a) with respect to $z$ gives

$$ w^{\prime}(z) = C_{1} \left( {(C + A)S^{\prime}_{1} (z) + (A - C)S^{\prime}_{2} (z)} \right) $$

(A10)

where

$$ S^{\prime}_{1} \left( z \right) = - \kappa (2\kappa + 1)\left( {\sqrt z + 1} \right)^{ - 2\kappa - 2} $$

(A10a)

and

$$ S^{\prime}_{2} \left( z \right) = \kappa (2\kappa + 1)\left( {1 - \sqrt z } \right)^{ - 2\kappa - 2} $$

(A10b)

Introducing (A1), (A3) and (A6) into (23), we obtain

$$ f(z) = - 2(1 - z)\left( {\frac{1}{w}\frac{{{\text{d}}w}}{{{\text{d}}z}} - \frac{\kappa }{1 - z}} \right) $$

(A11)

Substituting (A9a), (A10), (A10a) and (A10b) into (A11), we obtain

$$ f(z) = \frac{{ - 4\kappa (\kappa + 1)\left( {1 - \tilde{C}E(z)} \right)}}{{\tilde{C}E(z)\left( {(2\kappa + 1)\sqrt z + 1} \right) + (2\kappa + 1)\sqrt z - 1}} $$

(A12)

where

$$ \tilde{C} = \frac{A + C}{{A - C}} $$

(A12a)

and

$$ E(z) = \left( {\frac{1 + \sqrt z }{{1 - \sqrt z }}} \right)^{ - 2\kappa - 1} $$

(A12b)

Substituting (A1) into (A12), using (A4), we obtain for $\lambda < 1$

$$ f(\xi ) = \frac{{\lambda \left( {1 - \tilde{C}E(\xi )} \right)}}{{\tilde{C}E(\xi )\left( {\sqrt {1 - \lambda } \xi + 1} \right) + \sqrt {1 - \lambda } \xi - 1}} $$

(A13)

where

$$ E(\xi ) = \left( {\frac{1 + \xi }{{1 - \xi }}} \right)^{{ - \sqrt {1 - \lambda } }} $$

(A14)

subjected to the limitation that appears in (A6d).

Introducing $\xi = 0$ into (A13) and (A14) we obtain $\hat{Q}_{t0}$ appearing in (13a)

$$ f(\xi = 0) = \hat{Q}_{t\;0} = - \lambda $$

(A15)

where the integration constant $\lambda$ can be defined as the transient discharge parameter.

We will now equalize A(13) to zero

$$ f(\xi_{d} ) = 0 $$

(A16)

to obtain the constant $\tilde{C}$ as follows

$$ \tilde{C} = \left( {\frac{{1 - \xi_{d} }}{{1 + \xi_{d} }}} \right)^{{ - \sqrt {1 - \lambda } }} {\text{ for }}\lambda < 1. \, $$

(A17)

where $\xi_{d}$ is the downstream moving boundary parameter, as is explained in Sect. 5. Introducing (A14) and (A17) into (A13), we obtain (after several mathematical manipulations) that

$$ f(\xi ) = \frac{ - \lambda }{{1 + \sqrt {1 - \lambda } \xi \coth \frac{\theta }{2}}} $$

(A18)

where

$$ \theta = \sqrt {1 - \lambda } \ln \left[ {\frac{{(1 - \xi )(1 + \xi_{d} )}}{{(1 + \xi )(1 - \xi_{d} )}}} \right] $$

(A18a)

Appendix B

A new variable $z(\xi )$ is defined now as follows

$$ z = \frac{1}{{1 - \xi^{2} }} $$

(B1)

We will confine ourselves to the following case

$$ \left| z \right| < 1 $$

(B2)

Introducing (B1) into (B2), we obtain the following limitation for $\xi$

$$ \xi > 1 $$

(B2a)

Substituting (B1) into (24) then gives the following hypergeometric equation

(Polyanin and Zaitsev 2003)

$$ z(1 - z)\frac{{{\text{d}}^{{2}} u}}{{{\text{d}}z^{2} }} + \frac{1}{2}\frac{{{\text{d}}u}}{{{\text{d}}z}} - \frac{\lambda }{4}u = 0 $$

(B3)

Under the limitation defined in (B2), equation (B3) possesses the following solution

$$ u(z) = C_{1} \left( {CF_{1} (z) + z^{1/2} F_{2} (z)} \right) $$

(B4)

where

$$ F_{1} \left( z \right) = F\left( { - \frac{1}{2} + \frac{{\sqrt {1 - \lambda } }}{2}, - \frac{1}{2} - \frac{{\sqrt {1 - \lambda } }}{2},\frac{1}{2};z} \right) $$

(B4a)

$$ F_{2} \left( z \right) = F\left( {\frac{{\sqrt {1 - \lambda } }}{2}, - \frac{{\sqrt {1 - \lambda } }}{2},\frac{3}{2};z} \right) $$

(B4b)

are expressed via hypergeometric functions (Polyanin and Zaitsev 2003); $C$ and $C_{1}$ are constants to be determined below. Using the properties of the hypergeometric series, we obtain from (B4) and (B4a) and (B4b) the expression for $\frac{{{\text{d}}u(z)}}{{{\text{d}}z}}$

$$ \frac{{{\text{d}}u}}{{{\text{d}}z}} = C_{1} \left( {C\frac{\lambda }{{2}}F_{3} (z) + \frac{1}{2\sqrt z }F_{2} (z) + \frac{(\lambda - 1)\sqrt z }{6}F_{4} (z)} \right) $$

(B5)

where the hypergeometric functions $F_{3} (z)$ and $F_{4} (z)$ are given by

$$ F_{3} \left( z \right) = F\left( {\frac{1}{2} + \frac{{\sqrt {1 - \lambda } }}{2},\frac{1}{2} - \frac{{\sqrt {1 - \lambda } }}{2},\frac{3}{2};z} \right) $$

(B5a)

$$ F_{4} \left( z \right) = F\left( {1 + \frac{{\sqrt {1 - \lambda } }}{2},1 - \frac{{\sqrt {1 - \lambda } }}{2},\frac{5}{2};z} \right) $$

(B5b)

By using a computer algebra system such as in www.wolframalpha.com., we obtain simple forms for the above hypergeometric functions

$$ F_{1} \left( z \right) = \sqrt {1 - z} \cos \theta + \frac{1}{{\sqrt {1 - \lambda } }}\sqrt z \sin \theta $$

(B6a)

$$ F_{2} \left( z \right) = \frac{1}{\lambda }\left( {\cos \theta - \frac{{\sqrt {1 - \lambda } \sqrt {1 - z} }}{\sqrt z }\sin \theta } \right) $$

(B6b)

$$ F_{3} \left( z \right) = \frac{\sin \theta }{{\sqrt {1 - \lambda } \sqrt z }} $$

(B6c)

and

$$ F_{4} \left( z \right) = \frac{3}{{\lambda z^{3/2} }}\left( { - \frac{{\sqrt {1 - z} }}{{\sqrt {1 - \lambda } }}\sin \theta + \sqrt z \cos \theta } \right) $$

(B6d)

where

$$ \theta = \sqrt {1 - \lambda } \sin^{ - 1} \sqrt z $$

(B6e)

Introducing (B1) into (23) we obtain

$$ f(z) = - 2z\frac{1}{u}\frac{{{\text{d}}u}}{{{\text{d}}z}} $$

(B7)

Substituting (B4) and (B5) together with (B6a)-(B6e) into (B7), we obtain after several mathematical manipulations

$$ f(z) = \frac{ - \lambda }{{1 - \sqrt {1 - \lambda } \sqrt {\frac{1 - z}{z}} \tan (\theta - \alpha )}} $$

(B8)

where $\alpha$ is a constant related to the constant $C$(e.g., the detailed relationship $C(\alpha )$ is unimportant).

Introducing of (B1) into (B6e), we obtain and further use the following mathematical equalities (Polyanin and Zaitsev 2003)

$$ \sinh^{ - 1} \sqrt {\frac{1}{{\xi^{2} - 1}}} = \frac{1}{2}\ln \frac{\xi + 1}{{\xi - 1}} $$

(B8a)

and

$$ \sqrt {\frac{1 - z}{z}} = i\xi $$

(B8b)

Introducing (B8a) and (B8b) into Eq. (B8), we obtain with basic mathematics, the final solution to $f(\xi )$ in the domain $1 < \xi < \infty$

$$ f(\xi ) = \frac{ - \lambda }{{1 + \xi \sqrt {1 - \lambda } \coth \left( {\frac{{\sqrt {1 - \lambda } }}{2}\log \left[ {K\frac{\xi - 1}{{\xi + 1}}} \right]} \right)}} $$

(B9)

where $K$ is a constant related to the constant $C$ (e.g., also here, the detailed relationship $K(C)$ is unimportant).