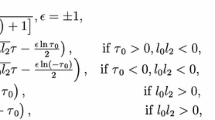Abstract
The flow of liquid relative to the bubbles is called drainage. This paper presents a study of the numerical solution of a non-linear foam drainage equation with time-fractional derivative. We use the two-scale approach which is formulated by combining the fractional complex transform and the homotopy perturbation method (HPM). With the aid of the fractional complex transform, first, we transform the problem into its differential partner and then HPM is applied to obtain the He’s polynomials which are highly and powerful support for non-linear problems. Further, we put forward the theory of the two-scale approach which reveals the sketch between fractional complex transform and the solution of non-linear foam drainage equation. The significant results illustrate that this approach does not require any assumption while it reduces the heavy calculation without any restrictive variable. This approach also sheds a bright light on practical applications of fractal calculus.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Underground fluid flow in fractured and porous media exhibits a variety of hydromechanical phenomena, which have been intriguing the research community for several decades (Schmidt and Steeb 2019). Foam drainage equation is observed one of the most important partial differential equation which in everyday of activities, both natural and industrial. The study of foam drainage equation is a simple model which leads to the flow of liquid through channels and nodes between the bubbles. Consider the non-linear foam drainage equation with time-fractional derivative such as
with initial condition
\(\Omega\) is the cross-section of a channel formed where three films meet which usually indicated as Plateau border, \(x\) denotes the scaled position and \(t\) be the time respectively. \(\alpha\) is fractal dimension and \(\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}\) is He’s fractional derivative (He 2018, 2020a, b; Ain et al. 2020; Shen and He 2020).
Recent research in foams and emulsions has focused on three topics often treated individually but are, in fact, interdependent: drainage, coarsening, and rheology; see Fig. 1. For \(\alpha = 1\), Eq. (1) can be reduced to classical foam drainage equation which has wide applications in particular care of commodities such as creams, oil, lotions, scrubbing and clothes cleaning (Stone et al. 2002), chemical industries, mineral processing, and structural material sciences (Hilgenfeldt et al. 2001), aluminum metals (Schultz et al. 2000), thin porous layer (Koursari et al. 2019). During the manufacturing of foam, the substance is in the liquid state, and fluid can change round while the bubble arrangement remains relatively unchanged. Alam (2015) applied \(G^{\prime}/G\)-expansion method to obtain the exact solution of the foam drainage equation. Parand and Delkhosh (2018) used the collocation method to find the semi-analytical solution of the nonlinear foam drainage equation. Islam and Akbar (2018) used \(G^{\prime}/G\)- expansion method with the assistance of the fractional complex transformation to find the wave solution of the space–time fractional foam drainage equation. Various approaches have been established to identify the approximate and analytical solution of foam drainage equation such Adomian decomposition method (Helal and Mehanna 2007), reduced differential transform method (Gubes et al. 2015), homotopy analysis method (Singh et al. 2016), and Haar wavelets method (Arbabi et al. 2016). The main focus of the present work is to formulate the strategy being pursued and to obtain the numerical solution of the fractal foam drainage equation. We also aim to confirm that the two-scale method is powerful, efficient, and promising in handling scientific and engineering problems (Elias-Zuniga et al. 2021a, b, c, d; He 2020c; Wang 2021; Wang et al. 2019).
Schematic illustration of the interdependence of drainage, coarsening, and rheology of foams (Hilgenfeldt et al. 2001)
2 Basic idea of the homotopy perturbation method
To illustrate the basic concept of the homotopy perturbation method, consider the following non-linear functional equation (Li and Nadeem 2019; Nadeem and Li 2019),
with boundary conditions
where \(A\) is a general functional operator, \(B\) is a boundary operator, \(f(r)\) is a known analytic function, and \(\Gamma\) is the boundary of the domain \(\Omega\). The operator \(A\) can generally be divided into two operators, \(L\) and \(N\), where \(L\) is a linear and \(N\) being a nonlinear operator. Therefore, Eq. (3) can be written as follows
Using the homotopy technique, we construct a homotopy \(v(r,p):\Omega \times [0,1] \to {\mathbb{R}}\) that satisfies
or
where \(p \in [0,1]\), is called homotopy parameter, and \(u_{0}\) is an initial approximation for the solution of Eq. (3), which satisfies the boundary conditions. According to HPM, we can use \(p\) as a small parameter and assume that the solution of Eq. (7) can be written as a power series in \(p\)
Considering \(p = 1\), the approximate solution of Eq. (3) will be obtained as follows
Additionally, some recent applications of HPM can be viewed in (He et al. 2020a, b; He and Dib 2020a, b; Skrzypacz et al. 2020; Anjum and He 2020; He and Jin 2020).
3 Fractional complex transform
During the modeling of a problem, the dimension and scale are extremely valuable things since the various scales and dimensions will lead to remarkable results and properties for the same configuration. A fractional complex transform is a scientific approach that converts a fractional differential equation into a fractal space in a continuous space and is defined as (He et al. 2012; Li and He 2010; Wang and Yao 2020)
where \(\Delta S\) is the smaller scale and \(\Delta t\) is the larger scale. On a smaller scale, the time-fractional foam drainage equation behaves discontinuously, especially at the peak of the solitary wave. On the other hand, the larger scale predicts a smooth solitary wave. The transformation is given in Eq. (10) is an approximate one to convert a fractal space on a small scale to a smooth space with a large scale. To under this, consider an example of a tree that stops growing at night, so when we use a scale of 24 h, it grows continuously, while when we measure it in 12 h, it becomes discontinuous. So, Eq. (10) is also called the two-scale transform (Ain and He 2019; He and Ji 2019; He and Ain 2020), which was geometrically studied using fractal theory. The results of any particular problem depend on the scale. For example, on an observable scale, the liquid is steady; accordingly, Newton’s laws can be executed, otherwise invalid in case of molecular scale. For example, on an observable scale, Newton’s law is effective only if the liquid is steady, otherwise, it is illegitimate. In other words, if the flow is independent of time, then Newton's law is valid while if the flow is dependent on time, then Newtons' law becomes invalid. So, the two-scale transform is to convert a fractal space on a small scale to an approximate smooth space on a larger scale. Some recent work on fractal calculus can be studied in Wang (2020a, b), Wang and Wang (2020a, b, 2021) andd Wang et al. (2021).
4 Analysis of the method
In this section, we obtain an analytical solution of Eq. (1). We first use the transformation
Thus, Eq. (1) becomes as
which may also be written as
with initial condition
where \(c\) is the velocity of the wavefront (Alquran 2014). The initial condition (13) is taken in such a way that it satisfies the problem to find a particular solution. Initially, we will apply the fractional complex transform to write it in its partner differential equation such as
So, Eq. (12) can be written as
The initial guess will be taken as \(u_{0} = - \sqrt c \tanh (\sqrt c x)\). The HPM together with He’s polynomials will be applied on Eq. (15) as follows
Proceeding in the same way, we can obtain the high-order approximations.
the rest of the components can also be found in the same manner. Thus, the approximate solution according to HPM has the following form
Thus, by using Eq. (14), we get
This series leads to the exact solution for Eq. (1) when \(\alpha = 1.\)
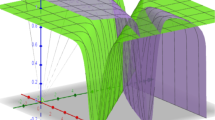
Using the Mathematica package 11.0.1, we illustrate the graphical representations and physical behaviors of the fractal foam drainage equation. For case \(\alpha = 1\), we compare the obtained results of the approximate solution of Eq. (1) and the exact solution of Eq. (16), which is depicted in Figs. 2 and 3. From Fig. 2, it is obvious that when α = 1, the solution is nearly identical to the exact solution. The solution graphs have declared that the obtained results are almost identical and confirm worthy contact with the exact solution, which aids us to understand the nature of the fractal foam drainage equation. Moreover, Fig. 4 shows the error distribution of the approximate solution and the exact solution which helps us to capture the behavior of the obtained solution. Some recent developments in fractal vibration models can be studied from somewhere else (Chun-Hui et al. 2021a, b; He et al. 2021a, He et al. 2021b).
5 Conclusion
In this paper, we suggested a hybrid scheme such as fractional complex transform is coupled with HPM to obtain the analytic solution of the nonlinear time-fractional foam drainage equation, which is a simple model of the flow of liquid through channels and nodes between the bubbles. The fractional complex transform performed a simple and excellent approach to convert a fractional differential equation into its differential partner which is suitable for the development of the two-scale method. This method is applied directly without any discretization, linearization, and small parameter assumptions, which in actual ruins the physical nature of the problems. The results show that the proposed method is very efficient and powerful. The graphical representation shows that the solution procedure is simple and might be found in wide applications of engineering. The procedure reveals that the semi-inverse method is highly efficient and powerful, and can be generalized to other nonlinear evolution equations with fractal derivatives in future applications.
References
Ain, Q.T., He, J.H.: On two-scale dimension and its applications. Therm. Sci. 23(3 Part B), 1707–1712 (2019)
Ain, Q.T., He, J.H., Anjum, N., Ali, M.: The fractional complex transform: a novel approach to the time-fractional Schrödinger equation. Fractals 28(07), 2050141 (2020)
Alam, M.N.: Exact solutions to the foam drainage equation by using the new generalized (G’/G)- expansion method. Results Phys. 5, 168–177 (2015)
Alquran, M.: Analytical solutions of fractional foam drainage equation by residual power series method. Math. Sci. 8(4), 153–160 (2014)
Anjum, N., He, J.H.: Homotopy perturbation method for N/MEMS oscillators. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6583
Arbabi, S., Nazari, A., Darvishi, M.T.: A semi-analytical solution of foam drainage equation by Haar wavelets method. Optik 127(13), 5443–5447 (2016)
Chun-Hui, H., Chao, L., He, J.H., Sedighi, H.M., Shokri, A., Gepreel, K.A.: A fractal model for the internal temperature response of a porous concrete. Appl. Comput. Math. 20(2), 1871–1875 (2021a)
Chun-Hui, H., Chao, L., He, J.H., Gepreel, K.A.: Low frequency property of a fractal vibration model for a concrete beam. Fractals (2021b). https://doi.org/10.1142/S0218348X21501176
Elias-Zuniga, A., Palacios-Pineda, L.M., Jimenez-Cedeno, I.H., Martinez-Romero, O., Olvera Trejo, D.: Equivalent power-form representation of the fractal toda oscillator. Fractals 29(1), 2150034 (2021a)
Elias-Zuniga, A., Palacios-Pineda, L.M., Jimenez-Cedeno, I.H., Martinez-Romero, O., Olvera Trejo, D.: Equivalent power-form transformation for fractal Bratu’s equation. Fractals 29(1), 2150019 (2021b)
Elias-Zuniga, A., Palacios-Pineda, L.M., Jimenez-Cedeno, I.H., Martinez-Romero, O., Olvera Trejo, D.: A fractal model for current generation in porous electrodes. J. Electro Anal. Chem. 880, 114883 (2021c)
Elias-Zuniga, A., Palacios-Pineda, L.M., Jimenez-Cedeno, I.H., Martinez-Romero, O., Olvera Trejo, D.: Analytical solution of the fractal cubic-quintic duffing equation. Fractals (2021d). https://doi.org/10.1142/S0218348X21500808
Gubes, M., Keskin, Y., Oturanc, G.: Numerical solution of time-dependent foam drainage equation (fde). Comput. Methods Differ. Equ. 3(2), 111–122 (2015)
He, J.H.: Fractal calculus and its geometrical explanation. Results Phys. 10, 272–276 (2018)
He, J.-H.: A fractal variational theory for one-dimensional compressible flow in a microgravity space. Fractals 28(2), 2050024 (2020c)
He, J.H.: A short review on analytical methods for a fully fourth-order nonlinear integral boundary value problem with fractal derivatives. Int. J. Numer. Methods Heat Fluid Flow (2020a). https://doi.org/10.1108/HFF-01-2020-0060
He, J.H.: On the fractal variational principle for the telegraph equation. Fractals (2020b). https://doi.org/10.1142/S0218348X21500225
He, J.H., Ain, Q.T.: New promises and future challenges of fractal calculus: from two-scale thermodynamics to fractal variational principle. Therm. Sci. 24(2), 659–681 (2020)
He, J.H., El Dib, Y.O.: The reducing rank method to solve third-order Duffing equation with the homotopy perturbation. Numer. Methods Partial Differ. Equ. (2020a). https://doi.org/10.1002/num.22609
He, J.H., El Dib, Y.O.: Homotopy perturbation method for Fangzhu oscillator. J. Math. Chem. 58(10), 2245–2253 (2020b)
He, J.H., Elagan, S., Li, Z.: Geometrical explanation of the fractional complex transform and derivative chain rule for fractional calculus. Phys. Lett. A 376(4), 257–259 (2012)
He, J.H., Ji, F.Y.: Two-scale mathematics and fractional calculus for thermodynamics. Therm. Sci. 23(4), 2131–2133 (2019)
He, J.H., Ji, F.Y., Sedighi, H.: Difference equation vs differential equation on different scales. Int. J. Numer. Methods Heat Fluid Flow (2020b). https://doi.org/10.1108/HFF-03-2020-0178
He, J.H., Jin, X.: A short review on analytical methods for the capillary oscillator in a nanoscale deformable tube. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6321
He, J.H., Kou, S.J., He, C.H., et al.: Fractal oscillation and its frequency-amplitude property. Fractals (2021). https://doi.org/10.1142/S0218348X2150105X
He, J.H., Skrzypacz, P.S., Zhang, Y., Pang, J.: Approximate periodic solutions to microelectron mechanical system oscillator subject to magnetostatic excitation. Math. Methods Appl. Sci. (2020a). https://doi.org/10.1002/mma.7018
He, J.H., Qie, H., Chun-Hui, N., Saeed, T.: On a strong minimum condition of a fractal variational principle. Appl. Math. Lett. Article number 107199 (2021)
Helal, M., Mehanna, M.S.: The tanh method and Adomian decomposition method for solving the foam drainage equation. Appl. Math. Comput. 190(1), 599–609 (2007)
Hilgenfeldt, S., Koehler, S.A., Stone, H.A.: Dynamics of coarsening foams: accelerated and self-limiting drainage. Phys. Rev. Lett. 86(20), 4704 (2001)
Islam, M.N., Akbar, M.A.: New exact wave solutions to the space-time fractional-coupled Burger’s equations and the space-time fractional foam drainage equation. Cogent Phys. 5(1), 1422957 (2018)
Koursari, N., Arjmandi-Tash, O., Johnson, P., Trybala, A., Starov, V.M.: Foam drainage placed on a thin porous layer. Soft Matter 15(26), 5331–5344 (2019)
Li, Z.B., He, J.H.: Fractional complex transform for fractional differential equations. Math. Comput. Appl. 15(5), 970–973 (2010)
Li, F., Nadeem, M.: He–Laplace method for nonlinear vibration in shallow water waves. J. Low Freq. Noise Vib. Active Control 38(3–4), 1305–1313 (2019)
Nadeem, M., Li, F.: He–Laplace method for nonlinear vibration systems and nonlinear wave equations. J. Low Freq. Noise Vib. Active Control 38(3–4), 1060–1074 (2019)
Parand, K., Delkhosh, M.: An efficient numerical method for solving nonlinear foam drainage equation. Indian J. Phys. 92(2), 231–243 (2018)
Schmidt, P., Steeb, H.: Numerical aspects of hydro-mechanical coupling of fluid-filled fractures using hybrid-dimensional element formulations and non-conformal meshes. GEM Int. J. Geomath. 10(1), 1–36 (2019)
Schultz, O., des Ligneris, A., Haider, O., Starke, P.: Fatigue behavior, strength, and failure of aluminum foam. Adv. Eng. Mater. 2(4), 215–218 (2000)
Shen, Y., He, J.H.: Variational principle for a generalized KdV equation in a fractal space. Fractals 28(4), 2050069–2050276 (2020)
Singh, M., Naseem, M., Kumar, A., Kumar, S.: Homotopy analysis transform algorithm to solve time- fractional foam drainage equation. Nonlinear Eng. 5(3), 161–166 (2016)
Skrzypacz, P., He, J.H., Ellis, G., Kuanyshbay, M.: A simple approximation of periodic solutions to microelectron mechanical system model of oscillating parallel plate capacitor. Math. Methods Appl. Sci. (2020). https://doi.org/10.1002/mma.6898
Stone, H., Koehler, S., Hilgenfeldt, S., Durand, M.: Perspectives on foam drainage and the influence of interfacial rheology. J. Phys.: Condens. Matter 15(1), S283–S290 (2002)
Wang, K.-J.: A new fractional nonlinear singular heat conduction model for the human head considering the effect of febrifuge. Eur. Phys. J. Plus 135, 871 (2020a)
Wang, K.J.: Variational principle and approximate solution for the generalized Burgers-Huxley equation with fractal derivative. Fractals (2020b). https://doi.org/10.1142/S0218348X21500444
Wang, K.: Variational principle and its fractal approximate solution for fractal Lane-Emden equation. Int. J. Numer. Methods Heat Fluid Flow Fractals (2021). https://doi.org/10.1108/HFF-09-2020-0552
Wang, K.J., Wang, G.-D.: Variational principle and approximate solution for the fractal generalized Benjamin–Bona–Mahony-burgers equation in fluid mechanics. Fractals (2020a). https://doi.org/10.1142/S0218348X21500754
Wang, K.J., Wang, K.-L.: Variational principles for fractal Whitham-Broer-Kaup equations in shallow water. Fractals (2020b). https://doi.org/10.1142/S0218348X21500286
Wang, K.J., Wang, G.-D.: Variational principle, solitary and periodic wave solutions of the fractal modified equal width equation in plasma physics. Fractals (2021). https://doi.org/10.1142/S0218348X21501152
Wang, K.-L., Wang, K.-J., He, C.-H.: Physical insight of local fractional calculus and its application to fractional KdV–Burgers–Kuramoto equation. Fractals 27(07), 1950122 (2019)
Wang, K.J., Wang, G.-D., Zhu, H.-W.: A new perspective on the study of the fractal coupled Boussinesq–Burger equation in shallow water. Fractals (2021). https://doi.org/10.1142/S0218348X2150122X
Wang, K.L., Yao, S.W.: He’s fractional derivative for the evolution equation. Therm. Sci. 24(4), 2507–2513 (2020)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Habib, S., Islam, A., Batool, A. et al. Numerical solutions of the fractal foam drainage equation. Int J Geomath 12, 7 (2021). https://doi.org/10.1007/s13137-021-00174-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13137-021-00174-2