Combined effects of suction/injection and exponentially decaying/growing time-dependent pressure gradient on unsteady Dean flow: a semi-analytical approach

Abstract

A two-dimensional mathematical model is developed and solved semi-analytically in order to theoretically examine the impact of suction/injection and an exponentially decaying/growing time-dependent pressure gradient on unsteady Dean flow through a coaxial cylinder. The walls of the cylinders are porous so as to enable the superimposition of the radial flow. The solution of the governing momentum and continuity equations are derived using a two-step process, the Laplace transformation in conjunction with the Riemann Sum-Approximation (RSA). For accuracy check, the steady state solution is computed and numerical values obtained using the Riemann-Sum Approximation (RSA) is compared with the already established results. It is found out that for an increasing time, a growing pressure gradient enhances the flow formation for both suction and injection, although the effect on the azimuthal velocity profile is subtle when suction is applied on porous walls. Moreover, the skin frictions on the walls can be minimized by imposing a decaying pressure gradient for suction/injection, however the behaviour is seen clearly when fluid particles are injected through the porous cavity.

1 Introduction

The study of unsteady two-dimensional viscous incompressible flows in horizontal permeable/non-permeable and non-rotating concentric cylinders have been the interest of many investigators in the past decades. This can be ascribed to the widespread application in biomedical engineering, biofluid mechanics where the circumferential flow is seen in most of the apparatuses transporting fluids, nuclear engineering, electrical and mechanical engineering.

The analysis of steady laminar flow in a curved channel on account of a constant circumferential pressure gradient was pioneered by Dean (1928). Some authors such as Dryden et al. (1956), Hamza (2017), Gupta and Gupta (1996), Fan and Chao (1965), Tsangaris (1984) have studied oscillatory flows in various geometries driven by an imposed circumferential pressure gradient. Tsangaris et al. (2006) discussed laminar fully developed flow in the gap between two coaxial cylinders with an imposed oscillating circumferential pressure gradient (finite gap oscillating Dean flow). Later on, Tsangaris and Vlachakis (2007) presented the exact solutions for Navier–Stokes Equations (NSE) responsible for the motion of a Newtonian fluid between two concentric cylinders taking into consideration the effect of an oscillating pressure gradient on the flow formation.

It is well known that the phenomenon of time-dependent pressure gradient flow through channels as well as annulus may help in understanding many technological problems such as pumping mechanisms, polymer technology, petroleum industry and purification of crude oil. These mechanisms produce, in general, pressure gradient flow which is not constant but pulsates in some way about a non-zero time-dependent pressure gradient.

In recent the past, some studies have been carried out in order to have an insight on the influence of time-dependent pressure gradient on various flow formation and physical situation. Yen and Chang (1961) in their article, considered the role of time-dependent pressure gradient on magnetohydrodynamic flow in a channel, in which three cases of time-dependent pressure gradient were considered namely; periodic, step and pulse pressure gradient. Unsteady flow of a viscous incompressible and electrically conducting fluid in the region between two porous cylinders under an external radial magnetic field with an exponentially decreasing/increasing time-dependent pressure gradient was investigated by Nandi (1970). McGinty et al. (2009) presented the general analytic solutions of Newtonian and Non-Newtonian fluid flows in cylindrical and annular pipes subject to an arbitrary time-dependent pressure gradient and arbitrary steady initial flow. In another work, Mendiburu et al. (2009) using a combination of Fourier series and integral transforms, analytically examined the unsteady one-dimensional flow between parallel plates with constant and time-dependent pressure gradient in which one of the plates is moving. They obtained that the time-dependent component of the pressure gradient decreases and eventually disappears, tending towards the constant pressure gradient as time increases. Other related literature can be found in references (Womersley 1995; Uchida 1956; Nowruzi et al. 2018; Manos et al. 2006; Mishra and Roy 1968; Yang and Wang 2001).

The importance of Dean number cannot be overruled in the study of the motion of fluids in curved pipes and channel. The Dean number is a dimensionless parameter and an important constituent of Dean flow which arises in motion of fluid in curved geometries. In an attempt to understand the role of Dean number and curvature on the motion of magnetohydrodynamics fluid flow, Hoque and Alam (2013) reported numerically the motion of fluid in a circular curved pipe of uniform cross section. From their investigations, result shows the existence of a two-vortex solution and increasing Dean number triggers an increase in the axial velocity flow. Generally, this is true since an increase in the dimensionless Dean number in turn generates an adverse pressure gradient along the curvature which prompts a secondary flow superimposed by the primary motion. Mondal et al. (2014), scrutinized numerically unsteady fully developed two-dimensional flow of viscous incompressible fluid flow in a rotating curved duct of small curvature. They vetted the impact of Coriolis and centrifugal instability on the flow formation for higher Dean number. In another related work, Mondal et al. (2015) employing the spectral method, performed a numerical analysis on the behavior of unsteady solutions of a two-dimensional fully developed flow of a viscous incompressible fluid through a curved rectangular duct of aspect ratios for varying Dean number. It is seen that as Dean number is increased, the nature of the flow changes progressively from chaotic, periodic, multi-periodic to steady-state.

In furtherance of the aforementioned investigation, the unsteady solution accountable for motion of a viscous incompressible fluid through a rotating curved rectangular channel was proposed by Islam et al. (2018). Sayed-Ahmed et al. (2010) undertook a numerical analysis in order to understand the effect of time-dependent pressure gradient on unsteady MHD Couette flow and heat transfer on Casson fluid in a porous channel with uniform suction/injection. In their work, they assumed the fluid is acted upon by an exponentially decaying pressure gradient $\left( {\frac{\partial P}{\partial x}} \right)$ in the x-direction. In another related work, Azad and Andallah (2016) evaluated numerically the unsteady flow of one-dimensional Navier–Stokes Equation (NSE) with time-dependent pressure gradient using an explicit exponential finite difference scheme (Expo FDS).

Afterward, several theoretical and experimental investigations have been carried out to better understanding this phenomenon. The semi-analytical evaluation for transient pressure-driven flow in a composite annulus due to circumferential pressure gradient (azimuthal pressure gradient) was reported by Jha and Yusuf (2018). Using the methods of Laplace transformation and Riemann-Sum Approximation (RSA), they obtained the solution of the governing momentum equations. Employing the same approach, Jha and Yahaya (2018) conducted a study on laminar fully developed transient flow through two horizontal and impermeable concentric tubes. The flow is set in by the applied circumferential pressure gradient in the annular gap. Their result shows that as time passes, the velocity is enhanced progressively as it attains a steady state. Jha and Yahaya (2019) further extended the work to the case when the walls of the tubes are porous. They concluded that in addition to the results obtained from their previous work, (see Jha and Yahaya (2018)) as the suction/injection parameter increases, the velocity increases. Other related articles can be seen in references (Mondal et al. 2013; Islam et al. 2017).

The concern of this analysis is to theoretically investigates the role of suction/injection and an exponentially decaying/growing time-dependent pressure on Dean flow.

The novelty of this examination is to deliberate the impact of decaying/growing time-dependent pressure gradient on unsteady Dean flow through a concentric cylinder forming an annulus with porous cavities on the wall. It is anticipated that this work will help in better understanding drag minimization on the walls of the annulus and enhancing the flow formation. The transient solutions of the velocity field and skin frictions has been obtained using a two-step approach; the Laplace transformation and the Riemann-Sum Approximation (RSA), the steady state solution has been equally derived. In justification of the present investigation, theoretical results obtained are compared with already established results. The effect of the various dimensionless flow parameters on the flow formation is studied with the aid of line graphs.

2 Mathematical analysis

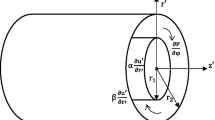
The flow considered is a two-dimensional fully developed laminar transient circumferential flow of viscous incompressible Newtonian fluid in the annular gap between two porous coaxial horizontal cylinders of infinite length. It is assumed that the two cylinders are fixed. The Z′-axis is assumed to be on the axis of the cylinders. The radii of the inner and outer cylinder are signified by a and b respectively as shown in Fig. 1. Initially, it is assumed that at time $t^{{\prime }} \le 0$ the fluid is at rest. At $t^{{\prime }} > 0$, the fluid is set in motion by the applied circumferential time-dependent pressure gradient in presence of suction/injection.

Fig. 1

Geometry of annular system

Since flow is fully developed and time-dependent, azimuthal velocity $v\left( {r^{{\prime }} ,t^{{\prime }} } \right)$ is a function of radial coordinate and time only. Following Yen and Chang (1961) and Jha and Yahaya (2019), the momentum and continuity equations for azimuthal exponential time-dependent pressure gradient in dimensional form are:

$$ \rho \left[ {\frac{{U_{1}^{2} a^{2} }}{{r^{{{\prime }3}} }} + \frac{{v^{2} }}{{r^{{\prime }} }}} \right] = \frac{\partial P}{{\partial r^{{\prime }} }} $$

(1)

$$ \rho \left[ {\frac{\partial v}{{\partial t^{{\prime }} }} + \frac{{U_{1} a}}{{r^{{\prime }} }}\frac{\partial v}{{\partial r^{{\prime }} }} + \frac{{U_{1} a}}{{r^{{\prime }} }}\frac{v}{{r^{{\prime }} }}} \right] = - \frac{{{ \exp }\left( { - \delta_{0} t^{{\prime }} } \right)}}{{r^{{\prime }} }}\frac{\partial P}{\partial \varphi } + \mu \left[ {\frac{{\partial^{2} v}}{{\partial r^{{{\prime }2}} }} + \frac{1}{{r^{{\prime }} }}\frac{\partial v}{{\partial r^{{\prime }} }} - \frac{v}{{r^{{{\prime }2}} }}} \right] $$

(2)

The initial and boundary conditions for the problem under consideration are $t^{{\prime }} \le 0:v = 0$ for $a \le r^{{\prime }} \le b$

$$ t^{{\prime }} > 0\left\{ {\begin{array}{*{20}l} {v = 0} \hfill & {at\;r^{{\prime }} = a} \hfill \\ {v = 0} \hfill & {at\;r^{{\prime }} = b} \hfill \\ \end{array} } \right. $$

(3)

2.1 Dimensionless analysis

Equations (1)–(3) are transformed into their respective dimensionless form by introducing the following dimensionless quantities

$$ \begin{aligned} & R = \frac{{r^{{\prime }} }}{a};\;\lambda = \frac{b}{a};\;t = \frac{{vt^{{\prime }} }}{{a^{2} }};\;V = \frac{v}{{U_{0} }}; \\ & U_{0} = \frac{{ - a\frac{\partial P}{\partial \varphi } }}{\rho v};\;Re = \frac{{U_{1} a}}{v};\;\delta = \frac{{a^{2} \delta_{0} }}{v}\;D_{n} = Re\sqrt {\frac{D}{{2R_{c} }}} \\ \end{aligned} $$

(4)

Equations (1) and (2) in the dimensionless form can be written as

$$ \frac{\partial V}{\partial t} + \frac{{\left( {Re - 1} \right)}}{R}\frac{\partial V}{\partial R} + \frac{{\left( {1 + Re} \right)}}{{R^{2} }} V = \frac{{{ \exp }\left( { - \delta t} \right)}}{R} + \frac{{\partial^{2} V}}{{\partial R^{2} }} $$

(5)

Subject to the following dimensionless initial and boundary conditions $t \le 0:V = 0$ for $1 \le R \le \lambda$

$$ t > 0\left\{ {\begin{array}{*{20}l} {V = 0} \hfill & {at\;R = 1} \hfill \\ {V = 0} \hfill & {at\;R = \lambda } \hfill \\ \end{array} } \right. $$

(6)

2.2 Analytical solution

It will be convenient to use classical Laplace transform technique in transforming Eqs. (5) and (6) since the governing momentum equation is time-dependent. Employing $\bar{V}\left( {R,s} \right) =\int_{0}^{\infty } V\left( {R,t} \right)e^{ - st} dt$ where s is the Laplace parameter and $s > 0$, the expression for Eqs. (5) and (6) are given as:

$$ \frac{{d^{2} \bar{V}}}{{dR^{2} }} + \frac{{\left( {1 - Re} \right)}}{R}\frac{{d\bar{V}}}{dR} - \left( {\left[ {1 + Re} \right] + sR^{2} } \right)\frac{{\bar{V}}}{{R^{2} }} = - \frac{1}{{R\left( {s + \delta } \right)}} $$

(7)

Subject to

$$ \begin{array}{*{20}l} {\bar{V} = 0} \hfill & {{\text{at}}\;R = 1} \hfill \\ {\bar{V} = 0} \hfill & {{\text{at}}\;R = \lambda } \hfill \\ \end{array} $$

(8)

Following Tsangaris et al. (2006), the linear non-homogeneous differential equation in Eq. (7) can be reduced using the given transformation below

$$ \bar{V}\left( {R,s} \right) = \bar{V}_{h} \left( {R,s} \right)R^{{\frac{Re}{2}}} + \frac{1}{{Rs\left( {s + \delta } \right)}} $$

(9)

where $\bar{V}_{h} \left( {R,s} \right)$ is the homogeneous solution of Eq. (7).

The exact solution of Eq. (7) in the Laplace domain under (8) is obtained by substituting the homogeneous solution of Eq. (7) into Eq. (9) and is given below

$$ \bar{V}\left( {R,s} \right) = \left[ {A_{1} I_{n} \left( {R\sqrt s } \right) + A_{2} K_{n} \left( {R\sqrt s } \right)} \right]R^{{\frac{Re}{2}}} + \frac{1}{{Rs\left( {s + \delta } \right)}} $$

(10)

where

$$ \begin{aligned} & A_{1} = \frac{{ - \left[ {\lambda^{ - n} K_{n} \left( {\sqrt s } \right) - K_{n} \left( {\lambda \sqrt s } \right)} \right]}}{{s\left( {s + \delta } \right)\left[ {I_{n} \left( {\lambda \sqrt s } \right)K_{n} \left( {\sqrt s } \right) - I_{n} \left( {\sqrt s } \right)K_{n} \left( {\lambda \sqrt s } \right)} \right]}}, \\ & A_{2} = \frac{{\left[ {\lambda^{ - n} I_{n} \left( {\sqrt s } \right) - I_{n} \left( {\lambda \sqrt s } \right)} \right]}}{{s\left( {s + \delta } \right)\left[ {I_{n} \left( {\lambda \sqrt s } \right)K_{n} \left( {\sqrt s } \right) - I_{n} \left( {\sqrt s } \right)K_{n} \left( {\lambda \sqrt s } \right)} \right]}}, \\ & n = \left( {\frac{Re}{2} + 1} \right). \\ \end{aligned} $$

Utilizing Eq. (10), the skin friction at $R = 1$ and $R = \lambda$ in the Laplace domain are given respectively as follows:

$$ \bar{\tau }_{1} \left( {R,s} \right) = R\frac{d}{dR}\left. {\left( {\frac{{\bar{V}\left( {R,s} \right)}}{R}} \right)} \right|_{R = 1} = \sqrt s \left[ {A_{3} - A_{4} } \right] - 2\left[ {A_{5} + A_{6} } \right] - \frac{2}{{s\left( {s + \delta } \right)}} $$

(11)

$$ \bar{\tau }_{\lambda } \left( {R,s} \right) = R\frac{d}{dR}\left. {\left( {\frac{{\bar{V}\left( {R,s} \right)}}{R}} \right)} \right|_{R = \lambda } = \sqrt s \left[ {A_{7} - A_{8} } \right]\lambda^{n - 1} - 2\lambda^{n - 2} \left[ {A_{9} + A_{10} } \right] - \frac{2}{{\lambda^{2} s\left( {s + \delta } \right)}} $$

(12)

where

$$ \begin{aligned} & A_{3} = A_{1} I_{n - 1} \left( {\sqrt s } \right),\;A_{4} = A_{2} K_{n - 1} \left( {\sqrt s } \right),\;A_{5} = A_{1} I_{n} \left( {\sqrt s } \right),\;A_{6} = A_{2} K_{n} \left( {\sqrt s } \right), \\ & A_{7} = A_{1} I_{n - 1} \left( {\lambda \sqrt s } \right),\;A_{8} = A_{2} K_{n - 1} \left( {\lambda \sqrt s } \right),\;A_{9} = A_{1} I_{n} \left( {\lambda \sqrt s } \right),\;A_{10} = A_{2} K_{n} \left( {\lambda \sqrt s } \right). \\ \end{aligned} $$

It is paramount to note that the Laplace domain solutions presented in Eqs. (10)–(12) are to be transformed to the time domain. Due to the complex nature of these solutions, a numerical Laplace inversion technique used in Jha and Yusuf (2018), Jha and Yahaya (2018, 2019) known as Riemann-Sum Approximation (RSA) has been adopted. In this method, any function in the Laplace domain can be transformed to the time domain as follows:

$$ V\left( {R,t} \right) = \frac{{e^{\varepsilon t} }}{t}\left[ {\frac{{\bar{V}\left( {R,\varepsilon } \right)}}{2} + {\text{Re}}\left( {\mathop \sum \limits_{n = 1}^{Q} \bar{V}(R,\varepsilon + \frac{in\pi }{t}} \right)\left( { - 1} \right)^{n} } \right] $$

(13)

where ${\text{Re}}$ is the real part of the summation, $i = \sqrt { - 1}$ the imaginary number, $Q$ is the number of terms involves in the summation and $\varepsilon$ is the real part of the Bromwich contour that is used in inverting Laplace transforms. The Riemann-Sum Approximation (RSA) for the Laplace inversion involves a single summation for the numerical computation, of which its exactness is dependent on the value of ε and the truncation error prescribed by $Q$. Following Tzou (1997), taking εt to be 4.7 gives the most desirable result.

2.3 Validation of the method

In an attempt to ascertain the effectiveness of the numerical inversing scheme used in transforming the Laplace domain solutions to time domain, the steady state solution is computed as a limit case. This is achieved by making $\delta = 0$ and $\frac{\partial V}{\partial t} = 0$ in Eq. (5). For large value of the dimensionless time $\left( t \right)$, the steady state solution is expected to synchronize with the transient solution for different flow regimes. Thus, the required ordinary differential equation is given as

$$ \frac{{d^{2} V}}{{dR^{2} }} + \frac{1}{R}\left( {1 - Re} \right)\frac{dV}{dR} - \frac{1 + Re}{{R^{2} }}V = - \frac{1}{R} $$

(14)

Under the no-slip boundary conditions

$$ \begin{array}{*{20}l} {V = 0} \hfill & {{\text{at}}\;R = 1} \hfill \\ {V = 0} \hfill & {{\text{at}}\;R = \lambda } \hfill \\ \end{array} $$

(15)

Employing the transformation $InR = \psi$ as follows, Eq. (14) can be written as

$$ \frac{{d^{2} V}}{{d\psi^{2} }} - Re\frac{dV}{d\psi } - \left( {1 + Re} \right)V = - \text{exp}(\psi) $$

(16)

The solution of the steady state momentum Eq. (16) under boundary conditions (15) is given as

$$ V\left( R \right) = \frac{1}{2Re}\left( {R - \frac{1}{R}} \right) - \frac{1}{2Re}\frac{{\left( {\lambda^{2} - 1} \right)\left( {R^{Re + 1} - \frac{1}{R}} \right) }}{{\left( {\lambda^{{\left( {Re + 2} \right)}} - 1} \right)}} $$

(17)

Utilizing Eq. (17), the steady state skin frictions on the walls of the inner and outer cylinders respectively is derived by differentiating Eq. (17) and evaluating at $R = 1$ and $R = \lambda$ and are given as follows

$$ \tau_{1} = R\frac{d}{dR}\left. {\left( {\frac{V}{R}} \right)} \right|_{R = 1} = \frac{1}{Re} - \frac{{\lambda \left( {\lambda^{2} - 1} \right)}}{{2Re\left( {\lambda^{{\left( {Re + 2} \right)}} - 1} \right)}}\left( {Re + 2} \right) $$

(18)

$$ \tau_{\lambda } = R\frac{d}{dR}\left. {\left( {\frac{V}{R}} \right)} \right|_{R = \lambda } = \frac{{(\lambda^{2} - 1)}}{{2Re\left( {\lambda^{{\left( {Re + 2} \right)}} - 1} \right)}}\left( {Re\lambda^{Re} + \frac{2}{{\lambda^{2} }}} \right) - \frac{1}{{Re\lambda^{2} }} $$

(19)

In order to show how good the numerical approach used in transforming the closed form exact solutions from the Laplace domain to time domain, a table of comparison is presented below (see Tables 1, 2, 3) between the current result established when the coefficient of time in the time-dependent component of the pressure gradient is taken to be zero $\left( {\delta = 0} \right)$ and results given by Jha and Yahaya (2019). It is noted that a perfect correlation is seen between the numerical values.

Table 1 Comparison of the present results obtained using the Riemann-Sum Approximation approach (RSA) with those of Jha and Yahaya (2019) for the transient state velocity

Table 2 Comparison of the present results obtained using the Riemann-Sum Approximation approach (RSA) with those of Jha and Yahaya (2019) for the transient state skin friction $\left( {R = 1} \right)$

Table 3 Comparison of the present results obtained using the Riemann-Sum Approximation approach (RSA) with those of Jha and Yahaya (2019) for the transient state skin friction $\left( {R = \lambda } \right)$

3 Results and discussions

The combined effects of suction/injection and an exponentially decaying/growing time-dependent pressure gradient on unsteady Dean flow in a horizontal concentric cylinder are examined semi-analytically. In order to understand the effect of the various dimensionless controlling parameters on the flow formation, a MATLAB program is written to determine and generate line graphs and numerical values for the velocity, skin frictions and vorticity. Throughout this analysis, the suction/injection parameter is taken over $- 8.0 \le Re \le 8.0$ and the coefficient of time in the time-dependent component of the pressure gradient is taken over $- 2.0 \le \delta \le 2.0$.

Figures 2 and 3 shows the velocity distribution in the direction of flow as time passes with suction applied for an exponentially increasing time-dependent pressure gradient and an exponentially decreasing time-dependent pressure gradient respectively. It is observed in both cases that as time increases, the velocity increases when the coefficient of time in the time-dependent pressure gradient is increased/decreased, but a higher velocity profile is perceived with an increasing coefficient of time in the exponential time-dependent pressure gradient.

Fig. 2

Velocity distribution for different values of time $\left( {\delta = - 2.0,\;{\text{Re}} = 4.0} \right)$

Fig. 3

Velocity distribution for different values of time $\left( {\delta = 2.0,\;{\text{Re}} = 4.0} \right)$

Figures 4 and 5 indicates the influence of injection, time and a growing/decaying exponential time-dependent pressure gradient on the velocity profile. It is seen from Fig. 4, the velocity increases as time and the coefficient of time in the exponential time-dependent pressure gradient increase. This is attributed to the fact that fluid particles are injected into the annular gap through the porous wall and the coefficient of time in the exponential time-dependent pressure gradient grows, thus enhancing the fluid velocity in the direction of flow. On the other hand, the increase in the fluid velocity is less significant with decaying coefficient of time in the exponential time-dependent pressure gradient compared to when it is growing as seen in Fig. 5.

Fig. 4

Velocity distribution for different values of time $\left( {\delta = - 2.0,\;{\text{Re}} = - 4.0} \right)$

Fig. 5

Velocity distribution for different values of time $\left( {\delta = 2.0,\;{\text{Re}} = - 4.0} \right)$

The effect of Reynolds number $\left( {Re} \right)$ on the steady velocity profile has been presented in Fig. 6. It is clear from Fig. 6, that increasing Reynolds number $\left( {Re} \right)$ accelerates the flow for both suction and injection. This behaviour can also be said for an increasing Dean number $\left( {Dn} \right)$ since there exists a direct proportionality between Dean number $\left( {Dn} \right)$ and Reynolds number $\left( {Re} \right)$. However, the increase is more pronounced with fluid injection. The effects of time and exponential time-dependent pressure gradient on skin friction on the outer surface of the inner cylinder with suction applied on the porous wall is seen in Figs. 7 and 8. It is evident from Figs. 7 and 8 that skin friction increases with time and a growing/decaying exponential time-dependent pressure gradient across the annular gap. In addition, the magnitude of the skin friction is higher when the coefficient of time in the exponential time-dependent pressure gradient is increasing.

Fig. 6

Steady state velocity profile showing the effect of Reynolds number $\left( {Re} \right)$

Fig. 7

Variation of skin friction $\left( {{\text{R}} = 1} \right)$ for different values of time $\left( {\delta = - 2.0,\;{\text{Re}} = 4.0} \right)$

Fig. 8

Variation of skin friction $\left( {{\text{R}} = 1} \right)$ for different values of time $\left( {\delta = 2.0,\;{\text{Re}} = 4.0} \right)$

The variation of skin friction on the outer surface of the inner cylinder with combined effects of time, exponentially increasing/decreasing time-dependent pressure gradient and injection are seen in Figs. 9 and 10. We note that as time and the coefficient of time in the exponential pressure gradient increases/decreases, the skin friction on the wall increases as fluid particles are injected through the porous cavity. It is interesting to note that the role of the coefficient of time in the exponential time-dependent pressure gradient is more pronounced with injection.

Fig. 9

Variation of skin friction $\left( {{\text{R}} = 1} \right)$ for different values of time $\left( {\delta = - 2.0,\;{\text{Re}} = - 4.0} \right)$

Fig. 10

Variation of skin friction $\left( {{\text{R}} = 1} \right)$ for different values of time $\left( {\delta = 2.0,\;{\text{Re}} = - 4.0} \right)$

The drag on the outer wall of the inner cylinder for different values of Reynolds number $\left( {Re} \right)$ at steady state is seen in Fig. 11. It is observed that increasing Reynolds number $\left( {Re} \right)$ in turn results to increase in skin friction on the surface of the inner wall.

Fig. 11

Steady state skin friction at $R = 1$ showing the effect of Reynolds number $\left( {Re} \right)$

Figures 12 and 13 illustrates the effect of time, suction and time-dependent pressure gradient on skin friction on the inner surface of the outer cylinder. As time passes, it is observed that the skin friction increases as the coefficient of time in the exponential time-dependent pressure gradient grows as exhibited in Fig. 12. On the other hand, as time increases and coefficient of the time-dependent pressure gradient decays, the skin friction is seen to slowly increases within the annular gap and gradually declining as we further away within the annular gap as viewed in Fig. 13. This is due to the fact that an exponentially decaying time-dependent pressure gradient and suction on the porous wall play an important role in weakening the skin friction as time passes.

Fig. 12

Variation of skin friction $\left( {{\text{R}} = \lambda } \right)$ for different values of time $\left( {\delta = - 2.0,\;{\text{Re}} = 4.0} \right)$

Fig. 13

Variation of skin friction $\left( {{\text{R}} = \lambda } \right)$ for different values of time $\left( {\delta = 2.0,\;{\text{Re}} = 4.0} \right)$

Figures 14 and 15 shows the variation of skin friction on the inner surface of the outer cylinder for different values of time with an increasing/decreasing pressure gradient and fluid particles injected through the porous walls. From Fig. 14, it is evident that the skin friction increases as time and the coefficient of time in the exponential time-dependent pressure gradient are increased. On the hand, the drag on the wall is seen to increase and slowly drops as time increases and the coefficient of time in the exponential time-dependent pressure gradient decreases as shown in Fig. 15.

Fig. 14

Variation of skin friction $\left( {{\text{R}} = \lambda } \right)$ for different values of time $\left( {\delta = - 2.0,\;{\text{Re}} = - 4.0} \right)$

Fig. 15

Variation of skin friction $\left( {{\text{R}} = \lambda } \right)$ for different values of time $\left( {\delta = 2.0,\;{\text{Re}} = - 4.0} \right)$

Figure 16 illustrates the action of Reynolds number $\left( {Re} \right)$ on the steady state skin friction on the wall of the outer cylinder for both suction and injection. We note that increasing the suction/injection parameter retards the drag effect on the wall of the outer cylinder.

Fig. 16

Steady state skin friction at $R = \lambda$ showing the effect of Reynolds number $\left( {Re} \right)$

The influence of time on fluid rotation produced in the annular gap by the secondary flow otherwise known as vorticity or Dean vortex with suction applied on the porous wall for a decreasing and increasing time-dependent pressure gradient respectively are exhibited in Figs. 17 and 18. As time passes, it is observed that the fluid rotation increases around the region of the inner cylinder and slightly drop with further distance from the wall of the inner cylinder. It interesting to note that the rotation is at its maximum on the wall of the inner cylinder when the time-dependent component of the pressure gradient is exponentially growing. Figures 19 and 20 depicts the Dean vortex for different values of time for a decaying and growing time-dependent pressure gradient when fluid particles are injected through the porous cavities. We find that Dean vortex is increasing as time is increased around the inner wall and abruptly decrease as it near the outer wall. As expected, a higher Dean vortex is seen when a growing time-dependent pressure gradient and fluid injection are considered.

Fig. 17

Vorticity profile showing the effect of time $\left( {Re = 4.0, \delta = 2.0} \right)$

Fig. 18

Vorticity profile showing the effect of time $\left( {Re = 4.0, \delta = - 2.0} \right)$

Fig. 19

Vorticity profile showing the effect of time $\left( {Re = - 4.0, \delta = 2.0} \right)$

Fig. 20

Vorticity profile showing the effect of time $\left( {Re = - 4.0, \delta = - 2.0} \right)$

4 Conclusion

A theoretical analysis on unsteady Dean flow in an annulus with suction/injection and an exponentially decaying/growing time-dependent pressure gradient is carried out. The flow in the annular region is induced by the sudden application of the Azimuthal pressure gradient and the exponential time-dependent pressure gradient. A combination of Laplace transforms technique and Riemann-Sum Approximation (RSA) has been used in order to solve the governing momentum equation responsible for the flow. Tables has been presented in order to compare the results obtained from the current analysis with previously established results, which demonstrate excellent agreement. Based on the solutions as well as pictorial representations, we concluded that:

• i. The fluid velocity can be optimized with an increasing time and fluid injection as it gradually attains steady state.

• ii. The skin friction on the wall of the inner cylinder can be enhanced by increasing time and careful selection of a growing pressure gradient and fluid injection through the permeable wall.

• iii. The action of the skin drag on the wall of the outer cylinder can be rendered less effective with a decaying time-dependent pressure gradient induced and fluid injection through the porous cavity.

• iv. Dean vortex can be amplified by increasing time and fluid injection.