Entropy based optimal scale selection and attribute reduction in multi-scale interval-set decision tables

Abstract

One of the current research gaps in multi-scale data analysis is studying information systems characterized by attributes with interval sets as attribute values and multiple scales. To address this gap, we first introduce the concepts of a multi-scale interval-set information system (MISIS) and a multi-scale interval-set decision table (MISDT). We then define the similarity relation between objects in an MISIS and the corresponding rough approximations. We further propose the positive region optimal scale, the modified conditional entropy optimal scale, and the positive complementary conditional entropy optimal scale in an MISDT. We examine the relationships among these optimal scales in consistent and inconsistent MISDTs and show that the positive region optimal scale and the modified conditional entropy optimal scale are equivalent in a consistent MISDT, while in an inconsistent MISDT, the positive region optimal scale is the same as the positive complementary conditional entropy optimal scale, and the modified conditional entropy optimal scale is not greater than the positive complementary conditional entropy optimal scale. Based on the optimal scale, we also develop attribute reduction approaches in MISDTs. Finally, through experimental analysis of data on the UCI dataset, we verify the effectiveness and reasonableness of our proposed methods.

1 Introduction

Granular computing (GrC) [16, 21, 42, 43] is crucial for knowledge discovery in big data. The primary idea of GrC is to decompose large data sets or complex problems into granules through information granulation [44], and to integrate and represent the information at different granularity levels to solve complex problems effectively.

One of the fundamental models in GrC is rough set theory, initiated by Pawlak [19], which shows promise in handling uncertain information [1, 2, 20]. This theory specifically focuses on information systems (ISs) [18], which consist of datasets composed of objects and their associated attribute values. For a target set of objects in an IS, we can represent it by a pair of operators called upper and lower approximations. We can find a similar way of expressing information in the interval sets [40]. An interval set is an extended interval number. The main idea of an interval set is to represent uncertain information by using two definite sets as upper and lower bounds. In real life, achieving an accurate representation of information or data is challenging due to the uncertainty and redundancy of the information and data volume. For example, in the course selection of students [48], we take the set of compulsory courses as the lower bound and the set of required courses and elective subjects as the upper bound. Therefore, the course selection of students constitutes an interval set. There are many similar situations. To represent ISs in which attribute values are interval sets, Yao and Liu [41] proposed the concept of an interval-set information system (ISIS), which has gained significant attention in recent research [10, 14, 26, 45,46,47,48].

Nevertheless, current equivalence relations used in ISISs impose on strict conditions that limit the comprehensive representation of relationships between objects. To overcome this limitation, Wang and Yue [26] proposed fuzzy dominance relations to define four uncertainty measures. They further explored the relationships among these uncertainty measures. Similarly, Zhang et al. [48] introduced similarity relations for objects in an ISIS.

In real-life situations, information is understood at various levels and depths. Objects in ISs may own different attribute values at different scales. To describe such multi-scale information, Wu and Leung [31] employed rough set methods to investigate knowledge discovery in multi-scale information systems (MISs) and multi-scale decision tables (MDTs), known as Wu–Leung model. In an MIS, there is a granular information transformation mapping to ease the transformation of object attribute values across different scales. Thus, the selection of an optimal scale is a key step for final decision in MDTs and has become a main direction in multi-scale data analysis [4, 11, 17, 25, 27, 33, 35, 49, 51]. Wu and Leung [32] defined seven types of optimal scales in an MDT and examined their relationships. These optimal scales are equivalent when an MDT is consistent, but they may be no longer equivalent in an inconsistent MDT. On the base of the Wu–Leung model, Li and Hu [9] proposed a generalized MIS, which relaxes the requirement that all attributes in MIS have the same scale level. A key step to rule acquisition in a generalized MDT is to seek for an optimal scale for each attribute to determine a single scale decision table with some requirement for final decision, which is called the optimal scale combination selection. For example, Wu and Leung [34] discussed seven optimal scale combinations in a generalized MDT. In addition, the optimal scales or optimal scale combinations based on matrix [6] and cost [50] were studied.

Information entropy [23] is an important measure to evaluate uncertainty of information. Various information entropies were used to study attribute reduction and rule acquisition in rough set data analysis [7, 8, 22, 37,38,39, 52]. Recently, information entropies have also been utilized to select optimal scales in multi-scale data analysis [3, 30]. Bao et al. [3] introduced a method of optimal scale combination, using Shannon entropy as the guiding principle that maintains the measurement of uncertainty in knowledge. Wang et al. [30] introduced multi-scale fuzzy entropy to integrate granular information across different scales.

With the increasing application of rough set data analysis, attribute values in data sets were emerged as sets [24], intervals [5], and fuzzy numbers [29]. Various types of attribute values were also found in multi-scale date analysis, see e.g. [12, 13, 28]. Despite the increasing interest of researchers in multi-scale data analysis models and ISISs, the issue of attribute multi-scale problems in ISISs has received limited attention. Furthermore, the problem of entropy optimal scale selection is also worth investigating. These facts have motivated our research on knowledge discovery in multi-scale interval-set information systems (MISISs). In [36], Xie et al. introduced the notion of MISISs and defined optimal scale in multi-scale interval-set decision tables (MISDTs). The main objective of this paper is to study further the selection of entropy optimal scales and the corresponding attribute reductions in MISDTs.

In the next section, we review some basic notions related to ISISs and information entropies. In Sect. 3, we introduce MISISs with the representations of information granules as well as rough approximations in MISISs. In Sect. 4, we give some concepts with their properties in MISDTs. In Sect. 5, we discuss optimal scale selection and attribute reduction in MISDTs. In Sect. 6, we give experiments evaluating algorithms. We summarize this research in Sect. 7.

2 Preliminaries

In this section, we overview the fundamental concepts of interval sets, interval-set information systems and information entropies. Throughout this paper, we adopt $C\left( n,m\right) =\frac{n!}{m!\left( n-m\right) !}$ to represent the combination number formula and $|\varvec{\cdot }|$ to denote the cardinality of a set.

2.1 Interval sets

Definition 1

[40] Let V be a finite set and $2^V$ the power set of V, a closed interval set on $2^V$ is defined as follows:

$$\begin{aligned} \mathcal {X}=[{X_1},{X_2}]=\{X \in 2^V | X_1 \subseteq X \subseteq X_2 \}, \end{aligned}$$

(1)

where $X_1$ and $X_2$ are the lower and upper bounds of $\mathcal {X}$, respectively, and satisfy $X_1 \subseteq X_2 \subseteq V$. Note that $[{X_1},{X_2}]$ degenerates into an ordinary set ${X_1}$ when ${X_1}={X_2}$.

In this paper, we use $\mathcal {I}(2^{V})$ to represent the set of all interval sets on the power set of a finite set V. For two interval sets $\mathcal {X}=[{X_1},{X_2}]$ and $\mathcal {Y}=[{Y_1},{Y_2}]$ on $2^V$, the interval-set intersection and union operations are defined, respectively, as follows [40]:

$$\begin{aligned}{} & {} \mathcal {X} \sqcap \mathcal {Y}=[X_1 \cap Y_1,X_2 \cap Y_2]=\{X \cap Y | X \in \mathcal {X}, Y \in \mathcal {Y}\}, \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \mathcal {X} \sqcup \mathcal {Y}=[X_1 \cup Y_1,X_2 \cup Y_2]=\{X \cup Y | X \in \mathcal {X}, Y \in \mathcal {Y}\}. \end{aligned}$$

(3)

Definition 2

[48] Let $\mathcal {X}=[{X_1},{X_2}]$ and $\mathcal {Y}=[{Y_1},{Y_2}]$ be two interval sets on the power set of a finite set V, the similarity degree of $\mathcal {X}$ and $\mathcal {Y}$ is defined as follows:

$$\begin{aligned} GS(\mathcal {X},\mathcal {Y})=\frac{1}{2}(PD_{\mathcal {X}-\mathcal {Y}}+ PD_{\mathcal {Y}-\mathcal {X}}), \end{aligned}$$

(4)

where

$$\begin{aligned} PD_{\mathcal {X}-\mathcal {Y}}=\frac{1}{2}(\frac{|X_1 \bigcap Y_1|}{|X_1|}+\frac{|X_2 \bigcap Y_2|}{|X_2|}). \end{aligned}$$

(5)

Moreover, note that the function $GS(\mathcal {X},\mathcal {Y})$ is symmetric. We assume that $\mathcal {X} \sqcap \mathcal {Y}=[Z_1,Z_2]$, then Eq. (4) can be represented as follows:

$$\begin{aligned} GS(\mathcal {X},\mathcal {Y})=\frac{1}{4}\sum \limits _{i=1}^{2}\left( \frac{|Z_i|}{|X_i|}+\frac{|Z_i|}{|Y_i|}\right) . \end{aligned}$$

(6)

2.2 Interval-set information systems

Definition 3

[18] An information system (IS) is a pair $S=(O,C)$, where $O=\{o_1,o_2, \ldots ,o_n\}$ is a nonempty finite set of objects called the universe of discourse, and $C=\{c_1,c_2, \ldots ,c_m\}$ a nonempty finite set of attributes such that $c_j: O \rightarrow V_j$ for all $c_j \in C$, where $V_j$ is the domain of attribute $c_j$.

Definition 4

[41] An interval-set information system (ISIS) is a pair $S=(O,C)$, where $O=\{o_1,o_2, \ldots ,o_n\}$ is the universe of discourse, and $C=\{c_1,c_2, \ldots ,c_m\}$ the nonempty finite set of attributes such that $c_j: O \rightarrow \mathcal {I}(2^{V_j})$ for all $c_j \in C$, i.e. $c_j(o)=[A_j^{1}(o),A_j^{2}(o)] \in \mathcal {I}(2^{V_j})$, $o \in O$, where $V_j$ is the domain of attribute $c_j$, and $A_j^{1}(o) \subseteq A_j^{2}(o) \subseteq V_j$.

In Definition 4, $c_j(o)=[A_j^{1}(o),A_j^{2}(o)]$ indicates that, under attribute $c_j$, object o must contain $A_j^{1}(o)$ and possibly $A_j^{2}(o)$. For example, Table 1 depicts an ISIS, in which $O=\{o_1,o_2,\ldots ,o_8\}$ represents eight residents, with $c_1$ and $c_2$ show the abilities of listening and writing, respectively. The attribute values “E”, “G”, “R”, “V”, “T” mean “English”, “German”, “Russian”, “Ukrainian”, “Tibetan”, respectively. We can observe that the attribute value of $o_3$ under $c_1$ is $[{\{E,G\}},{\{E,G,T\}}]$. The attribute value $[{\{E,G\}},{\{E,G,T\}}]$ indicates that in terms of the ability of listening, resident $o_3$ has definitely mastered English and German, while possibly done Tibetan.

Table 1 An interval-set information system

Let $S=(O,C)$ be an ISIS, $\tau \in [0,1]$, and $B \subseteq C$, a similarity relation w.r.t. $\tau$ and B is defined as follows [48]:

$$\begin{aligned} R_B^\tau =\{(o,p) \in O \times O|GS(c(o),c(p))\ge \tau , \forall c \in B \}. \end{aligned}$$

(7)

Based on the similarity relation $R_B^\tau$, it can be inferred that the similarity class of each object $o \in O$ w.r.t. $\tau$ and B is denoted as [48] $SC_B^\tau (o)=\{p|(o,p)\in R_B^\tau ,p \in O\}$. Additionally, the granular structure w.r.t. $\tau$ and B is defined as [48] $SC_B^\tau =\{SC_B^\tau (o_1),SC_B^\tau (o_2),\ldots ,SC_B^\tau (o_n)\}$.

It is obvious that $o \in SC_B^\tau (o)$ for all $o \in O$, i.e., $\bigcup \limits _{o \in O} SC_B^\tau (o) = O$ and $SC_B^\tau (o) \not = \varnothing$, so the granular structure $SC_B^\tau$ forms a covering on O.

An interval-set decision table (ISDT) [48] is a pair $S=(O,C \cup \{d\})$, where (O, C) is an ISIS, and $d\notin C$ the decision such that $d: O \rightarrow V_d$, where $V_d$ is the domain of d. A binary relation on objects induced by d is defined as follows:

$$\begin{aligned} R_d=\{(o,p) \in O \times O|d(o)=d(p)\}. \end{aligned}$$

(8)

Then, the $R_d$ constitutes a partition $O/R_d$ on O, written as $O/R_d=\{R_{d}(o)|o \in O\}=\{D_1,D_2,\ldots ,D_t\}$, where $R_{d}(o)=\{p|(o,p) \in R_d, p \in O\}$.

Definition 5

Let $S = (O,C \cup \{d\})$ be an ISDT and $\tau \in [0,1]$, if $SC_{C}^{\tau } (o) \subseteq R_d (o)$ for all $o \in O$, then we say that S is consistent. Otherwise, S is inconsistent.

Definition 6

[48] Let $S = (O,C \cup \{d\})$ be an ISDT, $\tau \in [0,1]$, and B, $F \subseteq C$, if $SC_B^\tau (o) \subseteq \ SC_F ^\tau (o)$ for all $o \in O$, then we say that $SC_B^\tau$ is finer than $SC_F ^\tau$ and mark it as $SC_B^\tau \preceq SC_F^\tau$.

Proposition 1

[48] Let $S = (O,C \cup \{d\})$ be an ISDT, $\tau \in [0,1]$, and $B,F \subseteq C$. If $F \subseteq B$, then

• (1) $R_B^\tau \subseteq R_F^\tau$,

• (2) $SC_B^\tau \preceq SC_F^\tau$.

2.3 Information entropies

Entropy measurement has become an important method to describe uncertainty in rough set theory. In this subsection, to better quantitatively analyze the information in ISISs, we review two types of conditional entropies.

Definition 7

[48] Let $S=(O,C\cup \{d\})$ be an ISDT, $\tau \in [0,1]$, and $B \subseteq C$, a modified conditional entropy w.r.t. B and $\tau$ is defined as follows:

$$\begin{aligned} H^{\tau }(d|B)=-\sum \limits _{i=1}^{n} \sum \limits _{j=1}^{t} \frac{|SC_{B}^{\tau }(o_i) \cap D_j|}{n^2} \log _{2} {\left( \frac{|SC_{B}^{\tau }(o_i) \cap D_j|}{|SC_{B}^{\tau }(o_i)|}\right)} , \end{aligned}$$

(9)

where n and t are the cardinalities of O and $O/R_d$, respectively. In this paper, we define $\frac{|SC_{B}^{\tau }(o_i) \cap D_j|}{n^2} \log _{2} {\left( \frac{|SC_{B}^{\tau }(o_i) \cap D_j|}{|SC_{B}^{\tau }(o_i)|}\right)} =0$ when $|SC_{B}^{\tau }(o_i) \cap D_j|=0$.

According to Definition 7, the range of the modified conditional entropy is $[0,\log _{2}{n}]$.

Definition 8

[15] Let O be a nonempty finite set, with $\mathcal {Q}=\{Q_1,Q_2,\ldots , Q_{n_1}\}$ and $\mathcal {P}=\{P_1,P_2,\ldots , P_{n_2}\}$ as two partitions of O, a complementary conditional entropy of $\mathcal {Q}$ about $\mathcal {P}$ is defined as follows:

$$\begin{aligned} CH(\mathcal {Q}|\mathcal {P})=\sum \limits _{i=1}^{n_1} \sum \limits _{j=1}^{n_2} \frac{|Q_i \cap P_j|}{|O|} \frac{|Q_i^\complement \cap P_j|}{|O|}, \end{aligned}$$

(10)

where $Q_i^\complement =O-Q_i=\{o \in O|o \not \in Q_i\}$ is the complement of $Q_i$ in O.

3 Multi-scale information systems and multi-scale interval-set information systems

In practical applications, attribute values of an object may exhibit variations across different scales. Therefore, Wu and Leung introduced MISs [31]. To facilitate the description in this paper, we assume that each attribute has L scale levels.

Definition 9

[31] An MIS is a pair $S = (O,C)$, where $O = \{o_1,o_2, \ldots ,o_n\}$ is the universe of discourse and $C = \{ {c_1,c_2, \ldots ,c_m} \}$ the set of attributes. Both O and C are nonempty finite sets, and each attribute in C has L scale levels. Therefore, an MIS can be represented as follows:

$$\begin{aligned} S=(O,C) = (O,\{c_j^l| j = 1,2, \ldots ,m,l = 1,2, \ldots ,L\}), \end{aligned}$$

(11)

where $c_j^l:O \rightarrow V_j^l$ and $V_j^l$ is the domain of attribute $c_j$ at the l-th scale. For each $l \in \{1,2, \ldots ,L-1\}$ and $j \in \{1,2, \ldots ,m\}$, there exists a surjective mapping $g_j^{l,l + 1}:V_j^l \rightarrow V_j^{l + 1}$ such that $c_j^{l + 1}=g_j^{l,l + 1} \circ c_j^{l}$, i.e.

$$\begin{aligned} c_j^{l + 1}(o) = g_j^{l,l + 1}(c_j^l(o)), \, o \in O, \end{aligned}$$

(12)

where $g_j^{l,l + 1}$ is called a granular information transformation mapping.

For $l \in \{1,2, \ldots ,L\}$, we denote the attribute set under the l-th scale as $C^l=\{c_j^l | j=1,2, \ldots ,m \}.$ Therefore, an MIS can be decomposed into L single-scale sub-ISs, denoted as $S^{l}=(O,C^{l})$, $l=1,2, \ldots ,L$.

Definition 10

[31] A multi-scale decision table (MDT) is a pair $S = (O,C \cup \{d\}) = (O,\{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L\} \cup \{d\})$, where $(O,C) = ( O,\{ c_j^l| j = 1,2, \ldots , m,l = 1,2, \ldots ,L \} )$ is an MIS, and $d \notin \{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L\}$ the decision such that $d:O \rightarrow V_d$, where ${V_d}$ is the domain of d.

When all attribute values in an MIS are interval sets, we refer to this system as a multi-scale interval-set information system (MISIS).

Definition 11

An MISIS is a pair $S= (O,C)$, where $O=\{o_1,o_2, \ldots ,o_n\}$ is the universe of discourse, and $C=\{c_1,c_2, \ldots ,c_m\}$ the set of attributes. Both O and C are nonempty finite sets, and each attribute in C has L scale levels, i.e., C can be represented as $\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}$ such that $c_j^l:O \rightarrow \mathcal {I} (2^{V_j^l})$ for all $j \in \{1,2,\ldots ,m\}$ and $l \in \{1,2,\ldots ,L\}$, i.e. $c_j^l(o)=[A_{j,l}^1(o),A_{j,l}^{2}(o)]$, where $V_j^l$ is the domain of the attribute $c_j$ at the l-th scale, and $A_{j,l}^1(o) \subseteq A_{j,l}^{2}(o) \subseteq V_j^l$.

For each $l \in \{1,2, \ldots ,L-1\}$ and $j \in \{1,2,\ldots ,m\}$, there exist two surjective mappings, one is $h_j^{l,l+1}:V_j^l \rightarrow V_j^{l+1}$ such that

$$\begin{aligned} v_j^{l+1}=h_j^{l,l+1} (v_j^{l}), \, v_j^{l} \in V_j^{l}, \end{aligned}$$

(13)

and the other is $\psi _j^{l,l+1}:\mathcal {I} (2^{V_j^l}) \rightarrow \mathcal {I} (2^{V_j^{l+1}})$ such that $c_j^{l+1}=\psi _j^{l,l+1} \circ c_j^{l}$, i.e.

$$\begin{aligned} \begin{aligned} c_j^{l+1} (o)&=\psi _j^{l,l+1} (c_j^{l}(o)) \\&=\psi _j^{l,l+1}([A_{j,l}^1(o),A_{j,l}^{2}(o)]) \\&=[h_j^{l,l+1}(A_{j,l}^1(o)),h_j^{l,l+1}(A_{j,l}^{2}(o))] \\&=[A_{j,l+1}^1(o),A_{j,l+1}^{2}(o)], \, o \in O, \end{aligned} \end{aligned}$$

(14)

where $h_j^{l,l+1}$ is the granular information transformation mapping and $\psi _j^{l,l+1}$ is the domain information transformation mapping.

Remark 1

Let $S = ({O,C}) = (O,\{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L\})$ be an MISIS. For any $l \in \{1,2,\ldots ,L-1\}$ and $c_j \in C$, we employ the granular information transformation mapping $h_j^{l,l+1}$ to assign every element in $V_j^{l}$ to its corresponding element in $V_j^{l+1}$, with the cardinality of $V_j^{l+1}$ must not surpass the cardinality of $V_j^{l}$. We use the domain information transformation mapping $\psi _j^{l,l+1}$ to map each element from attribute value $c_j^l(o)=[A_{j,l}^1(o),A_{j,l}^{2}(o)]$ of object o under the l-th scale of attribute $c_j$ to attribute value $c_j^{l+1}(o)=[A_{j,l+1}^1(o),A_{j,l+1}^{2}(o)]$ under the ($l+1$)-th scale. The cardinality of $A_{j,l+1}^1(o)$ must not exceed the cardinality of $A_{j,l}^1(o)$, and the cardinality of $A_{j,l+1}^{2}(o)$ can not be greater than the cardinality of $A_{j,l}^{2}(o)$.

For any $l \in \{1,2,\ldots ,L\}$, $c_j \in C$ and $k \le |V_j^l|$, the elements in $V_{j}^{l}$ can generate $C(|V_{j}^{l}|,k)$ different subsets with a cardinality of k, with each subset serving as an upper bound for a different interval set. According to Definition 1, there are at most $2^k$ different lower bounds for an upper bound of cardinality k. Therefore, we conclude that $|\mathcal {I} (2^{V_{j}^{l}})|=\sum \limits _{k = 0}^{| {{V_{j}^{l}}} |} {2^{k} C(|V_{j}^{l}|,k)}$.

Proposition 2

Let $S = ({O,C}) = (O,\{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L\})$ be an MISIS. For $l \in \{1,2, \ldots ,L-1\}$ and $c_j \in C$, we have

• (1) $| {V_{j}^{l+1}} | \leqslant | {V_{j}^{l}} |$,

• (2) $|\mathcal {I} (2^{V_{j}^{l+1}})| \leqslant |\mathcal {I} (2^{V_{j}^{l}})|$.

Proof

(1) For any ${v^{l + 1}}, {w^{l + 1}} \in {V_{j}^{l + 1}}$, if ${v^{l+1}} \ne {w^{l+1}}$, according to the property of surjective mappings, there exist ${v^l}, {w^l} \in {V_{j}^l}$, where ${v^l} \ne {w^l}$, such that $v^{l + 1} = h^{l,l+1}(v^l)$ and $w^{l + 1} = h^{l,l+1}(w^l)$, therefore $|V_{j}^{l + 1}| \le |V_{j}^{l}|$.

(2) For any $k \leqslant |V_{j}^{l + 1}|$, according to (1), we have $2^{k} C(|V_j^{l + 1}|,k) \leqslant 2^{k} C(|V_j^{l}|,k)$, then

$$\begin{aligned} \sum \limits _{k = 0}^{|{{V_j^{l+1}}}|} {2^{k} C(|V_j^{l + 1}|,k)} \leqslant \sum \limits _{k = 0}^{| {{V_j^{l+1}}}|} {2^{k} C(|V_j^{l}|,k)} \leqslant \sum \limits _{k = 0}^{| {{V_j^{l}}} |} {2^{k} C(|V_j^{l}|,k)}. \end{aligned}$$

Therefore, we conclude that $| {\mathcal {I} (2^{V_j^{l+1}})} | \leqslant | {\mathcal {I} (2^{V_j^{l}})} |$. $\square$

Like MISs, an MISIS can be decomposed into L single-scale sub-ISISs, denoted as $S^{l}=(O,C^{l})$, $l=1,2, \ldots ,L$.

Table 2 A multi-scale interval-set information system

For an MISIS, the similarity degree between objects may decrease as the scale becomes coarse. For example, in Table 2, $o_3$ and $o_6$ are two objects in O, where $c_1^1 (o_3)= [\{E,G\},\{E,G,T\}]$, $c_1^2 (o_3)= [\{Wb\},\{Wb,Tb\}]$, $c_1^1 (o_6)= [\{E,G\},\{E,G,R\}]$, and $c_1^2 (o_6)= [\{Wb\},\{Wb,Eb\}]$. Then we have

$$\begin{aligned} {GS}({c_1^1}(o_3),{c_1^1}(o_6))=\frac{5}{{6}} > \frac{3}{4} = {GS}({c_1^2}(o_3),{c_1^2}(o_6)). \end{aligned}$$

Therefore, if the threshold $\tau$ in Eq. (7) remains unchanged, there is a possibility of smaller similarity classes as the scale becomes coarse. To address this issue, we define a similarity relation that changes with the scale.

Proposition 3

Let $S = (O,C) = (O,\{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L \})$ be an MISIS and $B \subseteq C$. For $l \in \{1,2, \ldots ,L\}$ and $\tau ^{l} \in (0,1]$, we define

$$\begin{aligned} R_{B^l}^{\tau ^l}=\{ (o,p) \in O \times O|GS(c^{l} (o),c^{l}(p))\ge \tau ^{l},\forall c \in B \}. \end{aligned}$$

(15)

If $\tau ^{l+1} \le \lambda ^{l+1} \le \tau ^{l}$ for all $l \in \{1,2, \ldots ,L-1\}$, where

$$\begin{aligned} \lambda ^{l+1}=\min \left( {\min _{c \in C}}\left( \min _{(o,p) \in R_{C^l}^{\tau ^l}} \left( GS(c^{l+1} (o),c^{l+1}(p))\right) \right) , \tau ^{l}\right) , \end{aligned}$$

(16)

then we have $R_{C^l}^{\tau ^l}\subseteq R_{C^{l+1}}^{\tau ^{l+1}}$.

Proof

For any $(o,p) \in R_{{C^l}}^{{\tau ^l}}$ and $c \in C$, we have

$$\begin{aligned} GS(c^{l+1} (o),c^{l+1}(p)) \ge {\min _{a \in C}}\left( {{\min _{( x,y) \in R_{{C^l}}^{{\tau ^l}}}}\left( {GS(a^{l+1} (x),a^{l+1}(y))} \right) } \right) , \end{aligned}$$

i.e., $GS(c^{l+1} (o),c^{l+1}(p)) \ge {\lambda ^{l + 1}} \ge \tau ^{l+1}$, hence $(o,p) \in R_{C^{l+1}}^{\tau ^{l+1}}$, therefore $R_{C^l}^{\tau ^l} \subseteq R_{C^{l + 1}}^{\tau ^{l + 1}}$. $\square$

Remark 2

In Proposition 3, $\lambda ^{l+1}$ denotes the maximum value of threshold $\tau ^{l+1}$, ensuring that the similarity relations between objects at the l-th scale hold at the ($l+1$)-th scale. For example, suppose that in Table 2, the set of attributes only includes $c_1$, the universe of discourse only consists of objects $o_3$ and $o_6$, i.e., $C=\{c_1\}$, $O=\{o_3,o_6\}$, and $\tau ^{1}=\frac{5}{{6}}$. Objects $o_3$ and $o_6$ have the similarity relation $R_{C^1}^{\tau ^1}$ at the 1-th scale since ${GS}({c_1^1}(o_3),{c_1^1}(o_6))=\frac{5}{{6}} \ge \tau ^{1}$. By Eq. (16), we obtain $\lambda ^{2}=\frac{3}{4}$. If $\tau ^{2} \le \lambda ^{2}$, then $o_3$ and $o_6$ remain similarity relation $R_{C^2}^{\tau ^2}$ at the 2-th scale.

Based on the above discussion, hereafter we always assume that

• (1) ${\tau ^{l + 1}} \le {\lambda ^{l + 1}} \le {\tau ^l}$ for all $l \in \{1,2, \ldots ,L - 1\}$,

• (2) $\tau ^{l} \in (0,1]$ for all $l \in \{1,2, \ldots ,L\}$.

Proposition 4

Let $S = (O,C) = (O,\{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L \})$ be an MISIS, for $l \in \{1,2, \ldots ,L\}$, and $B \subseteq C$, we have

• (1) $R_{{B^l}}^{{\tau ^l}}$ is reflexive, i.e., $(o,o) \in R_{{B^l}}^{{\tau ^l}}$ for all $o \in O$,

• (2) $R_{{B^l}}^{{\tau ^l}}$ is symmetric, i.e., if $(p,o) \in R_{{B^l}}^{{\tau ^l}}$, then $(o,p) \in R_{{B^l}}^{{\tau ^l}}$.

By adjusting the threshold, we define a similarity relation that adapts to the scale change, like Eq. (7), we then give the concepts of similarity class and granular structure in an MISIS, and we can directly derive the monotonicity of these concepts with scale according to Proposition 3.

Proposition 5

Let $S = (O,C) = (O,\{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L \})$ be an MISIS, for $l \in \{1,2, \ldots ,L\}$, and $B \subseteq C$, we define

$$\begin{aligned}{} & {} SC_{B^l}^{\tau ^l}(o) = \{p|(o,p) \in R_{B^l}^{\tau ^l},p \in O \}, \, \forall o \in O, \,\, \,\, \,\, \, \, \end{aligned}$$

(17)

$$\begin{aligned}{} & {} SC_{B^l}^{\tau ^l} = \{SC_{B^l}^{\tau ^l}(o_1),SC_{B^l}^{\tau ^l}(o_2), \ldots ,SC_{B^l}^{\tau ^l}(o_n) \}. \end{aligned}$$

(18)

Then, for $l \in \{1,2, \ldots ,L-1\}$, we have

• (1) $SC_{C^l}^{\tau ^l}( o ) \subseteq SC_{C^{l + 1}}^{\tau ^{l + 1}}( o )$ for all $o \in O$,

• (2) $SC_{C^l}^{\tau ^l} \preceq SC_{C^{l + 1}}^{\tau ^{l + 1}}$.

Proposition 5 establishes the monotonicity of the granular structure in an MISIS, which indicates that, as the scale increases, the covering on the universe becomes coarse.

Definition 12

Let $S = (O,C) = (O,\{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L \})$ be an MISIS, for $l \in \{1,2,\ldots ,L\}$, $T \subseteq O$ and $B \subseteq C$, the lower and upper approximations of T w.r.t. $B^l$ and $\tau ^l$ are defined as follows:

$$\begin{aligned}{} & {} \underline{R}_{B^l}^{\tau ^l}(T)=\{o \in O|SC_{B^l}^{\tau ^l}(o)\subseteq T\}, \end{aligned}$$

(19)

$$\begin{aligned}{} & {} \overline{R}_{B^l}^{\tau ^l}(T)=\{o \in O|SC_{B^l}^{\tau ^l}(o)\cap T\not = \varnothing \}. \end{aligned}$$

(20)

Proposition 6

Let $S = (O,C) = (O,\{c_j^l|j = 1,2, \ldots ,m,l = 1,2, \ldots ,L \})$ be an MISIS and $T \subseteq O$. For $l \in \{1,2, \ldots ,L-1\}$, we have

• (1) $\underline{R} _{C^{l + 1}}^{\tau ^{l + 1}}( T ) \subseteq \underline{R} _{C^l}^{\tau ^l}( T ) \subseteq T$,

• (2) $T \subseteq {\overline{R}} _{C^l}^{\tau ^l}( T ) \subseteq {\overline{R}} _{C^{l + 1}}^{\tau ^{l + 1}}( T )$.

4 Multi-scale interval-set decision Tables

In this section, we introduce basic notions of multi-scale interval-set decision tables (MISDTs) and present their properties.

Definition 13

An MISDT is a pair $S=(O, C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\} \cup \{d\})$, where $(O,C) = (O,\{ c_j^l| j = 1,2, \ldots ,m,l = 1,2, \ldots ,L \} )$ is an MISIS, and $d \notin \{ c_j^l| j = 1,2, \ldots ,m,l = 1,2, \ldots ,L \}$ a decision with a single scale such that $d:O \rightarrow V_d$, where $V_d$ is the domain of d.

Remark 3

For an MISDT $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$, it can be decomposed into L sub-ISDTs with the same decision, denoted as $S^{l}=(O,C^{l}\cup \{d\})$, $l=1,2, \ldots ,L$.

Definition 14

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT, S is said to be consistent if $S^1 = ( O,C^1 \cup \{ d \} )$ is consistent, i.e., $SC_{C^1}^{\tau ^1} (o) \subseteq R_d (o)$ for all $o \in O$. Otherwise, S is inconsistent.

Definition 15

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT, for $l \in \{1,2, \ldots ,L\}$, and $B \subseteq C$, the positive region of d w.r.t. $B^l$ and $\tau ^l$ is defined as follows:

$$\begin{aligned} Pos_{B^l}^{\tau ^l}(O/R_d) = \bigcup \limits _{1 \le j \le t} {\underline{R} _{B^l}^{\tau ^l}( D_j )}, \end{aligned}$$

(21)

where t is the cardinality of $O/R_d$.

Proposition 7

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l \in \{1,2, \ldots ,L-1\}$, we have

$$\begin{aligned} Pos_{C^{l + 1}}^{\tau ^{l + 1}}( O/R_d ) \subseteq Pos_{C^l}^{\tau ^l}( O/R_d ). \end{aligned}$$

Definition 15 of the positive region is employed for the qualitative analysis in MISDTs. Meanwhile, information entropy is a quantitative analysis method widely used in the uncertainty measurement of rough sets. In what follows, we study the monotonicity of the modified conditional entropy in Definition 7 and its related properties.

Proposition 8

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT, for $l \in \{1,2, \ldots ,L\}$, and $B \subseteq C$, we define

$$\begin{aligned} H^{\tau ^l}(d|B^l)= & {} -\sum \limits _{i=1}^{n} \sum \limits _{j=1}^{t} \frac{|SC_{B^l}^{\tau ^l}(o_i) \cap D_j|}{n^2} \log _2 \nonumber \\{} & {} \left( \frac{|SC_{B^l}^{\tau ^l}(o_i) \cap D_j|}{|SC_{B^l}^{\tau ^l}(o_i)|}\right) , \end{aligned}$$

(22)

where n and t are the cardinalities of O and $O/R_d$, respectively. Then, for $l \in \{1,2, \ldots ,L-1\}$, we have $H^{\tau ^l}(d|C^l) \le H^{\tau ^{l+1}}(d|C^{l+1})$.

Proof

On the one hand, according to [48], we see that $f(x,y) = - x {\log _2}\frac{x}{x + y}$ is a monotonically increasing function when $x > 0$ and $y \ge 0$. And Eq.  (22) can be expressed as follows:

$$\begin{aligned} H^{\tau ^l}(d|C^l) = \sum \limits _{i = 1}^n \sum \limits _{j = 1}^t \frac{1}{n^2} f( | SC_{C^l}^{\tau ^l}(o_i) \cap D_j |,| SC_{C^l}^{\tau ^l}(o_i) \cap D_j^{\complement } | ). \end{aligned}$$

(23)

On the other hand, according to Proposition 5, for any $o_i \in O$ and $D_j \in O/R_d$, we have

$$\begin{aligned} | SC_{C^l}^{\tau ^l}(o_i) \cap D_j | \le | SC_{C^{l + 1}}^{\tau ^{l + 1}}(o_i) \cap D_j |, \end{aligned}$$

(24)

and

$$\begin{aligned} | SC_{C^l}^{\tau ^l}( o_i ) \cap D_j^{\complement } | \le | SC_{C^{l + 1}}^{\tau ^{l + 1}}(o_i) \cap D_j^{\complement } |. \end{aligned}$$

(25)

Hence $0 \le f( | SC_{C^l}^{\tau ^l}( o_i) \cap D_j |,| SC_{C^l}^{\tau ^l}(o_i) \cap D_j^{\complement } | ) \le f( | SC_{C^{l + 1}}^{\tau ^{l + 1}}( o_i) \cap D_j |,| SC_{C^{l + 1}}^{\tau ^{l + 1}}(o_i) \cap D_j^{\complement } | )$. Therefore, by Eq. (23), we obtain that $H^{\tau ^l}(d|C^l) \le H^{\tau ^{l+1}}(d|C^{l+1})$.

$\square$

Proposition 9

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l_1,\, l_2 \in \{1,2, \ldots ,L\}$, if $SC_{C^{l_1}}^{\tau ^{l_1}} = SC_{C^{l_2}}^{\tau ^{l_2}}$, then $H^{\tau ^{l_1}}( d|C^{l_1} )= H^{\tau ^{l_2}}( d| C^{l_2} )$.

Table 3 A multi-scale interval-set decision table

Example 1

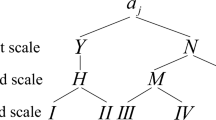
Table 3 is an MISDT $S=(O,C\cup \{d\})$, in which the MISIS (O, C) is Table 2, $O=\{o_1,o_2,\ldots ,o_8\}$ represents eight residents, with $c_1$ and $c_2$ show the abilities of listening and writing, respectively. The attribute values “E”, “G”, “R”, “V”, “T”, “Eb”, “Wb”, “Tb” mean “English”, “German”, “Russian”, “Ukrainian”, “Tibetan”, “East Slavic branch”, “West Germanic branch”, “Tibetan branch”, respectively. The granular information transformation mappings of the MISDT in Table 3 are as follows:

$$\begin{aligned} \begin{aligned} h_{j}^{1,2}(v)= \left\{ \begin{array}{ll} Wb, &{} v \in {\{G,E\}},\\ Eb, &{} v \in {\{V,R\}},\\ Tb, &{} v \in {\{T\}}, \end{array} \right. \end{aligned} j=1,2. \end{aligned}$$

Figure 1 shows the flowcharts of granular information transformation mappings and domain information transformation mappings from the 1-th scale to the 2-th scale in Table 3, respectively, where $j=1,2$. We assume that $\tau ^1 =\tau ^2=0.5$. It can be calculated that

$$\begin{aligned} O/R_d= & {} \big \{\{o_1,o_3,o_6\},\{o_2,o_4,o_5,o_7,o_8\}\big \},\\ SC_{C^{1}}^{\tau ^{1}}= & {} \big \{\{o_1\},\{o_2\},\{o_3,o_6\}, \{o_4\},\{o_5,o_7,o_8\},\\{} & {} \{o_3,o_6\}, \{o_5,o_7,o_8\},\{o_5,o_7,o_8\}\big \},\\ SC_{C^{2}}^{\tau ^{2}}= & {} \big \{\{o_1\},\{o_2\},\{o_3,o_6\}, \{o_4\},\{o_5,o_7,o_8\},\\{} & {} \{o_3,o_6\}, \{o_5,o_7,o_8\},\{o_5,o_7,o_8\}\big \}. \end{aligned}$$

And,

$$\begin{aligned}{} & {} Pos_{C^{1}}^{\tau ^{1}}(O/R_d)=O, \, H^{\tau ^{1}}(d|C^{1})=0,\\{} & {} Pos_{C^{2}}^{\tau ^{2}}(O/R_d)=O, \, H^{\tau ^{2}}(d|C^{2})=0. \end{aligned}$$

Fig. 1

Conversion flowchart of the granular information transformation mappings and the domain information transformation mappings

5 Optimal scale selection and attribute reduction in MISDTs

In this section, we discuss optimal scale selection with attribute reduction in MISDTs. It is well known that entropy is a tool for quantitatively analyzing and measuring uncertainty in information. We aim to investigate optimal scale selection and attribute reduction from the perspective of information uncertainty and quantitative analysis. To achieve this, we introduce the concept of entropy in the process of optimal scale selection and attribute reduction. Furthermore, this section suggests choosing the optimal scale according to the positive region.

Definition 16

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l \in \{1,2, \ldots ,L\}$, we say that

(1) $S^l = ( {O,C^l \cup \{ d \}})$ is positive region consistent to S if $Pos_{C^l}^{\tau ^l}(O/R_d)= Pos_{C^1}^{\tau ^1}(O/R_d)$. If $S^l$ is positive region consistent to S and $S^{l+1}$ is not positive region consistent to S (if $l + 1 \le L$), then l is the positive region optimal scale (we hereafter represent it using $l_{Pos}^{\tau ^l}$) of S.

(2) ${S^l} = (O,C^l \cup \{ d \})$ is modified conditional entropy consistent to S if $H^{\tau ^l}( d| C^l ) = H^{\tau ^1}( d| C^1 )$. If $S^l$ is modified conditional entropy consistent to S and $S^{l+1}$ is not modified conditional entropy consistent to S (if $l + 1 \le L$), then l is the modified conditional entropy optimal scale (we hereafter depict it using $l_H^{\tau ^l}$) of S.

Remark 4

According to Definition 16, we explain the optimal scale as follows:

(1) The positive region optimal scale $l_{Pos}^{\tau ^l}$ is the coarsest scale to ensure that the positive region of $S^{l_{Pos}^{\tau ^l}}$ is the same as the positive region of $S^1$.

(2)The modified conditional entropy optimal scale $l_H^{\tau ^l}$ is the coarsest scale which guarantees that the modified conditional entropy w.r.t. $\tau ^{l_{H}^{\tau ^l}}$ and $C^{l_{H}^{\tau ^l}}$ is equal to the modified conditional entropy w.r.t. $\tau ^{1}$ and $C^{1}$.

5.1 Optimal scale selection in consistent MISDTs

Proposition 10

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l \in \{1,2, \ldots ,L\}$, $H^{\tau ^l}( d| C^l) = 0$ iff $S^l$ is consistent.

Proof

“$\Rightarrow$” Assume that $H^{\tau ^l}( d| C^l) = 0$. By Proof of Proposition 8, for any $o \in O$ and $D \in O/{R_d}$, we have $f( | SC_{C^l}^{\tau ^l}( o ) \cap D |,| SC_{C^l}^{\tau ^l}( o ) \cap D^{\complement } |) = 0$. Hence, there are two, and only two outcomes, one is $| SC_{C^l}^{\tau ^l}( o ) \cap D | = 0$ and $|SC_{C^l}^{\tau ^l}( o ) \cap D^{\complement } | = | SC_{C^l}^{\tau ^l}( o ) |$, and the other is $| SC_{C^l}^{\tau ^l}( o ) \cap D | = | SC_{C^l}^{\tau ^l}( o ) |$ and $|SC_{C^l}^{\tau ^l}( o ) \cap D^{\complement } | = 0$. It follows that $SC_{C^l}^{\tau ^l}( o ) \subseteq R_d( o )$ for all $o \in O$, i.e., $S^l$ is consistent.

“$\Leftarrow$” It is a direct consequence of Definition 5 and Proof of Proposition 8. $\square$

Proposition 11

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l \in \{1,2, \ldots ,L\}$, we have

$$\begin{aligned} H^{\tau ^l}( d| C^l ) = 0 \Leftrightarrow {\overline{R}} _{C^l}^{\tau ^l}( D )-\underline{R} _{C^l}^{\tau ^l}( D ) = \emptyset , \, \forall D \in O/R_d. \end{aligned}$$

Proof

“$\Rightarrow$” Assume that $H^{\tau ^l}( d| {C^l} ) = 0$. For any $D \in O/R_d$ and $o \in {\overline{R}} _{C^l}^{\tau ^l}( D )$, according to Proof of Proposition 10, we have $SC_{C^l}^{\tau ^l}( o ) \subseteq {R_d}( o ) = D$, i.e., $o \in \underline{R} _{C^l}^{\tau ^l}( D )$, which means ${\overline{R}} _{C^l}^{\tau ^l}( D ) \subseteq \underline{R} _{C^l}^{\tau ^l}( D )$. By Proposition 6, we have ${\overline{R}} _{C^l}^{\tau ^l}( D ) = D = \underline{R} _{C^l}^{\tau ^l}( D )$. Therefore, we conclude that ${\overline{R}} _{C^l}^{\tau ^l}( D )-\underline{R} _{C^l}^{\tau ^l}( D ) = \emptyset$.

“$\Leftarrow$ ” Assume that ${\overline{R}} _{C^l}^{\tau ^l}( D )-\underline{R} _{C^l}^{\tau ^l}( D ) = \emptyset$ for all $D \in O/R_d$. For any $o \in O$, according to Proposition 6, there exists $D \in O/R_d$ such that $R_d( o ) = D={\overline{R}} _{C^l}^{\tau ^l}( D )$. Since ${\overline{R}} _{C^l}^{\tau ^l}( D ) = D$, for any $D_1 \in O/R_d - \{ D \}$, we have $o \notin D_1 = {\overline{R}} _{C^l}^{\tau ^l}( D_1)$, i.e., $SC_{C^l}^{\tau ^l}( o ) \cap D_1 = \emptyset$, hence $SC_{C^l}^{\tau ^l}( o ) \subseteq D = R_d( o )$, which means $S^l$ is consistent, thus $H^{\tau ^l}( d| C^l ) = 0$. $\square$

Proposition 12

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l \in \{1,2, \ldots ,L\}$, we have

$$\begin{aligned} H^{\tau ^l}( d| C^l ) = 0 \Leftrightarrow Pos_{C^l}^{\tau ^l}(O/R_d) = O. \end{aligned}$$

By Proposition 12, we can obtain Theorem 1.

Theorem 1

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be a consistent MISDT, we have

$$\begin{aligned} l_{Pos}^{\tau ^l} = l_H^{\tau ^l}. \end{aligned}$$

(26)

Algorithm 1

Calculate the modified conditional entropy optimal scale in an MISDT

Algorithm 1 is to search for the modified conditional entropy optimal scale in an MISDT. The time complexity (TC) of calculating both $SC_{C^l}^{\tau ^l}$ and $O/R_d$ in Algorithm 1 is $O( n^2 )$. The TC of step 5 is $O(n^2)$ because each object itself forms a decision class and a similarity class in the worst case. The worst case for step 12 is all similarity classes are the universe itself. Therefore, the TC of step 12 is $O(mn^2)$. Additionally, in the worst case, the modified conditional entropy optimal scale is the coarsest. Consequently, $O( Lmn^2 )$ is the overall TC of Algorithm 1.

Example 2

In Example 1, it is easy to observe that $S^1$ is consistent. It can be calculated that $Pos_{C^1}^{\tau ^1}(O/R_d) = Pos_{C^2}^{\tau ^2}(O/R_d)$ and $H^{\tau ^1}( d|C^1 ) = H^{\tau ^2}( d| C^2 )$, we then conclude that $l_{Pos}^{\tau ^l} = l_H^{\tau ^l} = 2$.

5.2 Optimal scale selection in inconsistent MISDTs

In this subsection, we discuss the optimal scales in an inconsistent MISDT. Firstly, by strengthening the conditions of Proposition 9, we obtain Proposition 13.

Proposition 13

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an inconsistent MISDT, for $l_1,\, l_2 \in \{1,2, \ldots ,L\}$ and $l_1 \le l_2$, we have

(1) $H^{\tau ^{l_1}}( d| C^{l_1} ) = H^{\tau ^{l_2}}( d| C^{l_2} )$ iff $SC _{C^{l_1}}^{\tau ^{l_1}}(o) = SC _{C^{l_2}}^{\tau ^{l_2}}(o)$ for all $o \in \{p \in O|p \not \in Pos_{C^{l_2}}^{\tau ^{l_2}}( O/R_d )\}$,

(2) If $H^{\tau ^{l_1}}( d| C^{l_1} ) = H^{\tau ^{l_2}}( d| C^{l_2} )$, then $Pos_{C^{l_1}}^{\tau ^{l_1}}( O/R_d ) = Pos_{C^{l_2}}^{\tau ^{l_2}}( O/R_d )$.

Proposition 13 shows that, in an inconsistent MISDT, if $S^l$ is modified conditional entropy consistent to S, then $S^l$ must be positive region consistent to S. Therefore, we obtain Theorem 2.

Theorem 2

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an inconsistent MISDT, we have

$$\begin{aligned} l_H^{\tau ^l} \le l_{Pos}^{\tau ^l}. \end{aligned}$$

(27)

According to Theorem 2, the modified conditional entropy optimal scale in an inconsistent MISDT is not greater than the positive region optimal scale. For this reason, we propose a new entropy based on Eq. (10) to quantify the amount of information in each scale and select a coarser scale to simplify the complexity.

Definition 17

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT and $B \subseteq C$. For $l \in \{1,2, \ldots ,L\}$, the positive complementary conditional entropy is defined as follows:

$$\begin{aligned} PCH^{\tau ^l}(d|B^l)= & {} \frac{1}{th}\sum \limits _{o \in Pos_{C^1}^{\tau ^1}( O/R_d )}\nonumber \\{} & {} {\sum \limits _{j = 1}^t {\frac{| SC_{B^l}^{\tau ^l}( o ) \cap D_j |}{| D_j |}} \frac{| SC_{B^l}^{\tau ^l}( o ) \cap D_j^{\complement }|}{| D_j^{\complement } |}}, \end{aligned}$$

(28)

where t and h are, respectively, the cardinalities of $O/R_d$ and $Pos_{C^1}^{\tau ^1}( O/R_d )$. Additionally, we define $PCH^{\tau ^l}( d| B^l ) = 0$ when $| O/R_d| = 1$ and specify $PCH^{\tau ^l}( d| B^l ) = 1$ when $| Pos_{C^1}^{\tau ^1}( O/R_d ) |= 0$. Note that in the following we always assume that the positive region of d w.r.t. C¹ and τ¹ is a nonempty set.

Proposition 14

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT, for $l \in \{1,2, \ldots ,L-1\}$, we have

$$\begin{aligned} PCH^{\tau ^l}( d| C^l ) \le PCH^{\tau ^{l+1}}( d| C^{l+1} ). \end{aligned}$$

Proof

Let $g( x,y) = xy$ be a monotonically increasing function for $x \ge 0$ and $y \ge 0$. In this case, Eq. (28) can be expressed as follows:

$$\begin{aligned} PCH^{\tau ^l}(d| C^l)= & {} \frac{1}{th } \sum \limits _{o \in Pos_{C^1}^{\tau ^1}( O/R_d )} \nonumber \\{} & {} {\sum \limits _{j = 1}^t {\frac{g( | SC_{C^l}^{\tau ^l}( o ) \cap D_j |,| SC_{C^l}^{\tau ^l}( o ) \cap D_j^{\complement } | )}{| D_j | | D_j^{\complement } |}} }. \end{aligned}$$

(29)

Then, for any $o \in Pos_{{C^1}}^{{\tau ^1}}\left( {O/{R_d}} \right)$ and $D \in O/{R_d}$, Eqs. (24) and (25) hold. According to the monotonicity of g(x, y), we have

$$\begin{aligned}{} & {} g( | SC_{C^l}^{\tau ^l}( o ) \cap D |,| SC_{C^l}^{\tau ^l}( o ) \cap D^{\complement } | )\\{} & {} \quad \le g( {| SC_{C^{l + 1}}^{\tau ^{l + 1}}( o ) \cap D |,| SC_{C^{l + 1}}^{\tau ^{l + 1}}( o ) \cap D^{\complement } |} ). \end{aligned}$$

Therefore, we conclude that $PCH^{\tau ^l}( d| C^l ) \le PCH^{\tau ^{l + 1}}( d| {C^{l + 1}} )$. $\square$

Proposition 15

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l \in \{1,2, \ldots ,L\}$, if $S^l$ is consistent, then $PCH^{\tau ^l}( d| C^l ) = 0$.

Proof

Since $S^l$ is consistent, by Propositions 7, 10, and 12, we have $Pos _{C^{l}}^{\tau ^{l}}( O /R_d ) = Pos _{C^{1}}^{\tau ^{1}}( O/R_d )=O$. Hence, for any $o \in O$ and $D \in O/R_d$, we have $g( | SC_{C^l}^{\tau ^l}( o ) \cap D |,| SC_{C^l}^{\tau ^l}( o ) \cap D^{\complement } | )=0$. Thus, by Eq. (29), we conclude that $PCH^{\tau ^l}(d|C^l) = 0$. $\square$

Proposition 16

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an inconsistent MISDT, for $l_1,\, l_2 \in \{1,2, \ldots ,L\}$ and $l_1 \le l_2$, if $PCH^{\tau ^{l_1}}( d| C^{l_1} ) = PCH^{\tau ^{l_2}}( d| C^{l_2} )$, then $Pos _{C^{l_1}}^{\tau ^{l_1}}( O/R_d ) = Pos _{C^{l_2}}^{\tau ^{l_2}}( O/R_d )$.

Proof

Since $PCH^{\tau ^{l_1}}( d| C^{l_1} ) = PCH^{\tau ^{l_2}}( d| C^{l_2} )$, on the one hand, for any $o \in Pos_{C^{l_1}}^{\tau ^{l_1}}( O/R_d )$, by Proof of Proposition 14, we have $g( | SC_{C^{l_2}}^{\tau ^{l_2}}( o ) \cap D |,| SC_{C^{l_2}}^{\tau ^{l_2}}( o ) \cap D^{\complement } | )=g( | SC_{C^{l_1}}^{\tau ^{l_1}}( o ) \cap D |,| SC_{C^{l_1}}^{\tau ^{l_1}}( o ) \cap D^{\complement } | )=0$ for all $D \in O/R_d$, i.e., $SC_{C^{l_2}}^{\tau ^{l_2}}( o ) \subseteq R_d( o )$, which means $o \in Pos_{C^{l_2}}^{\tau ^{l_2}}(O/R_d)$, hence $Pos_{C^{l_1}}^{\tau ^{l_1}}( O/R_d ) \subseteq Pos_{C^{l_2}}^{\tau ^{l_2}}( O/R_d )$. On the other hand, by Proposition 7, we have $Pos_{C^{l_2}}^{\tau ^{l_2}}( O/R_d ) \subseteq Pos_{C^{l_1}}^{\tau ^{l_1}}( O/R_d )$. Thus, we conclude that $Pos_{C^{l_1}}^{\tau ^{l_1}}( O/R_d ) = Pos_{C^{l_2}}^{\tau ^{l_2}}( O/R_d )$. $\square$

Definition 18

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l \in \{1,2, \ldots ,L\}$, if $PCH^{\tau ^l}( d| C^l ) = PCH^{\tau ^1}( d| C^1 )$, then $S^l = ( U,C^l \cup \{ d \} )$ is said to be positive complementary conditional entropy consistent to S. If $S^l$ is positive complementary conditional entropy consistent to S and $S^{l+1}$ is not positive complementary conditional entropy consistent to S (if $l + 1 \le L$), then l is called the positive complementary conditional entropy optimal scale (we hereafter represent it using $l_{PCH}^{\tau ^l}$) of S.

Remark 5

Based on Definition 18, we obtain that the positive complementary conditional entropy optimal scale $l_{PCH}^{\tau ^l}$ is the coarsest scale to ensure that the positive complementary conditional entropy w.r.t. $\tau ^{l_{PCH}^{\tau ^l}}$ and $C^{l_{PCH}^{\tau ^l}}$ is equal to the positive complementary conditional entropy w.r.t. $\tau ^{1}$ and $C^{1}$.

Proposition 17

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an inconsistent MISDT. If $l \in \{1,2, \ldots ,l_{PCH}^{\tau ^l}\}$, then $PCH^{\tau ^l}( d| C^l ) = 0$.

Proof

For $l \in \{1,2,\ldots ,l_{PCH}^{\tau ^l}\}$, according to Definition 18 and Proposition 14, we have $PCH^{\tau ^1}( d| C^1 )=PCH^{\tau ^l}( d| C^l )$. Then, by Proof of Proposition 15, we have $g( | SC_{C^{1}}^{\tau ^{1}}( o ) \cap D |,| SC_{C^{1}}^{\tau ^{1}}( o ) \cap D^{\complement } | )=0$ for all $o \in Pos_{C^{1}}^{\tau ^{1}}( O/R_d )$ and $D \in O/R_d$, which means $PCH^{\tau ^1}( d| C^1 ) = 0$. Therefore, $PCH^{\tau ^l}( d| C^l ) = 0$. $\square$

Proposition 18

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an inconsistent MISDT. If $l \in \{1,2, \ldots ,l_{PCH}^{\tau ^l}\}$, then $PCH^{\tau ^l}( d| C^l ) \le H^{\tau ^l}( d| C^l )$.

Proof

It is evident. $\square$

By using Propositions 12, 13, and 16, we can obtain the relationship between $H^{\tau ^l}( d| C^l )$ and $PCH^{\tau ^l}( d| C^l )$ as Proposition 19.

Proposition 19

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l,l_1,l_2 \in \{1,2, \ldots ,L\}$, we have

(1) If S is consistent, then $H^{\tau ^l}( d| C^l ) = 0$ iff $PCH^{\tau ^l}( d| C^l )=0$,

(2) If $H^{\tau ^{l_1}}( d| C^{l_1} ) = H^{\tau ^{l_2}}( d| C^{l_2} )$, then $PCH^{\tau ^{l_1}}( d| C^{l_1} ) = PCH^{\tau ^{l_2}}( d| C^{l_2} )$,

(3) If $l_1 < l_2$ and $0< PCH^{\tau ^{l_1}}( d| C^{l_1} ) < PCH^{\tau ^{l_2}}( d| C^{l_2} )$, then $H^{\tau ^{l_1}}( d| C^{l_1} ) < H^{\tau ^{l_2}}( d| C^{l_2} )$.

Proof

(1) Assume that S is consistent, according to Definition 14 and Proof of Proposition 15, we obtain $Pos_{C^1}^{\tau ^1}(O/R_d) = O$ and $PCH^{\tau ^1}( d| C^1 )=0$. If $PCH^{\tau ^l}( d| C^l )=0$, then Proposition 16 implies that $Pos_{C^l}^{\tau ^l}(O/R_d) = O$. As a result, $S^l$ is consistent, and it follows that $H^{\tau ^l}( d| C^l ) = 0$. Conversely, if $H^{\tau ^l}( d| C^l ) = 0$, then by Proposition 12, we have $Pos_{C^l}^{\tau ^l}(O/R_d) = O$. Therefore, based on Proof of Proposition 15, we deduce that $PCH^{\tau ^l}( d| C^l )=0$.

(2) It is direct consequence of Proposition 13 and Proof of Proposition 14.

(3) Assume that $0< PCH^{\tau ^{l_1}}( d| C^{l_1} ) < PCH^{\tau ^{l_2}}( d| C^{l_2} )$. Based on Proof of Proposition 14, there exists at least one $o \in U$ such that $SC _{C^{l_1}}^{\tau ^{l_1}}(o) \subset SC _{C^{l_2}}^{\tau ^{l_2}}(o)$ and $o \notin Pos_{C^{l_2}}^{\tau ^{l_2}}(O/R_d)$. Therefore, by Proposition 13, we have $H^{\tau ^{l_1}}( d| C^{l_1} ) < H^{\tau ^{l_2}}( d| C^{l_2} )$. $\square$

Theorem 3

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an inconsistent MISDT, we have

$$\begin{aligned} l_{PCH}^{\tau ^l} = l_{Pos}^{\tau ^l}. \end{aligned}$$

(30)

Proof

Suppose $l = l_{PCH}^{\tau ^l}$, we have $PCH^{\tau ^1}( d| C^1 ) = PCH^{\tau ^l}( d| C^l )$. By Proposition 16, we obtain $Pos_{C^l}^{\tau ^l}( O/R_d ) = Pos_{C^1}^{\tau ^1}( O/R_d )$, hence $l_{PCH}^{\tau ^l} \le l_{Pos}^{\tau ^l}$. Now, we are to prove $l_{Pos}^{\tau ^l} \le l_{PCH}^{\tau ^l}$. Suppose $l = l_{Pos}^{\tau ^l}$, we see that $Pos_{C^l}^{\tau ^l}( O/R_d ) = Pos_{C^1}^{\tau ^1}( O/R_d )$. Then, by Proof of Proposition 15, we observe that $PCH^{\tau ^l}( d| C^l )=0=PCH^{\tau ^1}( d| C^1 )$, thus $l_{Pos}^{\tau ^l} \le l_{PCH}^{\tau ^l}$. Therefore, $l_{Pos}^{\tau ^l} = l_{PCH}^{\tau ^l}$. $\square$

Remark 6

According to Theorems 2 and 3, we conclude that $l_{H}^{\tau ^l} \le l_{Pos}^{\tau ^l} = l_{PCH}^{\tau ^l}$ in an inconsistent MISDT.

Algorithm 2

Calculate the positive complementary conditional entropy optimal scale in an MISDT

Algorithm 2 is utilized to seek for the positive complementary conditional entropy optimal scale when the positive region under the finest scale is a nonempty set. In step 6, the TC of identifying the positive region is $O( n^2 )$. The TC of steps 7 and 18 is $O(n^2)$ because the universe is equal to the positive region in the worst case. Consequently, the overall TC is $O( L m n^2 )$.

Table 4 An inconsistent multi-scale interval-set decision table

Example 3

Table 4 depicts an inconsistent MISDT. We assume that $\tau ^{1}=\tau ^{2}=0.5$. It can be calculated that

$$\begin{aligned} O/R_d= & {} \big \{\{o_1,o_4,o_7\},\{o_2,o_3,o_5\},\{o_6,o_8\}\big \},\\ SC_{C^{1}}^{\tau ^{1}}= & {} \big \{\{o_1,o_3, o_7\},\{o_2,o_4,o_5,o_7,o_8\},\{ o_1, o_3\}, \\{} & {} \{o_2, o_4, o_5, o_8\},\{o_2, o_4, o_5\},\{ o_6\},\{ o_1, o_2, o_7\},\{ o_2, o_4, o_8\}\big \},\\ SC_{C^{2}}^{\tau ^{2}}= & {} \big \{\{o_1,o_3,o_4,o_5,o_7\},\{o_2,o_4,o_5,o_7,o_8\},\{ o_1,o_3,o_4,o_5,o_7\}, \\{} & {} O-\{o_6\}, O-\{o_6\},\{o_6\}, O-\{o_6\},\{o_2,o_4,o_5,o_7,o_8\}\big \}. \end{aligned}$$

And,

$$\begin{aligned}{} & {} Pos_{C^{1}}^{\tau ^{1}}(O/R_d)= \{o_6\}, \, H^{\tau ^{1}}(d|C^{1})=0.45, \, PCH^{\tau ^{1}}(d|C^{1})=0,\\{} & {} Pos_{C^{2}}^{\tau ^{2}}(O/R_d)= \{o_6\}, \, H^{\tau ^{2}}(d|C^{2})=0.86, \, PCH^{\tau ^{2}}(d|C^{2})=0. \end{aligned}$$

Since $Pos_{C^2}^{\tau ^2}( O/R_d ) = Pos_{C^1}^{\tau ^1}( O/R_d )$ and $PCH^{\tau ^2}( d| C^2 ) = PCH^{\tau ^1}( d| C^1 )$, we obtain that $l_{Pos}^{\tau ^l} = l_{PCH}^{\tau ^l} = 2$. Subsequently, notice that $H^{\tau ^2}( d| C^2 ) \ne H^{\tau ^1}( d| C^1 )$, we conclude that $l_H^{\tau ^l} = 1$. Thus, $l_H^{\tau ^l} \le l_{Pos}^{\tau ^l} = l_{PCH}^{\tau ^l}$.

5.3 Attribute reduction in MISDTs

In [48], the reduction of single-scale decision tables based on modified conditional entropy was discussed. In this subsection, based on the positive region optimal scale and the positive complementary conditional entropy optimal scale, we study attribute reduction in MISDTs.

Definition 19

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT and $\emptyset \not = B \subseteq C$. For the positive complementary conditional entropy optimal scale $l_{PCH}^{\tau ^l}$ and the positive region optimal scale $l_{Pos}^{\tau ^l}$, we say that

(1) B is an $l_{PCH}^{\tau ^l}$-reduct if $PCH^{\tau ^{l_{PCH}^{\tau ^l}}}(d|C^{l_{PCH}^{\tau ^l}})=PCH^{\tau ^{l_{PCH}^{\tau ^l}}}(d|B^{l_{PCH}^{\tau ^l}})$ and $PCH^{\tau ^{l_{PCH}^{\tau ^l}}}(d|C^{l_{PCH}^{\tau ^l}}) \ne PCH^{\tau ^{l_{PCH}^{\tau ^l}}}(d|\{B-c\}^{l_{PCH}^{\tau ^l}})$ for all $c \in B$.

(2) B is an $l_{Pos}^{\tau ^l}$-reduct if $Pos_{C^{l_{Pos}^{\tau ^l}}}^{\tau ^{l_{Pos}^{\tau ^l}}}(O/R_d)=Pos_{B^{l_{Pos}^{\tau ^l}}}^{\tau ^{l_{Pos}^{\tau ^l}}}(O/R_d)$ and $Pos_{C^{l_{Pos}^{\tau ^l}}}^{\tau ^{l_{Pos}^{\tau ^l}}}(O/R_d) \ne Pos_{\{B-c\}^{l_{Pos}^{\tau ^l}}}^{\tau ^{l_{Pos}^{\tau ^l}}}(O/R_d)$ for all $c \in B$.

Proposition 20

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $B \subseteq C$ and $l\in \{1,2, \ldots ,L\}$, we have

(1) $Pos_{B^l}^{\tau ^l}( O/R_d ) \subseteq Pos_{C^{l}}^{\tau ^{l}}( O/R_d )$,

(2) $PCH^{\tau ^{l}}( d| C^{l} ) \le PCH^{\tau ^l}( d| B^l )$.

Proof

(1) It follows immediately from Proposition 1 and Definition 15.

(2) For any $o \in Pos_{C^1}^{\tau ^1}( O/R_d )$, and $R_d(o)=D \in O/R_d$, according to Propositions 1 and 7, we have $SC_{C^{l}}^{\tau ^{l}}(o) \subseteq SC_{B^{l}}^{\tau ^{l}}(o)$, and $Pos_{B^l}^{\tau ^l}( O/R_d ) \subseteq Pos_{C^l}^{\tau ^l}( O/R_d ) \subseteq Pos_{C^1}^{\tau ^1}( O/R_d )$. When $o \in Pos_{C^1}^{\tau ^1}( O/R_d )-Pos_{C^l}^{\tau ^l}( O/R_d )$, we have $SC_{C^{l}}^{\tau ^{l}}(o) \not \subset D$, which means

$$\begin{aligned}{} & {} 0 <g( | SC_{C^{l}}^{\tau ^{l}}( o ) \cap D |,| SC_{C^{l}}^{\tau ^{l}}( o ) \cap D^{\complement } | ) \\{} & {} \quad \le g( | SC_{B^{l}}^{\tau ^{l}}( o ) \cap D |,| SC_{B^{l}}^{\tau ^{l}}( o ) \cap D^{\complement } | ). \end{aligned}$$

When $o \in Pos_{C^l}^{\tau ^l}( O/R_d )-Pos_{B^l}^{\tau ^l}( O/R_d )$, we have $SC_{C^{l}}^{\tau ^{l}}(o) \subseteq D$ and $SC_{B^{l}}^{\tau ^{l}}(o) \not \subset D$, thus

$$\begin{aligned}{} & {} 0 =g( | SC_{C^{l}}^{\tau ^{l}}( o ) \cap D |,| SC_{C^{l}}^{\tau ^{l}}( o ) \cap D^{\complement } | ) \\{} & {} \quad < g( | SC_{B^{l}}^{\tau ^{l}}( o ) \cap D |,| SC_{B^{l}}^{\tau ^{l}}( o ) \cap D^{\complement } | ). \end{aligned}$$

When $o \in Pos_{B^l}^{\tau ^l}( O/R_d )$, we have $SC_{B^{l}}^{\tau ^{l}}(o) \subseteq D$, which shows that

$$\begin{aligned}{} & {} 0 =g( | SC_{C^{l}}^{\tau ^{l}}( o ) \cap D |,| SC_{C^{l}}^{\tau ^{l}}( o ) \cap D^{\complement } | ) \\{} & {} \quad = g( | SC_{B^{l}}^{\tau ^{l}}( o ) \cap D |,| SC_{B^{l}}^{\tau ^{l}}( o ) \cap D^{\complement } | ). \end{aligned}$$

Therefore, by Proof of Proposition 14, we have $PCH^{\tau ^{l}}( d| C^{l} ) \le PCH^{\tau ^l}( d| B^l )$. $\square$

Propositions 21 and 22 can be derived similar to Propositions 15, 16, and 17.

Proposition 21

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $B \subseteq C$ and $l\in \{1,2, \ldots ,L\}$, if $PCH^{\tau ^{l}}( d| C^{l} ) = PCH^{\tau ^{l}}( d| B^{l} )$, then $Pos _{C^{l}}^{\tau ^{l}}( O/R_d ) = Pos _{B^{l}}^{\tau ^{l}}( O/R_d )$.

Proposition 22

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $B \subseteq C$ and $l\in \{1,2, \ldots ,L\}$, if $Pos _{C^{1}}^{\tau ^{1}}( O/R_d ) = Pos _{B^{l}}^{\tau ^{l}}(O/R_d )\not = \emptyset$, then $PCH^{\tau ^{l}}( d| B^{l} ) =0$.

Proposition 23

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $l_1,\, l_2\in \{1,2, \ldots ,L\}$ and $A,\, B \subseteq C$, if $SC_{B^{l_1}}^{\tau ^{l_1}}( o ) = O$ for all $o \in Pos_{C^1}^{\tau ^1}( O/R_d )$, then $PCH^{\tau ^{l_2}}( d| A^{l_2} ) \le PCH^{\tau ^{l_1}}( d| B^{l_1} )$.

Proof

Since $SC_{B^{l_1}}^{\tau ^{l_1}}( o ) = O$ for all $o \in Pos_{C^1}^{\tau ^1}( O/R_d )$, we obtain that $| SC_{A^{l_2}}^{\tau ^{l_2}}( o ) \cap D^{\complement } | \le | D^{\complement } |=| SC_{B^{l_1}}^{\tau ^{l_1}}(o) \cap D^{\complement } |$ and $| SC_{A^{l_2}}^{\tau ^{l_2}}( o ) \cap D| \le | D|=| SC_{B^{l_1}}^{\tau ^{l_1}}(o) \cap D|$ for all $D \in O/R_d$. Then, by Proof of Proposition 14, we conclude that $PCH^{\tau ^{l_2}}( d| A^{l_2} ) \le PCH^{\tau ^{l_1}}( d| B^{l_1} )=1$. $\square$

Remark 7

By Propositions 22 and 23, we see that the domain of positive complementary conditional entropy is [0, 1].

According to Propositions 16, 17, 21, and 22, we can obtain the relationship between an $l_{Pos}^{\tau ^l}$-reduct and an $l_{PCH}^{\tau ^l}$-reduct as Theorem 4.

Theorem 4

Let $S=(O,C \cup \{d\})=(O,\{c_j^l | j=1,2,\ldots ,m,l=1,2, \ldots ,L\}\cup \{d\})$ be an MISDT. For $B \subseteq C$, B is an $l_{Pos}^{\tau ^l}$-reduct iff B is an $l_{PCH}^{\tau ^l}$-reduct.

Algorithm 3

Calculate an $l_{PCH}^{\tau ^l}$-reduct in an MISDT

Compared to $l_{Pos}^{\tau ^l}$-reduct, the advantage of $l_{PCH}^{\tau ^l}$-reduct lies in its ability to measure the information content of a dataset as a whole and represent the overall information content of the data with a single numerical value. Algorithm 3 is used to find an $l_{PCH}^{\tau ^{l}}$-reduct. The TC of steps 12 to 14 is $O(n^2 m)$. Additionally, in the worst case, each attribute forms an $l_{PCH}^{\tau ^{l}}$-reduct. Therefore, the overall TC of Algorithm 3 is $O(n^2\,m^2)$.

Example 4

In Example 3, we have $l_{Pos}^{\tau ^l} = l_{PCH}^{\tau ^l} = 2$. It can be calculated that

$$\begin{aligned} SC_{\{c_1\}^{2}}^{\tau ^{2}}= & {} \big \{\{o_1,o_3, o_4, o_5,o_7\},\{o_2,o_4, o_5, o_7,o_8\},\{o_1,o_3, o_4, o_5,o_7\}, \\{} & {} O-\{o_6\},O-\{o_6\},\{o_6\},O-\{o_6\},\{o_2,o_4, o_5, o_7,o_8\}\big \},\\ SC_{\{c_2\}^{2}}^{\tau ^{2}}= & {} \big \{O-\{o_2\},\{o_2,o_4, o_5, o_7,o_8\}, O-\{o_2\}, \\{} & {} O,O,O-\{o_2\},O,O\big \}. \end{aligned}$$

And,

$$\begin{aligned}{} & {} Pos_{\{c_1\}^{2}}^{\tau ^{2}}(O/R_d)=\{o_6\}, \, PCH^{\tau ^{2}}(d|\{c_1\}^{2})=0,\\{} & {} Pos_{\{c_2\}^{2}}^{\tau ^{2}}(O/R_d)=\emptyset , \, PCH^{\tau ^{2}}(d|\{c_2\}^{2})=0.77. \end{aligned}$$

Since $Pos_{C^2}^{\tau ^2}( O/R_d ) = Pos_{\{c_1\}^{2}}^{\tau ^{2}}(O/R_d)$ and $PCH^{\tau ^{2}}(d|\{c_1\}^{2})= PCH^{\tau ^2}( d| C^2 )$, we conclude that $\{c_1\}$ is both an $l_{Pos}^{\tau ^l}$-reduct and an $l_{PCH}^{\tau ^l}$-reduct.

6 Experiments

In this section, we validate the feasibility and effectiveness of the proposed MISDT model, as well as its corresponding optimal scale selection algorithm and attribute reduction algorithm with experiments. All experimental hardware setups are configured as Windows 10, Intel(R) Core(TM) i7-6700HQ CPU @ 2.60GHz, and 8GB memory. The software environment for executing the algorithm is MATLAB R2019a.

The experimental data is obtained from 8 datasets in the UCI database, as shown in Table 5. Since no existing MISDTs are available in the datasets, it is necessary to preprocess the data and construct the corresponding MISDTs.

Table 5 A description of data sets

The construction of MISDTs is based on the data construction methods analogized in [9] and [47]. The specific construction processes are as follows:

step 1. If an object’s attribute value is a semantic data value, it must be converted to an integer value.

step 2. Following the construction method of MDTs in [9], we determine the domain of any attribute under any scale. In this experiment, we first standardize all attribute values of the initial ISs, and we then adjust the cardinality to 8 within the domain of each attribute at the finest scale. As the scale becomes coarse by one unit, the cardinality of the domain of each attribute decreases by one unit until they reach 3, completing the construction of domains of each attribute under each scale. Hence, in this experiment, the scales of each conditional attribute in all the datasets are uniformly set to 6.

step 3. Following the construction method of ISDTs in [47], we construct an ISIS for each IS that has been standardized at the finest scale. In construction, a fixed number of missing values are randomly assigned to an original IS to create interval sets. Here, the parameter $\delta$ represents the extent of missing data, where, for example, $\delta =0.25$ indicates a $25\%$ loss of items c(o) in the original information system.

step 4. We achieve the interval set transformation at each scale using the domain information transformation mapping $\psi _j^{l,l+1}$ defined in Definition 11, which results in an MISDT. Moreover, we describe the parameter $\tau ^1$ as the threshold in the similarity relation $R_{C^1}^{\tau ^1}$ at the finest scale.

Our experiments utilize Algorithms 1 and 2 to obtain the modified conditional entropy optimal scale and the positive complementary conditional entropy optimal scale, respectively. Then, we obtain an $l_{PCH}^{\tau ^l}$-reduct through Algorithm 3. In this experiment, we employ the ten-fold cross-validation method and the K-Nearest Neighbor (KNN) classifier to evaluate the classification performance of two optimal scales and $l_{PCH}^{\tau ^l}$-reduct. To obtain the best classification accuracy in the KNN classifier, we select the k values for each dataset, as shown in Table 6. Additionally, Eq. (4) is employed to construct the distance function $Dis(\mathcal {X},\mathcal {Y})$ between any two interval sets $\mathcal {X}$ and $\mathcal {Y}$ on the power set of a finite set V. The specific expression of the distance function $Dis(\mathcal {X},\mathcal {Y})$ is as follows:

$$\begin{aligned} Dis(\mathcal {X},\mathcal {Y})=1-GS(\mathcal {X},\mathcal {Y}). \end{aligned}$$

(31)

Table 6 A description of k value selection for data sets

6.1 Similarity measures comparison experiments

In [48], the authors compared the effects of different similarity measures on the classification performance of attribute reduction. However, there needs to be more research on the impact of distinct similarity measures on the classification performance of the optimal scale in MISDTs. To address this gap, we compare the performance of entropy optimal scales with three similarity measures. These similarity measures are derived from Eq. (4), [14] and [46]. For any two interval sets $\mathcal {X}=[{X_1},{X_2}]$ and $\mathcal {Y}=[{Y_1},{Y_2}]$ on the power set of a finite set V, the similarity degree in [46] is denoted as follows:

$$\begin{aligned} GS(\mathcal {X},\mathcal {Y}) = \frac{| X_1 \cap Y_1 |}{2| X_1 \cup Y_1 |} + \frac{| X_2 \cap Y_2 |}{2| X_2 \cup Y_2 |}, \end{aligned}$$

(32)

while the similarity degree in [14] is described as follows:

$$\begin{aligned} GS(\mathcal {X},\mathcal {Y}) = \frac{1}{3}\sum \limits _{i = 1}^3 {\frac{| U_i(\mathcal {X}) \cap U_i(\mathcal {Y}) |}{| U_i(\mathcal {X}) \cup U_i(\mathcal {Y}) |}}, \end{aligned}$$

(33)

where ${U_1}(\mathcal {X}) = {X_1}$, ${U_2}(\mathcal {X}) = {X_2} - {X_1}$, and ${U_3}(\mathcal {X}) = O - {X_2}$.

Additionally, we provide specific experimental results depicted in Figs. 2, 3, 4, 5, 6, 7, 8, 9, in which the parameter $\tau ^1 \in \{0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9\}$ and the parameter $\delta =0.25$. In the legends of Figs. 2, 3, 4, 5, 6, 7, 8, 9, M1, M2, and M3 indicate the classification accuracy achieved by the optimal scale obtained via formulas Eqs.  (4), (32), and (33) as similarity measures, respectively. Figures 2, 3, 4, 5, 6, 7, 8, 9 demonstrate that using the similarity in Eq. (4) as a benchmark, the positive complementary conditional entropy optimal scale yields the highest classification accuracy for most datasets. Similarly, the performance evaluation of the modified conditional entropy optimal scale also leads to the same conclusion. Figures 2, 3, 4, 5, 6, 7, 8, 9 suggest that the similarity formula used in this paper can better evaluate the relationship between different interval sets, thus we obtain an appropriate scale for knowledge discovery and rule extraction. In addition, in Figs. 6 and 7, the classification accuracy based on the optimal scales of two entropies is the same, which indicates positive complementary conditional entropy simplifies information complexity while ensuring classification capability.

Fig. 2

A comparison of the performance of optimal scales obtained from three similarity benchmarks in the dataset Breast cancer

Fig. 3

A comparison of the performance of optimal scales obtained from three similarity benchmarks in the dataset Breast tissue

Fig. 4

A comparison of the performance of optimal scales obtained from three similarity benchmarks in the dataset Ecoli

Fig. 5

A comparison of the performance of optimal scales obtained from three similarity benchmarks in the dataset Fertility

Fig. 6

A comparison of the performance of optimal scales obtained from three similarity benchmarks in the dataset Glass identification

Fig. 7

A comparison of the performance of optimal scales obtained from three similarity benchmarks in the dataset Iris

Fig. 8

A comparison of the performance of optimal scales obtained from three similarity benchmarks in the dataset Wholesale customers (region)

Fig. 9

A comparison of the performance of optimal scales obtained from three similarity benchmarks in the dataset Vertebral column

6.2 Optimal scale performance experiments

For each dataset, we compare the classification accuracies under the finest scale $l_{Fin}$, the coarsest scale $l_{Coa}$, the modified conditional entropy optimal scale $l_{H}^{\tau ^{l}}$, and the positive complementary conditional entropy optimal scale $l_{PCH}^{\tau ^{l}}$.

Experimental results are shown in Table 7, where the parameters used are $\delta =0.25$ and $\tau ^1=0.5$. From Table 7, the proposed optimal scales perform well on most datasets. Among the eight datasets, the positive complementary conditional entropy optimal scale achieves the highest classification accuracy in seven datasets. In comparison, the modified conditional entropy optimal scale achieves the highest classification accuracy in five datasets. Experimental results indicate that the optimal scale balances the fitting effect on training data and the generalization ability, resulting in higher classification accuracy on test datasets.

Additionally, under the conditions of $\delta =0.25$ and $\tau ^1=0.5$, Table 8 illustrates the average optimal scale obtained through ten-fold cross-validation, while Table 9 shows the classification accuracy achieved through an $l_{PCH}^{\tau ^l}$-reduct.

Table 7 A comparison of classification performance at various scales

Table 8 A description of the optimal scale of the data sets

Table 9 A description of the $l_{PCH}^{\tau ^l}$-reduct classification performance

6.3 Parameter evaluation experiments

Finally, we discuss the impact of parameters $\delta$ and $\tau ^1$ on the performance of the positive complementary conditional entropy optimal scale. Figures 10 and 11 describe the effect of parameter variations. The x-axis represents parameter $\tau ^1$, ranging from 0.5 to 0.9. The y-axis indicates parameter $\delta$, ranging from 0.25 to 0.55. Furthermore, the z-axis expresses the classification accuracy obtained using the KNN classifier. From Figs. 10 and 11, we can observe that parameter $\delta$ significantly impacts the classification accuracy across all datasets. However, parameter $\tau ^1$ minimizes classification accuracy for specific datasets, as shown in Fig. 10a. Moreover, different combinations of parameter values result in varying classification accuracy. For instance, in Fig. 11a, the classification accuracy reaches its minimum value of 93.23% when $\delta =0.4$ and $\tau ^1=0.65$, and the classification accuracy reaches its maximum value of 95.79% when $\delta =0.3$ and $\tau ^1=0.9$ in Fig. 10b.

Fig. 10

The impact of different parameter settings on the optimal scale performance

Fig. 11

The impact of different parameter settings on the optimal scale performance

7 Conclusion

Multi-scale data analysis has attracted significant attention in the research of GrC. However, the study of information systems that involve multiple scales and interval sets of attribute values still needs to be explored. In this paper, we have studied optimal scale selection and attribute reduction in MISDTs. We have first introduced the concept of an MISIS, and have defined a scale-adaptive similarity relation for each attribute set with each scale. In consistent MISDTs, we have proposed two optimal scale selection methods based on the positive region and modified conditional entropy, and examined their equivalence through rigorous proof. For inconsistent MISDTs, we have defined a new entropy measure called positive complementary conditional entropy, established the positive complementary conditional entropy optimal scale, and investigated its relationship with those above two optimal scales. Based on an optimal scale, we have also developed attribute reduction methods in MISDTs. Finally, we have conducted experiments on our proposed algorithms to verify three points, i.e., the reasonableness of the similarity formula used in this paper, the advantages of the effectiveness of the proposed optimal scale, and the productivity of the presented algorithm.

Our future research will consider optimal scale selection by integrating various measures of uncertainty and will focus on rule extraction in MISDTs. Moreover, we will aim to investigate knowledge acquisition in generalized MISDTs and incomplete MISDTs.