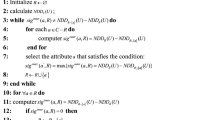Semi-supervised attribute reduction via attribute indiscernibility

Abstract

Attribute reduction based on rough sets plays an important role in data preprocessing. Discernibility pair, as an effective information measurement, has received extensive attention in attribute reduction. Unfortunately, the existing attribute importance measurement strategies based on discernibility pairs do not apply well to partially labeled data. Meanwhile, most of the existing attribute reduction algorithms focus on the relationships between objects and neglect the relationships between attributes, which may bring highly redundant attributes. Under the background of rough set theory, this paper studies the issue of semi-supervised attribute reduction, i.e. attribute reduction for partially labeled data. Firstly, we introduce the concept of discernibility pair based on object indiscernibility and propose a semi-supervised attribute reduction algorithm via the maximum discernibility pair by combining supervised and unsupervised discernibility pair strategies. Secondly, considering the relationships between attributes, we put forward new methods to define the similarity and distinction between attributes by discernibility pairs. Thirdly, we propose a semi-supervised attribute reduction algorithm by indiscernible attribute classes. Finally, comparative experiments indicate that the proposed algorithms are effective.

1 Introduction

Rough set theory, proposed by Pawlak [1, 2], is a new mathematical tool to deal with fuzzy and uncertain information. One of the core contents of rough set theory is attribute reduction, also called feature selection, which is a very important data preprocessing procedure. Attribute reduction removes irrelevant attributes to reduce the difficulty of learning tasks [3, 4].

The most of rough set methods partition the universe based on the indiscernibility relation between objects. Chen et al. [5] proposed a selection method of sample pairs in rough sets. Dai et al. [6] defined the discernibility relationship between objects in the framework of fuzzy rough sets, namely the maximal discernibility pair. Dai and Xu [7] proposed an attribute reduction method based on information gain ratio. Wang et al. [8] presented a new information term denoted as independent classification information. Susmaga [9] applied both indiscernibility relation and discernibility relation to attribute reduction. Based on the relative indiscernibility relation and relative discernibility relation of decision systems, Qin and Jing [10] proposed the concepts of $\lambda$ reduction and $\mu$ reduction. Dai et al. [11] constructed two feature selection methods through label symmetric uncertainty correlation learning and feature redundancy evaluation. Qian et al. [12] proposed a mixed attribute reduction algorithm based on indiscernibility relation and differential relation.

It is worth noting that relationships exist not only between objects, but also between attributes. When studying attribute reduction algorithms, most researchers only consider the indiscernibility relation between objects and neglect the relationships between attributes. Actually, relationships between attributes are also very important for attribute reduction. Based on the relationships between attributes, attribute redundancy can be reduced by removing needless attributes and attribute independence can be improved by selecting high-quality attributes. Relationships between attributes have attracted the attention of some scholars in the machine learning community [13, 14]. Mitra et al. [13] proposed the definition of attribute similarity based on the maximum information compression index to carry out attribute clustering. Restrepo and Cornelis [15] adopted functional dependency relations to get the reducts. Jia et al. [16] defined an attribute reduction method based on similarity from the perspective of clustering. Kudo and Murai [17] proposed a binary relationship between different attribute values of the same object.

Attribute reduction methods for complete data have been extensively studied in the field of rough sets. Unfortunately, because it is not easy to obtain the labels of objects, partially labeled data are more common in the real world. Some scholars have studied semi-supervised attribute reduction [18]. Dai et al. [19] proposed a semi-supervised attribute reduction method based on dual-dependency. In [20], Saha et al. used the simulated annealing method to deal with the multi-objective optimization problem consisting of feature selection and semi-supervised clustering. Chang and Yang [21] improved the performance of feature selection by mining the correlation among multiple tasks. Mi et al. [22] achieved dynamic classification learning over the semi-supervised data through concept-cognitive computing system. Xu et al. [23] studied a semi-supervised feature selection algorithm based on Pearson’s correlation coefficient. Mi et al. [24] proposed a semi-supervised concept learning method from the perspective of concept space. Dai et al. [25] proposed two semi-supervised attribute reduction algorithms by applying discernibility pairs to partially labeled data sets.

Based on the above analysis, the motivations of this paper are as follows:

• 1. When studying semi-supervised attribute reduction algorithms, some researchers [25, 26] regarded the importance of attribute subsets as the sum of the importance on labeled data and unlabeled data. However, these methods have a certain shortcoming, that is, they cannot well represent the change of the importance of attribute subsets at different missing rates of datasets. In view of this, in order to measure the discernibility ability of attributes in partially labeled decision information systems, we introduce the concept of discernibility pair based on object indiscernibility. Inspired by the supervised and unsupervised discernibility pair strategies proposed by Dai et al. [25], we combine discernibility pairs from labeled data with discernibility pairs from unlabeled data, and propose a semi-supervised attribute reduction algorithm based on the maximum discernibility pair. Therefore, the combined discernibility pairs can better explain the discernibility ability of attributes and adapt to the change of missing rate.

• 2. In the field of rough sets, most studies regard a single attribute as a granularity, and many attribute reduction algorithms are proposed. In this process, however, attributes that contain similar discernibility information may be selected into the attribute subset. In other words, redundant attributes are selected into the attribute subset. To handle this issue, this paper proposes a new attribute reduction method. Firstly, we introduce the concept of discernibility pair as a criterion for quantifying the discernibility ability of attributes. Considering the relationship between attributes, we define new fuzzy similarity relation and fuzzy discernibility relation between attributes based on discernibility pairs. Further, inspired by the attribute granulation, we regard the fuzzy discernibility relationship as a distance function and divide the attribute set into indiscernible attribute classes. For the attributes in an indiscernible attribute class, a representative attribute is selected. Therefore, we can delete redundant attributes by selecting representative attributes and propose a semi-supervised attribute reduction algorithm based on attribute indiscernibility.

The rest of this paper is organized as follows. Section 2 reviews some basic notations of rough set theory. In Section 3, new methods to measure the similarity and distinction between attributes are advanced and attribute reduction algorithms based on the maximum discernibility pair and attribute indiscernibility are proposed. Experiments are carried out to verify the performance of the proposed algorithms in Section 4. Conclusion is presented in Section 5.

2 Preliminary knowledge

2.1 Some basic concepts of rough sets

Rough set theory is an effective mathematical tool for processing uncertain information. This section reviews some basic symbols of rough set theory [1, 2].

Definition 1

An information system and a decision information system are respectively represented as $IS=<U,C,V,f>$ and $DS=<U,C\cup \{ d\} ,V,f>$, where $U=\{x_1,x_2,\ldots ,x_n\}$ is a nonempty finite set of objects; $C=\{a_1,a_2,\ldots ,a_m\}$ is a nonempty finite set of conditional attributes, and d is a label of an object; $V=\cup _{a\in C\cup \{ d\}}V_{a}$ and $V_{a}$ is the domain of attribute a; f is a mapping function, which maps an object in U to exactly one value from domains of an attribute such as $\forall a \in C\cup \{ d\},x\in U,f(a,x)\in V_{a}$ and f(a, x) is the value of the object x on attribute a. If $\exists x\in U$ such that f(d, x) is equal to a missing value denoted as $*$, then we call it a partially labeled decision information system $PLDS=<U,C\cup \{ d\},V^*,f>$.

For simplicity, we use a(x) to denote f(a, x) and d(x) to denote f(d, x) in this paper.

Definition 2

Let $IS=<U,C,V,f>$ be an information system. $S\subseteq C$ is a subset of the conditional attribute set C. The indiscernibility relation on S is defined as follows:

$$\begin{aligned} IND(S)=\{(x,y)\in U\times U~|~\forall a\in S, a(x)=a(y)\}. \end{aligned}$$

(1)

The indiscernibility relation IND(S) means that x and y are indistinguishable by the attribute subset S. Thus, the partition on U induced from IND(S) is expressed as either U/IND(S) or U/S.

Based on the indiscernibility relation, for $X\subseteq U$, the lower approximation and the upper approximation are defined as follows.

Definition 3

Let $IS=<U,C,V,f>$ be an information system, $X\subseteq U$ and $S\subseteq C$. The lower approximation and the upper approximation of X with respect to S can be defined as follows:

$$\begin{aligned} \begin{aligned} {\underline{S}}(X)& =\{x\in U~|~[x]_S\subseteq X \} ;\\ {\overline{S}}(X)& = \{x\in U~|~[x]_S\cap X\ne \varnothing \} . \end{aligned} \end{aligned}$$

(2)

The lower approximation of a set X with respect to IND(S) is the set of the objects which certainly belongs to X. The upper approximation of a set X with respect to IND(S) is the set of the objects which possibly belongs to X.

Definition 4

Let $IS=<U,C,V,f>$ be an information system. The discernibility matrix IM is a $|U|\times |U|$ matrix. For $S\subseteq C$, each item IM(x, y) represents the attribute set that can distinguish object x from object y.

$$\begin{aligned} IM(x,y)=\{ a\in S~|~a(x)\ne a(y)\} . \end{aligned}$$

(3)

Definition 5

Let $IS=<U,C,V,f>$ be an information system. $S\subseteq C$ is a reduct of IS if and only if:

• (1) $\forall x,y\in U,if \ IM(x,y)\ne \varnothing , then \ S\cap IM(x,y)\ne \varnothing$;

• (2) $\forall S'\subset S, \exists IM(x,y)\ne \varnothing , S'\cap IM(x,y)= \varnothing$.

Definition 6

Let $DS=<U,C\cup \{ d\},V,f>$ be a decision information system. The discernibility matrix DM is a $|U|\times |U|$ matrix. For $S\subseteq C$, each item DM(x, y) represents the attribute set that can distinguish object x from object y.

$$\begin{aligned} DM(x,y)=\{ a\in S~|~a(x)\ne a(y) \ \wedge \ d(x)\ne d(y)\} . \end{aligned}$$

(4)

Obviously, the discernibility matrix is anti-reflexive and symmetric, namely $DM(x,x)=\varnothing$ and $DM(x,y)=DM(y,x)$. Therefore, in order to reduce the computational complexity, we only need to calculate the upper or lower trigonometric part of the discernibility matrix.

Definition 7

Let $DS=<U,C\cup \{ d\},V,f>$ be a decision information system. $S\subseteq C$ is a reduct of DS with respect to d if and only if:

• (1) $\forall x,y\in U,if \ DM(x,y)\ne \varnothing , then \ S\cap DM(x,y)\ne \varnothing$;

• (2) $\forall S'\subset S,\exists DM(x,y)\ne \varnothing , S'\cap DM(x,y)= \varnothing$.

Definition 8

Let $IS=<U,C,V,f>$ and $DS=<U,C\cup \{ d\},V,f>$ be an information system and a decision information system, respectively. The core of attribute reduction can be defined as:

$$\begin{aligned} \begin{aligned}&Core_I(C)=\{a\in C~|~a\in IM(x,y) \wedge |IM(x,y)| = 1 \} ;\\&Core_D(C\cup \{ d\})=\{a\in C~|~a\in DM(x,y) \wedge \\&~~~~~~~~~~~~~~~~~~~~~~~~~~|DM(x,y)| = 1 \} . \end{aligned} \end{aligned}$$

(5)

The intersection of all the reducts is called the core. Therefore, we can first find the core to reduce the complexity of subsequent calculations.

2.2 Discernibility pair

In this section, we introduce the concept of discernibility pair which will be used as a criterion for quantifying the discernibility ability of attributes. The number of discernibility pairs produced by an attribute set reflects the discernibility ability of this attribute set.

Definition 9

[25] Let $IS=<U,C,V,f>$ be an information system. $S\subseteq C$ is a subset of the conditional attribute set C. The discernibility pair set with respect to attribute subset S is defined as follows:

$$\begin{aligned} DisP_I(S)=\{ (x,y)~|~\exists a\in S, a(x)\ne a(y) \} . \end{aligned}$$

(6)

Proposition 1

Let $IS=<U,C,V,f>$ be an information system. Given $S'\subseteq S$, then

• (1) $DisP_I(S') \subseteq DisP_I(S)$;

• (2) $DisP_I(S) - DisP_I(S') \subseteq DisP_I(S-S')$.

Proof

• (1) For any $(x,y)\in DisP_I(S'), \exists a\in S', s.t. ~ a(x) \ne a(y)$. Since $S'\subseteq S$, $\exists a\in S, a(x) \ne a(y)$. Hence, $(x,y)\in DisP_I(S), DisP_I(S') \subseteq DisP_I(S)$.

• (2) According to (1), we know $DisP_I(S') \subseteq DisP_I(S)$. For any $(x,y)\in [DisP_I(S) - DisP_I(S')]$, $DisP_I(S') \subseteq DisP_I(S)$, thus $(x,y)\in DisP_I(S)$ but $(x,y)\notin DisP_I(S')$. That is, for any $a\in S',a(x) = a(y)$. Since $S'\subseteq S$, $\exists b\in S-S', b(x) \ne b(y)$. Hence, $(x,y)\in DisP_I(S-S')$.

$\square$

Definition 10

[25] Let $IS=<U,C,V,f>$ be an information system. $S\subseteq C$ is a reduct of IS if and only if:

• (1) $|DisP_I(S)|=|DisP_I(C)|$;

• (2) $\forall S'\subset S, |DisP_I(S')|<|DisP_I(S)|$.

In Definition 10, condition (1) indicates that the attribute subset S can generate the same discernibility pairs as the attribute set C. That is, the attribute subset S has the same discernibility ability as the attribute set C. Condition (2) is used to ensure that the attribute subset S is the minimum, that is, the number of attributes is the least.

Definition 11

[25] Let $DS=<U,C\cup \{ d\},V,f>$ be a decision information system. $S\subseteq C$ is a subset of the conditional attribute set C. The discernibility pair set with respect to attribute subset S relative to decision attribute d is defined as follows:

$$\begin{aligned} \begin{aligned} DisP_D(S,d)&=\{ (x,y)~|~\exists a\in S, a(x)\ne a(y) \ \wedge \\&\ d(x)\ne d(y)\} . \end{aligned} \end{aligned}$$

(7)

Proposition 2

Let $DS=<U,C\cup \{ d\},V,f>$ be a decision information system. Given $S'\subseteq S$, then

• (1) $DisP_D(S',d) \subseteq DisP_D(S,d)$;

• (2) $DisP_D(S,d) - DisP_D(S',d) \subseteq DisP_D(S-S',d)$.

Proof

• (1) For any $(x,y)\in DisP_D(S',d), \exists a\in S', s.t. ~ a(x)\ne a(y), d(x) \ne d(y)$. Since $S'\subseteq S$, $\exists a\in S, a(x) \ne a(y), d(x) \ne d(y)$. Hence, $(x,y)\in DisP_D(S,d), DisP_D (S',d)\subseteq DisP_D(S,d)$.

• (2) According to (1), we know $DisP_D(S',d) \subseteq DisP_D (S,d)$. For any $(x,y)\in [DisP_D(S,d) - DisP_D(S',d)]$, $DisP_D(S',d) \subseteq DisP_D(S,d)$, thus $(x,y)\in DisP_D(S,d)$ but $(x,y)\notin DisP_D(S',d)$. That is, for any $a\in S',a(x) = a(y) \wedge d(x) \ne d(y)$. Since $S'\subseteq S$, $\exists b\in S-S', b(x) \ne b(y) \wedge d(x) \ne d(y)$. Hence, $(x,y)\in DisP_D(S-S',d)$.

$\square$

Based on Propositions 1 and 2, we can find that discernibility pairs satisfy monotonicity with respect to attribute subset S. Moreover, as the same as information entropy and positive domain, the number of discernibility pairs produced by an attribute can also be considered as the amount of information carried by the attribute. The more discernibility pairs an attribute generates, the more information that attribute carries, and vice versa.

Definition 12

[25] Let $DS=<U,C\cup \{ d\},V,f>$ be a decision information system. $S\subseteq C$ is a reduct of DS with respect to d if and only if:

• (1) $|DisP_D(S,d)|=|DisP_D(C,d)|$;

• (2) $\forall S'\subset S,|DisP_D(S',d)|<|DisP_D(S,d)|$.

In Definition 12, condition (1) indicates that relative to decision attribute d, the attribute subset S can generate the same discernibility pairs as the attribute set C. That is, the attribute subset S has the same discernibility ability as the attribute set C relative to decision attribute d. Condition (2) is used to ensure that the attribute subset S is the minimum, that is, the number of attributes is the least.

3 Semi-supervised attribute reduction based on relations of objects and attributes

3.1 Semi-supervised attribute reduction by the maximum discernibility pair

From the above discussion, we know that discernibility pairs can be used to evaluate the discernibility ability of an attribute subset $S\subseteq C$ in IS and DS. In this section, we propose a semi-supervised attribute reduction algorithm by dividing partially labeled data into a labeled part and an unlabeled part. In order to deal with partially labeled data, the discernibility pair set induced by the attribute subset $S\subseteq C$ is defined as follows:

Definition 13

Let $PLDS=<U,C\cup \{ d\},V^*,f>$ be a partially labeled decision information system. $S\subseteq C$ is a subset of the conditional attribute set C. The discernibility pair set with respect to attribute subset S relative to decision attribute d is defined as follows:

$$\begin{aligned} DisP_P(S,d) = DisP_I(S,d)\cup DisP_D(S) . \end{aligned}$$

(8)

Based on Definition 13, the discernibility pair set with respect to attribute subset S relative to decision attribute d combines discernibility pairs from labeled data with discernibility pairs from unlabeled data. It can better express the discernibility ability of attribute subset S than Definitions 9 and 11 in partially labeled decision information system.

Proposition 3

Let $PLDS=<U,C\cup \{ d\},V^*,f>$ be a partially labeled decision information system. Given $S'\subseteq S$, then

• (1) $DisP_P(S',d) \subseteq DisP_P(S,d)$;

• (2) $DisP_P(S,d) - DisP_P(S',d) \subseteq DisP_P(S-S',d)$.

Proof

• (1) For any $(x,y)\in DisP_P(S',d)$,

  • (a) if $d(x) = * \wedge d(y) = *$, $\exists a\in S', s.t. ~ a(x) \ne a(y)$. Since $S'\subseteq S$, $\exists a\in S, a(x) \ne a(y)$. Hence, $(x,y)\in DisP_P(S,d), DisP_P(S',d) \subseteq DisP_P(S,d)$;

  • (b) if $d(x) \ne * \wedge d(y) \ne *$, $\exists a\in S', s.t. ~ a(x) \ne a(y), d(x) \ne d(y)$. Since $S'\subseteq S$, $\exists a\in S, a(x) \ne a(y), d(x) \ne d(y)$. Hence, $(x,y)\in DisP_P(S,d), DisP_P(S',d) \subseteq DisP_P(S,d)$;

  • (c) if $d(x) \ne * \wedge d(y) = *$ or $d(x) = * \wedge d(y) \ne *$, $(x,y)\notin DisP_P(S',d)$. In summary, $DisP_P(S',d) \subseteq DisP_P(S,d)$.

    • (2) According to (1), we know $DisP_P(S',d) \subseteq DisP_P (S,d)$. For any $(x,y)\in [DisP_P(S,d) - DisP_P(S',d)]$, $DisP_P(S',d) \subseteq DisP_P(S,d)$, thus $(x,y)\in DisP_P(S,d)$ but $(x,y)\notin DisP_P(S',d)$.

    • (a) If $d(x) = * \wedge d(y) = *$, for any $a\in S',a(x) = a(y)$. Since $S'\subseteq S$, $\exists b\in S-S', b(x) \ne b(y)$. Hence,$(x,y) \in DisP_P(S-S')$;

    • (b) If $d(x) \ne * \wedge d(y) \ne *$, for any $a\in S',a(x) = a(y) \wedge d(x) \ne d(y)$. Since $S'\subseteq S$, $\exists b\in S-S', b(x) \ne b(y) \wedge d(x) \ne d(y)$. Hence,$(x,y)\in DisP_P(S-S',d)$;

    • (c) If $d(x) \ne * \wedge d(y) = *$ or $d(x) = * \wedge d(y) \ne *$, $(x,y)\notin [DisP_P(S,d) - DisP_P(S',d)]$. In summary, $DisP_P(S,d) - DisP_P(S',d) \subseteq DisP_P (S-S',d)$.

$\square$

Based on Proposition 3, we can find that discernibility pairs satisfy monotonicity with respect to the attribute subset S in partially labeled decision information systems. Therefore, we can use discernibility pairs to study semi-supervised attribute reduction method.

Theorem 1

$Dis_I(S)\cap DisP_D(S,d)=\varnothing .$

Proof

For any $(x,y)\in Dis_D(S,d), d(x)\ne * \ and \ d(y)\ne *$. However, for any $(x,y)\in Dis_I(S), d(x)=* \ and \ d(y) =*$. Hence, $(x,y)\notin Dis_I(S)$. $\square$

Based on Theorem 1, we can find that discernibility pair set from labeled data and discernibility pair set from unlabeled data have no intersection. Because discernibility pair set satisfies monotonicity with respect to attribute subset S in both labeled data and unlabeled data, Theorem 1 also indicates that the union of discernibility pair sets induced by the attribute subset S is monotonically increasing.

Proposition 4

Let S and d be a non-empty attribute subset and a decision attribute, respectively. For any $x,y\in U$, $DisP_P(S,d)$ meets the following properties:

• (1) Irreflexivity. If $x=y$, then $(x,y)\notin DisP_P(S,d)$;

• (2) Symmetric. If $(x,y)\in DisP_P(S,d)$, then $(y,x)\in DisP_P(S,d)$.

Proof

• (1) Since $x=y$, for any $a\in S$, $a(x)=a(y)$. Thus, $(x,y)\notin Dis_I(S)$ and $(x,y)\notin Dis_D(S,d)$. Hence, $(x,y)\notin Dis_P(S,d)$.

• (2) If $(x,y)\in DisP_P(S,d)$, it satisfies that $\exists a\in S, a(x) \ne a(y)$ or $a(x)\ne a(y) \ \wedge \ d(x)\ne d(y)$. Thus, $\exists a\in S, a(y) \ne a(x)$ or $a(y)\ne a(x) \ \wedge \ d(y)\ne d(x)$. Hence, $(y,x)\in DisP_P(S,d)$.

$\square$

Based on Proposition 4, we can find that discernibility pairs satisfy irreflexivity and symmetry. It can be used to reduce the computational complexity of the algorithm by only calculating the upper or lower triangle of the matrix.

Definition 14

Let $PLDS=<U,C\cup \{ d\},V^*,f>$ be a partially labeled decision information system. $S\subseteq C$ is a reduct of PLDS with respect to d if and only if:

• (1) $|DisP_P(S)|=|DisP_P(C)|$;

• (2) $\forall S'\subset S, |DisP_P(S')|<|DisP_P(S)|$.

In Definition 14, condition (1) indicates that the attribute subset S can generate the same discernibility pairs as the attribute set C relative to decision attribute d. That is, the attribute subset S has the same discernibility ability as the attribute set C. Condition (2) is used to ensure that the attribute subset S is the minimum, that is, the number of attributes is the least.

$DisP_P(S,d)$ combines discernibility pair set from labeled data with discernibility pair set from unlabeled data, and reflects the discernibility ability of S in partially labeled data. According to Definition 14, a semi-supervised attribute reduction algorithm based on the maximum discernibility pair is proposed as Algorithm 1.

Classical supervised or unsupervised algorithms consider either labeled information or unlabeled information alone, which often leads to insufficient use of information. Furthermore, it may influence the evaluation of the discernibility ability of attribute and increase the number of core attributes. Semi-DP uses both labeled information and unlabeled information by the metric of discernibility pairs, which fully reflects the amount of information carried by the attribute subset S.

In order to better understand the algorithm Semi-DP, we give an example as shown in Table 1. We only need to calculate the upper or lower triangle of the matrix because of the irreflexivity and symmetry of discernibility pairs.

Table 1 The first partially labeled decision information system

Example 1

Considering a partially labeled decision information system $PLDS=<U,C\cup \{ d\},V^*,f>$ shown in Table 1, $U=\{x_1,x_2,\ldots x_7 \}$ is the object set, $C=\{a_1,a_2,a_3,a_4 \}$ is the attribute set , and d is the decision attribute.

• (1) We calculate the discernibility pair set defined in Definition 13. $DisP_P(C,d) =\{(x_1,x_2),(x_1,x_3),(x_4,x_5), (x_4,x_6),(x_4,x_7),(x_5,x_6),(x_5,x_7) \}$.

• (2) In the first round, we set $R=\varnothing$. For any $a_k\in C-R$ and calculate the number of discernibility pairs $|DisP_P(a_k,d)|$ as follows: $|DisP_P(a_1,d)|=3$, $|DisP_P (a_2,d)|=2$, $|DisP_P(a_3,d)|=4$ and $|DisP_P(a_4,d)|=4$. We can conclude that attribute $a_3$ should be selected, $R=R\cup \{a_3 \}$, and $|DisP_P(R,d)|<|DisP_P(C,d)|$.

• (3) In the second round, we can get $|DisP_P(R\cup \{a_1 \},d)|=6, |DisP_P(R\cup \{a_2 \},d)|=5$ and $|DisP_P(R\cup \{a_4 \},d)|=4$. We can conclude that attribute $a_1$ should be selected, $R=R\cup \{a_1 \}$, and $|DisP_P(R,d)|<|DisP_P (C,d)|$.

• (4) In the third round, we can get $|DisP_P(R\cup \{a_2 \},d)| =7$ and $|DisP_P(R\cup \{a_4 \},d)|=6$. We can conclude that attribute $a_2$ should be selected, $R=R\cup \{a_2 \}$, and $|DisP_P(R,d)|=|DisP_P(C,d)|$.

• (5) Finally, because $|DisP_P(R-{a_3},d)| < |DisP_P(R,d)|$, $|DisP_P(R-{a_1},d)| < |DisP_P(R,d)|$ and $|DisP_P(R-{a_2},d)| < |DisP_P(R,d)|$, there are no redundant attributes in R. We get the attribute subset $R=\{a_3,a_1,a_2 \}$.

3.2 Semi-supervised attribute reduction by attribute indiscernibility

Considering the importance of the relationships between attributes such as the implication relation and the indiscernibility relation in the attribute reduction, we define the concept of similarity for measuring the relationships between attributes as follows:

Definition 15

Let $PLDS=<U,C\cup \{ d\},V^*,f>$ be a partially labeled decision information system. For any $a,b\in C$, the similarity between attribute a and attribute b with respect to decision attribute d is defined as follows:

$$\begin{aligned} Simatt(a,b,d)=\frac{|DisP_P(a,d)\cap DisP_P(b,d)|}{|DisP_P(a,d)\cup DisP_P(b,d)|} . \end{aligned}$$

(9)

If $DisP_P(a,d) = \varnothing \ and \ DisP_P(b,d) = \varnothing$, which means we cannot distinguish between any two objects through attribute a and attribute b, then we default $Simatt(a,b,d) = 1$.

Definition 15 is different from the definition of the classical distance-based similarity. The reason is that the similarity between attribute a and attribute b is determined by the number of discernibility pairs induced by attribute a and attribute b. As shown in Fig. 1, the shadowed part indicates the redundant information induced by attribute a and attribute b with respect to decision attribute d (formulate $|DisP_P(a,d)\cap DisP_P(b,d)|$). From another perspective, this part of redundant information is also a reflection of the similarity between attribute a and attribute b with respect to attribute d. After getting the definition of similarity, we can easily get the definition of the distinction between attribute a and attribute b with respect to attribute d.

Proposition 5

Let S and d be a non-empty attribute subset and a decision attribute, respectively. For any $a,b\in S$, Simatt(a, b, d) meets the following properties:

• (1) Non-negativity. $Simatt(a,b,d) \geqslant 0$;

• (2) Reflexivity. $Simatt(a,a,d) = 1$;

• (3) Symmetric. $Simatt(a,b,d) = Simatt(b,a,d)$.

Proof

• (1) Since $|DisP_P(a,d)\cap DisP_P(b,d)| \geqslant 0$, $|DisP_P (a,d)\cup DisP_P(b,d)| \geqslant 0$. Thus, $Simatt(a,b,d) \geqslant 0$.

• (2)
  $$\begin{aligned} \begin{aligned} Simatt(a,a,d)&= \frac{|DisP_P(a,d)\cap DisP_P(a,d)|}{|DisP_P(a,d)\cup DisP_P(a,d)|} \\&= \frac{|DisP_P(a,d)|}{|DisP_P(a,d)|} = 1 . \end{aligned} \end{aligned}$$

  (10)
• (3)
  $$\begin{aligned} \begin{aligned} Simatt(a,b,d)&= \frac{|DisP_P(a,d)\cap DisP_P(b,d)|}{|DisP_P(a,d)\cup DisP_P(b,d)|}\\&= \frac{|DisP_P(b,d)\cap DisP_P(a,d)|}{|DisP_P(b,d)\cup DisP_P(a,d)|} \\&= Simatt(b,a,d) . \end{aligned} \end{aligned}$$

  (11)

$\square$

Based on Proposition 5, we can find that Simatt(a, b, d) satisfies reflexivity and symmetry. It can be used to reduce the computational complexity of the algorithm by only calculating the upper or lower triangle of the matrix. At the same time, it also indicates that Simatt(a, b, d) satisfies the properties of fuzzy similarity relation which can be used to measure the similarity between attributes.

Fig. 1

The amount of common information between attribute a and attribute b with respect to d

Definition 16

Let $PLDS=<U,C\cup \{ d\},V^*,f>$ be a partially labeled decision information system. For any $a,b\in C$, the distinction between attribute a and attribute b with respect to decision attribute d is defined as follows:

$$\begin{aligned} Disatt(a,b,d)=\frac{|DisP_P(a,d)\vartriangle DisP_P(b,d)|}{|DisP_P(a,d)\cup DisP_P(b,d)|} . \end{aligned}$$

(12)

$\vartriangle$ means symmetrical difference. $DisP_P(a,d)\vartriangle DisP_P(b,d)=(DisP_P(a,d)-DisP_P(b,d))\cup (DisP_P(b,d)-DisP_P(a,d))$. If $DisP_P(a,d) = \varnothing \ and \ DisP_P(b,d) = \varnothing$, which means we cannot distinguish between any two objects through attribute a and attribute b, then we default $Disatt(a,b,d) = 0$.

Definition 16 is different from the definition of the classical distance-based distinction. The reason is that the distinction between attribute a and attribute b is determined by the number of discernibility pairs induced by attribute a and attribute b. As shown in Fig. 2, the shadowed parts indicate the unique classification information induced by attribute a and attribute b with respect to decision attribute d (formulate $|DisP_P(a,d)\vartriangle DisP_P(b,d)|$). From another perspective, the amount of differentiated information in this part is also the reflection of the distinction between attribute a and attribute b with respect to attribute d.

Fig. 2

The amount of differentiated information between attribute a and attribute b with respect to d

Proposition 6

Let S and d be a non-empty attribute subset and a decision attribute, respectively. For any $a,b\in S$, Disatt(a, b, d) meets the following properties:

• (1) Non-negativity. $Disatt(a,b,d) \geqslant 0$;

• (2) Irreflexivity. $Disatt(a,a,d) = 0$;

• (3) Symmetric. $Disatt(a,b,d) = Disatt(b,a,d)$;

• (4) Triangle inequality. $Disatt(a,b,d) + Disatt(b,c,d) \geqslant Disatt(a,c,d)$.

Proof

• (1) Since $|DisP_P(a,d)\vartriangle DisP_P(b,d)| \geqslant 0$, $|DisP_P (a,d)\cup DisP_P(b,d)| \geqslant 0$. Thus, $Disatt(a,b,d) \geqslant 0$.

• (2)
  $$\begin{aligned} \begin{aligned} Disatt(a,a,d)&= \frac{|DisP_P(a,d)\vartriangle DisP_P(a,d)|}{|DisP_P(a,d)\cup DisP_P(a,d)|}\\&= \frac{0}{|DisP_P(a,d)|} = 0. \end{aligned} \end{aligned}$$

  (13)
• (3)
  $$\begin{aligned} \begin{aligned} Disatt(a,b,d)&=\frac{|DisP_P(a,d)\vartriangle DisP_P(b,d)|}{|DisP_P(a,d)\cup DisP_P(b,d)|}\\&= \frac{|DisP_P(b,d)\vartriangle DisP_P(a,d)|}{|DisP_P(b,d)\cup DisP_P(a,d)|}\\&= Disatt(b,a,d). \end{aligned} \end{aligned}$$

  (14)

• (4) As can be seen from the Venn diagram in Fig. 3,$Disatt(a,b,d) + Disatt(b,c,d) \geqslant Disatt(a,c,d)$ which can be written as

  $$\begin{aligned} \begin{aligned} \frac{x+y+e+f}{x+y+h+e+f+g} + \frac{y+z+h+f}{y+z+h+e+f+g} \geqslant \frac{x+z+h+e}{x+z+h+e+f+g}. \end{aligned} \end{aligned}$$

  (15)

  By reduction of fractions to a common denominator, we have $(x^2y+xy^2+x^2z+2xyz+y^2z+xz^2+yz^2+x^2h+2xyh+y^2h+2xzh+2yzh+xh^2+yh^2+2xye+y^2e+2xze+2yze+z^2e+xhe+2yhe +zhe+ye^2+ze^2+x^2f+4xyf+2y^2f+4xzf+4yzf+z^2f+4xhf+5yhf+3zhf+2h^2f+3xef+5yef+4zef +4hef+2e^2f+3xf^2+4yf^2+3zf^2+4hf^2+4ef^2+2f^3+2xyg+2y^2g+2xzg+2yzg+xhg+3yhg+3yeg+zeg+3xfg+6yfg+3zfg+4hfg+4efg+4f^2g+2yg^2+2fg^2) /[(x+y+h+e+f+g)(x+z+h+e+f+g)(y+z+h+e+f+g)] \geqslant 0.$ Since $x,y,z,h,e,f,g \geqslant 0$, the above inequality is always true.

$\square$

Fig. 3

The Venn diagram of triangle inequality

Based on Proposition 6, we can find that Disatt(a, b, d) satisfies non-negativity, irreflexivity, symmetry and triangle inequality. It can be used to reduce the computational complexity of the algorithm by only calculating the upper or lower triangle of the matrix. At the same time, it also indicates that Disatt(a, b, d) satisfies the properties of the distance function which can be used to measure the distinction degree between attributes .

Theorem 2

$Simatt(a,b,d) + Disatt(a,b,d) = 1 .$

Proof

It can be easily proved by Definitions 15 and 16. $\square$

Theorem 2 shows that the sum of Simatt(a, b, d) and Disatt(a, b, d) is equal to 1, just like other fuzzy similarity relations and fuzzy distinction relations. Thus, similarity (distinction) can be obtained by 1- distinction (similarity).

At this point, we have a definition of distinction (also known as distance) between any two attributes. Next, we propose an attribute reduction algorithm based on attribute indiscernibility. This will be divided into two steps. In the first step, we divide the attribute set C into p ($p\leqslant |C|$) different classes. In the second step, we select an attribute from each class that can generate the most discernibility pairs as the representative attribute of the corresponding class.

Before clustering, core attributes need to be preprocessed. When calculating the discernibility matrix, an entry in the discernibility matrix contains a core attribute if it has only one attribute. In order to prevent multiple core attributes from being divided into the same class, we incorporate the attributes into the reduct in the first place. For the remaining attributes, the attribute clustering algorithm [13] is used.

Through the attribute clustering algorithm, we can divide the attribute set into indiscernible attribute classes $IndF(IndF_1,IndF_2,\ldots IndF_m,m\leqslant |C|)$, which are similar to the division of the equivalence classes in rough set theory.

Proposition 7

Let $PLDS=<U,C\cup \{ d\},V^*,f>$ be a partially labeled decision information system. Given $C' = C-[Core_I(C)\cup Core_D(C\cup \{d \} )]$, then

• (1) $\cup _{F_i\in F}IndF_i=C'$;

• (2) $IndF_i\cap IndF_j=\varnothing$.

Proof

• (1) For any $a\in \cup _{F_i\in F}IndF_i$, since $a \in C'$, $\cup _{F_i\in F} IndF_i\subseteq C'$. For any $a\in C'$, $\exists IndF_i \subseteq \cup _{F_i\in F}IndF_i$, s.t. $a\in IndF_i$. Thus, $C'\subseteq \cup _{F_i\in F}IndF_i$. In conclusion, $\cup _{F_i\in F}IndF_i=C'$.

• (2) Assuming that $\exists a\in IndF_i\cap IndF_j$, then $a\in IndF_i$ and $a\in IndF_j$. Since the clustering process only puts each attribute into a certain class, the assumption is wrong. Thus, $IndF_i\cap IndF_j=\varnothing$.

$\square$

Based on Proposition 7, we can find that indiscernible attribute classes have the same properties as equivalence class, that is, the intersection is empty and the union is the universal set. When we choose representative attributes, it ensures that we will consider all attributes and will not choose duplicate attributes.

The indiscernible attribute classes are obtained by the attribute clustering algorithm. Then, we propose a semi-supervised attribute reduction algorithm based on attribute indiscernibility as shown in Algorithm 2. It mainly contains the following parts. Firstly, for each indiscernible attribute class $IndF_i$ , we get the attribute that generates the most discernibility pairs. Secondly, we get a new attribute subset FS (each element in FS is from different indiscernible attribute classes, that is $|FS|=|IndF|$). Finally, we select the attributes with the most discernibility information in the FS.

Table 2 The second partially labeled decision information system

Semi-AI considers not only the indiscernibility relationship between objects, but also the indiscernibility relationship between attributes. In order to better understand the algorithm Semi-AI, we give an example as shown in Table 2. We only need to calculate the upper or lower triangle of the matrix because of the irreflexivity and symmetry of discernibility pairs.

Example 2

Considering a partially labeled decision information system $PLDS=<U,C\cup \{ d\},V^*,f>$ shown in Table 2, $U=\{x_1,x_2,\ldots x_7 \}$ is the object set, $C=\{a_1,a_2,\ldots a_6 \}$ is the attribute set and d is the decision attribute.

• (1) We calculate the discernibility pair sets defined in Definition 13.

  $$\begin{aligned} DisP_P(C,d) & = \{(x_1,x_2),(x_1,x_4),(x_2,x_3),(x_2,x_4),\\&(x_3,x_4),(x_5,x_6),(x_5,x_7),(x_6,x_7) \} ;\\ DisP_P(a_1,d) & = \{(x_1,x_2),(x_1,x_4),(x_2,x_3),(x_3,x_4),\\&(x_5,x_7),(x_6,x_7) \} ;\\ DisP_P(a_2,d) & = \{(x_1,x_4),(x_2,x_4),(x_3,x_4),(x_5,x_6),\\&(x_5,x_7) \} ;\\ DisP_P(a_3,d) & = \{(x_1,x_2),(x_2,x_3),(x_2,x_4),(x_5,x_6),(x_5,x_7) \} ;\\ DisP_P(a_4,d) & = \{(x_1,x_2),(x_2,x_3),(x_2,x_4),(x_5,x_6),(x_5,x_7) \} ;\\ DisP_P(a_5,d) & = \{(x_1,x_4),(x_2,x_4),(x_3,x_4),(x_5,x_6),(x_6,x_7)\} ;\\ DisP_P(a_6,d) &= \{(x_1,x_4),(x_2,x_4),(x_3,x_4),(x_5,x_6),(x_5,x_7) \} ;\\ Core_I(C) & = \varnothing , Core_D(C\cup \{d \}) = \varnothing . \end{aligned}$$

• (2) We calculate the distinction between attributes according to Definition 16 and obtain the distinction matrix DtM.

  $$\begin{aligned} DtM =\left( \begin{matrix}{} 0.0000 &{}0.6250 &{}0.6250 &{}0.6250 &{}0.6250 &{}0.6250\\ 0.6250 &{}0.0000 &{}0.5714 &{}0.5714 &{}0.3333 &{}0.0000\\ 0.6250 &{}0.5714 &{}0.0000 &{}0.0000 &{}0.7500 &{}0.5714\\ 0.6250 &{}0.5714 &{}0.0000 &{}0.0000 &{}0.7500 &{}0.5714\\ 0.6250 &{}0.3333 &{}0.7500 &{}0.7500 &{}0.0000 &{}0.3333\\ 0.6250 &{}0.0000 &{}0.5714 &{}0.5714 &{}0.3333 &{}0.0000\\ \end{matrix} \right) \end{aligned}$$

  (16)

• (3) We set $k = 3$. By using the attribute clustering algorithm to the cluster attribute set $C=\{a_1,a_2,a_3,a_4,a_5, a_6 \}$, we obtain the indiscernible attribute classes $\{a_2,a_6, a_5 \},\{a_3,a_4 \}$ and $\{a_1 \}$.

• (4) We set $FS = \varnothing$ and select attribute $a_k$ from each indiscernible attribute class by calculating $DisP_P(a_k,d)$ to represent the indiscernible attribute class. For $\{ a_2,a_6,a_5\}$, we can get $|DisP_P(a_2,d)|=5$, $|DisP_P(a_6,d)|=5$ and $|DisP_P(a_5,d)|=5$. We choose attribute $a_2$ as the representative attribute of $\{ a_2,a_6,a_5\}$, and set $FS = FS\cup \{a_2 \}$. For $\{ a_3,a_4\}$, we can get $|DisP_P(a_3,d)|=5$ and $|DisP_P(a_4,d)|=5$. We choose attribute $a_3$ as the representative attribute of $\{a_3,a_4 \}$, and set $FS = FS\cup \{a_3 \}$. For $\{a_1 \}$, we can get $|DisP_P(a_1,d)|=6$. We choose attribute $a_1$ as the representative attribute of $\{a_1 \}$, and set $FS = FS\cup \{a_1 \}$. Finally, a new attribute subset $FS=\{a_2,a_3,a_1 \}$ is obtained.

• (5) In the first round, we set $R = \varnothing$. For any $a_j\in FS-R$ and calculate the number of discernibility pairs $|DisP_P(a_j,d)|$ as follows: $|DisP_P(a_2,d)|=5$, $|DisP_P(a_3,d)|=5$, $|DisP_P(a_1,d)|=6$. We can conclude that attribute $a_1$ should be selected, $R=R\cup \{a_1 \}$, and $|DisP_P(R,d)|<|DisP_P(C,d)|$.

• (6) In the second round, we can get $|DisP_P(R\cup \{a_2 \},d)|=8$ and $|DisP_P(R\cup \{a_3 \},d)|=8$. We can conclude that attribute $a_2$ should be selected, $R=R\cup \{a_2 \}$, and $|DisP_P(R,d)|=|DisP_P(C,d)|$.

• (7) Finally, because $|DisP_P(R-{a_1},d)| < |DisP_P(R,d)|$ and $|DisP_P(R-{a_2},d)| < |DisP_P(R,d)|$, there are no redundant attributes in R. We get the attribute subset $R=\{a_1,a_2 \}$.

4 Experiments

In this section, several experiments are performed to verify the performance of the proposed algorithms. The data sets used in the experiments are from the UCI Machine Learning Database [27]. The types of attribute values used in the experiments are nominal and numeric, and we adopt the equal width operation to discretize the attribute value into four values for numeric data. The characteristics of the data sets are summarized in Table 3.

Table 3 A description of datasets

In order to get partially labeled decision information systems, decision attribute values of original complete data sets have been randomly selected to delete. Then every processed data set is divided into a labeled part and an unlabeled part, and decision attribute values in the unlabeled part are denoted as $*$.

In order to verify the effectiveness of proposed algorithms in processing symbolic data, we compare our algorithms with some classical supervised attribute reduction algorithms, unsupervised attribute reduction algorithm and semi-supervised attribute reduction algorithms, listed as follows:

• 1. Positive region POS. An attribute reduction algorithm based on attribute dependence [28].

• 2. Conditional entropy H(D$\vert$A). An attribute reduction algorithm based on conditional entropy [29].

• 3. LDP. An attribute reduction algorithm for labeled data based on the maximum discernibility pair [25].

• 4. UDP. An attribute reduction algorithm for unlabeled data based on the maximum discernibility pair [25].

• 5. DualPOS. A semi-supervised attribute reduction algorithm using dual positive regions [19].

• 6. Semi-mRMR. A semi-supervised attribute reduction algorithm based on maximum relevance and minimum redundancy [30].

• 7. Semi-rough-P. A semi-supervised attribute reduction algorithm that processes labeled data with dependence and unlabeled data with discernibility pair [25].

• 8. Semi-rough-D. A semi-supervised attribute reduction algorithm that processes labeled data with discernibility pair and unlabeled data with discernibility pair [25].

The nearest neighbor classifier (KNN, K = 5) and decision tree classifier (CART) are used to evaluate the attribute reduction results. By using ten-fold cross-validation, the higher the accuracies under KNN classifier and CART classifier are, the more reasonable the selected attribute subset is.

4.1 Compared with supervised and unsupervised algorithms

In this section, the proposed algorithms are compared with classical supervised and unsupervised algorithms mentioned above. For the data sets used in the experiment, the missing rate is 20%.

The specific experimental results are shown in Tables 4 and 5. The optimal classification accuracy of each data set under different algorithms is shown in bold. In most cases, Semi-AI achieves the best accuracy compared with both supervised and unsupervised algorithms. The average accuracy of Semi-DP on all data sets is 0.49% higher than the average accuracy of the other algorithms by KNN classifier through ten-fold cross-validation. The average accuracy of Semi-AI on all data sets is 3.69% higher than the algorithm with the highest average accuracy on given data sets and 15.67% higher than the lowest average accuracy on given data sets by KNN classifier through ten-fold cross-validation. The average accuracy of Semi-AI on all data sets is 2.00% higher than the algorithm with the highest average accuracy on given data sets and 12.17% higher than the lowest average accuracy on given data sets by CART classifier through ten-fold cross-validation. Unsupervised algorithms can only process 20% of the data and ignore the remaining 80% of the data. Supervised algorithms can only process 80% of the data and ignore the remaining 20% of the data. The proposed algorithms take both labeled data and unlabeled data into consideration and the reducts can better describe the information contained in partially labeled data. From Tables 4 and 5, it can be seen that Semi-DP and Semi-AI can deal with the problem caused by missing labels well.

Table 4 Accuracy results ($mean\% \pm std$) under KNN classifier with 20% missing labels compared with supervised and unsupervised algorithms

Fig. 4

Intuitive results of the data set Wine

Table 5 Accuracy results ($mean\% \pm std$) under CART classifier with 20% missing labels compared with supervised and unsupervised algorithms

Fig. 5

Intuitive results of the data set Sonar

4.2 Compared with semi-supervised algorithms

In this section, the proposed algorithms are compared with classical semi-supervised algorithms mentioned above. For the data sets used in the experiment, the missing rate is 20%.

Table 6 Accuracy results ($mean\% \pm std$) under KNN classifier with 20% missing labels compared with semi-supervised algorithms

Table 7 Accuracy results ($mean\% \pm std$) under CART classifier with 20% missing labels compared with semi-supervised algorithms

The specific experimental results are shown in Tables 6 and 7. The optimal classification accuracy of each data set under different algorithms is shown in bold. In most cases, Semi-AI achieves the best accuracy compared with semi-supervised algorithms. The average accuracy of Semi-DP on all data sets is 3.32% higher than the average accuracy of the other algorithms by KNN classifier through ten-fold cross-validation. The average accuracy of Semi-DP on all data sets is 2.09% higher than the average accuracy of the other algorithms by CART classifier through ten-fold cross-validation. The average accuracy of Semi-AI on all data sets is 5.04% higher than the algorithm with the highest average accuracy on given data sets and 18.94% higher than the algorithm with the lowest average accuracy on given data sets by KNN classifier through ten-fold cross-validation. The average accuracy of Semi-AI on all data sets is 5.32% higher than the algorithm with the highest average accuracy on given data sets and 14.00% higher than the algorithm with the lowest average accuracy on given data sets by CART classifier through ten-fold cross-validation. The reason why the accuracies of the proposed algorithm on given data sets are higher than the other algorithms is that the other algorithms only consider the relationships between objects, but rarely consider the relationships between attributes. From Tables 6 and 7, it can be seen that Semi-DP and Semi-AI are effective in dealing with the problem caused by missing labels.

4.3 Classification performance of the selected attribute subset

To further demonstrate the discernibility ability of attribute subset selected by Semi-AI, we show the intuitive results of the data sets Wine and Sonar through two-dimensional feature space in Figs. 4 and 5. Subgraph (a) and Subgraph (b) show the data distribution induced by the first two selected attributes and the last two selected attributes, respectively. Subgraph (c) and Subgraph (d) show the data distribution induced by two random attributes. As we can see from the figures, the attributes selected by Semi-AI achieve better discernibility ability than randomly selected attributes from original data.

4.4 Robustness of the proposed method

In this section, we show the robustness of Semi-AI by setting different missing rates (10%, 20%, $\ldots$, 50%) of datasets. As shown in Figs. 6, 7, 8 and 9, the X-axis shows the different missing rates and the Y-axis represents the classification accuracy under certain classifier. Compared with the representative supervised, unsupervised and semi-supervised algorithms, Semi-AI has achieved better classification accuracy results on most datasets. Moreover, Semi-AI has better adaptability to different missing rates, that is, it has better stability. Therefore, we can conclude that the proposed algorithm is effective and robust.

Fig. 6

Classification accuracy line charts (5NN) compared with supervised and unsupervised algorithms

Fig. 7

Classification accuracy line charts (CART) compared with supervised and unsupervised algorithms

Fig. 8

Classification accuracy line charts (5NN) compared with semi-supervised algorithms

Fig. 9

Classification accuracy line charts (CART) compared with semi-supervised algorithms

5 Conclusion

The work of this paper mainly has the following two contributions. On the one hand, we define discernibility pair set in partially labeled decision information system as a criterion for quantifying the discernibility ability of attributes. This provides researchers with a more intuitive perspective to evaluate the amount of information contained in attributes. On the other hand, we propose new fuzzy similarity relation and fuzzy discernibility relation between attributes by discernibility pairs. Further, we construct the concept of indiscernible attribute class which describes an indiscernibility relationship among attributes. This provides a good direction for researchers to explore the relationships between attributes. Experimental results demonstrate the effectiveness of the proposed algorithms compared with other representative algorithms.

In the future, there are two main directions worth exploring. On the one hand, influenced by the attribute clustering algorithm [13], the acquisition of the optimal indiscernible attribute class defined in this paper has the problem of high time complexity. Inspired by the gap neighborhood relation proposed by Zhou et al. [31] and the granular-ball rough set model proposed by Xia et al. [32, 33], we hope to explore an attribute reduction method in terms of relationships between attributes with adaptive neighborhood radius and low time complexity. On the other hand, since discernibility pairs can be regarded as the criterion for quantifying the discernibility ability of attributes, we hope to explore an attribute reduction method by combining discernibility pair with mutual information.