1 Introduction

Ensemble learning has attracted more and more attention from researchers recently, because it trains multiple weak learners to solve the same problem and achieves stability and accuracy [1]. With the development of Big Data, machine learning methods with increasing data size are usually employed to build the ensemble models, which would bring heavy computational burdens for the ensemble learning [2]. To decrease the computational overheads and improve the accuracy of ensemble methods, ensemble pruning (also known as ensemble selection or selective ensemble) provides a new perspective [3]. And it has been widely used to solve the binary classification problems [4,5,6]. The goal of ensemble pruning is to select a subset of base classifiers, which have been shown to perform better in both complexity and accuracy than the full ensemble [7]. Searching for the best subset of an ensemble using an exhaustive method is an NP-complete problem, which is not suitable for ensemble pruning [8]. Therefore, a lot of studies have been done to solve this problem. Among them, we find that the selection criterion and selection or searching method are the two key points for ensemble pruning. Tsoumakas et al. presented a taxonomy of ensemble pruning methods, and concluded that ensemble pruning evaluation measures consists of two major categories: diversity based and performance based [9].

The basic idea of ensemble learning is to combine various classifiers, which may offer complementary information about the patterns to be classified [10]. Thus, the diversity among the base classifiers has been widely applied to build the selection criterion, and it has been proved to have a positive correlation to the ensemble’s accuracy [11]. Many diversity measures have been investigated to build the selection criterion, such as Q statistic, the correlation, the disagreement, the double fault, etc. The choice of diversity measures will directly influence the final ensemble [12]. However, Kuncheva et al. found that diversity is not always beneficial, and sometimes it may work toward deterioration of the ensemble’s performance [13]. In their another work, they compared ten diversity measures, and found that the motivation for designing diverse classifiers is correct, but how to choose diversity measures and use them effectively for ensemble pruning is still an open problem [12]. Motivated by that, Cavalcanti et al. found that one diversity measure is not enough to capture all the diversities of ensemble, and combined five diversity measures for ensemble pruning [14].

Besides, accuracy is another important factor in building the selection criterion, because it is the ultimate pursuit of ensemble methods [15]. Santos et al. made a further investigation of GA-based selection method to get the subset of the ensemble with the highest accuracy, and implied that controlling overfitting is an important task [16]. Zhang et al. designed an accuracy guided ensemble pruning strategy for pruning the component classifiers with low complementarity [17]. However, accuracy is unable to capture all the different factors that characterize the performance of a classifier. To evaluate the competence of base classifiers, some other performance measures are also considered, such as Brier score (BS), the area under the receiver operating characteristic (ROC) curve (AUC), etc. The BS measures the classifier’s degree of deviation from the true label, which is more accurate to measure the classification ability of the classifiers [18]. The AUC is commonly regarded as a more suitable measurement for evaluating the classifier’s overall performances than accuracy [19, 20].

All of the above methods only use diversity or accuracy to build the selection criteria for ensemble pruning. Even though Dai et al. considered both of them for ensemble pruning, they employed only one algorithm to measure the diversity [21], which may be insufficient to capture all the relevant diversities of the base classifiers [14]. Moreover, Bian et al. only employed the mutual information to measure the accuracy, and the normalized variation to measure the diversity to balance the accuracy and diversity [22]. Using a single algorithm is insufficient to measure the classification ability of the base classifiers. Therefore, it is necessary to adopt multiple diversity and performance measures to build the selection criterion simultaneously.

Moreover, Hashemi et al. considered the ensemble feature selection as a Multi-Criteria Decision-Making (MCDM) process [23]. Kou et al. employed MCDM methods for evaluating classification algorithms and suggested that MCDM methods are feasible tools for ensemble pruning [24]. However, they pay less attention to the diversity and performance measures, and do not compare the MCDM methods to other ranking-based selection methods. Motivated by its preferable performance on decision making, we carry out research on considering the ensemble pruning as a MCDM problem based on multiple diversity and performance measures. In addition, Dempster-Shafer (D-S) theory of evidence is a useful tool for combining accumulative evidence of changing prior opinions [25], and solving the MCDM problems effectively [26]. Meanwhile, fuzzy soft set (FSS), proposed by Maji et al. has also been proved to handle MCDM problems effectively [27]. It provides a theoretic framework to arrange multiple diversity and performance measures of the base classifiers [28]. Therefore, we build a multiple criteria ensemble pruning method by using a MCDM method with FSS and D-S theory of evidence in this paper.

In this study, we use multiple diversity and performance measures to evaluate the competence level of the base classifiers, and then use the fuzzy soft set to organize them. Secondly, we use the D-S theory of evidence to obtain a final score for each base classifier, and then rank the classifiers according to their scores. Finally, we use the greedy ensemble pruning strategy with forward expansion to select the final ensemble from the ordered classifiers. The main contributions of this work are as follows:

  • The ensemble pruning method is proposed by considering multiple diversity and performance measures simultaneously, which can evaluate the base classifiers sufficiently.

  • The use of a MCDM method for ensemble pruning can make a good trade-off between the diversity and performance measures.

  • The D-S theory of evidence is applied to build the combinational rule of the MCDM method. The fuzzy soft set is used to arrange the multiple diversity and performance measures, which help to build the decision matrix.

The rest of this paper is organized as follows. Section 2 gives a preview of the multi-criteria decision making method based on D-S theory of evidence and fuzzy soft set. Section 3 reviews some definitions of diversity and performance measures. Section 4 introduces the research process of the proposed multiple criteria ensemble pruning method. Section 5 displays a detailed description of the experimental setup and Sect. 6 gives a full discussion of the experimental results. Finally, conclusions and avenues for future research are presented in Sect. 7.

2 Multi‑criteria decision making based on D-S theory of evidence and fuzzy soft set

2.1 Fuzzy soft set

Suppose that U is a universe set, and E is the parameters set. Then, let IU denote the power set of all fuzzy sets of U. Let A be a subset of E, i.e., \(A \subset E\). A pair \((F,A)\) is regarded as a fuzzy soft set (FSS in short) over U, where F is a mapping showed by:

$$F:A \to I^{U} .$$

The F is the fuzzy approximate function of the \((F,A)\), and it is usually defined according to the characteristics of the problem [28]. For \(e \in A\), \(F(e)\) is an fuzzy subset of U, which is a fuzzy number set regarding to parameter-e. We can show \(F(e)\) with the form of fuzzy set, \(\left( {F,A} \right) = \left\{ {(e,F(e)):e \in A,F(e) \in I^{U} } \right\}\).

2.2 D-S theory of evidence

Dempster-Shafer (D-S) theory of evidence is originated by the idea of upper probability and lower probability introduced by Dempster [29] and developed by Shafer [30]. It makes the measurement by using belief function and plausible reasoning, which is distinct from other aggregators. The D-S theory of evidence can express the random uncertainty information, the incomplete information and the subjective uncertainty information directly without any prior probability [4], which is similar to the way human collect evidences. Therefore, it has been regard as an increasingly important tool for decision making, because of its advantage in aggregating the information. Some basic concepts of D-S theory of evidence will be recalled in this subsection.

Supposed that Θ is a nonempty set of alternatives, which is regarded as a frame of discernment. Let A be one proposition over the power set 2Θ, the basic belief assignment (BBA) is a mapping [30], presented by \(m:2^{\Theta } \to [0,\,\,1]\). It is a mass function, and m satisfies:

$$m(\emptyset ) = 0,\,\,\sum\limits_{A \subseteq \Theta } {m(A) = 1} .$$

The m(A) means the evidence which is in support of the proposition A.

On the frame of discernment Θ, the belief function (Bel) and plausibility function (Pls) are respectively [30] defined as:

$$Bel(A) = \sum\limits_{B \subseteq A} {m(B)} ,A \subseteq \Theta ,$$
$$Pls:2^{\Theta } \to [0,1],Pls(A) = \sum\limits_{B \cap A \ne \emptyset } {m(B)} .$$

The Bel means decision maker’s the full confidence in A, and \(Pls(A)\) means the extent of no objection to A.

Besides, the D-S theory of evidence provides a way to combine bodies of evidence. Supposed that \(A_{1} ,A_{2} ,...A_{m}\) and \(B_{1} ,B_{2} ,...B_{n}\) are evidences on the frame of discernment Θ. The corresponding basic probability assignment functions are \(m_{1}\) and \(m_{2}\) respectively. If \(\sum\limits_{{A_{i} \cap B_{j} = \emptyset }} {m_{1} (A_{i} )m_{2} (A_{j} )} < 1\), the evidence combinational rule is given by:

$$m(A) = m_{1} \oplus m_{2} (A) = \frac{1}{1 - K}\sum\limits_{{A_{i} \cap B_{j} = A}} {m_{1} (A_{i} )m_{2} (B_{j} )} ,\forall A \subset \Theta ,A \ne \emptyset ,$$
(1)
$$m(A) = m_{1} \oplus m_{2} (A) = 0,A = \emptyset .$$

The \(K = \sum\limits_{{A_{i} \cap B_{j} }} {m_{1} (A_{i} )m_{2} (B_{j} )}\). K is regarded as the conflict probability, and it indicates the degree of the conflict between the evidences. Coefficient \(\frac{1}{1 - K}\) is regarded as normalized factor, and its role is to avoid the probability of assigning non-0 to empty set \(\emptyset\) in the combination [30].

2.3 Multi‑criteria decision making method

In general, a MCDM method usually consists two stages [31]: (1) information input and construction; (2) aggregation and exploitation. In the first stage, a decision matrix is usually built as the mathematical expression of the MCDM problem, which is defined as follows [32].

Given a MCDM problem with n distinct alternatives \(A_{1} , \ldots ,A_{n}\) and m criteria \(C{\text{r}}_{1} , \ldots ,C{\text{r}}_{m}\), where the level of achievement of \(A_{{\text{i}}} \left( {i = 1, \ldots ,n} \right)\) with regard to \(C{\text{r}}_{k} \left( {k = 1, \ldots ,m} \right)\) is denoted by \(C{\text{r}}_{k} (A_{i} )\):

$$\left[ {\begin{array}{*{20}c} {C{\text{r}}_{1} (A_{1} )} & {C{\text{r}}_{2} (A_{1} )} & {} & {C{\text{r}}_{m} (A_{1} )} \\ {C{\text{r}}_{1} (A_{2} )} & {C{\text{r}}_{2} (A_{2} )} & {} & {C{\text{r}}_{m} (A_{2} )} \\ {} & {} & \ddots & {} \\ {C{\text{r}}_{1} (A_{n} )} & {C{\text{r}}_{2} (A_{n} )} & {} & {C{\text{r}}_{m} (A_{n} )} \\ \end{array} } \right],$$

which is called the decision matrix of the problem.

In the second stage, the aggregation and exploitation are carried out based on the decision matrix, which are used for combining the criteria, such as an utility function \(u(A_{i} ) = \sum\nolimits_{k = 1}^{m} {w_{k} Cr_{k} (A_{i} )}\). From above, we can find that the decision matric is similar to FSS and D-S theory of evidence provides a novel aggregation rule. Thus, we use the FSS to build the decision matrix and D-S theory of evidence to build the combine rule, which is inspired by Xiao’s work [33].

3 Diversity and performance measures

3.1 Diversity measures

Even though diversity is widely applied for ensemble pruning, it does not have a generally accepted formal definition. Many diversity measures are presented in previous literatures, and summarized into pairwise measures and non-pairwise measures [12]. Meanwhile, the definition of a “criterion” is “a means or standard of judging” by which one particular choice or course of action could be judged to be more desirable than another in the area of MCDM [34]. Thus, we employ multiple well-known pairwise diversity measures to calculate the classifiers’ diversity.

Suppose a set of s trained classifiers \(C{ = }\left\{ {c_{1} , \ldots ,c_{s} } \right\}\) and N samples, we let \(c_{i} = 1\), if \(c_{i}\) predicts the sample correctly, and 0, otherwise, \(i = 1, \ldots ,s\). Then, we can get a contingency table (Table 1). \(N^{11}\) indicates the number of samples which are correctly classified by both \(c_{i}\) and \(c_{j}\). \(N^{10}\) indicates the number of samples which are correctly classified by \(c_{j}\) and incorrectly classified by \(c_{i}\). \(N^{01}\) indicates the number of samples which are correctly classified by \(c_{i}\) and incorrectly classified by \(c_{j}\). \(N^{00}\) indicates the number of samples which are incorrectly classified by both \(c_{i}\) and \(c_{j}\), \(i,j = 1, \ldots ,s\). With Table 1, we can get following diversity measures [14]:

Table 1 Contingency table for the relationship between a pair of classifiers
Full size table

Disagreement measure (Dis): Its value is calculated by Eq. (2), and the high value of \(dis_{i,j}\) indicates high diversity between \(c_{i}\) and \(c_{j}\).

$$Dis_{i,j} = \frac{{N^{01} + N^{10} }}{{N^{11} + N^{00} + N^{01} + N^{10} }}$$
(2)

The Q statistics (Q): It is a statistic to assess the similarity of two classifiers, and it ranges from -1 to 1, where the positive values indicate similar predictions and the negative values indicate different predictions made by them. The Q statistic of \(c_{i}\) and \(c_{j}\) is calculated as follows:

$$Q_{i,j} = \frac{{N^{11} N^{00} - N^{01} N^{10} }}{{N^{11} N^{00} + N^{01} N^{10} }}$$
(3)

The Kappa-statistic (Kappa): It is widely used in statistics and also applied to measure the diversity. The value is 1, if the classifiers completely agree. Moreover, it is 0, if they randomly agree. Less than 0 is a rare case. The Kappa-statistic of \(c_{i}\) and \(c_{j}\) is calculated as follows:

$$Kappa_{i,j} = \frac{{\Theta_{1} - \Theta_{2} }}{{1 - \Theta_{2} }},$$
(4)

where

$$\Theta_{1} = \frac{{N^{11} + N^{00} }}{{N^{11} + N^{00} + N^{01} + N^{10} }},\,\,\Theta_{2} = \frac{{(N^{11} + N^{10} )(N^{11} + N^{01} ) + (N^{00} + N^{10} )(N^{00} + N^{01} )}}{{\left( {N^{11} + N^{00} + N^{01} + N^{10} } \right)^{2} }}$$

The double-fault measure (DF): It indicates the proportion of the samples that have been incorrectly predicted by both classifiers, showed as follows:

$$DF_{i,j} = \frac{{N^{00} }}{{N^{11} + N^{00} + N^{01} + N^{10} }}$$
(5)

3.2 Performance measures

As mentioned in the introduction, there are three types of performance measures: some assess the discriminatory ability of the classifiers, some assess the accuracy of the classifiers’ probability predictions, and some assess the correctness of the classifiers’ categorical predictions [18, 35]. In order to evaluate the classifiers’ performance in all directions, we select at least one measure for each type of them. Meanwhile, to keep a balance between diversity and performance measures, we select four performance measures. Considering the set \(C{ = }\left\{ {c_{1} , \ldots ,c_{s} } \right\}\) and N samples, we can get the performance measures as follows.

Accuracy (ACC): It is the most commonly used measure to evaluate the classifier and build the ensemble pruning method. The ACC is usually measured using the percentage of correctly classified observations. It is gained upon a confusion matrix for binary classification presented in Table 2. The ACC of \(c_{i}\) is calculated as follows [18]:

$$ACC_{i} = \frac{TN + TP}{{TN + FP + FN + TP}}$$
(6)
Table 2 Confusion matrix
Full size table

Brier score (BS): It measures the classifier’s degree of deviation from the true probability. For binary classification, if \(p_{j}\) indicates the estimated probability of \(j{\text{th}}\) sample to the negative class, and \(f_{j}\) indicates its true probability of negative, then the BS for \(c_{i}\) is calculated as follows [18]:

$$BS_{i} = \frac{{\sum\nolimits_{i = 1}^{N} {\left( {f_{i} - p_{i} } \right)^{2} } }}{N}$$
(7)

The area under the receiver operating characteristic (ROC) curve (AUC): The ROC shows the tradeoff between TP rate and FP rate. The larger the AUC, the better the classifier. A simple method to calculate the AUC of a classifier is showed as follows [36]:

$$AUC = \frac{{\sum\limits_{i = 1}^{TP + FN} {rank_{i} - \frac{(TP + FN) \times (TP + FN + 1)}{2}} }}{{(TP + FN) \times \left( {TN + FP} \right)}},$$
(8)

where \(rank_{i}\) indicates the rank of \(i^{{{\text{th}}}}\) positive sample in the ordered list, which is usually built based on the predicted scores or posterior probability of the positive samples.

H-measure (H): It gives a normalized classifier assessment based on expected minimum misclassification loss [36]. Its cost ratio distribution is given based on a beta distribution and equal parameter values, which use different distributions to different classifiers different from AUC. Thus, it improves the AUC.

4 The proposed method: DSFSS-P

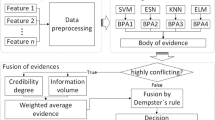
In this section, a detailed description of the proposed method is presented. The base classifiers are generated based on heterogeneous binary classification algorithms, which are given in Sect. 5.2. To prune the best subset of the ensemble, a multiple criteria ensemble pruning method is proposed by combining multiple diversity and performance measures of the base classifiers. Meanwhile, we solve this problem from the perspective of MCDM with FSS and D-S theory of evidence. In general, with the base classifiers’ diversity and performance measures on validation set, the FSS is built, which is a decision matrix of the MCDM problem. Then the D-S theory of evidence is used to fuse the multiple criteria and get the selection criterion for each base classifiers. Finally, we apply the greedy selection strategy with forward expansion to search the best ensemble. We call the proposed method DSFSS-P for short, and the research process of it can be divided into three phases shown in Fig. 1.

  1. (a)

    In phase 1, the s base classifiers are trained based on training set, and the eight diversity and performance measures, denoted by \(E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{8} } \right\}\), are used to evaluate them based on the validation set. The evaluation results are organized by the fuzzy soft set, which is the decision matrix of the MCDM problem, denoted by \((F,E) = \left\{ {\begin{array}{*{20}c} {F_{{{\text{e}}_{1} }} (c_{1} )} & {F_{{{\text{e}}_{2} }} (c_{1} )} & {...} & {F_{{{\text{e}}_{8} }} (c_{1} )} \\ {F_{{{\text{e}}_{1} }} (c_{2} )} & {F_{{{\text{e}}_{2} }} (c_{2} )} & {...} & {F_{{{\text{e}}_{8} }} (c_{2} )} \\ {...} & {...} & {...} & {...} \\ {F_{{{\text{e}}_{1} }} (c_{s} )} & {F_{{{\text{e}}_{2} }} (c_{s} )} & {...} & {F_{{{\text{e}}_{8} }} (c_{s} )} \\ \end{array} } \right\}\).

  2. (b)

    In phase 2, the basic probability assignment functions are built to compute the basic probability of the classifiers, and the evidences from the eight measures are combined with D-S theory of evidence to get the ordered classifiers \(C^{^{\prime}} = \left\{ {c^{^{\prime}}_{1} ,c^{^{\prime}}_{2} , \ldots ,c^{^{\prime}}_{s} } \right\}\).

  3. (c)

    In phase 3, the greedy selection strategy with forward expansion is used to search the top t classifiers with the best ensemble classification accuracy.

Fig. 1
figure 1

Overview of the proposed DSFSS-P method

Full size image

4.1 Build the decision matrix using multiple diversity and performance measures

One diversity measure is not enough to capture all the diversities of ensemble, and accuracy is not the most effective measure to evaluate classifier’s overall performances, as introduced in Sect. 1. Thus using one single criterion to select an ensemble classifier is biased [37]. Meanwhile, diversity and performance measures are two key points to build the selection criterion. It would be comprehensive and reasonable to consider multiple diversity and performance measures. In this work, four diversity measures and four performance measures are selected to estimate the base classifiers’ performance showed in Sect. 3. To select the best ensemble, we solve the problem from the perspective of the MCDM, and the FSS is used to build the decision matrix based on the classifiers’ performance. So the base classifiers are the alternatives of the MCDM problem. Meanwhile, the diversity and performance measures are selection criteria. Then we can get the universe \(C{ = }\left\{ {c_{1} , \ldots ,c_{s} } \right\}\), and the set of parameters \(E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{8} } \right\}\), where \(e_{1} = Dis\), \(e_{2} = Q\), \(e_{3} = Kappa\), \(e_{4} = DF\), \(e_{5} = ACC\), \(e_{6} = BS\), \(e_{7} = AUC\), and \(e_{8} = H\). Then a pair \(\left( {F,E} \right) = \left\{ {(e,F(e)):e \in E,F(e) \in I^{C} } \right\}\) is a FSS, and for each \(e_{j} \in E\) \((j = 1,2, \ldots ,8)\), we can get \(F(e_{j} ) = \left\{ {(c,F_{{e_{j} }} (c)):c \in C,F_{{e_{j} }} (c) \in \left[ {0,1} \right]} \right\}\), which is the mapping under the parameter \(e_{j}\).

With the purpose of building the decision matrix based on the FSS, constructing the fuzzy set corresponding to each parameter are required primarily. The crucial step is building the fuzzy approximate function F. However, the data dimension and meaning of it corresponding to the parameters are diverse, where some drops into the scope of [− 1, 1], and some drops into the scope of [0, 1]. Therefore, the functions should be built adaptively.

Suppose s base classifiers \(C{ = }\left\{ {c_{1} , \ldots ,c_{s} } \right\}\), \(c_{i} (e_{j} )\) indicates the value of \(c_{i}\) corresponding to the parameter \(e_{j}\) based on validation set, \(i = 1,...,s\),\(j = 1,...,8\). For \(e_{5} ,e_{6} ,e_{7} ,e_{8}\), the \(c_{i} (e_{j} )\) is computed based on their definitions. For \(e_{1} ,e_{2} ,e_{3} ,e_{4}\), the \(c_{i} (e_{j} )\) is computed by Eq. (9):

$$c_{i} \left( {e_{j} } \right){ = }\sum\limits_{k = 1}^{s} {diversity_{ik} \left( {e_{j} } \right)}$$
(9)

The \(diversity_{ik} \left( {e_{j} } \right)\) indicates the pairwise diversity of \(c_{i}\) and \(c_{k}\) under parameter \(e_{j}\), which is calculated by using Eqs. (2, 3, 4, 5) respectively, \(i,k = 1, \ldots ,s\), \(j = 1,2,3,4\).

The high values of disagreement measure of them indicate high diversity. Meanwhile, the high values of the ACC, AUC, H indicate good performance of the classifiers. Therefore, for parameters \(e_{1} ,e_{5} ,e_{7} ,e_{8}\), the fuzzy approximate function \(F(e)\) is built as follows:

$$F_{{e_{j} }} (c_{i} ) = \frac{{c_{i} (e_{j} ) - c_{\min } (e_{j} )}}{{c_{\max } (e_{j} ) - c_{\min } (e_{j} )}}$$
(10)

The \(c_{\min } (e_{j} )\) and \(c_{\max } (e_{j} )\) indicates the minimal and maximal value of the s base classifiers corresponding to the parameter \(e_{j}\) respectively, and \(F_{{e_{j} }} (c_{i} )\) indicates the fuzzy value or membership of \(c_{i}\) corresponding to the parameter \(e_{j}\).

However, the high values of the Q statistics, Kappa-statistic and double-fault measure of them indicate low diversity, and high value of Brier score indicates high posterior probability error. Therefore, for parameters \(e_{{2}} ,e_{{3}} ,e_{{4}} ,e_{6}\), the fuzzy approximate function \(F(e)\) is built as follows:

$$F_{{e_{j} }} (c_{i} ) = \frac{{c_{\max } (e_{j} ) - c_{i} (e_{j} )}}{{c_{\max } (e_{j} ) - c_{\min } (e_{j} )}}$$
(11)

Therefore, the FSS \((F,E)\) over C is presented by Table 3, which is the decision matrix.

Table 3 Matrix representation of fuzzy soft set \(\left( {F,E} \right)\) over C
Full size table

4.2 Combine multiple criteria using the D-S theory of evidence

In the decision matrix, the attributes or criteria are sometimes inconsistent because of the fuzzy relations of the diversity and the accuracy [20, 38]. The D-S theory of evidence can deal with imprecise and uncertain information without prior information, and sometimes can handle the conflicts among evidences [26]. Thus the combinational rule of D-S theory of evidence is an effective tool to fuse the multiple criteria based on the diversity and performance measures.

According to the definition of D-S theory of evidence and the decision matrix \((F,E)\), the frame of discernment of best classifiers is denoted by \(\Theta { = }C{ = }\left\{ {c_{1} , \ldots ,c_{s} } \right\},\) and \(E = \left\{ {e_{1} ,e_{2} , \ldots ,e_{8} } \right\}\) are the eight performance measures to provide the evidences denoted by \(\left( {F,E} \right) = \left\{ {(e,F(e)):e \in E,F(e) \in I^{C} } \right\}\). In order to combine the multiple measures by the D-S theory of evidence based combinational rule, the study defines the basic probability assignment functions based on Gong and Hua’s work [39] of basic utility assignments:

$$m\left( {F_{{e_{j} }} (c_{i} )} \right) = \frac{{F_{{e_{j} }} (c_{i} )}}{{\sum\nolimits_{i = 1}^{s} {F_{{e_{j} }} (c_{i} ) + \beta } }},$$
(12)

where \(\beta\) ranges in \([0,\,\,1]\) and usually takes 1 [40]. \(m\left( {F_{{e_{j} }} (c_{i} )} \right)\) indicates basic probability assignment function for degree of membership of \(c_{i} (i = 1,2,...,s)\) respectively under \(e_{j} (j = 1,2,...,8)\). From the perspective of D-S theory of evidence, it indicates the BPA of the singleton set \(\left\{ {c_{i} } \right\},i = 1,2, \ldots ,s\), and \(\beta\) is used to represent the comprehensive evidence of the other subsets of the power set of \(\Theta\). Since searching for the best subset from the \(\Theta\) using an exhaustive method is an NP-complete problem, it is hard to derive the evidences of all the elements of the power set of \(\Theta\). Besides, the purpose of this section is to select the best classifier under the \(\Theta\). Thus the BPAs of the singleton sets are mainly built.

In order to fuse the BPAs, the Eq. (8) is usually used to combine \(m\left( {F_{{e_{j} }} (c_{i} )} \right)\). The result can be regarded as a fuzzy set \(C^{^{\prime\prime}} = \left\{ {(c,F_{DS} (c)):c \in C,F_{DS} (c) \in [0,1]} \right\}\), where \(F_{DS} (c)\) is a fuzzy value. It is the final score of classifier c, indicating the membership of it belonging to best alternative of the ensemble. The algorithm of combing multiple criteria using D-S theory of evidence to get \(F_{DS} (c)\) is showed detailedly in Fig. 2. With the fuzzy set \(C^{^{\prime\prime}}\), we rank the classifiers by the descending order of the \(F_{DS} (c)\), and get the ordered set \(C^{^{\prime}} { = }\left\{ {c^{^{\prime}}_{1} ,c^{^{\prime}}_{2} , \ldots ,c^{^{\prime}}_{s} } \right\}\).

Fig. 2
figure 2

Algorithm of combining multiple criteria using D-S theory of evidence

Full size image

4.3 Select best ensemble using greedy selection strategy with forward expansion

Greedy selection strategy is a commonly used method to search for the optimal choice of ensemble based on the selection criteria, which can reduce the search space appropriately [21]. For ensemble pruning, this method greedily selects the classifier by searching the neighbors of the current ensemble according to the selection criteria. Therefore, there are usually two steps involved: building the selection criteria and determining the direction of the search [41]. With the FSS \((F,E)\) and D-S theory of evidence, we build a new selection criteria \(F_{DS} (c)\) and rank the base classifiers to get the ordered set \(C^{^{\prime}} { = }\left\{ {c^{^{\prime}}_{1} , \ldots ,c^{^{\prime}}_{s} } \right\}\). Meanwhile, forward expansion and backward shrinkage are the common search directions, which have been extensively studied and proved to be an efficient method for finding the optimal solution. In this paper, we employ the forward expansion to select classifiers to form the final ensemble, and the algorithm is showed in Fig. 3.

Fig. 3
figure 3

Algorithm of selecting the best ensemble using greedy selection strategy with forward expansion

Full size image

5 Experimental setup

5.1 Datasets

For evaluating the performance of the DSFSS-P, sixteen binary datasets are gathered from the UC Irvine Machine Learning Repository [42], which are broadly applied for assessing the ensemble models’ results. A descriptive outline of the databases is presented in Table 4. For the concision of the experiment, normalization is implemented after missing data imputation by mean value of all data sets. For robustness check, a 2 × 5-fold cross-validation is used to diminish the effect of variability created by random partitioning on forecasting results. In particular, the samples are randomly split into five folds at first. In each time for validation, we use one fold to evaluate the results of the methods, and the last four folds are randomly divided equally for training and pruning respectively. The validation experiments are conducted for five times with different fold for testing. Meanwhile, 5-fold cross-validation are conducted for two times based on different partitions. The final experimental results are averaged over the 10 validations.

Table 4 Descriptive outline of the databases
Full size table

5.2 Base classifiers and benchmark methods development

Base classifiers play an essential role in the ensemble model’s performance, as every classifier has its merits and advantages. A trade-off is demanded between synthesizing all the base classifiers’ advantages and the complexity of the ensemble model. Fruitful results have been gained for building classifiers with machine learning methods, such as DT, SVM, NN [43], and comparative studies are also implemented to show their better performances [35]. Therefore, they are employed to build the base classifiers. They are generated by using bagging and various parameters, and the ensemble size is 300 at the first place. Table 5 displays the settings of the classification algorithms’ parameters used for training base classifiers [35].

Table 5 Settings of the classification algorithms’ parameters
Full size table

In order to investigate the effectivity of the proposed ensemble pruning method based on multiple diversity and performance measures, six benchmark methods are selected. Two common selection methods, single best (SB) and fusing all base classifiers (ALL), are chosen as benchmarks. Four other popular ensemble pruning methods are selected. Hill-climbing ensemble selection (HCES) and Kappa pruning (Kappa) are two ordered based ensemble pruning methods, which build the selection criteria based on ACC and Kappa respectively. One ensemble pruning method built based on simultaneous diversity and ACC (SDAcc) is selected, which is proposed by [21]. Moreover, the method combining multiple diversity measures for ensemble pruning (DivP) is also selected [14].

The experiments described in this study are conducted on a PC with a 3.2 GHz Intel Core 4 CPU and 8 GB RAM, using the Windows 10 operating system. MATLAB, version 2020b, is used for modelling.

5.3 Performance indicators measures and statistical tests of significance

For the credibility and robustness, the ACC is selected to measure its classification ability, and the disagreement measure is selected to measure diversity of the ensemble classifiers generated by it.

Next, a non-parametric test was used to assess the statistical differences between models [44]. To be specific, Friedman test was carried out to check the differences of models’ ranking performance. The null hypothesis is that all classifiers perform identically, which indicates the average ranks of them are same. If the hypothesis is rejected, a post-hoc test called Holm’s method is employed to take pairwise comparisons among them, which show significant differences [45].

6 Experimental results

6.1 Ensemble performance and diversity evaluation

Comparison of the average accuracies of the DSFSS-P method and 6 state-of-the-art benchmark methods on the 16 datasets over 10 validations are showed in Table 6. As we can see from it, the DSFSS-P achieves the highest classification accuracy in most cases by 13 times, which is much higher than SB, ALL, HCES, Kappa, SDAcc and DivP with 0, 1, 2, 0, 1, 0 times. On datasets AReM3, Diabetic and EyeState, though DSFSS-P is not the best one, it is second only to HCES, SDAcc and HCES respectively in terms of the average accuracy. On dataset Wisconsin, the DSFSS-P and ALL get the same accuracy, which is highest among the seven methods. Distinct differences are hardly found between seven methods.

Table 6 Comparison of the models’ average accuracy on the 16 datasets
Full size table

In order to compare the diversities of the six ensemble methods in a clearer way, we summarize the results in Table 7. Bold values indicate the highest diversity among the six ensemble models. We can find that diversity of the ensemble pruned by DSFSS-P is at a medium level among the six methods on all datasets, but it obtains the best accuracy in most cases. The Kappa achieves the most diversified ensembles on most of the datasets, since it prunes the ensemble based on the Kappa. However, the accuracy of their measurements is very unstable and unsatisfactory, that may be due to the fact that only Kappa is insufficient to capture all the diversity of the ensemble. Divp, pruning the ensemble based on multiple diversity measures, achieves the lower diversity than SDAcc, which prunes the ensemble based on accuracy and diversity. They both obtain the lower diversity than the HCES on all datasets except for ILPD, which selects the ensemble only based on accuracy. It's an interesting and surprising discovery. Furthermore, it is found that there is no obvious correlation between the accuracy and the diversity of the ensemble.

Table 7 Comparison of the ensemble models’ average diversity on the 16 datasets
Full size table

Meanwhile, the averaged run-time of ensemble pruning modes is recorded in Table 8. From the results, we can see that the DSFSS-P is much faster than the other ensemble pruning methods in all datasets. It is attribute to that our proposed method does not use iterative methods for the ensemble pruning, and the D-S combine rule is also a fast algorithm. The overall time complexity of the proposed method is O(MS), where M is the number of criteria, and S is the number of the base classifiers.

Table 8 Comparison of the ensemble pruning models’ average runtime(s) on the 16 datasets
Full size table

6.2 Statistical tests of significance

Friedman test was carried out to check the significant differences of the methods’ results, which is shown in Table 9. With the level of significance \(\alpha \,\,{ = }\,\,0.05\), i.e., 95% confidence, the chi-square statistic is 40.781, and the degree of freedom is 6. The results show that the null hypotheses are rejected with the statistical results p value = 0.000, and it can be concluded that all the models play significantly different role in solving the binary classification problems. Moreover, it can be seen that DSFSS-P obtains the first rank whereas SB obtains the seventh rank, which again proves the superiority of the ensemble methods. SDAcc and HCES obtains the second and third rank respectively. They beat the other two pruning methods, i.e., Kappa and Divp, which select the ensembles only based on diversity measures. Kappa is worse than DivP and ALL, which indicates that one diversity measure is unstable for ensemble pruning, and it is unable to capture all diversities of the ensemble.

Table 9 Friedman test based on accuracy values (significance level of 0.05)
Full size table

Then, a post-hoc test called Holm’s method was carried out for a pairwise comparison between the rankings achieved by each model. Table 10 shows the results of post-hoc test on the confidence level \(\alpha \,\,{ = }\,\,0.05\), and all the hypotheses are rejected. We can state that DSFSS-P performance significantly better than any other benchmark model in terms of accuracy values.

Table 10 Results of post-hoc test after rejection of null hypothesis based on accuracy values (significance level of 0.05)
Full size table

6.3 Analysis of the selection criteria

In order to analyze the influence of the selection criteria on the performance the ensemble pruning method, we conduct the experiment by combining different number of the criteria. The result is shown in Fig. 4, where the horizontal axis shows the number of selection criteria. The sequence of the criteria is according to \(\left\{ {DF, \, Kappa, \, Q, \, Dis, \, H, \, AUC, \, BS, \, ACC} \right\}\). Specifically speaking, 1 means use DF as the criteria to build the ensemble pruning method, 2 means combine DF and Kappa as the criteria to build the method, and so on in a similar fashion. The vertical axis represents the result of methods based on ACC.

Fig. 4
figure 4

The influence of the number of selection criteria on the performance the ensemble pruning method

Full size image

From the results, we can see that combining all the eight criteria obtains the highest ACC 9 times and second high ACC 6 times among the 16 datasets. Meanwhile, the 16 lines of the experiment show an upward trend, which means the more criteria, the better performance the ensemble pruning method. It shows the multiple criteria ensemble pruning method’s effectivity and superiority. Moreover, only combining the criteria with diversity measures for ensemble pruning doesn’t obtain the highest accuracy for any dataset. Combining multiple diversity and performance measures for ensemble pruning (DSFSS-P) can generate more accurate ensemble than that only considering one performance or diversity measure and that combing multiple diversity measures.

7 Conclusions and future work

In this study, we propose a multiple criteria ensemble pruning method for binary classification by combining multiple diversity and performance measures simultaneously with a MCDM method. The Q statistics, Kappa-statistic, double-fault and disagreement measure are used to capture the base classifiers’ diversity. The accuracy, Brier score, ROC and H-measure are used to measure their classification ability. They are the criteria giving a full evaluation to the base classifier and the relation of them. In order to achieve a trade-off between the diversity and performance measures, the FSS is applied to arrange the base classifiers’ levels of achievements with regard to the criteria, which provides a mathematical theory support to build the decision matrix. The D-S theory of evidence is applied to aggregate the uncertainty and conflicting information of the criteria, which help to give a comprehensive evaluation to the base classifiers.

To validate the performance of the proposed ensemble pruning method, a comprehensive empirical evaluation is carried out on 16 binary datasets from UCI. Compared to 6 state-of-the-art benchmark methods, the proposed method DSFSS-P achieves better performance in 13 out of the 16 data sets than other methods do in terms of classification accuracy, which show its effectivity and superiority for ensemble pruning. Thus, ensemble pruning by considering multiple diversity and performance measures can bring more accurate and generalized ensemble. In our further research, there are two tasks for investigation to make the proposed ensemble pruning method more promising. On one hand, the choice of diversity and performance measures is still an open problem. On the other hand, the MCDM based ensemble pruning method’s classification performance can be further improved with more customized design.