Abstract
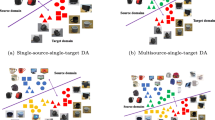
As an emerging research topic in the field of machine learning, unsupervised domain adaptation (UDA) aims to transfer prior knowledge from the source domain to help training the unsupervised target domain model. Although a variety of UDA works have been proposed, they mainly concentrate on scenarios from one source to one target (1S1T) or multi-source to one target domain (mS1T), the works on UDA from one source to multi-target (1SmT) is rare and they are mainly designed for ordinary problems. When countered with ordinal 1SmT tasks where there exists order relationship among the data labels, the existing methods degenerate in performance since the label relationships are not preserved. In this article, we propose an ordinal 1SmT UDA model which transfers both explicit and implicit knowledge from the supervised source and unsupervised target domains respectively via distribution alignment and dictionary transmission. We also design an efficient algorithm to solve the model and evaluate its convergence and complexity. Finally, the effectiveness of the proposed method is evaluated with extensive experiments.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In machine learning, the models are typically trained by default under the hypothesis that training and test data comply with the same statistical distribution [1, 2]. Nevertheless, in real world applications, such assumption often does not hold, resulting in degenerated model. To overcome this issue, the paradigm of unsupervised domain adaptation (UDA) [3,4,5,6,7,8,9,10] was proposed to mitigate the distribution inconsistency between the training and test data domains.
In UDA, the supervised domains with knowledge to be transferred are defined as source domains, while the other unsupervised domains are distinguished as target domains. According to the modeling methodology, the existing UDA methods can be grouped into three categories [11], i.e. instance-level, feature-level and model-level UDA. Specifically, the instance-level UDA [12,13,14,15,16] typically assigns the source instances weights in terms of their similarity to the target domains, and takes weighted source instances to help training the target model. Such methodology usually works effectively when the cross-domain divergence is small, otherwise they may lose efficacy especially when the distributions of the source and target domains do not intersect. The feature-level UDA [17,18,19,20,21,22] typically transforms the source and target domains into a common correlated representation space, in which the cross-domain distributions are pulled as near as possible. Although such feature-level UDA usually can achieve better results, its efficacy greatly depends on the choice of the representation space. As for the model-level UDA [23,24,25,26], it fulfils knowledge adaptation from the source model parameters. Although such kind of UDA can distill the source knowledge to the target domain, the data distribution priors are usually ignored.
Most of the existing UDA works concentrate on such task scenarios where merely one source and one target domain (1S1T) are involved, while few researches implement UDA from multiple sources to one target domain (mS1T). To generalize knowledge from one source to multiple target domains (1SmT), Yu et al. [27] proposed the 1SmT UDA method (PA-1SmT), which implements domain adaptation by reconstructing the source model with the target model parameters and relates the targets with a shared representation dictionary. Nevertheless, the PA-1SmT tends to fail when the union of the targets is proper subset of the source domain so that the latter cannot be completely approximated by the former. Even worse, the PA-1SmT is designed for ordinary problems, such that it may degenerate when facing the ordinal data problems. Let us take human age as an example, it exhibits ordinal relationships among different ages, e.g., the person aged 20 is younger than somebody aged 25, but elder than the people aged 18. In other words, the severity of misclassifying age 20 to 25 is more serious than to 18. Such order relationships are not preserved in existing UDA methods so that they cannot be directly employed to handle the cross-domain ordinal problems.
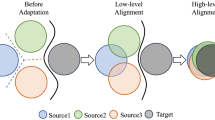
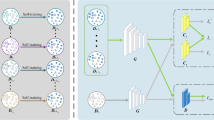
To implement 1SmT UDA for ordinal data scenarios, as shown in Fig.1, we construct an ordinal unsupervised domain adaptation through transferring both implicit and explicit knowledge from data distribution and model parameters perspectives, coined as OrUDA. In addition, we design an optimization algorithm to solve the OrUDA model alternatingly, with theoretically convergence guarantee. Finally, through extensive evaluations on artificial and real datasets, we demonstrate the effectiveness of the proposed method. In summary, the main contributions of this work are four-fold as follows:
-
1.
A kind of 1SmT UDA for ordinal data is proposed (OrUDA), which transfers both explicit and implicit knowledge from the supervised source and unsupervised target domains respectively via distribution alignment and dictionary transmission.
-
2.
The unknown ordinal prior of the target domains is transferred from the already trained source model via source model adaptation in the process of 1SmT UDA.
-
3.
An alternating optimization algorithm is designed to solve the OrUDA model, with convergence guarantee.
-
4.
Extensive evaluations are conducted to demonstrate the effectiveness and superiority of the proposed method.
The rest of this article is organized as follows. Section 2 briefly reviews the related work. Section 3 elaborates the proposed method. Section 4 experimentally evaluates the proposed method with analysis. Finally, Section 5 concludes this article and gives future research directions.
2 Related work
In this section, we present the related researches on UDA including 1S1T, mS1T and the most related 1SmT UDA methods.
2.1 1S1T UDA
Thanks to the broad practice prospects, a large number of 1S1T UDA methods are proposed based on non-deep architecture and deep architecture, which can be grouped into three categories [11], i.e. instance-level, feature-level and model-level UDA. For the instance-level UDA, most methods [12,13,14,15,16] reweight the source instances according to the similarity of samples, which work effectively when the cross-domain divergence is small otherwise these methods may fail. A typical example is KLIEP [28], which reweights the instances by solving a convex optimization problem with a sparse solution. The model-level methods [23,24,25,26] mitigate the domain shift by transferring the parameters of the source model. For example, DAN [29] conducts domain adaptation by sharing parameters of the probability distribution match layer. Additionally, most UDA methods [17,18,19,20,21,22] refer to the feature-level, which transfer knowledge by distribution alignment, such as MMD [30], CORAL [31], CMD [32] and so on. Recently, CMMS [21] captures the feature consistency by the class centroid matching and SALFL [22] aligns the domains by incorporating the projection clustering, label propagation and distributional alignment into a unified optimization framework.
2.2 mS1T UDA
Recently, more and more mS1T-UDA methods emerge which aim to transfer knowledge from multiple source domains at the same time to better assist the learning of the target domain. Specifically, mDA [33] aligns all the domains by selecting the shared latent sub-space. Differently, SSF [34] samples the sub-space along with the spline flow from the source domains to the target domain which associates the domains on the Grassmann manifold. Later, UMDL [35] realizes the domain adaptation by training the constructed task-shared and task-specific jointly. Additionally, to transfer the source decision model to the target domain without the bias, MDAN [36] learns the aligned cross-domain semantic network by the generative adversarial scheme. Further, WS-UDA [37] and CMSS [38] trains the adversarial network by reweighting the samples and spaces of the source domains respectively, which transfer the source knowledge effectively. Moreover, DistanceNet [39] conducts 1SmT UDA by the dynamic distance measure and the Bandit controller. And LtC-MSDA [40] constructs an adjacent relationship graph of the mixed knowledge domain to realize the consistent transfer of mS1T UDA.
2.3 1SmT UDA
Although a variety of 1S1T and mS1T UDA methods have been proposed, the research on 1SmT is quite rare. To our knowledge, PA-1SmT [27] is the first and representative 1SmT UDA method that transfers knowledge between the source and target domains via model parameter adaptation. More specifically, it performs clustering in the label space of multiple target domains simultaneously through the soft large-margin clustering. It also assumes the label space of target domains is subset of the source domain. To transfer the source domain knowledge to help clustering these unlabeled target instances, the PA-1SmT bridges the single source domain with each of the target domains with individual representing factor. Besides, a correlation dictionary is embedded in the model to capture the correlations between the target domains. Finally, when these considerations are taken into account, the objective function of PA-1SmT is achieved as follows:
where \(\varvec{W}_S\) and \(\varvec{W}_T^m\) respectively denote the projection matrices for the source and target domains, \(\varvec{V}^m\) and \(\varvec{V}_T^m\) indicate the individual selection matrices, \(\varvec{D}\) stands for the shared dictionary among the target domains, \(u_{ki}^m\) is the clustering membership of instance \(\varvec{x}_i^m\) to the kth class in the mth target domain. \(\alpha\), \(\beta\), \(\gamma\) and \(\eta\) are the tradeoff parameters. For more details about the PA-1SmT model and its algorithm, please refer to [27].
Although PA-1SmT has incorporated the knowledge relationship between the source and the target domains, it fails to preserve the cross-target relationships, whose performance may be limited especially in scenarios where the target domains are closely related to each other. Even worse, it does not characterize the ordinal relationships of the data.
3 The Proposed method
In this section, we propose an unsupervised domain adaptation for ordinal data scenario (OrUDA) that transfers implicit and explicit knowledge from source domain.
3.1 Notation and hypothesis
For convenience of elaboration, we systematically define the notations to be used in the remainder sections in Table 1.
Without loss of generality, we also comply with the hypothesis that the source data set \(\varvec{X}_S \in \mathbb {R}^{d\times N_S}\) follows distribution \(\mathcal {P}_S(\varvec{x}_S)\), while the data set of the mth target follows distribution \(\mathcal {P}_T^m(\varvec{x}_T^m)\). We concentrate on the UDA scenario where the supervised source and unsupervised target domains share the same original feature space and label space, i.e. \(\mathcal {X}_S = \mathcal {X}_T^m\) and \(\mathcal {Y}_S = \mathcal {Y}_T^m\). Considering the domain shift between the source and target domains, the marginal distributions \(\mathcal {P}_S(\varvec{x}_S) \ne \mathcal {P}_T^m(\varvec{x}_T^m)\) and conditional distributions \(\mathcal {P}_S(\varvec{y}_S \mid \varvec{x}_S) \ne \mathcal {P}_T^m(\varvec{y}_T^m \mid \varvec{x}_T^m)\).
3.2 Ordinal UDA with implicit and explicit knowledge transfer
3.2.1 Implicit knowledge transfer from the source domain
For ordinal classification or regression (e.g. human age estimation), one of the mainstream methods is to project the estimation samples into an ordered feature subspace and then make decisions in this space. Following this principle, the KDLOR method [41] was proposed to seek discriminative ordinal projection. Furthermore, in order to obtain orthogonal projections with complementary components, a multi-direction counterpart of KDLOR [42] was derived, with objective function formulated as
where \(\varvec{w}_{p+1}\) denotes the (p+1)th ordinal projection direction who is restricted to be orthogonal to the previous p directions, with \(\rho _{p+1}\) being the class margin along this projection, \(\varvec{S}_W\) is the intra-class scatter matrix, \(\varvec{m}_{k}\) indicates the data centroid of the kth class. \(\lambda\) is the tradeoff parameter.
The projections \(\varvec{W}_S = [\varvec{w}_{p+1}, \varvec{w}_{p}, \cdot \cdot \cdot , \varvec{w}_{1}]\) can be obtained by solving the variable \(\varvec{w}_{p+1}\) of (2) in the source domain. Then, we can transfer knowledge from the source domain via \(\varvec{W}_S\) to the target domains. Nevertheless, considering the distribution shift between the source and the target domain, as well as the individuality divergence between different targets, it is not reasonable to directly assign \(\{\varvec{W}_T^m\}_{m=1}^M\) with \(\varvec{W}_S\). To this end, we propose to adaptively transfer positive components from the source to the target domains through designing the individual transfer matrices \(\{\varvec{V}^m\}_{m=1}^M\), and consequently formulate it as
where the transfer matrix \(\varvec{V}^m\) acts to adaptively extract components from the source model \(\varvec{W}_S\) to represent the mth target module \(\varvec{W}_T^m\). The constraint aims to preserve the discriminant component of the transfer matrix, with \(\varvec{I}\) being an identity matrix. Modeling individual transfer matrix \(\varvec{V}^m\) for each of the target domains can effectively preserve their personality. Since knowledge transfer from \(\varvec{W}_S\) to \(\varvec{W}_T^m\) is implemented in an implicit manner, so we call it implicit knowledge transfer.
3.2.2 Explicit knowledge transfer from the source domain
Considering the distribution shift between the source and target domains, we need to align the domains by reducing their divergence in both marginal distribution and conditional distribution. To this end, we propose to introduce the maximum mean discrepancy (MMD) [43] to model the marginal distribution, while the conditional MMD [44] to characterize the conditional distribution between the domains. To seek a balance between the marginal divergence and conditional divergence, we seek a tradeoff between the domain distributions and thus formulate the objective as
where the first term characterizes the marginal distribution divergence between the source and the M target domains while the second term describes their conditional divergence, which are balanced by the parameter \(0 \le \mu \le 1\). \(\varvec{F}_S\) and \(\varvec{F}_T^m\) respectively store the class centroid in column for the source and target domains. It is worth noting that \(\varvec{F}_T^m\) is actually padded with “pseudo-centroid” for the target domains by classifying their instances using the classifier trained on the source domain. To boost the reliability, these pseudo-centroid are updated in iterative manner in the process of model optimization. To gain performance improvement, we adaptively calculate \(\mu\) according to the \(\mathcal {A}\)-distance [45] between the marginal and conditional distributions. Compared to the implicit knowledge transfer manner in Section 3.2.1, the domain distribution alignment is an explicit way of transferring prior knowledge from the source domain, so we distinguish it as explicit knowledge transfer.
3.2.3 Relation transfer between the target domains
For 1SmT UDA, there are usually potential correlations between the target domains. To explore these relations, we construct a shared representation dictionary to bridge the target domains as
where \(\varvec{D} \in \mathbb {R}^{d\times r}\) denotes the dictionary shared by the target domains, and \(\varvec{V}_T^m\) is the relation transfer matrix for the mth target domain. As formulated in (5), all the M target domains are related with knowledge transfer among them by the common dictionary.
3.2.4 Overall objective of OrUDA
For the concerned ordinal 1SmT UDA, we can consequently build the overall objective function for the OrUDA model by taking all the above considerations simultaneously, and formulate it as
where the first term denotes the empirical loss on the target domain, while the other terms regularize the learning by transferring knowledge from the source domain (implicit and explicit) and other target domains (relation). It is worth noting that implicit knowledge transfer constructs the individual transfer matrices for each target domain to learn the latent ordinal information from the source domain while the explicit knowledge transfer aims to mitigate the domain shift in the shared sub-space which is obtained according to the explicit measure of the domain distribution. In order to transfer from the source domain the ordinal structure for the target domains, we encode the target instance label through least-squares regression on their centroid. Then, we substitute (3), (4), (5) into (6) and consequently rewrite (6) as
where \(\lambda _1\) to \(\lambda _4\), as well as \(\mu\) are predefined tradeoff parameters. By the modeling manner of (7), the data ordinal characteristics, as well as other domain knowledge can be effectively transferred to the target domains.
3.3 Optimization of OrUDA
As shown in (7), the objective function is jointly convex w.r.t. the variables; therefore, we construct an alternating optimization to solve it, i.e. solving one variable while fixing the others.
-
Solve \(\varvec{W}_T^m\) with \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\), \(\varvec{D}\) fixed.
When \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\) and \(\varvec{D}\) are fixed, then (7) w.r.t. \(\varvec{W}_T^m\) can be equivalently written as
$$\begin{aligned} \begin{aligned} \mathcal {J}_{\varvec{W}_T^m}&= \min _{\varvec{W}_T^m} \; \frac{1}{2}\Vert (\varvec{W}_T^m)^T\varvec{X}_T^m-\varvec{F}_T^m(\varvec{G}_T^m)^T\Vert _F^2 \\&\qquad \quad + \frac{\lambda _1}{2}(1-\mu )\Vert \varvec{W}_T^m\overline{(\varvec{X}_T^m})^T - (\varvec{W}_S)^T\overline{\varvec{X}_S} \Vert _2^2 \\&\qquad \quad + \frac{\lambda _2}{2}\Vert \varvec{W}_T^m - \varvec{W}_S\varvec{V}^m\Vert _F^2 + \frac{\lambda _3}{2}\Vert \varvec{W}_T^m - \varvec{DV}_T^m\Vert _F^2 \\ \end{aligned} \end{aligned}$$(8)Calculating the derivative of (8) w.r.t. \(\varvec{W}_T^m\) and making it to zero yields the closed-form solution
$$\begin{aligned} \begin{aligned} \varvec{W}_T^m & = \left( \varvec{X}_T^m(\varvec{X}_T^m)^T+\lambda _1(1-\mu )\overline{\varvec{X}_T^m}(\overline{\varvec{X}_T^m})^T+(\lambda _2+\lambda _3)\varvec{I}_d\right) ^{-1}\\& \quad \cdot \left( \varvec{X}_T^m\varvec{G}_T^m(\varvec{F}_T^m)^T+\lambda _1(1-\mu )\overline{\varvec{X}_T^m}(\overline{\varvec{X}_S})^T\varvec{W}_S\right. \\&\quad \left. +\lambda _2\varvec{W}_S\varvec{V}^m+\lambda _3\varvec{DV}_T^m\right) \end{aligned} \end{aligned}$$(9) -
Solve \(\varvec{F}_T^m\) with \(\varvec{W}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\), \(\varvec{D}\) fixed.
When \(\varvec{W}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\) and \(\varvec{D}\) are fixed, then (7) w.r.t. \(\varvec{F}_T^m\) can be written as
Taking the derivative of (10) w.r.t. \(\varvec{F}_T^m\) to zero, yields the following closed-form solution
-
Solve \(\varvec{G}_T^m\) with \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\), \(\varvec{D}\) fixed.
When \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\) and \(\varvec{D}\) are fixed, then (7) w.r.t. \(\varvec{G}_T^m\) can be written as
Considering the (ij)th element, \(\varvec{G}_{T(ij)}^m\) of \(\varvec{G}_T^m\) stores the membership degree of the ith instance to the jth class, we compare the distance of the instance to each of the class centroids and assign it to the class with the closet distance, as formulated
-
Solve \(\varvec{V}^m\) with \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}_T^m\), \(\varvec{D}\) fixed.
When \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}_T^m\) and \(\varvec{D}\) are fixed, then (7) w.r.t. \(\varvec{V}^m\) can be written as
constrained by \((\varvec{V}^m)^T\varvec{V}^m = \varvec{I}\). We set the derivative of \(\mathcal {J}_{\varvec{V}^m}\) to zero, yielding
Then, performing Gram-Schmidt orthogonalization operation on \(\varvec{V}^m\) generates the solution.
-
Solve \(\varvec{V}_T^m\) with \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\), \(\varvec{D}\) fixed.
When \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\) and \(\varvec{D}\) are fixed, then (7) w.r.t. \(\varvec{V}_T^m\) can be written as
For convenience of optimization, we introduce a diagonal matrix
into (16) and reformulate it as
Setting the derivative of \(\mathcal {J}_{\varvec{V}_T^m}\) w.r.t. \(\varvec{V}_T^m\) to zero, yields
Since \(\varvec{V}_T^m\) is involved in \(\varvec{S}_v\), therefore we need to update them in an alternating manner.
-
Solve \(\varvec{D}\) with \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\) fixed.
When \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\) and \(\varvec{V}_T^m\) are fixed, then (7) w.r.t. \(\varvec{D}\) can be equivalently formulated as
Making the derivative of \(\mathcal {J}_{\varvec{D}}\) w.r.t. \(\varvec{D}\) to zero, yields the closed-form analytical solution
Through updating \(\varvec{W}_T^m\), \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\), \(\varvec{D}\) alternatively until convergence, we can eventually achieve their optimal solutions. The complete optimization algorithm is summarized in Algorithm 1.

3.4 Convergence analysis
Here, we analyze the convergence property of Algorithm 1. Specifically, denote by \(\mathcal {J}(\varvec{W}_T^{m(t)}, \varvec{F}_T^{m(t)}, \varvec{G}_T^{m(t)},\) \(\varvec{V}^{m(t)}, \varvec{V}_T^{m(t)}, \varvec{D}^{(t)})\) the objective value of (7) at the tth iteration. The objective is convex w.r.t. \(\varvec{W}_T^m\) when fixing \(\varvec{F}_T^m, \varvec{G}_T^m, \varvec{V}^m, \varvec{V}_T^m, \varvec{D}\). Therefore, after updating the solution of \(\varvec{W}_T^m\), it holds
Considering the objective of (7) is also convex w.r.t each of \(\varvec{F}_T^m\), \(\varvec{G}_T^m\), \(\varvec{V}^m\), \(\varvec{V}_T^m\), \(\varvec{D}\) when fixing all the other variables.Footnote 1 As a result, the following inequalities hold
and
Taking into account from (22) to (27), it appears that
It verifies that the entire objective value descends monotonously with increased iterations. In addition, (7) is definitely lower-bounded by nonnegative value since it is a linear sum of nonnegative norms, i.e. \(\Vert \cdot \Vert _F^2\), \(\Vert \cdot \Vert _2^2\) and \(\Vert \cdot \Vert _{2,1}\). As a result, we draw the conclusion that the objective function of (7), solved by Algorithm 1, converges in finite iterations.
3.5 Time complexity analysis
The time cost of Algorithm 1 mainly lies in updating the variables. More specifically, the cost of calculating the solution of \(\varvec{W}_T^m\) in line 3 is \(\mathcal {O}(d^3+d^2p)\), the cost of updating \(\varvec{F}_T^m\) in line 4 is \(\mathcal {O}({K_T^m}^3+{K_T^m}^2p)\). In line 6 and 8, calculating \(\varvec{V}^m\) and \(\varvec{V}_T^m\) respectively costs \(\mathcal {O}(d^3+p^2d)\) and \(\mathcal {O}(r^3+rdp)\). As for the time cost of solving the dictionary \(\varvec{D}\) in line 11, it is \(\mathcal {O}(Mr^3+Mdpr)\). Usually, it holds that \(d \ge p \ge r\). Assume the algorithm converges in L iterations. As a result, taking all the cost into account, the total time complexity of Algorithm 1 is \(\mathcal {O}\left( LMdpr+Ld^3+L(K_T^m)^2p+L(K_T^m)^3\right)\).
4 Experiment
In this section, we conduct experiments to evaluate the proposed method. Firstly, we introduce the setting and data set used for the evaluations. Secondly, we report the comparison with other related methods, with performance Hypothesis test and ablation study. Finally, we evaluate the convergence efficiency of the proposed algorithm.
4.1 Dataset and setting
Artificial dataset In order to verify the motivation of the proposed method, we construct an artificial dataset with known effects. As shown in Table 2, the artificial dataset consists of one source domain and two target domains with two classes. We fix the covariance matrix and generate randomly twenty samples that obey the Gaussian distribution for each class according to the given class centers. It is worth noting that compared with the source domain, the class center of target domain 2 is closer to target domain 1, which is designed to demonstrate the feasibility of target knowledge transfer.
Real dataset We evaluate on two types of ordinal image datasets: character dataset, i.e. Chars74k [47] and face aging datasets, i.e. AgeDB [48], Morph (album 2) [49], CACD [50]. For Chars74k, it is consisted of over 100000 images of three modalities of characters, i.e. Img, Hnd, Fnt, as shown in Fig. 2. We uniformly resize the images to \(32\times 32\), extracted the Hog coefficients from them with normalization and apply the generated 288-dimensional components as feature representation. For the AgeDB, Morph and CACD face datasets, they respectively contain 16,000, 55,000, and 160,000 face images with age annotation, as demonstrated in Fig. 3. We extract their normalized BIF visual features and retained 95% components for evaluation.
Setting To make extensive evaluations, we conduct comparison with the most related 1SmT UDA method PA-1SmT, as well as other related 1S1T UDA methods, i.e. STC [51], TSC [52], TFSC [53], CMMS [21], SLSA[22]. For fairness of comparison, the source modules of these methods are trained in supervised manner while the target unsupervised. The values of hyper parameters \(\lambda _1\), \(\lambda _2\), \(\lambda _3\), \(\lambda _4\) are searched in the range of (1e−3, 1e−2, 1e−1, 1e1, 1e2, 1e3, 1e4, 1e5, 1e6), the number p of source domain projection directions in KDLOR is selected in the range of [5, 10, 15, \(\ldots\), 100], the dimension r of the dictionary in the range of [5, 10, 15, \(\ldots\), p], all through five-fold cross-validation. The parameters in the compared methods are also tuned in cross-validation referring to the literature. To comprehensively evaluate the performance, we adopt the Normalized Mutual Information (NMI) and Rand Index (RI) [27], as well as the Mean Absolute Errors (MAE) [18] as performance measure. In order to mitigate the randomness of results, we run the evaluations ten times and report the average results.
4.2 Results and analysis
Artificial dataset recognition For comparison, we construct two 1S1T tasks “source \(\rightarrow\) target1”, “source \(\rightarrow\) target2” and one 1SmT task “source \(\rightarrow\) target1, target2”. The data distribution and classification bound of three tasks are shown in Fig. 4 (The classification bound is marked by the dashed line of the corresponding color of each domain. ). We can find that the classification result of target2 is worse than target1 in the 1S1T task while the performance improves in the 1SmT task, which is consistent with our expectation. Actually, in the process of 1SmT UDA, the target1 which is closer to the source could be seen as an intermediate domain between source and target2. And the dictionary learning can be regarded as a bias term in the linear space of this artificial dataset so that the discrimination information of target1 is utilized by the target2.
Ordinal character recognition We conduct ordinal character recognition evaluation on the Chars74k dataset. Specifically, we randomly choose one modality from Img, Fnt, Hnd as source domain while the rest as target domains. The results are shown in Table 3 and 4 (best in bold, second-best underlined).
We can observe the following findings. On the one hand, the proposed OrUDA model generated the best results in terms of both NMI and RI measures, with clear performance improvement. Moreover, in 1S1T setting, OrUDA still beats the other methods. It states that transferring both the implicit source model knowledge and explicit distribution information, as well as the inter-target relations effectively benefit the target domain learning. On the other hand, the improvement extent on different cases differs. It affirms the divergence between the target domains and verifies the rationality of modeling target-specific transfer matrix and relation matrix in OrUDA.
Human age estimation We also perform human age estimation in the setting of cross datasets. Specifically, we randomly take from AgeDB, Morph and CACD one dataset as the source dataset while the other two as target datasets. For the sake of domain knowledge transfer, we select their common age range of 16 to 62 years old, and divide them into several groups, i.e. 16–20, 21–25, \(\ldots\), 55–60, 61–62 for age group estimation. The averaged results on ten random runs are shown in Table 5.
We observe that in both 1S1T and 1SmT settings, the proposed OrUDA model generates the best age estimation results, compared to related methods. It demonstrates the effectiveness of the proposed model and its superiority to other compared models.
In order to estimate the effectiveness of the OrUDA method in improving performance, we perform hypothesis test [54] on the results in Table 3 to Table 5. The test results are shown in Fig. 5. We can observe that the proposed OrUDA method (i.e. OURS) generates a quite clear performance improvement than the others.
4.3 Ablation study
In order to explore the effectiveness of the modules of the proposed model (objective function), we additionally perform ablation study. Specifically, we estimate respectively the efficacy of orderly projection, implicit knowledge transfer, explicit knowledge transfer and target knowledge transfer in (7). As shown in Table 6, each of the four modules in OrUDA is significant, especially the explicit knowledge transfer. Moreover, though the target knowledge transfer could not improve the model as much as knowledge transfer from the labeled source domain in most tasks due to the absence of supervised information, it is far away from enough to transfer supervised knowledge only for a UDA model. Actually, various relationships of domains are crucial to benefit the process of domain adaptation, which acts as the complementary set of the source domain knowledge, such as relationship of target domains or the ordered relationship of samples. The results of the ablation study prove our hypothesis and explain why our model performs better than other UDA models.
4.4 Convergence evaluation
We also empirically evaluate the convergence efficiency of Algorithm 1. Without loss of generality, we conduct analysis experiments with the same setting aforementioned on the three face aging datasets and report the convergence results in Fig. 6. We can observe from the results that, the algorithm efficiently converges in about 15 iterations.
4.5 Parameter sensitivity analysis
To assess the parameters of the proposed model, we perform parameter sensitivity analysis for OrUDA on the face datasets. Specifically, we evaluate by just tuning the concerned parameter while fixing all the other ones. The evaluation results are shown in Fig. 7. We can observe the following findings. On the one hand, although OrUDA is sensitive to \(\lambda _1\), \(\lambda _2\) and \(\lambda _3\), the performance changes with good trends. In summary, the best performance can be achieved when \(1e5< \lambda _1 < 1e7\), \(\lambda _2 < 1e1\), \(\lambda _3 < 1e1\), regardless on which face dataset the source target sub-model is trained. On the other hand, the performance is preferably not sensitive to \(\lambda _4\), which can be fixed in practical applications.
5 Conclusion
In this work, we proposed an ordinal model of unsupervised domain adaptation, i.e. OrUDA, by transferring knowledge from both the implicit model parameters and explicit cross-domain data distributions, as well as the relations between the target domains. By this kind of model, the knowledge from the source and target has been exploited to training the concerned target model. In addition, we designed an alternating optimization algorithm to solve the OrUDA model and provided theoretical convergence proof. Finally, we experimentally evaluated the effectiveness of the proposed method in performance and the sensitivity of its parameters. We proved that this modeling method can effectively handle the UDA problem in ordinal and 1SmT scenarios. Compared with related existing UDA methods, the proposed OrUDA outperforms others thanks to the utilization of ordinal prior and related information in other target domains. Actually, there are more priors that could be taken into consideration such as sparsity, low-rank and so on. Hence, in the future, we will consider generalizing the proposed method by exploring more prior knowledge [55] and extending the method into the deep network architecture.
References
Zhao M, Zhan C, Wu Z, Tang P (2015) Semi-supervised image classification based on local and global regression. IEEE Signal Process Lett 22(10):1666–1670
Zhao MB, Chow TWS, Peng T, Wang Z, Zukerman M (2016) Route selection for cabling considering cost minimization and earthquake survivability via a semi-supervised probabilistic model. IEEE Trans Industr Inf 13(2):1–1
Gong B, Shi Y, Sha F, Grauman K (2012) Geodesic flow kernel for unsupervised domain adaptation. In: 2012 IEEE conference on computer vision and pattern recognition, pp. 2066–2073
Zhuang F, Luo P, Du C, He Q, Shi Z, Xiong H (2013) Triplex transfer learning: exploiting both shared and distinct concepts for text classification. IEEE Trans Cybern 44(7):1191–1203
Long M, Zhu H, Wang J, Jordan MI (2016) Unsupervised domain adaptation with residual transfer networks. In: Proceedings of the 30th international conference on neural information processing systems, pp. 136–144
Tahmoresnezhad J, Hashemi S (2016) Visual domain adaptation via transfer feature learning. Knowl Inf Syst 50(2):1–21
Zhang L, Zhang D (2016) Robust visual knowledge transfer via extreme learning machine-based domain adaptation. IEEE Trans Image Process 25(10):4959–4973
Liu J, Zhang L (2019) Optimal projection guided transfer hashing for image retrieval. In: Proceedings of the AAAI conference on artificial intelligence, vol. 33, pp. 8754–8761
Liang J, Hu D, Feng J (2020) Do we really need to access the source data? Source hypothesis transfer for unsupervised domain adaptation. In: International conference on machine learning, pp. 6028–6039
Tian Q, Sun H, Ma C, Cao M, Chu Y, Chen S (2021) Heterogeneous domain adaptation with structure and classification space alignment. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2021.3070545
Pan SJ, Yang Q (2009) A survey on transfer learning. IEEE Trans Knowl Data Eng 22(10):1345–1359
Cortes C, Mohri M, Riley M, Rostamizadeh A (2008) Sample selection bias correction theory. In: International conference on algorithmic learning theory, pp. 38–53
Yao Y, Doretto G (2010) Boosting for transfer learning with multiple sources. In: 2010 IEEE computer society conference on computer vision and pattern recognition, pp. 1855–1862
Tan B, Song Y, Zhong E, Yang Q (2015) Transitive transfer learning. In: Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining, pp. 1155–1164
Khan MNA, Heisterkamp DR (2016) Adapting instance weights for unsupervised domain adaptation using quadratic mutual information and subspace learning. In: 2016 23rd international conference on pattern recognition (ICPR), pp. 1560–1565
Tan B, Zhang Y, Pan SJ, Yang Q (2017) Distant domain transfer learning. In: Thirty-first AAAI conference on artificial intelligence, pp. 2604–2610
Long M, Wang J, Sun J, Philip SY (2014) Domain invariant transfer kernel learning. IEEE Trans Knowl Data Eng 27(6):1519–1532
Tian Q, Chen S (2017) Cross-heterogeneous-database age estimation through correlation representation learning. Neurocomputing 238:286–295
Li J, Lu K, Huang Z, Zhu L, Shen H (2019) Heterogeneous domain adaptation through progressive alignment. IEEE Trans Neural Netw Learn Syst 30(5):1381
Zhang L, Wang S, Huang G-B, Zuo W, Yang J, Zhang D (2019) Manifold criterion guided transfer learning via intermediate domain generation. IEEE Trans Neural Netw Learn Syst 30(12):3759–3773
Tian L, Tang Y, Hu L, Ren Z, Zhang W (2020) Domain adaptation by class centroid matching and local manifold self-learning. IEEE Trans Image Process 29:9703–9718
Wang W, Chen S, Xiang Y, Sun J, Li H, Wang Z, Sun F, Ding Z, Li B (2021) Sparsely-labeled source assisted domain adaptation. Pattern Recogn 112:107803
Zhao Z, Chen Y, Liu J, Liu M (2010) Cross-mobile elm based activity recognition. Int J Eng Ind 1(1):30–38
Zhao Z, Chen Y, Liu J, Shen Z, Liu M (2011) Cross-people mobile-phone based activity recognition. In: Twenty-second international joint conference on artificial intelligence, pp. 2545–2550
Sun S, Xu Z, Yang M (2013) Transfer learning with part-based ensembles. In: International workshop on multiple classifier systems, pp. 271–282
Wei Y, Zhu Y, Leung CW-k, Song Y, Yang Q (2016) Instilling social to physical: co-regularized heterogeneous transfer learning. In: Thirtieth AAAI conference on artificial intelligence, pp. 1338–1344
Yu H, Chen S (2019) Whole unsupervised domain adaptation using sparse representation of parameter dictionary. J Front Comput Sci Technol 13(05):822–833
Sugiyama M, Nakajima S, Kashima H, Buenau P, Kawanabe M (2007) Direct importance estimation with model selection and its application to covariate shift adaptation. In: NIPS'07: Proceedings of the 20th international conference on neural information processing systems, pp 1433–1440
Long M, Cao Y, Wang J, Jordan M (2015) Learning transferable features with deep adaptation networks. In: International conference on machine learning, pp. 97–105. PMLR
Pan SJ, Tsang IW, Kwok JT, Yang Q (2010) Domain adaptation via transfer component analysis. IEEE Trans Neural Netw 22(2):199–210
Sun B, Feng J, Saenko K (2016) Return of frustratingly easy domain adaptation. In: Proceedings of the AAAI conference on artificial intelligence, vol. 30
Zellinger W, Grubinger T, Lughofer E, Natschläger T, Saminger-Platz S (2017) Central moment discrepancy (cmd) for domain-invariant representation learning. arXiv preprint arXiv:1702.08811
Mancini M, Porzi L, Bulo SR, Caputo B, Ricci E (2018) Boosting domain adaptation by discovering latent domains. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 3771–3780
Caseiro R, Henriques JF, Martins P, Batista J (2015) Beyond the shortest path: Unsupervised domain adaptation by sampling subspaces along the spline flow. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 3846–3854
Peng P, Xiang T, Wang Y, Pontil M, Gong S, Huang T, Tian Y (2016) Unsupervised cross-dataset transfer learning for person re-identification. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 1306–1315
Zhao H, Zhang S, Wu G, Moura JM, Costeira JP, Gordon GJ (2018) Adversarial multiple source domain adaptation. Adv Neural Inf Process Syst 31
Dai Y, Liu J, Ren X, Xu Z (2020) Adversarial training based multi-source unsupervised domain adaptation for sentiment analysis. In: Proceedings of the AAAI conference on artificial intelligence, vol. 34, pp. 7618–7625
Yang L, Balaji Y, Lim S-N, Shrivastava A (2020) Curriculum manager for source selection in multi-source domain adaptation. In: European conference on computer vision. Springer, New York, pp. 608–624
Guo H, Pasunuru R, Bansal M (2020) Multi-source domain adaptation for text classification via distancenet-bandits. In: Proceedings of the AAAI conference on artificial intelligence, vol. 34, pp. 7830–7838
Wang H, Xu M, Ni B, Zhang W (2020) Learning to combine: knowledge aggregation for multi-source domain adaptation. In: European conference on computer vision. Springer, New York, pp. 727–744
Sun B-Y, Li J, Wu DD, Zhang X-M, Li W-B (2009) Kernel discriminant learning for ordinal regression. IEEE Trans Knowl Data Eng 22(6):906–910
Sun B-Y, Wang H-L, Li W-B, Wang H-J, Li J, Du Z-Q (2015) Constructing and combining orthogonal projection vectors for ordinal regression. Neural Process Lett 41(1):139–155
Pan SJ, Tsang IW, Kwok JT, Yang Q (2010) Domain adaptation via transfer component analysis. IEEE Trans Neural Netw 22(2):199–210
Wang J, Feng W, Chen Y, Yu H, Huang M, Yu PS (2018) Visual domain adaptation with manifold embedded distribution alignment. In: Proceedings of the 26th ACM international conference on multimedia, pp. 402–410
Ben-David S, Blitzer J, Crammer K, Pereira F (2007) Analysis of representations for domain adaptation. In: Advances in neural information processing systems, pp. 137–144
Nie F, Huang H, Cai X, Ding CH (2010) Efficient and robust feature selection via joint l2,1-norms minimization. In: Advances in neural information processing systems, pp. 1813–1821
De Campos TE, Babu BR, Varma M et al (2009) Character recognition in natural images. VISAPP 2(7):273–280
Moschoglou S, Papaioannou A, Sagonas C, Deng J, Kotsia I, Zafeiriou S (2017) Agedb: the first manually collected, in-the-wild age database. In: Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pp. 51–59
Ricanek K, Tesafaye T (2006) Morph: A longitudinal image database of normal adult age-progression. In: 7th international conference on automatic face and gesture recognition (FGR06), pp. 341–345
Chen B-C, Chen C-S, Hsu WH (2014) Cross-age reference coding for age-invariant face recognition and retrieval. In: European conference on computer vision, pp. 768–783
Dai W, Yang Q, Xue G-R, Yu Y (2008) Self-taught clustering. In: Proceedings of the 25th international conference on machine learning, pp. 200–207
Jiang W, Chung F-l (2012) Transfer spectral clustering. In: Joint European conference on machine learning and knowledge discovery in databases, pp. 789–803
Deng Z, Jiang Y, Chung F-L, Ishibuchi H, Choi K-S, Wang S (2015) Transfer prototype-based fuzzy clustering. IEEE Trans Fuzzy Syst 24(5):1210–1232
Demisar J, Schuurmans D (2006) Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res 7(1):1–30
Zhao M, Zhang Y, Zhang Z, Liu J, Kong W (2019) Alg: adaptive low-rank graph regularization for scalable semi-supervised and unsupervised learning. Neurocomputing 370:16–27
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant 62176128, the Open Projects Program of State Key Laboratory for Novel Software Technology of Nanjing University under Grant KFKT2022B06, the Fundamental Research Funds for the Central Universities No. NJ2022028, the Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD) fund, as well as the Qing Lan Project.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Tian, Q., Sun, H., Chu, Y. et al. Ordinal unsupervised multi-target domain adaptation with implicit and explicit knowledge exploitation. Int. J. Mach. Learn. & Cyber. 13, 3807–3820 (2022). https://doi.org/10.1007/s13042-022-01626-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-022-01626-3