Risk-Averse support vector classifier machine via moments penalization

Abstract

Support vector machine (SVM) has always been one of the most successful learning methods, with the idea of structural risk minimization which minimizes the upper bound of the generalization error. Recently, a tighter upper bound of the generalization error, related to the variance of loss, is proved as the empirical Bernstein bound. Based on this result, we propose a novel risk-averse support vector classifier machine (RA-SVCM), which can achieve a better generalization performance by considering the second order statistical information of loss function. It minimizes the empirical first- and second-moments of loss function, i.e., the mean and variance of loss function, to achieve the “right” bias-variance trade-off for general classes. The proposed method can be solved by the kernel reduced and Newton-type technique under certain conditions. Empirical studies show that the RA-SVCM achieves the best performance in comparison with other classical and state of art methods. The additional analysis shows that the proposed method is insensitive to the parameters, so abroad range of parameters lead to satisfactory performance. The proposed method is a general form of standard SVM, so it enriches the related studies of SVM.

1 Introduction

Support Vector Machine (SVM) [1, 2] and its extensions have always been one of the most successful machine leaning methods for supervised learning due to their accuracy, robustness and indifference towards the instance data type. They are widely used in classification and regression problems, such as face recognition [3, 4], spam recognition [5], handwriting number recognition [6], disease diagnosis [7,8,9], and pattern recognition [10], etc.

During the past few decades, many common improved methods based on SVM have been developed well, among which the most methods change the regularization terms, constraints, and loss functions to improve the learning ability of the model. For instance, the least-square SVM (LS-SVM) [11] method can be easily implemented due to the utilization of the equality constraints. A radius-margin-based SVM model with LogDet regularization considers the radius and introduce a negative LogDet term to improve the model accuracy [12]. A risk-averse classifier allows for associating distinct risk functional to each classes [13]. The sparse LSSVM in primal using cholesky factorization for large-scale problems and the random reduced P-LSSVM (RRP-LSSVM) achieves the sparse solutions of LSSVM [14]. The twin Support vectors [15,16,17] finds two hyperplanes, one for each class, and classifies points according to which hyperplane a given point is closest to. These methods are mainly based on margin theory [1] or structural risk minimization theory. They focus on margin of a few instances or first-order information of loss function instead of the characteristics of the data itself.

There are a few studies considered the effect of the information about data on the generalization ability of SVM-style algorithms. The SVM+ approach can lower the overall system’s VC-dimension and hence attain better generalization by taking advantage of the structure in the training data [18, 19]. But this model still consider only the samples that are in the class boundaries regardless of class distribution characteristics. The Support Vector Machines with multiview Privileged improve the performance of the classification tasks by exploiting the complementary information among multiple feature sets [20,21,22]. The margin distribution optimization (MDO) algorithm [23] optimizes margin distribution by minimizing the sum of exponential loss, but this method tends to get a local minima with slow convergence since the objective function is non-differential and non-differential. At the same time, more and more attention has been paid to the second-order statistical characteristics of training datas. A robust least-squares SVM [24] with minimization of mean and variance of modeling error distributes smaller weight to larger error training samples and lager weight to small error training samples, which is more robust in regards to random noise. The large margin distribution machine (LDM) [25] tries to optimize the margin distribution by maximizing the margin mean and minimizing the margin variance simultaneously. The optimal margin distribution machine (ODM) [26], which is a simpler but powerful formulation than LDM, were successively proposed by simplifing the variance term of LDM and introducing a insensitive loss. All studies of SVM above, however, focused on margin-based explanation or partial information of training data, whereas the influence of the loss distribution for SVM has not been well exploited.

Based on Hoeffding’s inequality, the SVM minimizes the structural risk that is upper bound of the generalization error. The empirical Bernstein bounds [27], however, disclosed that minimize the structural risk does not necessarily lead to better generalization performance, and instead the variance of loss function has been proven be more crucial. In other words, the empirical Bernstein bounds is a tighter upper bound of the generalization error. Inspired by the theory above, we propose a Risk-Averse support vector classifier machine(RA-SVCM). The RA-SVCM tries to achieve the “right” bias-variance trade-off for general classes by minimizing the empirical first- and second-moments of loss simultaneously, i.e., the mean and variance of loss. Comprehensive experiments on twelve regular scale data sets and eight large scale data sets show the superiority of RA-SVCM to SVM and many state-of-the-art methods, verifying that the minimum variance of loss function is more crucial for SVM-style learning approaches than minimum structural risk.

The remainder of this paper is organized as follows. An overview of the related work is introduced in Sect. 2. In Sect. 3, the details of the developed RA-SVCM are stated. In Sect. 4, the differences with related methods are presented. the details of the developed RA-SVCM are stated. The experimental results are then reported in Sect. 5 to validate the validity of the method. Finally, Sect. 6 concludes this paper.

2 Related work

2.1 SVM

This section briefly introduces SVM. For convenience, we first introduce some notations which are used throughout the paper. Let ${\mathcal {X}}\subset {\mathbb {R}}^d$ and ${\mathcal {Y}} = \{ + 1, - 1\}$ denote the input space and output space, respectively. Denote by ${\mathcal {D}}$ an (unknown) underlying probability distribution over the product space ${\mathcal {X}} \times {\mathcal {Y}}$. Let ${u_ + } = \max \{ 0,u\}$. For training set $S = \{ ({\varvec{x}_1},{y_1}) \cdots ({\varvec{x}_m},{y_m})\} \in {\{ {\mathcal {X}} \times {\mathcal {Y}}\} ^m}$, which drawn independently and identically (i.i.d) according to the distribution ${\mathcal {D}}$, the goal of soft SVM is to learn parameters $(\varvec{w},b)$ of a hypothesis $f(\varvec{x}) = \left\langle {\varvec{w},\phi (\varvec{x})} \right\rangle +b$ from the optimization problem:

$$\begin{aligned} \mathop {\min }\limits _{\varvec{w},b} \frac{C}{m}{\sum \limits _{i = 1}^m {[1 - {y_i}(\left\langle {\varvec{w},\phi ({\varvec{x}_i})} \right\rangle + b)]_ + } } + \frac{1}{2}{\left\| \varvec{w} \right\| ^2}, \end{aligned}$$

(1)

where $\varvec{w}\in {\mathbb {H}}, b\in {\mathbb {R}}$, tradeoff paramete $C> 0$ and $\phi ( \cdot )$ maps $\varvec{x}_i$ to a high dimensional feature space. ${\mathbb {H}}$ is the reproducing kernel Hilbert space (RKHS) associated with a kernel fuction $k:{{\mathbb {R}}^m} \times {{\mathbb {R}}^m} \rightarrow {\mathbb {R}}$ satisfying $k({\varvec{x}_i},{\varvec{x}_j}) = {\left\langle {\phi ({\varvec{x}_i}),\phi ({\varvec{x}_j})} \right\rangle }$. For convenience, SVM for learning a homgenous halfpace is considered, where the bias term b is set to be zero. Because Steinwart et al. [28] proved that SVMs without offset term b have convergence rates and classification performance that are comparable to SVMs with offset, while the absence of the offset gives more freedom in the algorithm design.

On the basis of the representation theorem [29,30,31], the learning result $\varvec{w}$ can be represented by a linear combination of the kernel functions:

$$\begin{aligned} \varvec{w} = \sum \limits _{i = 1}^m {{\varvec{\alpha } _i}} \phi ({\varvec{x}_i}), \end{aligned}$$

(2)

which is a finite linear combination of $\phi (\varvec{x}_i)$. Therefore, we can optimize problem (1) with respect to the coefficients ${\varvec{\alpha }}$ in ${\mathbb {R}}^m$ instead of the parameters $\varvec{w}$ in ${\mathbb {H}}$ as follows.

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha } \in {\mathbb {R}}^m} \frac{C}{m} \sum \limits _{i = 1}^m {\left( {1 - {y_i}{K_i}\varvec{\alpha } } \right) _+} + \frac{1}{2}{\varvec{ \alpha }^\top }K\varvec{\alpha }, \end{aligned}$$

(3)

where the kernel matrix K satisfies $K_{i,j}=k({\varvec{x}_i},{\varvec{x}_j}) = {\left\langle {\phi ({\varvec{x}_i}),\phi ({\varvec{x}_j})} \right\rangle }$ and ${K_i}$ is the i-th row of K. It is infeasible to get the whole kernel matrix when the sample size m is larger enough. According to sparse representation theorem [32, 33], the learning result can be represented as

$$\begin{aligned} \varvec{w} = \sum \limits _{i \in J} {{\varvec{\alpha } _i}} \phi ({\varvec{x}_i}), \end{aligned}$$

(4)

where a reduced set J is selected randomly from the index set $M = \{1,2,....m\}$, and $|J |\le 0.1 m$ [33, 34]. So the reduced version of standard SVM corresponding to (3) can be represented as

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha }_J \in {\mathbb {R}}^{|J |}} \frac{C}{m} \sum \limits _{i = 1}^m {\left( {1 - {y_i}{K_{Ji}}\varvec{\alpha }_J } \right) _+} + \frac{1}{2}\varvec{\alpha } _J^{\top }K_{JJ}{\varvec{\alpha } _J}. \end{aligned}$$

(5)

Here, $K_{JJ}$ is the sub-matrix of K, whose elements are $k({\varvec{x}_i},{\varvec{x}_j})$ for $i\in J$ and $j\in J$. $K_{JM}$ is a sub-matrix of K, whose elements are $k({\varvec{x}_i},{\varvec{x}_j})$ for $i\in J$ and $j\in M$ and $K_{Ji}$ is i-th column of $K_{JM}$.

2.2 LDM and ODM

Based on theoretical results that the margin distribution is more crucial to the generalization performance, the large margin distribution Machine (LDM) [25] is proposed to achieving a better generalization performance by optimizing the margin distribution of model characterized by the first and second order statistics, i.e., the margin mean and variance. The formulation of LDM is as following.

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{\varvec{w},{\varvec{\xi } _i}} \frac{1}{2}{\left\| \varvec{w} \right\| ^2} + {\mu _1}{\gamma _v} - {\mu _2}{\gamma _m} + \frac{\lambda }{m}\sum \limits _{i = 1}^m {{\varvec{\xi } _i}} \\ s.t.{y_i}{\varvec{w}^T}\phi ({\varvec{x}_i}) \ge 1 - {\varvec{\xi } _i},{\varvec{\xi } _i} \ge 0,\forall i, \end{array} \end{aligned}$$

(6)

where ${\gamma _m} = \frac{1}{m}\sum \nolimits _{i = 1}^m {{y_i}{\varvec{w}^T}\phi ({\varvec{x}_i})}$ and ${\gamma _v} = \frac{1}{m}\sum \nolimits _{i = 1}^m {{{({y_i}{\varvec{w}^T}\phi ({\varvec{x}_i}) - \gamma _m )}^2}}$ are the margin mean and margin variance respectively.

The optimal margin distribution machine (ODM) [26], which is a simpler but powerful formulation than LDM, were successively proposed by simplifying the variance term of LDM and introducing a insensitive loss.

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{\varvec{w},{\varvec{\xi } _i},{\varepsilon _i}} \frac{1}{2}{\left\| \varvec{w} \right\| ^2} + \frac{\lambda }{m}\sum \limits _{i = 1}^m {\frac{{\varvec{\xi } _i^2 + \mu \varvec{\varepsilon } _i^2}}{{{{(1 - D)}^2}}},} \\ s.t.\begin{array}{*{20}{c}} {}&{}{} \end{array}{y_i}{\varvec{w}^T}\phi ({\varvec{x}_i}) \ge 1 - D - {\varvec{\xi } _i},\\ \begin{array}{*{20}{c}} {}&{}{}&{}{{y_i}{\varvec{w}^T}\phi ({\varvec{x}_i}) \le 1 + D + {\varvec{\varepsilon } _i},} \end{array}\forall i. \end{array} \end{aligned}$$

(7)

where $\lambda$ and $\mu$ are trading-off parameters, and D is a parameter for controlling the number of support vectors. For kernel ODM, the objective function of primal problem (7) can be reformulated as the following form,

$$\begin{aligned} {f_O}(\varvec{w})&= \!\frac{1}{2}{\left\| \varvec{w} \right\| ^2}+ \frac{{\lambda }}{{m{{(1 - D)}^2}}} (\!\sum \limits _{i = 1}^m {(1 - D - {y_i}{\varvec{w}^T}\phi ({\varvec{x}_i}))_ + ^2} \nonumber \\&\quad + \mu \sum \limits _{i = 1}^m {({y_i}{\varvec{w}^T}\phi ({\varvec{x}_i}) - 1 - D)_ + ^2}). \end{aligned}$$

(8)

3 The proposed Risk-Averse SVCM

In this section, we begin with a discussion of the confidence bounds most frequently used in learning theory.

Suppose this underlying observation is modeled by a random variable $(\varvec{x},y)$ distributed in some space ${\mathcal {Z}}={\mathcal {X}} \times {\mathcal {Y}}$ according to law ${\mathcal {D}}$, then this underlying observation can be denoted as $l({y},f({\varvec{x}}))$. The ${{\mathbb {E}}_{(\varvec{x},y)\sim {\mathcal {D}}}}[l(y,f(\varvec{x}))]$ and $\frac{1}{m}\sum \nolimits _{i = 1}^m {l({y_i},f({\varvec{x}_i}))}$ are called expected risk and empirical risk of hypothesis f respectively.

According to the above-mentioned conditions and the related theorems in [27], some results can be given as:

Suppose that ${\mathcal {D}}$ is a distribution over ${\mathcal {X}} \times {\mathcal {Y}}$ such that with probability 1 we have that ${\left\| {\varvec{x}} \right\| _2} \le R$ . Let $l:{\mathcal {H}} \times {\mathcal {Z}}\rightarrow {\mathbb {R}}$ be a loss function, and $l({y_i},f({\varvec{x}_i}))$ be a sequence of i.i.d. random variables with values in [0, 1]. Then for any $\delta >0$, with probability at least $1-\delta$ we have

$$\begin{aligned} \mathop {{\mathbb {E}}_{(\varvec{x},y)\sim {\mathcal {D}}}}l(y,f(\varvec{x})) \le \frac{1}{m}\sum \limits _{i = 1}^m {l({y_i},f({\varvec{x}_i}))} + \sqrt{\frac{{\ln 1/\delta }}{{2m}}}, \end{aligned}$$

(9)

The inequation of (9) cited Hoeffding’s inequality probability in form of a confidence dependent bound on the deviation [35]. A drawback of this inequality is that the confidence interval is independent of the hypothesis in question, and of order $\sqrt{1/m}$.

And for any $\delta >0$, then with probability at least $1-\delta$ we aslo have

$$\begin{aligned}\mathop {{\mathbb {E}}_{(\varvec{x},y)\sim {\mathcal {D}}}}l(y,f(\varvec{x}))&\le \frac{1}{m}\sum \limits _{i = 1}^m {l({y_i},f({\varvec{x}_i}))} + \sqrt{\frac{{2{\mathbb {V}}(l)\ln 1/\delta }}{m}} \nonumber \\&\quad + \frac{{\ln 1/\delta }}{{3m}}, \end{aligned}$$

(10)

where ${\mathbb {V}}(l) = {\mathbb {E}}{(l - El)^2}$. The inequality of (10) is called Bennetts’s inequality, and the confidence interval of this inequality becomes $2\sqrt{{\mathbb {V}}l}$ times the confidence interval of the Hoeffding’s inequality. This bound proves us of higher accuracy for hypotheses of small variance, and of lower accuracy for hypotheses of large variance. But the first term on the right hand side depends the unmeasurable variance, leaving us with a uniformly blurred view of the hypothesis class. So Maurer and Pontil [27] provide empirical Bernstein bounds (11), which is a purely data-dependent bound with similar properties as Bennetts’s inequality. This bound makes the diameter of the confidence interval observable and provides us with a view of the loss class which is more in focus for hypotheses of small sample variance.

$$\begin{aligned}\mathop {{\mathbb {E}}_{(\varvec{x},y)\sim {\mathcal {D}}}}l(y,f(\varvec{x})) \!\le \!\frac{1}{m}\sum \limits _{i = 1}^m {l({y_i},f({\varvec{x}_i}))} + \!\sqrt{\frac{{2{\mathbb {V}}_m(l)\ln 2/\delta }}{m}} \! \nonumber \!+\!\frac{{7\ln 2/\delta }}{{3(m - 1)}} \end{aligned}$$

(11)

where ${\mathbb {V}}(l) = {\mathbb {E}}{(l - El)^2}$, ${\mathbb {V}}_m(l) = \frac{1}{{m - 1}}\sum \nolimits _{i = 1}^m {{{({l_i} - {\bar{l}})}^2}}$, and $l_i = l({y_i},f({\varvec{x}_i}))$. Minimizing this uniform convergence bound leads to the sample variance penalization principle:

$$\begin{aligned} \mathop {\arg \min }\limits _{f \in {\mathcal {F}}} \frac{1}{m}\sum \limits _{i = 1}^m {l({y_i},f({\varvec{x}_i}))} + \tau \sqrt{\frac{{V[l(y,f(\varvec{x}))]}}{m}} \end{aligned}$$

(12)

Based on this principle,we propose a new model, which allows for a reduction of mean of the hinge loss as well as the minimization of its variance. As the variance of model loss characterize the stability of the model at sample datas, we named it Risk-Averse support vector classifier machine(RA-SVCM).

Here we first analyze the relevant loss function. Given an i.i.d. training set $\{ {\varvec{x}_i},{y_i}\} _{i = 1}^m$, our aim is to minimize the future probability of error ${\mathbb {P}}_{\mathcal {D}}[yf(\varvec{x})\le 0]$ in classification problems. Note that ${\mathbb {E}}[{{\mathbf {I}}_{yf(\varvec{x}) \le 0}}] = {\mathbb {P}}_{\mathcal {D}}[yf(\varvec{x})\le 0]$, we can minimize the future probability of error by minimizing the mean of 0-1 loss:

$$\begin{aligned} l(y,f(\varvec{x})) = {I_{yf(\varvec{x}) \le 0}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {0,}&{}{yf(\varvec{x}) > 0} \end{array}}\\ {\begin{array}{*{20}{c}} {1,}&{}{yf(\varvec{x}) \le 0.} \end{array}} \end{array}} \right. \end{aligned}$$

(13)

However, the empirical risk minimization with the 0-1 loss is a difficult problem to deal with. Towards this end, we replace the 0-1 loss by the hinge loss :

$$\begin{aligned} l(y,f(\varvec{x})) = \max \{ 0,1 - yf(\varvec{x})\} = \left\{ {\begin{array}{*{20}{l}} 0&{}{yf(\varvec{x}) > 1}\\ {1 - yf(\varvec{x})}&{}{yh(\varvec{x}) \le 1}, \end{array}} \right. \end{aligned}$$

(14)

which is a convex approximation of the 0–1 loss. Therefore, we relate the future probability of error to the hinge loss:

$$\begin{aligned} {\mathbb {P}}_{\mathcal {D}}[yf(\varvec{x})\le 0]={\mathbb {E}}[{{\mathbf {I}}_{yf(\varvec{x}) \le 0}}] \le {E_{\mathcal {D}}}[{(1 - yf(\varvec{x}))_ + }]. \end{aligned}$$

(15)

That is, we can minimize the mean and standard deviation of hinge loss to improve the performance of the SVMs as follows:

$$\begin{aligned}&\mathop {\min }\limits _{f \in {\mathcal {F}}} \frac{1}{m}\sum \limits _{i = 1}^m {{{(1 - {y_i}f({\varvec{{x}_i}}))}_ +}}\nonumber \\&+ \tau \sqrt{\frac{{\sum \limits _{i = 1}^m {{{({{(1 - {y_i}f({\varvec{{x}_i}}))}_ +} - \frac{1}{m}\sum \limits _{j = 1}^m {{{(1 - {y_j}f({\varvec{{x}_j}}))}_ +}} )}^2}}}}{m(m-1)}}. \end{aligned}$$

(16)

Since there is an unknown trade-off parameter between the two terms in (16), and it is difficult to solve because of the standard deviation, we can minimize that cost by the following problem:

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{f \in {\mathcal {F}}} \frac{1}{m}\sum \limits _{i = 1}^m {{{(1 - {y_i}f({\varvec{x}_i}))}_ + }} \\ s.t.\sqrt{\frac{{\sum \limits _{i = 1}^m {{{({{(1 - {y_i}f({\varvec{x}_i}))}_ + } - \frac{1}{m}\sum \limits _{j = 1}^m {{{(1 - {y_j}f({\varvec{x}_j}))}_ + }} )}^2}} }}{m(m-1)}}\le B, \end{array} \end{aligned}$$

(17)

where ${\mathcal {F}}$ is a finite class of hypotheses $f:{\mathcal {X}}\rightarrow [0,1]$, and the trade-off parameter is now parametrized by B. For every $\tau$, there is a B that obtains the same optimal function. In particular, $B=\infty$ is equivalent to $\tau =0$. The problem above can be equivalent to the problem as follows:

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{f \in {\mathcal {F}}} \frac{{{\mu _1}}}{m}\sum \limits _{i = 1}^m {{{(1 - {y_i}f({\varvec{x}_i}))}_ + }} \\ s.t.\frac{\sum \nolimits _{i = 1}^m {{{({{(1 - {y_i}f({\varvec{x}_i}))}_ + } - \frac{1}{m}\sum \nolimits _{j = 1}^m {{{(1 - {y_j}f({\varvec{x}_j}))}_ + }} )}^2}}}{m(m-1)} \le {B^2}, \end{array} \end{aligned}$$

(18)

where $\mu _1\ge 0$ is trade-off parameters of mean term. By introducing the Lagrange multipliers $\mu _2$ for the constraints, the Lagrange of Eq.(19) lead to

$$\begin{aligned} \frac{\mu _1}{m}\sum \limits _{i = 1}^m {{{(1 \!- \!{y_i}f({\varvec{x}_i}))}_ + }} \! + \frac{\mu _2}{m(m-1)} \sum \limits _{i = 1}^m {{{\left({{(1 - {y_i}f({\varvec{x}_i}))}_ + }\! - \!\frac{1}{m}\sum \limits _{j = 1}^m {{{(1 - {y_j}f({\varvec{x}_j}))}_ + }} \right)}^2}} \! - \!\mu _2 {B^2}. \end{aligned}$$

(19)

Since the trird term does not involve the function f, we can merely optimize the first two items, and consider model regularization term, we can get new model as follows:

$$\begin{aligned} \mathop {\min }\limits _{f \in {\mathcal {F}}} {\lambda _1}\sum \limits _{i = 1}^m {{{(1 - {y_i}f({\varvec{x}_i}))}_ + }} + {\lambda _2}\sum \limits _{i = 1}^m {{{\left({{(1 - {y_i}f({\varvec{x}_i}))}_ + } - \frac{1}{m}\sum \limits _{j = 1}^m {{{(1 - {y_j}f({\varvec{x}_j}))}_ + }} \right)}^2}} + R(f) \end{aligned}$$

(20)

where $\lambda _1=\frac{\mu _1}{m},\lambda _2=\frac{\mu _2}{m(m-1)}$. This is the robust model we propose, and the specific forms of which are described in the next section.

3.1 New objective function of RA-SVCM

The objective function with the minimized mean and variance of the loss is constructed in order to improve generalization performance of SVM.

The new objective function of nonlinear RA-SVCM is

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha } \in {{\mathbb {R}}^m}} \lambda _1 \sum \limits _{i = 1}^m {({\varvec{r}_{i })_{+}}} + {\lambda _2}\sum \limits _{i = 1}^m {\left( {({\varvec{r}_{i })_{+ }} - \frac{1}{m}\sum \limits _{j = 1}^m {({\varvec{r}_{ j})_{+}}} } \right) }^2 + { \frac{1}{2}\varvec{\alpha ^\top } K{\varvec{\alpha } }}, \end{aligned}$$

(21)

where $\varvec{r}_i = 1-y_iK_i\varvec{\alpha }$. $\lambda _1$ and $\lambda _2$ are the regularization parameters, which are determined by using the cross-validation method [36, 37].

The new objective function has the following features:

• 1) The first term $\lambda _1 \sum \nolimits _{i = 1}^m {({\varvec{r}_{i})_{ + }}}$ is empirical risk that is minimized to make the points generated by the model closer to the sample datas, hence it can minimize the entirety of classification error in the training phase.

• 2) The second term ${\lambda _2}\sum \nolimits _{i = 1}^m {\left( {({\varvec{r}_{i})_{ + }} - \frac{1}{m}\sum \nolimits _{j = 1}^m {({\varvec{r}_{j})_{ + }}} } \right) }^2$ is the variance regularization that acts as a global loss stabilizer factor. This global loss adjusting factor is used to coordinate all of the samples in order to achieve a better modeling performance. It is clear that minimizing this term can improve the generalization performance of modeling based on the empirical Bernstein bounds. Obviously, when $\lambda _2$ is equal to zero, the objective function of (21) is same as that of standard SVM. This means that the standard SVM is a special case of RA-SVCM.

• 3) The third term $\frac{1}{2}\varvec{\alpha ^\top } K{\varvec{\alpha } }$ is the model regularization term that is used to avoid overfitting of the model.

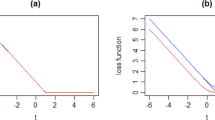
It is evident that the regularization term in this new objective function includes both the variance and model regularization term as show in Fig. 1. It is also well-known that there is an increase in the classification accuracy when the mean of the loss is minimized, and that minimizing its variance can lead to a classifier with higher generalization ability.

Fig. 1

RA-SVCM

For approximately separable dataset, the average loss of SVM tends to zero. Considering that the second-order central moment of loss is similar to the second-order origin moment, the linear and nonlinear RA-SVCM can be simplified as follow:

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha } \in {{\mathbb {R}}^m}} \lambda _1 \sum \limits _{i = 1}^m {({\varvec{r}_{ i })_{+}}} + {\lambda _2}\sum \limits _{i = 1}^m {({\varvec{r}_{ i })^2_{+}}} {}\mathrm{{ + }}\frac{1}{2}{\varvec{\alpha } ^T}K\varvec{\alpha }. \end{aligned}$$

(22)

These models are denoted as sRA-SVCM. When $\lambda _2 \rightarrow 0$ , the objective function of (22) is same as it is when using the standard SVM with hinge loss (SVM-H). And when $\lambda _1 \rightarrow 0$, the objective function of (22) is same as it is when using the standard SVM with squared hinge loss (SVM-SH), this means that both the standard SVM with hinge loss and squared hinge loss are special cases of sRA-SVCM.

3.2 Theoretical analysis

In this section, we study the statistical property of RA-SVCM. By applying the result from empirical bernstein bounds (11), for our model, i.e., $f(x) = \langle \varvec{w},\psi (\varvec{x})\rangle = G_i^T\varvec{\alpha }$, we can get a result as follows:

Theorem 1

Suppose that $(\varvec{x}_i,y_i)_{i = 1}^m$ be drawn i.i.d. according to the distribution ${\mathcal {D}}$ such that with probability 1 we have that ${\left\| \varvec{x} \right\| _2} \le R$, and let ${\left\| \varvec{\alpha } \right\| _2} \le C$, and the Gaussian kernel function $G_{i,j}= K(x_i,x_j)= \exp ( - h{\left\| {{x_i} - {x_j}} \right\| ^2})$ is bounded in the feature spaces, i.e., $\exists M > 0$ and $c>0$ such that ${\max _{ G_i^T\varvec{\alpha } \in [ - M,M]}}\{ 0,1 - y G_i^T\varvec{\alpha }\} \le {c}$. Then, for any $\delta >0$, with probability at least $1-\delta$, $\forall \varvec{\alpha }\in {R^m}$,

$$\begin{aligned}{{\mathbb {E}}_{\mathcal {D}}}[{(1 - y G_i^T\varvec{\alpha } )_ + }] &\le {\hat{p}} + \sqrt{\frac{{18 V[(1 - y G_i^T\varvec{\alpha } )_ +]\ln ({\mathcal {M}}(m)/\delta )}}{m }} \nonumber \\&\quad + \frac{{15 c\ln ({\mathcal {M}}(m)/\delta )}}{{m - 1}}, \end{aligned}$$

(23)

where ${\hat{p}} = {\hat{P}}[l(y,G_i^T\varvec{\alpha })] = \frac{1}{m}\sum \limits _{i = 1}^m {(1 - y G_i^T\varvec{\alpha })_+}$ is the empirical loss, and an extra c appears in the third term to normalize the hinge loss so that it has the range [0, 1].

Proof

Since ${\left\| \varvec{\alpha } \right\| _2} \le C$, ${\left\| \varvec{x} \right\| _2} \le R$, then the Gaussian kernel is bounded on ${\mathcal {X}}$, thus $\exists M > 0$, such that $G_i^T\varvec{\alpha }\in [ - M,M]$. So $\exists c > 0$, such that the loss function $l_{1}(G_i^T\varvec{\alpha },y)= (1 - yG_i^T\varvec{\alpha })_+\in [0,c]$. Then we can apply the empirical bernstein inequation (11) on hinge loss which is normalized. $\square$

It is clear that the bounds of theorem 1 has estimation errors which can be as small as O(1/n) for small sample variances, while the bound of Hoeffdings inequality on which SVMs are based is of order $1/\sqrt{n}$.

3.3 Solutions to RA-SVCM and sRA-SVCM

In this section, Newton-type algorithms, which has quadratic convergence rate, is used to train the RA-SVCM and sRA-SVCM. However, due to the hinge loss is not differentiable, the Newton-type methods do not work for it directly. Thus, some smooth loss function are chosen to approximate the hinge loss, such as least squares loss [11, 38], logistic loss [33] and Huber loss [1, 34]. According to SSVM presented by Lee and Mangasarian [32] and a Smoothing SVM with efficient reduced techniques proposed by Zhou [39], the logistic loss ${\varphi _p}(r) = \frac{1}{p}\log (1 + \exp (pr))$ is adopted to approximate hinge loss in this paper. To overcome any potential overflowing, a stable form is given as ${\varphi _p}(r) = \mathrm{{max}}\{ r,0\} + \frac{1}{p}\log (1 + \exp ( - |{pr} |))$.

For convenience, here we only introduce the solution of nonlinear models. The smooth forms of problem (21) and (22) can be formulated as:

$$\begin{aligned}\mathop {\min }\limits _{\varvec{\alpha } \in {{\mathbb {R}}^m}} {f_1}(\varvec{\alpha } )&: = {\varvec{\lambda } _1}\sum \limits _{i = 1}^m {{\varphi _p}({\varvec{r}_i})} + {\lambda _2}{\sum \limits _{i = 1}^m ({{\varphi _p}({\varvec{r}_i})} - \frac{1}{m}\sum \limits _{j = 1}^m {{\varphi _p}({\varvec{r}_j})} )^2} \nonumber \\&\quad + \frac{1}{2}{\varvec{\alpha } ^\top }K\varvec{\alpha } , \end{aligned}$$

(24)

and

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\alpha } \in {{\mathbb {R}}^m}} {f_2}(\varvec{\alpha } ): = \lambda _1 \sum \limits _{i = 1}^m {{\varphi _p }({\varvec{r}_i})} + {\lambda _2}\sum \limits _{i = 1}^m ({\varphi _p }({\varvec{r}_i}))^2 + \frac{1}{2}{\varvec{\alpha }^\top }K\varvec{\alpha }, \end{aligned}$$

(25)

respectively.

The gradient ${\nabla }f_1(\varvec{\alpha }^t)$ and Hessian matrix $\nabla ^2f_1(\varvec{\alpha }^t)$ of the objective function in problem (24) are

$$\begin{aligned} \nabla {f_1}(\varvec{\alpha } ) = {K_{{I_1}}}\varvec{u_1} + {K_{{I_2}}}\varvec{u_2} + K\varvec{\alpha }, \end{aligned}$$

(26)

and

$$\begin{aligned} {\nabla ^2}{f_1}(\varvec{\alpha }) = {K_{{I_3}}}^{\top } {\Lambda _{{I_3}}}{K_{{I_3}}} + 2{\lambda _2}{K_{{I_1}}}^{\top } {K_{{I_1}}} - \frac{{2{\lambda _2}}}{m}\varvec{qq^{\top }} + K. \end{aligned}$$

(27)

The gradient ${\nabla }f_2(\varvec{\alpha }^t)$ and Hessian matrix $\nabla ^2f_2(\varvec{\alpha }^t)$ of the objective function in problem (25) are

$$\begin{aligned} \nabla {f_2}(\varvec{\alpha } ) = {K_{{I_1}}}\varvec{u_1} + {K_{{I_3}}}\varvec{u_3} + K\varvec{\alpha }, \end{aligned}$$

(28)

and

$$\begin{aligned} {\nabla ^2}{f_2}(\varvec{\alpha }) = {K_{{I_3}}}^{\top } {\bar{\Lambda } _{{I_3}}}{K_{{I_3}}} + 2{\lambda _2}{K_{{I_1}}}^{\top } {K_{{I_1}}} + K. \end{aligned}$$

(29)

where $(u_1)_i = - 2{\lambda _2}r_i*y_i$, $(u_2)_i = \left( {\frac{{2{\lambda _2}}}{m}{\varphi _p(r_i)} - \lambda _1 } \right) {\varphi ' _p}(r_i)*y_i$, $(u_3)_i = \left( -\lambda _1 \right) {\varphi ' _p(r_i)}*y_i$, $\varvec{r} = {({r_1},....{r_m})^{\top }}$, $\varvec{{\varphi _p}(r)} = {({\varphi _p}({r_1}),....{\varphi _p}({r_m}))^{\top }}$, $\varvec{{\varphi '_p}(r)} = {({\varphi '_p}({r_1}),....{\varphi '_p}({r_m}))^{\top }}$, ${\Lambda } = \left( \lambda _1 - \frac{{2{\lambda _2}}}{m} \varvec{{\varphi _p}({r})}^{\top }\varvec{e}\right) diag[{\varphi ''_p}({r_1})...,{\varphi ''_p}({r_m})]$, ${{\bar{\Lambda }}} = \lambda _1 diag[{\varphi ''_p}({r_1})...,{\varphi ''_p}({r_m})]$,$q_i = (K\varvec{{\varphi '_p(r)}})_i*y_i$, $\varvec{e}=(1,...1)^{\top }$, and ${I_1} = \{ i \in M \mid {r_i} > 0\}$ To improve computational efficiency, let ${I_2} = \{ i \in M \mid {\varphi '_p}({r_i}) \ge \varsigma \}$, ${I_3} = \{ i \in M \mid {\varphi ''_p}({r_i}) \ge \varsigma \}$ for a tiny number $\varsigma$ like $10^{-10}$. ${\varphi '}(r)$ and ${\varphi ''}(r)$ are calculated as ${\varphi '}(r) = \frac{{\min \{ 1,{e^{pr}}\} }}{1 + {e^{ - p |r |}}}$, ${\varphi ''}(r) = \frac{{p\exp ( - p |r |)}}{{{{(1 + \exp ( - p|r |))}^2}}}$.

It solves Newton equation

$$\begin{aligned} {\nabla ^2}{f}(\varvec{\alpha ^t })\varvec{d} = - \nabla {f}(\varvec{\alpha ^t } ) \end{aligned}$$

(30)

to update the current solution. Let ${\varvec{\bar{d}}}$ is the solution of (30). If the full Newton step is acceptable, then ${\varvec{\alpha } ^{t + 1}} = \varvec{\alpha ^t }+\varvec{{\bar{d}} }$, otherwise ${\varvec{\alpha } ^{t + 1}} = \varvec{\alpha ^t }+\gamma \varvec{{\bar{d}} }$, where $\gamma$ is chosen by Armijo line search.

The reduced smoothing Algorithm for RA-SVCM and sRA-SVCM on large datasets is given as follows. For regular datasets, $J=M$, that is $\varvec{\alpha } =\varvec{\alpha }_J$.

Setting of approximate parameters p: In order to make the Newton method working well, the approximate parameters p should be set moderately. Such as $p=1$ at beginning, then $p:=10p$ if $\left\| {{g^t}} \right\|$ is small and repeat the algorithm until $p = {10^4}$ and $\left\| {{g^t}} \right\| \le \varepsilon$ for given $\varepsilon$.

Remark 1

The solution of problem (25) obtained by algorithm 1 is the globally optimal since the objective function in (25) is convex. And the solution of problem (24) obtained by algorithm 1 is almost globally optimal, because the objective function in (24) is convex in most cases. We defer the relevant proof to Appendix.

4 Differences with related methods

There are a few studies considered the effect of the moment penalization on the generalization ability of SVM-style algorithms. Zhang and Zhou [25, 26] proposed the LDM and ODM algorithm, whose idea is to optimize the margin distribution by considering the margin mean and variance simultaneously. Our method optimizes losses distribution by minimizing the mean and variance of loss function.

From the generalization error bound (23) of RA-SVCM we proposed, We can derive the statistical characteristics our methods. Under appropriate conditions on the loss l, parameter space $\Theta$, inequality (23) shows that the generalization bound of RA-SVM can be upper bounded by the sum of three components, among which, the first term is the average of empirical loss, and the last term is a by-product which can be ignored, so the main inspiration comes from the second term. It’s not difficult to find that the smaller ${{\mathbb {V}}_m}(l)$, the smaller this term, so that the tighter the bound. Thus to achieve good generalization performance, we should minimize the upper bound of loss. Hence minimizing the mean and variance of the loss can result in good generalization performance.

The generalization bound of ODM presented in the Theorem 5.1 of [26] shows that the generalization bound of ODM also can be upper bounded by the sum of three components, among which, the first term is the average of margin, and the last term is a by-product of McDiarmid inequality which can be ignored, but the second term is affected by four related parameters.

Meanwhile, the resultant objective function (6) of LDM is quite complex, and both LDM and ODM require tuning four parameters. Comparatively speaking, the objective function of our method is relatively simple, and fewer parameters need to be adjusted.

5 Empirical studies

In this section, we investigate the performance of our proposed methods using the artificial and benchmark datasets. We first introduce the experiment settings in Sect. 5.1. Then, we visualize the classifier SVM, ODM, RA-SVCM and sRA-SVCM on artificial dataset in Sect. 5.2, and then compare RA-SVCM and sRA-SVCM with standard SVM, LSSVM [11] (RRP-LSSVM [14]), SVM+ [19], SVM-2V [20] and ODM in Sect. 5.3. And the Friedman test is employed to compare the test accuracies of six methods on twenty datasets in Sect. 5.4. In addition, we also study the loss distribution and relevant results produced by sRA-SVCM, SVM, LSSVM (RRP-LSSVM) and ODM in Sect. 5.5. Finally, the sensitivity of parameters is analyzed in Sect. 5.6, and the time cost of four method are compared in 5.7.

5.1 Experimental setup

We evaluate the effectiveness of our models on a artificial dataset, twelve regular scale datasets and eight large scale datasets, including both UCI data sets and real-word data sets like KDD2010. Table 1 summarizes the statistics of these datasets. The size of the datasets ranges from 145 to 78823, and the dimensionality ranges from 2 to 784. All features are normalized into the interval [0,1]. Meanwhile, the optimal parameters are listed in table, and the abbreviations in table are explained at the bottom of the table. The Gaussian kernel function $K({x_1},{x_2}) = \exp ( - h{\left\| {{x_1} - {x_2}} \right\| ^2})$ is used for all datasets, kernel spread parameters h, regularization parameters $\lambda _1$ ,$\lambda _2$ are roughly chosen by 5-fold cross validation within $h \in \mathrm{{\{ }}{\mathrm{{2}}^{\mathrm{{-6}}}},{\mathrm{{2}}^{\mathrm{{-5}}}}.....,{\mathrm{{2}}^\mathrm{{5}}},{\mathrm{{2}}^{\mathrm{{6}}}}\mathrm{{\} }}$ and $\lambda _1,{\lambda _2} \in \mathrm{{\{ 1}}{\mathrm{{0}}^\mathrm{{6}}}\mathrm{{,1}}{\mathrm{{0}}^\mathrm{{5}}}......\mathrm{{1}}{\mathrm{{0}}^{\mathrm{{ - 6}}}}\mathrm{{\} }}$.

Table 1 Characteristics of experimental datasets and the optimal parameters

The regular scale datasets and Adult, IJCNN of larger datasets are original binary classification problems, the other five datasets are muti-class datasets. Specifically, the task of separating class 3 from the rest is trained on Vechile dataset. For Shuttle data set, a binary classification problem is solved to separate class 1 from the rest. And for MNIST and USPS dataset, here two binary classification problems are solved to separate class 3 from the rest and separate class 8 from the rest. For the datasets with partition of training sets and testing sets, we can adopt the original training sets and testing sets directly. And for the data sets without partition of training set and testing set, we can select eighty percent of the instances randomly as training data, and use the rest as testing data.

For standard SVM, LSSVM, SVM+ and SVM-2V, the regularization parameter $\lambda$ and Kernel spread parameter h are selected by 5-fold cross validation from the set of $\{{10^{ - 6}},{10^{ - 5}} \cdots {10^6}\}$ and $\{{2^{ - 6}},{2^{ - 5}} \cdots {2^6}\}$ respectively, and for RRP-LSSVM, 1000 of the training data is randomly selected as the working set for larger datasets. For ODM, the regularization parameter $\lambda _1$ are selected by 5-fold cross validation from the set of $\{{10^{-6}},{10^{-5}}{.....10^6}\}$, while the parameters D and $\mu$ is selected from the set of $\{0.2,0.4, 0.6,0.8\}$. For SVM-2V, other parameters are set as [20]. Experiments are repeated for 30 times, and the average accuracies as well as the standard deviations are recorded.

All the experiments are carried out on a desktop PC with Intel(R) Core(TM)i7-7700 CPU (3.60 GHz) and 16GB RAM under the MATLAB 2019b programming environment.

5.2 Experimental results with artificial data

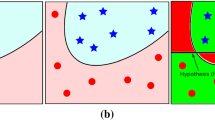
We visualize the classification hyperplanes determined by SVM (7), ODM, RA-SVCM and the sRA-SVCM model (10) on a two-moon dataset with 800 samples (400 for training, 400 for testing) and d = 2 features. Figure 2 shows the experimental results.

From the comparisons of Fig. 2a–d, it can be seen that for the two moon dataset, the classification boundaries of ODM, RA-SVCM, and sRA-SVCM are relatively similar, and the classification boundaries of these three methods are obviously better than that of standard SVM. Meanwhile, the classification accuracies of these three methods are higher than that of standard SVM. Compared with standard SVM, the margin of RA-SVCM that we proposed is wider than that of SVM, and the classification confidence of our methods are obviously higher than that of SVM on Data from the end of the crescent moon. Compared with ODM, the margin of RA-SVCM that we proposed is narrower than that of ODM but the number of support vector is smaller than ODM. We can also find that the classification performance of RA-SVCM and sRA-SVCM is similar. It can be concluded that our method has good generalization performance.

Fig. 2

Plots for comparing the classification boundaries of SVM, ODM, RA-SVCM and SRA-SVCM on the two moon dataset. For this dataset, the test accuracies of these four algorithms are 97.00%, 97.50%, 97.75% and 97.50%

5.3 Experimental results with regular scale and large benchmark Datasets

According to the experimental setup in Sect. 4.1, experiments were carried out on the twenty datasets above, the results summarized in Table 2 (the experimental result of the SVM-2V and SVM+ on the eight scale data is missing because the quadratic programming is difficult to deal with large kernel matrix).

Table 2 Accuracy (mean ± td) comparison on regular and large scale data sets

As can be seen, the overall performance of our models are superior to the other compared methods. According to the test accuracy, these twenty datasets can be divided into Two levels: The datasets which test accuracy less than $95\%$ are “hard” datasets; The rest are belonging to “easy” datasets. As showing in Table 2, For “easy” datasets, the test accuracy of our methods can do up to $1.95\%$ better than the standard SVM; For “hard” datasets, the test accuracy of our methods can do up to $4.71\%$ better than the standard SVM. This indicates that our methods have a better generalization ability than the standard SVM, especially for the “hard” datasets.

Meanwhile, it can be seen from the experimental results that sRA-SVCM and RA-SVCM behave almost similarly. For simplicity, the sRA-SVCM will be used to compare with other models.

5.4 Statistical comparisons by friedman test

In order to evaluate multiple methods systematically, the Friedman test [40] is employed to compare the test accuracies of the five methods over the 20 benchmark datasets. For the different datasets, Friedman test at significance level $\alpha = 0.05$ rejects the null hypothesis of equal performance, which leads to the use of post-hoc tests to find out which algorithms are actually different. The Nemenyi test is used to further distinguish different methods. Specifically, Nemenyi test is used where the performance of two algorithms is significantly different if their average ranks over all datasets differ by at least one critical difference

$$\begin{aligned} CD = {q_\alpha }\sqrt{{\frac{{k(k + 1)}}{{6M}}}}, \end{aligned}$$

(31)

where critical values ${q_\alpha }$ are based on the studentized range statistic, K is the number of comparison algorithms, and M is the number of datasets.

Take Fig. 3a as an example, for the five methods on twelve datasets, according to

$$\begin{aligned} {\tau _{{\chi ^2}}}\mathrm{{ = }}\frac{{12M}}{{k(k + 1)}}\left(\sum \limits _{\mathrm{{i}} = 1}^k {o_i^2} - \frac{{k{{(k + 1)}^2}}}{4}\right) \end{aligned}$$

(32)

and

$$\begin{aligned} {\tau _F}\mathrm{{ = }}\frac{{(M - 1){\tau _{{\chi ^2}}}}}{{M(k - 1) - {\tau _{{\chi ^2}}}}}, \end{aligned}$$

(33)

the friedman statistic ${\tau _F} = 25.60$, which at significance level $\alpha = 0.05$ rejects the null hypothesis of equal performance, where $o_i$ is the average ordinal number of the ith algorithm, and k is the number of algorithms. Then, the critical difference ($CD = 1.3640$) is calculated by (31). If the difference between the average ranks of the two algorithms exceeds the critical value 1.3640, the assumption that “the two algorithms have the same performance” is rejected with corresponding confidence.

Fig. 3

CD diagrams of the comparison approaches on the certain datasets. Groups of methods that are not significantly different according to Nemenyi test are connected with a red line

Figure 3 illustrates the CD diagrams for the comparison methods on the twenty benchmark datasets, where the average rank of each comparing method is marked along the axis. The axis is turned so that the best ranks are to the right. Groups of methods that are not significantly different according to Nemenyi test are connected with a red line. The critical difference is also shown above the axis in each subfigure.

As can be seen from Fig. 3, our methods achieve the statistically superior performance on the whole twenty datasets. Our two methods are not significantly different from ODM on “easy” datasets, but are significantly superior to the other methods. The sRA-SVCM are significantly different from ODM, SVM and R-LSSVM on“hard” datasets, and our two methods are significantly different from SVM, LSSVM, SVM+ and SVM-2v on regular datasets. Meanwhile, we can also see that the generalization performance of our method is best on the whole datasets, and our two methods (sRA-SVCM and sRA-SVCM) are not significantly different. So for simplicity, the sRA-SVCM will be used to compare with other models in the following experiments.

5.5 Specific results and loss distribution on four datasets

In this section, the experiments of sRA-SVCM, standard SVM, ODM and LSSVM (RRP-LSSVM) are performed on svmguide1, Adult, Vechile and IJCNN datasets (the optimal parameters of four models are used). Some specific results of these experiments are listed in Table 3.

Table 3 Experimental results on four representative datasets

Fig. 4

Plots for comparing positive loss distribution on training datasets of svmguide1, Adult,Vechile and IJCNN

Fig. 5

Plots for comparing r distribution on test datasets of svmguide1, Adult, Vechile and IJCNN datasets

As can be seen from Table 3, the training accuracy of our model are not always the best, but the test accuracy is always the largest. This is because the mean of loss of sRA-SVCM is slightly larger than that of SVM, but the variance of loss of sRA-SVCM is slightly less than that of SVM. The differences bring good results that the test accuracy of sRA-SVCM have been improved than the standard SVM. ODM optimizes the distribution of margin, to a certain extent, and it also optimizes the distribution of loss. SVM does not care about the variance of the loss, so the variances of loss are lager than RA-SVCM and ODM. For the LSSVM, the loss of most points are concentrated between 0 and 1, which makes too many points near the classification hyperplane. In this case, their generalization performance will be slightly lower than sRA-SVCM. Meanwhile, the AUC and F1-score of RA-SVCM are superior to SVM. The above show that our method have a good generalization ability and better performance.

Figure 4 plots the positive loss distribution of sRA-SVCM and standard SVM on training sets of four representative datasets. It can be seen that the positive loss of SVM is relatively scattered and the maximum value larger than our models. That of RA-SVCM is relatively concentrated, and the number of sRA-SVCM between 0 and 1 is higher than SVM. And the Fig. 5 plots the corresponding results of r on test sets of the four datasets. It is obvious that the test error of our method is smaller than that of SVM, and the maximum error is much smaller than the standard SVM. So that our model has a better classification ability on the test sets. Namely, our model has a better generalization performance than standard SVM. A reasonable interpretation is that there have a suitable loss distribution of the new model on the training set, and thus it get a better generalization ability on test sets.

5.6 Sensitivity analysis of parameter of RA-SVCM

There are two tuned parameters in the proposed model, such as $\lambda _1$ and $\lambda _2$, which are used to balance the importance of the corresponding terms. The first term is used to make the points generated by the model closer to the sample datas. The second term guarantees the stability of the entire sample data in the model.

Fig. 6

Plots for relationships of the average test accuracies (%) and different combinations of parameters on the six larger datasets

To analyze the sensitivity of parameters in the proposed method, we first define a candidate set where the optimal parameter located for these parameters. We have performed the proposed model 20 times with the parameters in candidate set and report the mean classification accuracy. From the Fig. 6, it is obvious that the average test accuracies are almost steady with respect to different values of parameter $\lambda _1$ and $\lambda _2$, which indicates that those parameters do not require careful tuning, and a broad range of $\lambda _1$ and $\lambda _2$ lead to satisfactory performance.

Fig. 7

Plots for comparing average test accuracies on sRA-SVCM, SVM-H, and SVM-SH when the five different mean penalty parameters $\lambda _1$ are chosen on six large datasets. These seven mean penalty parameters are in interval which the optimal parameter is located, and the parameter $\lambda _2$ are fixed

Next, we fix parameter $\lambda _2$ and select the seven candidate parameters of $\lambda _1$ to compare with SVM-H and SVM-SH (standard SVM with hinge loss and squared hinge loss) on datasets above. The Fig. 7 shows the relationships of the average test accuracy and mean parameters $\lambda _1$ of sRA-SVCM, SVM-H and SVM-SH. And the Fig. 7 represents the average test accuracies of sRA-SVCM, SVM-H and SVM-SH by red line, magenta line, and green line respectively. It is obvious that the magenta and green lines fluctuate greatly with the change of the parameters $\lambda _1$, but the red lines are relatively stable, and the red lines are generally above the magenta and green lines. This indicates that compared with SVM-H and SVM-SH, the sRA-SVCM achieve a better generalization performance, and the sRA-SVCM is not sensitive to the parameter $\lambda _1$. The sensitivity analysis to $\lambda _1$ reveals that this conclusion is stable to reasonable pertubations of $\lambda _1$.

5.7 Time cost

We compare the cost of our methods with SVM and ODM on six large scale datasets(RRP-LSSVM, SVM+ and SVM-2v can be solved without iterative methods). All the experiments are carried out on a desktop PC with Intel(R) Core(TM)i7-7700 CPU (3.60 GHz) and 16GB RAM under the MATLAB 2019b programming environment. The average CPU time (in seconds) on each dataset is show in Fig. 8. The Newton algorithm is used to solve these four models. It can be seen that, except for the vechile datasets, our methods are faster than SVM and slightly faster than ODM. On vechile datasets, RA-SVCM is slightly slower than ODM, but sRA-SVCM is still faster than ODM. This show that our methods are computationally efficient.

Fig. 8

CPU time on the large scale datasets

6 Conclusion

Recent theoretical results suggested that the distribution of loss, rather than only mean of loss, is more crucial to the generalization performance. In this paper, based on the empirical Bernstein inequality, we propose a novel method, named Risk-Averse support vector classifier machine (RA-SVCM), which tries to optimize the loss distribution by considering the mean and variance of loss. Our models are general learning approach which can be used in any place where SVM can be applied. Comprehensive experiments on the artificial and benchmark datasets validate the superiority of our method to other classical models.

In the future, it will be interesting to further investigate the application of mean-variance minimization to other particular loss functions (Such as ramp loss, squares hinge loss, etc). And this raise a pressing issue to find an efficient implementation, which can deal with the case that the sample variance penalization is non-convex. In addition, it is necessary to automatically estimate the parameter $\lambda _2$ without cross-validation in order to make RA-SVCM free from additional parameters. And another line of future research is to refine these generalized boundaries with additional theoretical work.

Appendix A Proof of remark 1

Theorem 2

Under the condition of Theorem 1, the objective function $f_1({\varvec{\alpha }})$ in (24) is convex if

$$\begin{aligned} \frac{{{\lambda _1}}}{{{\lambda _2}}} \ge 2 \left(c + \frac{1}{p}\right). \end{aligned}$$

(A1)

Proof

Here, let ${g_i}({\varvec{\alpha }}) = \frac{1}{p}\log (1 + {e^{p{\varvec{r}_i}}}) = \max \{ {\varvec{r}_i},0\} + \frac{1}{p}\log (1 + {e^{ - p{|\varvec{r}_i |}}})$, the objective function of (24) can be written as

$$\begin{aligned} {f_1}(\varvec{\alpha } ) = {\lambda _1}\sum \limits _{i = 1}^m {{g_i}(\varvec{\alpha } )} + {\lambda _2}{g^\top }(\varvec{\alpha } )Qg(\varvec{\alpha } ) + \frac{1}{2}{\varvec{\alpha } ^\top }K\varvec{\alpha } \end{aligned}$$

(A2)

The Hessian matrix of $f_1(\varvec{\alpha })$ is:

$$\begin{aligned} {\nabla ^2}{f_1}(\varvec{\alpha } )= & {} {\lambda _1}\sum \limits _{i = 1}^m {{\nabla ^2}{g_i}(\varvec{\alpha } )} + 2{\lambda _2}\sum \limits _{i = 1}^m {{\varvec{\delta } _i}{\nabla ^2}{g_i}(\varvec{\alpha } )} \nonumber \\&+ 2{\lambda _2}\nabla g(\varvec{\alpha } )Q\nabla {g^\top }(\varvec{\alpha } ) + K\nonumber \\= & {} \sum \limits _{i = 1}^m {({\lambda _1} + 2{\lambda _2}{\varvec{\delta } _i}){\nabla ^2}} {g_i}(\varvec{\alpha } ) \nonumber \\&+ 2{\lambda _2}\nabla g(\varvec{\alpha } )Q\nabla {g^\top }(\varvec{\alpha } ) + K \end{aligned}$$

(A3)

where $Q=\varvec{I}-\frac{1}{m}\varvec{e}^\top \varvec{e}$, $\varvec{\sigma }=Qg(\varvec{\alpha })$, and

$$\begin{aligned} {\varvec{\delta } _i}= & {} {g_i}(\varvec{\alpha } ) - \frac{1}{m}\sum \limits _{i = 1}^m {{e^T}g(\varvec{\alpha } )} \nonumber \\= & {} \max \{ {\varvec{r}_i},0\} + \frac{1}{p}\log (1 + {e^{ - p{|\varvec{r}_i |}}}) - \frac{1}{m}\sum \limits _{j = 1}^m \max \{ {\varvec{r}_j},0\} \nonumber \\&+ \frac{1}{p}\log (1 + {e^{ - p{|\varvec{r}_j |}}}) \nonumber \\\ge & {} - \frac{1}{m}\sum \limits _{j = 1}^m {\max \{ {\varvec{r}_j},0\} - \frac{1}{{mp}}\sum \limits _{j = 1}^m {\log (1 + {e^{ - p{|\varvec{r}_j |}}})} } \nonumber \\\ge & {} - {c} - \frac{1}{{mp}}\sum \limits _{j = 1}^m {\log (1 + {e^{ - p(1+M)}})} \nonumber \\\ge & {} - {c} - \frac{{\log 2}}{p}\nonumber \\\ge & {} - {c} - \frac{1}{p}. \end{aligned}$$

(A4)

To prove that the objective function in Eq.(A2) is convex, it suffices to show that ${\nabla ^2}{f_1}(\varvec{\alpha } ) \succeq 0$ for every $\varvec{\alpha }$. It’s obvious that $2{\lambda _2}\nabla g(\varvec{\alpha } )Q\nabla {g^T}(\varvec{\alpha } ) + K\succeq 0$. That is, we need to prove that $\sum \nolimits _{i = 1}^m {({\lambda _1} + 2{\lambda _2}{\varvec{\delta } _i}){\nabla ^2}} {g_i}(\varvec{\alpha } ) \succeq 0$. Thus, let $\varvec{\mu }_i=\lambda _1+2\lambda _2 \varvec{\delta } _i$, then we need to prove $\varvec{\mu }_i\ge 0$, based on (A4), we get $\frac{{{\lambda _1}}}{{{\lambda _2}}} \ge 2(c + \frac{1}{p})$. That is, when $\frac{{{\lambda _1}}}{{{\lambda _2}}} \ge 2(c + \frac{1}{p})$, for each $\varvec{\alpha }\in R^m$, we have ${\nabla ^2}{f_1}(\varvec{\alpha } ) \succeq 0$. Therefore, the objective function $f_1(\varvec{\alpha })$ in (24) is convex. $\square$

It is obvious that the objective function in Eq.(25) is convex since ${\varphi _p}(r)$ and ${({\varphi _p}(r))^2}$ are convex functions. When $\frac{{{\lambda _1}}}{{{\lambda _2}}} \ge 2(c + \frac{1}{p})$, the solution of problem (24) obtained by algorithm 1 is globally optimal based on the Theorem 2. In fact, we have rarely encountered non-convergence in a large number of experiments. Of course we can also make a simple rule for selecting a optimal superparameter that satisfies the conditions given above.