A novel feature selection method using generalized inverted Dirichlet-based HMMs for image categorization

Abstract

Hidden Markov Models (HMMs) have consistently been a powerful tool for performing numerous challenging machine learning tasks such as automatic recognition. The latter perceives all objects of the universe through information carried by their characteristics or features. However, not all available data is always valuable for distinguishing between the different objects, scenes, scenarios; referring analogically to states. More often than not, automatic recognition is accompanied by a feature selection to reduce the number of collected features to a relevant subset. Although sparse, the majority of literature resources available on feature selection for HMMs, presuppose either a single Gaussian or employ a Gaussian mixture model (GMM) as emission distribution. The proposed method builds upon the feature saliency model introduced by Adams, Cogill, and Beling (in IEEE Access 4:1642–1657), and is adjusted to handle complex multidimensional data by using as a novel experiment, GID (Generalized Inverted Dirichlet) mixture models) as emission probabilities. We make use of an Expectation-Maximization (EM) algorithm (Dempster et al. in J R Stat Soc 39(1):1–22) to compute maximum a posteriori (MAP) [Gauvain and Lee in IEEE Transact Speech Audio Process 2(2):291–298] estimates for model parameters. The complete inference and parameter estimation of our GID-FSHMM (GID Feature Selection-based HMM) are detailed in this work. Automatic recognition applications such as facial expression recognition and scenes categorization demonstrate comparable to higher performance compared to the extensively used Gaussian mixture-based HMM (GHMM), the Dirichlet-based (DHMM) and the inverted Dirichlet-based HMM (IDHMM) without feature selection and also when the latter is embedded in all of the aforementioned models.

1 Introduction

The successful application of HMMs to a great number of areas ranging from speech recognition to image categorization broke new grounds by bringing many extensions and novelties not only in terms of the methods used along with HMMs to better their performance but also in the volume and diversity of data collected for analysis using these methods. There is no doubt that this expansion of data, types of information, and features contributed enormously to refining and improving machine learning tasks and methods. Nevertheless, it has triggered a considerable amount of problems and challenges namely the formidable curse of dimensionality often resulting from the manipulation of high-dimensional data. For example, in clustering tasks, it is a widely held view that the more information, data, and features we manipulate, the better an algorithm is expected to perform [48]. However, this is not the case in practice. Many features can be just “noise” and may cause the finest pattern recognition and machine learning techniques to struggle as a result of irrelevancy and thus degrade the modelling performance [18]. Thereby, feature selection is used to increase modelling performance since it allows eliminating noise in the data, speeding up the models’ training and prediction, decreasing overfitting odds and most importantly reducing the computational cost after disregarding many features.

We intend by feature selection, the process of decreasing the number of gathered features to a relevant subset of features and is usually used to counter the curse of dimensionality [3]. Aside from feature extraction, which is a separate problem, feature selection determines relevant features from a given set of features, whereas feature extraction generates new features from a given set. Unlike feature extraction, feature selection does not come up with new features nor does it amend the primary features.

The primary inducement for adopting feature selection strategies is their important potential to improve modelling and generalization capabilities if performed reliably and properly [4]. Applying feature selection permits taking into consideration the significant contribution of feature screening to the classification process. In fact, each different feature contributes differently to the classification structure based on its degree of relevance [21, 68]. The latter is intended to be determined to improve our models’ performance, in particular using simultaneous feature selection and classification in the course of an unsupervised process which is considered to be one of the most challenging problems in data mining and machine learning. In practice, the said case implies selecting features without a priori knowledge about data labels.

In most applications of HMM, features are pre-selected based on domain knowledge, and the feature selection procedure is completely omitted. Usually, to train HMMs, even in the case where feature selection is considered features are selected traditionally. That is, features are selected in advance either based on already available data or relying on experts’ knowledge. These practices are the result of the scarcity of literature in terms of unsupervised feature selection methods specific for HMMs [3] [30], not to mention the high computational cost of wrapping methods. Despite the extensive research and investigations that are made on feature selection in their general case, methods specific for HMMs are lacking. Feature selection methods for HMMs and mixture models are seldom treated as a joint topic. Most importantly, the use of generalized inverted Dirichlet mixtures to model the emission probabilities within the HMM framework together with feature selection as an embedded process is unprecedented. In this work, we propose a fully customized feature selection methodology with a complete empirical and experimental study of Feature Saliency embedding into the GID-based HMM.

Feature selection plays a major role in speeding the learning process and refining the models’ interpretation. It can drastically minimize the risk of overfitting and mitigates the effects of the curse of dimensionality [39]. Above-mentioned, the feature selection process is embedded in the training of the HMM, which represents the main takeaway from this research work.

Our vision of integrating feature selection in the HMM framework holds beyond the simple procedure of solely combining state of the art feature selection methods such as in the case of [55], where several ranking methods like Bhattacharyya distance [43], entropy and Wilcoxon [33], have been used to reduce the number of features fed to the HMM. As far as we are concerned, we are resolute to use the feature saliency as in [1], thoroughly embedded in the HMM framework making only one core method ready for use directly to treat any set of features.

The work presented in this manuscript can also be viewed intellectually at two different levels. First, it allows the integration of the non-conventional feature selection techniques into the framework of HMM, second, it allows the use of GID mixtures as a premiere to model data fed to HMM specifically emission distributions.

The remainder of this paper is organized as follows: In section 2 we summarize the previous works adopting HMMs. Then, we outline some of the applications using general feature selection methods along with HMMs as a predictive model. In section 3, we present our GID-FSHMM and explain all the corresponding integration steps. The subsequent section 4 showcases real-life problems experimentation and analyses obtained results. Finally, the paper closes with a summary of work and concluding remarks.

2 Related work

2.1 Hidden Markov models

In this section, we recall a handful of background information on HMMs, while focusing on previous related work using HMMs conjointly with feature selection. Hidden Markov models are a ubiquitous tool commonly utilized to model time series data [34] [37] with applications across numerous areas. Used for decades in speech recognition [62], text classification [15, 44], face recognition [58] and fMRI data analysis [26], HMMs represent a powerful statistical tool that have proven to be not only useful but also efficient in various machine learning-based applications.

An HMM consists mainly of two distinct sequences of states. The first is a sequence of hidden states modelled by a Markov chain [7], the second is a sequence of observed events or features related to the hidden states. The typical purpose behind using HMMs is to represent probability distributions over sequences of observations, with the assumption that the observations are discrete. Therefore, the hidden states sequence can be estimated from the sequence of correlated observations. It is possible to specify an HMM by an initial probability, a matrix of transition probabilities between the states, and a set of parameters of the emission probability distribution which will be more focused on later in this paper. Most importantly, an HMM is outlined by two fundamental proprieties. Firstly, it assumes that an observation at time t is generated by some process whose state $h_t$ is hidden from the observer. Second, it implied that the state of the said hidden process fulfills the Markov property [31]; that is, given the value of $h_{t-1}$, the current state $h_t$ is independent of all the states before the time $t-1$. Thus, the observed features are modelled meeting the property of conditional independence given the state sequence. At the application level, the learning of parameters is simply finding the best set of state transitions and emission probabilities amid the states of the model. Consequently, an output sequence or a set of sequences is specified. At each time a state sequence is handled, there is a corresponding vector of observations composed of features collected from various sources. However, not all features are likely to be useful to the model. That is why, to build a rigorous model, we ought to remove all features that do not contribute to its usefulness, without degrading its accuracy.

2.2 Feature selection and its application with HMMs

Feature selection is a wide research area and many methods to reduce a given set of features have been implemented in both supervised and unsupervised contexts [47].

Typically, feature selection techniques are present in the state of the art under three main categories, namely, filters, wrappers, metaheuristic methods and embedded [3]. While filter methods such as information gain [49, 71], Pearson’s correlation coefficient [35] and variance threshold [72], treat the evaluation of all features and return a relevant subset out of them apart from the model building process, wrapper methods tend to optimize the classifier’s performance for the most part. Wrappers, which commonly adopt either forward selection [45], backward elimination [20] or recursive feature elimination [22, 53, 78], identify the relevant features depending on the learning algorithm. That is, when using wrappers, the model itself is built depending on a certain subset of features and its performance is measured upon particular criteria. Methods relying on metaheuristic algorithms tackle feature selection as an optimization problem. Composed but not limited to evolution-based algorithms such as Genetic Algorithm [42], these methods obtain the optimal solution thanks to their simplicity, flexibility and their capability to avoid local optima [59]. They start their feature selection process by generating random solutions that do not require heavy derivatives calculations and carry on an exploration phase to thoroughly investigate search space and identify promising areas. Embedded methods namely $L_1$ regularization and decision trees [9, 36] aspire to simultaneously select the features and build the model. Although filter methods exhibit a significant low time complexity, they are usually criticized for ignoring certain informative features [63]. On the other hand, metaheuristic and wrapper-based methods evaluate the usefulness of selected features using learner’s performance and can thus be more complex but still not very time-consuming. However, it has been proved that other optimization algorithms, namely embedded methods, can be more efficient given the fact that they not only improve the performance of the model but also facilitate results analysis. Indeed, there is a significant complexity compromise when it comes to using embedded methods, but these methods succeeded in adapting to several types of data and can be used with the majority of machine learning models. Embedded methods are also very useful when investigating relationships between features, which is an arising challenge nowadays.

In particular, feature selection for HMMs is driven by a crucial need to determine which feature to use in the model. Despite being investigated in numerous general and mixture models-based studies [25] [48], feature selection methods dedicated to HMMs are particularly limited. In fact, in the majority of applications, features are selected beforehand based on domain knowledge, and a consonant feature selection procedure is fully lacking [56] [74]. Clearly, transformation methods such as Principal Component Analysis (PCA) and Independent Component Analysis (ICA) do reduce the number of features in the model and for this same reason, they have been integrated into HMMs in [6, 80]. However, the mentioned methods do not really act as feature selection techniques as they are not able to eliminate data streams, and hence they merely are considered feature extraction techniques.

Embedded or integrated feature selection approaches, which are the main focus in this manuscript, ought to consider the whole set of features at once. These features serve as an input to the maximizing learning algorithm that is deployed to optimize the models’ performance. As an output, the reduced set of features, as well as the models’ parameters, are generated. Hence, an embedded feature selection method is identified as a simultaneous selection of features and model construction. This combines both the wrappers and filters advantages of respectively selecting feature subsets concerning a specific learning algorithm and the computational efficiency [1]. As previously indicated, one of the embedded methods for feature selection is the classification and regression trees [57]. The latter applies a recursive splitting of the feature space to generate a classification model. Features identified as the ones being involved in improving the model will exclusively be included in the learning algorithm. In contrast to the mixture models, context [11, 24, 48], literature about feature selection integration into the HMM framework is somewhat narrow. Nearly all HMM-based adaptations of feature selection were based on what is also known as the concept of feature saliency, which has been defined by [48] as a metric associated with a given feature, that is the probability that the said feature is relevant. Zhu et al. [81] are among the first to use a jointly embedded estimation and feature selection method, where they apply a variational Bayesian framework to the end of salient features inference. They use the implemented method to simultaneously infer the number of hidden states as well as the models’ parameters. The adopted approach showed interesting results, however, the use of the variational Bayesian sometimes manifested a significant underestimation of the variance for the approximate distribution. Adams et al. [1] put forward a feature saliency model using hidden Markov models. The main idea is to use feature saliency variables to represent the probability that a given feature is relevant, by drawing a distinction between state-dependent and state-independent distributions. The said model operates in the case where the number of hidden states is known. For the matter, it provides a maximum a posteriori based estimation that selects the most relevant features using an Expectation-Maximization (EM) algorithm. This approach takes advantage of the already specified number of states to provide maximum a posteriori estimates and save the most relevant features by applying an Expectation-Maximization algorithm [14]. Moreover, Zheng et al. [79] adopted a strategy that combines a hidden Markov model, a localized feature saliency measure, and two t Student distributions for the purpose of distinguishing between relevant and non-relevant features. This strategy made it possible to accurately model emission parameters for each hidden state. Similarly to [81], the parameter estimation was operated using a variational Bayes framework. More recently, Fons et al. [30] incorporated Adams’ feature saliency HMM (FSHMM) [2] into a dynamic asset allocation system. The authors applied their HMM-based feature selection method to train their systematic trading system by testing its performance on real-life data. It showed that even without a financial expert involvement, the results reached a decent accuracy allowing the model to objectively contribute to portfolio construction and to prevent biases in the feature selection process. From their side, authors in [12] proposed a feature selection algorithm embedded in an HMM applied to gene expression time-course data, and they succeeded in reducing the feature domain by up to 90% leaving only a few but relevant features. The notable drawback of the mentioned work is that features deemed as irrelevant are eliminated and hence can drastically affect the models’ accuracy in the case the aforementioned features seem to be relevant after treatment.

There is indubitably a significant challenge when analyzing dense data, that is dealing with the saliency parameters besides those imperative for the model itself. As a consequence, the parameter estimation can sometimes be a sensitive task, not to mention the huge impact that the number of needed hidden states has on the said estimation. For this particular reason, we need to adapt the model in a way that it can handle the modelling of the data using a lower number of parameters to come up with the most relevant features from the candidate sets.

3 The proposed GID-FSHMM model

3.1 Feature selection integration in Hidden Markov model

In this section, we start by presenting the Hidden Markov Model and we recall the feature saliency concept that we will embed in the HMM. Then, we

3.1.1 The Hidden Markov model

We consider a HMM with continuous emissions and K states. We put $y=\{y_0,y_1,...,y_T\}$ the sequence of observed data with $y_t \in {\mathbb {R}}^L$, where T designates the time factor and L is the number of features. The observation for the l-th feature at time t, which is represented by the the l-th component of $y_t$, is denoted by $y_{lt}$.

Let $x=\{x_0,x_1,..., x_T\}$ be the sequence of hidden data. The transition matrix of the Markov chain associated to this sequence is denoted as $B=\{b_{ij}=P(x_t=j|x_{t-1}=i)\}$ and $\pi$ is the initial state probability. Thus the complete data likelihood can be expressed as:

$$\begin{aligned} p(x,y|\Lambda )=\pi _{x_{0}}c_{{x_0}}(y_0)\prod _{t=1}^{T}b_{x_{t-1},x_t}c_{x_t}(y_t) \end{aligned}$$

(1)

where $\Lambda$ is the set of model parameters, and $c_{x_t}(y_t)$ is the emission probability given state $x_t$.

Fig. 1

The Hidden Markov model: Grey squares represent latent variable, pink circles are observations, and blue circles represent model parameters where $\alpha$ and $\beta$ are GID parameters (colour figure online)

In our feature selection hidden Markov model (FSHMM) we apply a feature saliency approach over the emission probability distribution in order to select the relevant features and to estimate our parameters [48]

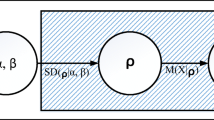
The graphical model of the GID Hidden Markov model can be seen in Fig. 1.

3.1.2 Feature saliency-based Hidden Markov model

The feature-saliency based HMM measures the relevancy of a certain feature as follows; if the latter’s distribution is dependent on the underlying state, the feature is believed to be relevant. In the case where its distribution is independent of the state, the feature is considered irrelevant [1].

Thus, we put a set of binary variables $z=\{z_1,..., z_L\}$ indicating the relevancy of features, that is $z_1=1$ if the l-th feature is relevant and $z_1=0$ if it’s irrelevant. The feature saliency $\rho _l$ is the probability that the l-th feature is relevant.

In this work we assume that all features are conditionally independent given the state. Hence, the conditional distribution of $y_t$ given z and x can be written as follows:

$$\begin{aligned} p(y|z,x_t=i, \Lambda )=\prod _{l=1}^{L}r(y_{lt}|\theta _{il})^{z_l}q(y_{lt}|\lambda _l)^{1-z_l} \end{aligned}$$

(2)

where $r(y_{lt}|\theta _{il})$ is the conditional feature distribution for the l-th feature with state-dependent parameters $\theta _{il}$ which later will be detailed with depending on the adopted type of mixture, and $q(y_{lt}|\lambda _l)$ is the state independent feature distribution with parameters $\lambda _l$.

$\Lambda =\{\theta ,\rho ,\lambda \}$ is the set of all our FSHMM model parameters. The marginal probability of z is:

$$\begin{aligned} p(z|\Lambda )=\prod _{l=1}^{L}\rho _l^{z_l}(1-\rho _l)^{1-z_l} \end{aligned}$$

(3)

The joint distribution of $y_t$ and z given x can be expressed as:

$$\begin{aligned} p(y_t,z|x_t=i, \Lambda )=\prod _{l=1}^{L}[\rho _l r(y_{lt}|\theta _{il})]^{z_l}[(1-\rho _l)q(y_{lt}|\lambda _l)]^{1-z_l} \end{aligned}$$

(4)

The marginal distribution for $y_t$ given x over all values of z is:

$$\begin{aligned} \begin{aligned} c_{x_t}(y_t)&=p(y_t|x_t=i, \Lambda )\\ {}&=\prod _{l=1}^{L}\big (\rho _l r(y_{lt}|\theta _{il})+(1-\rho _l)q(y_{lt}|\lambda _l)\big ) \end{aligned} \end{aligned}$$

(5)

The complete data likelihood of the FSHMM can thus be written as:

$$\begin{aligned} p(x,y,z|\Lambda )=\pi _{x_0}p(y_0,z|x_0,\Lambda )\prod _{t=1}^{T}b_{x_{t-1},x_t}p(y_t,z|x_t,\Lambda ) \end{aligned}$$

(6)

The form of q(.|.) indicates our prior knowledge about the distribution of the non-salient features. We put q(.|.) and r(.|.) to follow an inverted generalized Dirichlet distribution, as this can lead to better results for the reasons explained earlier in this paper.

In this work, the state-dependent and the state-independent distributions are assumed to be GID mixtures. Accordingly, the set of model parameters for the GID-FSHMM is $\Lambda =\{\pi , B, \alpha , \beta , \rho , \lambda \}$. Figure 2 shows the feature saliency GID-based HMM.

Fig. 2

The feature saliency GID-based Hidden Markov Model: Grey squares represent latent variable, pink circles are observations, and blue circles represent model parameters (colour figure online)

3.2 GID mixtures and integration into the FSHMM framework

3.2.1 Generalized Inverted Dirichlet

The choice of GID is backed by the several interesting mathematical properties that this distribution has. These properties allow for a representation of GID samples in a transformed space where features are independent and follow inverted Beta distributions. Adopting this distribution lets us take advantage of conditional independence among features. This interesting strength is used in this paper to develop a statistical model that handles not only positive data but also feature selection.

Let $\overrightarrow{X}$ a D-dimensional positive vector following a GID distribution. The joint density function is given by Lingappaiah [52] as:

$$\begin{aligned} p(\overrightarrow{X}|\overrightarrow{\alpha },\overrightarrow{\beta })=\prod _{d=1}^{D}\frac{\Gamma (\alpha _{d}+\beta _{d})}{\Gamma (\alpha _{d})\Gamma (\beta _{d})}\frac{X_{d}^{\alpha _{d}-1}}{\bigg (1+\sum _{l=1}^{d}X_d\bigg )^{\eta _{d}}} \end{aligned}$$

(7)

where $\overrightarrow{\alpha }=[\alpha _{1}, ..., \alpha _{D}]$, $\overrightarrow{\beta }=[\beta _{1}, ..., \beta _{D}]$. $\eta$ is defined such that $\eta _{d}=\alpha _{d}+\beta _{d}-\beta _{d+1}$ for $d=0, ..., D$ with $\beta _{D+1}=0$.

The GID estimation is made simple thanks to an essential propriety, that is if there exists a vector $\overrightarrow{X}$ that follows a GID distribution, then we can come up with another vector $\overrightarrow{W}_n=[\overrightarrow{W}_{n1}, ..., \overrightarrow{W}_{nD}]$ where each element follows an inverted Beta (IB) distribution following the transformation:

$$\begin{aligned} W_{nd}= f(X_{nd}) = {\left\{ \begin{array}{ll} X_{nd}, &{} \text{ d=1 } \\ \frac{X_{nd}}{1+X_{n1}+, ..., +X_{nd-1}}, &{} \text{ d=2, } \text{..., } \text{ D } \end{array}\right. } \end{aligned}$$

(8)

Then, the multivariate extension of the 2-parameters inverted Beta distribution is given by:

$$\begin{aligned} p_{IBeta}(W_{nd}|\alpha _{jd}, \beta _{jd})=\frac{\Gamma (\alpha _{jd} +\beta _{jd})}{\Gamma (\alpha _{jd})\Gamma (\beta _{jd})} \frac{W_{nd}^{\alpha _{jd} -1}}{(1+W_{jd})^{(\alpha _{jd}+\beta _{jd})}} \end{aligned}$$

(9)

The mean of IB is given by:

$$\begin{aligned} E(W_d)=\frac{\alpha _d}{\beta _{d}-1} \end{aligned}$$

(10)

The variance of IB is given by:

$$\begin{aligned} Var(W_d)=\frac{\alpha _d(\alpha _d + \beta _{d} -1)}{(\beta _{d}-2)(\beta _{d} -1)^2 } \end{aligned}$$

(11)

3.2.2 GID mixture model

Let us consider a data set ${\mathcal {X}}$ of N D-dimensional positive vectors, ${\mathcal {X}}=(\overrightarrow{X_1}, \overrightarrow{X_2}, ..., \overrightarrow{X_N})$. We assume that ${\mathcal {X}}$ is governed by a weighted sum of M GID component densities with parameters $\Theta =(\overrightarrow{\theta _1}, \overrightarrow{\theta _1}, ..., \overrightarrow{\theta _M}, p_1, p_2, ..., p_M)$ with $\overrightarrow{\theta _j}$ is the vector of parameters of the j-th component and ${p_j}$ are the mixing weights which are positive and sum to one [4]:

$$\begin{aligned} p(\overrightarrow{X_i}|\Theta )=\sum _{j=1}^{M}p_jp(\overrightarrow{X_i}|\overrightarrow{\Theta _j}) \end{aligned}$$

(12)

where $p(\overrightarrow{X_i}|\overrightarrow{\Theta _j})$ is the GID distribution with $\Theta _j=(\alpha _{j1},\beta _{j1},\alpha _{j2},\beta _{j2}, ..., \alpha _{jD},\beta _{jD})$ is the set of parameters defining the j-th component. Furthermore, in mixture-based clustering, each data point $\overrightarrow{X_i}$ can be assigned to all classes with different posterior probabilities $p(j|\overrightarrow{X_i})$. Therefore, a factorization of the posterior probability can simply be expressed as:

$$\begin{aligned} p(j|\overrightarrow{Y_i})\propto p_j\prod _{l=1}^{D}p_{IBeta}(X_{il}|\theta _{jl}) \end{aligned}$$

(13)

where $X_{i1}=Y_{i1}$ et $X_{il}=\frac{Y_{il}}{1+\sum _{l=1}^{D}Y_{il}}$ for $l>1$, $p_{IBeta}(X_{il}|\theta _{jl})$ is an inverted Beta distribution with $\theta _{jl}=(\alpha _{jl},\beta _{jl})$, $l=1, ..., D$

In this fashion, the clustering structure underlying ${\mathcal {X}}$ is the same as that underlying ${\mathcal {Y}}=(\overrightarrow{Y_1}, ..., \overrightarrow{Y_N})$, and it can be described by the following mixture model with conditionally independent features:

$$\begin{aligned} p(\overrightarrow{X}_i|\Theta )=\sum _{j=1}^{M} p_j\prod _{l=1}^{D}p_{IBeta}(X_{il}|\theta _{jl}) \end{aligned}$$

(14)

3.2.3 GID mixture-based FSHMM

As a first attempt in the context of feature saliency-driven HMMs, to the extent of our knowledge, we are using a mixture of GID as emission probabilities of our FSHMM. Gaussian mixtures, in particular, have seldom been tested previously and applied successfully [48] [81]. Assuming the relevant feature distribution is represented by a mixture of M GID distributions, we let $\Phi =\{\phi _{1t}, ..., \phi _{Mt}\}$ be the set of variables indicating the mixture component, where $\phi _{m}=1$ if observation t comes from the $m^th$ mixture and $\phi _{mt}=0$ otherwise. To indicate the probability that the observation comes from the $m^th$ mixture, given the state, we put $\omega _{im}$. In this regard, the set of model parameters $\Lambda$ becomes $\{\pi , B, \alpha , \beta , \rho , \lambda , \omega \}$. The idea behind the GID-based FSHMM is to suppose that a given feature $y_{lt}$ is generated from a mixture of two univariate distributions. The first one is supposed to generate relevant features and is distinct for each cluster. The second is common to all clusters in a way that it is independent of class labels, and generates irrelevant features. This purpose can be formulated as follows.

The marginal probability of $\phi _t$ can be expressed as

$$\begin{aligned} p(\Phi |\Lambda )=\prod _{m=1}^{M}\omega _{im}^{\phi _{mt}} \end{aligned}$$

(15)

In the same manner as in (3), we assume the features are conditionally independent given the state. Thus, the conditional distribution of $y_t$ given x, y and $\Phi$ can be formulated as

$$\begin{aligned} p(y_t|\Phi , z, x_t=i, \Lambda )=\prod _{l=1}^{L}\big [r(y_{lt}|\alpha _{ilm}, \beta _{ilm})^{z_l}q(y_{lt}|\alpha _{\lambda , ilm}, \beta _{\lambda , ilm})^{1-z_l}\big ]^{\phi _{mt}} \end{aligned}$$

(16)

The joint distribution of $y_t$, $\Phi$, and z given x is

$$\begin{aligned} \begin{aligned} p(y_t, \Phi ,&z|x_t=i, \Lambda )=p(y_t|\Phi , z, x_t=i, \Lambda )p(\Phi |\Lambda )p(z|\Lambda )\\&=\prod _{m=1}^{M}\Bigg [\omega _{im}\prod _{l=1}^{L}\big [\rho _l r(y_{lt}|\alpha _{ilm},\beta _{ilm})^{z_l}\big ]\big [(1-\rho _l)q(y_{lt}|\alpha _{\lambda , ilm}, \beta _{\lambda , ilm})^{1-z_l}\big ]^{\phi _{mt}}\Bigg ] \end{aligned} \end{aligned}$$

(17)

The marginal distribution for $y_t$ given x is obtained by summing (17) over z and $\Phi$ such as

$$\begin{aligned} \begin{aligned} c_{x_t}(y_t)&=p(y_t|x_t=i, \Lambda )\\ {}&= \sum _{m=1}^{M}\omega _{im}\prod _{l=1}^{L}(\rho _l r(y_{lt}|\alpha _{ilm},\beta _{ilm})+(1-\rho _l)q(y_{lt}|\alpha _{\lambda , ilm}, \beta _{\lambda , ilm}) \end{aligned} \end{aligned}$$

(18)

The complete data likelihood for the FSHMM with GID emissions is

$$\begin{aligned} p(x, y, z, \Phi |\Lambda )=\pi _{x_1}p_{IBeta}(y_1,\Phi ,z|x_1, \Lambda )\prod _{t=2}^{T} b_{x_{t-1},x_t}p_{IBeta}(y_t, \Phi , z|x_t, \Lambda ) \end{aligned}$$

(19)

3.3 Parameter estimation of the GID-FSHMM

3.3.1 Update equations for FSHMM parameters

In order to perform the estimation of parameters, we opt for using the EM algorithm, referred to as Baum-Welch when applied in the context of HMMs [8, 62]. We use this algorithm to calculate the maximum-likelihood (ML) estimates for the model parameters. For the part where we evaluate the features, we are bound to place priors on the parameters to compute the maximum a posteriori (MAP) estimates [32]. We need to go over the two steps of the Baum-Welch algorithm. First, in the E-step we need to find the expected value of the complete log-likelihood taking into consideration the data and the underlying model parameters. Second, in the M-step we proceed to maximize the expectation computed in the previous step in order to figure the next set of model parameters out. The Baum-Welch is iterated until an experimentally determined stopping threshold is met. The $\mathcal {Q}$ function designates the expectation of the complete log-likelihood and is given by:

$$\begin{aligned} \begin{aligned} \mathcal {Q}(\Lambda ,\Lambda ')&={\mathbb {E}}\big [log p(x, y, z, \Phi |\Lambda )|y,\Lambda '\big ]\\ {}&=\sum _{x,z,\Phi }log (p(x, y, z, \Phi |\Lambda )|\Lambda ')p(x, z, \Phi |y, \Lambda ') \end{aligned} \end{aligned}$$

(20)

where $\Lambda$ and $\Lambda '$ represent the set of model parameters for the current iteration and the set of parameters from the previous iteration respectively. We place priors on the parameters and calculate the MAP estimates with an eye toward the automatic feature assessment and selection. Hence the $\mathcal {Q}$ is changed by adding $G(\Lambda )$ the prior on the model parameters such as:

$$\begin{aligned} \mathcal {Q}(\Lambda ,\Lambda ')+log G(\Lambda ) \end{aligned}$$

(21)

By analogy to the previously explained EM procedure, the complete log-likelihood $\mathcal {Q}$ is calculated in the E-step (20), then the $log G(\Lambda )$ is added up and equation (21) is maximized in the M-step. For this matter, several probabilities are needed for the FSHMM, the E-step takes in charge the computation of the following quantities:

$$\begin{aligned} \zeta _t(i)= & {} {\mathbb {P}}(x_t=i|y,\Lambda ), \end{aligned}$$

(22)

$$\begin{aligned} \xi _t(i,j)= & {} {\mathbb {P}}(x_t=i,x_{t+1}=j|y,\Lambda ) \end{aligned}$$

(23)

where $\zeta _t(i)$ et $\xi _t(i,j)$ are respectively the conditional state probabilities and the conditional transition probabilities. These quantities are calculated using the forward-backward algorithm. As a result, the following quantities are what the E-step probabilities turn out to be after iterating the forward-backward algorithm

$$\begin{aligned} \begin{aligned} \delta _{ilmt}&=p(y_{lt},z_l=1|\phi _{mt}=1, x_t=i,\Lambda ')\\ {}&=\rho _l p(y_{lt}|\alpha _{ilm}, \beta _{ilm}), \end{aligned} \end{aligned}$$

(24)

$$\begin{aligned} \begin{aligned} \epsilon _{ilmt}&=p(y_{lt},z_l=0|\phi _{mt}=1, x_t=i,\Lambda ')\\ {}&=(1-\rho _l)q(y_{lt}|\alpha _{\lambda , ilm}, \beta _{\lambda , ilm}), \end{aligned} \end{aligned}$$

(25)

$$\begin{aligned} \begin{aligned} \tau _{ilmt}&=p(y_{lt}|\phi _{mt}=1, x_t=i,\Lambda ')\\ {}&=\delta _{ilmt}+\epsilon _{ilmt}, \end{aligned} \end{aligned}$$

(26)

$$\begin{aligned} \begin{aligned} u_{ilmt}&=p(z_l=1, x_t=i, \phi _{mt}=1|y, \Lambda ')\\ {}&=\zeta _t(i)\Bigg (\frac{\delta _{ilmt}}{\tau _{ilmt}}\Bigg )\Bigg (\frac{\omega _{im}\prod _{l=1}^{L}\tau _{ilmt}}{\sum _{m}^{M}\omega _{im}\prod _{l=1}^{L}\tau _{ilmt}}\Bigg ), \end{aligned} \end{aligned}$$

(27)

and

$$\begin{aligned} \begin{aligned} v_{ilmt}&={\mathbb {P}}(z_l=0, x_t=i, \phi _{mt}=1|y, \Lambda ')\\ {}&=\zeta _t(i)\Bigg (\frac{\epsilon _{ilmt}}{\tau _{ilmt}}\Bigg )\Bigg (\frac{\omega _{im}\prod _{l=1}^{L}\tau _{ilmt}}{\sum _{m}^{M}\omega _{im}\prod _{l=1}^{L}\tau _{ilmt}}\Bigg ), \end{aligned} \end{aligned}$$

(28)

The $\mathcal {Q}$ function is expanded into a sum of terms where each term can be maximized independently. These terms are the $\mathcal {Q}$ function applied to the initial state $\pi$, the state-transition b, and the parameters for the emission distribution $\theta =\{\alpha , \beta , \lambda , \rho \}$. Consequently, for all parameters, except for the GID distribution ones, the maximization step gives, as a result, the following parameters and their updates

$$\begin{aligned} \hat{\pi _i}=\zeta _t(i), \end{aligned}$$

(29)

$$\begin{aligned} \hat{b_{ij}}=\frac{\sum _{t=1}^{T-1}\xi _t(i, j)}{\sum _{t=1}^{T-1}\zeta _t(i)}, \end{aligned}$$

(30)

$$\begin{aligned} \hat{\omega _{im}}=\frac{\sum _{t=1}^{T-1}\sum _{l=1}^{L}u_{ilmt}}{\sum _{t=1}^{T-1}\sum _{l=1}^{L}\sum _{m=1}^{M}u_{ilmt}} \end{aligned}$$

(31)

$$\begin{aligned} \begin{aligned} {\hat{\rho }}_l&=\frac{\sum _{t=1}^{T-1}\sum _{l=1}^{L}\sum _{m=1}^{M}u_{ilmt}}{\sum _{t=1}^{T-1}\sum _{l=1}^{L}\sum _{m=1}^{M}u_{ilmt}+\sum _{t=1}^{T-1}\sum _{l=1}^{L}\sum _{m=1}^{M}v_{ilmt}}\\ {}&=\frac{\sum _{t=1}^{T-1}\sum _{l=1}^{L}\sum _{m=1}^{M}u_{ilmt}}{T} \end{aligned} \end{aligned}$$

(32)

Complete estimation of GID parameters, as well as the MAP estimation, can be consulted respectively in Appendix sections A and B.

4 Experiments and results

In this section, extensive experiments are conducted and we have implemented several real-world topical yet challenging applications using the FSHMM with GID emission probabilities. We are mainly comparing our new approach to its classical FSHMM competitors and other new adaptations that we executed for the sake of comparison and testing, e.g., inverted Dirichlet-based FSHMM (ID-FSHMM) and Dirichlet-based FSHMM (Dir-FSHMM), not to mention the widely used GMM-FSHMM. It is noteworthy that the learning of the mentioned adaptations has been based on the same methodology described in the previous section to learn the GID mixture-based FSHMM. Two real-world applications, facial expressions recognition, and scene categorization are here tested and explained. Experimentation and results presented in this section have been yielded on a macOS environment over a 2.3 GHz Dual-Core Intel Core i5 MacBook Pro, using Python.

4.1 Facial expressions recognition

Facial expression recognition is a powerful process that usually commends the way we interact with other people. It is one of the non-verbal communication media that humans naturally use in everyday interactions. Besides its role in supporting humans’ understanding of people’s intentions and feelings, facial expression recognition plays a major role in making decisions about relationships or situations. For all these reasons, substantial efforts have been devoted to automating this recognition [19, 23] and using it as a fundamental step within multiple decision-making systems. A human being is naturally empowered to interpret these expressions and make his decisions in a real-time matter. Nonetheless, this task is still approached as a complex and challenging process in the field of machine learning [27, 38]. Facial Expression Recognition is applied in a wide range of contexts and is used in numerous applications such as Human-Computer Interaction [65], student automatic E-learning [54], Behavioural Science [46], psychological studies [50], image understanding, and synthetic face animation. The principal purpose of researchers working on these applications is to produce automated systems capable of automatically recognizing the emotional state of a person and further draw an analysis or take a decision based on a specific context [16].

4.1.1 HMM-based facial expression recognition

Classification is the most significant part of a facial expression recognition system [69]. Methods applied to classify this type of images are generally sorted into static or dynamic [77]. Static methods are based on the information acquired from the input image, they take benefit from the use of support vector machine, neural network, Bayesian network to perform the assigned task. HMMs are dynamic classifiers that exploit temporal records to analyze facial expressions. Hence, they are highly recommended by psychological experiments carried out as indicated in [5].

As early as 1990, [66] used HMMs to come up with a solution for the challenging task of automating facial expressions recognition. Authors in [66], used an HMM along with the integration of a priori structural knowledge with statistical information. HMMs offer a perfect analogous representation to the experience of observing a particular feeling through the way they statistically handle the behaviour of an observable symbol sequence. These models provide a specification of the probability distribution over all hidden events that are behind a certain symbol sequence. The performances of HMMs when dealing with such challenges are promising, especially in the case when they learn through an entire sequence of images describing a group of actions taken by a person when undergoing a certain feeling. The learning process is conducted in a much smoother way thanks to HMMs capability of handling the Spatio-temporal nature of the debated application. In fact, there is a metaphorical resemblance between human performance when naturally processing the recognition task, and the stochastic nature of the HMM process inasmuch as it analyses the measurable (observable) actions in order to infer the immeasurable (hidden) feelings of the person.

In this particular context, we choose to apply our model on the challenging Dollar facial expression database [17] 3. This application is unprecedented as it uses for the first time and embedded model-based feature selection into the HMM structure.

Fig. 3

Samples of facial frames from the Dollar facial expressions dataset

4.1.2 Experimental trials and results

The Dollar database is composed of 192 sequences performed by 2 individuals, each expressing 6 different basic emotions 8 times under 2 lighting setups. Each subject starts with a neutral expression, then expresses emotion, and returns to a neutral expression. For our simulations, we follow the experimental setting considered in [58], which consists of using three peak frames of each sequence for 6-class expression recognition (576 images: anger, disgust, fear, joy, sadness, and surprise). The pre-processing steps are also the same and consist of extracting features from the whole face region by cropping original face images into 110$\times$150 pixels, keeping only the central part of facial extraction. A Local Binary Pattern (LBP) descriptor [60], is used for feature extraction. More specifically, each cropped face image is first divided into small regions from which LBP histograms are extracted and then concatenated altogether into a single feature histogram representing the face image. We use a 59-bin LBP operator in the (8, 2) neighbourhood. This means 8 sampling points on a circle of radius 2, then we divide each image (110 $\times$ 150) into 18 $\times$ 21 pixels regions. Therefore, each face image is divided into 42 (6 $\times$ 7) regions and is then represented by LBP histograms with a length of 2478 (59 $\times$ 42). After that, these histograms are normalized. The procedure is applied as the one originally used in [67]. We figured that if we reduce the feature vector the algorithm tends to early diverge, however since features will later be reduced by the model itself, and in order to give the algorithm the time to learn we will not reduce the feature vector ourselves and will leave it as it is. The obtained feature vector is actually handled with our GIDHMM where the feature saliency is considered. Hence, recognition is carried out via a single HMM recognizer. A collection of HMMs each representing a different subject is matched against the test image and the highest match is selected as explained in figure 4. For the sake of comparison, we conduct several experiments with different used models, with and without taking into consideration of feature relevancy, then we report the results including features relevancies and the confusion matrix for each experiment.

Fig. 4

Block diagram for FSHMM-based face recognizer

In order to evince the advantages of the proposed approach and most importantly underline the crucial role of feature selection integration in improving results, we compare the latter with other emotion recognition approaches that are mainly based on mixture models. These approaches, have been personally implemented, and include inverted Dirichlet-based HMM without feature selection (IDHMM) [58], inverted Dirichlet-based HMM with feature selection (ID-FSHMM), generalized inverted Dirichlet-based HMM without feature selection (GIDHMM), and generalized inverted Dirichlet-based HMM with feature selection (GID-FSHMM). On top of that, we put a special emphasis on the improvements noticed from the use of GID mixtures measured against the Gaussian mixtures-based HMM with feature selection (GM-FSHMM). Results obtained are displayed in Fig. 5, where we present the average recognition rates for the different used methods.

Fig. 5

Average recognition rates for facial expressions recognition with and without applying feature selection (colour figure online)

There is an interesting observation to make after nailing these results, that is the amelioration in average recognition results after using the GIDHMM as a model. Initially, using only the latter allowed for a slight but worth mentioning amelioration in the average recognition rate from 96.11% to 96.16%, this itself shows that the GIDHMM is better in modelling our data than the IDHMM. Further, we noticed when incorporating feature selection into our previously established IDHMM model, the average recognition rate improved from 96.11 to 96.44%. On top of that, we plainly succeeded to bear out our theoretically anticipated projections regarding recognition rates. In fact, the feature selection-based GIDHMM executed the task of recognizing each facial expression considerably better than GIDHMM without FS. This conclusion comes after several trials on each emotion type separately. The individual recognition rates per category and confusion matrices for the mentioned trials are displayed in Table 1 and Fig. 6.

Fig. 6

Confusion matrices for facial expressions recognition with and without applying feature selection for GID-FSHMM

Table 1 Detailed recognition rates in the case of facial recognition application with and without applying feature selection for GIDHMM

As indicated in Fig. 5, average recognition rates for GIDHMM with and without feature selection integration are respectively 97.33% and 96.16% with the corresponding average misclassified images of 22.11 and 15.32 per dataset. There is also a significant variation in the run time when using each of the cited methods, 36.4 min for GIDHMM, and 41.6 min for GIDHMM-FS.

Needless to say, the integration of feature selection in our models brought an obvious amelioration to the yielded results for all adopted distributions, this shows the important role of taking into consideration the feature saliency when dealing with image classification tasks. Further investigations with respect to features relevancy are conducted in the following applications to emphasize this role.

4.2 Scene categorization

Recently, there has been an abundance of research works and experimental trials aiming to bridge the semantic gap between the perceptual ability of human vision and the capacity of automated systems when performing the same related tasks. This challenge is prompted by the impressive trait of the human visual system to rapidly, accurately, and comprehensively recognize and understand a complex scene [28, 29, 76]. Thus, it would be worthwhile if each image in a studied collection could be annotated with semantic descriptions allowing for a better automatic interpretation and hence an improved visual recognition ability. In this section, we work on a challenging problem related to the mentioned area of research, which is recognizing scene categories. Visual scenes classification has many applications in robot navigation and robot path planning [70], video analysis [73], content-based image retrieval [13].

Inasmuch as this application is complex due to the variety of scenes and variations of viewing angles and changing backgrounds, choosing efficient features plays a major role in the accuracy level of the recognition task.

In this section, we test the effectiveness of our proposed feature-selection-based GIDHMM, in categorizing images of real-world scenes from the notorious MIT benchmark [61].¹ The indicated database contains about 2688 diverse outdoor scene images in colours from 8 categories: coast (360 images), mountain (374 images), forest (328 images), open country (410 images), inside city (308 images), street (292 images), tall building (356 images) and highways (260 images). Images come in 256 $\times$ 256 pixels resolution. We choose to randomly select 200 images from each category for training and leave the rest for testing purposes. Figure 7, shows example images from the MIT outdoor data set.

Fig. 7

Sample images from the 8 categories MIT data set: (a) Tall buildings, (b) Mountain, (c) Street, (d) Forest, (e) Open country, (f) Highway, (g) Inside city, (h) Coast

A crucial step for the scene categorization task is feature extraction. For this matter, we adopt a process where we normalize images which will afterward be represented each by a collection of local image patches. These patches are scanned and low-level feature vectors are thereafter extracted. We then use the bag of words approach (BOW) method, adapted likewise by [75] for scene classification, in which Yang et al. mapped the key points of an image into visual words. Hence, each image could be represented as a “bag of visual words” BoVW, and in this instance as a vector of counts of each visual word in that image. This will allow for an overall representation for each image through a feature vector, upon which the task of image classification is built. Following [10], and after obtaining the intended histograms, we apply a probabilistic Latent Semantic Analysis (pLSA) [40, 41] in order to represent each image by a D-dimensional vector with D being the number of latent aspects (hidden aspects, features, or hidden states in our analogy). Ultimately, our objective is to identify the right category for each image by applying our previously developed model.

In this work, we use dense SIFT 16 $\times$ 16-pixel patches calculated over a grid of 8 pixels. Besides, we build a bag of words dictionary using a K-means algorithm [41] to cluster our descriptors in a V visual words vocabulary. For each SIFT point in a candidate image, the nearest neighbour within the vocabulary is computed, and thereby a feature vector with dimension V is built. Hence, each image can be represented as a frequency histogram over the V visual words. As previously explained, in this work we apply pLSA to allow for a description through a D-dimensional vector where D is the number of aspects. We employ our GIDHMM to model the set of images designated for training. We compute the class-relationship likelihood of each input image and classify it to the class that maximizes more its likelihood. In our approach, each image class is characterized by its own behaviour, therefore each class is described by its own HMM. That being the case, for each scenery type, a distinct 8-state HMM is trained. Experiments are carried out 30 times with the average accuracy reported for both feature-saliency-based and non-feature-saliency-based methods.

Through these experiments, we aim to evaluate not only the effectiveness of GIDHMM measured against IDHMM and GHMM but also the effectiveness of embedding the process of feature selection in the core of each of the aforementioned models. Experiments are chosen to be conducted in the following order: first, we compare the performance of GIDHMM, IDHMM, and GHMM without taking into consideration the relevancy of features. Then we reproduce the same experiments by taking into account feature relevancy. Table 2 presents the confusion matrix when GIDHMM is applied without feature selection. According to this table, we get an average accuracy of 91.37%. On the other hand, Table 3 shows the confusion matrix when GIDHMM is used along with feature selection: the average accuracy is 93.12%.

Table 2 The confusion matrix in the case of MIT scene recognition problem when applying GIDHMM without feature selection

Table 3 The confusion matrix in the case of MIT scene recognition problem when applying GIDHMM with feature selection

Results of other experimentation on the different used models are presented in Table 4 and confirm our previous assumptions about the role of feature selection in improving recognition rates. Our algorithm analyzed all extracted features and succeeded to determine their saliency, hence the use of the better features yielded better results. Figure 8 shows the feature saliencies obtained by our GID-FSHMM.

Table 4 Average recognition rates for different used HMMs in the context of natural scenes recognition, with and without feature selection

Fig. 8

Feature saliencies obtained in the case of fnatural scenes recognition problem when performing feature selection-based GIDHMM (colour figure online)

5 Conclusion

While there are multiple general techniques of applying feature selection, and despite the buildup of standardized procedures for features and dimensionality reduction, the literature reveals time and again that custom methods keep outperforming the general methods. Besides there is an overwhelming need for some sort of supervised data and knowledge when applying general feature selection models. In our context, this supervised data can take the form of information about the class, a label of each observation, or even a piece of knowledge about the latent variable. This additional information is often not readily accessible especially in areas where mixture models and HMMs are applied, considering that those models account for the fact that supervised data is unavailable. Therefore, unsupervised feature selection methods are essentially needed when using HMMs, allowing for significantly better performing models compared to those based upon general feature selection methods. Further, the interest in adopting the GID for modelling our data arose from the limitations encountered when inverted Dirichlet is adopted, in particular its restraining strictly positive covariance. In this paper, we proposed a framework in which all the aforementioned problems are addressed simultaneously in the case of automatic recognition. The developed approach applies feature selection to a GID-based HMM. Parameters are learned via a MAP method adding a huge advantage in raising both accuracies of parameter estimates and feature saliencies. Experimental results involving challenging real-life applications such as facial expressions recognition and natural outdoor scene recognition showed that the proposed approach is highly promising. Future works are intended to be done in the near future extending this work to different flexible distributions and considering online learning for more precise results.

Appendices

Estimation of GID parameters

Here, the estimation of the GID parameters is equivalent to maximization of the following log-likelihood function

$$\begin{aligned} \begin{aligned} log(p(\overrightarrow{X}_i|\Theta )&=\sum _{i=1}^{N}\sum _{j=1}^{M} p_j\prod _{l=1}^{D}p_{IBeta}(X_{il}|\theta _{jl}))\\&=\sum _{i=1}^{N}\sum _{j=1}^{M}\sum _{l=1}^{D}(log(p_j)+log p_{IBeta}(X_{il}|\theta _{jl})) \end{aligned} \end{aligned}$$

(33)

In the E-step, we compute the conditional expectation of log-likelihood, which is reduced to the computation of the posterior probabilities meaning the probability that a vector $\overrightarrow{X}_i$ is assigned to a cluster j, such as following

$$\begin{aligned} p(j|\overrightarrow{X}_i,\Theta ,\overrightarrow{p}_j)=\frac{p_jp(\overrightarrow{X}_i|\theta _j)}{\sum _{j=1}^{M}p_jp(\overrightarrow{X}_i|\theta _j)}=\frac{p_j\prod _{l=1}^{D}p_{IBeta}(X_{il}|\theta _{jl})}{\sum _{j=1}^{M}p_j\prod _{l=1}^{D}p_{IBeta}(X_{il}|\theta _{jl})} \end{aligned}$$

(34)

where $\overrightarrow{p}_j=(p_1, ..., p_M), p_j > 0$ and $\sum _{j=1}^{M} p_j =1$

Hence, we have

$$\begin{aligned} log p({\mathcal {X}}|\Theta ,\overrightarrow{p}_j)=\sum _{i=1}^{N}\sum _{j=1}^{M}\sum _{l=1}^{D}p(j|\overrightarrow{X_{i}},\Theta ,\overrightarrow{p_j})(log(p_j)+log p_{IBeta}(\overrightarrow{X_{i}}|\theta _{jl})) \end{aligned}$$

(35)

Whence, the conditional expectation of the complete-data log likelihood

$$\begin{aligned} {\mathbb {Q}}({\mathcal {X}},\Theta ,\overrightarrow{p}_j,\Upsilon )=log p({\mathcal {X}}|\Theta ,\overrightarrow{p}_j)+\Upsilon (1-\sum _{j=1}^{M}p_j) \end{aligned}$$

(36)

where $\Upsilon$ is the Lagrange multiplier.

We move forward in maximizing the log-likelihood function by finding the roots to its derivations with respect to the set of parameters. The mixture weights can be easily estimated as follows

$$\begin{aligned} p_j=\frac{\sum _{i=1}^{N}p(j|\overrightarrow{X}_i,\Theta ,\overrightarrow{p}_j)}{N} \end{aligned}$$

(37)

Regarding the derivatives with respect to $\alpha _{jl}$ and $\beta _{jl}$, we have

$$\begin{aligned} \begin{aligned} \frac{\partial {\mathbb {Q}}}{\partial \alpha _{jl}}&=\sum _{i=1}^{N}p(j|\overrightarrow{X}_i, \Theta , \overrightarrow{p}_j)\frac{\partial log p_{IBeta}(\overrightarrow{X}_i|\theta _{jl})}{\partial \alpha _{jl}}\\&=\sum _{i=1}^{N}p(j|\overrightarrow{X}_i, \Theta , \overrightarrow{p}_j)(\Psi (\alpha _{jl}+\beta _{jl})-\Psi (\alpha _{jl})+log(\frac{X_{il}}{1+X_{il}})) \end{aligned} \end{aligned}$$

(38)

$$\begin{aligned} \begin{aligned} \frac{\partial {\mathbb {Q}}}{\partial \beta _{jl}}&=\sum _{i=1}^{N}p(j|\overrightarrow{X}_i, \Theta , \overrightarrow{p}_j)\frac{\partial log p_{IBeta}(\overrightarrow{X}_i|\theta _{jl})}{\partial \beta _{jl}}\\&=\sum _{i=1}^{N}p(j|\overrightarrow{X}_i, \Theta , \overrightarrow{p}_j)(\Psi (\alpha _{jl}+\beta _{jl})-\Psi (\beta _{jl})+log(\frac{1}{1+X_{il}})) \end{aligned} \end{aligned}$$

(39)

where $\Psi (.)$ is the digamma function. We can clearly see that a closed form solution to estimate $\theta _{jl}$ does not exist. Therefore, we ought to use the Newton-Raphson method [51] such as

$$\begin{aligned} \theta _{jl}^{old}=\theta _{jl}^{new}-H_{jl}^{-1} \end{aligned}$$

(40)

where $H_{jl}$ is the Hessian matrix associated with ${\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )$ with first derivatives vector $G_{jl}=\Bigg (\frac{\partial {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \alpha _{jl}},\frac{\partial {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \beta _{jl}}\Bigg )$

$$\begin{aligned} H_{jl}=\begin{pmatrix} \frac{\partial ^2 {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \alpha _{jl}^2} &{} \frac{\partial ^2 {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \alpha _{jl} \partial \beta _{jl}}\\ \frac{\partial ^2 {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \alpha _{jl}\partial \beta _{jl}} &{} \frac{\partial ^2 {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \beta _{jl}^2} \end{pmatrix} \end{aligned}$$

(41)

with the following second and mixed derivatives

$$\begin{aligned} \frac{\partial ^2 {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \alpha _{jl}^2}=\sum _{i=1}^{N}p(j|\overrightarrow{X}_i, \Theta , \overrightarrow{p}_j)\Big (\Psi '(\alpha _{jl}+\beta _{jl})-\Psi '(\alpha _{jl})\Big ) \end{aligned}$$

(42)

$$\begin{aligned} \frac{\partial ^2 {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \beta _{jl}^2}=\sum _{i=1}^{N}p(j|\overrightarrow{X}_i, \Theta , \overrightarrow{p}_j)\Big (\Psi '(\alpha _{jl}+\beta _{jl})-\Psi '(\beta _{jl})\Big ) \end{aligned}$$

(43)

$$\begin{aligned} \frac{\partial ^2 {\mathbb {Q}}({\mathcal {X}}, \Theta , \overrightarrow{p}_j, \Upsilon )}{\partial \alpha _{jl}\partial \beta _{jl}}=\sum _{i=1}^{N}p(j|\overrightarrow{X}_i, \Theta , \overrightarrow{p}_j)\Big (\Psi '(\alpha _{jl}+\beta _{jl})\Big ) \end{aligned}$$

(44)

MAP estimation

A standard choice for the mixing parameters vector $\overrightarrow{p}_j$ is the Dirichlet distribution (Dir), given its definition on the simplex $\{(p_1, ..., p_M):\sum _{j=1}^{M-1}p_j<1\}$ [64]. We pick the same distribution for both initial and transition probabilities $\pi$ and B as well as for the observation weights such that

$$\begin{aligned} \pi \sim Dir(\pi |p) \\ B_i \sim Dir(B_i|b_i) \\ \omega _i \sim Dir(\omega _i|\Omega _i) \\ \rho _l \sim \frac{1}{{\mathbf {Z}}}e^{-{k_l \rho _l}} \end{aligned}$$

where ${\mathbf {Z}}$ is the normalizing constant and $\Omega _i$ is the hyperparameter vector of the observation weights.

The prior for the mixing parameters vector $\overrightarrow{p}_j$ can be written as follows

$$\begin{aligned} p(\overrightarrow{p}_j|M,\overrightarrow{\Delta })=\frac{\Gamma (\sum _{j=1}^{M}\Delta _j)}{\prod _{j=1}^{M}\Gamma \Delta _j}\prod _{j=1}^{M}p_j^{\Delta _j-1} \end{aligned}$$

(45)

where $\overrightarrow{\Delta }=\{\Delta _1, ...,\Delta _M\}$ is the Dirichlet parameters vector.

For the GID parameters, the Gamma (G) function is chosen as a prior given its exponential nature under the assumption of parameters independence. Thus we have the priors

$$\begin{aligned} p(\alpha _{jl})=G(\alpha _{jl}|\nu _{jl}, \vartheta _{jl})=\frac{\vartheta _{jl}^{\nu _{jl}}}{\Gamma (\nu _{jl})}\alpha _{jl}^{\nu _{jl}-1}e^{-\nu _{jl}\alpha _{jl}} \end{aligned}$$

(46)

$$\begin{aligned} p(\beta _{jl})=G(\beta _{jl}|\kappa _{jl}, \varsigma _{jl})=\frac{\varsigma _{jl}^{\kappa _{jl}}}{\Gamma (\kappa _{jl})}\beta _{jl}^{\kappa _{jl}-1}e^{-\kappa _{jl}\beta _{jl}} \end{aligned}$$

(47)

where $\nu$, $\vartheta$, $\kappa$ and $\varsigma$ are positive hyperparameters.