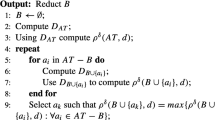1 Introduction

Up to now, in the field of Granular Computing (GrC) [14, 20, 41, 42, 49, 54], multigranulation has witnessed great success in knowledge representation [28], distributive information processing [63], groups of intelligent agents [29] and so on. Following the basic principle of multigranulation, various studies have been reported and then most of them can be divided into the following two phases.

  1. 1.

    On the one hand, the structure related topics are explored in view of the multiple different granulations [15, 47, 59]. For example, by examining the relationships among different information granulations, Yang et al. [55] have systematically revealed the hierarchical structures of the multigranulation space; Qian et al. [30] have proposed a serious of measures for characterizing the coarser or finer relationships over the multigranulation space, immediately, the order structure of the multigranulation space can be quantitatively represented; Lin et al. [18] have investigated the uncertainty measures in multigranulation space based on the hierarchical structure.

  2. 2.

    On the other hand, the modelling and data analysis related topics are also investigated in the framework of multigranulation. For instance, Lin et al. [21] have introduced the neighborhood based multiple information granulations into the rough modelling; Sun et al. [35] have studied the fuzzy based multiple information granulations over two universes for decision making; Li et al. [22] have introduced the Dempster-Shafer evidence theory into the multigranulation framework for improving the effectiveness of clustering ensemble; Qian et al. [34] also proposed the local modelling in cost-sensitive [17] environment for realizing quick feature selection.

Though reviewing various modelling strategies in terms of multigranulation, it is not difficult to point out that Multigranulation Rough Set (MGRS) [16, 61, 62] aims to approximate the target through using multiple different results of information granulation [37, 57]. Up to now, though a lot of MGRS have been proposed and carefully studied, most of the used information granulations only come from the homogeneous mechanism. For example, through appointing different values of radius, different neighborhood relations [10] can be obtained and these neighborhood relations are considered as the results of multiple information granulation for constructing MGRS; by using different values of threshold, the multigranulation decision-theoretic rough set [33] can be constructed, in which the thresholds are used to rule the granularity of the information granulation; through using a set of the coverings [19] for representing the results of information granulation, the covering based MGRS and the corresponding properties can also be studied. Nevertheless, it must be emphasized that most of the these researches lack the multi-view [56] which is rooted in the heterogeneous information granulation.

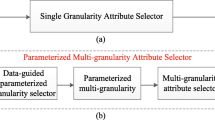
From discussions above, a new MGRS called Triple-G MGRS (covers three different “G”, i.e., neiGhborhood, Gap and Granular ball) will be developed in the context of this paper. Different from previous MGRS, our Triple-G MGRS employs the following three different information granulations: (1) a neiGhborhood [25, 46, 53] based parameterized information granulation; (2) a Gap [65] based data-adaptive information granulation; (3) a Granular ball [50, 51] based data-adaptive information granulation. Obviously, since both parameterized information granulation and data-adaptive information granulations have been used, our Triple-G MGRS does reflect the fundamental principle of heterogeneous information granulation. Therefore, the main structure of such Triple-G MGRS model can be elaborated in the following Fig. 1.

Fig. 1
figure 1

The structure of Triple-G MGRS model

Full size image

Moreover, it must be pointed out that in the field of rough set, the neighborhood, gap and granular ball are three widely accepted techniques for performing information granulation when facing data with continuous values or mixed data with both continuous and categorical values. Not only the computations of these information granulations are straightforward because only the distances among samples are required, but also the semantic explanations of these information granulations are clear. For example, the neighborhood based information granulation characterizes the similarity or dissimilarity [38] between any two samples through using only one justifiable parameter, it follows that different parameters offer different scales of such similarity or dissimilarity; the granular ball based information granulation characterizes the similarity or dissimilarity between samples through using the labels of samples, it follows that such mechanism can figure the distribution of data in some degree.

As the core of the rough set [8, 23, 36, 43, 44, 48], the problem of attribute reduction [9, 39, 45, 52, 60] can also be further explored in terms of Triple-G MGRS. However, since obtaining reduct based on Triple-G MGRS requires three different types of the information granulation, the elapsed time of searching reduct may be huge. For such a reason, an acceleration mechanism [12, 24, 58] called attribute grouping [3] will be further introduced into the process of searching reduct for reducing the computation overhead. Without loss of generality, the essence of such an accelerator is to partition the raw attributes into different groupings and then attributes in those groupings which contain at least one attribute in the potential reduct will not be evaluated in the process of deriving reduct. This is why the searching space of candidate attributes can be compressed and the computational efficiency will be improved.

The main contribution of our research can be summarized as the following aspects: (1) the proposed Triple-G is a novel development of MGRS, which can characterize the universe not only from the perspective of multigranulation, but also from the perspective of heterogeneity based multi-view; (2) since three comprehensively different mechanisms of information granulation are employed, the proposed Triple-G model is more explanatory than other rough set models; (3) to further improve the efficiency of searching Triple-G related reduct, the attribute grouping [3] based acceleration mechanism is introduced into the procedure of searching reduct; (4) as a framework of accelerator, the attribute grouping is with strong expansibility and then different approaches for partitioning the attributes may generate different attribute grouping based accelerators.

The rest of this paper is organized as follows. In Sect. 2, basic notions related to neighborhood, gap, granular ball and multigranulation rough sets are briefly reviewed. Our proposed Triple-G MGRS and the corresponding attribute reduction will be addressed in Sect. 3. Comparative experimental results are reported in Sect. 4, as well as the corresponding analyses. This paper is ended in Sect. 5 by summarizing the novelties and scheduling some further perspectives.

2 Preliminaries

In this section, we will review some basic concepts such as neighborhood rough set, gap rough set, granular ball rough set, multigranulation rough set and the corresponding attribute reductions.

In researching rough set for the classification task, a decision system is denoted as \({\mathcal {D}}=\langle U,AT,d\rangle \), in which U is a finite non-empty set which consists of m samples, AT is the set of all condition attributes, d is the decision attribute and d(x) indicates the label of sample x. In other words, the values over d are categorical and then such a decision attribute can be used to derive an equivalence relation such that \(\text{ IND }(d)=\{(x_i,x_j)\in U^2: d(x_i)=d(x_j)\}\), it follows that the universe can be partitioned into serval disjoint decision classes such that U/IND(d)={\(X_1,X_2,\cdots ,X_n\)}.

2.1 Neighborhood rough set and attribute reduction

Definition 1

[10] Given a decision system \({\mathcal {D}}\), \(\forall A\subseteq AT\), the neighborhood relation related to A over U can be defined as:

$$\begin{aligned} {\mathcal {N}}_A^\delta =\{(x_i,x_j)\in U\times U:\varDelta _A(x_i,x_j)\le \delta \}, \end{aligned}$$
(1)

in which \(\varDelta _A(x_i,x_j)\) is the distance between \(x_i\) and \(x_j\) by using the set of the attributes A, \(\delta \) is the assigned radius which determines the scale of the neighborhood.

Furthermore, in the light of the information provided by neighborhood relation \({\mathcal {N}}_A^\delta \), \(\forall x_i \in U\), the neighborhood of \(x_i\) related to A can be easily derived such that \({\mathcal {N}}_A^\delta (x_i)=\{x_j\in U:(x_i,x_j)\in {\mathcal {N}}_A^\delta \}\).

Definition 2

[10] Given a decision system \({\mathcal {D}}\), \(\forall A\subseteq AT\) and \(\forall X_p \in U/\text{IND }(d)\), the neighborhood lower and upper approximations of \(X_p\) related to A are defined as:

$$\begin{aligned}&\underline{{{\mathbf {\mathsf{{N}}}}}_A^\delta }(X_p)=\{x_i\in U:{\mathcal {N}}_A^\delta (x_i)\subseteq X_p\}, \end{aligned}$$
(2)
$$\begin{aligned}&\overline{{{\mathbf {\mathsf{{N}}}}}_A^\delta }(X_p)=\{x_i\in U:{\mathcal {N}}_A^\delta (x_i)\cap X_p \ne \emptyset \}. \end{aligned}$$
(3)

Following the basic notions of neighborhood and the corresponding rough set, various forms about attribute reduction have been proposed. Generally speaking, two representative trends of neighborhood rough set related measures are frequently used in defining attribute reductions. Therefore, a formal description of attribute reduction can be given as follows.

Definition 3

Given a decision system \({\mathcal {D}}, \forall A\subseteq AT\), \(\varepsilon \) is a given non-zero measure,

  1. 1.

    if the measure \(\varepsilon \) is expected to be as higher as possible, then A is referred to as a reduct if and only if the following two conditions hold:

    1. (a)

      \(\displaystyle \frac{\varepsilon (A)}{\varepsilon (AT)}\ge \zeta \),

    2. (b)

      \(\forall A' \subset A,\displaystyle \frac{\varepsilon (A')}{\varepsilon (AT)}<\zeta \);

  2. 2.

    if the measure \(\varepsilon \) is expected to be as lower as possible, then A is referred to as a reduct if and only if the following two conditions hold:

    1. (a)

      \(\displaystyle \frac{\varepsilon (AT)}{\varepsilon (A)}\ge \zeta \),

    2. (b)

      \(\forall A' \subset A,\displaystyle \frac{\varepsilon (AT)}{\varepsilon (A')}<\zeta \);

in which \(\zeta \) is a given threshold, \(\varepsilon (A)\) is the value of the measure \(\varepsilon \) determined by A.

Following Def. 3, it can be observed that the reduct A is actually the minimum subset of the condition attributes which will not bring great changes to the considered measure \(\varepsilon \). Up to now, in view of the neighborhood rough set, various measures have been proposed, e.g., approximation quality [10], neighborhood conditional entropy [64], neighborhood conditional discrimination index [40], neighborhood decision error rate [11] and so on. For example, the approximation quality is used to evaluate the degree of certainty in data and then such measure is expected to be as higher as possible; the neighborhood decision error rate is used to estimate the ratio of misclassifications in data and then such measure is expected to be as lower as possible.

2.2 Gap rough set and attribute reduction

Though the neighborhood relation has been widely concerned for its flexibility, the determination or selection of the radius is an open problem. In view of this, Zhou et al. [65] have proposed the gap rough set which can also derive the information granules of samples without assigning the radii. In their approach, the gap based information granulation can automatically select the neighbors for each sample by the surrounding instances distribution. For such a reason, the process of deriving gap information granules is data-adaptive. The detailed notions related to gap information granulation will be shown as follows.

Definition 4

[65] Given a decision system \({\mathcal {D}}, \forall A\subseteq AT\), \(\forall x_i\in U\), the rest of samples are sorted by ascending order based on the distances between these samples and \(x_i\), they are denoted as a set such that \(Dis_A(x_i)\), the width of gap is then denoted as \(Wid_A(x_i)\):

$$\begin{aligned}Dis_A(x_i)=\{x_i^1,x_i^2,\cdots ,x_i^{m-1}\}, \end{aligned}$$
(4)
$$\begin{aligned}Wid_A(x_i)=\frac{\sum _{j=1}^{m-1} \varDelta _A(x_i^j,x_i)}{m-1}, \end{aligned}$$
(5)

in which \(\varDelta _A(x_i,x_i^1)\le \varDelta _A(x_i,x_i^2)\le \cdots \le \varDelta _A(x_i,x_i^{m-1})\).

Following Def. 4, if the distance between two samples \(x_i^j\) and \(x_i^{j+1}\) is bigger than \(Wid_A(x_i)\), it is called a Gap between \(x_i^j\) and \(x_i^{j+1}\) and denoted as \({\mathcal {G}}_A(x_i^j,x_i^{j+1})\).

Definition 5

[65] Given a decision system \({\mathcal {D}}, \forall A\subseteq AT\), \(\forall x_i\in U\), the gap information granule of \(x_i\) over A is defined as:

$$\begin{aligned} {\mathcal {G}}_A(x_i)=\{x_i^k\in Dis_A(x_i):{\mathcal {G}}_A(x_i^{k-1},x_i^k)<Wid_A(x_i),2\le k\le w\} \cup \{x_i\}, \end{aligned}$$
(6)

in which \(w=\min \{t: {\mathcal {G}}_A(x_i^{t-1},x_i^t)\ge Wid_A(x_i),2\le t\le (m-1)\}\).

Definition 6

[65] Given a decision system \({\mathcal {D}}\), \(\forall A\subseteq AT\) and \(\forall X_p \in U/\text{IND }(d)\), the gap lower and upper approximations of \(X_p\) related to A are defined as:

$$\begin{aligned}&\underline{{{\mathbf {\mathsf{{G}}}}}_A}(X_p)=\{x_i\in U:{\mathcal {G}}_A(x_i)\subseteq X_p\}, \end{aligned}$$
(7)
$$\begin{aligned}&\overline{{{\mathbf {\mathsf{{G}}}}}_A}(X_p)=\{x_i\in U:{\mathcal {G}}_A(x_i)\cap X_p \ne \emptyset \}. \end{aligned}$$
(8)

Following Def. 6, Zhou et al. [65] have designed a forward greedy searching for deriving reduct based on gap rough set. The specific steps are shown as follows.

  1. (1)

    The potential reduct red is initialed to be \(\emptyset \).

  2. (2)

    By the considered measure \(\varepsilon \), calculate the measure value \(\varepsilon (AT)\) over AT.

  3. (3)

    \(\forall a\in AT-red\), compute \(\varepsilon (red \cup \{a\})\).

  4. (4)

    Select an appropriate attribute b from \(AT-red\) and add it into red.

  5. (5)

    If the constraint in attribute reduction is fulfilled, then return red; otherwise, go to (3).

2.3 Granular ball rough set and attribute reduction

Besides the gap rough set, Xia et al. [50, 51] have also developed a novel concept called granular ball for adaptively acquiring the information granules of samples. Furthermore, it should be emphasized that the sizes of the information granules in terms of different samples may be different. Such a case also characterizes the internal structure of the samples in some degree.

For Xia et al.’s [50, 51] work, the concept of granular ball mainly involves two phases: (1) the center point; (2) the radius.

Definition 7

[50, 51] Given a decision system \({\mathcal {D}}\), \(\forall A\subseteq AT\), \(\forall {\mathcal {B}}_s\subseteq U\), \({\mathcal {B}}_s\) is a granular ball induced by A in which c is the center point of \({\mathcal {B}}_s\), r is the mean distance among all samples in \({\mathcal {B}}_s\) and the central point c, that is:

$$\begin{aligned}&c=\frac{1}{|{\mathcal {B}}_s|}\sum _{i=1}^{|{\mathcal {B}}_s|}x_i, \end{aligned}$$
(9)
$$\begin{aligned}&r=\frac{1}{|{\mathcal {B}}_s|}\sum _{i=1}^{|{\mathcal {B}}_s|}\varDelta _A(x_i,c), \end{aligned}$$
(10)

in which \(\varDelta _A(x_i,c)\) is the distance between \(x_i\) and the center point c over A.

Following the concept of granular ball, the procedure of generating granular balls can be realized by using the unsupervised learning. For instance, the universe can be gradually partitioned by using 2-meaning clustering [5] until the purities of the granular balls reach the expected values. The details are elaborated as follows.

  1. (1)

    The universe U is regarded as a grouping.

  2. (2)

    Each grouping is divided by 2-means clustering [5].

  3. (3)

    The center point c and the mean distance r are calculated.

  4. (4)

    Obtain granular balls based on the centers and radii of grouping, calculate the purity [50, 51] of each granular ball.

  5. (5)

    If the purity of each granular ball achieves the expected value, then all the granular balls are generated; otherwise, go to step (2).

Based on the above process, the set of all obtained granular balls induced by A is denoted as \({\mathcal {B}}_A\) in the context of this paper.

Definition 8

[50, 51] Given a decision system \({\mathcal {D}}\), \(\forall A\subseteq AT\) and \(\forall X_p \in U/\text{IND }(d)\), the granular ball lower and upper approximations of \(X_p\) related to A are defined as:

$$\begin{aligned}&\underline{{{\mathbf {\mathsf{{B}}}}}_A}(X_p)=\{x_i:\exists {\mathcal {B}}_s\in {\mathcal {B}}_A,x_i\in {\mathcal {B}}_s,{\mathcal {B}}_s\subseteq X_p\}, \end{aligned}$$
(11)
$$\begin{aligned}&\overline{{{\mathbf {\mathsf{{B}}}}}_A}(X_p)=\{x_i:\exists {\mathcal {B}}_s\in {\mathcal {B}}_A,x_i\in {\mathcal {B}}_s,{\mathcal {B}}_s\cap X_p\ne \emptyset \}. \end{aligned}$$
(12)

Following the granular ball rough set shown in Def. 8, an immediate problem is to calculate the corresponding reduct. Therefore, Xia et al. [50, 51] have designed a backward greedy searching for deriving granular ball rough set related reduct. The specific steps are shown as follows.

  1. (1)

    The potential reduct red is initialized to be AT.

  2. (2)

    By the considered measure \(\varepsilon \), calculate the measure value \(\varepsilon (AT)\) over AT.

  3. (3)

    \(\forall a\in AT-red\), compute \(\varepsilon (red-\{a\})\).

  4. (4)

    Select an appropriate attribute b from red and remove it from red.

  5. (5)

    If the constraint in attribute reduction is fulfilled, then return red; otherwise, go to (3).

2.4 Multigranulation rough set and attribute reduction

From the perspective of GrC, the neighborhood rough set, the gap rough set and the granular ball rough set can be regarded as the similar model which is constructed based on one and only one strategy of information granulation. Nevertheless, in many real-world applications, the single information granulation is insufficient to characterize the multi-level or multi-view over data. For such reasons, Qian et al. [32] have developed a framework called MGRS which aims to further expand the applications of rough set. Different from conventional researches, MGRS is constructed based on multiple different information granulations. The following definitions show us two representative models of MGRS.

Definition 9

[32] Given a decision system \({\mathcal {D}}, \forall A\subseteq AT\), \(\forall X_p \in U/\text{IND }(d)\), the optimistic neighborhood multigranulation lower and upper approximations of \(X_p\) related to A are defined as:

$$\begin{aligned} \underline{{{\mathbf {\mathsf{{MG}}}}}_{\sum _{k= 1}^{|A|}a_k}^{Opt}}(X_p)=&\{x_i\in U: {\mathcal {N}}_{a_1}^\delta (x_i)\subseteq X_p\vee \dots \vee {\mathcal {N}}_{a_{|A|}}^\delta (x_i)\subseteq X_p\}, \end{aligned}$$
(13)
$$\begin{aligned} \overline{{{\mathbf {\mathsf{{MG}}}}}_{\sum _{k=1}^{|A|}a_k}^{Opt}}(X_p)=&\sim \underline{{{\mathbf {\mathsf{{MG}}}}}_{\sum _{k= 1}^{|A|}a_k}^{Opt}}(\sim X_p), \end{aligned}$$
(14)

in which \(\sim X_p\) is the complement of \(X_p\).

Definition 10

[32] Given a decision system \({\mathcal {D}}, \forall A\subseteq AT\), \(\forall X_p \in U/\text{IND }(d)\), the pessimistic neighborhood multigranulation lower and upper approximations of \(X_p\) related to A are defined as:

$$\begin{aligned} \underline{{{\mathbf {\mathsf{{MG}}}}}_{\sum _{k=1}^{|A|}a_k}^{Pes}}(X_p)=&\{x_i\in U: {\mathcal {N}}_{a_1}^\delta (x_i)\subseteq X_p\wedge \dots \wedge {\mathcal {N}}_{a_{|A|}}^\delta (x_i)\subseteq X_p\}, \end{aligned}$$
(15)
$$\begin{aligned} \overline{{{\mathbf {\mathsf{{MG}}}}}_{\sum _{k=1}^{|A|}a_k}^{Pes}}(X_p)=&\sim \underline{{{\mathbf {\mathsf{{MG}}}}}_{\sum _{k=1}^{|A|}a_k}^{Pes}}(\sim X_p). \end{aligned}$$
(16)

Following the definitions of optimistic and pessimistic MGRS, some crucial measures related to rough set can also be generalized, e.g., approximation quality, conditional entropy, etc. Following these measures, the problem of attribute reduction then can be addressed over such two MGRS. The following Algorithm 1 shows us the detailed process of searching MGRS related reduct.

figure a

The above algorithm shows us the procedure of deriving reduct if the measure \(\varepsilon \) is expected to be as higher as possible. Similarly, if the measure is expected to be as lower as possible, then the terminal condition in Algorithm 1 should be replaced by \(\displaystyle \frac{\varepsilon (AT)}{\varepsilon (red)}<\zeta \).

In Algorithm 1, it is not difficult to observe that each candidate attribute in \(AT-red\) is required to be evaluated. In the worst case, all the conditional attributes must be added into the reduct. Therefore, the number of all iterations is \((|AT|+(|AT|-1)+(|AT|-2)+\cdots +1)\). In addition, in the process of calculating the value of measure, the samples in the whole universe U should be scanned and any two samples in U should be compared. In summary, the number of iterations required in Algorithm 1 is \(|U|^2\times (|AT|+(|AT|-1)+(|AT|-2)+\cdots +1)\), i.e., the time complexity of Algorithm 1 is \({\mathcal {O}}(|U|^{2}\times |AT|^{2})\).

3 Attribute reduction based on Triple-G MGRS

3.1 Triple-G MGRS

In Sect. 2.4, it is not difficult to observe that such two MGRS models take one and only one form of the information granulation into account, which can characterize the rough set related uncertainties. This is mainly because the process of deriving neighborhood relation is unique though different attributes have been employed. For such reason, we can observe that the MGRS shown in Defs. 9 and 10 do not comprehensively grasp the fundamental principle of multi-view which is the core in the theory of GrC.

Fortunately, following what have been addressed in Sect. 2, besides the neighborhood based information granulation which heavily depends on the value of the radius, two state-of-the-art data-adaptive information granulations have been presented. Therefore, to further characterize the uncertainty from multi-view in the framework of MGRS, both the neiGhborhood rough set, Gap rough set and Granular ball rough set will be simultaneously used for constructing MGRS, such type of the rough set will be referred to as the Triple-G MGRS. The following definition shows us two representative models of Triple-G MGRS.

Definition 11

Given a decision system \({\mathcal {D}},\forall A\subseteq AT\), \(\forall X_p \in U/\text{IND }(d)\), the Triple-G optimistic lower and upper approximations of \(X_p\) related to A are defined as:

$$\begin{aligned} \underline{{{\mathbf {\mathsf{{TG}}}}}_A^{Opt}}(X_p)&=\{x_i\in U: {\mathcal {N}}_A^\delta (x_i)\subseteq X_p\vee {\mathcal {G}}_A(x_i)\subseteq X_p\vee \nonumber \\&{\mathcal {B}}_s\subseteq X_p \text{ where } {\mathcal {B}}_s\in {\mathcal {B}}_A \text{ and } x_i\in {\mathcal {B}}_s\}, \end{aligned}$$
(17)
$$\begin{aligned} \overline{{{\mathbf {\mathsf{{TG}}}}}_A^{Opt}}(X_p)&=\sim \underline{{{\mathbf {\mathsf{{TG}}}}}_A^{Opt}}(\sim X_p). \end{aligned}$$
(18)

Theorem 1

Given a decision system \({\mathcal {D}},\forall A\subseteq AT\), \(\forall X_p \in U/IND (d)\), we have

$$\begin{aligned} \begin{aligned} \overline{{{\mathbf {\mathsf{{TG}}}}}_A^{Opt}}(X_p)&=\{x_i\in U: {\mathcal {N}}_A^\delta (x_i)\cap X_p \ne \emptyset \wedge {\mathcal {G}}_A(x_i)\cap X_p \ne \emptyset \\&\quad \wedge {\mathcal {B}}_s\cap X_p \ne \emptyset {\hbox { where }} {\mathcal {B}}_s\in {\mathcal {B}}_A{\hbox { and }}x_i\in {\mathcal {B}}_s\}. \end{aligned} \end{aligned}$$
(19)

Proof

By Def. 11, we have

$$\begin{aligned} x\in \overline{{{\mathbf {\mathsf{{TG}}}}}_A^{Opt}}(X_p)&\Leftrightarrow x\notin \underline{{{\mathbf {\mathsf{{TG}}}}}_A^{Opt}}(\sim X_p)\\&\Leftrightarrow {\mathcal {N}}_A^\delta (x_i)\nsubseteq (\sim X_p)\wedge {\mathcal {G}}_A(x_i)\nsubseteq (\sim X_p)\wedge {\mathcal {B}}_s\nsubseteq (\sim X_p)\\&\quad ~ \text{ where } {\mathcal {B}}_s\in {\mathcal {B}}_A \text{ and } x_i\in {\mathcal {B}}_s\\&\Leftrightarrow {\mathcal {N}}_A^\delta (x_i)\cap X_p \ne \emptyset \wedge {\mathcal {G}}_A(x_i)\cap X_p \ne \emptyset \wedge {\mathcal {B}}_s\cap X_p \ne \emptyset \\&\quad ~ \text{ where } {\mathcal {B}}_s\in {\mathcal {B}}_A \text{ and } x_i\in {\mathcal {B}}_s. \end{aligned}$$

\(\square \)

By Theorem 1, we can observe that though the Triple-G optimistic upper approximation is defined by the complement of the Triple-G optimistic lower approximation, it can also be considered as a set, in which samples have non-empty intersection with the target in terms of each used information granulation.

Definition 12

Given a decision system \({\mathcal {D}},\forall A\subseteq AT\), \(\forall X_p \in U/\text{IND }(d)\), the Triple-G pessimistic lower and upper approximations of \(X_p\) related to A are defined as:

$$\begin{aligned} \underline{{{\mathbf {\mathsf{{TG}}}}}_A^{Pes}}(X_p)&=\{x_i\in U: {\mathcal {N}}_A^\delta (x_i)\subseteq X_p\wedge {\mathcal {G}}_A(x_i)\subseteq X_p\nonumber \\&\quad \wedge {\mathcal {B}}_s\subseteq X_p \text{ where } {\mathcal {B}}_s\in {\mathcal {B}}_A \text{ and } x_i\in {\mathcal {B}}_s\}, \end{aligned}$$
(20)
$$\begin{aligned} \overline{{{\mathbf {\mathsf{{TG}}}}}_A^{Pes}}(X_p)&=\sim \underline{{{\mathbf {\mathsf{{TG}}}}}_A^{Pes}}(\sim X_p). \end{aligned}$$
(21)

Theorem 2

Given a decision system \({\mathcal {D}},\forall A\subseteq AT\), \(\forall X_p \in U/IND (d)\), we have

$$\begin{aligned} \begin{aligned} \overline{{{\mathbf {\mathsf{{TG}}}}}_A^{Pes}}(X_p)&=\{x_i\in U: {\mathcal {N}}_A^\delta (x_i)\cap X_p \ne \emptyset \vee {\mathcal {G}}_A(x_i)\cap X_p \ne \emptyset \\&\vee {\mathcal {B}}_s\cap X_p \ne \emptyset {\hbox { where }} {\mathcal {B}}_s\in {\mathcal {B}}_A{\hbox { and }}x_i\in {\mathcal {B}}_s\}. \end{aligned} \end{aligned}$$
(22)

Proof

The proof of Theorem 2 is similar to that of Theorem 1.\(\square \)

Similar to Defs. 9 and 10, the structures of MGRS shown in Defs. 11 and 12 are preserved, i.e., one sample belongs to the Triple-G optimistic lower approximation if and only if at least one type of the information granule related to such sample is contained in the target, one sample belongs to the Triple-G pessimistic lower approximation if and only if all the information granules related to such sample are contained in the target. Nevertheless, it must be pointed out that different from previous MGRS, our new Triple-G MGRS uses multiple different mechanisms for performing information granulation and then derive the information granules for constructing rough sets.

Similar to Algorithm 1, we can also design the following Algorithm 2 for searching reduct based on Triple-G MGRS.

figure b

Similar to Algorithm 1, if the measure is expected to be as lower as possible, then the terminal condition in Algorithm 1 should be replaced by \(\displaystyle \frac{\varepsilon (AT)}{\varepsilon (red)}<\zeta \).

By observing Algorithm 2, in the worst case, all the conditional attributes must be added into the reduct. Therefore, the number of iterations is \((|AT|+(|AT|-1)+(|AT|-2)+\cdots +1)\). In addition, the lower approximations should be obtained by the neighborhood, gap and granular ball based information granulations simultaneously, it follows that in the calculation of the value of measure, the required number of iterations is \((|U|^2+|U|\times |{\mathcal {B}}_{AT}|+|U|^2)\). In summary, the number of iterations in Algorithm 2 is \((|U|^2+|U|\times |{\mathcal {B}}_{AT}|+|U|^2)\times (|AT|+(|AT|-1)+(|AT|-2)+\cdots +1)\), i.e., the time complex of Algorithm 2 is \({\mathcal {O}}(|U|^2\times |AT|^2)\).

3.2 Attribute reduction based on Triple-G MGRS with attribute grouping

As what can be observed in Sect. 3.2, the number of iterations used in Algorithm 2 is greater than that is required in Algorithm 1, this is mainly because both the strategies of gap and granular ball are further introduced into the process of information granulation. From this point of view, Algorithm 2 may be very time-consuming and then the quick searching has become a necessary.

Presently, in the field of rough set, various acceleration strategies [7, 13] have been proposed for speeding up the procedure of searching reduct. Most of them can be roughly grouped into two phases: (1) accelerator based on the perspective of sample; (2) accelerator based on the perspective of attribute. For example, the bucket [26] and positive approximation [31] are two typical representations of the sample based accelerators, the attribute grouping [3] is the typical representation of the attribute based accelerator. Through comparing these state-of-the-art accelerators, it can be observed that Chen et al.’s [3] attribute grouping based accelerator is superior to the sample based accelerators. This is mainly because most of the sample based accelerators are vulnerable to the distribution of the samples. For instance, the bucket will be useless if the samples are extremely concentrated.

From discussions above, for further speeding up the searching of Triple-G MGRS related reduct, the attribute grouping will be introduced into Algorithm 2. Fundamentally, the essence of attribute grouping is to partition the raw set of the condition attributes into different groupings, it follows that attributes in those groupings which contain at least one attribute in the potential reduct will not be evaluated. Such a mechanism will significantly reduce the times of evaluating candidate attributes and then the elapsed time of calculating reduct can be saved. Immediately, the following Algorithm 3 will be designed.

figure c

In Algorithm 3, if all condition attributes are divided into \(q(1<q<|AT|)\) groupings, then the numbers of attributes in those q groupings are \(|AT_1|, |AT_2|,\cdots , |AT_q|\), respectively, i.e., \(|AT_1|+|AT_2|+\cdots+|AT_q|=|AT|\). Therefore, in the “While” loop, the number of iterations is \((|AT|+(|AT|-|AT_1|)+(|AT|-|AT_1|-|AT_2|)+\cdots +1)\). Moreover, both Algorithm 2 and Algorithm 3 require the same number of iterations in the step of calculating the value of measure, i.e., \((|U|^2+|U|\times |{\mathcal {B}}_{AT}|+|U|^2)\). Finally, the number of iterations in Algorithm 3 is \((|U|^2+|U|\times |{\mathcal {B}}_{AT}|+|U|^2)\times (|AT|+(|AT|-|AT_1|)+(|AT|-|AT_1|-|AT_2|)+\cdots +1)\), i.e., the time complexity of Algorithm 3 is \({\mathcal {O}}(|U|^2\times |AT|^2)\). Though the time complexity of Algorithm 3 is the same as that of Algorithm 2, it must be pointed out that such a case can only be observed if each grouping contains only one attribute. In most of the cases, we can set \(|AT_q|\ge 1\), then \((|AT|+(|AT|-1)+(|AT|-2)+\cdots +1)\ge (|AT|+(|AT|-|AT_1|)+(|AT|-|AT_1|-|AT_2|)+\cdots +1)\) holds, it follows that the number of iterations used in Algorithm 3 is less than or equal to that used in Algorithm 2.

4 Experiments

4.1 Data sets

To demonstrate the effectiveness of our proposed algorithms, experimental comparisons will be conducted in the context of this section. All experiments will be carried out on a personal computer with Windows 10, Intel Core(TM) i5-4210U (2.60 GHz) and 8.00 GB memory. The programming language is Matlab R2018a. Moreover,

20 UCI data sets have been selected to conduct the experiments. The details of these data sets are shown in the following Table 1.

Table 1 Data sets description
Full size table

Besides Algorithms 1–3 which have been explored in this paper, the algorithms related to gap and granular ball rough sets for calculating reducts will also be tested in this section. Since Algorithms 1–3 should be performed by inputting the radius and then in our experiments, 20 different radii such as 0.02, 0.04, \(\cdots \), 0.40 are selected with the step size of 0.02.

Notably, in our experiments, the K-means clustering is adopted to generate attribute groups. The value of K is set to be \(K = \lceil |AT|/3\rceil \) based on numerous previous testings.

4.2 Comparisons of classification accuracy

In this subsection, 10-fold cross-validation [6, 27] is used to calculate the reducts by using different algorithms. That is, we divide each data set into 10 parts with the same size, they are denoted by \(U_1,U_2,\cdots , U_{10}\). For the first round of computation, \(U_1\cup \cdots \cup U_9\) is considered as the set of training samples for deriving reduct and then \(U_{10}\) is regarded as the set of testing samples for obtaining the classification accuracy related to such obtained reduct; \(\cdots \); for the last round of computation, \(U_2\cup \cdots \cup U_{10}\) is considered as the set of training samples for deriving reduct and then \(U_1\) is regarded as the set of testing samples for obtaining the classification accuracy related to such obtained reduct. Immediately, the average classification accuracies related to different reducts can be obtained.

It must be pointed out that since 20 different radii have been selected for calculating reducts through using Algorithms 1–3, the following Tables 2 and 3 show us the maximal values of classification accuracies which are selected from the results related to such 20 radii. Tab. 2 is based on the KNN \((k=3)\) [2] classifier while Table 3 is based on the SVM (libSVM) classifier [1]. And in our experiments, \(\zeta =0.95\).

Table 2 Maximal classification accuracies based on KNN classifier (higher accuracies are indicated in bold)
Full size table
Table 3 Maximal classification accuracies based on SVM classifier (higher accuracies are indicated in bold)
Full size table

In Tables 2 and 3,

  1. 1.

    “Algorithm 1(O)” indicates the result of attribute reduction based on optimistic classical MGRS through using Algorithm 1;

  2. 2.

    “Algorithm 1(P)” indicates the result of attribute reduction based on pessimistic classical MGRS through using Algorithm 1;

  3. 3.

    “Algorithm 2(O)” indicates the result of attribute reduction based on optimistic Triple-G MGRS through using Algorithm 2;

  4. 4.

    “Algorithm 2(P)” indicates the result of attribute reduction based on pessimistic Triple-G MGRS through using Algorithm 2;

  5. 5.

    “Algorithm 3(O)” indicates the result of attribute reduction based on optimistic Triple-G MGRS through using Algorithm 3;

  6. 6.

    “Algorithm 3(P)” indicates the result of attribute reduction based on pessimistic Triple-G MGRS through using Algorithm 3;

  7. 7.

    “Gap” indicates the result of attribute reduction based on gap rough set;

  8. 8.

    “GB” indicates the result of attribute reduction based on granular ball rough set.

Therefore, it is not difficult to observe the following.

  1. 1.

    No matter optimistic or pessimistic case is considered, compared with classical MGRS, gap and granular ball rough sets, the reduct obtained by using our Triple-G MGRS can provide higher classification accuracies. Take the “Parkinson Multiple Sound Recording” data set as an example, in Table 2, the classification accuracy derived from the reduct related to optimistic Triple-G MGRS is 0.7003, it is superior to the classification accuracy derived from the reduct related to classical optimistic MGRS, i.e., 0.6847, it is also superior to the classification accuracies derived from the reducts related to both gap and granular ball rough sets, i.e., 0.6630 and 0.6084. Furthermore, take the “Forest Type Mapping” data set as an example, in Table 3, the classification accuracy derived from the reduct related to pessimistic Triple-G MGRS is 0.8929, it is superior to the classification accuracy derived from the reduct related to classical pessimistic MGRS, i.e., 0.4856, it is also superior to the classification accuracies derived from the reducts related to both gap and granular ball rough sets, i.e., 0.8164 and 0.6693.

  2. 2.

    By comparing with Algorithm 2, though Algorithm 3 is designed based on the consideration of accelerating of the process of calculating Triple-G based MGRS reduct, such improved algorithm can also offer well-matched classification performances. Take the “Cardiotocography” data set and the optimistic model as an example, in Table 2, the classification accuracy derived from the reduct related to Algorithm 3 is 0.8045 while the classification accuracy derived from the reduct related to Algorithm 2 is 0.8024. Furthermore, Take the “Statlog (Heart)” data set and the pessimistic model as an example, in Table 3, the classification accuracy derived from the reduct related to Algorithm 3 is 0.8333 while the classification accuracy derived from the reduct related to Algorithm 2 is 0.8307.

  3. 3.

    From discussions above, we can conclude that the reducts derived by using our optimistic(pessimistic) Triple-G MGRS are better than the reducts derived by using optimistic(pessimistic) classical MGRS, gap and granular ball rough sets because higher classification abilities can be achieved.

Furthermore, to compare the above algorithms from the viewpoint of statistic, the Wilcoxon signed rank test [4] is employed. Note that the significant level is set as 0.05, that is, if the returned p-value is lower than 0.05, then it indicates that algorithms perform significantly different. The detailed results are shown in the following Table 4 and the italic portion is the data with a p-value greater than 0.05.

Table 4 p-values for comparing classification accuracies based on different reducts
Full size table

\(\divideontimes \) In Table 4, the value “NaN” indicates that the classification accuracies related to the two comparison algorithms over 20 different radii are exactly the same. Therefore, the value of Wilcoxon signed rank test is incalculable.

With a deep investigation of Table 4, it is not difficult to observe the follows.

  1. (1)

    No matter optimistic or pessimistic case is considered, there is a great difference between the classification accuracies obtained by reducts related to our Algorithms 2–3 and those obtained by reducts related to conventional MGRS, gap and granular ball rough sets. Take “Yeast” data set as an example, whether the optimistic or pessimistic case is used, all of the corresponding p-values are lower than 0.05. Furthermore, by combing with the observations over Tables 2–3, we can conclude that our proposed model does provide reducts which can significantly improve the classification performances.

  2. (2)

    In our Triple-G model, there is a great difference between the classification accuracies obtained by reduct related to our pessimistic case and that obtained by reduct related to optimistic case. For example, when the Algorithm 2 and Algorithm 1 are compared, over 20 data sets, the p-values of 4 data sets are greater than 0.05 in optimistic case. Similarly, the p-value of all the data sets are lower than 0.05. Furthermore, by combing with the observations over Tables 2–3, we can conclude that our proposed model in the pessimistic case can improve the classification performance better.

4.3 Comparisons of elapsed time

In this experiment, the elapsed time of obtaining reduct by using two different algorithms in optimistic and pessimistic cases will be compared.

Fig. 2
figure 2figure 2figure 2

The elapsed time of deriving reducts

Full size image

With a deep investigation of Fig. 2, it is not difficult to observe the follows.

  1. (1)

    In most cases, by comparing with optimistic Triple-G MGRS, the pessimistic Triple-G MGRS requires more elapsed time for deriving reduct. Take “Dermatology” data set as an example, in Fig. 2, if \(\delta = 0.2\), the elapsed time of obtaining reduct related to pessimistic Triple-G MGRS is 11.9529 s, it is superior to the elapsed time of obtaining reduct related to optimistic Triple-G MGRS, i.e., 4.5848 s.

  2. (2)

    By comparing with Algorithm 2, Algorithm 3 is designed based on the consideration of accelerating the process of obtaining reduct by Triple-G MGRS. Therefore, such improved algorithm can significantly reduce the elapsed time of obtaining reduct. Take “Waveform Database Generator(Version 1)” data set as an example, in Fig. 2, if \(\delta = 0.2\), the elapsed time of obtaining reducts related to optimistic and pessimistic Triple-G MGRS, i.e., 680.0876 and 869.5392 s, it is superior to the elapsed time of obtaining reducts related to optimistic and pessimistic Triple-G MGRS with attribute grouping, i.e., 442.3297 and 353.2678 s.

  3. (3)

    From discussions above, we can conclude that the time consumption of obtaining reduct will be effectively reduced by introducing the acceleration mechanism. Furthermore, through combing the analyses shown in both Sects. 4.2 and 4.3, either optimistic or pessimistic case is considered, the improved Algorithm 3 can effectively reduce the time consumption of obtaining reduct without reducing the classification performance.

5 Conclusions and future perspectives

In the field of researching MGRS, to characterize the uncertainty of the target in terms of multi-view based heterogeneous information granulation, a Triple-G MGRS is developed. Different from previous models, our proposed model is actually constructed by using both the parameterized and data-adaptive information granulations. Therefore, our Triple-G MGRS presents not only the principle of multi-view, but also the mechanism of heterogeneous information granulation. Additionally, by considering the efficiency of searching Triple-G MGRS based reduct, an acceleration strategy called attribute grouping is introduced into the procedure of forward greedy searching. The experimental results have not only demonstrated the effectiveness of our new model in terms of the classification ability, but also verified the effectiveness of our accelerator for quickly deriving reduct. The following topics deserve our further investigations.

  1. (1)

    In this paper, we have only used three neighborhood related techniques for realizing heterogeneous information granulation, diversified forms for obtaining information granulations will be further selected and used in our future study.

  2. (2)

    Though the attribute grouping strategy can significantly reduce the time consumption of obtaining our Triple-G MGRS based reduct, such accelerator is only designed based on the perspective of sample, it can be further improved by combining both the sample and attribute based perspectives.