hier2vec: interpretable multi-granular representation learning for hierarchy in social networks

Abstract

Network representation learning (NRL) maps vertices into latent vector space for further network inference. The existing algorithms concern more about whether the vectors of two similar nodes be close in latent vector space while the hierarchy proximity has been largely neglected by them. The distribution of the representation vectors needs to reflect the hierarchical structural properties which widely exist in networks. In this paper, we propose a novel network representation learning framework that can encode the interpretable hierarchical structural semantics into the representation vectors. Specifically, we measure the distance and importance degree of nodes in the original network and map the nodes to a tree space. This makes the hierarchical structural relations in the original network be clearly revealed by the tree which is also of good interpretability. In this paper, the local structural proximities and the interpretable hierarchy knowledge are encoded into vector space by optimizing the objective function. Extensive experiments conducted on the realistic data sets demonstrate that the proposed approach outperforms the existing state-of-the-art approaches on tasks of node classification, link prediction, and visualization. Finally, a case study is conducted for further analysis about how the proposed model works.

1 Introduction

Networks have wide applications on revealing the properties of relational objects [1,2,3]. Recently, network representation learning, also known as network embedding (NE) [4, 5], seeks to learn representations that encode the similarity between nodes (e.g. neighborhoods [6, 7], node attributes [8] and labels [9, 10]) in the original network. Representation learning approaches for machine learning on graphs offer a powerful alternative to traditional feature engineering. These approaches have consistently pushed the state of the art on tasks such as node classification, link prediction, community detection, etc. [5]. On the other hand, the communities in networks often compose a hierarchical organization, with communities embedded within other communities [11, 12]. This nesting property of communities is called the hierarchy that is ubiquitous in real networks [13]. Revealing the hierarchy knowledge about networks can help us learn about them on different granularity and handle the problems caused by the high complexity and the huge scale of networks [14]. However, the hierarchy in networks is paid less attention to. Simply doing the hierarchical clustering on the representation vectors fails to reveal the hierarchy of nodes because they concern more about the similarity between nodes rather than the hierarchical structural relationships. NRL algorithm focuses too much on local connection characteristics and fails to capture the hierarchy in the network. This can cause problems such as that shown in Fig. 1. The graph of network contains nodes of two classes, i.e. ‘class a’ (orange) and ‘class b’ (blue). NRL algorithm A focuses more on local connections and the edges (0,1) and (0,2) in the original graph have more influence on node ‘0’ than the edge (0,3). This makes the representation vector of node ‘0’ be closer with those of node ‘1’ and ‘2’ in latent vector space and node ‘0’ is finally classified into ‘class a’ through algorithm A. Nevertheless, of all the nodes with degrees larger than node ‘0’, node ‘5’ is the closest to it. If we consider the hierarchy in the original graph in algorithm B, as the graph shown in Fig. 1, we can establish a red dashed line representing the effect of node ‘5’ on node ‘0’. This can lead to classifying node ‘0’ into ‘class b’ in the end.

Fig. 1

The failure of modeling hierarchy in networks causes different classification results (Zoom for better view)

Tree structures play an important role in machine learning and statistics [15]. Learning a tree structure over data points gives a straightforward picture of how objects of interest are related. Trees are easily interpreted and intuitive to represent the hierarchy in data. Sometimes we may know that there is a true hierarchy underlying the data. For example, species in the tree of life or duplicates of genes in the human genome, known as paralogs [16]. In 2016, Xu et al. proposed a leading tree granular computing model, called DenPEHC [17]. Based on the density calculation given by Eq. 1, DenPEHC clearly separates the data points into different granular levels and reveals the hierarchy of the distributions of data by a tree structure (called leading tree). In the leading tree, a node has more child nodes means it is at the center of a community. Assume there is a set of data points distributed in 2-dimensional space, shown in Fig. 2a. We can obtain the leading tree via the distribution of samples, shown in Fig. 2b. In that tree, the node ‘10’ is at the root of the tree while the node ‘13’ is leading a subtree in green. It means that the node ‘10’ acts as the center of the entire community and the node ‘13’ acts as the center of a sub-community, which is at a lower granular level. We can even see the blue nodes, ‘19’ and ‘20’ can be split into the smaller community at a lower granular level than that of green nodes. Thus, the hierarchy revealed by in Fig. 2b matches the real distribution of sample points in Fig. 2a.

$$\begin{aligned} \rho _i = \sum _{j\in I\setminus \{i\}} e^{-\left( \frac{d_{i,j}}{d_c}\right) ^2} \end{aligned}$$

(1)

In Fig. 3, the original graph (Fig. 3a) is a relationship graph for the member of a karate club. Zachary et al. collected this data set [18]. They used these data and an information flow model for network conflict resolution to explain the split-up of this group following disputes among the members. In that graph, the person represented by node ‘33’ is the founder of whole community while the node ‘0’ is the core member of a split new community. The original graph (Fig. 3a) is represented in vectors (Fig. 3b) by local approximation preserving NRL, i.e. LINE, and the Fig. 3c shows the leading tree (which can be seen as a directed graph) that generated by representation vectors and thus extracting the hierarchy implicit in the distribution of the vectors. In Fig. 3a, the node ‘0’ is the center of a community. However, the Fig. 3c shows the node ‘0’ has no child node and its parent node is ‘12’. This means that node ‘12’ is a point that is more at the center of the community than node ‘0’, which clearly contradicts the reality. On the other hand, if the hierarchy in the original network is followed, using the method of this paper, a leading tree can be generated as shown in Fig. 3d and the contradiction is resolved. It indicates that the distribution of the representation vectors obtained by local structural approximation preserving NRL fails to represent the hierarchy of nodes in the original graph.

Fig. 2

From sample data points to its leading tree

Fig. 3

The leading tree generated from representation vectors (Zoom for better view)

This paper proposes a framework of interpretable multi-granular representation learning (hier2vec) which builds an interpretable multi-granular tree on the original graph structure and embeds the multi-granular semantic knowledge of hierarchy revealed by the leading tree to the representation vectors. In this way, the representation vectors encode not only the local linkage semantic but also the global multi-granular hierarchy semantic knowledge. The extensive experiments conducted on several networks demonstrate that the proposed approach is effective and it outperforms the existing state-of-the-art approaches on a variety of tasks, including node classification, link prediction, and node visualization.

The main contributions of this paper are summarized as follows.

• (1) This work embeds the multi-granular hierarchy knowledge into the representation vectors by using an interpretable model of the leading tree. This ameliorates the lack of interpretability of representation learning for the hierarchy in network.

• (2) It makes up for the fact that the traditional network representation learning only pays attention to the local structural similarity but ignores the global multi-level structural characteristics.

• (3) The multi-granularity hierarchical clustering model on Euclidian space is extended to graph data mining so that the structure on the graph can be intuitively displayed.

The remainder of this paper is organized as follows. In Sect.  2, related backgrounds of the proposed method are given. Section 3 gives the problem definition and formulation in hier2vec, while Sect. 4 deals with detailed descriptions of the proposed algorithm. Experimental results are analyzed in Sect. 5, and finally, we summarize in Sect. 6 with conclusions and future work.

2 Related works

2.1 Multi-granularity computing

Multi-granularity computing is a concept of intelligent computing which simulate the cognition law of human for solving the complex problems. It is an umbrella term to cover any theories, methodologies, techniques, and tools that departs and solve the complex problems on multi-scale, multi-complexity, multi-size, multi-resolution, etc. [19]. Multi-granularity computing (MGrC) emphasizes on jointly utilizing multiple levels of information granules in problem-solving, instead of only one optimal granular layer [20]. Heimann et al. [21] represents the multi-granular distribution of node embeddings in feature space, which enables the expressively and inductively comparison of graphs. Li et al. [22] propose an axiomatic approach to describe three-way concepts utilizing multi-granularity. By proposing a hierarchical cluster ensemble model, Hu et al. [23] provide a new way for the ensemble learning application of the knowledge granulation. Multi-granular computing has been one of the fastest-growing information-processing paradigms in the domain of computational intelligence.

2.2 Hierarchical clustering and the leading tree

Hierarchical clustering is regarded as a method to construct multi-granular information granules for the original finest-grained data from the perspective of granular computing [17]. The hierarchical clustering divides the data clustering into coarser to finer granule or verse versa. It offers people a good understanding of the distribution of data. Hierarchical clustering methods can be categorized into two types. One type presents a new method or methodology. Bouguettaya et al. improved the efficiency of agglomerative hierarchical clustering by building a hierarchy that was based on a group of centroids rather than raw data points [24]. F. de Morsier et al. propose a new cluster validity measure (CVM) [25] to quantify the clustering performance of hierarchical algorithms that handle overlapping clusters of any shape and in the presence of outliers. D. Knowles et al. introduce the Pitman Yor Diffusion Tree (PYDT), a Bayesian non-parametric prior over tree structures for hierarchical clustering [16]. X. Tang et al. develop some hierarchical clustering problems and analysis for fuzzy proximity relation by using rigorous mathematical descriptions, and an algorithm is obtained to compute the hierarchical clustering structure [26]. Based on the density and distance calculation in [27], Xu et al. [17] propose a method for multi-granular hierarchical clustering (called DenPEHC). By generating a tree structure (i.e. leading tree), the leading tree reveals the hierarchy in the distribution of data. The other type involves combinations and ensembles. Mirzaei et al. presented an algorithm called MATCH to combine multiple dendrograms (the presentation of a hierarchical clustering result) into one unit. This combination is performed by computing the min-transitive closure of the similarity matrices that correspond to the dendrograms to reach an aggregating matrix [28]. Rashedi and Mirzaei proposed a Bob-Hic algorithm to improve the performance of hierarchical clustering, whose key components involve computing the boosting values and updating the weights for objects [29].

2.3 Network representation learning

Network representation learning, also known as network embedding, maps the network instances into a low-dimensional latent vector space [4]. It has aroused a lot of research interest. Based on the representation vectors that preserve the properties of network instances, network analytic tasks can be easily and efficiently carried out by applying conventional vector-based machine learning algorithms. In the early 2000s, the representative works such as IsoMap [30], Locally Linear Embedding (LLE) [31] and Laplacian Eigenmap [32] calculate the similarity between pairwise data points to construct an affinity graph and then represent the affinity graph into a new space having much lower dimensionality. In recent years, the research efforts have shifted to scalable algorithms. The representative models like DeepWalk [33], LINE [7], SDNE [34], GraRep [6] embed the network structural proximities into latent, low-dimensional space while the models like [35, 36], and [37] attach the rich content and side information on attributes. Moreover, for the bipartite attributed networks, Huang et al. [38] model not only the inter-partition proximity but also the intra-partition proximity. Wu et al. [39] consider the information heterogeneity from the attributed networks and propose an algorithm that recursively aggregates the graph structure as well as individual node attributes in network. Those works show remarkable performance for various applications such as node classification, link prediction, community detection, visualization, etc. Nevertheless, the distribution of the representation vectors in latent space is rarely concerned and the hierarchy structural properties should be revealed by the distribution of the representation vectors. The knowledge of hierarchy can be represented as a tree structure and this work try to represent the hierarchy of network by encoding the tree into vector space.

3 Problem formulation

In this section, we define some notations, and the problem formulations for the framework of interpretable representation learning methodologies.

3.1 Definitions

Online social network An online social network is denoted as a graph ${{\mathcal{G}} = (V,E)}$ where ${\mathcal {V}}$ is a set of nodes and each node $v_i \in {\mathcal {V}}$ represents a user account $u_i$. ${\mathcal {E}} \subseteq {{\mathcal{V}} \times {\mathcal{V}}}$ is a set of weighted or unweighted edges, $e_{ij} \in {\mathcal {E}}$ represent the connection between $u_i$ and $u_j$ in social network. We have the binary adjacency matrix ${\mathbf {A}} \in {\mathbb {R}}^{|V|\times |V|}$, and ${\mathbf {A}}_{ij} = 1$ if and only if there exists an edge from $v_i$ to $v_j$.

Network representation learning (NRL) Given a network ${{\mathcal{G}}= (V,E)}$. The goal of Network representation learning is to learn a mapping function $f: v \mapsto {\mathbf {z}} \in {\mathbb {R}}^d$ where ${\mathbf {z}}$ is the learned representation vector, and $d \ll |V|$ is the dimension of ${\mathbf {z}}$. The transformation f preserves the original network information, such that two nodes similar in the original network should also be represented similarly in the learned vector space.

The granule in graph Each graph instance, such as a node or a community, can be taken as an information granule from the perspective of Granular Computing [19]. Given a network ${{\mathcal{G}}= (V,E)}$, in the finest granularity level, we define granule r as the member v in node set ${\mathcal {V}}$ and use R for denoting the set of all granules in this graph.

The distance matrix and importance degree The distance matrix ${\mathbf {D}} \in {\mathbb {R}}^{|R|\times |R|}$. Each element ${\mathbf {D}}_{ij}$ in ${\mathbf {D}}$ is the distance between two granules $r_i$ and $r_j$. ${\mathbf {D}}_{ij}$ is defined as follows:

$$\begin{aligned} {\mathbf {D}}_{ij} = \frac{l_s^{ij}}{\max \{l_s^{11}, l_s^{12}, \dots , l_s^{|R||R|}\}} \end{aligned}$$

(2)

where $l_s^{ij}$ is the length of shortest path between $v_i$ and $v_j$, and $\max (l_s^{ij})$ is the maximum length of shortest path between $v_i \in V$ and $v_j \in V$.

We also define the importance degree $\rho _i$ for granule $r_i$ as follows:

$$\begin{aligned} \rho _i = \frac{n_i}{\max \{n_1, n_2, \dots , n_{|R|}\}} \end{aligned}$$

(3)

where $n_i$ is the degree of node $v_i$.

This is one way of the generation of distance and importance degree. However, the original graph can contain different styles of the relationship of distance. We can even take multiple nodes as one granule and the distance between granules can be calculated by the similarity of multi-nodes granules.

3.2 The graph leading tree

The graph leading tree is a tree that contains $r_i \in R$ as its node and $(r_i,r_j)$ as its edge. The graph leading tree can be viewed as a graph ${{\mathcal{G}}_{LT}= (V_{LT},E_{LT})}$. The $(r_i, r_j) \in {\mathcal {E}}_{LT}$ represent the leading from the granule $r_i$ to granule $r_j$ while the granule $r_j$ is the parent of $r_i$. In the model of DenPEHC [17] and generalized leading tree [40], each granule in graph can be assigned by one parent granule except the root node in that tree. We will discuss how the parent granule is assigned in Sect.  4, and how does the graph leading tree contribute to the revealing of the hierarchy in network.

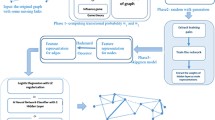
4 The hier2vec model

The hier2vec model is shown in Fig. 4. The original network can yield multiple graph leading trees on different granularities. All the leading trees will be merged into one leading tree and feed into a comparator for optimization. On the other side, the initial representation vectors are obtained by representation learning on local structural proximities. The final representation vectors are obtained by optimizing the objective function in the comparator.

Fig. 4

The framework of hier2vec model

4.1 The generation of graph leading tree

For any object, or granule, we define its importance degree and its distance from other granule. With these two elements, we can generate a tree structure. This tree structure will reveal the membership and hierarchy of all granule classes in a set. This tree structure will form a general lead tree and it’s not limited to data points in Euclidean space. Based on this argument, we defined the distance and importance degree for granule in graph. For granule $r_i$, we can select its parent $r_j$ from the set R. R is the set of all granules defined in Sect. 3. We can denote the process of assigning the parent node for granule $r_i$ as a mapping of $\varPsi : r_i \mapsto r_j$:

$$\begin{aligned} \varPsi (r_i) = r_j \;\; \mathrm {if} \;\; {\mathbf {D}}_{ij} = \min \{{\mathbf {D}}_{ij}: j \in R_{higher}^i \} \end{aligned}$$

(4)

where $R_{higher}^i := \{ r_k : \rho _k > \rho _i \; \forall \;r_k \in R \}$

Once the parent node for each granule is assigned, the graph leading tree ${{\mathcal{G}}_{LT}}$ is generated. Under different scope of granularities, we can obtain multiple ${{\mathcal{G}}_{LT}}$s, and the ${{\mathcal{G}}_{LT}}_{merge}$ can be obtained by merging all the edges in set of ${{\mathcal{G}}_{LT}}$s.

4.2 Interpretable hierarchical semantic

This subsection will discuss how does the leading tree reveals the hierarchical semantic in an interpretable way. Figure 5 shows the original graph and the graph leading tree generated from that graph. In the original graph, Figure 5a, we can find there are two main communities leader, i.e. node ‘32/33’ and ‘0’. The node ‘33’ has the biggest importance degree as the definition. It’s believed that the ‘33’ is the center of the whole graph while the node ‘0’ is the center of a smaller community at the right-bottom of the original graph. In the perspective of granular computing, there are at least two granular layers. In the coarsest layer, the graph is one community with ‘33’ as the center; in the finer layer, the graph consists of two communities lead by ‘32,33’ and ‘0’ respectively. In the graph leading tree, the ‘33’ is the root. This means the whole community is lead by it. The ‘0’ is leading the second large scale of communities and the ‘0’ is lead by ‘32’ while ‘32’ is lead by ‘33’. These hierarchy properties are revealed by the graph leading tree. This instance shows that the graph leading tree reveals the hierarchical semantic of the graph in an interpretable way.

Fig. 5

The graph leading tree reveals the hierarchy

4.3 Representation learning for the hierarchy semantic

The objective of representing the hierarchical semantic in graph is to find a mapping that maps the ${{\mathcal{G}}_{LT}}$ to a set of low-dimensional vectors under some initial conditions. The representation learning process can be denoted as:

$$\begin{aligned} \begin{aligned} \min \varTheta ({\mathbf {X}}_{new})&= \min \limits _{{\mathbf {X}}_{new}} \, \mathrm {Diff}({{\mathcal{G}}_{LT}}_{target}, {{\mathcal{G}}_{LT}}_{new}) \\&\quad + \alpha ||{\mathbf {X}}_{initial} - {\mathbf {X}}_{new}||_F \end{aligned} \end{aligned}$$

(5)

In Eq. 5, we have a given target graph leading tree ${{\mathcal{G}}_{LT}}_{target}$, and an initial set of representation vectors ${\mathbf {X}}_{initial}$ given by the algorithms for encoding the local structural proximities, e.g. LINE [7]. The goal of this algorithm is to find the ${\mathbf {X}}_{new}$ that can generate the ${{\mathcal{G}}_{LT}}_{new}$, and the ${{\mathcal{G}}_{LT}}_{new}$ needs to be as similar as the given target graph leading tree ${{\mathcal{G}}_{LT}}_{target}$. By solving the Eq. 5, the ${\mathbf {X}}_{new}$ can be obtained. Proper representation of the ${{\mathcal{G}}_{LT}}_{target}$ can contain the hierarchy semantic of the original graph in the obtained ${\mathbf {X}}_{new}$. However, directly solving the Eq. 5 poses great challenges because the gradient of the $\varTheta$ function of ${\mathbf {X}}_{new}$ can not be explicitly expressed. One workaround way for approximately solving this problem is to capture the structure of ${{\mathcal{G}}_{LT}}_{target}$ by maximizing the probability of the appearance of context for each node in the graph leading tree.

4.4 Optimization

We consider the direction of the edge as the finest difference of the importance degree for the graph leading tree generation since the being leading node has some information about priority such as one famous movie actor is followed by millions of fans. With this consideration, the graph leading tree can be viewed as a graph and we can encode the structures by maximizing the co-occurrence probability among the granules that appear within a window w. We follow the method [33] and samples a set of paths from the graph leading tree ${{\mathcal{G}}_{LT}}_{target}$ using truncated random walk. The objective function for approximately solving the Eq. 5 can be denoted as:

$$\begin{aligned} \min _{y} -\log P(\{ r_{i-w}, \dots , r_{i-1}, r_{i+1}, \dots , r_{i+w}\}|y_i), \end{aligned}$$

(6)

where w is the window size which restricts the size of random walk context and y is the representation vector for granule r. The Eq. 6 can be transformed to:

$$\begin{aligned} \min _{y} -\log {\sum }_{-w \le j \le w}P(r_{i+j}|y_i), \end{aligned}$$

(7)

where $P(r_{i+j}|y_i)$ is defined using the softmax function:

$$\begin{aligned} P(r_{i+j}|y_i) = \frac{\exp (y_{i+j}^T y_i)}{\sum _{k=1}^{|R|}\exp (y_k^T y_i)}. \end{aligned}$$

(8)

For a node (i.e. $r_i$), we want to distinguish the target node (i.e. $r_{i+j}$) from noise using the logistic regression. A noise distribution $P_n(r_i)$ is designed to draw the negative samples for node $r_i$ [41]. Then, each $\log P(r_{i+j}|y_i)$ in Eq. 8 can be calculated as:

$$\begin{aligned} \log \sigma (y_{i+j}^T y_i)) + \varSigma _{t=1}^{K} E_{r_t \sim P_n(r_i)}[\log \sigma (-y_{r_t}^T y_i)], \end{aligned}$$

(9)

Equation 9 represents the negative sampling process. For each node i, we sample K negative samples $r_t, t = 1, ... , K$ with a probability distribution of $P_n$. The value of K can be set as 2-5 if the number of nodes is larger than thousand. The noise distribution $P_n(r)$ is given by the unigram distribution U(r) raised to the 3/4 power. The time complexity of solving the Eq. 7 is ${\mathcal {O}}(K|R|)$.

From the calculation above, the representation vectors $\{y_i\}_{i=1}^{|R|} \subset {\mathbb {R}}^{\frac{d}{2}}$ for granules $\{r_i\}_{i=1}^{|R|}$ can be obtained and the d is dimension number of the final representation vector ${\mathbf {z}}_i \in {\mathbb {R}}^d$. The representation vectors that encoding the local structural proximities can be obtained by the LINE algorithm [7]. We denote that representation vectors as a set of $\{y'_k\}_{k=1}^{|V|}$. Because at the finest granular level, each node is a granule and the |R| equals |V|. We can obtain the final representation vector ${\mathbf {z}}_i \in {\mathbb {R}}^d$ for the nodes by concatenating the $y_i$ and $y'_i$.

The multi-granular graph trees can be obtained by making the granules that are far from the root granule share the representation vectors with the local root granule they are leading to. By controlling the degree of granule aggregation, we can control the generation of finer or coarser graph tree.

4.5 The hier2vec algorithm

The hier2vec algorithm first generate the target leading tree ${{\mathcal{G}}_{LT}= (V_{LT},E_{LT})}$ by the steps described in algorithm 1. The process of generating the ${{\mathcal{G}}_{LT}}$ is consisted by two steps: (1) generating the distance matrix ${\mathbf {D}}$ by calculating the distances between two nodes, i.e. ${\mathbf {D}}_{ij}$ and (2) assigning the parent for each node i with the mapping described in Eq .4

The Algorithm 1 shows how to obtain the final embedding vectors in hier2vec algorithm. Since the construction of the target tree ${{\mathcal{G}}_{LT}}_{target}$ in Eq. 5 cannot be explicitly expressed by a mathematical formula, we cannot directly optimize the target function Eq. 5 to obtain the embedding vectors. We approximate our initial goal by incorporating the hierarchy information contained in the target graph leading tree into the final embedding. As the Algorithm 1 shown, we treat the target graph leading tree as a graph and do random walk to obtain the node sequence ${\mathcal {S}}_{r_i}$. By optimizing the skip-gram model, the probability of co-occurrence of neighboring nodes in ${\mathcal {S}}_{r_i}$ is as high as possible. Such that the subordination between nodes on the leading tree supports the closeness of representation vectors in the latent feature space. After we obtain the initial vector $\{y'_i\}$, and the $\{y_i\}$, we concatenate them together. This incorporates the hierarchy information into the final node vector expression. Thus, the final expression vector have both the hierarchical structure of the network and the local structural proximity of the original network.

5 Experiments

In this section, the performance of the proposed hier2vec is presented. These results are obtained after conducting several experiments on three realistic social networks. To be convincing, we selected the most representative baseline methods and compared the performance under a wide-used metrics. Finally, a case study is given and discussed to show how hier2vec’s hierarchy knowledge boosts the realistic task of node classification.

5.1 Data sets

In order to verify the effectiveness of the proposed hier2vec model, we use the three publicly available network data sets as described below:

Wiki. Wikipedia is an online encyclopedia created and edited by volunteers around the world. The data set is a word co-occurrence network constructed from the entire set of English Wikipedia pages [42]. This data contains 2405 nodes, 17981 directed edges, and 19 labels.

Cora. The Cora data set [43] consists of 2708 scientific publications of 7 classes. The graph has 5429 links that indicate citation relations between documents. Each document has text attributes that are expressed by a binary-valued vector of 1433 dimensions. We only use its linkages and labels.

blogCatalog. The blogCatalog data set [44] is a social network. Nodes and edges represent the bloggers and the friendship between them respectively. It contains 10312 nodes, 333983 undirected edges, 39 labels.

5.2 Experimental settings

For the task of node classification, we evaluate our method using the same experimental procedure outlined in [33]. A portion of the labeled nodes are randomly picked out under the training ratio (TR) and they are used as training data with the rest being used for testing. The one-vs-rest logistic regression implemented by LibLinear [45] is utilized for node classification task and the Macro-F1 and Micro-F1 scores are reported. There are several parameters for Algorithm 2 that generate the representation vectors. The walk-length parameter ${\mathcal {L}}$ is set to 80 while the number of walks $\eta$ is set to 10 and the window size w is set to 4. The dimension d is set to 256.

5.3 Comparative methods

We compare the proposed hier2vec model with several most representative state-of-the-art methods, which are summarized as follows.

• DeepWalk DeepWalk [33] generates a context window for each node from random walks and adopts SkipGram [46] to model the probability of a node appearing in the context. It then learns node representations by optimizing the SkipGram objective function.

• LINE LINE [7] learns a $\frac{d}{2}$-dimensional representation to preserve first-order proximity (i.e. linked nodes tend to be similar) and another $\frac{d}{2}$-dimensional representation to preserve second-order proximity (i.e. nodes sharing common neighbors tend to be similar) for each node. It produces the final d-dimensional representation for a node by concatenating the two parts.

• node2vec node2vec [47] is a generalization of DeepWalk and uses a biased random walk sampler. The biased sampler can behave like either depth-first search (DFS) or breadth-first search (BFS), depending on its hyper-parameters.

• SDNE SDNE [34] learns a low-dimensional network-structure preserving representation by considering both the first order and the second-order proximities between vertexes using CNNs.

• Graph factorization (GF) GF [48] tries to directly factorize node proximity matrix. Node proximity can be approximated in a low-dimensional space using matrix factorization. The objective of preserving node proximity is to minimize the loss of approximation.

• Laplacian eigenmaps (Lap) LAP [32] technique minimizes a cost function to ensure that points close to each other on the manifold are mapped close to each other in the low-dimensional space to preserve local distances.

• MARINE The MARINE [49] algorithm uses not only graph structure information but also node features to learn the representation vectors. It shows the possibility that combining graph structure information and node attribute information can yield a more robust network embedding model which is suitable for different types of networks. In order to compare the performance, as with hier2vec, only the graph structure information is used to train MARINE. Note that the node attributes are either missing or not disclosed for privacy reasons in many practical cases.

5.4 Node classification

Node classification is to assign a class label to each node in network, based on the rules learned from the labeled nodes. Intuitively, “similar” nodes have the same labels. We conduct this by applying a linear SVM classifier on the set of labeled representation vectors for training. A portion of labeled nodes (i.e. training ratio, TR) is used for training the classifier and the rest of nodes are used for testing. This subsection shows the experiment result obtained by representing vectors learn by the proposed hier2vec algorithm and the other baseline methods. We calculate the precision by micro-F1 and macro-F1 score. The F1 scores on $TR = 0.5$ are proposed in Table 1.

Table 1 The performance of node classification, on three data sets

Table 2 The Micro-F1 scores for node-classification at different TR on blogCatalog

Table 3 The PR AUC scores on task of link prediction

Note that on the data set of Cora, hier2vec fails to outperform the representation learned by GF. We attribute this to that the citation network of Cora data set is quite well behaved. It exhibits highly homophonous behavior. The co-authors guarantee similar attributes and the two authors sharing publications are in very similar research areas. When the edges in the graph indicate a high degree of similarity (it is harder to create spurious edges), the GF’s direct factorizing node proximity matrix can yield high-performance gains. However, GF requires materializing a dense matrix, which is inherently unscalable.

At different training ratio, the Micro-F1 scores obtained by baselines on blogCatalog data set are shown in Table  2. It shows that on the node classification task, the proposed hier2vec algorithm outperforms the baselines.

5.5 Link prediction

Link prediction is one of the most important network inference tasks. It has a wide variety of applications such as predicting the outbreak of a disease, controlling privacy in networks, detecting spam emails, suggesting new friends or merchandise, etc. [50]. Link prediction aims to infer the existence of relationship or interaction among pairs of nodes in a graph. This requires the learned representation to help inferring the graph structure, especially when some links are missing. The learned representation should preserve the network proximity and the structural similarity among nodes. We conduct the link prediction experiment as the same procedure as that of [47] to facilitate the comparison between our method and the relevant baselines. The performance of link prediction is evaluated by the Precision-Recall area under the curve (PR AUC) [51, 52]. To verify the validity of this hier2vec model with different proportions of training samples, we conducted experiments at different TR values. A portion of labeled edges (i.e. training ratio, TR) is used for the training and the rest of edges are used testing. Since unknown links are far more than known ones, we randomly select disconnected edges as negative samples with an equal number of positive samples in both the training and testing phase. For each node pair, we take the average of embeddings of two nodes as the edge feature and then build a Logistic Regression binary classifier based on it using scikit-learn package [53]. The PR AUC scores under different training ratio on three data sets are shown in Table  3.

We can see that hier2vec obtains the higher PR AUC scores than the baselines. To be specific, on the data set of Wiki, our model is about 5% outperform the best performance among the baseline methods. With the increase of the training ratio, the performance improvement decreases slightly (from 5.1 to 4.4%). We attribute this to the greater performance gains obtained with the baseline approach in obtaining a larger percentage of the training sample. On the Cora dataset, the LINE method is a strong competitor to our method. Our hier2vec model only gained 1% performance advantage over it. This is because, as an academic citation network, Cora is very structured. The co-author relationships in academic networks tend to be made up of a very narrow domain of co-professionals. This makes the hier2vec method, which can encode global hierarchical structural properties, less advantageous than the LINE, a method that pays great attention to local structural features. We also found that the baseline approaches did not perform consistently across data sets. For example, LINE can get better performance on the CORA dataset, while not performing as well as SDNE on the Wiki data set. Whereas DeepWalk performs better on the blogCatalog data set and less well on the Cora data set than LINE and SDNE. We believe that, on the task of link prediction, the proposed hier2vec is more stable than the baseline methods on various data sets.

5.6 Visualization of layouts

The visualization that layout a network on a two-dimensional space is also an important application of representation vectors generated by network representation techniques. After the dimension of vectors is reduced, the layout of vectors can reveal the aggregation of nodes. The layout result on the Wiki data set is shown in Fig. 6. Different colors represent nodes belong to different classes.

From Fig. 6, we can see the community structure is mixed up for LINE, SDNE, GF, and Lap. For DeepWalk, node2vec, and hier2vec, the obtained boundaries are more indistinct and some nodes are diffused to other groups at the center of the layout. The layout given by the proposed hier2vec has a more distinctive layout at the center area than deepWalk and node2vec.

Fig. 6

Visualization of Wiki network. The nodes are mapped to the 2-D space using the t-SNE algorithm with learned vectors as input. Color of a node indicates the class of the node. (Zoom in for better view)

Fig. 7

The layout of the original sub-graph of 501 nodes. (Zoom for better view)

Fig. 8

The local zoomed graph for node ‘450’ and ‘78’ (cont.)

5.7 Case study

In this sub-section, we pick out a concrete instance of a sub-graph from the Wiki data set to explain how the muti-granularity preserving network representation learning obtains vectors for better-classifying nodes in networks. As shown in Fig. 7, the original structure of the Wiki sub-graph (501 nodes contained) has 3-4 instinct communities. In this network, the node ‘450’ and ‘78’ are two instances we take to explain the effect of the proposed hier2vec algorithm comparing with the local structure concern algorithm, LINE. The node ‘450’ and ‘78’ are correctly classified by the representation vectors obtained by hier2vec but not by that of LINE. More than ‘450’ and ‘78’, all the nodes that are marked by red are only correctly classified by hier2vec.

In order to see the ‘450’ and ‘78’ nodes more clearly, we zoom in the graph and visualize them in Fig. 8. In that figure, some of the nodes are used for training while the rest are used for testing. The label on the nodes for testing contains round brackets and square brackets. The round brackets means the prediction given by LINE model and the square brackets means the prediction given by hier2vec model. The number right after the ‘_’ means the true class label of that node. For example, ‘327_13’ means that node ‘327’ is used as training, and it belongs to class 13. The ‘78_3(1)[3]’ means that node ‘78’ is for testing and its true class is class 3. Moreover, the LINE gives an incorrect prediction of class 1, while hier2vec gives a correct prediction of class 3.

As the Fig. 8a shown, we take ‘450’ for more detailed analysis. We can see that node ‘450’ belongs to class 1, but it was misclassified by LINE to class 3 and hier2vec correctly. Of the points connected to ‘450’, node ‘82’ has the largest number of degrees and its true class is 3. LINE is misled by this representation and so also classifies ‘450’ to class 3. But in the ${{\mathcal{G}}_{LT {merge}}}$ construction in hier2vec, node ‘450’ takes the point connected to it with a slightly larger number of degrees, ‘451’, as its parent. So one edge of ${{\mathcal{G}}_{LT {merge}}}$ is (450,451), and as can be seen from the hier2vec-generated vectors, the closest cosine distance to the vector of ‘450’ is exactly ‘451’. Note the class of ‘451’ is 1. Therefore, compared to the LINE-generated vectors, the hier2vec-generated vectors plays a positive role in correctly classifying the node ‘450’.

Similarly, the subgraph centering node ‘78’ is shown in Fig. 8b. It belongs to class 3, but LINE’s vector leads to classifying it in class 1. The reason for this is that LINE’s vector generation process is affected by node ‘276’ connected to node ‘78’ and node ‘276’ belongs to class 1. In contrast, the vector for ‘78’ obtained by hier2vec leads to correctly classifying the ‘78’ into class 3, because the slightly larger of the degrees in the nodes connected to ‘78’ is ‘100’, while ‘100’ belongs to class 3. In ${{\mathcal{G}}_{LT merge}}$, there exists edge (78, 100), and the experimental results suggest that this has a positive effect on the correct classification of node ‘78’.

From the case of node ‘450’ and ‘78’, we can see that the process of constructing the ${{\mathcal{G}}_{LT merge}}$ considers the subordination of nodes in the hierarchy and avoids the classification error caused by a local connection with a neighbor which has higher degree.

6 Conclusion and future works

This paper presents a novel model, called ‘hier2vec’. It is an interpretable multi-granular representation learning algorithm for representing the hierarchy as well as local structural property in networks into low-dimensional vectors. The hier2vec model makes use of the pre-defined nodes’ importance degree and the similarity-transferred distance between nodes to build the graph leading tree. Through this way, the multi-granular semantic knowledge of hierarchy can be interpretably modeled into the graph leading tree. By optimizing the model, the representation vectors can finally encode not only the local linkage semantic but also the global multi-granular hierarchy semantic knowledge. Experimental results on various real-world network inferring tasks prove the effectiveness of hier2vec. The hier2vec model is based on structural information, and it is not able to utilize the content information to improve performance when it is available for the network. This does not limit the scenarios in which this model can be used, but in the presence of richer information, the model may not be able to take full advantage of all the available information. In the future, we plan to explore ways to utilize content information in networks and more accurate way to simulate the generation of the vectors that can match the objective graph leading tree.