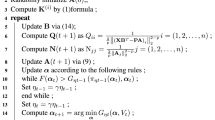1 Introduction

Feature selection is of great practical significance in real life. The purpose of feature selection is to select feature subset that can most effectively represent the decision from feature set of original data. Therefore, we can eliminate some attributes that are not related to decision, reduce the dimension of data, reduce over fitting, and improve the generalization ability of the model. Thus, feature selection has attracted the attentions of many researchers [1,2,3,4,5,6,7,8,9]. Especially in feature selection in numerical data, some researchers [10, 11] use discrete operation to preprocess numerical data. However, it is worth noting that discretization will lead to the loss of information in data. In order to avoid the discretization of numerical features, we can catch the distribution characteristics of numerical data and estimate the probability density of numerical data.

There are two types of probability density estimation: parametric estimation and non-parametric estimation. As for parametric estimation, it is necessary to assume the probability density model of the data. Then, the parameters in the model are solved by using the given data, and the probability density estimation can be obtained. It ought to note that the probability density function can not well reflect the rules of the experimental data if the hypothetical model does not conform to experimental data. However, the above situation will not occur in non-parametric estimation. Non-parametric estimation does not need to assume the model of experimental data in advance, but directly fits the probability density function in line with the law of the distribution. There are several common methods of nonparametric density estimation, including Histogram estimation [12], Kernel density estimation [13] (shortly KDE), Rosenblatt estimation [14] and so on. Kernel density estimation overcomes discontinuous disadvantage of probability density function in Histogram estimation and Rosenblatt estimation, so it has been widely used in many areas [15,16,17,18,19,20,21,22,23,24].

Among the applications of kernel density estimation, feature selection is an interesting and successful application. The reason why it is so widely used in feature selection is that it can overcome information loss caused by discretization. Therefore, Kwak et al. [24] proposed a feature selection method on basis of mutual information defined by kernel density estimation. Recently, Xu et al. [25] proposed a semi-supervised feature selection method with kernel purity and kernel density estimation. Zhang et al. [26] proposed a feature selection method in line with kernel density estimation for mixed data. It ought to notice that the above methods don’t consider interval-valued data and they can’t be used in feature selection in interval-valued data.

As a matter of fact, interval-valued data exist widely in real applications to describe uncertainty [27, 28]. Many scholars have studied interval-valued data from different perspectives. Especially in feature selection, many researchers have studied feature selection for inter-val-valued data. Dai et al. [27, 28] constructed uncertainty measurement and feature selection in interval-valued data. Du et al. [29] put forward an approximation distribution reduct in interval-valued ordered decision tables. Yang et al. [30] proposed an attribute reduction based on \(\alpha -\)dominance relation in interval-valued information systems. Dai et al. [31] constructed dominance-based fuzzy rough set model via probability approach in interval-valued decision systems and used the model to perform approximation distribution reduct. Guru et al. [32] constructed a novel feature selection model for supervised interval-valued data on basis of K-means clustering. Li [33] put forward multi-level attribute reductions in an interval-valued fuzzy formal context. Dai et al. [34] proposed a heuristic feature selection for interval-valued data based on conditional entropy. Dai et al. [35] introduced a feature selection method in incomplete interval-valued decision systems. Guru et al. [36] presented a feature selection of interval-valued data based on Interval Chi-Square Score.

However, so far, there are very few feature selection methods on basis of kernel density estimation entropy for interval-valued data. Focusing on handling interval-valued data by kernel density estimation entropy, a feature selection method based on kernel density estimation for interval-valued data is proposed in this paper. We first raise the kernel density estimation of interval-valued data, and then propose kernel density estimation probability structure. Based on the structure, kernel density estimation entropies are proposed and used in feature selection for interval-valued data. In addition, we improve the feature selection method and propose a fast feature selection method. Experiments indicate the effectiveness of the proposed feature selection methods for interval-valued data.

The rest of this paper is organized as below. In Sect. 2, the basic concepts of information theory and kernel density estimation are introduced. In Sect. 3, a kernel function for interval-valued data is proposed, and its theoretical properties are studied. In Sect. 4, the interval-valued kernel density estimation probability structure is raised with the proposed kernel function. In Sect. 5, the kernel density estimation information entropy, kernel density estimation conditional entropy and kernel density estimation joint entropy for interval-valued data are constructed by using the raised structure. In Sect. 6, we propose a feature selection method based on kernel density estimation conditional entropy. For improving efficiency of the feature selection method, a fast feature selection algorithm is further presented via the incremental expressions of the kernel function and the inverse of the covariance matrix. In Sect. 7, the validity of the fast feature selection method is verified from aspects of computing time, intuitional identifiability and classification performance by experiments. Section 8 summarizes the paper.

2 Preliminary knowledge

2.1 Basic concepts in information theory

Let X be a discrete random variable with a range of \({\mathbb {X}}\). \(p(x)=p(X=x)\) denotes the probability of occurrence of \(X=x\). Information entropy H(X) is defined as below [37]:

$$\begin{aligned} H\left( X \right) =-\sum _{x\in {\mathbb {X}}}{p\text {(}x\text {)}\log p\left( x \right) } \end{aligned}$$
(1)

Information entropy can measure the amount of information needed to eliminate uncertainty. The greater the uncertainty of discrete random variable X is, the greater its information entropy is.

Let X and Y be discrete random variables with ranges of \({\mathbb {X}}\) and \({\mathbb {Y}}\), respectively. \(p(x,y)=p(X=x,Y=y)\) denotes the joint probability of x and y, then the joint entropy is defined as follows:

$$\begin{aligned} H\left( X,Y \right) =-\sum _{x\in {\mathbb {X}}}{\sum _{y\in {\mathbb {Y}}}{}p\text {(}x,y\text {)}\log p\left( x,y \right) } \end{aligned}$$
(2)

Joint entropy can measure the amount of information needed to eliminate the uncertainty in the joint distribution of X and Y. The greater the uncertainty in X and Y is, the greater the joint entropy is.

Let X and Y be discrete random variables with ranges of \({\mathbb {X}}\) and \({\mathbb {Y}}\). \(p\left( y|x\right) =p\left( Y=y|X=x\right)\) denotes the probability of \(Y=y\) under \(X=x\). The definition of conditional entropy is shown as below:

$$\begin{aligned} H\left( Y|X \right) =-\sum _{x\in {\mathbb {X}}}{p\left( x \right) \sum _{y\in {\mathbb {Y}}}{}p\text {(}y|x\text {)}\log p\left( y|x \right) } \end{aligned}$$
(3)

Conditional entropy can measure the amount of information needed to eliminate uncertainty in Y under condition of X. The more information can X provide about Y, the less uncertainty Y has and the less the conditional entropy is.

The above forms of entropy are all for discrete features. Entropy of continuous features without discrete processing can be written in the form of integral:

$$\begin{aligned} H\left( X \right) =-\int _{x\in {\mathbb {X}}}{p\left( x \right) \log p\left( x \right) dx} \end{aligned}$$
(4)

Here X is a continuous random variable. p(x) represents the probability density function of a random variable X, and \({\mathbb {X}}\) denotes the range of X. From Eq. (4), we can see that the key to obtain the entropy of continuous features lies in the probability density function.

2.2 Feature selection

The curse of dimensionality is a problem which occurs in the applications of data mining, pattern recognition and machine learning [38,39,40]. In most cases, data sets coming from real life have many features in which there may exist irrelevant or redundant features that can consume a lot of computing time and storage space. Feature selection can deal with the problem effectively. Feature selection is to get rid of features which are irrelevant to decision and to select the features which are relevant to decision. In this way, the performances of learning algorithms can be improved.

In this paper, we mainly study the feature selection approach based information theory. In most cases, feature selection method based on information theory use condition entropy \(H(D|{\varvec{F}})\) to evaluate the degree of relevance between features and decision. In condition entropy \(H(D|{\varvec{F}})\), \({\varvec{F}}\) is a feature set and D denotes the decision. The smaller the value of \(H(D|{\varvec{F}})\) is, the greater relevance between \({\varvec{F}}\) and D is. Then, we intend to select feature set which have minimum \(H(D|{\varvec{F}})\) in the process of feature selection.

Definition 1

[34] In an information table \(<{\varvec{U}}\),\(~{\varvec{C}}>\), \({\varvec{U}}\) is the nonempty sample set and \({\varvec{C}}\) is the nonempty feature set. Let \({\varvec{F}}\) be a selected feature set. For \(\forall a,b\in {\varvec{C}}-{\varvec{F}}\) and \(a\ne b\), if \(H(D|{\varvec{F}}\cup a)< H(D|{\varvec{F}}\cup b)\), then a is more significant than b relative to decision D.

The detailed process about feature selection based on condition entropy \(H(D|{\varvec{F}})\) can be shown as follows.

figure a

2.3 Kernel density estimation

In one-dimensional continuous real data, the definition of kernel density estimation is as follows:

$$\begin{aligned} {\hat{f}}_{h_n}\left( x \right) =\frac{1}{nh_n}\sum _{i=1}^n{K_{h_n}\left( x-x_i \right) }=\frac{1}{nh_n}\sum _{i=1}^n{K\left( \frac{x-x_i}{h_n} \right) } \end{aligned}$$
(5)

where \(h_n\) denotes the window width; \(\underset{n\rightarrow \infty }{\lim }h_n=0\); n represents the number of samples; K(.) denotes a kernel function; \(x_i\) denotes the ith sample. The common kernel functions are Uniform kernel, Gauss kernel, Epanechnikov kernel and Quadric kernel. Gauss kernel \(\varPhi ( x-x_i,h ) =\frac{1}{\sqrt{2\pi }h}\exp \left( -\frac{\left( x-x_i \right) ^2}{2h^2} \right)\) is most commonly used in kernel density estimation. According to the properties of probability density function, it is realized that the integration of probability density function in definition domain is 1, that is to say, the integration of kernel function in its definition domain is equal to 1:\(\int {_{x\in {\mathbb {X}}}K( x )}dx=1\). Bandwidth h plays a smooth role in probability density function. The larger h is, the smoother the curve estimated by kernel density is. On the contrary, the steeper the curve is. From the definition of kernel function, we can see that the kernel density estimation actually calculates the average effect of all sample points on the point x probability density based on the distance. The closer the sample points are to the point x, the greater the contribution to the point x is. On the contrary, the farther the distance is, the smaller the contribution will be.

In m-dimensional continuous real data, the Gauss kernel function is defined as follows:

$$\begin{aligned} \begin{aligned} \varPhi \left( x-x_i,h \right)&=\frac{1}{\left( \sqrt{2\pi }h \right) ^m|\sum {}|^{\frac{1}{2}}}\\&\exp \left( -\frac{\left( x-x_i \right) ^T\sum {^{-1}}\left( x-x_i \right) }{2h^2} \right) \end{aligned} \end{aligned}$$
(6)

where \(x_i\) represents ith sample; \(\sum {}\) denotes the m-dimen-sional sample covariance; \(\sum {^{-1}}\) represents the inverse of the covariance matrix; \(|\sum {}|\) denotes the determinant of the covariance.

Definition 2

[41] In a \(t\times t\) dimension covariance matrix

$$\begin{aligned} \sum {_{{\varvec{t}}}=\left( \begin{matrix} \sum {_{t-1}}&{} {\varvec{r}}_t\\ {\varvec{r}}^{T}_t&{} 1\\ \end{matrix} \right) } \end{aligned}$$

\(\sum {_{t-1}}\) is the first \(t-1\) dimensional matrix of \(\sum {_{{\varvec{t}}}}\), \({\varvec{r}}_t\) is the first \(t-1\) row of the t column element. If \(\sum {_{{\varvec{t}}}}\) is reversible, the inverse matrix \(\sum {_{t}^{-1}}\) of \(\sum {_{{\varvec{t}}}}\) can be expressed as the following incremental formula:

$$\begin{aligned} \sum {_{t}^{-1}}=\left( \begin{matrix} \sum {_{t-1}^{-1}}&{} {\mathbf {0}}_t\\ {\mathbf {0}}_{t}^{T}&{} 0\\ \end{matrix} \right) +\frac{1}{\beta _t}\left( \begin{matrix} {\varvec{b}}_t{\varvec{b}}_{t}^{T}&{} {\varvec{b}}_t\\ {\varvec{b}}_{t}^{T}&{} 1\\ \end{matrix} \right) \end{aligned}$$
(7)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} {\varvec{b}}_t=-\sum {_{t-1}^{-1}{\varvec{r}}_t}\\ \beta _t=1-{\varvec{r}}_{t}^{T}\sum {_{t-1}^{-1}{\varvec{r}}_t=1+{\varvec{r}}_t{\varvec{b}}_t}\\ \end{array}\right. } \end{aligned}$$

Lemma 1

The determinant of the covariance matrix satisfies the following property:

$$\begin{aligned} |\sum {_t|=\beta _t|\sum {_{t-1}|}} \end{aligned}$$
(8)

Definition 3

[26] In data set U, the feature set \({\varvec{X}}\) contains \(t-1\) features, where \(t\geqslant 2\) and its inverse matrix is expressed as: \(\sum {_{t-1}^{-1}}\). The \({\varvec{X}}\)-feature part of sample x is represented as column vector \({\varvec{x}}\). When the feature set \({\varvec{Z}}={\varvec{X}}\cup Y\) is obtained by adding feature Y to the feature set \({\varvec{X}}\), its inverse matrix is expressed as \(\sum {_{t}^{-1}}\). The \({\varvec{Z}}\)-feature part of sample z is expressed as column vector \({\varvec{z}}=\left( \varvec{x,}y \right) =\left( x_1,x_2,...,x_{t-1},y \right) ^T\), and the incremental expression of each element in the kernel matrix is expressed as:

$$\begin{aligned} \phi \left( {\varvec{z}}_i-{\varvec{z}}_j,h \right) =\frac{\phi \left( {\varvec{x}}_i-{\varvec{x}}_j,h \right) }{\sqrt{2\pi \beta _t}h\exp \left( \frac{\left( \left( {\varvec{x}}_i-{\varvec{x}}_j \right) ^T{\varvec{b}}_{{\varvec{t}}}+\left( y_i-y_j \right) \right) ^2 }{2h^2\beta _t} \right) } \end{aligned}$$
(9)

3 Kernel density estimation for interval-valued data

Real-valued data can be regarded as a special form of interval-valued data, where the left and right boundaries of the interval form of real-valued data are equal. Inspired by the large contribution of close samples and the small contribution of far samples, the interval-valued Gauss kernel can be constructed.

Definition 4

In an interval-valued decision table \(IVDT=<{\varvec{U}},{\varvec{C}}\cup D>\), \({\varvec{U}}\) denotes the sample set, \(\left| {\varvec{U}}\right| =n\) denotes the base of \({\varvec{U}}\) is n; \({\varvec{C}}\) represents the conditional feature set; D denotes the decision feature. Feature values on conditional features are interval values and feature values on decision features are real values. Let \({\varvec{A}}\subseteq {\varvec{C}}\) and \(\left| {\varvec{A}}\right| =m\), the interval Gaussian kernel function of random interval variable x is defined as follows:

$$\begin{aligned} \begin{aligned} \varPhi ( x-x_i,h_n,{\varvec{A}} )&= \frac{1}{2( \sqrt{2\pi }h_n ) ^m|\sum {_{L,{\varvec{A}}}}|^{\frac{1}{2}}}\\&\exp \left( -\frac{( x-x_{i,{\varvec{A}}}^{-}) ^T\sum {_{L,{\varvec{A}}}^{-1}}( x-x_{i,{\varvec{A}}}^{-})}{2h_{n}^{2}}\right) \\&\quad +\frac{1}{2( \sqrt{2\pi }h_n ) ^m|\sum {_{R,A}}|^{\frac{1}{2}}}\\&\exp \left( -\frac{( x-x_{i,{\varvec{A}}}^{+}) ^T\sum {_{R,{\varvec{A}}}^{-1}}( x-x_{i,{\varvec{A}}}^{+})}{2h_{n}^{2}}\right) . \end{aligned} \end{aligned}$$
(10)

where \(h_n\) denotes the window width, \(h_n>0\) and \(\underset{n\rightarrow \infty }{\lim }h_n=0\); \(x_{i,{\varvec{A}}}^{-}\) represents the m-dimensional vector formed by the left bound of interval values of the ith sample on the feature set \({\varvec{A}}\); \(x_{i,{\varvec{A}}}^{+}\) represents the m-dimensional vector formed by the right bound of interval values of the ith sample in the feature set \({\varvec{A}}\); \(\sum {_{L,{\varvec{A}}}}\) is the left-bound covariance of m-dimensional on feature set \({\varvec{A}}\); \(\sum {_{R,{\varvec{A}}}}\) is the right-bound covariance of m-dimensional on feature set \({\varvec{A}}\); \(\sum {_{L,{\varvec{A}}}^{-1}}\) and \(|\sum {_{L,{\varvec{A}}}}|\) denote the inverse and the determinant of the left-bounded covariance matrix on feature set \({\varvec{A}}\); \(\sum {_{R,{\varvec{A}}}^{-1}}\) and \(|\sum {_{R,{\varvec{A}}}}|\) denote the inverse and the determinant of the right-bounded covariance matrix on feature set \({\varvec{A}}\).

We can rewrite Eq. 5 to \(\varPhi ( x-x_i,h_n,{\varvec{A}} )=L( x-x_i,h_n,{\varvec{A}} )+R( x-x_i,h_n,{\varvec{A}})\) where \(L( x-x_i,h_n,{\varvec{A}})=\frac{1}{( \sqrt{2\pi }h_n) ^m|\sum {_{L,{\varvec{A}}}}|^{\frac{1}{2}}} \exp ( -\frac{( x-x_{i,{\varvec{A}}}^{-}) ^T\sum {_{L,{\varvec{A}}}^{-1}}( x-x_{i,{\varvec{A}}}^{-})}{2h_{n}^{2}})\) and \(R( x-x_i,h_n,{\varvec{A}} )=\frac{ \exp (-\frac{( x-x_{i,{\varvec{A}}}^{+}) ^T\sum {_{R,{\varvec{A}}}^{-1}}( x-x_{i,{\varvec{A}}}^{+})}{2h_{n}^{2}})}{( \sqrt{2\pi }h_n) ^m|\sum {_{R,{\varvec{A}}}}|^{\frac{1}{2}}}\)

Table 1 An interval-valued decision table
Full size table

Example 1

An interval-valued decision table \(IVDT=<{\varvec{U}},{\varvec{C}}\cup D>\) is presented in Table 1 where \({\varvec{U}}=\{x_1,x_2,x_3, x_4\}\), \({\varvec{C}}=\{a,b,c\}\). In this example, we set \(h=1/log2(4)=0.5\) and \(A=\{a\}\). Then we can get the following results: \(L\left( x_1-x_2,\frac{1}{2},A \right) =0.1080\) \(R\left( x_1-x_2,\frac{1}{2},A \right) =0.0003\).

Similarly, we can get the following matrixes:

\(L \left( \frac{1}{2}, A\right) = \left( \begin{matrix} 0.7981&{} 0.1080&{} 0.1080&{} 0.7981\\ 0.1080&{} 0.7981&{} 0.7981&{} 0.1080\\ 0.1080&{} 0.7981&{} 0.7981&{} 0.1080\\ 0.7981&{} 0.1080&{} 0.1080&{} 0.7981\\ \end{matrix} \right)\) and

\(R \left( \frac{1}{2}, A\right) = \left( \begin{matrix} 0.7981&{} 0.0003&{} 0.1080&{} 0.7981\\ 0.0003&{} 0.7981&{} 0.1080&{} 0.0003\\ 0.1080&{} 0.1080&{} 0.7981&{} 0.1080\\ 0.7981&{} 0.0003&{} 0.1080&{} 0.7981\\ \end{matrix} \right)\)

Proposition 1

Interval Gaussian kernel function Eq. 10has the following properties:

  1. (1)

    Continuity;

  2. (2)

    \(\varPhi \left( x-x_i,h_n,{\varvec{A}} \right) >0\),\(\forall {\varvec{A}}\subseteq {\varvec{C}}\) ;

  3. (3)

    Symmetry:\(\phi \left( x-y,h_n,{\varvec{A}} \right) =\phi \left( y-x,h_n,{\varvec{A}} \right)\),

    \(\forall x,y\in U\),\(\forall {\varvec{A}}\subseteq {\varvec{C}}\);

  4. (4)

    \(\int {\phi \left( x-x_i,h_n,{\varvec{A}} \right) }dx=1\),\(\forall {\varvec{A}}\subseteq {\varvec{C}}\);

  5. (5)

    Semi-positive definiteness.

We can notice that the interval-valued Gaussian kernel raised in this paper will be reduced to real-valued Gaussian kernel when the interval values are reduced to real values and \(\sum {_{L,A}}\) and \(\sum {_{R,A}}\) are reversible. From this aspect, we can see that interval kernel function is an extension of classical Gaussian kernel.

Theorem 1

\(\forall {\varvec{A}}\subseteq {\varvec{B}}\subseteq {\varvec{C}}\), \(\exists \delta >\text {0,}\) if \(h_n\geqslant \delta\) and \(\sum {_{L,{\varvec{B}}}}\) and \(\sum {_{R,{\varvec{B}}}}\) are reversible, then \(\phi ( x-x_i,h_n,{\varvec{A}}) \geqslant \phi ( x-x_i,h_n,{\varvec{B}} )\).

Proof

Let \({\varvec{A}}\subseteq {\varvec{B}}\subseteq {\varvec{C}}\), \({\varvec{E}}={\varvec{A}}+b,\; b\in {\varvec{B}}\). We can get \(\varPhi \left( x-x_i,h_n,{\varvec{A}} \right) =L\left( x-x_i,h_n,{\varvec{A}} \right) +R\left( x-x_i,h_n,{\varvec{A}} \right)\). We can first prove the properties on L(.).

Suppose \(\sum {_{L,{\varvec{E}}}}\) is reversible, we can get \(\sum {_{L,{\varvec{A}}}}\) is reversible and \(\beta _{L,{\varvec{E}}}>0\) by Eq. 8 and the semi-positive definiteness of covariance matrix. Similarly, when \(\sum {_{L,{\varvec{B}}}}\) is reversible, we can get \(\sum {_{L,{\varvec{F}}}}\) is reversible and \(\beta _{L,{\varvec{F}}}>0\) for \(\forall {\varvec{F}}\subseteq {\varvec{B}}\).

\(L( x-x_i,h_n,{\varvec{A}} )=\frac{ \exp ( -\frac{( x-x_{i,{\varvec{A}}}^{-}) ^T\sum {_{L,{\varvec{A}}}^{-1}}( x-x_{i,{\varvec{A}}}^{-} )}{2h_{n}^{2}} )}{( \sqrt{2\pi }h_n ) ^m|\sum {_{L,{\varvec{A}}}}|^{\frac{1}{2}}}\)

\(L( x-x_i,h_n,{\varvec{E}} )=\frac{ \exp ( -\frac{( x-x_{i,{\varvec{E}}}^{-} ) ^T\sum {_{L,{\varvec{E}}}^{-1}}( x-x_{i,{\varvec{E}}}^{-} )}{2h_{n}^{2}})}{( \sqrt{2\pi }h_n ) ^m|\sum {_{L,{\varvec{E}}}}|^{\frac{1}{2}}}\)

Based on Definitions 2, 1 and 3, we can get:

$$\begin{aligned}&L( x-x_i,h_n,{\varvec{E}} ) =\frac{ \exp \left( -\frac{( x-x_{i,{\varvec{E}}}^{-} ) ^T\sum {_{L,{\varvec{E}}}^{-1}}( x-x_{i,{\varvec{E}}}^{-} )}{2h_{n}^{2}} \right) }{( \sqrt{2\pi }h_n ) ^m|\sum {_{L,{\varvec{E}}}}|^{\frac{1}{2}}}\\&\quad =\frac{ \exp \left( -\frac{( x-x_{i,{\varvec{A}}}^{-} ) ^T\sum {_{L,{\varvec{A}}}^{-1}}( x-x_{i,{\varvec{A}}}^{-} ) ) ^2}{2h_{n}^{2}} \right) }{( \sqrt{2\pi }h_n ) ^m|\sum {_{L,{\varvec{A}}}}|^{\frac{1}{2}}\beta _{L,{\varvec{E}}}^{\frac{1}{2}}}\\&\quad *\exp \left( -\frac{\frac{1}{\beta _{L,{\varvec{E}}}}( ( x-x_{i,{\varvec{A}}}^{-} ) ^Tb_{L,{\varvec{E}}}+( x-x_{i,b}^{-} ))^2}{2h_{n}^{2}}\right) \end{aligned}$$

\(L( x-x_i,h_n,{\varvec{A}})-L( x-x_i,h_n,{\varvec{E}} ) =\frac{1}{( \sqrt{2\pi }h_n ) ^m|\sum {_{L,{\varvec{A}}}}|^{\frac{1}{2}}} \exp ( -\frac{( x-x_{i,{\varvec{A}}}^{-} ) ^T\sum {_{L,{\varvec{A}}}^{-1}}( x-x_{i,{\varvec{A}}}^{-} )}{2h_{n}^{2}})\times ( 1-\frac{1}{\sqrt{2\pi }h_n\beta _{L,{\varvec{E}}}^{\frac{1}{2}}}\exp ( -\frac{( ( x-x_{i,{\varvec{A}}}^{-}) ^Tb_{L,{\varvec{E}}}+( x-x_{i,b}^{-} ) ) ^2}{2h_{n}^{2}\beta _{L,{\varvec{E}}}}))\). We can see that \(\frac{1}{( \sqrt{2\pi }h_n ) ^m|\sum {_{L,{\varvec{A}}}}|^{\frac{1}{2}}}\exp ( -\frac{( x-x_{i,{\varvec{A}}}^{-} ) ^T\sum {_{L,{\varvec{A}}}^{-1}}( x-x_{i,{\varvec{A}}}^{-} )}{2h_{n}^{2}} )>0\). \(\max \{\exp (-\frac{((x-x_{i,{\varvec{A}}}^{-}) ^Tb_{L,{\varvec{E}}}+(x-x_{i,b}^{-})) ^2}{2h_{n}^{2}\beta _{L,{\varvec{E}}}})\}=1\) for \(\beta _{L,{\varvec{E}}}>0\) and \(h_n>0\).  So when \(h_n\geqslant \frac{1}{\sqrt{2\pi }\beta _{L,{\varvec{E}}}^{\frac{1}{2}}}\), \(L( x-x_i,h_n,{\varvec{A}} )\geqslant L( x-x_i,h_n,{\varvec{E}} )\).  Let \(\delta _L=\max \{ \frac{1}{\sqrt{2\pi }\beta _{L,{\varvec{E}}}^{\frac{1}{2}}},\frac{1}{\sqrt{2\pi }\beta _{L,F}^{\frac{1}{2}}},...,\frac{1}{\sqrt{2\pi }\beta _{L,{\varvec{B}}}^{\frac{1}{2}}} \}\) where \({\varvec{F}}={\varvec{E}}+f,\;f\in {\varvec{B}}\). When \(h_n\geqslant \delta _L\), \(L( x-x_i,h_n,{\varvec{A}} )\geqslant L( x-x_i,h_n,{\varvec{B}} )\).

Similarly, let \(\delta _R=\max \{ \frac{1}{\sqrt{2\pi }\beta _{R,{\varvec{E}}}^{\frac{1}{2}}},\frac{1}{\sqrt{2\pi }\beta _{R,{\varvec{F}}}^{\frac{1}{2}}},\cdots , \frac{1}{\sqrt{2\pi }\beta _{R,{\varvec{B}}}^{\frac{1}{2}}} \}\). If \(h_n\geqslant \delta _R\), we have \(R( x-x_i,h_n,{\varvec{A}} )\,\geqslant \, R( x-x_i,h_n,{\varvec{B}} )\).

In summary, when \(\delta =max\{ \delta _L,\delta _R \}\) and \(h_n \geqslant \delta\), \(\phi ( x-x_i,h_n,{\varvec{A}} ) \geqslant \phi ( x-x_i,h_n,{\varvec{B}} )\) holds. \(\square\)

Definition 5

Given an interval-valued decision table \(IVDT=<{\varvec{U}},{\varvec{C}}\cup D>\), \({\varvec{A}}\subseteq {\varvec{C}}\) and \(\left| {\varvec{A}}\right| =m\), the probability density function estimation of interval values on \({\varvec{A}}\) is defined as below:

$$\begin{aligned} {\hat{p}}_{{\varvec{A}}}\left( x \right) = \frac{1}{n}\sum \limits _{i\in {\varvec{U}}}{\phi \left( x-x_i,h_n,{\varvec{A}} \right) } \end{aligned}$$
(11)

Proposition 2

(1)\(\int {{\hat{p}}_{{\varvec{A}}}\left( x \right) }dx=1\).

Proof

It can be proved by Proposition 1. \(\square\)

4 Kernel density estimation probability structure for interval values

Enlightened by Kwak et al. [24], the conditional probability and joint probability of kernel density estimation for interval values can be defined based on the interval kernel function.

Definition 6

Given an interval-valued decision table \(IVDT=<{\varvec{U}},{\varvec{C}}\cup D>\), \({\varvec{A}}\subseteq {\varvec{C}}\) and \(\left| {\varvec{A}}\right| =m\). In feature set \({\varvec{A}}\), the conditional probability of kernel density estimation under \({D = d}\) is defined as below

$$\begin{aligned} {\hat{p}}_{{\varvec{A}}}\left( x|d \right) =\frac{1}{n_d}\sum _{i\in I_d}{\phi \left( x-x_i,h,{\varvec{A}} \right) } \end{aligned}$$
(12)

where \(I_d=\left\{ x_i|\forall x_i\in {\varvec{U}},\;D\left( i \right) =d \right\}\) in which D(i) denotes decision value of ith sample; \(n_d=|I_d|\) represents the number of elements in set \(I_d\).

Definition 7

Given an interval-valued decision table \(IVDT=<{\varvec{U}},{\varvec{C}}\cup D>\), \({\varvec{A}}\subseteq {\varvec{C}}\) and \(\left| {\varvec{A}}\right| =m\). In feature set \({\varvec{A}}\), the joint probability is defined as follows by Eq. 12:

$$\begin{aligned} \begin{aligned} {\hat{p}}_{{\varvec{A}}}\left( x,d \right)&={\hat{p}}_{{\varvec{A}}}\left( d \right) {\hat{p}}_{{\varvec{A}}}\left( x|d \right) \\&=\frac{n_d}{n}\frac{1}{n_d}\sum _{i\in I_d}{\phi \left( x-x_i,h,{\varvec{A}} \right) }\\&=\frac{1}{n}\sum _{i\in I_d}{\phi \left( x-x_i,h,{\varvec{A}} \right) } \end{aligned} \end{aligned}$$
(13)

where n denotes the number of samples in sample set \({\varvec{U}}\).

Definition 8

Given an interval-valued decision table \(IVDT=<{\varvec{U}},{\varvec{C}}\cup D>\), \({\varvec{A}}\subseteq {\varvec{C}}\) and \(\left| {\varvec{A}}\right| =m\). In feature set \({\varvec{A}}\), the posterior probability is defined as follows by Eqs. 12 and 13:

$$\begin{aligned} \begin{aligned} {\hat{p}}_{{\varvec{A}}}\left( d|x \right)&=\frac{{\hat{p}}_{{\varvec{A}}}\left( x,d \right) }{{\hat{p}}_{{\varvec{A}}}\left( x \right) }=\frac{\frac{1}{n}\sum _{i\in I_d}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}{\frac{1}{n}\sum _{i\in {\varvec{U}}}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}\\&=\frac{\sum _{i\in I_d}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}{\sum _{i\in {\varvec{U}}}{\phi \left( x-x_i,h,{\varvec{A}} \right) }} \end{aligned} \end{aligned}$$
(14)

Proposition 3

  1. (1)

     \({\hat{p}}_{{\varvec{A}}}\left( x \right) =\frac{n_d}{n}\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}}\left( x|d \right)\);

  2. (2)

     \(\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}}\left( d|x \right) =1\);

  3. (3)

     \({\hat{p}}_{{\varvec{A}}}\left( d \right) =\frac{1}{n}\sum _{i=1}^n{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\);

  4. (4)

    \({\hat{p}}_{{\varvec{A}}}\left( x \right) \geqslant {\hat{p}}_{{\varvec{A}}}\left( x,d \right)\);

  5. (5)

    \({\hat{p}}_{{\varvec{A}}}\left( x,d \right) \leqslant {\hat{p}}_{{\varvec{A}}}\left( x|d \right)\).

Proof

(1) 

$$\begin{aligned}\frac{n_d}{n}\sum _{d\in D}{}{\hat{p}}_{{\varvec{A}}}(x|d)&=\frac{n_d}{n}\frac{1}{n_d}\sum _{d\in D}{}\sum _{i\in I_d}{}\phi ( x-x_i,h,{\varvec{A}})\\&=\frac{1}{n}\sum _{i\in U}^{}{\phi ( x-x_i,h,{\varvec{A}})}. \end{aligned}$$

(2) 

$$\begin{aligned} \sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x \right) }&=\sum _{d\in D}{\frac{\sum _{i\in I_d}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}{\sum _{i\in U}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}}\\&=\frac{\sum _{d\in D}{\sum _{i\in I_d}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}}{\sum _{i\in {\varvec{U}}}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}\\&=\frac{\sum _{i\in {\varvec{U}}}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}{\sum _{i\in {\varvec{U}}}{\phi \left( x-x_i,h,{\varvec{A}} \right) }}. \end{aligned}$$

(3)

$$\begin{aligned} {\hat{p}}_{{\varvec{A}}}\left( d \right)&=\int {{\hat{p}}_{{\varvec{A}}}\left( d,x \right) dx}\\&=\int {{\hat{p}}_{{\varvec{A}}}\left( x \right) {\hat{p}}_{{\varvec{A}}}\left( d|x \right) }dx\\&=\frac{1}{n}\sum _{i=1}^n{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) } \end{aligned}$$

(3)It can be proven by Eqs. 13 and 11. (4)It can be proven by Eqs. 13 and 12. \(\square\)

Theorem 2

\(\exists \delta >\text {0,}\;\forall {\varvec{A}}\subseteq {\varvec{B}}\subseteq {\varvec{C}}\) , if \(h_n\geqslant \delta\) and \(\sum {_{L,{\varvec{B}}}}\) and \(\sum {_{R,{\varvec{B}}}}\) are reversible, then:

  1. (1)

    \({\hat{p}}_{{\varvec{A}}}\left( x \right) \geqslant {\hat{p}}_{{\varvec{B}}}\left( x \right)\);

  2. (2)

    \({\hat{p}}_{{\varvec{A}}}\left( x,d \right) \geqslant {\hat{p}}_{{\varvec{B}}}\left( x,d \right)\) ;

  3. (3)

    \({\hat{p}}_{{\varvec{A}}}\left( x|d \right) \geqslant {\hat{p}}_{{\varvec{B}}}\left( x|d \right)\).

Proof

It can be proved according to Theorem 1. \(\square\)

5 Kernel density estimation entropy of interval values

According to the law of large numbers, the information entropy, joint entropy and conditional entropy of kernel density estimation for interval values can be defined.

Given an interval-valued decision table \(IVDT=<{\varvec{U}},{\varvec{C}}\cup D>\), \({\varvec{U}}\) denotes the sample set. Suppose the samples are independent and subject to the same distribution. \({{\varvec{A}}}\subseteq {\varvec{C}}\) denotes feature subset. \({\mathbb {A}}\) denotes the value domain of \({\varvec{A}}\).

Definition 9

The information entropy of interval values is defined as below:

$$\begin{aligned} \begin{aligned} {\hat{H}}\left( {\varvec{A}} \right)&=-\int _{{\varvec{x}}\in {\mathbb {A}}}{{\hat{p}}_{{\varvec{A}}}\left( x \right) \log {\hat{p}}_{{\varvec{A}}}\left( x \right) }dx\\&=-\frac{1}{n}\sum \limits _{i\in U}{\log {\hat{p}}_{{\varvec{A}}}\left( x_i \right) } \end{aligned} \end{aligned}$$
(15)

Theorem 3

\(\exists \delta >\text {0,}\;\forall {\varvec{A}}\subseteq {\varvec{B}}\subseteq {\varvec{C}}\) , if \(h_n\geqslant \delta\) and \(\sum {_{L,B}}\) and \(\sum {_{R,B}}\) are reversible, then \({\hat{H}}\left( {\varvec{A}} \right) \geqslant {\hat{H}}\left( {\varvec{B}} \right)\).

Proof

It can be proved according to Theorem 2. \(\square\)

Definition 10

The joint entropy of interval values is defined as:

$$\begin{aligned} \begin{aligned} {\hat{H}}\left( \varvec{A,}D \right)&=-\int _{x\in {\mathbb {A}}}{\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( x,d \right) \log {\hat{p}}_{{\varvec{A}}}\left( x,d \right) }}dx\\&=-\int _{x\in {\mathbb {A}}}{\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( x \right) {\hat{p}}_{{\varvec{A}}}\left( d|x \right) \log {\hat{p}}_{{\varvec{A}}}\left( x,d \right) }}dx\\&=-\frac{1}{n}\sum \limits _{i\in U}{\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }}\log {\hat{p}}_{{\varvec{A}}}\left( x_i,d \right) \end{aligned} \end{aligned}$$
(16)

Definition 11

The entropy of D under the condition \({\varvec{A}}\) is defined as follows:

$$\begin{aligned} \begin{aligned} {\hat{H}}\left( D|{\varvec{A}} \right)&=\int _{x\in {\mathbb {A}}}{{\hat{p}}_{{\varvec{A}}}\left( x \right) {\hat{H}}\left( D|{\varvec{A}}=x \right) dx}\\&=-\int _{x\in {\mathbb {A}}}{{\hat{p}}_{{\varvec{A}}}\left( x \right) \sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x \right) \log {\hat{p}}_{{\varvec{A}}}\left( d|x \right) }dx}\\&=-\frac{1}{n}\sum \limits _{i\in U}{\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }}\log {\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) \end{aligned} \end{aligned}$$
(17)

Conditional entropy \({\hat{H}}\left( D|{\varvec{A}} \right)\) can reflect the correlation between conditional feature set \({\varvec{A}}\) and decision feature D. The larger the condition entropy is, the smaller the correlation between \({\varvec{A}}\) and D is. Otherwise, the greater the correlation between \({\varvec{A}}\) and D is.

Definition 12

The entropy of \({\varvec{A}}\) under the condition D is defined as follows:

$$\begin{aligned} \begin{aligned}&{\hat{H}}( \varvec{A|}D ) =\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d \right) {\hat{H}}\left( \varvec{A|}D=d \right) }\\&\quad =-\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}}\left( d \right) \int _{x\in {\mathbb {A}}}{{\hat{p}}_{{\varvec{A}}}\left( x|d \right) \log {\hat{p}}_{{\varvec{A}}}\left( x|d \right) }dx\\&\quad =-\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}}\left( d \right) \int _{x\in {\mathbb {A}}}{\frac{{\hat{p}}_{{\varvec{A}}}\left( x \right) {\hat{p}}_{{\varvec{A}}}\left( d|x \right) }{{\hat{p}}_{{\varvec{A}}}\left( d \right) }\log {\hat{p}}_{{\varvec{A}}}}( x|d )dx\\&\quad =-\sum \limits _{d\in D}{\int _{x\in {\mathbb {A}}}{{\hat{p}}_{{\varvec{A}}}\left( x \right) {\hat{p}}_{{\varvec{A}}}\left( d|x \right) \log {\hat{p}}_{{\varvec{A}}}\left( x|d \right) }dx}\\&\quad =-\frac{1}{n}\sum _{d\in D}{\sum _{i\in U}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) \log {\hat{p}}_{{\varvec{A}}}\left( x_i|d \right) }} \end{aligned} \end{aligned}$$
(18)

Theorem 4

$$\begin{aligned} {\hat{H}}\left( \varvec{A,}D \right)&={\hat{H}}\left( \varvec{A|}D \right) +{{H}}\left( D \right) \\&={\hat{H}}\left( D|{\varvec{A}} \right) +{\hat{H}}\left( {\varvec{A}} \right) . \end{aligned}$$

Proof

Since \(\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}}( d|x ) =1\) and \(\frac{1}{n}\sum _{i\in U}{{\hat{p}}_{{\varvec{A}}}( d|x_i )}={\hat{p}}_{{\varvec{A}}}( d )\), we have:

$$\begin{aligned} \begin{aligned} {\hat{H}}\left( \varvec{A|}D \right) +{{H}}\left( D \right)&=-\frac{1}{n}\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d \right) \log {\hat{p}}_{{\varvec{A}}}\left( d \right) }\\&\quad -\frac{1}{n}\sum _{i\in {\varvec{U}}}{\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\log {\hat{p}}_{{\varvec{A}}}\left( x_i|d \right) }\\&=-\frac{1}{n}\sum _{d\in D}{\sum _{i\in U}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\log {\hat{p}}_{{\varvec{A}}}\left( d \right) }\\&\quad -\frac{1}{n}\sum _{i\in {\varvec{U}}}{\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\log {\hat{p}}_{{\varvec{A}}}\left( x_i|d \right) }\\&=-\frac{1}{n}\sum \limits _{i\in {\varvec{U}}}{\sum \limits _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }}\log {\hat{p}}_{{\varvec{A}}}\left( x_i,d \right) \\&={\hat{H}}\left( \varvec{A,}D \right) \\ {\hat{H}}\left( D|{\varvec{A}} \right) +{\hat{H}}\left( {\varvec{A}} \right)&=-\frac{1}{n}\sum _{i\in U}{\log{\hat{p}}_{{\varvec{A}}}\left( x_i \right) }\\&\quad -\frac{1}{n}\sum _{i\in {\varvec{U}}}{\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\log {\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\\&=-\frac{1}{n}\sum _{i\in {\varvec{U}}}{\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }{\log\hat{p}}_{{\varvec{A}}}\left( x_i \right) }\\&\quad -\frac{1}{n}\sum _{i\in {\varvec{U}}}{\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\log {\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\\&=-\frac{1}{n}\sum _{i\in U}{\sum _{d\in D}{{\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) }\log {\hat{p}}_{{\varvec{A}}}\left( d,x_i \right) }\\&={\hat{H}}\left( \varvec{A,}D \right) \end{aligned} \end{aligned}$$

In summary, \({\hat{H}}\left( \varvec{A,}D \right) ={\hat{H}}\left( \varvec{A|}D \right) +{{H}}\left( D \right) ={\hat{H}}\left( D|{\varvec{A}} \right) +{\hat{H}}\left( {\varvec{A}} \right)\). \(\square\)

6 Feature selection on basis of kernel density estimation entropy

6.1 Feature selection on basis of kernel density estimation entropy

Based on the definition (see Definition 11) of conditional entropy via interval kernel density estimation, we construct the original algorithm (see Algorithm 2) to calculate conditional entropy. In Step 3, we calculate the inverse of covariance matrix by gaussian elimination [42, 43] whose time complexity is \(O(|{\varvec{A}}|^3)\); the time complexity of the kernel matrix from Step 1 to Step 5 is \(O(n^2*|{\varvec{A}}|^3)\); from Step 6 to Step 11, the time complexity of conditional entropy is \(O(n^2+n*N_d)\). To sum up, the time complexity of Algorithm 2 is \(O(n^2*|{\varvec{A}}|^3+n^2+n*N_d)\).

figure b

Then, we construct a feature selection algorithm (see Algorithm 3) based on conditional entropy of kernel density estimation. The time complexity of Algorithm 3 is \(O(K*|{\varvec{C}}|*(|{\varvec{A}}|^3*n^2+n^2+n*N_d))\).

figure c

6.2 Fast feature selection on basis of kernel density estimation entropy

The computation of kernel matrix has high time complexity and low efficiency. Therefore, in this section, we first propose an incremental algorithm for interval-valued data (see Algorithm 4) to calculate kernel matrix and the inverse of covariance matrix. Secondly, we propose a concept of kernel partition matrix and an algorithm (see Algorithm 5) of calculating conditional entropy based on kernel partition matrix for interval-valued data. Finally, based on the above two algorithms, a fast feature selection algorithm (see Algorithm 6) is proposed by interval-valued kernel density estimation entropy.

figure d

In Algorithm 4, if conditional feature Q is the first candidate feature, then the inverse of left bound covariance matrix and right bound covariance matrix are both 1 and the kernel matrix \(\varvec{\Phi }_{{\varvec{S}}}^{L}\) and \(\varvec{\Phi }_{{\varvec{S}}}^{R}\) are calculated based on Eq. 10 where \({\varvec{S}}\) denotes the selected conditional features. If conditional feature Q is not the first candidate feature, then we need to calculate the inverse of covariance matrix based on Eq. 7 and two kernel matrices \(\varvec{\Phi }_{{\varvec{S}}}^{L}\), \(\varvec{\Phi }_{{\varvec{S}}}^{R}\) based on Eqs. 9 and 10, respectively. The main cost of Algorithm 4 is the calculation of the kernel matrix, so the time complexity of the algorithm is \(O(n^2)\).

figure e

In Algorithm 5, the time complexity of Step 1 is \(O(n^2)\); the time complexity of Step 3 to Step 6 is O(n). So the total time complexity of the algorithm is \(O(n^2+n)\).

Definition 13

In an interval-valued decision table \(IV DT=<{\varvec{U}},{\varvec{C}}\cup D>\), \({\varvec{U}}\) denotes the sample set and \(|{\varvec{U}}|=n\), \({\varvec{A}}\subseteq C\). \(\varvec{\varPhi }\left( {\varvec{A}} \right) =\left( \phi \left( x_i-x_j,h,{\varvec{A}} \right) \right) _{n\times n}=\left( L\left( x_i-x_j,h,{\varvec{A}} \right) +R\left( x_i-x_j,h,{\varvec{A}} \right) \right) _{n\times n}\) is a kernel matrix. The range of decision D is the integer of \(\left[ \text {1,}N_d \right]\). Then the definition of the kernel partition matrix \(\varvec{\varUpsilon }\left( \varvec{A,}D \right)\) is as follows:

$$\begin{aligned} \begin{aligned} \varvec{\Upsilon }\left( \varvec{A,}D \right)&=\left( \varUpsilon _{i,d}\left( \varvec{A,}D \right) \right) _{n\times N_d}=\left( \sum _{j=1}^n{\phi _{ij}m_{jd}} \right) _{n\times N_d}\\&=\left( \sum _{j=1}^n{\phi \left( x_i-x_j,h,{\varvec{A}} \right) m_{jd}} \right) _{n\times N_d}\\&=\left( \sum _{j=1}^n{L\left( x_i-x_j,h,{\varvec{A}} \right) m_{jd}} \right) _{n\times N_d}\\&\quad +\left( \sum _{j=1}^n{R\left( x_i-x_j,h,{\varvec{A}} \right) }m_{jd} \right) _{n\times N_d} \end{aligned} \end{aligned}$$
(19)

where \(m_{jd}={\left\{ \begin{array}{ll} 1&{} D\left( j \right) =d\\ 0&{} D\left( j \right) \ne d\\ \end{array}\right. }\).

Example 2

(Continued from Example 1) Based on Table 1, we can get \(M(D)=(m_{jd})_{4\times 2}\): \(M\left( D \right) =\left( \begin{matrix} 1&{} 0\\ 0&{} 1\\ 0&{} 1\\ 1&{} 0\\ \end{matrix} \right)\). \(\left( \varUpsilon _{1,1}\left( \varvec{A,}D \right) \right) =1.5962+1.5962=3.1924\). Similarly, we can get: \(\varvec{\Upsilon }\left( \varvec{A,}D \right) =\left( \begin{matrix} 3.1924&{} 0.3243\\ 0.2166&{} 2.5023\\ 0.432&{} 2.5023\\ 3.1924&{} 0.3243\\ \end{matrix} \right)\).

Remark 1

\(\varUpsilon _{i,d}\left( \varvec{A,}D \right) =\sum _{j=1}^n{\phi \left( x_i-x_j,h,{\varvec{A}} \right) m_{jd}}=\sum _{i\in I_d}{\phi \left( x-x_i,h,{\varvec{A}} \right) }=n*{\hat{p}}_{{\varvec{A}}}\left( x_i,d \right)\).

Theorem 5

\(|\varvec{\varUpsilon }\left( \varvec{A,}D \right) |_i\) represents the addition of the \(i\hbox {th}\) row elements of the kernel partition matrix. It satisfies the following property:

$$\begin{aligned} |\varvec{\varUpsilon }\left( \varvec{A,}D \right) |_i=\sum _{j\in U}{\phi \left( x_i-x_j,h,{\varvec{A}} \right) }=n*{\hat{p}}_{{\varvec{A}}}\left( x_i \right) \end{aligned}$$

Proof

\(|\varvec{\varUpsilon }\left( \varvec{A,}D \right) |_i\) \(=\sum _{d\in \left[ \text {1,}N_d \right] }{\varUpsilon _{id}\left( \varvec{A,}D \right) }\) \(=\sum _{d\in \left[ \text {1,}N_d \right] }{\sum _{j=1}^n{\phi \left( x_i-x_j,h,{\varvec{A}} \right) }}m_{jd}\)

\(=\sum _{j=1}^n{\phi \left( x_i-x_j,h,{\varvec{A}} \right) }\) \(=n*\frac{1}{n}*\sum _{j=1}^n{\phi \left( x_i-x_j,h,{\varvec{A}} \right) }\) \(=n*{\hat{p}}_{{\varvec{A}}}\left( x_i \right)\) \(\square\)

Remark 2

\({\hat{p}}_{{\varvec{A}}}\left( d|x_i \right) =\frac{\varUpsilon _{i,d}\left( \varvec{A,}D \right) }{|\varvec{\varUpsilon }\left( \varvec{A,}D \right) |_i}\)

figure f

Algorithm 6 describes a Fast Feature Selection based on Interval-Valued Kernel Density Estimation entropy (shortly \(FFS\_IVKDE\)). Step 8 calculates the inverse of the left bound covariance matrix \(\sum {_{L,\varvec{S\_X}}^{-1}}\) and the right bound covariance \(\sum {_{R,\varvec{S\_X}}^{-1}}\) on conditional feature \(\varvec{S\_X}\) where \(\varvec{S\_X}\) is the conditional feature set after adding a candidate conditional feature Q. In addition, the kernel matrix \(\varvec{\Phi }_{\varvec{S\_X}}^{L}\) about the left bound of interval values and the kernel matrix \(\varvec{\Phi }_{\varvec{S\_X}}^{R}\) about the right bound of interval values on the feature set \(\varvec{S\_X}\) are calculated. Step 9 calculates the conditional entropy \(new\_H\) on the conditional feature set \(\varvec{S\_X}\). Steps 10-17 determine whether the conditional entropy \(new\_H\) on the conditional feature set \(\varvec{S\_X}\) is smaller than the conditional entropy \(\min \text {\_}H\) on the original feature set \({\varvec{S}}\). If \(new\_H\) is less than \(\min \text {\_}H\), then candidate feature Q in \(\varvec{S\_X}\) can provide feature information about decision feature D and put Q in the selected feature set \({\varvec{S}}\). And, based on the time complexity analysis of the above Algorithms 5 and 4, we can get that the time complexity of Algorithm 6 is \(O(K*|{\varvec{C}}|*(n^2+n))\).

7 Experiments

In order to test the effectiveness of the proposed method, experiments are carried out on 14 data sets. The details of these 14 data sets are shown in Table 2. The first four of them are real-life interval-valued data sets [28, 44, 45]. SRBCT is real-valued data from [46]. Glioma is real-valued data from [47]. The other data sets are real-valued data from UCI [48].

Table 2 Interval-valued data sets
Full size table

Since the last ten data sets are real-valued data, we need to convert the real-valued data into interval-valued data. The specific operation about above converting is designed as follows: \(a_{i}^{-} \,= \,a_i-\sigma _d\), \(a_{i}^{+} \,= \,a_i+\sigma _d\) where \(a_i\) denotes the ith sample’s value on feature \(a \in C\), \(\sigma _d\) denotes the standard variance of feature values about samples whose labels are the same as ith sample [49].

In the experiment, we evaluate the effectiveness of the fast feature selection method proposed in this paper from three perspectives: (1). Feature selection via interval-valued kernel density estimation entropy mainly includes three aspects: computing of kernel matrix and the inverse of covariance matrix, computing of conditional entropy, feature selection. In order to test wheth-er the fast feature selection algorithm is faster than the original feature selection algorithm, we compare the running time of two methods from three aspects: the computing time of kernel matrix and the inverse of covariance matrix, the computing time of conditional entropy, and the computing time of feature selection. (2). Sample distribution by first two features selected by our method are compared with that of two features selected randomly. (3). Compare the classification performance of our method with other six comparative methods. Due to the limited number of samples in Fish, Face, Car and Glioma, leave-one-out cross validation is used. Other data sets use 10 fold cross validation.

7.1 Comparison of running time

Fig. 1
figure 1

Comparison of computing time of kernel matrix and inverse on covariance matrix on Face, Hill, Colon

Full size image
Fig. 2
figure 2

Comparison of computing time of conditional entropy on Face, Hill, Colon

Full size image

In order to test wether the fast feature selection algorithm is faster than the original feature selection method, we conduct experiments on three representative data, including Face data of 9 label classes, Hill data of 1212 samples and Colon data of 2000 features. Here we set window width parameter h as 1/log2(n) where n denotes the number of samples. In addition, the hardware platform for our experiments is a PC equipped with 12 G main memory and 3.41 GHZ CPU. The software is Matlab (Version R2019a).

The calculation of the kernel matrix and the inverse of covariance matrix in Steps 1-5 of Algorithm 2 is denoted as the Non Incremental strategy of Interval-Valued Data (shortly \(NI\_IVD\)). We compare \(NI\_IVD\) with Algorithm 4, in which the calculation of the kernel matrix and the inverse of covariance matrix is denoted Incremental algorithm of Interval-Valued Data (shortly \(I\_IVD\)). In Fig. 1, we show the time comparison results of \(NI\_IVD\) method and \(I\_IVD\) method on Face, Hill and Colon, where the red line represents \(I\_IVD\) and the black line represents \(NI\_IVD\). In each node (x, y), x represents the number of features, and y represents time of the method calculating the kernel matrix and inverse of covariance matrix under feature subset \(\{a_1, a_2,\cdots ,a_x\}\). From Fig. 1, we can find \(I\_IVD\) is much faster than \(IN\_IVD\) on the three data sets. Therefore, our incremental algorithm \(I\_IVD\) can greatly speed up the speed of calculating kernel matrix and the inverse of covariance matrix.

Fig. 2 shows the time comparison results of conditional entropy on Face, Hill and Colon. In Fig. 2, the black line represents the original conditional entropy calculation method (see Algorithm 2), and the red line represents the improved conditional entropy calculation (see Algorithm 5). What’s more, in each node (x, y), x represents the number of features, and y represents the running time of the method calculating condition entropy under feature subset \(\{a_1, a_2,\cdots ,a_x\}\). From the figure, we can see that the calculation time of \(CE\_IVD\) is significantly less than that of \(OCE\_IVD\). It indicates that algorithm \(CE\_IVD\) is faster than algorithm \(OCE\_IVD\).

Figure 3 shows the time comparison results of feature selection on Face, Hill and Colon data. Furthermore, in each node (x, y), x represents the number of features and y represents running time of the method selecting feature x. In Fig. 3, the black line represents the original feature selection method (see Algorithm 3), and the red line represents the fast feature selection method (see Algorithm 6). We can see that the red line is much lower than the black line. Therefore, the speed of \(FFS\_IVKDE\) is faster than that of \(OFS\_IVKDE\) in feature selection.

Fig. 3
figure 3

Comparison of computing time of feature selection on Face, Hill, Colon

Full size image
Fig. 4
figure 4

Comparison of sample distribution on two features from Face Dataset

Full size image
Fig. 5
figure 5

Comparison of sample distribution on two features from Iris Data set

Full size image
Fig. 6
figure 6

Comparison of sample distribution on two features from Colon Data set

Full size image

7.2 Intuitive effect

In order to intuitively display the effectiveness of the proposed fast feature selection, we select Face, Iris and Colon to show the intuitive effect of the method. We compare scatter plot constructed by the first two features selected through Algorithm 6 with scatter plot constructed by two random features from original data. Here we set window width parameter h as 3/log2(n) where n denotes the number of samples. Figs 4, 5, 6 show the comparison of scatter plots, where each rectangle represents a sample and different colors represent different classes.

Sub-figures (a) in Figs. 4–6 show sample distribution under the first two features selected by our method, while sub-figures (b) in Figs. 4-6 show sample distribution under two random features. The x-axis denotes the first selected feature and the y-axis denotes the second selected feature. We can find that the sample distribution of the first two features selected by our method is clear, while the sample distribution of two random features has many intersections. It suggests that the top two features selected by our method have higher identifiability than the two random features, visually. Hence, the proposed feature selection does be effective.

7.3 Classification performance

Most of the traditional classifiers are for real-valued data. To classify interval-valued data, Dai et al. [28] proposed the extensions of K-Nearest Neighbor(KNN) method and Probabilistic Neural Network(PNN).

Table 3 The accuracy results of KNN
Full size table
Table 4 The accuracy results on PNN
Full size table
Table 5 The precision results on KNN
Full size table
Table 6 The precision results on PNN
Full size table
Table 7 The recall results on KNN
Full size table

Definition 14

[28] \(u_i\) and \(u_j\) are two objects of interval-valued information table. \(u_i=\left[ u_{i}^{k,-},u_{i}^{k,+} \right]\) and \(u_j=\left[ u_{j}^{k,-},u_{j}^{k,+} \right]\) represent the interval values of object \(u_i\) and \(u_j\) in kth feature. The distance between \(u_i\) and \(u_j\) is defined as follows:

$$\begin{aligned} Dis\left( u_i,u_j \right) =\sqrt{\sum _{k=1}^m{\left( P_{\left( u_{i}^{k}\geqslant u_{j}^{k} \right) }-P_{\left( u_{i}^{k}\leqslant u_{j}^{k} \right) } \right) ^2}} \end{aligned}$$

Where m denotes the number of conditional features and \(P_{\left( u_{i}^{k}\geqslant u_{j}^{k} \right) }\) denotes the possible degree of the interval value \(u_i\) relative to the interval value \(u_j\), which is designed as follows: \(P_{( u_{i}^{k}\geqslant u_{j}^{k})}=\min \{ \text {1,}\max \{ \frac{{u_i}^{k,+}-{u_j}^{k,-}}{({u_i}^{k,+}-{u_i}^{k,-})+({u_j}^{k,+}-{u_j}^{b,-})} ,0 \} \}\).

In this paper, we compare our method with six representive methods. In [27], a similarity relation between two interval values based on the possible degree of interval value A relative to interval value B was proposed. In [30], the \(\alpha\) dominance relation was presented. In [34], the relative bound difference similarity degree between two interval values was proposed. In [50], the \(\alpha\)-weak similarity relation between two interval values was proposed. Then we use these four kinds of relations to define conditional entropy similar to [27] for feature selection, and obtain four feature selection methods, namely Feature Selection of the Similarity Relation (FSSR), Feature Selection of \(\alpha\) Dominance Relation (FSDR), Feature Selection of the Relative Bound Difference similarity degree (FSRBD) and Feature Selection of the \(\alpha\)-Weak Similarity relation (FSWS). Attribute reduction using conditional entropy based on dominance fuzzy rough sets was proposed by [35] , called Attribute Reduction of Dominance Relation (ARDR). Recently, feature selection based on Interval Chi-Square Score was presented by [36], called Feature Selection of Interval Chi-Square Score (FSICSS). We proposed Fast Feature Selection method of the Kernel Density Estimation entropy (FFSKDE) in this paper. The range of parameter \(\theta\) involved in FSSR, FSDR, FSRBD, FSWS is set to \(\{0.4,0.5,0.6,0.7,0.8\}\). According to literatures [24, 51], the range of parameter h involved in the proposed FFSKDE is set to \(\{\frac{1}{log2(n)}, \frac{2}{log2(n)}, \frac{3}{log2(n)}\}\) where n denotes the number of samples. In this experiment, FSSR, FSDR, FSRBD, FSWS, FFSKDE feature selection methods select the optimal classification results within its corresponding parameter range.

Table 8 The recall results of PNN
Full size table

In the following, we will compare FFSKDE with FSSR,FSDR, FSRBD, FSWS, FSCISS, ARDR and All features on the indexes of accuracy, precision, recall which can comprehensively and well reflect the classification performance of these methods.

First, the accuracy results are shown in Table 3 and Table 4 where the optimal classification accuracies of the data among the seven feature selection methods are represented in bold. From Table 3 and Table 4, the times of being the optimal of FFSKDE method is higher than other six methods on both KNN classifier and PNN classifier. Moreover, in terms of the average classification accuracy on the data sets, FFSKDE method is not only higher than the other six comparative methods, but also higher than the average classification accuracy of ALL features. Especially, in KNN classifier and PNN classifier, only our method has an average classification accuracy of more than \(80\%\). By KNN classifier, our method’s average classification accuracy is about \(6\%\) higher than the sub-optimal method’s average classification accuracy. By PNN classifier, our method’s average classification accuracy is about \(4\%\) higher than the sub-optimal method’s average classification accuracy.

Second, the precision results are displayed in Table 5 and Table 6 where the optimal classification precision results among the seven feature selection methods are denoted in bold. By KNN classifier, we can observe the times when FFSKDE achieves the optimal results is higher than other comparative methods. By PNN classifier, although the times that FFSKDE achieves the best equal to FFSR, the average classification precision of FFSKDE is obviously higher than FFSS. What’s more, the average value of classification precision on FFSKDE is not only higher that of other comparative methods, but also higher ALL features.

Finally, the classification recall results are shown in Table 7 and Table 8 where the optimal classification recall results are represented in bold.We can get the same conclusion as classification precision. Then, we can get result that the FFSKDE proposed in this paper performs better than other methods and All features in accuracy, precision and recall. Therefore, the fast feature selection method proposed in this paper is effective.

8 Conclusion

Kernel density estimation technology has been applied in feature selection to avoid discretization for real-valued data. However, there are few studies on feature selection based on kernel density estimation for interval-valued data. Therefore, a feature selection method based on kernel density estimation entropy for interval-valued data is proposed in this paper. Firstly, we raise kernel density estimation of interval-valued data and study its’ properties. The kernel density estimation probability structure is constructed. By the constructed structure, a series of kernel density estimation entropies are defined. Further we present a fast feature selection method by kernel partition matrix, incremental expressions of kernel matrix and inverse of covariance matrix. Experiments are conducted to verify the proposed approach. The results show that the proposed fast feature selection method is efficient.

It is worth noting that the proposed fast feature selection algorithm doesn’t consider the correlation among the selected features. Therefore, in the future work, we will construct an improved feature selection method via introducing the concept of mutual information which can not only evaluate the correlation between the selected features and decision feature, but also evaluate the correlation among the selected features. However, how to construct the mutual information by kernel density estimation is challenging. In the future, we intend to study this issue.