M_k-NNG-DPC: density peaks clustering based on improved mutual K-nearest-neighbor graph

Abstract

Clustering by fast search and detection of density peaks (DPC, Density Peaks Clustering) is a relatively novel clustering algorithm published in the Science journal. As a density-based clustering algorithm, DPC produces better clustering results while using less parameters than other relevant algorithms. However, we found that the DPC algorithm does not perform well if clusters with different densities are very close. To address this problem, we propose a new DPC algorithm by incorporating an improved mutual k-nearest-neighbor graph (M_k-NNG) into DPC. Our M_k-NNG-DPC algorithm leverages the distance matrix of data samples to improve the M_k-NNG, and then utilizes DPC to constrain and select cluster centers. The proposed M_k-NNG-DPC algorithm ensures an instance to be allocated to the fittest cluster. Experimental results on synthetic and real world datasets show that our M_k-NNG-DPC algorithm can effectively and efficiently improve clustering performance, even for clusters with arbitrary shapes.

1 Introduction

Clustering analysis is an unsupervised learning technique [1] that recognizes different groups (clusters) underlying data. Clustering analysis has been applied to many fields such as pattern recognition [2], information retrieval [3], business intelligence [4], and so on. In the literatures, there are many clustering algorithms published, see for example [5,6,7,8,9,10,11,12,13,14,15]. Among those algorithms, hierarchy-based clustering [8,9,10] builds a binary tree to group similar data points. In density-based clustering [11, 12], a cluster is defined as a contiguous region of high density of data in the space. Model-based clustering assumes that the data is generated by a mixture of probability models. In general, clustering analysis involves two phases including class and function (also called a model). For a given data sample D, the class conducts rule-based or concept-based partitioning of D, while the function returns an array of labels corresponding to different clusters of D. Despite the tremendous efforts in the past a few decades, clustering analysis needs continued efforts with the emergence of new types of data in the era of big data.

In this paper, we focus on the state-of-the-art density peaks clustering (DPC) [16, 33,34,35]. As a density-based clustering algorithm, DPC produces better results while using less parameters than other clustering algorithms. However, it is found that the performance of DPC deteriorates significantly if clusters with different densities are very near. To address this problem, we propose to incorporate the mutual k-nearest-neighbor graph into DPC, called M_k-NNG-DPC. This proposed method can avoid assigning neighboring instances belonging to different clusters into the same cluster. Through constructing a mutual nearest neighbor graph, the theoretical analysis and the experimental results show that our M_k-NNG-DPC algorithm outperforms the DPC algorithm. In addition, our M_k-NNG-DPC algorithm can deal with clusters with arbitrary shapes.

The rest of this paper is organized as follows. In Sect. 2, the classical and well-performed clustering algorithms are briefly reviewed. In Sect. 3, the mutual k-nearest-neighbor graph and the DPC algorithm are introduced. In Sect. 4, we present the improved DPC algorithm, M_k-NNG-DPC, which combines the improved mutual k-nearest-neighbor graph with DPC algorithm. In Sect. 5, experimental studies are conducted to verify the effectiveness of our proposed algorithm. Section 6 concludes the paper.

2 Related work

Clustering analysis commonly differentiates objects from various groups (clusters) by the similarities or distances between pairs of objects. Typically, clustering algorithms are categorized based on a different set of rules for defining the similarity among data points [1, 21, 40,41,42,43,44, 55, 56]. As an example, in density-based clustering, a cluster is defined as an area with higher density than the other areas. The algorithm DBSCAN [11] is a classic density-based clustering method and designed to find arbitrary-shaped clusters. Through quantifying the neighborhood of a data point, DBSCAN can find a cluster with high dense in data space. The main drawback is that it is hard to systematically detect the density border since the cluster density decreases continuously, so that most of the parameters on density need to be specified manually.

Hierarchical clustering is another well-known clustering method. Hierarchical clustering (HC) methods represent data objects in a hierarchy or “tree” structure of clusters [15]. Hierarchical processes have two strategies: bottom-up or agglomerative, and top-down or divisive [1, 45,46,47]. Generally, HC is categorized into distance-based method or density-based method. For example, Gabor et al. [21] proposed a distance-based hierarchical clustering method that extends Ward’s minimum variance by defining a cluster distance and objective function in terms of Euclidean distance. On the other hand, density-based HC applied the density connectivity to investigate the reachable distance of all data points and hierarchical structures. For example, Campello et al. [36] proposed HDBSCAN as an improvement over the classic OPTICS algorithm by measuring the clustering stability. They formalized the problem to maximize the overall stability of selected clusters. In addition, there are some theoretical studies on the above research areas [48,49,50,51,52,53,54].

In recent years, there are many research works focusing on improving the performance of the existing algorithms. For example, Li et al. [37] proposed a divisive projected clustering (DPCLUS) algorithm to partition the dataset into clusters in a top-down manner for detecting correlation clusters in highly noisy data. Zhang et al. [38] proposed a density-based multiscale analysis to reliably separate “noisy” objects from “clustered” objects and is applicable to clusters of arbitrary shapes. Clustering by fast search and detection of density peaks (abbrev. DPC) [16] is a novel algorithm published in Science by Rodriguez and Laio in 2014. DPC can find arbitrary shaped clusters without requiring multiple parameters. Moreover, it is insensitive to noise underlying the data. DPC is our interest and focus of this paper.

3 Preliminary

In this section, we introduce the standard DPC algorithm and the notion of mutual k-nearest-neighbor graph. Here, we will also investigate several improved DPC algorithms.

3.1 DPC Algorithm

DPC includes two distinct procedures. In the first procedure, DPC uses the input parameters to compute the local density of a group of data points and find the density peaks, which are considered as cluster centers. In the second procedure, each data point is assigned to the nearest cluster with the largest density peak. The best cluster center should satisfy two constraints: the largest density and the maximum margin. For data sample i, its local-density $\rho_{i}$ and mini-distance $\delta_{i}$ are defined in Eqs. (1) and (2), respectively:

$$ \rho_{i} = \sum\limits_{j \ne i} {\chi (d_{ij} - d_{c} )} $$

(1)

$$ \delta_{i} = \mathop {\hbox{min} }\limits_{{j:\rho_{j} > \rho_{i} }} (d_{ij} ) $$

(2)

where d_ij is the distance between sample i and j, d_c is the truncation distance. The piecewise function $\chi (x)$ is defined as:

$$ \chi \left( {\text{x}} \right){ = }\left\{ {\begin{array}{*{20}c} {1,} & {x < 0} \\ {0,} & {others} \\ \end{array} } \right. $$

Besides Eq. (1), there is another approach to compute $\rho_{i}$ by using Gaussian function as follows [6]:

$$ \rho_{i} = \sum\limits_{j \ne i} {e^{{ - (\frac{{d_{ij} }}{{d_{c} }})^{2} }} } \, $$

(3)

In Eq. (1) $\rho_{i}$ is actually the number of data samples whose distances to sample i is less than d_c. In Eq. (3), however,$\rho_{i}$ is the sum of weighted distance of all samples to sample i. Since the probability that different samples have the same local densities is small, Eq. (3) is a suitable measure of local density, especially for small-scale datasets. The value of d_c directly influences clustering results. In DPC algorithm, d_c is set to such a value that the number of neighbors of each data sample is about one to two percent of the total data. DPC uses $\rho$ and $\delta$ to construct decision graph, and then selects data points with the large $\rho$ and $\delta$ values as the cluster centers. Each cluster center represents a cluster, and each data point is assigned to its nearest cluster.

The prominent advantage of DPC algorithm is that it can detect noisy data more precisely than other algorithms. DPC defines the boundary of a cluster as the member data points of the cluster. DPC considers the maximum density in a boundary of one cluster as the upper bound $\rho_{b}$ of local density for this cluster. Then the data whose density is less than $\rho_{b}$ is defined as noisy data.

DPC can find clusters with arbitrary shapes and dimensionalities. It works well in finding convex clusters. For clusters with very different densities, DPC cannot work well with the unique parameter $\rho$ and the unique parameter $\delta$.

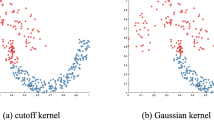
Figure 1 illustrates two clustering results obtained by Eqs. (1) and (3), respectively. In the dataset, there are three clusters with different densities including a ring structure and two circular structures. The density peaks of three cluster structures are greatly different, but their boundaries are not obvious. The result in Fig. 1a is generated by the algorithm using Eq. (1), where point A is a data point with maximum value of local density. Point B is another point with larger local density value than point A and is close to point A. Based on the assignment criterion of DPC, point A should be assigned to the circular cluster centered by Center1 that point B belongs to. Obviously, this is incorrect because point A belongs to the ring cluster centered by Center3. The clustering result illustrated in Fig. 1b reveals the similar problem.

Fig. 1

Clustering results by DPC

3.2 Mutual k-nearest-neighbor graph

A k-nearest-neighbor (abbrev. k-NN) graph [26] is a directed graph G_k-NN = (V, E), where V is the set of vertexes, each of which is a group of data points, and E is the set of edges. There is a connection from vertex X_i to X_j if X_j is the k-NN of X_i. Like the k-NN algorithm, in k-NN graph, the choice of k is crucial for a good performance.

In a k-NN graph G_k-NN = (V, E), for two arbitrary vertexes v_q and v_p, they are called k-mutual-neighbor if v_q belongs to k-NN (v_p) and v_p belongs to k-NN (v_q). For a dataset with the size n, a k-nearest-neighbor graph G_k-NN = (V, E) is called mutual k-nearest-neighbor graph [26, 27] (abbrev. M_k-NNG) if and only if v_q and v_p are k-mutual-neighbor, which is written as:

$$ M_{k - NN} G(v_{p} ,v_{q} ) = \left\{ {\begin{array}{*{20}c} {1,} & {{\text{if }}v_{q} \in k - NN(v_{p} )\;\;and\;\;v_{p} \in k - NN(v_{q} )} \\ {0,} & {\text{otherwise}} \\ \end{array} } \right. $$

(4)

From Eq. (4), we know that an edge generated in an M_k-NNG requires two vertexes of that edge to be k-mutual-neighbor for each other. Information are extracted from the relationships of vertexes in graph. In contrast with k-nearest-neighbor approach, information transmission of M_k-NNG is bidirectional and connected each other. For example, The data point B is one of the 2·k nearest neighbors of point A, while A does not belong to the set of 2·k nearest neighbors of point B. Then there is no connection between A and B. In other words, the condition that A is connected to B is that A and B belong to the set of the other 2·k nearest neighbors at the same time. So M_k-NNG is an undirected graph, while k-NN graph is a directed graph.

4 Our approach

The above examples show that the standard DPC algorithm incorrectly groups the data as illustrated in Fig. 1. One reason is that the standard DPC has limitation in data assignment. When clusters with different densities are very close, a data instance in the boundary region can be easily assigned incorrectly to a cluster with higher density. For example, in Fig. 1a, the point A locates at the area with higher density. In fact, A belongs to the ring-shape cluster with lower density. According to the chained allocation criteria of DPC algorithm the data point A will be assigned to the cluster that B locates in because that cluster has the highest density near to A. This will cause the consequent misallocation. Figure 1b illustrates the clustering result by using another estimation approach of local density, the estimation of Gaussian kernel function. Also, it is can be seen that the point C is erroneously assigned to the nearest cluster with higher density that D locates in.

Xie et al. proposed an improved DPC algorithm KNN-DPC to address the problem discussed above [28]. Although KNN-DPC considers the strength of k-nearest-neighbor approach, other problems emerge. First, when the densities of clusters are irregular, inappropriate assignment strategy may result in unreliable output. That is, the data instances in the lower density cluster are probably assigned to higher density cluster. Second, the existing DPC-based algorithms use a single instance as the cluster center (the representative of a cluster), which may be insufficient to represent the actual shape of the cluster.

To address these problems, we can consider the mutual k-nearest-neighbor graph (M_k-NNG). However, we found that if M_k-NNG is directly applied to DPC, the result is not much ideal, which will be illustrated in the following section. In this paper, we improve the basic M_k-NNG and fuse it into DPC to develop a novel DPC-based algorithm.

4.1 M_k-NNG and novel DPC

If the basic M_k-NNG is directly applied to clustering analysis, we find the benefit is limited. We illustrate this problem by using an experiment with a two-dimensional dataset shown in Fig. 2. There are four clusters with different densities and shapes in this dataset, but the marginal similarity between arbitrary two clusters is very high. In other words, the objects in the boundary regions are highly similar or “close to” each other.

Fig. 2

Plot of a two-dimensional dataset

There are two possible scenarios when using the basic M_k-NNG to deal with the dataset shown in Fig. 2. Figure 3 shows the clustering results when the parameter k is set to 3 and 4, respectively. For low-density clusters, if k is set as smaller values than the actual value, some points in low-density sections may become isolated points or clusters, for example, region C in Fig. 3a. If k is set as larger values, the points in the boundary regions may be connected to the same graph (the same cluster) even if they belong to different clusters. Region D in Fig. 3b is just such an example.

Fig. 3

Clustering results when using the basic M_k-NNG

To address the limitations of the basic M_k-NNG in handling clustering problems, we develop an improved version of M_k-NNG. Figure 4 shows the clustering result using the improved M_k-NNG. If k = 2 and k = 3, the improved M_k-NNG leads to better clustering results than the basic M_k-NNG.

Fig. 4

Clustering results when using the improved M_k-NNG

We now explain how to improve the basic M_k-NNG. We firstly give the following definitions.

Definition 1

Let i and j represent different data samples, and DS_knn(i) is a set which is formalized as Eq. (5). DS_knn(i) is a k-nearest-neighbor sample set, where knn(i) is the set containing k nearest neighbors of i, and 2·knn(j) represents a set having 2·k nearest neighbor samples of sample j.

$$ DS_{knn} (i) = \{ j|i \in 2 \cdot knn(j)\} $$

(5)

DS_knn(i) is an index set of other different data samples connected to sample i. According to Eq. (5), the size of DS_knn(i) is uncertain because of the different densities of data distribution. For those samples in a high-density space, there exists a great deal of nearest-neighbor samples of a sample i and the size of DS_knn(i) may be greater than 2·k. otherwise, for those samples in a low density space, DS_knn(i) may only include a few elements.

Definition 2

If the size of DS_knn(i) is larger than or equal to k, a distance-upper-bound pointp_DUB(i) is the k^th larger number, otherwise, p_DUB(i) is the data point of the most far nearest-neighbor. The description of p_DUB(i) is formalized as Eq. (6), where | DS_knn(i)| is the size of DS_knn(i), and distance(i, j) is a function which is used to calculate the distance of sample i and j.

$$ p_{DUB} (i) = \left\{ {\begin{array}{ll} {kth{\text{ nearest neighbor from }}DS_{knn} (i){ ,}} &\quad {{ |}DS_{knn} (i) |\ge k} \\ {\mathop {\text{argmax}}\limits_{{ \, j \in DS_{knn} (i)}} (distance (i,j ) ) { ,}} &\quad {otherwise} \\ \end{array} } \right. $$

(6)

Definition 3

The distance between sample i and p_DUB(i) is called distance level, dis_level(i), which is formalized as Eq. (7).

$$ dis_{level} (i) = distance(i,p_{DUB} (i)) $$

(7)

We use the nearest-neighbor set DS_knn to estimate the distance level of each data sample. According to Eq. (7), distance level dis_level(i) is actually a measure of density that can be used to distinguish those regions with different densities.

Definition 4

If the distance between sample i and j is less than the distance level dis_level(i) and dis_level(j), all such samples j constitute a set called mutual k-nearest-neighbor set ($S_{{M_{k - NN} }}$), which is formalized as Eq. (8). The graph generated from $S_{{M_{k - NN} }}$ is the improved M_k-NNG.

$$ S_{{M_{k - NN} }} (i) = \{ j|distance(i,j) < dis_{level} (j) \wedge distance(i,j) < dis_{level} (i)\} $$

(8)

According to Eq. (8), there is no upper bound of the connectivity for some nodes in the improved M_k-NNG because the number of mutual nearest neighbors for some samples in high density region may be greater than k.

The improved M_k-NNG has high significance to lift the clustering capacities, especially for density-based technique. When sample i is in the boundary of a high-density region and sample j is in the region of low-density, if i and j are “near”, the value of dis_level(i) is small and the value of dis_level(j) is large. Conseqently, i and j are not the mutual neighbors.

We next illustrate how to construct an improved M_k-NNG. When k = 2, Fig. 5a is the nearest neighbor graph of samples C and G, and (b) is the improved version of (a). For samples C and G, p_DUB(C) = {B, D, F, E}, and p_DUB(G) = {B, H}. According to Eq. (6) and (7), dis_level(C) = $\sqrt 2$, and dis_level(G) = 3. Figure 5 (b) can then be obtained according to Eq. (8). Because sample C is located in a high-density region, its mutual nearest neighbors are more than 2 k (k is 2, but the total number of neighbors is 5). For sample G, however, it is in a low-density region, and only has one neighbor.

Fig. 5

Illustration of M_k-NNG and its improved version

Figure 6 illustrates the results of using the basic M_k-NNG and its improved version to cluster the two-dimensional dataset illustrated in Fig. 2. Figure 6a, b are the results of the improved DPC algorithm with the improved M_k-NNG and the basic M_k-NNG, respectively. Obviously, the result in (a) is more accurate than the result in (b).

Fig. 6

Results of the improved DPC algorithm with the basic M_k-NNG and its improved version (k = 3)

We also test the DPC algorithm with the improved M_k-NNG using real-world datasets. Table 1 shows the NMI (Normalized Mutual Information) [30] results. By using the improved M_k-NNG, the DPC achieves much better results than it basic version for six real datasets.

Table 1 NMI Results of the improved DPC algorithm with different M_k-NNG on real datasets

The above results shows that DPC algorithm combined with the improved M_k-NNG outperforms the basic M_k-NNG. In the improved M_k-NNG, the distance level of each sample i must be calculated to decide whether two arbitrary samples are mutual nearest neighbors. We give Theorem 1 to state the relationship of mutual nearest neighbors and distance level.

Theorem 1

Samples i and j are mutual nearest neighbors, if and only if the distance between i and j is less than their distance levels dis_level(i) and dis_level(j).

Proof

Given an arbitrary sample i, let knn(i) be the set containing k nearest neighbors of i. According to the definition of DS_knn(i), if the size of DS_knn(i) is larger than k, written as | DS_knn(i)| > k, knn(i) ⊂ DS_knn(i); if | DS_knn(i)| = k, knn(i) = DS_knn(i); if | DS_knn(i)| < k, DS_knn(i) ⊂ knn(i). Therefore, if we want to prove that distance(i, j) ≤ dis_level(i) and distance(i, j) ≤ dis_level(j) hold, we need to prove that i belongs to knn(j) and j belongs to knn(i).

According to Definition 3, when |DS_knn(i)| ≥ k, the distance level dis_level(i) indicates the distance between sample i and the kth ordered neighbor in DS_knn(i); when | DS_knn(i)| < k, the dis_level(i) is the largest distance between sample i and the farthest neighbor. For sample i, let MaxDis(i) Eqals to $\mathop {\text{max}}\nolimits_{{j \in DS_{knn} \text{(}i\text{)}}} \text{(}distance\text{(}i\text{,}j\text{))}$, where j is an arbitrary sample in DS_knn(i). If distance(i, j) ≤ dis_level(i), j belongs to knn(i) according to Definition 3, thereby obtaining distance(i, j)≤ MaxDis(j). Similarly, j belongs to knn(i) and thereby obtaining distance(i, j)≤ MaxDis(i).

According to the above, we can prove that Theorem 1 holds.

Comparing the improved M_k-NNG with the basic M_k-NNG for DPC, the improved one prefers to those samples with similar density. Towards this nature, a traditional constraint should be added to the improved DPC algorithm.

Constraint 1

If samples i and j can be clustered together, one of the necessary constraints is that they are mutual k-nearest-neighbor.

Based on Constraint 1, the arbitrarily shaped and complex clusters can be obtained.

4.2 Assignment strategy

Through the above analysis, we know that the M_k-NNG for DPC needs Constraint 1 to improve its clustering performance. Thus, besides measuring the local density, distance and finding the cluster centers by decision graph, the DPC algorithm based on the improved M_k-NNG can take the advantage of the theories stated in Sect. 4.1 to assign data instances to those nearest clusters with the highest local densities. Especially, we need reasonable assignment strategy for those data instances in the boundary of clusters. We give Definition 5.

Definition 5

Let C₁, C₂, …, C_m be m different clusters, a set is called a cluster boundary if satisfying Eq. (9),

$$ S_{boundary} = \{ j|j \in S_{{M_{k - NN} }} \left( {i_{1} } \right),j \in S_{{M_{k - NN} }} \left( {i_{2} } \right), \ldots ,j \in S_{{M_{k - NN} }} \left( {i_{m} } \right),i_{1} \in C_{1} ,i_{2} \in C_{2} , \ldots ,i_{m} \in C_{m} \} $$

(9)

where i₁, i₂, …, i_m are m instances taken from C₁, C₂, …, C_m, respectively.

According to Definition 5, an instance j belonging to S_boundary means that j is the mutual nearest neighbor of other instances from multiple clusters. That is, there are multiple directed edges connected to node j. Then, the assignment strategy of j is that j is assigned to a cluster C if there are the maximum edges connected to it from C.

4.3 Proposed algorithm

In this section, we apply the improved mutual nearest neighbor graph and the assignment strategy for data instances to develop an improved DPC algorithm, called M_k-NNG-DPC. To avoid assigning neighboring instances belonging to different clusters into the same cluster, it is necessary to construct a mutual nearest neighbor graph to distinguish such neighbors. The idea is to use distance (near neighbors) and distribution density simultaneously, as stated in Sects. 4.1 and 4.2. The M_k-NNG-DPC algorithm is described in Fig. 7.

Fig. 7

Description of M_k-NNG-DPC algorithm

4.4 Analysis of computational complexity

For a data set D containing n instances, the computational complexities of calculating the distance matrix M and the parameter δ are all O(n²). The complexity of calculating local-density ρ using Eq. (1) is O(n²) as well. It is necessary to scan D to derive the distances between different instances less than a threshold d_c. If we use Eq. (3) to calculate ρ, the complexity is also O(n²) because the sum of weighted distances of all instances must be derived. Therefore, the overall complexity from Step 1–3 is O(n²). The calculation of DS_knn(i) in Step 4 involves finding 2 k neighbors of each instance i, and thus the complexity for n instances is O(n²). Because the complexity of deriving p_DUB(i) is O(2 kn), considering that the elements in p_DUB(i) needs to be ordered, the worst-case computational complexity of calculating dis_level(i) is O(n(2 k)²), where k is usually far less than n. According to Eq. (8), the computational complexity of Step 5 is O(n²). Thus, the overall complexity of the M_k-NNG-DPC algorithm is O(n²). In fact, the time complexities of DPC algorithm and its variations are all O(n²) [16, 28, 33, 34, 36], so the computational complexity of the proposed algorithm is approximate to or equal to the other DPC-based algorithms.

5 Experimental analysis

In this section, we test the proposed M_k-NNG-DPC algorithm on 18 datasets and compare it with nine classical clustering algorithms.

5.1 Experimental methodology

5.1.1 Data sets

We test our proposed algorithm M_k-NNG-DPC with eighteen benchmark datasets from UCI machine learning repository [29]. The important statistics of the benchmark datasets are summarized in Table 2. The datasets listed in Table 2 are all real and multi-dimensional. And all the class labels are removed from these datasets to generate unlabeled data.

Table 2 The benchmark datasets used in this paper

5.1.2 Compared algorithms

We compare the M_k-NNG-DPC algorithm with nine well-known clustering algorithms including the standard DPC [16], DBSCAN [11], Spectral clustering [19], BIRCH [8], Mean shift [18], Gaussian Mixture Model (GMM) [23], K-means [6], FCM [24] and Affinity Propagation (AP) [17].

DBSCAN is a representative method which models clusters as dense regions in the data space and can discover arbitrary clusters. Spectral clustering is a representative method in high dimensional data applications, which combines feature extraction approaches with clustering strategies. Spectral clustering uses matrix theory including affinity matrix, computation of eigenvectors, and transformation of vector spaces. BIRCH is another representative algorithm in hierarchical clustering. BIRCH integrates bottom-up strategy with a kind of data structure, namely, clustering feature tree, resulting in multiphase hierarchical clustering. Mean shift clustering is a typical non-parametric feature-space analysis technique with the characteristics of application-independence and non-assumption of any predefined shape on data clusters. The GMM can be viewed as a mixture of a number of Gaussian components. The aim of GMM is to maximum the log-likelihood function. The K-means clustering algorithm is based on distance measurement. FCM is based on Euclidean distance function and associated with fuzzy mathematics. The AP method is one of the state-of-the-art methods proposed recently, which takes as input measures of similarity between pairs of data points. These well-known models apply probability-, evolution-, or ML-based ideas, which is also applied in our proposed approaches.

5.1.3 Evaluation metrics

We use five metrics to evaluate the performances of the clustering algorithms:

(1) Clustering accuracy: the accuracy of a clustering algorithm is the ratio of correct assignments to the whole dataset. The computational equation of accuracy (Acc) is

$$ {\text{Acc}} = \frac{{\mathop \sum \nolimits_{i = 1}^{k} a_{i} }}{\left| D \right|} $$

(10)

In Eq. (10), the parameter a_i denotes the number of data objects that are correctly assigned to cluster C_i, k is the number of clusters, and |D| means the size of dataset D.

(2) Clustering F-score: a weighted average of the Precision and Recall, where it reaches its best value at 1 and worst at 0, or it is viewed as the harmonic mean of Precision and Recall. Precision means the precision of the clustering results, which is the degree to which repeated measurements show the same results if conditions unchanged. Precision (PR) is calculated by:

$$ {\text{PR}} = \frac{{\sum\nolimits_{i = 1}^{k} {\frac{{a_{i} }}{{a_{i} + b_{i} }}} }}{|D|} $$

(11)

In Eq. (11), if a data set D contains k clusters, a_i denotes the number of data objects that are correctly assigned to cluster C_i while the parameter b_i denotes the data objects that are incorrectly assigned to C_i.

Recall (RE) is the ratio of the number of data objects but are falsely clustered. Assuming that c_i denotes the number of data objects belonging to the ith cluster but are falsely assigned to other clusters, RE is defined as:

$$ {\text{RE}} = \frac{{\sum\nolimits_{i = 1}^{k} {\frac{{a_{i} }}{{a_{i} + c_{i} }}} }}{|D|} $$

(12)

Using Eq. (11) and (12), F-score is defined as:

$$ {\text{F-score}} = \frac{{2 * {\text{PR*RE}}}}{{{\text{PR}} + {\text{RE}}}} $$

(13)

(3) NMI (Normalized Mutual Information) [30]: a commonly used index in evaluating the effectiveness of a clustering algorithm. NMI is calculated by:

$$ {\text{NMI}}(X,Y) = \frac{I(X,Y)}{{\sqrt {H(X)H(Y)} }} $$

(14)

where X and Y are random variables, I(X, Y) means the mutual information between X and Y, and H(X) is the entropy of X. I(X, Y), H(X) and H(Y) are obtained by Eqs. (15), (16) and (17), respectively,

$$ I(X,{\kern 1pt} {\kern 1pt} {\kern 1pt} Y) = \sum\nolimits_{h = 1}^{{k^{(a)} }} {\sum\nolimits_{l = 1}^{{k^{(b)} }} {n_{h,l} \log \left(\frac{{n \cdot n_{h,l} }}{{n_{h}^{(a)} n_{l}^{(b)} }}\right)} } $$

(15)

$$ H(X) = \sum\nolimits_{h = 1}^{{k^{(a)} }} {n_{n}^{(a)} \log \frac{{n_{h}^{(a)} }}{n}} $$

(16)

$$ H(Y) = \sum\nolimits_{l = 1}^{{k^{(b)} }} {n_{l}^{(b)} \log \frac{{n_{l}^{(b)} }}{n}} $$

(17)

where $n_{h}^{(a)}$ is the number of data objects in cluster h when their class-label is a, and $n_{l}^{(b)}$ is the number of data instances in cluster l when their class-label is b. And n_h, _l is the number of objects that are in cluster h associated with a as well as in group l associated with b.

(4) Clustering Purity: a simple clustering index in evaluating the proportion of correctly clustered samples. Purity is calculated by:

$$ {\text{Purity}} = \mathop \sum \limits_{i = 1}^{K} \frac{{m_{i} }}{m}P_{i} $$

(18)

where m_i is the number of all members in cluster i, and m is the number of members involved in the whole cluster partition. P_i is proportion of the largest number of members in cluster i to all members of this cluster. And K is the number of clusters.

(5) ARI (adjusted rand index): a variation of clustering evaluation index RI, ARI is to calculate the similarity of random uniform distribution between real class label and predicted class label. The larger ARI is, the better the clustering effect is. RI and ARI are calculated by:

$$ RI = \frac{a + b}{{C_{2}^{{n_{samples} }} }} $$

(19)

$$ ARI = \frac{RI - E(RI)}{\hbox{max} (RI) - E(RI)} $$

(20)

where a is the sample log in same label between real label and predicted label, b is the sample log in different label between real label and predicted label. $C_{2}^{{n_{samples} }}$ is all possible combinations of pairs of samples. E(RI) is the expected value of RI.

5.2 Results and analysis on synthesis data

We first use three two-dimensional datasets to illustrate the performance of the standard DPC, the basic M_k-NNG-based and the improved M_k-NNG-based DPC. Each of these synthesis datasets contains several clusters with different shapes and distribution densities. In this section, we employ the Euclidean distance as the distance measure. To facilitate computation in the algorithm, the truncation distance d_c is represented by percentages. We sort all the distances in ascending order based on the distance matrix, and then take the value at position n % × size (D) of these ordered distances, where n is a tuning parameter and D is a dataset, as the value of d_c.

Figures 8, 9, and 10 illustrate the clustering results on three synthesis datasets, Zelnik6, Path-based1, and Compound, respectively, produced by the standard DPC, and the proposed M_k-NNG-DPC algorithms.

Fig. 8

Clustering results on the synthesis dataset Zelnik6

Fig. 9

Clustering results on the synthesis dataset Path-based1

Fig. 10

Clustering results on the synthesis dataset Compound

Zelnik6 dataset has 238 data instances and contains 3 clusters. The circle-shaped cluster in Zelnik6 has low-density, as shown in Fig. 8a, the clusters obtained by the standard DPC are not good enough (or has higher error rate). The main reason is that the density of this circle-shaped cluster is low but the standard DPC cannot solve this problem very well. Figure 8b shows the clusters clustered by M_k-NNG-DPC. There are edges between the circle-shaped cluster and other two high-density clusters, but the edges are sparse. This can help M_k-NNG-DPC generate arbitrary-shaped clusters with different densities. Figure 8c shows the clusters generated from M_k-NNG in (b).

Figure 9 shows the clustering results on the synthesis dataset Path-based1 which contains 300 data instances and 3 clusters. Figure 9a shows the results obtained from the standard DPC. Since the boundaries of the circle-shaped cluster and the other two clusters are not clear, the clusters generated by the standard DPC have many errors because the data instances in the boundaries are easily clustered erroneously. As shown in Fig. 9b, the clustering effect becomes much better when using the M_k-NNG-DPC than using the standard DPC. The result illustrated in Fig. 9c is generated from (b). The M_k-NNG-DPC algorithm focuses on the margin sections and there are few edges between different clusters, thereby obtaining very high accurate rate.

In Fig. 10a, c illustrate the clustering results generated by the standard DPC and the M_k-NNG-DPC algorithm, respectively, on dataset Compound which has 399 instances and 6 different shaped clusters with different densities. In Fig. 10a, there are two clusters in the left lower part of the coordinate, but the standard DPC cannot cluster them correctly because it only considers the factors of distance and density but does not consider the margin size between different clusters. The M_k-NNG-DPC algorithm produces the result illustrated in Fig. 10b, but there are only few edges in the margins of different clusters. Then we can obtain the clusters shown in Fig. 10c, from which we can see that the clustering effect is well.

From the above experiments on those synthesis data, our proposed algorithm is well-performed. Although the standard DPC and the M_k-NNG-DPC algorithms choose the same cluster centers, the effects are significantly different. This also validates the analysis for the M_k-NNG-DPC algorithm in Sect. 4. Due to the join of a constraint in the M_k-NNG-DPC algorithm, when data instances are assigned to a cluster, there is less chance for those instances with different local densities to be assigned to a same cluster. This alleviates the problem of the standard DPC and lifts the clustering performance.

5.3 Results and analysis on the benchmark datasets

In this section, we use the benchmark datasets, compared algorithms, and evaluation metrics listed in Sect. 5.1 to validate our proposed algorithm.

The comparison results on eight synthesis datasets are presented in Tables 3 and 4. These results are obtained by using five metrics and nine compared algorithms. From Table 3 the proposed algorithm M_k-NNG-DPC is better than most of the other algorithms.

Table 3 The comparison of Acc, F-Score and NMI for each clustering algorithms on synthetic datasets

Table 4 The comparison of purity and ARI for each clustering algorithms on synthetic datasets

For dataset zelnink6 and Path-based1, as illustrated in Figs. 8a and 9a, they contain multiple clusters with different shapes and densities. Obviously, M_k-NNG-DPC has the best clustering results. Because of the deficiencies of the standard DPC algorithm, as stated in Sect. 3, the lack of samples can limit the capability of allocation to the corresponding clusters, which increases the misclassification rates when there are clusters with low density. K-means, FCM and AP algorithms can cluster convex-shaped, especially spherical-shaped clusters, but are unsuitable for arbitrary-shaped ones. GMM is a Gaussian model-based algorithm, which can find those clusters with high density obeying normal distributions. However, for those sparse clusters, GMM has low clustering performances. Mean shift algorithm is a non-parametric feature-space clustering technique for finding the maxima of a density function by iteration. The mean shift algorithm has been widely used in many applications and has good clustering effect. However, there is no rigid proof for the convergence of the algorithm, especially in a high dimensional space.

The dataset Compound contains some different clusters with low-density and high-density, as illustrated in Fig. 10a. There are sparse clusters in the Compound, so M_k-NNG-DPC cannot perform very well because it uses the standard DPC to choose cluster centers, which is difficult to obtain the ideal centers. But M_k-NNG-DPC obtains the best result in F-score index. Nevertheless, the clustering results in all indexes are better than the standard DPC. The dataset Atom contains 3 features and 800 instances. Its shape looks like an atom, in the center of which there is the nucleus, that is, a cluster with the higher density than the surrounding neutrons (cluster). For this dataset, obviously, the distance-based clustering algorithms cannot perform well. Those non-distance-based algorithms, such as DBSCAN (density-based), Spectral clustering (graph-based), GMM (probability-based), and our proposed method, can obtain better results. Given a dataset in some space, DBSCAN groups together data points that are closely packed together with many nearby neighbors (“nearby” is measured by some parameters). Spectral clustering algorithm makes use of the eigenvalues (called spectrum) of the similarity matrix of the dataset to perform dimensionality reduction before clustering in fewer dimensions. M_k-NNG-DPC is also based on graph theory, as stated in the above section. The clustering results of these three algorithms are the best, that is, 100%.

The DIM256 and DIM1024 are two high-dimensional datasets, which contain 1024 and 10 clusters, 256 and 1024 dimensionalities, respectively. The clusters of these two datasets are separate in space and are all convex shapes, so most algorithms, including our proposed algorithm, obtain the highest values of all indexes. It indicates that M_k-NNG-DPC can deal with high-dimensional datasets. GMM algorithm cannot find the fittest parameters due to the high dimensionality, so there are no results on these two datasets. The S3 and S4 datasets all contains 5000 samples and 16 clusters. Although the cluster center of each cluster is obvious, the margins between the neighbored clusters are overlapped. K-means, FCM, and AP algorithms are fit for such datasets like S3 and S4, and they perform well on these data. The mean shift algorithm employs an iterative process to find those regions with high density, thereby having good performances on S3 and S4 data. However, the mean shift cannot effectively deal with the overlapping problems, so it is not the best. The GMM and Birch algorithms perform worse than other algorithms because the densities of many different clusters are similar and the density-based algorithms cannot distinguish these clusters well. M_k-NNG-DPC can overcome these disadvantages and improve the performance of the standard DPC, so it has the best clustering results on S3 and S4 data.

The experimental results on 10 real datasets are listed in Tables 5 and 6. The Iris dataset has 150 instances with 4 features and contains 3 clusters, two of which are nonlinear separable. The M_k-NNG-DPC algorithm is obviously more efficient on five indexes than all other algorithms. On the other hand, the standard DPC, K-means, FCM, spectral clustering, AP, and GMM can correctly allocate most of the instances to their clusters, so the clustering results are not very bad. The Seeds is a 7-dimensional dataset containing 210 instances which belong to three different clusters. Experimental results show that both the M_k-NNG-DPC and the standard DPC are able to find the correct number of clusters. Because the size of this dataset is small and the distribution of instances in space is too uniform, the results of M_k-NNG-DPC are slightly less than the standard DPC in Acc, Purity and F-score, but larger than the standard DPC in NMI and ARI indexes. The results of the other algorithms are almost similar except for DBSCAN that obtains the worst effect. The Art dataset has 300 instances with four attributes and contains three clusters. The clustering effect of M_k-NNG-DPC is clearly better than other algorithms in all indexes.

Table 5 Comparison of Acc, F-score and NMI for 10 clustering algorithms on UCI datasets

Table 6 Comparison of Purity and ARI for 10 clustering algorithms on UCI datasets

The Libras movement and Ionosphere are high-dimensional datasets in which the Ionosphere is an imbalanced dataset having 351 instances (containing one positive class and one negative class [31]). The M_k-NNG-DPC prefers to assign those smaller clusters to the larger ones. Therefore, for the imbalanced data, the positive instances are possibly merged to the negative clusters, which generates that the accurate rate (Acc) is slightly less than the standard DPC. But the clustering effects are better than other approaches for all indexes. The Libras movement is a time-sequential dataset. The spectral clustering algorithm achieves the best results on the F-score and NMI indexes because the spectral is fit for time sequence [32]. The M_k-NNG-DPC has the best value on the Acc and ARI indexes.

The WDBC is also a multi-dimensional dataset containing 30 features and has binary clusters. The M_k-NNG-DPC achieves the greater improvement than the standard DPC for all indexes, especially the NMI index. Some other algorithms obtain good performances with the Acc and F-score indexes, including K-means, FCM, spectral clustering, AP, and GMM algorithms. The Glass data contains 6 clusters and 214 instances with ten features. The M_k-NNG-DPC has the best effect on the Acc and NMI indexes and has similar result with DPC on F-score index. Some other algorithms have the similar performances on this dataset, including spectral clustering, AP, FCM, GMM, while the Mean shift method has the worst experimental values. The sizes of the Waveform and Image Segmentation datasets are larger than other datasets. The Waveform contains noisy values, which is a challenge for most of the algorithms. The graph-based techniques should be more suitable for this challenge due to the capacity of handling noisy data. From the experiments on the Waveform, the M_k-NNG-DPC, DPC, spectral clustering, and GMM have good performances because they are all graph-based algorithms, among which the M_k-NNG-DPC is the best. The Image Segmentation is a kind of image data on which our proposed algorithm achieves the best effect with the Acc, Purity, ARI and F-score indexes and the comparative result for the NMI, which is said to be able to deal with those complicated data. The Ecoli is a biological dataset containing protein localization sites. Particularly, the Ecoli is an imbalanced dataset that has several positive clusters, each of which only contains a few instances. The index values of the M_k-NNG-DPC exceed the counterparts of other algorithms. It is indicated that our proposed approach is able to handle the imbalanced problem and biological data. For those imbalanced problems, K-means, AP, FCM, and spectral clustering algorithms easily assign the positive clusters to the negative ones, thereby obtaining fewer clusters than the actual number.

The running time of DPC algorithm and M_k-NNG-DPC algorithm on UCI datasets are listed in Table 7. Most of the time cost of M_k-NNG-DPC algorithm is used to establish the mutual neighbor graph and merge the ‘negative classes’. For the same dataset, the time cost of the neighbor graph established by different parameters k is the same. If the value of parameter k is small, the probability that the samples in the nearest neighbor graph are near to each other will decrease, which leads to generate more ‘negative classes’, thereby spending more time to merge ‘positive classes’ and ‘negative classes’.

Table 7 The running time of DPC algorithm and M_k-NNG-DPC algorithm on UCI datasets

6 Conclusion and future work

As a widely used application field, clustering analysis is becoming more and more important, especially in the big data era. As the accumulation of data, the huge amounts of data mean that it is hard to obtain the training data because the enough labels and the actual number of classes might be hard to obtain, so that ‘labeled’ methods cannot be used normally. On the other hand, although there has been a great deal of clustering techniques, most of them are the specific data-oriented. That is, the generalization of many clustering algorithms is poor.

In this paper, we apply some classical and well-performed clustering algorithms, which can achieve good generalization, to perform the comparative analysis. In this study, we focus on DPC-based approach. We emply a mutual k-nearest-neighbor graph-based structure. The experimental analysis shows that, when the basic mutual k-nearest-neighbor graph is applied to DPC algorithm, the effects are not ideal and even much poor. Therefore, we improve the basic mutual k-nearest-neighbor graph to lift the DPC algorithm. This approach is to constrain the cluster assignment for data instances, which can distinguish the cluster membership of each instance more efficiently according to the densities of nodes in a graph. Typically, this technique can avoid such a case that the instances belonging to different densities of clusters are misclassified into the same cluster. It not only lifts the capacity of the DPC, but improve the performance of clustering the arbitrary shaped clusters.

The DPC-based algorithms are stable and robust in clustering many kinds of data. Our future work is to consider other complex data, such as Web data stream, video data, and DNA data, to be clustered by a series of the DPC-based algorithms.