DCSVM: fast multi-class classification using support vector machines

Abstract

Using binary classification techniques to perform multi-class classification of data is still of great practical interest due to the robustness and simplicity of binary classifiers. These techniques produce a single multi-class classification decision based on many binary decisions. Our work relies on the simple observation that as dimensionality increases so does the data sparsity and, consequently, a single binary classifier may separate multiple classes. Therefore, we claim that the number of binary decisions can be significantly reduced. We present Divide and Conquer Support Vector Machines (DCSVM), an efficient algorithm for multi-class classification using Support Vector Machines. DCSVM is a divide and conquer algorithm which relies on data sparsity in high dimensional space and performs a smart partitioning of the whole training data set into disjoint subsets that are easily separable. A single prediction performed between two partitions eliminates at once one or more classes in one partition, leaving only a reduced number of candidate classes for subsequent steps. The algorithm continues recursively, reducing the number of classes at each step, until a final binary decision is made between the last two classes left in the competition. In the best case scenario, our algorithm makes a final decision between k classes in $O(\log k)$ decision steps and in the worst case scenario DCSVM makes a final decision in $k{-}1$ steps, which is not worse than the existent techniques.

1 Introduction

Machine learning classification is the task of performing data categorization based on previously seen data categories (labels or classes). When only two classes are present it is called binary classification and for more than two classes it is called multiclass classification. Binary classification is inherently simpler to perform and decomposing a multiclass classification problem into a number of binary classification problems (called transformation to binary) has been a popular method for producing multiclass classification [12, 16]. The transformation to binary methods inherit the robustness and simplicity of the binary methods but suffer, in general, from producing many pairs of binary classifiers and typically using a large number of binary decisions for producing a single multiclass classification decision. In this article we propose a new method of performing multiclass classification using transformation to binary with a significantly reduced number of binary decisions. Our method relies on the key observation that in high dimensional space the sparsity of the data may increase significantly. As a consequence, a single binary classifier may accurately perform classification for more than the two classes the classifier was designed for. We show how to detect such practical situations and efficiently exploit them to perform multiclass classification with less binary decision.

According to Wikipedia [29], the curse of dimensionality refers to various phenomena that arise when analyzing and organizing data in high-dimensional spaces (often with hundreds or thousands of dimensions) that do not occur in low-dimensional settings such as the three-dimensional physical space. The expression was introduced by Richard E. Bellman in a highly acclaimed article considering problems in dynamic optimization [2, 3]. In essence, as dimensionality increases, the volume of the space increases rapidly, and the available data become sparser and sparser. In general, this sparsity is problematic for any method that requires statistical significance. In order to obtain a statistically sound and reliable result, the amount of data needed to support the result often grows exponentially with the dimensionality, which would prevent common data processing techniques from being efficient.

Fig. 1

Binary SVM classifier for classes 1 and 2 out of a dataset of six classes

Since its introduction, the Support Vector Machines (SVM) [7] has quickly become a popular tool for classification which has attracted a lot of interest in the machine learning community. However, SVM is primarily a binary classification tool. The multiclass classification with SVM is still an ongoing research problem (see, for example, [4, 24, 25, 30] for some recent work and [14, 20] for real-life applications). We present an SVM-based multi-class classification method that exploits the curse of dimensionality to efficiently perform classification of highly dimensional data.

Our method, the Divide and Conquer SVM (DCSVM) algorithm, exploits the curse of dimensionality and the power of SVM binary classifiers to produce faster multiclass classificaitons. The algorithm’s idea is described next using the example in Fig. 1. The figure shows 6 classes (1—red, 2—blue, 3—green, 4—black, 5—orange, and 6—maroon) of two-dimensional points and a linear SVM separation of classes 1 and 2 (the line that separates the points in these classes). It happens that the SVM model for classifying classes 1 and 2 completely separates the points in classes 4 (which takes class 2’s side) and 6 (which takes class 1’s side). Moreover, the classifier does a relatively good job classifying most points of the class 5 as class 2 (with relatively few points classified as 1) and a poor job on classifying the points of class 3 (as the points in this class are classified about half as 1’s and the other half as 2’s). With DCSVM we use the SVM classifier for classes 1 and 2 for a candidate of an unknown class: if the classifier predicts 1, then we next decide between classes 1, 6, 3, and 5; if the classifier predicts class 2, then we next decide between classes 2, 4, 3, and 5. Notice that in either case one or more classes are eliminated, and we are left to predict a fewer number of classes. That is, a multi-class classification problem of a smaller size (less classes). The algorithm then proceeds recursively on the smaller problem. In the best case scenario at each step half of the k classes will be eliminated and the algorithm will finish in $\lceil \log k\rceil$ steps. Notice that, in the above scenario, classes 2 and 4 are completely separated from classes 1 and 6, whereas classes 3 and 5 are not clearly on one side or the other of the separation line. For this reason, classes 3 and 5 are part of the next decision step, regardless of the prediction of the first classifier.

However, there is a significant difference between classes 3 and 5. While class 3 is almost divided in half by the separation line, class 5 can be predicted as “2” with a relatively small error. In DCSVM we use a threshold value $\theta$ to indicate the maximum classification error accepted in order to consider a class on one side or the other of a separation line. For instance, let us consider that only 2% of the points of class 5 are on the same side as class 1. With the threshold value set to 0.02, DCSVM will separate classes 1, 3, and 6 (when 1 is predicted) from classes 2, 3, 4, and 5 (when 2 is predicted). A higher threshold value will produce a better separation of classes (less overlapping) and less classes to process in the subsequent steps. This comes at the price of possibly sacrificing the accuracy of the final prediction.

Clearly, the method presented in the example above is suitable for multiclass classification using a binary classifier, in general. Our choice of using SVM is based on the SVM algorithm’s remarkable power in producing accurate binary classification. Our main contribution is producing a multiclass classification decision faster than the previously proposed methods, based on performing significantly less binary decisions. We do so without sacrificing the accuracy of the previously proposed methods. However, the accuracy of each binary decision and how fast a binary decision is produced depend solely on the performance of the binary classifier being used. Of course, using binary classifiers for multiclass classification has the obvious disadvantage of having to create a large number of classifiers ($k(k{-}1)/2$ for k classes), this process is highly parallelizable. A major challenge for our method was deciding which classifiers to use and in which order to achieve best results. For this purpose, we introduce some measures (Definitions 3 and 4) in Sect. 3.1 and explain how to use these measures to achieve our goals.

The content of this article is organized as follows. We give a brief description of binary classification with SVM and related work on using SVM for multi-class classification in Sect. 2. DCSVM is described in detail in Sect. 3 and experimental results (including performance comparisons with one-versus-one approach) are given in Sect. 4. We conclude in Sect. 5.

2 Preliminaries and related work

Support Vector Machines (SVM) [7] was primary developed as a tool for the binary classification problem by finding a separation hyperplane for the classes in feature space. If such a plane cannot be find, the “separating plane” requirement is softened and a maximal margin separation is produced instead. Formally, the problem of finding a maximal margin separation can be stated as a quadratic optimization problem. Given a set of L training vectors $\mathbf {x}_i\in {\mathbb {R}}^d$, $i = 1\ldots L$ with labels $y_i\in \{-\,1,1\}$ and a feature space projection $\varPhi : {\mathbb {R}}^d\rightarrow H$, the SVM method consists in finding the solution of the following:

$$\begin{aligned} {\begin{array}{ll} \min \limits _{\mathbf {w}\in H, b\in {\mathbb {R}},\xi _i\in {\mathbb {R}}} &{} \quad \frac{1}{2}\mathbf {w}^T\mathbf {w} + C\sum \limits _{i=1}^L\xi _i \\ \text{ subject } \text{ to } &{}\quad y_i\left( \left\langle \mathbf {w},\varPhi (\mathbf {x}_i)\right\rangle + b\right) \ge 1 - \xi _i \\ &{}\quad \xi _i \ge 0,\ i=1\ldots L\\ \end{array}} \end{aligned}$$

where $\mathbf {w}\in H$ is the weights vector and $C\in {\mathbb {R}}^+$ is a cost regularization constant. The corresponding decision function is:

$$\begin{aligned} f(\mathbf {x}) = sign\left( \left\langle \mathbf {w},\varPhi \left( \mathbf {x}\right) \right\rangle + b\right) \end{aligned}$$

An interesting property of the method is that the dot product can be represented by a kernel function:

$$\begin{aligned} k(\mathbf {x},\mathbf {x}') = \left\langle \varPhi (\mathbf {x}),\varPhi \left( \mathbf {x}' \right) \right\rangle \end{aligned}$$

which is computationally much less expensive than actually projecting $\mathbf {x}$ and $\mathbf {x}'$ into the feature space H.

In the case of multiple classes, the problem formulation becomes more complicated and inherently more difficult to address. Given a set of L training vectors $\mathbf {x}_i\in {\mathbb {R}}^d$, $i = 1\ldots L$ with labels $y_i\in \{1, \ldots , k\}$, one must find a way to distinguish between k classes.

Several approaches were proposed, which can be grouped into direct methods (a single optimization problem formulation for multi-class classification) and indirect methods (using multiple binary classifiers to produce multi-class classification). Many of the indirect methods were introduced, in fact, as methods for multi-class classification using binary classifiers, in general. They are not limited to the SVM method.

A comparison [16] of these methods of multi-class classification using binary SVM classifiers shows that one-versus-one method and its Directed Acyclic Graph improvement are more suitable for practical use.

2.1 Direct formulation of multi-class classification

Direct formulations to distinguish between k classes in a single optimization problem were given in [6, 8, 27, 28] or, more recently, in [15, 30]. Each of these formulations has a single objective function for training all k-binary SVMs simultaneously and maximize the margins from each class to the remaining ones. The decision function then chooses the “best classified” class.

For instance, Crammer et al. in [8] solve the following optimization problem for k classes:

$$\begin{aligned} {\begin{array}{ll} \min \limits _{\mathbf {w}_m\in H, \xi _i\in {\mathbb {R}}} &{} \quad \frac{1}{2}\sum \limits _{m=1}^k\mathbf {w}_m^T\mathbf {w}_m + C\sum \limits _{i=1}^L\xi _i\\ \text{ subject } \text{ to } &{} \quad \left\langle \mathbf {w}_{y_i},\varPhi (\mathbf {x}_i)\right\rangle - \left\langle \mathbf {w}_t,\varPhi (\mathbf {x}_i)\right\rangle \ge 1 -\delta _{y_i,t} - \xi _i \\ &{}\quad \xi _i \ge 0,\ i=1\ldots L,\ \ t = 1\ldots k \end{array}} \end{aligned}$$

(1)

where $\delta _{i,j}$ is the Kronecker delta function. The corresponding decision function is:

$$\begin{aligned} argmax_mf_m(\mathbf {x}) = argmax_m\left\langle \mathbf {w}_m,\varPhi (\mathbf {x})\right\rangle \end{aligned}$$

The original formulation addresses the classification without taking into account the bias terms $b_t$ (for each of the k classes). These can be easily included in the formulation using additional constraints (see, for instance, [16]). Crammer’s formulation is among the most compact optimization problem formulations for multi-class classification problem.

A common issue of the single optimization problem formulations for multi-class classification is the large number of variables involved. For instance, (1), although a compact formulation, includes $L\times k$ variables (not taking into account $b_i$’s, if included), which yields large computation complexity. In [15], Crammer’s formulation is extended by relaxing its constraints and subsequently solving a single l-variable quadratic programming problem for multi-class classification.

2.2 One-versus-rest approach

The one-versus-rest approach [5, 26, 27] is an indirect method relying on binary classifiers as follows. For each class $t \in \{1, \ldots , k\}$ a binary classifier $f_t$ is created between class t (as positive examples in the training set) and all the other classes, $\{1, \ldots , t-1, t+1, \ldots , k\}$ (all as negative examples in the training set). The corresponding decision function is then:

$$\begin{aligned} f(\mathbf {x}) = argmax_{1\le t\le k}f_t(\mathbf {x}) \end{aligned}$$

That is, the class label is determined by the binary classifier that gives maximum output value (the winner among all classifiers). A well-known shortcoming of the one-versus-rest approach is the highly imbalanced training set for each binary classifier (the more classes, the bigger the imbalance). Assuming equal number of training examples for all classes, the ratio of positive to negative examples for each binary classifier is $1 / (k{-}1)$. The symmetry of the original problem is lost and the classification results may be dramatically affected (especially for sparse classes).

2.3 One-versus-one approach

The one-versus-one approach ([11, 18, 19, 22] or the improvement by Platt et al. [23]) aims to remove the imbalance problem of the one-versus-rest method by training binary classifiers strictly with data in the two classifier’s classes. For each pair of classes, $s,t\in \{1, \ldots , k\}$ a binary classifier $f_{s,t}$ is created. This classifier is trained using all data in class s as positive examples and all data in class t as negative examples, hence all balanced binary classifiers. Each binary classifier is the result of a smaller optimization problem, at the cost of producing $k(k{-}1)/2$ classifiers. The corresponding decision function is based on majority voting. All classifiers $f_{s,t}$ are used on an input data item $\mathbf {x}$ and each class appears in exactly $k{-}1$ classifiers, hence an opportunity for up to $k{-}1$ votes out of the $k(k{-}1)/2$ binary classification rounds. The class with the majority of votes is the winner.

An improvement on the number of voting rounds was originally proposed by Platt et al. in [23] and more recently also used in [1, 17]. Their method, called Directed Acyclic Graph SVM (DAGSVM), forms a decision-graph structure for the testing phase and it takes exactly $k{-}1$ individual voting rounds to decide the label of a data item $\mathbf {x}$. In a nutshell, DAGSVM uses one binary classifier at the time and subsequently removes the losing class from all subsequent classifications. There is no particular criterion on the order of using each binary classifier in this process.

3 Divide and conquer SVM (DCSVM)

As noted in the introduction and illustrated in Fig. 1, the key idea is that any binary classifier may, in practice, separate more than two classes. Which raises a natural question: which classes are separated (and with what accuracy) by each binary classifier? DCSVM combines the one-versus-one method’s simplicity of producing balanced, fast binary classifiers with the classification speed of the DAGSVM’s decision graph. The essential difference consists of producing the most efficient decision tree capable of delivering the decision in at most $k{-}1$ steps in the worst case scenario, or $O(\log k)$ steps in the best case scenario.

3.1 DCSVM training

Let us introduce some notations and then we will proceed to the formal description of the algorithm. Given a data set D of k classes (labels) where to each data item $\mathbf {x}\in D$ has been assigned a label $l\in \{1,\ldots , k\}$, we want to construct a decision function $dcsvm : D \rightarrow \{1,\ldots , k\}$ so that $dcsvm(\mathbf {x}) = l$, where l is the corresponding label of $\mathbf {x}\in D$. As usual, by considering a split $D = R\cup T$ of the data set D into two disjoint sets R (the training set) and T (the test set), we will be using the data in R to construct our decision function dcsvm() and then the data in T to measure its accuracy. Furthermore, we consider $R = R_1\cup R_2\cup \dots \cup R_k$ as an union of disjoint sets $R_l$, where each $x\in R_l$ has label l, $l = 1,\dots , k$. (Similarly, we consider $T = T_1\cup T_2\cup \ldots \cup T_k$ as a union of disjoint sets $T_l$, where each $x\in T_l$ has label l, $l = 1,\ldots , k$.)

Let $svm_{i,j} : D\rightarrow \{i,j\}$, be a SVM binary classifier created using the training set $R_i\cup R_j$, $i < j$ and $i = 1,\dots ,k{-}1, j = 2,\dots ,k$. There are $k(k{-}1)/2$ such one-versus-one binary classifiers. We must clearly specify that the svm() decision function we consider here is not the ideal one, but the practical one, likely affected by misclassification errors. That is, for some $\mathbf {x}\in R_i\cup T_i$, we may have that $svm_{i,j}(\mathbf {x}) = j$.

Our goal is to create the dcsvm() decision function that uses a minimal number of binary decisions for k-classes classification, while not sacrificing the classification accuracy. While seeking to achieve this goal, we were exploring metrics from Decision Trees classification (such as Gini impurity, Information gain, etc). However, our situation is different. In most cases, DCSVM decision trees do not separate a set of classes into disjoint subsets. Some classes may appear in both subtrees rooted at the same decision node. We hence tried to identify other metrics that would help reaching our goal.

We start by defining a few measures we use in the process of identifying the shortest path to a multi-class classification decision.

Definition 1

(Class Predictions Likelihoods) The class predictions likelihoods of a SVM binary classifier $svm_{i,j}(\cdot )$ for a label $l\in \{1,\dots ,k\}$, denoted respectively as ${\mathcal {C}}_{i,j}(l, i)$ and ${\mathcal {C}}_{i,j}(l, j)$, are:

$$\begin{aligned} {\mathcal {C}}_{i,j}(l, i)= & {} \frac{|\{\mathbf {x}\in R_l\;|\;svm_{i,j}(\mathbf {x}) = i\}|}{|R_l|} \\ {\mathcal {C}}_{i,j}(l, j)= & {} \frac{|\{\mathbf {x}\in R_l\;|\;svm_{i,j}(\mathbf {x}) = j\}|}{|R_l|} = 1 - C_{i,j}(l,i) \end{aligned}$$

Each class prediction likelihood represents the expected outcome likelihood for i or j when a binary classifier $svm_{i,j}(\cdot )$ is used for prediction on all data items in $R_l$. These likelihoods are computed for each binary classifier and each class in the training data set.

All pairs of likelihood predictions, for every binary classifier $svm_{i,j}(\cdot )$ and classes are stored in a table, as follows.

Definition 2

(All-Predictions Table) We arrange all classes predictions likelihoods in rows (corresponding to each binary classifier $svm_{i,j}$) and columns (corresponding to each class $1,\ldots ,k$) to form a table ${\mathcal {T}}$ where each entry is given by a pair of predictions likelihoods as follows:

$$\begin{aligned} {\mathcal {T}}[svm_{i,j},l]=\left( {\mathcal {C}}_{i,j}(l, i), {\mathcal {C}}_{i,j}(l, j)\right) \end{aligned}$$

Figure 2 shows the All-Predictions Table computed for the glass data set in [9]. The data set contains 6 classes, labeled as 1, 2, 3, 5, 6, and 7 (notice that label 4 is skipped in the original glass data set). Each row corresponds to a binary classifier $svm_{1,2},\cdots ,svm_{6,7}$ and the columns correspond to the class labels. Each table cell contains a pair of likelihood predictions (as percentages) for the row classifier and class column. For instance, ${\mathcal {C}}_{1,2}(1, 1) = 100\%$, ${\mathcal {C}}_{1,2}(1, 2) = 0\%$ and ${\mathcal {C}}_{1,6}(2, 1) = 91.8\%$, ${\mathcal {C}}_{1,6}(2, 6) = 8.2\%$.

Fig. 2

The All-Predictions table for the glass data set in [9]

The table gives also a general overview of how good the binary classifiers are for separating other classes. As in the example described in Sect. 1, by setting precision goal (called precision threshold and denoted by $\theta$) one can enforce each binary classifier to perform with some accuracy, if possible. For instance, choosing $\theta = 5\%$ would require a precision of at least $1 - \theta = 95\%$, which in turn would allow “svm 1 vs. 7” (row 5 in Fig. 2) separate only classes 1, 5, and 7. For $\theta = 10\%$, the same binary classifier would separate classes 1, 3, 5, and 7. We must emphasize that while $\theta$ is clearly related to the multiclass classification accuracy, it does not indicate a guaranteed accuracy overall. $\theta$ can be considered an expected accuracy only for some classes: namely for those that can be decided with that accuracy by some binary classifiers.

We formally define next two measures for the quality of the classification of each $svm_{i,j}(\cdot )$. The impurity index measures how good the binary classifier is for classifying all classes as i or j for a given precision threshold $\theta$. In a nutshell, a class l is classified as “definitely” i by $svm_{i,j}(\cdot )$ if ${\mathcal {C}}_{i,j}(l, i) \ge 1-\theta$; as “definitely” j if ${\mathcal {C}}_{i,j}(l, j) \ge 1-\theta$; otherwise, it is classified as “undecided” i or j. The impurity index counts how many “undecided” decisions a binary classifier produces. The lower the index, the better the separation. The balance index measures how “balanced” a separation is in terms of the number of classes predicted as i and j. The larger the index, the better.

Definition 3

(SVM Impurity and Balance Indexes) For an accuracy threshold $\theta$ of a SVM classifier $svm_{i,j}(\cdot )$, we define:

• the impurity index, denoted as ${\mathcal {P}}_{i,j}(\theta )$, as:

  $$\begin{aligned} {\mathcal {P}}_{i,j}(\theta ) = \left( \sum _{l = 1}^{k}\left( \chi _\theta ({\mathcal {C}}_{i,j}(l, i)) + \chi _\theta ({\mathcal {C}}_{i,j}(l, j))\right) \right) -k \end{aligned}$$

• the balance index, denoted as ${\mathcal {B}}_{i,j}(\theta )$, as:

  $$\begin{aligned} {\mathcal {B}}_{i,j}(\theta ) = min\left( k-\sum _{l = 1}^{k}\chi _\theta ({\mathcal {C}}_{i,j}(l, j)), k-\sum _{l = 1}^{k}\chi _\theta ({\mathcal {C}}_{i,j}(l, i))\right) \end{aligned}$$

  where $\chi _\theta$ is the step function:

  $$\begin{aligned} \chi _\theta (x) = \left\{ \begin{array}{ll}1\ \ \ \ &{}\text{ if } x > \theta \\ 0 &{} \text{ if } x \le \theta \end{array}\right. \end{aligned}$$

For instance, the impurity index for row $svm_{1,6}$ and threshold $\theta = 0.05$ in Fig. 2 is:

$$\begin{aligned} {\mathcal {P}}_{1,6}(0.05)= & {} \big ((1+0) + (1+1) + (1+0) + (1+1) \\&+\, (0+1) + (1+1)\big ) - 6 = 3 \end{aligned}$$

and indicates that 3 of the classes (namely 2, 5, and 7) are undecided when the required precision is at least $\theta = 5\%$.

For accuracy threshold $\theta = 0.05$, the balance index for row $svm_{1,2}$ in Fig. 2 is ${\mathcal {B}}_{1,2} = 1$ and for row $svm_{5,6}$ is ${\mathcal {B}}_{5,6} = 2$.

The SVM score, defined next, is a measure of the precision of the binary classifier $svm_{i,j}(\cdot )$ for classifying classes i and j. The higher the score the better the classifier precision.

Definition 4

(SVM Score) The score of a SVM classifier $svm_{i,j}(\cdot )$, denoted as ${\mathcal {S}}_{i,j}$, is

$$\begin{aligned} {\mathcal {S}}_{i,j} = \frac{{\mathcal {C}}_{i,j}(i, i) + {\mathcal {C}}_{i,j}(j, j)}{2} \end{aligned}$$

For instance, the table in Fig. 2 shows that

$$\begin{aligned} {\mathcal {S}}_{1,2} = \frac{{\mathcal {C}}_{1,2}(1, 1) + {\mathcal {C}}_{1,2}(2, 2)}{2} = \frac{100\%+100\%}{2} = 100\%. \end{aligned}$$

Algorithm 1 describes the DCSVM training and proceeds as follows. In the main procedure, TrainDCSVM, the SVM binary classifiers for all class pairs are trained (line 4) and the predictions likelihoods are stored in the predictions table (line 5). The decision function dcsvm is created as an empty tree (line 8) and then recursively populated in the DCSVM-subtree procedure (line 10). The recursion procedure creates a left and/or a right node at each step (lines 12 and 19, respectively) or may stop with creating a left and/or a right label (lines 9 and 16, respectively). Each new node is associated to the binary $svm_{i,j}$ that is the decider at that node (line 5), or with a class label if an end node (lines 9 and 16).

An important part of the DCSVM-subtree procedure is choosing the “optimal” svm from a current predictions likelihoods table (line 4). For this purpose, we use the SVM Impurity Index, Balance, and Score from Definitions 3 and 4, respectively. The order these measures are used may influence the decision tree shape and precision. If Score is used then the Impurity and Balance Indexes are used to break a tie, the resulting tree favors accuracy over the speed of decisions (may yield bushier trees). If Impurity and Balance Indexes are used first, then Score, if a tie, the resulting tree may be more balanced. The decision speed is favored while possibly sacrificing accuracy.

A dcsvm decision tree for the glass data set is shown in Fig. 3. Clearly, the algorithm may produce highly unbalanced dcsvm decision trees (when some classes are decided faster than others) or very balanced decision trees (when most of class labels are leaves situated at about same depth). Regardless of outcome, the following result is almost immediate.

Proposition 1

(Worst case scenario) The dcsvm decision tree constructed in Algorithm 1 has depth at most $k{-}1$.

Proof

The lists of classes labeled i and j (lines 6, 7 in DCSVM-subtree procedure) contain at least one label each: i or j, respectively. Once a class column is removed from ${\mathcal {T}}$ at some tree node n, it will not appear again in a node or leaf in the subtree rooted at that node n. Hence with each recursion the number of classes decreases by at least one (lines 11, 18) from k to 2, ending the recursion with a left or a right label node in lines 9 or 16, respectively.

Notice that a scenario where each dcsvm decision tree label has depth k is possible in practice: when no $svm_{i,j}$ binary classifier is a good separator for classes other than i and j (and therefore at each node only classes i and j are separated, while the other are undecided and will appear in both left and right branches). We call this the worst case scenario, for obvious reasons. The opposite case scenario is also possible in practice: each $svm_{i,j}$ separates all classes into two disjoint lists of about same lengths. The dcsvm decision tree is also very balanced in this case, but a lot smaller.

Proposition 2

(Best case scenario) The dcsvm decision tree constructed in Algorithm 1 when each $svm_{i,j}$ produced balanced, disjoint separation between all classes has depth $\lceil \log k\rceil$.

Proof

Clearly, this is a case scenario where at each recursion step a node is created such that half of the classes are assigned to the left subtree and the other half to the right subtree. This produces a balanced binary tree (not necessarily complete) with k leaves. The tree has 1, then at each level the number of nodes doubles: 1, 2, 4, 8, etc. At the maximum depth h, there are exactly $2^h$ leaves (nodes) if the tree is complete. Since our tree is balanced (one level must be complete before moving to the next) but not necessary complete:

$$\begin{aligned} 2^{h-1}< k \le 2^h\ \ \Rightarrow \ \ h-1 < \log k \le h \ \ \Rightarrow \ \ \lceil \log k\rceil = h \end{aligned}$$

Hence the depth is $\lceil \log k\rceil$.

The DCSVM classifier Algorithm 2 relies on the dcsvm decision tree produced by Algorithm 1 to take any data item $\mathbf {x}$ and predict its label. The algorithm starts at the decision tree root node (line 4) then each node’s associated svm predicts the path to follow (lines 6–12) until a leaf node is reached. The label of the leaf node is the DCSVM’s prediction (line 14) for the input data item $\mathbf {x}$. An example of a prediction path in a dcsvm tree is illustrated in Fig. 3b.

Propositions 1 and 2 directly justify the following result.

Theorem 1

The Algorithm 2 performs multi-class classification of any data item $\mathbf {x}$ in at most $k{-}1$ binary decisions steps (in the worst case scenario) and at most $\lceil \log k\rceil$ binary decision steps (in the best case scenario).

We illustrate next how the dcsvm decision tree is created and how a prediction is computed using a working example.

3.2 A working example

We use the glass data set [9] to illustrate DCSVM at work. This data set contains 6 classes, labeled 1, 2, 3, 5, 6, and 7 (notice there is no label 4). Consequently, $6 * (6 - 1) / 2 = 15$ binary svm classifiers are created and then the “all predictions likelihoods” table ${\mathcal {T}}$ is computed (Fig. 2). Let us choose the accuracy threshold $\theta = 0$, for simplicity. That is, a class l is classified by an $svm_{i,j}$ as only i if $svm_{i,j}$ predicts that all data items in $R_l$ have class i; l is classified as only j if $svm_{i,j}$ predicts that all data items in $R_l$ have class j; else, l is undecided and will appear on both sides of the decision tree node associated with $svm_{i,j}$.

Fig. 3

DCSVM decision tree (a) with a decision process example (b), for the glass data set

We have chosen the “glass” data set as the working examples mostly based on its size: not trivially small, not artificial, and not too big to have a visual representation of the method so that the reader can follow. The “glass” data set is not necessary the best case scenario (Fig. 3 shows a decision tree that is not perfectly balanced) but also not the worst case scenario. We consider it has the advantage of showing both sides.

We follow next the DCSVM-subtree procedure in Algorithm 1 and construct the dcsvm decision tree. Notice that $S_{i,j} = 100\%$ for all $svm_{i,j}$, so score does not matter for choosing the optimal $svm_{i,j}$ in line 4. The choice will be solely based on the impurity and balance indexes. Table 1 shows all values for these measures for the initial predictions likelihoods table. The table shows rows 1, 13, and 14 as candidates with minimum impurity indexes. Then a tie between rows 13 and 14 as the winners among these. Row 13 comes first and hence $svm_{5,6}$ is selected as the root node. Figure 3a shows the full decision tree, with $svm_{5,6}$ as the root node. Subsequently, $svm_{5,6}$ labels classes 1, 2, 3, and 5 as “5” (left), and classes 6 and 7 as “6” (right). The algorithm continues recursively with classes $\{1, 2, 3, 5\}$ to the left, and classes $\{6, 7\}$ to the right. The right branch will be completed immediately with one more tree node (for $svm_{6,7}$) and two corresponding leaf nodes (for labels 6 and 7).

Table 1 svm optimality measures for glass data set and the initial All-Predictions table

For the left branch the algorithm will proceed with a reduced All-Predictions table: rows 4, 5, 8, 9, 11, 12, 13, 14, and 15 and columns for classes 6 and 7 are removed. The optimality measures will be subsequently computed for all svm and classes still in competition (1, 2, 3, and 5) in the left branch. The corresponding measures are given in Table 2 (for an easier identification, the indices in the first column are kept the same as the original indices in the All-Predict table in Fig. 2). There is a tie between $svm_{1,2}$ and $svm_{2,5}$, and $svm_{1,2}$ is being used first. A node is consequently created, with a leaf as a left child. The rest of the tree is subsequently created in the same manner.

Table 2 Optimality measures in the second step of creating the decision tree in Fig. 3b

4 Experimental results

Table 3 Data sets

Fig. 4

Multi-class prediction accuracy comparison: built-in SVM, one-versus-one, and DCSVM

We implemented DCSVM in R v3.4.3 using the e1071 library [10], running on Windows 10, 64-bit Intel Core i7 CPU @3.40GHz, 16GB RAM. For testing, we used 14 data sets from the UCI repository [9] (as listed in Table 3). We performed three sets of experiments: (1) multi-class prediction accuracy comparison, (2) prediction performance in terms of speed (time and number of binary decisions) and resources (number of support vectors), and (3) DCSVM performance comparisons for different data sets and accuracy threshold parameter values. For the first set of experiments we compared three multi-class predictors: the built-in multi-class SVM (from the e1071 library), our R implementation of one-versus-one, and the R implementation of DCSVM. For a fair comparison, in the second set of experiments we compared only the R implementations of one-versus-one and DCSVM. The built-in multi-class SVM would benefit of the inherent speed of native code it relies on. Finally, the third set of experiments focused on the DCSVM’s R implementation performance and fine tuning.

4.1 Accuracies comparison: built-in multi-class SVM, one-versus-one, and DCSVM

The main goal of DCSVM is to improve multi-class prediction performance while not sacrificing the prediction accuracy. The first experimental results compare multi-class prediction accuracy of: (1) built-in SVM multi-class prediction (in the e1071 package), (2) one-versus-one implementation in R, and (3) DCSVM implementation in R. For the experiment, we used cross-validation with 80% data for training and 20% for testing, for each data set. We ran 10 trials and averaged the results. The results are displayed in Fig. 4 and show no significant differences between the three methods.

Next, we performed the Wilcoxon signed rank test on sequences of accuracies from each trial and compared accuracies of DCSVM vs. built-in SVM (BI), and of DCSVM vs. one-versus-one implementation in R (OvsO). The p-value of the results, for each data set, are presented in Table 4. The results in Table 4 show that there is no compelling evidence to conclude the median of the accuracies of the DCSVM trials differ from the median of one-versus-one method (the null hypothesis is not rejected, according to values in the “OvsO—DCSVM” column of the table). Interestingly, there are likely differences in the median when comparing DCSVM and the built-in method for a few data sets (as usual, we consider the null hypothesis being rejected when p value $< 0.05$). For instance, one of the smallest p value corresponds to the “svmguide4” data set: 0.00585709908528413. However, as Fig. 4 shows, all these instances correspond to situations where DCSVM’s average accuracy is better than the built-in method’s accuracy (including the case of the “svmguide4” data set). These conclusions (and data presented in Table 4) are consistent with the prediction accuracies over all data sets in our experiments in Fig. 5: on median, DCSVM performs similarly to the one-versus-one implementation and slightly better than the built-in method.

Table 4 p values from Wilcoxon signed rank test

Fig. 5

Prediction accuracies comparison for all data sets

4.2 Prediction performance comparison

Fig. 6

Average number of Support Vectors for multi-class predictions

Fig. 7

Average number of binary decisions for multi-class predictions

Fig. 8

Average prediction times for multi-class predictions

For this purpose, we compared the R implementations of one-versus-one method and DCSVM. We analyzed prediction performance in three aspects: the average number of support vectors, the average number of binary decisions, and time. The number of support vectors used was computed by summing up all support vectors from every binary decider, over all steps of binary decisions until the multi-class prediction was achieved. The number of such support vectors is clearly proportional not only to the number of decision steps (which are illustrated separately), but also to the configuration of data separated by each binary classifier. The corresponding performance results are presented in Figs. 6, 7, and 8, respectively. Due to large variations in size between the data sets we used, we split the data sets into two size-balanced groups and displayed each graph side-by-side for each group. DCSVM significantly outperforms one-versus-one, clearly being much less computationally intensive (number of support vectors for prediction) and faster (number of binary decisions and prediction times).

From the first two sets of experimental results we can conclude already that DCSVM achieved the goal of being a faster multi-class predictor without sacrificing prediction accuracy. This conclusion is also supported by the overall comparison (for all data sets in our experiments) of the number of support vectors used for prediction, as illustrated in Fig. 9.

Fig. 9

Total number of Support Vectors for multi-class predictions (aggregated over all data sets and for one-versus-one and DCSVM methods)

4.3 DCSVM performance fine tuning

Fig. 10

Accuracy and the average number of prediction steps for different thresholds

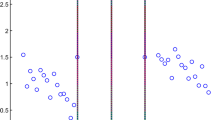
In this set of experiments we analyze in close detail DCSVM’s performance in terms of the accuracy threshold parameter. Figure 10 shows the trade-off between accuracy (top) and the average prediction steps (bottom) with various threshold values. Clearly, the accuracy threshold parameter permits a trade-off between accuracy and speed. However, this is largely data dependent. The more separable the data is, the less influence the threshold has on speed. For less separable data (such as the letter data set), fine adjustment of the threshold permits trade-off between prediction accuracy and prediction speed. This is not the case for the vowel data set, which is highly separable: changes in the threshold influence neither the accuracy of prediction nor the average number of prediction steps.

Fig. 11

Accuracy for predicting “letter” with each method, for different split thresholds

Figure 11 shows how DCSVM accuracy compares to other multi-class classification methods (BI, built-in; OvsO, one-against-one) for various threshold values. For less separable data (such as letter) DCSVM’s accuracy drops sharply with the threshold (starting at some small threshold value) compared to the accuracy of one-against-one method, which we found to perform better than the built-in method. The built-in and one-against-one methods do not depend on the threshold value, of course. They are shown on the same graph for comparison purpose. However, it is interesting to notice that by increasing the threshold the prediction accuracy of DCSVM on letter data sets decreases from a comparable value with one-versus-one method’s accuracy (which performs best on this data set) to the accuracy of the built-in method. With a threshold value $\theta = 2\%$ the prediction accuracy of DCSVM is still above the accuracy of the built-in method (for the letter data set).

Table 5 Prediction accuracies for different split thresholds

Table 6 DCSVM average number of steps per decision, for different split thresholds vs. “1 vs. 1” and DAGSVM number of steps per decision

Table 7 DCSVM: Average support vectors per decision, for different split thresholds

Fig. 12

Number of separated classes for different thresholds

Table 5 shows side-by-side accuracies of multi-class classification using (1) built-in (BI), (2) one-against-one (OvsO), and (3) DCSVM (for a few threshold values $\theta$). DCSVM performs very well in terms of accuracy (compared to the other methods) for all data sets, for threshold values $\theta \in \{ 2\%, 1\%, 0.1\%, 0.01\%\}$ (the smaller the threshold, the better the accuracy, in general). A larger threshold $\theta$ may increase the prediction speed (Table 6) and reduce the computation effort (Table 7). Interesting to notice: Table 6 shows that in all cases displayed in the table the number of decision steps is less than $k{-}1$, where k is the number of classes in the respective data set. In terms of the number of SVM binary decisions DCSVM outperforms (even when the threshold $\theta$ is not very small) one-against-one and its improvement DAGSVM, which reaches multi-class prediction after $k{-}1$ steps. In this context it worth mentioning that recent work on improving DAGSVM performance [1, 13, 21] focus on combining DAGSVM with other methods or learning the optimal DAG structure for computational efficiency, not on reducing the number of binary decisions. Moreover, previous work ([16] and more recently [1, 13, 21]) indicates that DAGSVM performs similarly to one-against-one in terms of accuracy and all recent efforts were concentrated on improving its computational efficiency.

The All-Predictions table in Fig. 2 collects all information used by DCSVM to construct its multi-class prediction strategy (the dcsvm decision tree in Algorithm 1). The same information can be used to predict how much separation can be achieved for different threshold values. For instance, for the glass data set All-Predictions table in Fig. 2 and for a threshold value $\theta = 2\%$ there are 58 entries in the table where the percentage of predicting one class or the other is at least $100 - \theta = 98\%$ (out of a total of $15\times 6 = 90$ entries in the table). The percentage $58/90=64.4\%$ is a good indicator of purity for DCSVM with threshold $\theta = 2\%$: the higher the percentage, the more separation is produced at each step and hence a shallow decision tree. Figure 12 shows the class separation percentages for threshold values $0\le \theta \le 5$ and four data sets (letter, vowel, usps, and sensorless). Intuitively, as threshold increases so does the separation percentage. The letter and usps data sets display an almost linear increase of separation with threshold. sensorless displays a sharp increase for small threshold values, then it tends to flatten, that is, not much gain for significant increase in threshold (and hence possibly less accuracy). Lastly, vowel displays a step-like behavior: not much gain in separation until threshold value reaches approx $\theta = 2.3\%$, a steep increase until $\theta$ approaches $3\%$, then nothing much happens again. One can use these indicators to decide the trade-off between speed and accuracy of predictions.

5 Conclusion and future work

In this paper we present DCSVM, a fast algorithm for multi-class classification using Support Vector Machines. Our method relies on dividing the whole training data set into two partitions that are easily separable by a single binary classifier. Then, a prediction between the two training set partitions would eliminate one or more classes at the time. The algorithm continues recursively until a final binary decision is made between the last two classes left in the competition. Our algorithm performs consistently better than the existent methods on average. In the best case scenario, our algorithm makes a final decision between k classes in $O(\log k)$ decision steps between different partitions of the training data set. In the worst case scenario, DCSVM makes a final decision in $k{-}1$ steps, which is not worse than the existent techniques.

The SVM divide and conquer technique we present for multi-class classification can be easily used with any binary classifier. It is rather a consequence of increasing data sparsity with the dimensionality of the space, which can be exploited, in general, in favor of producing fast multi-class classification using binary classifiers. Our experimental results on a few popular data sets show the applicability of the method.

A clear limitation of using binary classifiers to produce multiclass classification is the large number of binary classifiers to be created (quadratic in the number of classes). This can be very computationally expensive for large number of classes. However, this is a general problem for multiclass classifiers, in general. In the case of using binary classifiers the limitation can be partially overcome by using parallelization (binary classifiers can be independently created, in parallel).

Our choice of using SVMs as binary classifiers relies on the fact that SVM binary classifiers produce optimal separation hyperplanes (the underlaying optimization problem finds a global minimum, rather than a local minimum). It would be interesting, as future work, to compare with techniques that produce direct multiclass classification (using neural networks, decision trees, k-nearest neighbours, etc) rather than relying on binary classifiers. Also, possibly adapting some decision trees metrics (Gini impurity, Information gain) for producing better DCSVM decision trees would be another direction to explore in future work. Yet, other directions to further investigate would be related to the precision threshold $\theta$: a data-driven procedure for its selection and the possible benefits of using variable $\theta$ values on different decision tree branches (the shallow ones). The former would help practitioners understand trade-offs between different values, while the latter may improve classification accuracy for some classes with the price of a small increase of tree-branch depth (hence more decision steps).