1 Introduction

Online video services have surged to an unprecedented level in recent years. The number of users and videos have been increasing constantly, together with the number of video contents, genres, and concepts, which leads to the difficulties of video clustering analysis task. The effective social web video clustering method can automatically organize the video corpus into a meaningful cluster (category) hierarchy for efficient searching and browsing. Social web video clustering is widely studied and much work has been done by using different types of videos’ information. The standard approach consists of three main stages: (1) extracting features (videos’ contents or the surrounding text information of videos) and representing videos as feature vectors; (2) similarity measurement based on video representations; (3) applying the clustering algorithm to cluster web videos based on similarity measured. However, web video clustering suffers well-known difficulty due to the calculation of the similarity between videos which comprises two problems, i.e., the video similarity which differs from visual features’ similarity, and the low quality of text information because videos on video sharing website has been uploaded by unlimited levels of users. Text information, e.g., title, tag, and description, contains many synonyms, noise, ambiguous or is totally absent. Previous studies try to address this problem by using single features or merging them together. Zhang et al. [1] applied spectral clustering (SC) to cluster videos by merging two types of features such as speech transcripts and visual features. Guil et al. [2] used visual features to compare videos efficiently based on the keyframe selection. Hindle et al. [3] proposed a model for web video clustering based on two clustering algorithms, i.e., affinity propagation (AP) and normalization cut (NC) by using text metadata and visual features. Another useful videos’ information, i.e., co-watched videos was used together with text information in [4]. Kamie et al. [5] presented a method for web video clustering by using videos’ playlist information. Mahmood et al. [6] developed a framework by utilizing textual information and external support from the web to enhance the semantic relation of terms then incorporated must-link constraints into different clustering algorithms and combined clustering results by CSPA to deal with the web video categorization problem. Different types of features of web videos data have been utilized (e.g., textual features, semantic features and visual features) which are regarded as multi-modality for clustering purpose in [7].

Those studies are based on single-view data implemented in the models. However, real data usually comes from multiple sources along with the phenomenon of concept drift [8]. In many real-world applications, data is naturally comprised of different heterogeneous representations or views. For example, video data can be represented by using a collection of heterogeneous features (views), e.g., text-tag-unigrams, audio-spectrogram-stream, and vision-cuboids-histogram, which can be regarded as three views. Similarly, image data is presented by color descriptor, local shape descriptor, and local binary patterns, etc. A metadata of documents can be represented by the title, author, journals’ name and etc. Usually, multiple representation or views provide compatible and complementary information for the semantically same data. By exploiting the characteristics of multi-view data, multi-view learning can obtain better performance than that relies only on a single view.

Generally, real-world datasets contain missing values, such as instances with some views missing. Trivedi et al. [9] firstly attempted to deal with incomplete views by using information from one complete view to infer the essential incomplete views. Li et al. [10] tried to solve multi-view clustering with the incomplete views by establishing a latent subspace where the instances corresponding to the same example in different views are close to each other, and similar instances (belonging to different examples) in the same view are well grouped. Shao et al. [11] learned a latent representation for all views and then generated a consensus matrix based on weighted NMF with L2,1 regularization to deal with the multiple incomplete views. However, multi-view data in existing methods needs to fit into the memory.

Nonnegative matrix factorization (NMF) is one of the most popular techniques for dimensionality reduction of clustering by extracting latent features from high-dimensional data. NMF has become an imperative tool in conventional data analysis and widely used in the fields of data mining [12], machine learning [13], text mining [14], and so on. Zhou et al. [15, 16] proposed a new algorithm for sentiment classification to enable unsupervised sentiment analysis by constructing the nearest neighbor graphs. The formulation of a joint NMF process with the consistency constraint that pushes the clustering solution of each view towards a common consensus for multi-view data was presented in [17]. A method for feature extraction by the matrix factorization objective function by constructing a nearest neighbor to integrate local geometrical information of each view via NMF was proposed in [18]. The graph regularized NMF for data representation by encoding the geometrical information and seeking a matrix factorization was shown in [19]. Different variations of NMF were proposed to handle very large data in the last few years. Wang et al. presented an algorithm for document clustering based on online NMF by utilizing the second-order Hessian matrix to optimize the objective function [20]. Guan et al. proposed a novel online NMF algorithm with the robust stochastic approximation that accepts one sample or a chunk of samples and updates the bases per step [21]. Shao et al. [22] developed an online algorithm by adding graph regularization to joint NMF to help select discriminative features for multi-view feature selection.

Recently, multi-view clustering has gained increasing attention due to its high performance which performs with the information from multiple views to generate clusters [23, 24]. In order to enforce the indicator matrices from different views, Akata et al. [25] extended the NMF [26] to multi-view settings. To combine multi-view information in the NMF framework, Akata et al. [25] enforced a shared indicator matrix among different views to perform multi-view clustering in NMF framework. In order to keep the clustering solutions across different views meaningful and comparable, Liu et al. [17] enforced a constraint to push each view indicator matrix towards a common indicator matrix and normalization constraint inspired by the connection between NMF and probability latent semantic. A number of NMF-based multi-view algorithms have been proposed, such as factorizing each view as a linear combination of a shared latent representation in [27] or establishing a latent subspace in [10] where the instances corresponding to the same example in different views are close to each other and similar instances in the same view are well grouped. The disagreement between each pair of views is minimized the loss function of NMF in [28] by indicating that the vectors from two different views should be similar if they belong to the same cluster and dissimilar otherwise. A weighted extension of multi-view NMF in [29] imposed consensus constraint on the efficient matrices across different features (views) for image annotation.

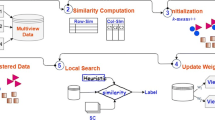
In this paper, we tackle the problem of Social Web Video Clustering based on Multi-View Clustering via NMF (SOMVCS). SOMVCS deals with large-scale multi-view data of web videos. The framework of SOMVCS is illustrated in Fig. 1.

Fig. 1
figure 1

The proposed framework of SOMVCS

Full size image

The contributions of this paper are as follows:

  • We propose SOMVCS, which models the multi-view clustering as a joint weighted NMF problem, that can capture relation between heterogeneous views.

  • SOMVCS incorporates the graph regularization to preserve the local structure of data and processes the multi-view data chunk by chunk, which will be fit into the memory.

  • It learns latent feature matrices across all views and drives them towards to a common consensus. By applying clustering algorithm, SOMVCS provides accurate results.

The rest of this paper is organized as follows. In Sect. 2, a brief review of NMF is described. The formulation and the algorithm of SOMVCS are presented in Sect. 3. The experimental study is provided in Sect. 4. The results and discussion are shown in Sect. 5. The paper ends with conclusions and future work in Sect. 6.

2 A brief review of NMF

In this section, we will introduce some knowledge about clustering based NMF. It is well understood that NMF is used for feature extraction in data mining and it is a method to factorize a nonnegative data matrix into two nonnegative matrix factors where the product of these two factors is an approximation of the original matrix. As the decomposition result is nonnegative, the interpretability of NMF outputs makes it fit on large-scale and time-varying datasets.

Given a nonnegative data matrix \(X \in R_{+}^{{D \times N}},\) where each row represents a feature and each column represents an instance. NMF aims to transform the data matrix X into two rank-r nonnegative matrices, that is a basis matrix \(U \in R_{+}^{{D \times r}}\) and a feature matrix \(V \in R_{+}^{{N \times r}}\). U and V are determined by minimizing the cost function as follows:

$$\begin{gathered} \mathop {\hbox{min} }\limits_{{U,V}} L=\left\| {X - U{V^T}} \right\|_{F}^{2} \hfill \\ s.t.\ U \geq 0,\ V \geq 0, \hfill \\ \end{gathered}$$
(1)

where \(\left\| \cdot \right\|\) is the matrix Frobenius norm.

In general, solving Eq. (1) is difficult as the objective function is not convex for U and V jointly. One of the well-known algorithms for implementing the alternate update rules is Lee and Seung’s multiplicative update approach in [26] which updates U and V by

$${U_{i,j}} \leftarrow {U_{i,j}}\frac{{{{(XV)}_{i,j}}}}{{{{(U{V^T}V)}_{i,j}}}}$$
(2)
$${V_{i,j}} \leftarrow {V_{i,j}}\frac{{{{({X^T}U)}_{i,j}}}}{{{{(V{U^T}U)}_{i,j}}}}.$$
(3)

However, NMF still does not produce satisfactory results in clustering tasks because it cannot theoretically guarantee the composition results to be sparse. The existing NMF solutions require the entire data matrix to reside in the memory which is problematic when the datasets are very large or streaming. To address this issue, Wang et al. [20] proposed an online NMF algorithm based on a stochastic approximation to efficiently handle streaming data by processing one chunk of data points at a time.

3 A novel online multi-view clustering algorithm

3.1 Formulation

In this section, we present the SOMCVS which processes multi-view data chunk by chunk in a streaming fashion with low storage complexity. In order to deal with incomplete views (missing instances), dynamic weights from online multi-view clustering [30] were used to assign lower weights to less informative estimations and higher weights to more informative estimations. SOMVCS provides us a common consensus matrix with a latent representation of the original data points. Finally, k-means algorithm is applied to generate the result.

Suppose we have a multi-view data set (incomplete) \(X=\{ {X^{(1)}},{X^{(2)}}, \ldots ,{X^{({n_v})}}\}\) denoting the data of all the views, where \({X^{(v)}}=\{ x_{1}^{{(v)}},x_{2}^{{(v)}}, \ldots ,x_{n}^{{(v)}}\} \in {R^{{D_v} \times N}}\) represents the data of the v-th view. In NMF, the coefficient matrices \({V^{(v)}}\) is learned from different views which give forward a common consensus matrix \({V^*}\). This consensus matrix is considered to reflect simultaneously the latent structure shared by every view [17].

In the study of manifold learning theory, it has shown that respecting the intrinsic geometrical structure is an effective method that can improve clustering quality [19]. Therefore, we introduce additional graph regularization. Given a similarity matrix S, one can define a smoothness penalty term for each view using the following function f:

$$\begin{aligned} f&=\sum\limits_{{i,j=1}}^{N} {{{\left\| {V_{{i,:}}^{{(v)}} - V_{{j,:}}^{{(v)}}} \right\|}^2}} \times S_{{ij}}^{{(v)}} \hfill \\ &=Tr\left( {{V^{{{(v)}^T}}}{D^{(v)}}{V^{(v)}}} \right) - Tr\left( {{V^{{{(v)}^T}}}{S^{(v)}}{V^{(v)}}} \right) \hfill \\ &=Tr\left( {{V^{{{(v)}^T}}}{L^{(v)}}{V^{(v)}}} \right) \hfill \\ \end{aligned}$$
(4)

where \(Tr( \cdot )\) denotes the trace of a matrix and \({D^{(v)}}\) is a diagonal matrix such that, \(D_{{i,i}}^{{(v)}}=\mathop \sum \nolimits_{i} S_{{i,j}}^{{(v)}}\) or \(D_{{i,i}}^{{(v)}}=\mathop \sum \nolimits_{j} S_{{i,j}}^{{(v)}}\). \({L^{(v)}}={D^{(v)}} - {S^{(v)}}\) is called graph Laplacian matrix. Therefore, SOMCVS for multi-view clustering is formulated as

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{U^{(v)}},{V^{(v)}},{V^{( * )}}}} L & =\sum\limits_{{v=1}}^{{{n_v}}} {\left\| {{X^{(v)}} - {U^{(v)}}{V^{{{(v)}^T}}}} \right\|_{F}^{2}} +\sum\limits_{{v=1}}^{{{n_v}}} {{\alpha _v}Tr\left( {{V^{{{(v)}^T}}}{L^{(v)}}{V^{(v)}}} \right)} {\kern 1pt} \\ & \quad {\kern 1pt} +\sum\limits_{{v=1}}^{{{n_v}}} {{\beta _v}} \left\| {{V^{(v)}} - {V^*}} \right\|_{F}^{2} \\ & \quad {\kern 1pt} s.t.{\text{ }}{U^{(v)}} \geq 0,{\text{ }}{V^{(v)}} \geq 0,{\text{ }}{V^ * } \geq 0,{\text{ }}v=1,2, \ldots ,{n_v} \\ \end{aligned}$$
(5)

where \({U^{(v)}} \in {R^{{D_v} \times K}}\) and \({V^{(v)}} \in {R^{N \times K}}\) are the basis matrix and the latent feature matrix for the v-th view, \({V^*} \in {R^{N \times K}}\) is the consensus latent feature matrix across all views, \({\alpha _v}\) and \({\beta _v}\) are the trade-off parameters used to control the contribution of the manifold regularization and reconstruction error between view v and the consensus, and K is the number of clusters.

In order to support incompleteness, the assigning of dynamic weights in [30] such as assigning lower weights to less informative estimations and higher weights to more informative estimations have been used. After adding the weight matrices, Eq. (5) becomes:

$$\begin{aligned} L & =\sum\limits_{{v=1}}^{{{n_v}}} {\left\| {{\omega ^{(v)}}\left( {{X^{(v)}} - {U^{(v)}}{V^{{{(v)}^T}}}} \right)} \right\|_{F}^{2}} +\sum\limits_{{v=1}}^{{{n_v}}} {{\alpha _v}Tr\left( {{V^{{{(v)}^T}}}{L^{(v)}}{V^{(v)}}} \right)} {\kern 1pt} \\ & \quad +\sum\limits_{{v=1}}^{{{n_v}}} {{\beta _v}} \left\| {{\omega ^{(v)}}\left( {{V^{(v)}} - {V^*}} \right)} \right\|_{F}^{2} \\ & \quad s.t.{\text{ }}{\kern 1pt} {U^{(v)}} \geq 0,{\text{ }}{V^{(v)}} \geq 0,{\text{ }}{V^ * } \geq 0,{\text{ }}v=1,2, \ldots ,{n_v}. \\ \end{aligned}$$
(6)

Because SOMVCS is for social web videos clustering, the data matrices are too large to fit into the memory. Hence, it is crucial to solving the above optimization in an incremental way. Let \(X_{t}^{{(v)}} \in {R^{z \times {D_v}}}\) denote the data received at time t, where z is the number of instances (size of the data chunk). Equation (6) can be written as follows:

$$\begin{aligned} L & =\sum\limits_{{v=1}}^{{{n_v}}} {\sum\limits_{{t=1}}^{{[N/z]}} {\left\| {\omega _{t}^{{(v)}}\left( {X_{t}^{{(v)}} - {U^{(v)}}V_{t}^{{{{(v)}^T}}}} \right)} \right\|_{F}^{2}} } +\sum\limits_{{v=1}}^{{{n_v}}} {\sum\limits_{{t=1}}^{{[N/z]}} {{\alpha _v}Tr\left( {V_{t}^{{^{{{{(v)}^T}}}}}L_{t}^{{(v)}}V_{t}^{{(v)}}} \right)} } {\kern 1pt} \\ & \quad +\sum\limits_{{v=1}}^{{{n_n}}} {\sum\limits_{{t=1}}^{{[N/z]}} {{\beta _v}} } \left\| {\omega _{t}^{{(v)}}\left( {V_{t}^{{(v)}} - V_{t}^{*}} \right)} \right\|_{F}^{2} \\ & \quad s.t.{\text{ }}{\kern 1pt} {U^{(v)}} \geq 0,{\text{ }}V_{t}^{{(v)}} \geq 0,{\text{ }}V_{t}^{ * } \geq 0,{\text{ }}v=1,2, \ldots ,{n_v} \\ \end{aligned}$$
(7)

where \(X_{t}^{{(v)}}\) is a data chunk at time t in the v-th view, \(\omega _{t}^{{(t)}} \in {R^{z \times z}}\) is the diagonal weight matrix for data chunk at time t, \(V_{t}^{{(v)}} \in {R^{z \times K}}\) is the latent feature matrix for t-th data chunk in the v-th view, and \(V_{t}^{{(v)}} \in {R^{z \times K}}\) is the consensus latent feature matrix for t-th data chunk across all the views.

3.2 Algorithm

In this section, we solve the objective function of SOMVCS derived in the above section. From Eq. (7), we can see that for each time t, we need to update \({U^{(v)}}\), \({V^{(v)}}\) and \(V_{t}^{*}\) in an alternate way since the objective function is not jointly convex. The optimization problem of SOMVCS is described as follows:

(1) Optimize \({U^{(v)}}\) with \(V_{t}^{{(v)}}\) and \(V_{t}^{*}\) fixed: To optimize \({U^{(v)}}\) for v-th view at time t, we only need to minimize the following objective function:

$$\begin{aligned} {T_t}\left( {{U^{(v)}}} \right) & =\sum\limits_{{i=1}}^{t} {\left\| {\omega _{i}^{{(v)}}\left( {X_{i}^{{(v)}} - {U^{(v)}}V_{i}^{{{{(v)}^T}}}} \right)} \right\|_{F}^{2}} \\ & \quad s.t.{\text{ }}{\kern 1pt} {U^{(v)}} \geq 0. \\ \end{aligned}$$
(8)

Taking the derivative of the \({T_t}\) with respect to \({U^{(v)}}\), we have:

$$\frac{{\partial {T_t}}}{{\partial {U^{(v)}}}}=2{U^{(v)}}\sum\limits_{{i=1}}^{t} {V_{i}^{{{{(v)}^T}}}} \tilde {\omega }_{i}^{{(v)}}V_{i}^{{(v)}} - 2\sum\limits_{{i=1}}^{t} {X_{i}^{{(v)}}} \tilde {\omega }_{i}^{{(v)}}V_{i}^{{(v)}}$$
(9)

where \(\tilde {\omega }_{i}^{{(v)}}=\omega _{i}^{{(v)}}\omega _{i}^{{{{(v)}^T}}}=\omega _{i}^{{{{(v)}^T}}}\omega _{i}^{{(v)}}\).

We introduce two terms \(M_{t}^{{(v)}}\) and \(N_{t}^{{(v)}}\) as

$$M_{t}^{{(v)}}=\sum\limits_{{i=1}}^{t} {V_{i}^{{{{(v)}^T}}}\tilde {\omega }_{i}^{{(v)}}V_{i}^{{(v)}}}$$
(10)
$$N_{t}^{{(v)}}=\sum\limits_{{i=1}}^{t} {X_{i}^{{(v)}}\tilde {\omega }_{i}^{{(v)}}V_{i}^{{(v)}}} .$$
(11)

Using the Karush–Kuhn–Tucker condition for the nonnegativity constraint on \({U^{(v)}}\), the update rule for \({U^{(v)}}\) is:

$$U_{{i,k}}^{{(v)}} \leftarrow U_{{i,k}}^{{(v)}}\sqrt {\frac{{{{\left( {N_{t}^{{(v)}}} \right)}_{i,k}}}}{{{{\left( {{U^{(v)}}\left( {M_{t}^{{(v)}}} \right)} \right)}_{i,k}}}}} .$$
(12)

(2) Optimize \(V_{t}^{{(v)}}\) with \(V_{t}^{*}~\) and \({U^{(v)}}\) fixed: Using the same steps as before, then let \({\psi _{ij}}\) be the Lagrange multiplier for nonnegative constraint \(V_{t}^{{(v)}}\) and \(\Psi=[{\psi _{ij}}]\), and using the Kuhn–Tucker condition \({\psi _{ij}}{(V_{t}^{{(v)}})_{ij}}=0\). The objective function becomes

$$\begin{aligned} T\left( {V_{t}^{{(v)}}} \right) & =\left\| {\omega _{t}^{{(v)}}\left( {X_{t}^{{(v)}} - {U^{(v)}}V_{t}^{{{{(v)}^T}}}} \right)} \right\|_{F}^{2}+{\alpha _v}Tr\left( {V_{t}^{{{{(v)}^T}}}L_{t}^{{(v)}}V_{t}^{{(v)}}} \right) \\ & \quad +{\beta _v}\left\| {\omega _{t}^{{(v)}}\left( {V_{t}^{{(v)}} - V_{t}^{*}} \right)} \right\|_{F}^{2}+Tr\left( {\Psi V_{t}^{{{{(v)}^T}}}} \right). \\ \end{aligned}$$
(13)

Taking the partial derivative of T with respect to \(V_{t}^{{(v)}}\), we have

$$\begin{aligned} \frac{{\partial T}}{{\partial V_{t}^{{(v)}}}} & =2\tilde {\omega }_{t}^{{(v)}}{U^{{{(v)}^T}}}V_{t}^{{(v)}}{U^{(v)}} - 2\tilde {\omega }_{t}^{{(v)}}X_{t}^{{{{(v)}^T}}}{U^{(v)}}+2{\alpha _v}L_{t}^{{(v)}}V_{t}^{{(v)}} \\ & \quad +2{\beta _v}\tilde {\omega }_{t}^{{(v)}}V_{t}^{{(v)}} - 2{\beta _v}\tilde {\omega }_{t}^{{(v)}}V_{t}^{ * }+\Psi . \\ \end{aligned}$$
(14)

Following the steps as above, the update rule for \(V_{t}^{{(v)}}\) is as following Eq. (15) by giving the graph Laplacian matrix \(L_{t}^{{(v)}}=D_{t}^{{(v)}} - S_{t}^{{(v)}}\):

$${\left( {V_{t}^{{(v)}}} \right)_{j,k}} \leftarrow {\left( {V_{t}^{{(v)}}} \right)_{j,k}}\sqrt {\frac{{{{\left( {\tilde {\omega }_{t}^{{(v)}}X_{t}^{{{{(v)}^T}}}{U^{(v)}}+{\alpha _v}S_{t}^{{(v)}}V_{t}^{{(v)}}+{\beta _v}\tilde {\omega }_{t}^{{(v)}}V_{t}^{ * }} \right)}_{j,k}}}}{{{{\left( {\tilde {\omega }_{t}^{{(v)}}{U^{{{(v)}^T}}}V_{t}^{{(v)}}{U^{(v)}}+{\alpha _v}D_{t}^{{(v)}}V_{t}^{{(v)}}+{\beta _v}\tilde {\omega }_{t}^{{(v)}}V_{t}^{{(v)}}} \right)}_{j,k}}}}} .$$
(15)

(3) Optimize \(V_{t}^{*}\) with \(V_{t}^{{(v)}}~\) and \({U^{(v)}}\) fixed: To optimize the consensus \(V_{t}^{*}\), it requires minimizing the following objective function:

$$\begin{aligned} T(V_{t}^{ * }) & =\sum\limits_{{v=1}}^{{{n_v}}} {{\beta _v}} \left\| {\omega _{t}^{{(v)}}\left( {V_{t}^{{(v)}} - V_{t}^{*}} \right)} \right\|_{F}^{2} \\ & \quad s.t.{\text{ }}{\kern 1pt} V_{t}^{ * } \geq 0. \\ \end{aligned}$$
(16)

Taking the derivative of the objective function \(T(V_{t}^{*})\), we have

$$\frac{{\partial T}}{{\partial V_{t}^{ * }}}=\sum\limits_{{v=1}}^{{{n_v}}} {{\beta _v}} \tilde {\omega }_{t}^{{(v)}}\left( { - 2V_{t}^{{(v)}}+2V_{t}^{ * }} \right)=0.$$
(17)

Therefore, we have a closed form solution:

$$V_{t}^{ * }=\frac{{\sum\nolimits_{{v=1}}^{{{n_v}}} {{\beta _v}\tilde {\omega }_{t}^{{(v)}}V_{t}^{{(v)}}} }}{{\sum\nolimits_{{v=1}}^{{{n_v}}} {{\beta _v}\tilde {\omega }_{t}^{{(v)}}} }}=\sum\limits_{{v=1}}^{{{n_v}}} {{\beta _v}\tilde {\omega }_{t}^{{(v)}}V_{t}^{{(v)}}} .$$
(18)
figure a

4 Experimental study

4.1 Dataset

In this paper, we use a publicly available real-world large-scale dataset (YouTubeFootnote 1) that is named YouTube Multiview Video Games. This dataset consists of feature values and class labels about 120,000 videos. Each video is described by up to 13 feature types from 3 high-level feature families such as auditory, textual and visual features. There are 31 class labels corresponding to 30 popular video games and the remaining correspond to other games [31]. The data is very valuable to do web videos clustering due to their quality of the feature representation. The subset of the dataset used in the experiments is shown in Table 1.

Table 1 A description of the dataset
Full size table

4.2 Performance evaluation

In our experiments, the clustering performance is measured by using two popular evaluation metrices. The first metric is the ACCuracy (ACC) [32, 33]. Given a video zi, let li and ci be the cluster label and the label provided by the data corpus, respectively. The ACC is defined as follows:

$$ACC=\frac{{\sum\nolimits_{{i=1}}^{N} {\delta ({c_i},map({l_i}))} }}{N}$$
(19)

where N is the total number of videos in the test, \(\delta (a,b)\) is the delta function that equals to one if \(a=b~\) and equals to zero otherwise, and \(map({l_i})\) is the permutation mapping function that maps each cluster label li to the equivalent label from the data corpus. The best mapping can be found by using the Kuhn–Munkres algorithm [34].

The second metric is normalized mutual information (NMI) [32, 33]. Let \(C\) is the set of clusters obtained from the ground truth and \({C^\prime }\) is the clusters obtained from our algorithm. Their mutual information metric \(MI(C,{C^\prime })\) is defined as follows:

$$MI(C,C^{\prime})=\sum\limits_{{{c_i} \in C,{{c^{\prime}}_j} \in C^{\prime}}} {p({c_i},{{c^{\prime}}_j})} \cdot {\log _2}\frac{{p({c_i},{{c^{\prime}}_j})}}{{p({c_i}) \cdot p({{c^{\prime}}_j})}}$$
(20)

where \(p({c_i})\) and \(p(c_{j}^{\prime })\) are the probabilities that a video arbitrarily selected from the corpus belongs the clusters \({c_i}\) and \(c_{j}^{\prime }\), respectively, and \(p({c_i},c_{j}^{\prime })\) is the joint probability that the arbitrarily selected video belongs to the clusters \({c_i}\) as well as \(c_{j}^{\prime }\) at the same time. In our experiments, we use the NMI as follows:

$$NMI(C,C^{\prime})=\frac{{MI(C,C^{\prime})}}{{\hbox{max} (H(C),H(C^{\prime}))}}$$
(21)

where \(H(C)\) and \(H({C^\prime })\) are the entropies of \(C\) and \({C^\prime }\), respectively. \(NMI(C,{C^\prime })\) takes values between 0 and 1. \(NMI=1\) if the two sets of clusters are identical, and \(NMI=0\) if the two sets of clusters are independent.

The dataset used in our experiments is so big to fit in the memory that it is impossible to keep this data in the memory while running the model. We compare the results of the proposed SOMVCS with ONMF [20] and OMVC [30]. The other existing methods such as GMNMF [18], MIC [11] and MultiNMF [17] are the off-line methods based on NMF which can not apply to the above dataset since these methods are designed for keeping the data in the memory. ONMF is proposed for solving the problem of single-view. In order to apply ONMF to the above dataset, we concatenate views into one single-view. After the concatenation of views of the original datasets, data becomes so large that it will take too much time to process. Therefore, in the experiments, we omit DS5 and DS6 since both of them comprise 7 and 9 views, respectively.

5 Results and discussion

5.1 Results

To show the clustering performance of the proposed SOMVCS, we set the chunk size z to be 2500 for the datasets DS1–DS6 and 3000 for the datasets DS7 and DS8. In our experiments, we notice that applying multiple passes is better than applying one pass. This is because, with the first input few data point the performance of clustering may not be satisfactory, and if multiple passes are feasible, the performance of clustering may get a chance to improve. We report the ACC and NMI in Table 2. In Table 2, based on our introduce of additional manifold regularization term, we give the results with \(\alpha =0\) as a baseline.

Table 2 Accuracy and NMI of ONMF, OMVC, and SOMVCS
Full size table

From Table 2, we can observe that the performance of the proposed SOMVCS outperforms the compared method for all the datasets in terms of ACC and NMI. According to the different significance of each feature type, some of them have a high performance while some have a low performance as reported by Madani et al. [31] in UCI dataset. The performance on DS2 is worse than the others because it consists of feature types from only the feature family such as “text”. The performance becomes better when the dataset includes feature types from up to two or three feature families together (e.g., DS1 and DS3). Therefore, in this experiment, we design the dataset comprising feature types from variant numbers of feature families. It means that when the data consists of feature types from more feature families, it will perform better for clustering purpose. The maximum number of feature type we include in the dataset in our experiments is 9 (DS6); Otherwise, the datasets would be too large for batch learning.

The results demonstrate that the proposed method can learn a better feature representation. It is good for learning with the large-scale data, especially the data from real-world applications as YouTubeFootnote 2. In SOMVSC, the performance improves when the number of passes increases. We set the number of passes to be 10 because after the several passes the result has already improved and then varies a little up and down. The graph for comparing the performance between SOMVCS, ONMF, OMVC is shown in Figs. 2, 3 (ACC) and Figs. 4, 5 (NMI).

Fig. 2
figure 2

Accuracy on DS-1, 2 and 3

Full size image
Fig. 3
figure 3

Accuracy on DS-4, 7 and 8

Full size image
Fig. 4
figure 4

NMI on DS-1, 2 and 3

Full size image
Fig. 5
figure 5

NMI on DS-4, 7 and 8

Full size image

From these figures, we can observe that the proposed SOMVCS gets close performance within the first pass and continue to improve after several passes. The advantages of the SOMVCS is that it utilizes a weight matrix for each view (possibly incomplete view), the intrinsic geometry of the data distribution and sparsity of the latent features, while OMVC and ONMF does not consider the intrinsic geometry, and also ONMF does not consider the possibly incomplete data and sparsity of the data.

5.2 Parameter study

The parameters selection aims to provide a practical guidance of the proposed method. There are two essential parameters, \(\{ {\alpha _v}\}\) and \(\{ {\beta _v}\}\) in SOMVCS. Basically, we set \({\alpha _v}\) to be the same for all the views and also set \({\beta _v}\) the same as \({\alpha _v}\). We run SOMVCS with different values for \(\{ {\alpha _v}\}\) and \(\{ {\beta _v}\}\) on DS1. We only show the results in ACC and NMI on DS1 since we have similar observation on the other datasets.

From Fig. 6, assume that \({\alpha _v}=\alpha\) and \({\beta _v}=\beta\) we can see that the proposed SOMVCS method is sensitive to the parameters \(\alpha\) and \(\beta\). Parameter \(\alpha\) controls the contribution of the manifold regularization of the views. Parameter \(\beta\) controls the co-regularization between views and the consensus. We can observe that when \(\beta\) becomes small, the consensus has more contributed to the learning of each view, meanwhile when it is too small, the performance will not be stable (ACC) and finally will decline. When the value of parameter \(\beta\) increases, the consensus has more influence to each view and the performance will decrease. SOMVCS achieves stably good performance when \(\beta\) is in [10−6, 10−7] (NMI). From these results, the selection of an appropriate value of \(\alpha\) and \(\beta\) shows that a combination of these two parameters affects the performance of the SOMVCS.

Fig. 6
figure 6

ACC and NMI of SOMVCS with different \({\alpha _v}\), \({\beta _v}\) on DS1

Full size image

5.3 Results discussion

In summary, we have the following conclusions for our proposed method:

  1. (a)

    The idea of utilizing the multi-view clustering via NMF technique for social web video clustering has shown a promising performance.

  2. (b)

    Multi-view data with multi-view learning can achieve better performance than relying on just single-view or either multi-view data from the same feature family (Videos).

  3. (c)

    The results of multi-view data comprising more feature types from different feature families can achieve better results (e.g., the result of DS6 is better than that of DS2).

  4. (d)

    The performance improves when multiple passes are feasible.

  5. (e)

    The proposed SOMVCS has outperformed the state-of-the-art in most cases. The ACC and NMI are not high since the method does not hold all data in the memory but split the data into the chunks. The results are obtained at the time t according to the number of passes.

6 Conclusion

In this paper, we presented a novel online multi-view clustering algorithm based on NMF called (SOMVCS), which processes the incoming data chunk by chunk at a time. SOMVCS does not require to hold the whole data matrix in the memory, which can reduce the storage complexity. It learns the latent feature matrices for each view (possibly incomplete view) and merges them into a common consensus. Graph Laplacian regularization enables SOMVCS to exploit the intrinsic geometry of the data distribution in each incomplete view. Our method can scale up to large-scale video datasets. The experimental results demonstrated the effectiveness of the proposed SOMVCS. As the SOMVCS algorithm is designed for dealing with the data in high-dimensional space, we will looking for other real-world datasets of social media as the benchmark and try to extend our algorithm with other clustering algorithms to further improve its performance in the future work.