$H_{\infty }$ filter design for delayed static neural networks with Markovian switching and randomly occurred nonlinearity

Abstract

The paper is concerned with the problem of $H_{\infty }$ filter design for delayed static neural networks with Markovian switching and randomly occurred nonlinearity. The random phenomenon is described in terms of a Bernoulli stochastic variable. Based on the reciprocally convex approach, a lower bound lemma is proposed to handle the double- and triple-integral terms in the time derivative of the Lyapunov function. Finally, the optimal performance index is obtained via solving linear matrix inequalities(LMIs). The result is not only less conservative but the time derivative of the time delay can be greater than one. Numerical examples with simulation results are provided to illustrate the effectiveness of the developed results.

1 Introduction

As the characteristic of distributed storage, parallel processing and self-learning ability, the neural networks have been successfully applied to signal processing, static image processing and associative memories etc. But the change of the actual project, such as time delay [1–3] which is the main element of many physical processes, may lead to significantly deteriorated performances of the underlying neural networks. Therefore, the stability of the neural network is the core problem that needs to be considered. When the external states of neurons are taken as basic variables, the neural networks can be transformed into static neural networks, because of its extensive application, such as recursive back propagation neural network and the optimization of neural network etc., a number of papers have focus on static neural networks [4–10]. Guaranteed generalized H ₂ performance state estimation problems of delayed static neural networks are studied in [4], and a H ₂ filter is designed for a class of static neural networks in [5]. Furthermore, guaranteed $H_{\infty }$ performance state estimation problems are added in [6]. The state estimation of static neural networks with delay-dependent and delay-independent criteria is presented in [7]. While in [8], by constructing a suitable augmented Lyapunov-Krasovskii function, the $H_\infty$ state estimation problem of static neural network was further researched. On the other hand, the stability analysis of static recurrent neural networks has been researched in [9, 10].

On the other hand, the Markovian jumping system is very suitable for random mutation model, such as the change of the working point, sudden environmental interference, and biomedical error [11, 12]. In order to further study neural networks, many related results on stability analysis and filter design for neural networks with Markovian jumping parameters have been reported in [13–23]. However, more attention should be paid to these disturbances such as uncertainty, which is caused by the randomness. Strictly speaking, any actual system contains random factors. It is worth to know that the nonlinear disturbances may occur in a probabilistic way and are randomly changeable in terms of their types. Both time-delay and random disturbance have great influence in the stability of system, so a lot of reserach on them have been done in [24–30]. For examples, asynchronous $l_2$–$l_\infty$ filter is designed for discrete-time stochastic systems where the sensor nonlinearities is considered in [24]. The randomly occurring parameter uncertainties with certain mutually uncorrelated Bernoulli distributed white noise sequences is introduced in [25]. $H_\infty$ filtering for a class of discrete-time stochastic system with randomly occurred sensor nonlinearity has been researched in [26]. The effect of both variation range and distribution probability of the time delay is taken into account in [27]. Stochastic switched static neural networks with randomly occurring nonlinearities and stochastic delay is introduced and its mean square exponential stability proved in [28]. The problem of mean square asymptotic stability of stochastic Markovian jump neural networks with randomly occurred nonlinearities has been solved in [29]. Moreover, the analysis for the asymptotic stability of stochastic static neural networks is proposed in [30], where the time-delays are variable.

In this paper, according to the reciprocally convex approach [32, 33], which is a special type of function combination obtained by applying the inequality lemma to partitioned single integral terms, we will quote the lower bounder lemma in [5] instead of Wirtinger inequality in [31] for such a linear combination of the Lyapunov functional with the double- and triple-integral. Based on this lemma, we will get the lower prescribed level of noise attenuation compared with [31]. One needs to be noted is that the time derivative of the time delay can be greater than one in this paper. Motivated by the above discussion, the randomly occurred nonlinearity function will be taken into account with a Bernoulli stochastic variable in the paper. $H_{\infty }$ filter is designed to ensure the resultant error systems are globally stochastic stable. And the $H_{\infty }$ filter performance indexes are obtained by solving linear matrix inequalities (LMIs). Finally, numerical examples are given to demonstrate the validity and effectiveness of the proposed approach.

Throughout this paper, $\mathbb {R}^n$ denotes the n-dimensional Euclidean space. I is the identity matrix. $||\cdot ||$ denotes Euclidean norm for vectors. $A^T$ stands for the transpose of the matrix A. For symmetric matrices X and Y, the notation $X>Y$ (respectively $X\ge Y$ ) means that the $X-Y$ is positive definite (respectively, positive semi-definite). The symmetric terms in a symmetric matrix are denoted by $*$ and $diag\{Z_1,Z_2,\ldots ,Z_n\}$ denotes a blockdiagonal matrix. $\mathbf {E}\{x\}$ stands for the expectation of the stochastic variable. $L_{2}[0, \infty )$ is the space of the square integrable vector functions over $[0, \infty )$.

2 Problem description

Firstly, for $t\ge 0$, $r_t$, taking values from a finite set $\mathcal {N}=\{1,2,\ldots ,n\}$, is a right-continuous Markov chain defined on a complete probability space $(\Omega ,\mathcal {F}, \mathcal {P})$. Its transition probability between different modes are given by

$$\begin{aligned}&\mathcal {P}_{r}(r_{t+\Delta }=j |r_{t}=i) = \left\{ \begin{array}{ll} \pi _{ij}\Delta +o(\Delta )&{}i\ne j,\\ 1+\pi _{ii}\Delta +o(\Delta )&{}i=j \end{array}\right.. \end{aligned}$$

where $\Delta >0$, $\lim _{\Delta \rightarrow 0}\frac{o(\Delta )}{\Delta }=0$; $\pi _{ij}\ge 0$, $\forall i\ne j$, and for $i\in \mathcal {N}$, $\pi _{ii}=-\sum _{j=1,j\ne i}^n\pi _{ij}$.

Next, we consider the following static neural networks with Markovian switching and randomly occurred nonlinearity:

$$\begin{aligned} \dot{x}(t)= & {} -A(r_{t})x(t)+f(W(r_t)x(t-d(t))+J(r_{t}))+B_1(r_{t})w(t),\end{aligned}$$

(1)

$$\begin{aligned} y(t)=\; & {} \alpha (t)\psi (C(r_{t})x(t))+(1-\alpha (t))C(r_{t})x(t)+D(r_{t})x(t-d(t))+B_2(r_{t})w(t),\end{aligned}$$

(2)

$$\begin{aligned} z(t)=\; & {} E(r_{t})x(t),\end{aligned}$$

(3)

$$\begin{aligned} x(t)=\; & {} \phi (t), \quad t\in [-d,0], \end{aligned}$$

(4)

where $x(t)=[x_1(t)~x_2(t)~\cdots ~x_n(t)]^T\in \mathbb {R}^{n}$ is the state vector of the neural networks with n neurons, $A(r_{t})=diag\{a_1(r_{t}),a_2(r_{t}),\ldots ,a_n(r_{t})\}$ is a constant diagonal matrix with $a_m(r_{t})>0$, $w(t)\in \mathbb {R}^p$ is the disturbance input in $L_{2}[0,\infty )$, $y(t)\in \mathbb {R}^q$ is the measured output and z(t) is the signal to be estimated, $f(x(t))=[f_1(x_1(t)),f_2(x_2(t)),\ldots ,f_n(x_n(t))]$ denotes the neuron activation function, for r(t) $\in$ $\mathcal {N}$, $W(r_{t}),C(r_{t}),D(r_{t}),B_1(r_{t}),B_2(r_{t}),E(r_{t})$ are the constant matrices with compatible dimensions, and $J(r_{t})$ is an external input vector. $\psi (x(t))=[\psi _1(x_1(t)),\psi _2(x_2(t)),\ldots ,\psi _n(x_n(t))]$ is an output nonlinear signal. $\phi (t)$ is a real valued initial function. d(t) is a time-varying delay with an upper bound $d>0$ and scalar $\mu$, such that d(t) satisfies

$$\begin{aligned} 0\le {d(t)}\le {d},\dot{d}(t)\le \mu . \end{aligned}$$

(5)

To simplify the notations, in the sequel, for each $r(t)=i\in \mathcal {N}$, we denote the matrix $A(r_t)$ to be $A_i$ and so on.

For the neural network (1)–(4), the state estimator is constructed as follows:

$$\begin{aligned}&\dot{\hat{x}}(t)=-A_i\hat{x}(t)+f(W_i\hat{x}(t-d(t))+J_i)+K_i[y(t)-(1-\alpha )C_i\hat{x}(t)-D_i\hat{x}(t-d(t))\nonumber \\&\quad \quad \quad -\alpha \psi (C_i\hat{x}(t))],\end{aligned}$$

(6)

$$\begin{aligned} \hat{z}(t)=E_i\hat{x}(t),\end{aligned}$$

(7)

$$\begin{aligned} \hat{x}(0)=0,\quad t \in [-d,0], \end{aligned}$$

(8)

where $\hat{x}(t)\in \mathbb {R}^{n}$ and $\hat{z}(t)\in \mathbb {R}^q$, and $K_i$ are to be designed matrices with compatible dimensions.

Defining the error signals to be $\tilde{x}(t)=x(t)-\hat{x}(t)$, and $\tilde{z}(t)=z(t)-\hat{z}(t)$. It is easy to follow the above discussion that the estimation error systems are

$$\begin{aligned} \dot{\tilde{x}}(t)= & {} (-A_i-(1-\alpha )K_iC_i)\tilde{x}(t)+g(W_i\tilde{x}(t-d(t)))\nonumber \\ &- {} K_iD_i\tilde{x}(t-d(t))+(B_{1i}-K_iB_{2i})w(t)\nonumber \\ & - {} \alpha K_i\psi _s(C_i\tilde{x}(t))+(\alpha (t)-\alpha )(K_iC_ix(t)-K_i\psi (C_ix(t))),\end{aligned}$$

(9)

$$\begin{aligned} \tilde{z}(t)= & E_i \tilde{x}(t), \end{aligned}$$

(10)

where

$$\begin{aligned}&g(W_i\tilde{x}(t-d(t)))=f(W_ix(t-d(t)+J_i)-f(W_i\hat{x}(t-d(t)+J_i),\end{aligned}$$

(11)

$$\begin{aligned}&\psi _s(C_i\tilde{x}(t))=\psi (C_ix(t))-\psi (C_i\hat{x}(t)). \end{aligned}$$

(12)

The following presentation will give us a detailed understanding of the problem.

Remark 1

Markovian switching systems are considered in this paper, but the state of Markovian switching may be different with the state of systems. For example, many papers [1, 2, 11, 13, 18] have considered the impulsive neural network model, which belongs to a new category of dynamical systems, so it is neither purely continuous-time nor purely discrete-time.

Remark 2

According to the given hypothesis [25, 29], $\alpha (t)$ is a Bernoulli process white sequence taking values of 1 and 0, and indicating that the output of the plant y(t) is linear or not, with $Pr[\alpha (t)=1]=\alpha$, $Pr[\alpha (t)=0]=1-\alpha$, where $\alpha \in [0,1]$ is a known constant, for further calculation, we get

$$\begin{aligned}&\mathbf {E}(\alpha (t))=\alpha \quad \quad \mathbf {E}(\alpha (t)-\alpha )=0,\end{aligned}$$

(13)

$$\begin{aligned}&\mathbf {E}((\alpha (t)-\alpha )^2)=\bar{\alpha }^2,\quad \bar{\alpha }=\sqrt{\alpha (1-\alpha )}. \end{aligned}$$

(14)

Remark 3

Following from Remark 2, $\alpha (t)$ is not constant and time-varying, which means the output nonlinear signal will randomly appear in the measured output y(t). Therefore, the advantage of the model is more flexible and adapt to changes of the working conditions, even in some unexpected situations.

Assumption 1

The activation function f(t) in (1) and nonlinear function $\psi (t)$ in (2) are both continuous and satisfy

$$\begin{aligned}&l_i ^- \le \frac{f_i(u)-f_i(v)}{u-v} \le l_i^+ ,\end{aligned}$$

(15)

$$\begin{aligned}&m_i ^- \le \frac{\psi _i(u)-\psi _i(v)}{u-v} \le m_i^+ , \end{aligned}$$

(16)

where $f(0)=0$, $\psi (0)=0,\quad i=1, 2, \ldots , n$. $u\ne v$, $l_i^-$ and $l_i^+$, $m_i ^-$ and $m_i ^+$ are real scalars, and they maybe positive, negative, or zero.

Remark 4

From Assumption 1, we know that the bound of activation function f(t) can be positive or negative, which means it will be more general than usual Lipschitz condition in [7].

Remark 5

The randomly occurred disturbance of neural network has been deeply researched in literatures [24, 26, 28, 29], where the nonlinear function $\psi (t)$ satisfies the sector bounded condition. In this paper, in order to compare with [31], we will consider the same assumption for the activation function in [31]. Here the nonlinear functions f(t) and $\psi (t)$ satisfy the conditions (15)–(16). Then with the stochastic variable $\alpha (t)$, the occurrence probability of the event of $\psi (t)$ is defined.

The following lemmas are given which will be used in our main results.

Lemma 1

[34] If there exists function $v(t):[0,d]\rightarrow \mathbb {R}^n$ , such that $\int ^d_0v^T(s)Xv(s)ds$ and $\int ^d_0v(s)ds$ are well defined, the following inequality holds for any pair of symmetric positive definite matrix $X\in \mathbb {R}^{n\times n}$ and $d>0$.

$$\begin{aligned} -\int _0^dv^{T}(s)Xv(s)ds\le -\frac{1}{d}\left( \int _0^dv(s)ds\right) ^{T}X\int _0^dv(s)ds. \end{aligned}$$

Lemma 2

[5] For the given scalar $d > 0$ , real matrix S and G satisfy

$$\begin{aligned} \left[ \begin{array}{cc} S &{} G \\ *&{} S \end{array} \right] \ge\; 0, \end{aligned}$$

then with $e(t)=[x^T(t)\quad \tilde{x}^T(t)]^T$, $\bar{w}(t)=[w^T(t) \quad w^T(t)]^T$, one has

$$\begin{aligned}&-d\int _{t-d}^t\dot{e}^{T}(s)S\dot{e}(s)ds \le -\xi ^{T}(t)\mathcal {I}^{T}\left[ \begin{array}{cc} S &{} G \\ *&{} S \end{array} \right] \mathcal {I}\xi (t). \end{aligned}$$

where

$$\begin{aligned}&\xi (t)=[e^T(t)\quad e^T(t-d)\quad e^T(t-d(t))\\ \quad \times \int ^t_{t-d}e^T(s)ds\quad \delta _{1i}^T(t)\quad \bar{w}^T(t)\quad \delta _{2i}^T(t)]^T\\&\delta _{1i}(t)=[f^T(W_ix(t-d(t)))\quad g^T(W_i\tilde{x}(t-d(t)))]^T,\nonumber \\&\delta _{2i}(t)=[\psi ^T(C_ix(t))\quad \psi _s(C_i\tilde{x}(t))]^T,\nonumber \\&\mathcal {I}=\left[ \begin{array}{cccccccc} 0 &{} -I &{} I &{} 0 &{} 0 &{} 0 &{} 0\\ I &{} 0 &{} -I &{} 0 &{} 0 &{} 0 &{} 0 \end{array}\right] .\nonumber \end{aligned}$$

(17)

$H_\infty$ filter problem can be utilized as: given a prescribed level of noise attenuation $\rho > 0$, such that the following conditions hold.

• 1. The error systems (9)–(10) with $w(t) \equiv 0$ are globally stochastic stable.

• 2. Under the zero-initial condition

  $$\begin{aligned}&\Vert \tilde{z}(t)\Vert _{2}<\rho \Vert w(t)\Vert _{2}. \end{aligned}$$

  (18)

  holds for any nonzero $w(t)\in L_{2}[0,\infty ).$

3 Main results

Theorem 1

For the given scalar $d>0$ and $\mu$ , the resulting estimation error systems (9)–(10) are globally stochastic stable with $H_{\infty }$ performance $\rho$ , if there exist positive matrices $P_{i1}$, $P_{i2}$, $Q_{11i}$, $Q_{13i}$, $Q_{21i}$, $Q_{23i}$, $Q_{11}$, $Q_{22}$, $R_{11}$, $R_{22}$, $R_{i11}$, $R_{i22}$, $S_{11}$, $S_{22}$, $S_{i11}$, $S_{i22}$ , diagonal matrices $T_i=diag\{t_{i1},t_{i2},\ldots ,t_{in}\}>0$, $U_i=diag\{u_{i1},u_{i2},\ldots ,u_{in}\}>0$, and $X_i$, $Q_{12}$, $Q_{12i}$, $Q_{22i}$, $R_{12}$, $R_{i12}$, $S_{12}$, $S_{i12}$, $G_i=\left[ \begin{array}{cc}G_{i11} &{} G_{i12}\\ G_{i21} &{} G_{i22} \end{array}\right]$ with appropriate dimension, such that the following LMIs hold for $i\in \mathcal {N}$:

$$\begin{aligned}&P_i=\left[ \begin{array}{cc} P_{i1} &{} 0\\ *&{} P_{i2} \end{array} \right]>0,\quad Q_{1i}=\left[ \begin{array}{cc} Q_{11i} &{} Q_{12i}\\ *&{} Q_{13i} \end{array} \right] >0,\end{aligned}$$

(19)

$$\begin{aligned}&Q_{2i}=\left[ \begin{array}{cc} Q_{21i} &{} Q_{22i}\\ *&{} Q_{23i} \end{array} \right]>0,\quad Q=\left[ \begin{array}{cc} Q_{11} &{} Q_{12}\\ *&{} Q_{22} \end{array} \right] >0,\end{aligned}$$

(20)

$$\begin{aligned}&R=\left[ \begin{array}{cc} R_{11} &{} R_{12}\\ *&{} R_{22} \end{array} \right]>0,\quad R_i=\left[ \begin{array}{cc} R_{i11} &{} R_{i12}\\ *&{} R_{i22} \end{array} \right] >0,\end{aligned}$$

(21)

$$\begin{aligned}&S=\left[ \begin{array}{cc} S_{11} &{} S_{12}\\ *&{} S_{22} \end{array} \right]>0,\quad S_i=\left[ \begin{array}{cc} S_{i11} &{} S_{i12}\\ *&{} S_{i22} \end{array} \right] >0,\end{aligned}$$

(22)

$$\begin{aligned}&\left[ \begin{array}{cc} S_i &{} G_i\\ *&{} S_i \end{array} \right] \ge 0,\end{aligned}$$

(23)

$$\begin{aligned}&\sum _{j=1,j\ne i}^{n}\pi _{ij}Q_{1j}+\sum _{j=1}^{n}\pi _{ij}Q_{2j}<Q,\end{aligned}$$

(24)

$$\begin{aligned}&\sum _{j=1}^{n}\pi _{ij}R_j\le R, \quad \sum _{j=1}^{n}\pi _{ij}S_j\le S,\end{aligned}$$

(25)

$$\begin{aligned}&\Sigma =\left[ \begin{array}{ccc} \gamma _{i1} &{} \gamma _{i2} &{} \gamma _{i3}\\ *&{} \gamma _{i4} &{} \gamma _{i5}\\ *&{} *&{} \gamma _{i6} \end{array} \right] <0. \end{aligned}$$

(26)

where

$$\begin{aligned} \gamma _{i1}= & {} \left[ \begin{array}{cccc} \Omega _{i1} &{} \Omega _{i2} &{} \Omega _{i3} &{} 0 \\ *&{} \Omega _{i4} &{} \Omega _{i5} &{} 0 \\ *&{} *&{} \Omega _{i6} &{} 0\\ *&{} *&{}*&{} \Omega _{i7} \end{array} \right] , \end{aligned}$$

$$\begin{aligned} \gamma _{i2}= & {} \left[ \begin{array}{cccccc} P_{i1} &{} 0 &{} P_{i1}B_{1i} &{} 0 &{} \Lambda _{i7} &{} 0 \\ 0 &{} P_{i2} &{} 0 &{} \Lambda _{i8} &{} 0 &{} \Lambda _{i9} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ \Lambda _{i10} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \Lambda _{i10} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right] ,\\ \gamma _{i3}= & {} \left[ \begin{array}{cccc} -dA_i^TP_{i1} &{} 0 &{} 0 &{} \bar{\alpha }dC_i^TX_i^T\\ 0 &{} \Lambda _{i11} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} -dD_iX_i^T &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] ,\\ \gamma _{i4}= \,& {} diag\{-T_i ,-T_i,-{\rho }^2I,-{\rho }^2I ,-U_i,-U_i\},\\ \gamma _{i5}= & {} \left[ \begin{array}{cccc} dP_{i1} &{} 0 &{} 0 &{} 0\\ 0 &{} dP_{i2} &{} 0 &{} 0\\ dB_{1i}^TP_{i1} &{} 0 &{} 0 &{} 0\\ 0 &{} dB_{1i}^TP_{i2}-dB_{2i}^TX_i^T &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} -{\bar{\alpha }}dX_i^T\\ 0 &{} -{\alpha }dX_i^T &{} 0 &{} 0 \end{array} \right] ,\\ \gamma _{i6}= & {} \left[ \begin{array}{cccc} \Lambda _{i12}&{} \Lambda _{i13} &{} 0 &{} 0\\ *&{} \Lambda _{i14} &{} 0 &{} 0\\ *&{} *&{} \Lambda _{i12} &{} \Lambda _{i13}\\ *&{} *&{} *&{} \Lambda _{i14} \end{array} \right] ,\\&\Omega _{i1}=\left[ \begin{array}{cc} \Lambda _{i1} &{} \Lambda _{i2}\\ *&{} \Lambda _{i3} \end{array} \right] ,\quad \Omega _{i2}=\left[ \begin{array}{cc} \frac{1}{d}G_{i11}^T &{} \frac{1}{d}G_{i21}^T\\ \frac{1}{d}G_{i12}^T &{} \frac{1}{d}G_{i22}^T \end{array} \right] ,\\&\Omega _{i3}=\left[ \begin{array}{cc} -\frac{1}{d}G_{i11}^T+\frac{1}{d}S_{i11} &{} -\frac{1}{d}G_{i21}^T+\frac{1}{d}S_{i12}\\ -\frac{1}{d}G_{i12}^T+\frac{1}{d}S^T_{i12} &{} -\frac{1}{d}G_{i22}^T+\frac{1}{d}S_{i22}-X_iD_i \end{array} \right] ,\\&\Omega _{i4}=\left[ \begin{array}{cc} -Q_{21i}-\frac{1}{d}S_{i11} &{} -Q_{22i}-\frac{1}{d}S_{i12}\\ *&{} -Q_{23i}-\frac{1}{d}S_{i22} \end{array} \right] ,\\&\Omega _{i5}=\left[ \begin{array}{cc} -\frac{1}{d}G_{i11}+\frac{1}{d}S_{i11} &{} -\frac{1}{d}G_{i12}+\frac{1}{d}S_{i12}\\ -\frac{1}{d}G_{i21}+\frac{1}{d}S^T_{i12} &{} -\frac{1}{d}G_{i22}+\frac{1}{d}S_{i22} \end{array} \right] ,\\&\Omega _{i6}=\left[ \begin{array}{cc} \Lambda _{i4} &{} \Lambda _{i5}\\ *&{} \Lambda _{i6} \end{array} \right] ,\quad \Omega _{i7}=\left[ \begin{array}{cc} -\frac{1}{d}R_{i11} &{} -\frac{1}{d}R_{i12}\\ *&{} -\frac{1}{d}R_{i22} \end{array} \right] ,\\&\Lambda _{i1}=-P_{i1}A_i-A_i^TP_{i1}+\sum _{j=1}^{n}\pi _{ij}P_{j1}+Q_{11i}+Q_{21i}\\& \quad \quad +dQ_{11}+dR_{i11}+\frac{1}{2}d^{2}R_{11}-\frac{1}{d}S_{i11}-C^T_iU_iM_{i1}C_i,\\&\Lambda _{i2}=Q_{12i}+Q_{22i}+dQ_{12}+dR_{i12}+\frac{1}{2}d^{2}R_{12}-\frac{1}{d}S_{i12},\\&\Lambda _{i3}=-P_{i2}A_i-A_i^TP_{i2}-(1-\alpha )X_iC_i-(1-\alpha )C_i^TX^T_i+\sum _{j=1}^{n}\pi _{ij}P_{j2}+Q_{13i}\\& \quad \quad +Q_{23i}+dQ_{22}+dR_{i22}+\frac{1}{2}d^{2}R_{22}-\frac{1}{d}S_{i22}-C^T_iU_iM_{i1}C_i+E_i^TE_i,\\&\Lambda _{i4}=-\frac{2}{d}S_{i11}+\frac{1}{d}G_{i11}+\frac{1}{d}G_{i11}^{T}-(1-\mu )Q_{11i}-W^T_iT_iN_{i1}W_i,\\&\Lambda _{i5}=-\frac{2}{d}S_{i12}+\frac{1}{d}G_{i12}+\frac{1}{d}G_{i21}^{T}-(1-\mu )Q_{12i},\\&\Lambda _{i6}=-\frac{2}{d}S_{i22}+\frac{1}{d}G_{i22}+\frac{1}{d}G_{i22}^{T}-(1-\mu )Q_{13i}-W^T_iT_iN_{i1}W_i.\\&\Lambda _{i7}=-C^T_iU_iM_{i2},\quad \Lambda _{i8}=P_{i2}B_{1i}-X_iB_{2i},\\&\Lambda _{i9}=-C^T_iU_iM_{i2}-{\alpha }X_i, \quad \Lambda _{i10}=-W^T_iT_iN_{i2},\\&\Lambda _{i11}=-dA_i^TP_{i2}-d(1-\alpha )C_i^TX_i^T, \quad \Lambda _{i12}=-2P_{i1}+\frac{1}{d}S_{i11}+\frac{1}{2}S_{11},\\&\Lambda _{i13}=\frac{1}{d}S_{i12}+\frac{1}{2}S_{12}, \quad \Lambda _{i14}=-2P_{i2}+\frac{1}{d}S_{i22}+\frac{1}{2}S_{22},\\&N_{i1}=l_i^-l_i^+, \quad N_{i2}=-\frac{l_i^- +l_i^+}{2},\\&M_{i1}=m_i^-m_i^+, \quad M_{i2}=-\frac{m_i^- +m_i^+}{2}. \end{aligned}$$

The gain matrices $K_i$ can be designed as

$$\begin{aligned} K_i=P_{i2}^{-1}X_i. \end{aligned}$$

(27)

Proof

Combing (1)–(4) and (9)–(10), one has $e(t)=[x^T(t)\quad \tilde{x}^T(t)]^T$, $\bar{z}(t)=[z^T(t) \quad \tilde{z}^T(t)]^T$, we get the following augmented system governing the estimation error dynamics:

$$\begin{aligned}&\dot{e}(t)= \xi _{1i}(t)+(\alpha (t)-\alpha )\xi _{2i}(t),\end{aligned}$$

(28)

$$\begin{aligned}&\bar{z}(t)=\bar{E}_ie(t), \end{aligned}$$

(29)

where

$$\begin{aligned}&\xi _{1i}(t)={\bar{A}}_{i}e(t)+{\bar{D}}_{i}e(t-d(t))+{\bar{B}}_{i}{\bar{w}}(t)+{\delta }_{1i}(t)+{\bar{G}}_{i}{\delta }_{2i}(t),\\&\xi _{2i}(t)={\bar{C}}_{i}e(t)+{\bar{K}}_{i}{\delta }_{2i}(t), \end{aligned}$$

$$\begin{aligned}&{\bar{A}}_{i}=\left[ \begin{array}{ll} -A_{i} &{} 0\\ 0 &{} -A_{i}-(1-{\alpha })K_{i}C_{i}\end{array}\right] , \quad {\bar{B}}_{i}=\left[ \begin{array}{ll} B_{1i} &{} 0 \\ 0 &{} B_{1i}-K_{i}B_{2i}\end{array}\right] ,\end{aligned}$$

(30)

$$\begin{aligned}&{\bar{C}}_{i}=\left[ \begin{array}{ll} 0 &{} 0 \\ K_{i}C_{i} &{} 0 \end{array}\right] , \quad {\bar{D}}_{i}=\left[ \begin{array}{ll} 0 &{} 0 \\ 0 &{} -K_{i}D_{i} \end{array}\right] , {\bar{E}}_{i}=\left[ \begin{array}{ll} 0&E_{i} \end{array}\right] ,\end{aligned}$$

(31)

$$\bar{G}_{i} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill \\ 0 \hfill & { - \alpha K_{i} } \hfill \\ \end{array} } \right],{\text{ }}\quad \bar{K}_{i} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill \\ { - K_{i} } \hfill & 0 \hfill \\ \end{array} } \right].{\text{ }}$$

(32)

Now we need to show the augmented error systems (28)–(29) are globally stochastic stable, we choose the following Lyapunov functions to begin this proof

$$\begin{aligned} V(t)= & {} V_1(t)+V_2(t)+V_3(t)+V_4(t), \end{aligned}$$

(33)

where

$$\begin{aligned} V_1(t)=\; & {} e^T(t)P_ie(t),\end{aligned}$$

(34)

$$\begin{aligned} V_2(t)= & {} \int ^t_{t-d(t)}e^T(s)Q_{1i}e(s)ds+\int ^t_{t-d}e^T(s)Q_{2i}e(s)ds +\int ^0_{-d}\int ^t_{t+\theta }e^T(s)Qe(s)dsd\theta ,\end{aligned}$$

(35)

$$\begin{aligned} V_3(t)= & {} \int ^0_{-d}\int ^t_{t+\theta }e^T(s)R_ie(s)dsd\theta +\int ^0_{-d}\int ^{0}_{\theta }\int ^t_{t+\alpha }e^T(s)Re(s)dsd{\alpha }d\theta ,\end{aligned}$$

(36)

$$\begin{aligned} V_4(t) & = \int ^0_{-d}\int ^t_{t+\theta }\dot{e}^T(s)S_i\dot{e}(s)dsd\theta \\&\quad+\int ^0_{-d}\int ^{0}_{\theta }\int ^t_{t+\alpha }\dot{e}^T(s)S\dot{e}(s)dsd{\alpha }d\theta . \end{aligned}$$

(37)

Firstly, we define the weak infinitesimal operator $\mathcal {L}$ as

$$\begin{aligned} \mathcal {L}V(t,e_t,i)=\lim _{\Delta \rightarrow 0}\frac{1}{\Delta }[\mathbf {E}(V(t+\Delta ,e_{t+\Delta },r_{t+\Delta }|e_t,r_t=i)-V(t,e_t,i)]. \end{aligned}$$

where $\mathbf {E}$ is defined as

$$\begin{aligned} \mathbf {E}\{V(t,e_t,r_t)\}=V(0,e_0,r_t)+\mathbb {E}\left\{\int ^t_{0}V(s,e_s,r_s)ds\right\}. \end{aligned}$$

Then for each $i\in \mathcal {N}$, according to the weak infinitesimal operator $\mathcal {L}$, we have the stochastic differential

$$\begin{aligned} \mathcal {L}V(t)=\mathcal {L}V_1(t)+\mathcal {L}V_2(t)+\mathcal {L}V_3(t)+\mathcal {L}V_4(t), \end{aligned}$$

(38)

where

$$\begin{aligned} \mathcal {L}V_1(t)=\; & {} 2e^T(t)P_i\dot{e}(t)+\sum _{j=1}^{n}\pi _{ij}e^{T}(t)P_je(t), \\ \mathcal {L}V_2(t) & = e^T(t)Q_{1i}e(t)-(1-\dot{d}(t))e^T(t-d(t))Q_{1i}e(t-d(t))+\sum _{j=1}^{n}\pi _{ij}\int ^{t}_{t-d(t)}e^T(s)Q_{1j}e(s)ds\\&\quad+e^{T}(t)Q_{2i}e(t)-e^T(t-d)Q_{2i}e(t-d)+\sum _{j=1}^{n}\pi _{ij}\int ^{t}_{t-d}e^T(s)Q_{2j}e(s)ds\\&\quad+de^T(t)Qe(t)-\int ^{t}_{t-d}e^T(s)Qe(s)ds,\\ \mathcal {L}V_3(t)=\; & {} de^T(t)R_ie(t)-\int ^{t}_{t-d}e^T(s)R_ie(s)ds+\sum _{j=1}^{n}\pi _{ij}\int ^{0}_{-d}\int ^{t}_{t+\theta }e^T(s)R_je(s)dsd\theta \\&\quad +\frac{1}{2}d^2e^T(t)Re(t)-\int ^{0}_{-d}\int ^{t}_{t+\theta }e^T(s)Re(s)dsd\theta ,\\ \mathcal {L}V_4(t)=\; & {} d\dot{e}^T(t)S_i\dot{e}(t)+\frac{1}{2}d^2\dot{e}^T(t)S\dot{e}(t)-\int ^{t}_{t-d}\dot{e}^T(s)S_i\dot{e}(s)ds\\&\quad+\sum _{j=1}^{n}\pi _{ij}\int ^{0}_{-d}\int ^{t}_{t+\theta }\dot{e}^T(s)S_j\dot{e}(s)dsd\theta -\int ^{0}_{-d}\int ^{t}_{t+\theta }\dot{e}^T(s)S\dot{e}(s)dsd\theta . \end{aligned}$$

Noting that $\pi _{ij}\ge 0$, when $j\ne i$, and $\pi _{ii}\le 0$, one has

$$\begin{aligned}&\sum _{j=1}^{n}\pi _{ij}\int ^{t}_{t-d(t)}e^T(s)Q_{1j}e(s)ds\le \sum _{j=1,j\ne i}^{n}\pi _{ij}\int ^{t}_{t-d(t)}e^T(s)Q_{1j}e(s)ds\\&\quad \le \sum _{j=1,j\ne i}^{n}\pi _{ij}\int ^{t}_{t-d}e^T(s)Q_{1j}e(s)ds. \end{aligned}$$

In the view of (24), we obtain

$$\begin{aligned}&\sum _{j=1}^{n}\pi _{ij}\int ^{t}_{t-d(t)}e^T(s)Q_{1j}e(s)ds+\sum _{j=1}^{n}\pi _{ij}\int ^{t}_{t-d}e^T(s)Q_{2j}e(s)ds-\int ^{t}_{t-d}e^T(s)Qe(s)ds \le 0. \end{aligned}$$

(39)

From (25), we also have the following calculation:

$$\begin{aligned}&\sum _{j=1}^{n}\pi _{ij}\int ^{0}_{-d}\int ^{t}_{t+\theta }e^T(s)R_je(s)dsd\theta -\int ^{0}_{-d}\int ^{t}_{t+\theta }e^T(s)Re(s)dsd\theta \le 0,\end{aligned}$$

(40)

$$\begin{aligned}&\sum _{j=1}^{n}\pi _{ij}\int ^{0}_{-d}\int ^{t}_{t+\theta }\dot{e}^T(s)S_j\dot{e}(s)dsd\theta -\int ^{0}_{-d}\int ^{t}_{t+\theta }\dot{e}^T(s)S\dot{e}(s)dsd\theta \le 0. \end{aligned}$$

(41)

By Lemma 1 and 2, it is known that

$$\begin{aligned}&-\int ^{t}_{t-d}e^T(s)R_ie(s)ds \le -\frac{1}{d}\left(\int ^{t}_{t-d}e(s)ds\right)^TR_i\int ^{t}_{t-d}e(s)ds,\end{aligned}$$

(42)

$$\begin{aligned}&-\int ^{t}_{t-d}\dot{e}^T(s)S_i\dot{e}(s)ds\le -\frac{1}{d}\xi ^{T}(t)\mathcal {I}^{T}\left[ \begin{array}{cc} S_i &{} G_i \\ *&{} S_i \end{array} \right] \mathcal {I}\xi (t). \end{aligned}$$

(43)

For any $T_i=diag\{t_{i1},t_{i2},\ldots ,t_{in}\}>0$, $U_i=diag\{u_{i1},u_{i2},\ldots ,u_{in}\}>0$, considering the conditions in (15)–(16), similar to [27], we obtain

$$\begin{aligned}&\left[ \begin{array}{c} \bar{W}_ie(t-d(t))\\ \delta _{1i}(t) \end{array} \right] ^T\left[ \begin{array}{cc} \mathcal {T}_i\mathcal {N}_{i1} &{} \mathcal {T}_i\mathcal {N}_{i2}\\ \mathcal {T}_i\mathcal {N}_{i2} &{} \mathcal {T}_i \end{array} \right] \left[ \begin{array}{c} \bar{W}_ie(t-d(t))\\ \delta _{1i}(t) \end{array} \right] \le 0,\end{aligned}$$

(44)

$$\begin{aligned}&\left[ \begin{array}{c} \tilde{C}_i e(t)\\ \delta _{2i}(t) \end{array} \right] ^T\left[ \begin{array}{cc} \mathcal {U}_i\mathcal {M}_{i1} &{} \mathcal {U}_i\mathcal {M}_{i2}\\ \mathcal {U}_i\mathcal {M}_{i2} &{} \mathcal {U}_i \end{array} \right] \left[ \begin{array}{c} \tilde{C}_ie(t)\\ \delta _{2i}(t) \end{array} \right] \le 0, \end{aligned}$$

(45)

where

$$\begin{aligned}\mathcal {T}_i &=diag\{T_i,T_i\}, \quad \mathcal {U}_i=diag\{U_i,U_i\},\\ \mathcal {N}_{i1}& =diag\{N_{i1},N_{i1}\}, \quad \mathcal {M}_{i1}=diag\{M_{i1},M_{i1}\},\\ \mathcal {N}_{i2} & =diag\{N_{i2},N_{i2}\}, \quad \mathcal {M}_{i2}=diag\{M_{i2},M_{i2}\},\\ \bar{W}_i & =diag\{W_{i},W_{i}\}, \quad \tilde{C}_i=diag\{C_{i},C_{i}\}. \end{aligned}$$

Considering the (39)–(45) and noting (5), then we take the mathematical expectation of $\mathcal {L}V(t)$ with the conditions (13)–(14), and we finally get

$$\begin{aligned}&\mathbf {E}\{\mathcal {L}V(t)\}\le \mathbf {E}\{2e^T(t)P_i(\bar{A}_ie(t)+\bar{D}_ie(t-d(t))+\bar{B}_i\bar{w}(t)+\delta _{1i}(t)+\bar{G}_i\delta _{2i}(t))\\&\quad \quad \quad \quad \quad +\sum _{j=1}^{n}\pi _{ij}e^{T}(t)P_je(t)+e^T(t)Q_{1i}e(t)-(1-\mu )e^T(t-d(t))Q_{1i}e(t-d(t))\\&\quad \quad \quad \quad \quad +e^{T}(t)Q_{2i}e(t)-e^T(t-d)Q_{2i}e(t-d)+de^T(t)Qe(t)+de^T(t)R_ie(t)\\&\quad \quad \quad \quad \quad -\frac{1}{d}\left(\int ^{t}_{t-d}e(s)ds\right)^TR_i\int ^{t}_{t-d}e(s)ds+\frac{1}{2}d^2e^T(t)Re(t)-\frac{1}{d}\xi ^{T}(t)\mathcal {I}^{T}\left[ \begin{array}{cc} S_i &{} G_i \\ *&{} S_i \end{array} \right] \mathcal {I}\xi (t)\\&\quad \quad \quad \quad \quad +\xi _{1i}^T(t)\left(dS_i+\frac{1}{2}d^2S\right)\xi _{1i}(t)+{\bar{\alpha }}^2\xi _{2i}^T(t)\left(dS_i+\frac{1}{2}d^2S\right)\xi _{2i}(t)\\&\quad \quad \quad \quad \quad -\left[ \begin{array}{c} \bar{W}_ie(t-d(t))\\ \delta _{1i}(t) \end{array} \right] ^T\left[ \begin{array}{cc} \mathcal {T}_i\mathcal {N}_{i1} &{} \mathcal {T}_i\mathcal {N}_{i2}\\ \mathcal {T}_i\mathcal {N}_{i2} &{} \mathcal {T}_i \end{array} \right] \left[ \begin{array}{c} \bar{W}_ie(t-d(t))\\ \delta _{1i}(t) \end{array} \right] \\&\quad \quad \quad \quad \quad -\left[ \begin{array}{c} \tilde{C}_ie(t)\\ \delta _{2i}(t) \end{array} \right] ^T\left[ \begin{array}{cc} \mathcal {U}_i\mathcal {M}_{i1} &{} \mathcal {U}_i\mathcal {M}_{i2}\\ \mathcal {U}_i\mathcal {M}_{i2} &{} \mathcal {U}_i \end{array} \right] \left[ \begin{array}{c} \tilde{C}_ie(t)\\ \delta _{2i}(t) \end{array} \right] \} \end{aligned}$$

Now, we define a function:

$$\begin{aligned} \mathcal {J}=\mathcal {L}V(t)+\tilde{z}^T(t)\tilde{z}(t)-{\rho ^2}\bar{w}^T(t)\bar{w}(t). \end{aligned}$$

Taking (17) into consideration, it is not difficult to obtain

$${\mathbf{E}}\{{\mathcal{J}}\} \le {\mathbf{E}}\left\{ {\xi ^{T} (t)\left[ {\Sigma _{{1i}} + d^{2} \Xi _{{1i}}^{T} \left( {\frac{1}{d}S_{i} + \frac{1}{2}S} \right)\Xi _{{1i}} + d^{2} \bar{\alpha }^{2} \Xi _{{2i}}^{T} \left( {\frac{1}{d}S_{i} + \frac{1}{2}S} \right)\Xi _{{2i}} } \right]} \right\}\xi (t).$$

(46)

Letting $\bar{S_i}=\frac{1}{d}S_i+\frac{1}{2}S$, and we obtain

$$\begin{aligned}&\mathbf {E}\{\mathcal {J}\}\le \mathbf {E}\{\xi ^T(t)[\Sigma _{1i} +d^2\Xi _{1i}^T\bar{S_i}\Xi _{1i}+d^2{\bar{\alpha }}^2\Xi _{2i}^T\bar{S_i}\Xi _{2i}]\xi (t)\} =\mathbf {E}\{\xi ^T(t)\tilde{\Sigma }_{1i}\xi (t)\} \end{aligned}$$

(47)

where

$$\begin{aligned} \Xi _{1i}= & {} \left[ \begin{array}{ccccccc} \bar{A_i}&0&\bar{D_i}&0&I&\bar{B_i}&\bar{G_i} \end{array} \right] ,\\ \Xi _{2i}= & {} \left[ \begin{array}{ccccccc} \bar{C_i}&0&0&0&0&0&\bar{K_i} \end{array} \right] ,\\ \tilde{\Sigma }_{1i}= & {} \Sigma _{1i}+d^2\Xi _{1i}^T\bar{S_i}\Xi _{1i}+d^2{\bar{\alpha }}^2\Xi _{2i}^T\bar{S_i}\Xi _{2i},\\ \Sigma _{1i}= & {} \left[ \begin{array}{ccccccc} \bar{\Omega }_{i1} &{} \bar{\Omega }_{i2} &{} \bar{\Omega }_{i3} &{} 0 &{} P_i &{} P_i\bar{B_i} &{} P_i\bar{G_i}-\tilde{C}^T_i\mathcal {U}_i\mathcal {M}_{i2}\\ *&{} \bar{\Omega }_{i4} &{} \bar{\Omega }_{i5} &{} 0 &{} 0 &{} 0 &{} 0\\ *&{} *&{} \bar{\Omega }_{i6} &{} 0 &{} -\bar{W}^T_i\mathcal {T}_i\mathcal {N}_{i2} &{} 0 &{} 0\\ *&{} *&{} *&{} \bar{\Omega }_{i7} &{} 0 &{} 0 &{} 0\\ *&{} *&{} *&{} *&{} -\mathcal {T}_i &{} 0 &{} 0\\ *&{} *&{} *&{} *&{} *&{} -{\rho }^2I &{} 0\\ *&{} *&{} *&{} *&{} *&{} *&{} -\mathcal {U}_i \end{array} \right] , \end{aligned}$$

$$\begin{aligned} \bar{\Omega }_{i1}=\; & {} P_i\bar{A_i}+\bar{A}^T_iP_i+\sum _{j=1}^{n}\pi _{ij}P_j+Q_{1i}+Q_{2i}+dQ+dR_i \\&+\frac{1}{2}d^{2}R-\tilde{C}^T_i\mathcal {U}_i\mathcal {M}_{i1}\tilde{C}_i+\bar{E_i}^{T}\bar{E_i}-\frac{1}{d}S_i,\\ \bar{\Omega }_{i2}=\; & {} \frac{1}{d}G_i^T, \quad \bar{\Omega }_{i3}=-\frac{1}{d}G_i^T+\frac{1}{d}S_i+P_i\bar{D_i},\\ \bar{\Omega }_{i4}= & {} -Q_{2i}-\frac{1}{d}S_i, \quad \bar{\Omega }_{i5}=-\frac{1}{d}G_i+\frac{1}{d}S_i,\\ \bar{\Omega }_{i6}= & {} -\frac{2}{d}S_i+\frac{1}{d}G_i+\frac{1}{d}G_i^{T}-(1-\mu )Q_{1i}-\bar{W}^T_i\mathcal {T}_i\mathcal {N}_{i1}\bar{W}_i,\\ \bar{\Omega }_{i7}= & {} -\frac{1}{d}R_i. \end{aligned}$$

If $\tilde{\Sigma }_{1i}<0$, by Schur complement, it follows from (47) that

$$\begin{aligned} \left[ \begin{array}{ccccccccc} \bar{\Omega }_{i1} &{} \bar{\Omega }_{i2} &{} \bar{\Omega }_{i3} &{} 0 &{} P_i &{} P_i\bar{B_i} &{} P_i\bar{G_i}-\tilde{C}^T_i\mathcal {U}_i\mathcal {M}_{i2} &{} d\bar{A_i}^T\bar{S_i} &{} d\bar{\alpha }\bar{C_i}^T\bar{S_i}\\ *&{} \bar{\Omega }_{i4} &{} \bar{\Omega }_{i5} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ *&{} *&{} \bar{\Omega }_{i6} &{} 0 &{} -\bar{W}^T_i\mathcal {T}_i\mathcal {N}_{i2} &{} 0 &{} 0 &{} d\bar{D_i}^T\bar{S_i} &{} 0\\ *&{} *&{} *&{} \bar{\Omega }_{i7} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ *&{} *&{} *&{} *&{} -\mathcal {T}_i &{} 0 &{} 0 &{} d\bar{S_i} &{} 0\\ *&{} *&{} *&{} *&{} *&{} -{\rho }^2I &{} 0 &{} d\bar{B_i}^T\bar{S_i} &{} 0\\ *&{} *&{} *&{} *&{} *&{} *&{} -\mathcal {U}_i &{} d\bar{G_i}^T\bar{S_i} &{} d\bar{\alpha }\bar{K_i}^T\bar{S_i}\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} -\bar{S_i} &{} 0\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} -\bar{S_i} \end{array} \right] <0, \end{aligned}$$

(48)

Then pre- and post-multiplying (48) by $diag\{I,I,I,I,I,I,I,P_i\bar{S_i}^{-1},P_i\bar{S_i}^{-1}\}$ and its transpose, we get

$$\begin{aligned} \left[ \begin{array}{ccccccccc} \bar{\Omega }_{i1} &{} \bar{\Omega }_{i2} &{} \bar{\Omega }_{i3} &{} 0 &{} P_i &{} P_i\bar{B_i} &{} P_i\bar{G_i}-\tilde{C}^T_i\mathcal {U}_i\mathcal {M}_{i2} &{} d\bar{A_i}^TP_i &{} d\bar{\alpha }\bar{C_i}^TP_i\\ *&{} \bar{\Omega }_{i4} &{} \bar{\Omega }_{i5} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ *&{} *&{} \bar{\Omega }_{i6} &{} 0 &{} -\bar{W}^T_i\mathcal {T}_i\mathcal {N}_{i2} &{} 0 &{} 0 &{} d\bar{D_i}^TP_i &{} 0\\ *&{} *&{} *&{} \bar{\Omega }_{i7} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ *&{} *&{} *&{} *&{} -\mathcal {T}_i &{} 0 &{} 0 &{} dP_i &{} 0\\ *&{} *&{} *&{} *&{} *&{} -{\rho }^2I &{} 0 &{} d\bar{B_i}^TP_i &{} 0\\ *&{} *&{} *&{} *&{} *&{} *&{} -\mathcal {U}_i &{} d\bar{G_i}^TP_i &{} d\bar{\alpha }\bar{K_i}^TP_i\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} -P_i\bar{S_i}^{-1}P_i &{} 0\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} *&{} -P_i\bar{S_i}^{-1}P_i \end{array} \right] <0, \end{aligned}$$

(49)

Thus, $\mathcal {J}<0$, in the view of the fact that $-P_i\bar{S_i}^{-1}P_i\le -2P_i+\bar{S_i}$, by noting (27), (19)–(23) and (30)–(32), it is noting that $\Sigma <0$ implies (26) holds, since $w(t)\ne 0$, we have $\mathcal {J}<0$, that is $\Vert \tilde{z}(t)\Vert _{2}<\rho \Vert w(t)\Vert _{2}$.

When $\bar{w}(t)=0$, the augmented system will be:

$$\begin{aligned}&\dot{e}(t)= \bar{\xi }_{1i}(t)+(\alpha (t)-\alpha )\xi _{2i}(t), \end{aligned}$$

where

$$\begin{aligned}&\bar{\xi }_{1i}(t)=\bar{A}_ie(t)+\bar{D}_ie(t-d(t))+\delta _{1i}(t)+\bar{G}_i\delta _{2i}(t),\\&\xi _{2i}(t)=\bar{C}_ie(t)+\bar{K}_i\delta _{2i}(t), \end{aligned}$$

We choose the same Lyapunov functions (33) and calculate the weak infinitesimal operator $\mathcal {L}V(t)$. In this case, by the similar line of the derivative of (46), we get:

$$\begin{aligned}&\mathbf {E}\{\mathcal {J}\}\le \mathbf {E}\{\bar{\xi }^T(t)[\bar{\Sigma }_{1i} +d^2\bar{\Xi }_{1i}^T\bar{S_i}\bar{\Xi }_{1i}+d^2{\bar{\alpha }}^2\bar{\Xi }_{2i}^T\bar{S_i}\bar{\Xi }_{2i}]\bar{\xi }(t)\} \end{aligned}$$

where

$$\begin{aligned}&\bar{\xi }(t)=[e^T(t)\quad e^T(t-d)\quad e^T(t-d(t))\quad \int ^t_{t-d}e^T(s)ds\quad \delta _{1i}^T(t)\quad \delta _{2i}^T(t)]^T,\\&\bar{\Xi }_{1i}=\left[ \begin{array}{cccccc} \bar{A_i}&0&\bar{D_i}&0&I&\bar{G_i} \end{array}\right] ,\\&\bar{\Xi }_{2i}=\left[ \begin{array}{cccccc} \bar{C_i}&0&0&0&0&\bar{K_i} \end{array}\right] ,\\&\bar{\Sigma }_{1i}=\left[ \begin{array}{cccccc} \bar{\Omega }_{i1} &{} \bar{\Omega }_{i2} &{} \bar{\Omega }_{i3} &{} 0 &{} P_i &{} P_i\bar{G_i}-\tilde{C}^T_i\mathcal {U}_i\mathcal {M}_{i2}\\ *&{} \bar{\Omega }_{i4} &{} \bar{\Omega }_{i5} &{} 0 &{} 0 &{} 0\\ *&{} *&{} \bar{\Omega }_{i6} &{} 0 &{} -\bar{W}^T_i\mathcal {T}_i\mathcal {N}_{i2} &{} 0\\ *&{} *&{} *&{} \bar{\Omega }_{i7} &{} 0 &{} 0\\ *&{} *&{} *&{} *&{} -\mathcal {T}_i &{} 0\\ *&{} *&{} *&{} *&{} *&{} -\mathcal {U}_i \end{array}\right] . \end{aligned}$$

With similar step (48)–(49), we get the following matrix inequality:

$$\begin{aligned}&\left[ \begin{array}{cccccccc} \bar{\Omega }_{i1} &{} \bar{\Omega }_{i2} &{} \bar{\Omega }_{i3} &{} 0 &{} P_i &{} P_i\bar{G_i}-\tilde{C}^T_i\mathcal {U}_i\mathcal {M}_{i2} &{} d\bar{A_i}^TP_i &{} d\bar{\alpha }\bar{C_i}^TP_i\\ *&{} \bar{\Omega }_{i4} &{} \bar{\Omega }_{i5}&{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ *&{} *&{} \bar{\Omega }_{i6} &{} 0 &{} -\bar{W}^T_i\mathcal {T}_i\mathcal {N}_{i2} &{} 0 &{} d\bar{D_i}^TP_i &{} 0\\ *&{} *&{} *&{} \bar{\Omega }_{i7} &{} 0 &{} 0 &{} 0 &{} 0\\ *&{} *&{} *&{} *&{} -\mathcal {T}_i &{} 0 &{} dP_i &{} 0\\ *&{} *&{} *&{} *&{} *&{} -\mathcal {U}_i &{} d\bar{G_i}^TP_i &{} d\bar{\alpha }\bar{K_i}^TP_i\\ *&{} *&{} *&{} *&{} *&{} *&{} -P_i\bar{S_i}^{-1}P_i &{} 0\\ *&{} *&{} *&{} *&{} *&{} *&{} *&{} -P_i\bar{S_i}^{-1}P_i \end{array} \right] <0, \end{aligned}$$

(50)

In the view of the fact that $-P_i\bar{S_i}^{-1}P_i\le -2P_i+\bar{S_i}$, by noting (27), (19)–(23) and (30)–(32), it is noting that (26) implies (50) holds. Therefore, the estimation error systems with $\bar{w}(t)=0$ are stochastically stable, this ends the proof. $\square$

Remark 6

The measurement model is proposed in (2), which provides a novel unified framework for the phenomenon of randomly occurred nonlinearities. The stochastic variable $\alpha (t)$ characterizes the random nature of nonlinearities, when $\alpha (t)\ne 0$, it works normally. When $\alpha (t)=0$, the static neural networks (1)–(4) have the following form in [31]:

$$\begin{aligned}&\dot{x}(t)=-A(r_{t})x(t)+f(W(r_t)x(t-d(t))+J(r_{t}))+B_1(r_{t})w(t),\end{aligned}$$

(51)

$$\begin{aligned}&y(t)=C(r_{t})x(t)+D(r_{t})x(t-d(t))+B_2(r_{t})w(t),\end{aligned}$$

(52)

$$\begin{aligned}&z(t)=E(r_{t})x(t),\end{aligned}$$

(53)

$$\begin{aligned}&x(t)=\phi (t), \quad t\in [-d,0]. \end{aligned}$$

(54)

the state estimator is constructed as follows:

$$\begin{aligned}\dot{\hat{x}}(t)&=-A_i\hat{x}(t)+f(W_i\hat{x}(t-d(t))+J_i)+K_i[y(t)-C_i\hat{x}(t)-D_i\hat{x}(t-d(t))],\\&\quad \hat{z}(t)=E_i\hat{x}(t),\\&\hat{x}(0)=0,\quad t \in [-d,0]. \end{aligned}$$

and we finally get the error systems:

$$\begin{aligned}&\dot{\tilde{x}}(t)=-(A_i+K_iC_i)\tilde{x}(t)+g(W_i\tilde{x}(t-d(t))-K_iD_i\tilde{x}(t-d(t))+(B_{1i}-K_iB_{2i})w(t),\end{aligned}$$

(55)

$$\begin{aligned}&\tilde{z}(t)=E_i\tilde{x}(t). \end{aligned}$$

(56)

Corollary 1

For the given scalars $d>0$ and $\mu$ in (5), considering (51)–(54), the resulting error systems (55)–(56) are globally stochastic stable with $H_{\infty }$ performance $\rho$ , if there exist real matrices $P_i>0$ , $Q_{1i}>0$ , $Q_{2i}>0$ , $Q>0$ , $R>0$ , $R_i>0$ , $S>0$, $S_i>0$ , diagonal matrix $T_i=diag\{t_{i1},t_{i2},\ldots ,t_{in}\}>0$, $G_i$ and $X_i$. Such that the following LMIs hold for $i\in \mathcal {N}$:

$$\begin{aligned}&\sum _{j=1,j\ne i}^{n}\pi _{ij}Q_{1j}+\sum _{j=1}^{n}\pi _{ij}Q_{2j}<Q,\end{aligned}$$

(57)

$$\begin{aligned}&\sum _{j=1}^{n}\pi _{ij}R_j\le R, \quad \sum _{j=1}^{n}\pi _{ij}S_j\le S,\end{aligned}$$

(58)

$$\begin{aligned}&\left[ \begin{array}{cc}S_i &{} G_i\\ *&{} S_i \end{array}\right] \ge 0,\end{aligned}$$

(59)

$$\begin{aligned}&\left[ \begin{array}{ccccccc} \tilde{\Omega }_{i1} &{} \frac{1}{d}G_i^T &{} \tilde{\Omega }_{i2} &{} 0 &{} P_i &{} \tilde{\Omega }_{i3} &{} \tilde{\Omega }_{i4}\\ *&{} \tilde{\Omega }_{i5} &{} -\frac{1}{d}G_i+\frac{1}{d}S_i &{} 0 &{} 0 &{} 0 &{} 0\\ *&{} *&{} \tilde{\Omega }_{i6} &{} 0 &{} \tilde{\Omega }_{i7} &{} 0 &{} -dD_i^{T}X_i^{T}\\ *&{} *&{} *&{} -\frac{1}{d}R_i &{} 0 &{} 0 &{} 0\\ *&{} *&{} *&{} *&{} -T_i &{} 0 &{} dP_i\\ *&{} *&{} *&{} *&{} *&{} -{\rho }^2I &{} \tilde{\Omega }_{i8}\\ *&{} *&{} *&{} *&{} *&{} *&{} \tilde{\Omega }_{i9}\\ \end{array} \right] <0, \end{aligned}$$

(60)

where

$$\begin{aligned}\tilde{\Omega }_{i1} & =-P_iA_i-A_i^TP_i-X_iC_i-C_i^TX_i^T+\sum _{j=1}^{n}\pi _{ij}P_j\\&\quad+Q_{1i}+Q_{2i}+dQ+dR_i\\&\quad +\frac{1}{2}d^{2}R+E_i^{T}E_i-\frac{1}{d}S_i, \\&\tilde{\Omega }_{i2}=-\frac{1}{d}G_i^T+\frac{1}{d}S_i-X_iD_i,~~ \tilde{\Omega }_{i3}=P_iB_{1i}-X_iB_{2i},\\&\tilde{\Omega }_{i4}=-dA_i^{T}P_i-dC_i^{T}X_i^{T},~~ \tilde{\Omega }_{i5}=-Q_{2i}-\frac{1}{d}S_i,\\&\tilde{\Omega }_{i6}=-\frac{2}{d}S_i+\frac{1}{d}G_i+\frac{1}{d}G_i^{T}-(1-\mu )Q_{1i}-W_i^{T}T_iN_{i1}W_i,\\&\tilde{\Omega }_{i7}=-W_i^{T}N_{i2}T_i,~~ \tilde{\Omega }_{i8}=d(B_{1i}^{T}P_i-B_{2i}^{T}X_i^{T}),\\&\tilde{\Omega }_{i9}=-2P_i+\frac{1}{d}S_i+\frac{1}{2}S. \end{aligned}$$

Then the gain matrices $K_i$ is designed as $K_i=P_i^{-1}X_i$.

Remark 7

Compared with [31], in order to handle the integral terms in the time derivative of the Lyapunov function, the number of time variable is reduced by the Wirtinger inequality at the expense of conservatism in [31]. The number of decision variables for time complexity is $\frac{i}{2}(5n^2+9n)+\frac{3}{2}n(n+1)$. While in Corollary 1, by employing Jensens inequality and the reciprocally convex combination technique [32, 33], a lower bounder inequality in Lemma 2 is qutoed to reduce conservativeness with the number $\frac{i}{2}(7n^2+9n)+\frac{3}{2}n(n+1)$. The difference of the number of decision variables are $\Delta N=in^2$, which caused by the freely matrices $G_i$. Here, $G_i$ in (59) is introduced in the reciprocally convex approach. However, the less conservativeness are achieved at the expense of introducing more number of variables with $\Delta N=in^2$, which will bring computational burdens.

Remark 8

It is noticed that the filter design problem studied in [31] is a special case of this paper, and we can easily obtain the much less conservative result in Corollary 1. It should be noted that the derivative of delay $\mu$ in [31] will be invalid if $\mu \ge 1$. But in this paper, the finally condition holds for any $\mu$ (see Table 3).

4 Numerical examples

Example 1

Considering the neural networks (51)–(54) with parameters in [31]:

Mode 1:

$$\begin{aligned}&A_{1}=\left[ \begin{array}{ll} 0.74 &{} 0 \\ 0 &{} 0.98 \end{array} \right] , \quad W_{1}=\left[ \begin{array}{cc} 0.32 &{} -0.17 \\ 0.29 &{} 0.43 \end{array} \right] , \quad B_{11}=\left[ \begin{array}{ll} -0.05 &{} 0.21 \\ 0.13 &{} -0.32 \end{array} \right] \\&B_{21}=\left[ \begin{array}{cc} 0.08&0.25 \end{array} \right] , \quad C_{1}=\left[ \begin{array}{ll} 0.20&-0.11 \end{array} \right] , \quad D_{1}=\left[ \begin{array}{ll} -0.10&0.14 \end{array} \right] \\&E_{1}=\left[ \begin{array}{cc} 0.78 &{} -0.53 \\ -1.02 &{} 0.46 \end{array} \right] , \quad l^{-}_1=0.3I, \quad l^{+}_1=0.8I. \end{aligned}$$

Mode 2:

$$A_{2} = \left[ {\begin{array}{*{20}c} {0.82} & 0 \\ 0 & {0.67} \\ \end{array} } \right],\quad W_{2} = \left[ {\begin{array}{*{20}c} { - 0.13} & {0.74} \\ { - 0.48} & { - 0.17} \\ \end{array} } \right],\quad B_{{12}} = \left[ {\begin{array}{*{20}c} {0.12} & { - 0.30} \\ { - 0.54} & {0.06} \\ \end{array} } \right]\quad B_{{22}} = \left[ {\begin{array}{*{20}c} {0.18} & { - 0.20} \\ \end{array} } \right],\quad C_{2} = \left[ {\begin{array}{*{20}c} {0.26} & {0.09} \\ \end{array} } \right],\quad D_{2} = \left[ {\begin{array}{*{20}c} {0.37} & { - 0.51} \\ \end{array} } \right]\quad E_{2} = \left[ {\begin{array}{*{20}c} {0.63} & {0.35} \\ {0.99} & { - 0.41} \\ \end{array} } \right],\quad l_{2}^{ - } = 0.2I,\quad l_{2}^{ + } = 0.6I.$$

Suppose the transition probability matrix is given by

$$\begin{aligned} \Pi _1=\left[ \begin{array}{cc} -3 &{} 3 \\ 5 &{} -5 \end{array} \right] \end{aligned}$$

Firstly, we let $\mu =0.3$, and change the upper bounder d of time delay with $\Pi _1$, the results are listed in Table 1. Then according to [31], we have $\mu =0.8$, $d=0.9$, for different $\pi _{22}$ with $\pi _{11}=-\pi _{12}=-0.5$, the results are shown in Table 2. Finally, we let $d=0.7$, $\mu =1.2$ with $\pi _{11}=-\pi _{12}=-0.5$, for different $\pi _{22}$, the results are summarized in Table 3. And “–” means that the result is not applicable to the corresponding case. In this Corollary 1, utilizing the inequality in Lemma 2 of this paper which is different from Lemma 2 of [31], the conservatism of the results is reduced when compared with the method in [31]. From these tables, we can see the prescribed level of noise attenuation $\rho$ is much lower and the time derivative of the time-varying delay is no longer required to be smaller than one. The number of decision variables for time complexity in [31] are 47, while in Cor ollary 1 are 55 for the reason of the introduced matrices $G_1$ and $G_2$.

The activation functions are chosen as $f(W_1x(t-d(t))=0.25sin( W_1t)+0.55$, and $f(W_2x(t-d(t))=0.2sin(W_2t)+0.4$, the noise disturbance is chosen as $w(t)=e^{-2t}sin(0.6t)$, when $\mu =0.3$, $d=1.2$, $\rho =0.72$, and $\Pi _1$ are taken with the initial condition $x(0)=[~-1~~2~]^T$, $\hat{x}(0)=[~0.5~~1~]^T$, the simulation results are plotted in Figs. 1, 2. One needs to pay attention is that the value of $K_1$ and $K_2$ in Tables 1, 2 are calculated from Corollary 1.

Example 2

Considering the delay static neural networks (1)–(4) with the following parameters:

Mode 1:

$$A_{1} = \left[ {\begin{array}{*{20}l} {0.84} & 0 \\ 0 & {0.98} \\ \end{array} } \right],\quad W_{1} = \left[ {\begin{array}{*{20}l} {0.12} & { - 0.37} \\ {0.22} & {0.13} \\ \end{array} } \right],\quad B_{{11}} = \left[ {\begin{array}{*{20}l} { - 0.15} & {0.22} \\ { - 0.33} & { - 0.62} \\ \end{array} } \right]\quad B_{{21}} = \left[ {\begin{array}{*{20}l} {0.01} & { - 0.21} \\ {0.01} & {0.2} \\ \end{array} } \right],\quad C_{1} = \left[ {\begin{array}{*{20}l} {0.40} & { - 0.11} \\ { - 0.11} & {0.21} \\ \end{array} } \right],\quad D_{1} = \left[ {\begin{array}{*{20}l} { - 0.23} & {0.14} \\ {0.1} & {0.1} \\ \end{array} } \right]\quad E_{1} = \left[ {\begin{array}{*{20}l} {0.14} & { - 0.22} \\ {0.02} & { - 2.46} \\ \end{array} } \right],\quad l_{1}^{ - } = 0.3I,\quad l_{1}^{ + } = 0.8I,\quad m_{1}^{ - } = 0.3I,\quad m_{1}^{ + } = 0.5I.$$

Mode 2:

$$A_{2} = \left[ {\begin{array}{*{20}l} {0.62} & 0 \\ 0 & {0.87} \\ \end{array} } \right],\quad W_{2} = \left[ {\begin{array}{*{20}l} {0.22} & {0.14} \\ { - 0.28} & { - 0.47} \\ \end{array} } \right],\quad B_{{12}} = \left[ {\begin{array}{*{20}l} { - 0.12} & { - 0.20} \\ { - 0.14} & {0.26} \\ \end{array} } \right]B_{{22}} = \left[ {\begin{array}{*{20}l} {0.28} & { - 0.45} \\ {0.02} & {0.31} \\ \end{array} } \right],\quad C_{2} = \left[ {\begin{array}{*{20}l} {1.36} & {1.09} \\ { - 0.3} & {0.04} \\ \end{array} } \right],\quad D_{2} = \left[ {\begin{array}{*{20}l} {0.17} & { - 0.51} \\ {0.13} & {0.21} \\ \end{array} } \right]\quad E_{2} = \left[ {\begin{array}{*{20}l} {0.23} & { - 0.55} \\ {0.19} & { - 0.21} \\ \end{array} } \right],\quad l_{2}^{ - } = 0.2I,\quad l_{2}^{ + } = 0.6I,\quad m_{2}^{ - } = 0.1I,\quad m_{2}^{ + } = 0.3I.$$

Suppose the transition probability matrix is given by

$$\begin{aligned} \Pi _2=\left[ \begin{array}{cc} -5 &{} 5 \\ -3 &{} 3\end{array}\right] . \end{aligned}$$

Let $\alpha =0.82$, for $\mu =0.4$ and $\mu =1.1$, we change the values of time delay d with $\Pi _2$ respectively. The results are presented in Table 4. From Table 4, when the time-delay d increase, the optimal $H_\infty$ performance indices $\rho _{min}$ is increasing for different $\mu$.

We choose the same activation functions $f(W_1x(t-d(t))$ and $f(W_2x(t-d(t))$, noise disturbance w(t) in Example 1, initial conditions $x(0)=[~-1~~2~]^T$, $\hat{x}(0)=[~0.5~~1~]^T$. When $\psi (C_1x(t))=0.1sin(C_1t)+0.4$, $\psi (C_2x(t))=0.1sin(C_2t)+0.2$, $\mu =1.1$, $d=2.5$, $\rho =1.7266$ with $\Pi _2$, then the simulation results are plotted in Figs. 3, 4.

Fig. 1

State trajectories, estimation and Markov chain $r_t$ (Corollary 1)

Fig. 2

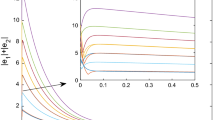
Estimation error (Corollary 1)

Table 1 The optimal $H_\infty$ performance indices $\rho _{min}$ for different d

Table 2 The optimal $H_\infty$ performance indices $\rho _{min}$ for different $\pi _{22}$

Table 3 The optimal $H_\infty$ performance indices $\rho _{min}$ for $\mu =1.2$

Fig. 3

State trajectories, estimation and Markov chain $r_t$ (Theorem 1)

Fig. 4

Estimation error (Theorem 1)

Table 4 The optimal $H_\infty$ performance indices $\rho _{min}$ for different d and $\mu$

5 Conclusions

This paper has addressed the problem of $H_{\infty }$ filter design for delayed static neural networks with Markovian switching and randomly occurred nonlinearity. Bernoulli stochastic variable and the double- and triple-integral terms of the Lyapunov functions are taken into account. In the process of the derivation without the Bernoulli stochastic variable, the double integral terms will be easy to handled and we end up with a smaller prescribed level of noise attenuation. Two numerical examples have demonstrated the effectiveness of the proposed approach. Based on the analysis in this paper, the other further results can be extended to more complex systems. For example, it is possible to generalize reciprocally convex approach subject to the asymmetric static neural networks with Markovian jumping or fuzzy neural networks with Markovian jumping. It will be interesting to be investigated in future.