Backstepping control of MEMS gyroscope using adaptive neural observer

Abstract

In this paper, a backstepping controller with an adaptive neural states observer is proposed for MEMS (Micro-Electro-Merchanical-System) gyroscopes in the presence of model uncertainties and external disturbance. Gyroscope states are usually assumed to be available in controller design procedure. However, gyroscope states may be unavailable in some circumstances. In this paper, an adaptive neural states observer is employed to estimate gyroscope states without physical sensors and thus can help reducing complexity of the gyroscope system. A backstepping controller is utilized to control the vibrating amplitude and frequency of the mass proof and the control law is carried out with states estimation rather than actual gyroscope states. Adaptive laws are investigated in the Lyapunov stability framework to guarantee the stability of the observer. Numerical simulation results demonstrate the effectiveness of the proposed control scheme.

1 Introduction

Gyroscopes are one of the most common sensors used to measure angular velocity and they are widely used in areas such as navigation, automobiles and so on. The principle of gyroscopes is that the device can transfer energy from driving axis to sensing axis by the Coriolis force when gyroscopes are rotating at some angular velocity. In practical situations, temperature change, manufacturing errors, quadrature errors are all factors that will deteriorate the performance of gyroscopes and will lead to false output; thus, it is necessary to use advanced control methods to control gyroscopes.

To handle the factors that will hinder the measurement and improve the performance of gyroscopes, many professionals have done much research in the field. Adaptive control, sliding mode control, intelligent control all have been used to improve the performance of gyroscopes. Juan et al. [1] introduced an adaptive fuzzy approach for the MEMS gyroscope where non-linear parts are compensated. Fazlyab et al. [2] applied fuzzy sliding mode control to a z-axis MEMS gyroscope and the parameters of the system can be estimated. Wang et al. [3] proposed a T-S fuzzy model based robust adaptive sliding mode control for the MEMS gyroscope. Besides, adaptive control and intelligent control [4–12] are commonly combined in control methods to improve control performances.

Usually, position and velocity signals are essential in the design of control force. Sometimes, it is difficult or even impossible to measure the states and adding physical sensors will add to the complexity of the system. So, states observer is a feasible method to solve the problem and it has been developed in many areas. Laurent et al. [13] derived an adaptive controller with observer for the magnetic guided microrobot. Kim et al. [14] investigated disturbance-observer-based position tracking controller and carried out the method in electrohydraulic actuators. Jiang et al. [15] proposed an adaptive neural observer-based backstepping fault tolerant control and applied the method in the near space vehicle under control effector damage. Chen et al. [16] proposed a direct adaptive neural control based on disturbance observer for a class of uncertain nonaffine nonlinear systems. Li et al. [17] presented an adaptive fuzzy backstepping control of static var compensator based on state observer. An adaptive observer backstepping control using neural networks was proposed for the single-input–single-output system by Choi [18]. Yao et al. [19] introduced extended-state-observer-based output feedback nonlinear robust control of hydraulic systems with backstepping. Tong et al. [20] derived an observer-based adaptive fuzzy backstepping output feedback control of uncertain multiple-input-multiple-output pure-feedback nonlinear systems. A novel SPR-filter approach using indirect adaptive fuzzy control scheme based on observer was investigated by Boulkroune [21]. An observer-based adaptive neural network control was derived by Zhou et al. [22] and was applied in nonlinear stochastic systems. Ting et al. [23] studied the model of linear stepping motor and derived an observer-based back-stepping control. Xu et al. [24] proposed an observer-based fuzzy adaptive control of nonlinear systems with actuator fault and unmodeled dynamics. An output feedback dynamic surface control was derived by Yoo et al. [25] in the application of flexible-joint robots. Na et al. [26] proposed an adaptive control for nonlinear pure-feedback systems with high-order sliding mode observer.

It can be found from [1] and [3] that the states of the gyroscope are assumed to be measurable and the states are directly used in the design of control forces. If the states are assumed to be unmeasurable and the states can not be used directly, the control forces can hardly be carried out, thus a states observer can be used to estimate system states and the states estimation can be used in the design process. This paper proposes a backstepping controller using states observer for z-axis gyroscopes. All the states are replaced by the states estimation. Adaptive laws in both states observer and controller are derived in framework of Lyapunov stability theory, so the stability of the entire system can be guaranteed. The contribution of the control scheme can be concluded as follows:

• 1. In the presence of disturbances, an adaptive neural observer is proposed to estimate gyroscope states. The complexity of the gyroscope system will be reduced for not installing physical sensors. Lyapunov stability theorem guarantees bounded estimation error.

• 2. A backstepping controller is carried out with states estimation rather than actual gyroscope states. This solves the problem when gyroscope states are essential in controller design procedure while they are unavailable in actual circumstances.

• 3. The combination of backstepping controller and states observer is applied to MEMS gyroscopes for the first time.

The paper is organized by 5 parts in all. In Sect. 2, the dynamics of MEMS gyroscope are studied through non-dimensional transformation. The design of the states observer is presented in Sect. 3 where the stability of the observer is analyzed with Lyapunov stability theory as well. In Sect. 4, the backstepping controller using states estimation is proposed. Simulation results are shown in Sect. 5 to verify the effect of the control method and observer. Section 6 gives the conclusion.

2 Dynamics of MEMS gyroscope

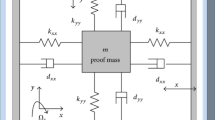
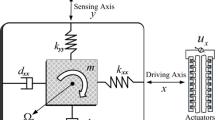
Generally, a vibratory gyroscope consists of a proof mass suspended by springs, the driving mechanism and the sensing mechanism. The proof mass is two-degree-free which means that the proof mass can only move on the plane of X–O–Y. The electrostatic driven mechanism is set to force the proof mass to oscillate while the sensing mechanism is set to sense the position and velocity of the proof mass. A z-axis vibratory gyroscope is shown in Fig. 1.

Fig. 1

Schematic model of a z-axis vibratory gyroscope

We assume that the gyroscope is rotating about the z axis at a constant velocity over a long time interval. The dynamics of the Gyroscope can be described as:

$$ \begin{aligned} m{\ddot{x}} + d_{xx} \dot{x} + d_{xy} \dot{y} + k_{xx} x + k_{xy} y = u_{x} + 2m\varOmega_{z} \dot{y} \hfill \\ m {\ddot{y}} + d_{xy} \dot{x} + d_{yy} \dot{y} + k_{xy} x + k_{yy} y = u_{y} - 2m\varOmega_{z} \dot{x} \hfill \\ \end{aligned} $$

(1)

where $x$ and $y$ are the coordinates of the proof mass in the direction of $X$ and $Y$,$k_{xx}$, $k_{yy}$ are the spring coefficients and $d_{xx}$,$d_{yy}$ are the damping coefficients along the $X$ and $Y$ axis. For the fabrication imperfection and the fact that the structure of the gyroscope is not totally symmetric and the asymmetric structure contributes mainly to the cross spring term $k_{xy}$ and cross damping term $d_{xy}$. $m$ is the weight of the proof mass, and $u_{x}$ and $u_{y}$ are the control forces in the $X$ and $Y$ direction.

We can get the non-dimensional form of the dynamics by dividing both sides of (1) with $m,q_{0} ,\omega_{0}^{2}$ where $m,q_{0} ,\omega_{0}^{2}$ represent the reference mass, length and natural resonance frequency respectively. The dynamics of the gyroscope can be rewritten in non-dimensional form as:

$$ \begin{aligned} {\ddot{x}} + d_{xx} \dot{x} + d_{xy} \dot{y} + \omega_{x}^{2} x + \omega_{xy} y = ux + 2\varOmega_{z} \dot{y} \hfill \\ {\ddot{y}} + d_{xy} \dot{x} + d_{yy} \dot{y} + \omega_{xy} x + \omega_{y}^{2} y = u_{y} - 2\varOmega_{z} \dot{x} \hfill \\ \end{aligned} $$

(2)

where $\frac{{d_{xx} }}{{m\omega_{0} }} \to d_{xx}$, $\frac{{d_{xy} }}{{m\omega_{0} }} \to d_{xy}$, $\frac{{d_{yy} }}{{m\omega_{0} }} \to d_{yy}$, $\frac{{\varOmega_{z} }}{{\omega_{0} }} = \varOmega_{z}$, $\sqrt {\frac{{k_{xx} }}{{m\omega_{0}^{2} }}} \to \omega_{x}$, $\sqrt {\frac{{k_{yy} }}{{m\omega_{0}^{2} }}} \to \omega_{y}$, $\frac{{k_{xy} }}{{m\omega_{0}^{2} }} \to \omega_{xy}$.

The dynamics of the model can be rewritten in the vector form as

$$ {\ddot{q}} + D\dot{q} + Kq = u - 2\varOmega \dot{q} $$

(3)

where $q = \left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right]$, $u = \left[ {\begin{array}{*{20}c} {u_{x} } \\ {u_{y} } \\ \end{array} } \right]$, $D = \left[ {\begin{array}{*{20}c} {d_{xx} } & {d_{xy} } \\ {d_{xy} } & {d_{yy} } \\ \end{array} } \right]$, $K = \left[ {\begin{array}{*{20}c} {\omega_{x}^{2} } & {\omega_{xy} } \\ {\omega_{xy} } & {\omega_{y}^{2} } \\ \end{array} } \right]$, $\varOmega = \left[ {\begin{array}{*{20}c} 0 & { - \varOmega_{z} } \\ {\varOmega_{z} } & 0 \\ \end{array} } \right]$.

3 Adaptive neural observer design

In this section, an adaptive observer based on RBF (Radial Basis Function) neural network is proposed to estimate the states of the gyroscope. In order to avoid using the states in the design of control force, the states estimation from the observer is used to replace the position and velocity signals of the proof mass, thus the control force can be achieved without using gyroscope states. The nonlinear part in the model caused by parameter variation can be approximated by the neural network, and arbitrary small estimation error can be achieved.

Rewrite the dynamics in state space form as

$$ \left\{ \begin{aligned} \dot{X} = AX + Bu \hfill \\ y{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = C^{T} X \hfill \\ \end{aligned} \right. $$

(4)

where $A = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ { - \omega_{x}^{2} } & { - d_{xx} } & { - \omega_{xy} } & { - (d_{xy} - 2\varOmega_{z} )} \\ 0 & 0 & 0 & 1 \\ { - \omega_{xy} } & { - (d_{xy} + 2\varOmega_{z} )} & { - \omega_{y}^{2} } & { - d_{yy} } \\ \end{array} } \right]$, $B = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 1 & 0 \\ 0 & 0 \\ 0 & 1 \\ \end{array} } \right]$, $C = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 0 \\ 0 & 1 \\ 0 & 0 \\ \end{array} } \right]$, $u = \left[ {\begin{array}{*{20}c} {u_{x} } \\ {u_{y} } \\ \end{array} } \right]$ $X = [x_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{x}_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} x_{2} {\kern 1pt} {\kern 1pt} {\kern 1pt} \dot{x}_{2} ]^{T}$.

By taking the parameters variation and external disturbance into account, the model can be rewritten as:

$$ \begin{aligned} \dot{X} = (A + \Delta A)X + Bu + d(t) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = AX + Bu + \Delta AX + d(t) \hfill \\ \end{aligned} $$

(5)

where $X \in R^{n}$, $y \in R^{m}$, $A \in R^{n \times n}$, $B \in R^{n \times m}$, $u \in R^{m}$; $\Delta A$ represents unknown parameters variation in $A$,$d(t)$ is an external disturbance.

Assumption 1

There exist some appropriate functions $f_{m}$, $d_{u}$ such that $\Delta AX = Bf_{m}$ and $d(t) = Bd_{u}$. Therefore, the dynamics can be expressed as

$$ \dot{X} = AX + Bu + B(f_{m} + d_{u} ) $$

(6)

where $f_{m}$, $d_{u}$ represent the parameter uncertainties and external disturbance.

The observer is proposed as

$$ \left\{ \begin{aligned} \dot{\hat{X}} = A\hat{X} + B[\hat{f}_{m} + u - v] + K(y - C^{T} \hat{X}) \hfill \\ \hat{y} = C^{T} \hat{X} \hfill \\ \end{aligned} \right. $$

(7)

where $\hat{X}$ is the estimation of $X$,$\hat{y}$ is the estimation of the gyroscope output $y$, $\hat{f}_{m}$ is the estimation of the unknown function $f_{m}$, $u$ is the control force, the robust term $v$ is set to address the parameter variation and disturbance, $K$ is the gain vector.

Define the states estimation error as

$$ \tilde{X} = X - \hat{X} $$

The derivative of the states estimation error becomes

$$ \dot{\tilde{X}} = \dot{X} - \dot{\hat{X}} $$

Substitute the gyroscope model (6) and the observer (7) into the derivative of the states estimation error gives

$$ \begin{aligned} \dot{\tilde{X}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= (AX + BU + B(f_{m} + d_{u} )) - \hfill \\& {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (A\hat{X} + B(\hat{f}_{m} + u - v) + K(y - C^{T} \hat{X})) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= (A - KC^{T} )\tilde{X} + B(\tilde{f}_{m} + d_{u} + v). \hfill \\ \end{aligned} $$

(8)

Define the output estimation error as $\tilde{y} = y - \hat{y}$, then the states estimation error and output estimation error become

$$ \left\{ \begin{aligned} \dot{\tilde{X}} = (A - KC^{T} )\tilde{X} + B(\tilde{f}_{m} + d_{u} + v) \hfill \\ \tilde{y} = C^{T} \tilde{X} \hfill \\ \end{aligned} \right. $$

(9)

where $\tilde{f}_{m}$ is the nonlinear function approximation error, which is expressed as

$$ \tilde{f} = f_{m} - \hat{f}_{m} . $$

(10)

The Laplace transform of $\dot{\tilde{X}}$ in (9) becomes

$$ S\tilde{X}(S) = (A - KC^{T} )\tilde{X}(S) + B(\tilde{f}_{m} + d_{u} + v) . $$

(11)

The Laplace transform of $\tilde{y}$ in (9) becomes

$$ \begin{aligned} \tilde{y}(S) = \frac{{C^{T} B}}{{S - (A - KC^{T} )}}(\tilde{f}_{m} + d_{u} + v){\kern 1pt} {\kern 1pt} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = H(S)(\tilde{f}_{m} + d_{u} + v). \hfill \\ \end{aligned} $$

(12)

Lemma 1

[26] Meyer-Kalman-Yokubovic (MKY) If a proper transfer function $H(S) = C^{T} (SI - A)^{ - 1} B$ with $A$ a Hurwitz matrix is SPR (strictly positive real), then for any given $Q = Q^{T} > 0$, there exist a $P = P^{T} > 0$ such that

$$ A^{T} P + PA = - Q,\quad PB = C. $$

Lemma 2

[26] Consider the linear time-invariant system in the form

$$ \dot{x}(t) = Ax(t) + Bu,x(0) = x_{0} $$

with $x(t) \in R^{n}$,$u(t) \in R^{m}$ and the matrices $A \in R^{n \times n}$,$B \in R^{n \times m}$. Then, every solution $x(t)$ of the system is such that

$$ \left\| {x(t)} \right\| \le k_{1} + k_{2} \left\| u \right\|_{2}^{\alpha } \forall t \ge 0 $$

with $k_{1}$ decaying exponentially to zero and $k_{2}$ a positive constant that depends on the eigenvalues of $A$.

For the great advantage of neural network in dealing with nonlinear systems, a RBF neural network is adopted to approximate the unknown function $f_{m}$.

The structure of a RBF network is a three-lawyer feed forward network. The input layer passes input signals without any operation; the hidden layer performs activation function in each node of the layer and the output layer gives the output. The structure of a RBF network is shown in Fig. 2.

Fig. 2

Architecture of a RBF network

The output of the NN can be described as

$$ y = \omega^{T} \phi $$

(13)

where $\omega = [\omega_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} \omega_{2} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} \omega_{n} ]^{T}$ is the weight vector and $\omega_{n}$ is the neural weight connecting the nth neuron in the hidden layer and the output neuron. $\phi$ represents the activation function that is performed in every node in the hidden layer; $\phi = [\phi_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \phi_{2} {\kern 1pt} \ldots {\kern 1pt} \phi_{n} ]^{T}$ is the output vector of the hidden layer. Gaussian function is usually chosen as the activation function and the output of the nth node in the hidden layer is given by

$$ \phi_{n} (x) = \exp \left( - \frac{{\left\| {x - c_{n} } \right\|^{2} }}{{b_{n}^{2} }}\right) $$

(14)

where $c_{n}$ and $b_{n}$ are the center and the width of the Gaussian function respectively.

The $f_{m}$ can be expressed as

$$ f_{m} = W_{{}}^{T} \sigma (X) + \varepsilon (X) $$

(15)

where $W$ is the optimal weight of the network, $\sigma (X)$ is the Gaussian function in terms of the states $X$, $\varepsilon (X)$ is the approximation error.

We assume that the approximation error and the weight are bounded by known bounds, such as $\left| {\varepsilon (X)} \right| \le \varepsilon_{d}$, $\left\| W \right\|_{F} \le W_{M}$, where $\varepsilon_{d}$,$W_{M}$ are positive constants.

Let the estimation of $f_{m}$ be given by

$$ \hat{f}_{m} = \hat{W}_{{}}^{T} \sigma (\hat{X}) $$

(16)

where the input of the Gaussian function is the states estimation instead of the states of the gyroscope for the purpose of avoiding to use the gyroscope states.

Substituting (15) and (16) into (10) yields

$$ \tilde{f}_{m} = f_{m} - \hat{f}_{m} = W_{{}}^{T} \sigma (X) + \varepsilon (X) - \hat{W}_{{}}^{T} \sigma (\hat{X}). $$

(17)

Define the Gaussian function error as

$$ \tilde{\sigma }(X) = \sigma (X) - \sigma (\hat{X}). $$

(18)

Substituting (18) into (17) yields

$$ \begin{aligned} \tilde{f}_{m} = f_{m} - \hat{f}_{m} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = W_{{}}^{T} (\tilde{\sigma }(X) + \sigma (\hat{X})) - \hat{W}_{{}}^{T} \sigma (\hat{X}) + \varepsilon (X) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \tilde{W}_{{}}^{T} \sigma (\hat{X}) + W_{{}}^{T} \tilde{\sigma }(X) + \varepsilon (X) \hfill \\ \end{aligned} $$

(19)

where the weight error is given by $\tilde{W} = W - \hat{W}$, the disturbance term is defined as $W_{{}}^{T} \tilde{\sigma }(X) = \rho$, and $\rho$ is bounded such as $\left\| \rho \right\| \le \beta$, where $\beta$ is a positive constant.

Substituting $\hat{f}_{m}$ in (16) into the observer in (7), we can get

$$ \left\{ \begin{aligned} \dot{\hat{X}} = A\hat{X} + B[\hat{W}_{{}}^{T} \sigma (\hat{X}) + u - v] + K(y - C^{T} \hat{X}) \hfill \\ \hat{y} = C^{T} \hat{X} \hfill \\ \end{aligned} \right.. $$

(20)

Substituting $\tilde{f}_{m}$ in (17) into the states estimation error in (9) yields

$$ \left\{ \begin{aligned} \dot{\tilde{X}} &= (A - KC^{T} )\tilde{X} + B(\tilde{W}_{{}}^{T} \sigma (\hat{X}) \hfill \\ &{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \rho (t) + \varepsilon (X) + d_{u} + v) \hfill \\ &\tilde{y} = C^{T} \tilde{X} \hfill \\ \end{aligned} \right. . $$

(21)

Substituting (17) into (12), the output estimation error becomes

$$ \begin{aligned} \tilde{y}(S) &= H(S)(\tilde{f}_{m} + d_{u} + v(t)) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= H(S)(\tilde{W}_{{}}^{T} \sigma (\hat{X}) + \rho (t) + \varepsilon (X) + d_{u} + v) \hfill \\ \end{aligned} $$

(22)

where $H(S)$ is a transfer function with stable poles which are realized by $(A - KC^{T} ,B,C)$.

The output estimation error (22) can be rewritten as

$$ \begin{aligned} \tilde{y}(S) &= H(S)L(S)L^{ - 1} (S)(\tilde{f}_{m} + d_{u} + v) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= H(S)L(S)(L^{ - 1} (S)(\tilde{W}_{{}}^{T} \sigma + \delta ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad+ L^{ - 1} (S)(\rho + \varepsilon + d_{u} + v)) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= H(S)L(S)(\tilde{W}_{{}}^{T} \bar{\sigma } + \bar{\delta } + \bar{\rho } + \bar{\varepsilon } + \bar{d}_{u} + \bar{v}) \hfill \\ \end{aligned} $$

(23)

where $L^{ - 1} (S)$ is a transfer function with stable poles and the over bar means that all the signals are filtered by $L^{ - 1} (S)$,such as $\bar{\sigma } = L^{ - 1} (S)\sigma$, $\bar{\rho } = L^{ - 1} (S)\rho$, $\bar{\varepsilon } = L^{ - 1} (S)\varepsilon$, $\bar{d}_{u} = L^{ - 1} (S)d_{u}$, $\bar{v} = L^{ - 1} (S)v$.

And in (23), the term $\delta$ is defined as

$$ \begin{aligned} L^{ - 1} (S)\tilde{W}_{{}}^{T} \sigma &= \{ L^{ - 1} (S)[\tilde{W}_{{}}^{T} \sigma ] - \tilde{W}_{{}}^{T} [L^{ - 1} (S)\sigma ]\} \\&\quad+ \tilde{W}_{{}}^{T} [L^{ - 1} (S)\sigma ] \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= \delta + \tilde{W}_{{}}^{T} \bar{\sigma } \hfill \\ \end{aligned} $$

Rewrite $\delta$ in the form $\delta = L^{ - 1} (S)(\tilde{W}_{{}}^{T} \sigma ) - \tilde{W}_{{}}^{T} L^{ - 1} (S)\sigma$, it can be concluded that $\delta$ is bounded such as $\left\| \delta \right\| \le c_{1} \left\| {\tilde{W}} \right\|_{F}$, where $c_{1}$ is a computable positive constant.

The error dynamics can be realized as

$$ \left\{ \begin{aligned} \dot{\tilde{z}} = A_{c} \tilde{z} + B_{c} (\tilde{W}_{{}}^{T} \bar{\sigma } + \bar{\delta } + \bar{\rho } + \bar{\varepsilon } + \bar{d}_{u} + \bar{v}) \hfill \\ \tilde{y} = C_{c}^{T} \tilde{z}. \hfill \\ \end{aligned} \right. $$

(24)

Remark 1

$A_{c} \in R^{n \times n}$,$B_{c} \in R^{n \times m}$, $C_{c} = C$ is the minimal state space representation of $H(S)L(S)$ such as

$$ H(S)L(S) = C_{c}^{T} (SI - A_{c} )^{ - 1} B_{c} = ((SI - A_{c} )(C_{c}^{T} )^{ - 1} )^{ - 1} B_{c} . $$

(25)

Define a Lyapunov function candidate as:

$$ V_{1} = \frac{1}{2}\tilde{z}^{T} P\tilde{z} + \frac{1}{2}tr(\tilde{W}_{{}}^{T} F_{{}}^{ - 1} \tilde{W}) $$

(26)

where $P = P_{{}}^{T} > 0$ , $F = F_{{}}^{T} > 0$.

Differentiating $V_{1}$ with respect to time yields

$$ \begin{aligned} \dot{V}_{1} &= \frac{1}{2}\dot{\tilde{z}}^{T} P\tilde{z} + \frac{1}{2}\tilde{z}^{T} P\dot{\tilde{z}} + tr(\tilde{W}_{{}}^{T} F_{{}}^{ - 1} \dot{\tilde{W}}) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= \frac{1}{2}\tilde{z}^{T} Q\tilde{z} + \tilde{y}\Delta + tr(\tilde{W}_{{}}^{T} F_{{}}^{ - 1} \dot{\tilde{W}}). \hfill \\ \end{aligned} $$

(27)

Remark 2

Lemma 1 is referred to in the reasoning process of (27). For $H(S)L(S)$ is SPR, according to Lemma 1, there exists a proper matrix $P = P_{{}}^{T} > 0$ such that $A_{c}^{T} P + PA_{c} = - Q$,$PB_{c} = C_{c}$,$Q = Q_{{}}^{T} > 0$ .

$$ \begin{aligned} \dot{\tilde{z}}^{T} P\tilde{z} + \tilde{z}^{T} P\dot{\tilde{z}} &= (A_{c} \tilde{z} + B_{c} \Delta )^{T} P\tilde{z} + \tilde{z}^{T} P(A_{c} \tilde{z} + B_{c} \Delta ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= \tilde{z}^{T} (A_{c}^{T} P + PA_{c} )\tilde{z} + \Delta^{T} B_{c}^{T} P\tilde{z} + \tilde{z}^{T} PB_{c} \Delta \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= - \tilde{z}^{T} Q\tilde{z} + 2\tilde{z}^{T} PB_{c} \Delta \\&= - \tilde{z}^{T} Q\tilde{z} + 2\tilde{z}^{T} C_{c} \Delta \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = &- \tilde{z}^{T} Q\tilde{z} + 2\tilde{y}^{T} \Delta = - \tilde{z}^{T} Q\tilde{z} + 2\tilde{y}\Delta \hfill \\ \end{aligned} $$

(28)

and $\Delta = \tilde{W}_{{}}^{T} \bar{\sigma } + \bar{\delta } + \bar{\rho } + \bar{\varepsilon } + \bar{d}_{u} + \bar{v}$. Thus, the Eq. (27) is proved.

To make $\dot{V}_{1} \le 0$, we can choose the adaptive law as

$$ \dot{\hat{W}} = F\bar{\sigma }\tilde{y} - KF\left| {\tilde{y}} \right|\hat{W} $$

(29)

Substituting (29) into (27) gives

$$ \begin{aligned} \dot{V}_{1} &= \frac{1}{2}\tilde{z}^{T} Q\tilde{z} + \tilde{y}\Delta + tr(\tilde{W}_{{}}^{T} F_{{}}^{ - 1} ( - F\bar{\sigma }\tilde{y} + KF\left| {\tilde{y}} \right|\hat{W})) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= \frac{1}{2}\tilde{z}^{T} Q\tilde{z} + \tilde{y}(\bar{\delta } + \bar{\rho } + \bar{\varepsilon } + \bar{d}_{u} + \bar{v}) + tr(\tilde{W}_{{}}^{T} K\left| {\tilde{y}} \right|\hat{W}) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\le - \frac{1}{2}\lambda_{\hbox{min} } (Q)\left\| {\tilde{z}} \right\|^{2} + \tilde{y}(\bar{\varepsilon } + \bar{d}_{u} + C\left\| {\tilde{W}} \right\|_{F} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &+ K\left| {\tilde{y}} \right|tr(\tilde{W}_{{}}^{T} (W - \tilde{W})) \hfill \\ \end{aligned} $$

(30)

where $tr( - \tilde{W}_{{}}^{T} \bar{\sigma }\tilde{y}) = - \tilde{y}\tilde{W}_{{}}^{T} \bar{\sigma }$

Remark 3

In the reasoning process of (30), the design of robust term in the observer in (7) is set as

$$ v = - D\frac{{\tilde{y}}}{{\left| {\tilde{y}} \right|}} $$

(31)

where $D \ge \beta \sigma_{M}$,$\sigma_{M} = \sigma_{\hbox{max} } [L^{ - 1} (S)]$. And the result in (32) is derived to finish the proof of (30)

$$ \begin{aligned} \tilde{y}(\bar{\rho }_{1} + \bar{v} + \delta ) &= \tilde{y}(\bar{\rho } - D\text{sgn} (\tilde{y})) + \tilde{y}\delta \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= \tilde{y}L^{ - 1} (S)\rho - D\left| {\tilde{y}} \right| + \tilde{y}\delta \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\le \left| {\tilde{y}} \right|\beta \sigma_{M} - D\left| {\tilde{y}} \right| + \tilde{y}\delta \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\le 0 + c\left| {\tilde{y}} \right|\left\| {\tilde{W}} \right\|_{F} = c\left| {\tilde{y}} \right|\left\| {\tilde{W}} \right\|_{F} \hfill \\ \end{aligned} $$

(32)

with $\left\| \delta \right\| \le c\left\| {\tilde{W}} \right\|_{F}$ mentioned above. If $\tilde{y}$ is 0, $v$ is set as 0, (32) can still be derived to finish the proof of (30).

With the inequality derived in (32) and using the norm inequality below

$$ - \frac{1}{2}\lambda_{\hbox{min} } (Q)\left| {\tilde{z}} \right|^{2} \le - \frac{1}{2}\lambda_{\hbox{min} } (Q)\left| {\tilde{y}} \right|^{2} $$

$$ tr[W_{{}}^{T} (W - \tilde{W})] \le W_{M} \left\| {\tilde{W}} \right\|_{F} - \left\| {\tilde{W}} \right\|_{F}^{2} $$

(30) becomes

$$ \begin{aligned} \dot{V}_{1} &\le - \frac{1}{2}\lambda_{\hbox{min} } (Q)\left\| {\tilde{y}} \right\|^{2} + \left| {\tilde{y}} \right|(\bar{\varepsilon } + \bar{d}_{u} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad+ \left| {\tilde{y}} \right|c\left\| {\tilde{W}} \right\|_{F} + K\left| {\tilde{y}} \right|(W_{M} \left\| {\tilde{W}} \right\|_{F} - \left\| {\tilde{W}} \right\|_{F}^{2} ). \hfill \\ \end{aligned} $$

(33)

For $\sigma_{M} = \sigma_{\hbox{max} } (L^{ - 1} (S))$, $\bar{\varepsilon } = L^{ - 1} (S)\varepsilon$, $\bar{d}_{u} = L^{ - 1} (S)d_{u}$ and $\varepsilon_{d}$, $d_{ud}$ are the bounds of $\varepsilon$, $d_{u}$, we can get:

$$ (\bar{\varepsilon } + \bar{d}_{u} ) \le \sigma_{M} (\varepsilon_{d} + d_{ud} ) $$

(34)

Substituting (34) into (33) yields

$$ \begin{aligned} \dot{V}_{1} &\le - \frac{1}{2}\lambda_{\hbox{min} } (Q)\left| {\tilde{y}} \right|^{2} + \left| {\tilde{y}} \right|\sigma_{M} (\varepsilon_{d} + d_{ud} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad+ \left| {\tilde{y}} \right|C\left\| {\tilde{W}} \right\|_{F}^{{}} + K\left| {\tilde{y}} \right|(W_{M} \left\| {\tilde{W}} \right\|_{F}^{{}} - \left\| {\tilde{W}} \right\|_{F}^{2} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= - \left| {\tilde{y}} \right|[\frac{1}{2}\lambda_{\hbox{min} } (Q)\left| {\tilde{y}} \right| - \sigma_{M} (\varepsilon_{d} + d_{ud} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad- (C + KW_{M} - K\left\| {\tilde{W}} \right\|_{F}^{{}} )\left\| {\tilde{W}} \right\|_{F}^{{}} ] \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= - \left| {\tilde{y}} \right|[\frac{1}{2}\lambda_{\hbox{min} } (Q)\left| {\tilde{y}} \right| - \sigma_{M} (\varepsilon_{d} + d_{ud} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad+ K(\left\| {\tilde{W}} \right\|_{F}^{{}} - \frac{1}{2}\alpha )^{2} - \frac{1}{4}K\alpha^{2} ] \hfill \\ \end{aligned} $$

(35)

where

$\alpha = W_{M} + \frac{c}{K},$

$$ - K(\alpha - \left\| {\tilde{W}} \right\|_{F}^{{}} )\left\| {\tilde{W}} \right\|_{F}^{{}} = K(\left\| {\tilde{W}} \right\|_{F}^{{}} - \frac{1}{2}\alpha )^{2} - \frac{1}{4}K\alpha^{2} . $$

To make $\dot{V}_{1} < 0$, we get the following conditions to be satisfied

$$ \left| {\tilde{y}} \right| \ge \frac{{\sigma_{M} (\varepsilon_{d} + d_{ud} ) + \frac{1}{2}K\alpha^{2} }}{{\lambda_{\hbox{min} } (Q)}} $$

(36)

Or

$$ \left\| {\tilde{W}} \right\|_{F}^{{}} \ge \frac{1}{2}\alpha + (\frac{{\sigma_{M} (\varepsilon_{d} + d_{ud} )}}{K} + \frac{1}{4}\alpha^{2} )^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} $$

(37)

$\dot{V}_{1}$ is negative outside the set defined by (36) and (37). This demonstrates that $\tilde{y}$, $\tilde{W}$ are UUB (uniformly ultimately bounded); any excursion of $\tilde{y}$, $\tilde{W}$ beyond the bounds set by the conditions in (36) and (37) will cause decrease in the Lyapunov function. That is to say the bounds defined by the right side of Eqs. (36) and (37) can be taken as the bounds on $\left| {\tilde{y}} \right|$ and $\left\| {\tilde{W}} \right\|_{F}^{{}}$; and arbitrary small error bounds can be achieved by setting large $K$ and small $\sigma_{M}$.

Consider the estimation error dynamics in (21), according to Lemma 2, the bounds of $\tilde{x}$ can be expressed such that $\left\| {\tilde{x}(t)} \right\| \le m_{0} + m_{1} \left\| u \right\|_{2}^{\alpha }$. For $\tilde{u} = \tilde{W}_{{}}^{T} \hat{\bar{\sigma }} + \bar{\delta } + \bar{\rho } + \bar{\varepsilon } + \bar{d}_{u} + \bar{v}$, it can be seen that all the terms in $\tilde{u}$ are all bounded and mostly relative to the neural weight error $\tilde{W}$, using Lemma 2 and norm inequality yields $\left\| {\tilde{x}(t)} \right\| \le m_{0} + m_{1} (c_{1} + c_{2} \left\| {\tilde{W}_{F} } \right\|_{F}^{\alpha } )$ with $m_{0}$ decaying exponentially to zero and $m_{1}$ a positive constant that depends on the eigenvalues of $A$; $c_{1}$, $c_{2}$ are computable constants. It has been proven that $\left\| {\tilde{W}} \right\|_{F}^{{}}$ is bounded, thus $\left\| {\tilde{x}(t)} \right\|$ is also bounded.

4 Backstepping controller using states estimation

In this section, a backstepping controller is proposed using the states estimation. The control objective is to make the states $X_{1}$ to track the reference trajectory $X_{1d}$. And the novelty is that the controller is designed with the states estimation in stead of practical states.

The block diagram of the backstepping controller with neural states observer is depicted in Fig. 3. States estimation is incorporated in the controller to replace the states of the gyroscope. The design procedure of the backstepping controller using states estimation is investigated step by step as follows:

Fig. 3

Block diagram of the backstepping controller with neural states observer

We consider the Eq. (4) as the system model, the states are defined as $X_{1} = q$ and $X_{2} = \dot{q}$. The system model can be rewritten in state-space form as

$$ \left\{ \begin{aligned} \dot{X}_{1} &= X_{2} \hfill \\ \dot{X}_{2} &= - (D + 2\varOmega )X_{2} - KX_{1} + u \hfill \\ \end{aligned} \right. $$

(38)

The output is expressed as

$$ y = X_{1} $$

(39)

Consider the model with parameter variation and external disturbances, according to (4), the system model can be rewritten as

$$ \dot{X}_{2} = - (D + 2\varOmega )X_{2} - KX_{1} + u + f_{m} + d_{u} $$

(40)

Step 1. Define the tracking error as

$$ e_{1} = \hat{X}_{1} - X_{1d} $$

(41)

Differentiating the tracking error with respect to time yields

$$ \dot{e}_{1} = \dot{\hat{X}}_{1} - \dot{X}_{1d} = \hat{X}_{2} - \dot{X}_{1d} . $$

(42)

Define the tracking error of $\hat{X}_{2}$ as

$$ e_{2} = \hat{X}_{2} - \hat{X}_{2d} $$

(43)

where $\hat{X}_{2d}$ is the virtual control force

The virtual control $\hat{X}_{2d}$ is chosen as

$$ \hat{X}_{2d} = \dot{\hat{X}}_{1d} - a_{1} e_{1} $$

(44)

where $a_{1}$ is a positive constant.

Substituting (44) into (42) gives

$$ \begin{aligned} \dot{e}_{1} = \hat{X}_{2} - \dot{X}_{1d} = e_{2} + X_{2d} - \dot{X}_{1d} \hfill \\ = e_{2} + \dot{X}_{1d} - a_{1} e_{1} - \dot{X}_{1d} = e_{2} - a_{1} e_{1} . \hfill \\ \end{aligned} $$

(45)

Choose the first Lyapunov function as

$$ V_{2} = \frac{1}{2}e_{1}^{2} $$

(46)

and the derivative of $V_{2}$ is

$$ \dot{V}_{2} = e_{1} \dot{e}_{1} = e_{1} e_{2} - a_{1} e_{1}^{2} $$

(47)

If $e_{2} \to 0$, then

$\dot{V}_{2} = - a_{1} e_{1}^{2} < 0$.

As can be seen in (7), the observer is designed as

$$ \dot{\hat{X}}_{2} = - (D + 2\varOmega )\hat{X}_{2} + k_{1} \hat{X}_{1} + \hat{f} + u - v + G_{1} \tilde{y}. $$

(48)

Step 2. Differentiating $e_{2}$ with respect to time and using (48), we obtain

$$ \begin{aligned} \dot{e}_{2} &= \dot{\hat{X}}_{2} - \dot{\hat{X}}_{2d} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= - (D + 2\varOmega )\hat{X}_{2} + k_{1} \hat{X}_{1} + \hat{f} + u - v + G_{1} \tilde{y} - \dot{\hat{X}}_{2d} \hfill \\ \end{aligned} . $$

(49)

Define the second Lyapunov candidate as

$$ V_{3} = \frac{1}{2}e_{1}^{2} + \frac{1}{2}e_{2}^{2} $$

(50)

and the derivative of $V_{3}$ is expressed as

$$ \begin{aligned} \dot{V}_{3} &= e_{1} \dot{e}_{1} + e_{2} \dot{e}_{2} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= e_{1} (e_{2} - a_{1} e_{1} ) + e_{2} ( - (D + 2\varOmega )\hat{X}_{2} + k_{1} \hat{X}_{1} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad+ \hat{f} + u - v + G_{1} \tilde{y} - \dot{\hat{X}}_{2d} ) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &= - a_{1} e_{1}^{2} + e_{2} ( - (D + 2\varOmega )\hat{X}_{2} + k_{1} \hat{X}_{1} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} &\quad+ \hat{f} + u - v + G_{1} \tilde{y} - \dot{\hat{X}}_{2d} + e_{1} ) \hfill \\ \end{aligned} $$

(51)

According to (51), to make $\dot{V}_{3}$ negative, the control law can be designed as

$$ u = (D + 2\varOmega )\hat{X}_{2} - k_{1} \hat{X}_{1} - \hat{f} + v - G_{1} \tilde{y} + \dot{\hat{X}}_{2d} - a_{2} e_{2} - e_{1} $$

(52)

where $a_{2}$ is a non-zero positive constant.

Theorem 1

If the control force in (52) is applied to gyroscope model described in (40), the entire system is stable.

Proof

Substituting the controller (52) into (51) gives

$$ \dot{V}_{3} = - a_{1} e_{1}^{2} - a_{2} e_{2}^{2} \le 0 $$

This implies that $\dot{V}_{3}$ is a negative semi-definite function; $\dot{V}_{3}$ is negative semi-definite ensures that $e_{1}$, $e_{2}$ are bounded. For $\dot{V}_{3} \le 0$, the integral of $\dot{V}_{3}$ is $\int\limits_{0}^{t} {\dot{V}_{3} (t)} dt = V_{3} (t) - V_{3} (0) \le 0$. Since $V_{3} (0)$ is bounded and $V_{3} (t)$ is a non-increasing and bounded function, $e_{1}$, $e_{2}$ are bounded. So, ${\ddot{V}}_{3} (t) = - 2a_{1} e_{1} \dot{e}_{1} - 2a_{2} e_{2} \dot{e}_{2}$ is also bounded.${\ddot{V}}_{3} (t)$ is bounded implies that $\dot{V}_{3}$ is uniformly continuous in the time domain. According to Barbalat lemma, it can be concluded that $\dot{V}_{3} (t)$ will converge to zero, which means that $e_{1}$, $e_{2}$ will converge to zero. Thus, with arbitrary small error between gyroscope states and their estimation, the trajectory tracking object can be achieved and the tracking error will converge to zero.

5 Simulation study

According to the proposed observer based backstepping control approach, the simulation is performed in MATLAB/Simulink software. The parameters of the MEMS gyroscope are set as follows:

$$ m = 1.8 \times 10^{ - 7} {\text{kg}},\quad k_{xx} = 63.955\;{\text{N/m,}}\quad k_{yy} = 95.92\;{\text{N/m}},\quad k_{xy} = 12.779\;{\text{N/m}} $$

$$ d_{xx} = 1.8 \times 10^{ - 6} {\text{N}} \cdot {\text{s/m,}}\quad d_{yy} = 1.8 \times 10^{ - 6} {\text{N}} \cdot {\text{s/m}},\quad d_{xy} = 3.6 \times 10^{ - 7} {\text{N}} \cdot {\text{s/m}} $$

choose the reference length $q_{0} = 1$ μm, the reference frequency $\omega_{0} = 1\;{\text{kHz}}$, and the angular velocity $\varOmega_{z} = 100\;{\text{rad/s }}$. Through non-dimensional transform, the parameters can be obtained:

$$ \omega_{x}^{2} = 355. 3 ,\quad \omega_{y}^{2} = 532.9,\quad \omega_{xy} = 70.99,\quad d_{xx} = 0.01,\quad d_{yy} = 0.01,\quad d_{xy} = 0.002,\quad d_{xy} = 0.002,\quad \varOmega_{{}} = 0.1 $$

The control objective is to make the system states to track the desired trajectory given by:

$$ q_{m} = \left[ {\begin{array}{*{20}c} {x_{m} } \\ {y_{m} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sin (4.17t)} \\ {1.2\sin (5.11t)} \\ \end{array} } \right] $$

We choose the initial states as $X_{0} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ \end{array} } \right]$, the external disturbances as $d = \left[ {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {10\sin (\omega_{1} t)} \\ {10\sin (\omega_{2} t)} \\ \end{array} } \right]$. For comparison, another case is provided where the disturbance is chosen as $d = \left[ {\begin{array}{*{20}c} {d_{1} } \\ {d_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {10{\text{random}}(1)} \\ {10{\text{random}}(1)} \\ \end{array} } \right]$.

Parameters of the observer are set as follows:

The gain of the observer $K = \left[ \begin{aligned} K_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K_{2} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} 900{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 900 \hfill \\ \end{aligned} \right]$, gain of the robust part $D = \left[ \begin{aligned} D_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D_{2} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} 900{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 900 \hfill \\ \end{aligned} \right]$, and the transfer function with stable pole is set as $L^{ - 1} (s) = \frac{1}{S + 3}.$

Parameters in the backstepping control are set as:$a = \left[ \begin{aligned} a_{1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a_{2} \hfill \\ \end{aligned} \right] = \left[ \begin{aligned} 5{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 5 \hfill \\ \end{aligned} \right]$

In the design of the adaptive neural network part, the parameters are set as: $F = \left[ \begin{aligned} F1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} F2 \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} {0.01} & 0 \\ 0 & {0.01} \\ \end{array} } \right]$. The center and width of the Gaussian function of the neural network is chosen as $c = 0.1*{\text{ones}}\;(1,{\text{node}})$ and $b = 0.3*ones(1,node)$ and node is the number of neurons in the hidden layer where $node = 40$.

Figures 4, 5, 6, 7, 8, 9 are simulation results where the disturbance is chosen as $d = 10*\sin (\omega t)$ and Figs. 10, 11, 12, 13 present tracking and estimation performance where a random signal with zero mean and unity variance is chosen as the disturbance.

Fig. 4

Position tracking of X and Y axis ($d = 10 \times \sin (\omega t)$)

Fig. 5

Tracking errors of X and Y axis ($d = 10 \times \sin (\omega t)$)

Fig. 6

Position estimation of X and Y axis ($d = 10 \times \sin (\omega t)$)

Fig. 7

Position estimation error of X and Y axis ($d = 10 \times \sin (\omega t)$)

Fig. 8

Control inputs of X and Y axis ($d = 10 \times \sin (\omega t)$)

Fig. 9

Partial enlarged drawing of control inputs of X and Y axis ($d = 10 \times \sin (\omega t)$)

Fig. 10

Position tracking of X and Y axis ($d = 10 \times {\text{random}}(1)$)

Fig. 11

Tracking error of X and Y axis ($d = 10 \times {\text{random(}}1)$)

Fig. 12

Position estimation of X and Y axis ($d = 10 \times {\text{random}}(1)$)

Fig. 13

Position estimation error of X and Y axis ($d = 10 \times {\text{random}}(1)$)

Figure 4 depicts the position tracking performance with backstepping control. It can be observed from Figs. 4 and 5 that the position in the $X$,$Y$ direction can track the given trajectory in a short time and the tracking error converges to zero asymptotically. That is to say that the designed backstepping controller can maintain the proof mass to oscillate in the $X$, $Y$ direction at the given frequency and amplitude.

Figure 6 depicts the position estimation performance and Fig. 7 depicts the estimation error in the $X$, $Y$ direction. It can be observed from Figs. 6 and 7 that the position estimation can track the gyroscope position in a short time and the tracking error is within a small bound. Thus, the states estimation can be adopted to replace the position of the gyroscope. Figures 8 and 9 depict the control force along the $X$ axis and $Y$ axis where the control force is very smooth.

Figures 10 and 11 depict the trajectory tracking and tracking error where the disturbance is chosen as $d = 10*random(1)$. It can be observed form Fig. 10 that the system states can still track the desired trajectory although a random signal is a much stronger disturbance. But it can also been seen that the bound of tracking error becomes larger.

The states estimation and estimation error are shown in Figs. 12 and 13. It can be found form Fig. 12 that the states estimation(blue dotted line) almost overlap with system states(read line) which means that the states observer can correctly estimate the system states. And the bound of estimation error also becomes larger because the random signal disturbance is a stronger disturbance.

It can be concluded that the proposed estimator can correctly estimate gyroscope states in the presence of disturbance and estimation errors under different disturbances in Figs. 7 and 13 show that the proposed estimator has very good robustness. Tracking errors in Figs. 5 and 11 show that it is feasible to use states estimation in controller design.

6 Conclusion

In the paper, a backstepping control scheme with adaptive neural observer is proposed for MEMS gyroscopes. The states estimation is used to replace actual gyroscope states in the controller design. Thus, the control force can be derived without using gyroscope states and this can help to reduce the complexity of the system for not installing physical sensors in the system. Both the controller and the observer are designed in the sense of Lyapunov stability theory, so bounded states estimation error can be achieved and the stability of the entire control system is guaranteed.

Numerical simulations demonstrate that the gyroscope trajectory can track the command trajectory very well. Small estimation error and tracking error indicate that it is feasible to use states estimation in controller design procedure. Simulation results also show strong robustness to different disturbances.