1 Introduction

Machine scheduling problem is concerned with finding an efficient schedule during an uninterrupted period of time for a set of machines to process a set of jobs. Machine scheduling problems arise in a wide field of real life and so are important from both theoretical and practical viewpoints. Since the pioneering work of Johnson [9] and Naughton [23], theory for machine scheduling has been greatly enlarged and improved. In 1977, Lenstra et al. [12] studied the complexity of machine scheduling problems, and showed that most classical machine scheduling problems were NP-complete. In 1979 Graham et al. [6] proposed an expression of three parameters \(\alpha \mid \beta \mid \gamma\) where \(\alpha\), \(\beta\) and \(\gamma\) represented machine environment, job characteristic and optimality criteria respectively to describe scheduling problems.

In a machine scheduling problem, processing time and release date are important factors that affect scheduling plan. Originally, release dates and processing times were assumed to be exact numbers. A great deal of models and algorithms have been developed, such as Baker and Scudder [2], Mokotoff [22], Lam and Xing [11], Pinedo [27] and Xing et al. [32]. Since in real life processing times and release dates are usually difficult to be crisp numbers, the indeterminacy is taken into account. With the proposition of probability theory by Kolmogorov in 1933, Banerjee [3] was the first who investigated a single machine scheduling problem with random processing times. Later, different machine scheduling problems with random processing times were researched. In 1977, Hodegson [7] described a single machine scheduling problem with random processing times, in which he showed that Lawler’s efficient algorithm was optimal even when the processing times were random. Seo et al. [29] studied the single machine scheduling problem for the objective of minimizing the expected number of tardy jobs where the jobs had normally distributed processing times and a common deterministic due date. Scheduling problems with random release dates were also studied by many researchers. Pinedo [26] studied stochastic scheduling problems in which the processing times of jobs, the release dates and the due dates were random variables and the objectives were minimization of the expected weighted sum of completion times and the expected weighted number of late jobs. Ahmadizar et al. [1] dealt with a stochastic group shop scheduling problem in which both the release date of each job and the processing time of each job on each machine were random variables with known distributions, and the objective was to find a job schedule which minimized the expected makespan.

Since the concept of fuzzy set was proposed by Zadeh in 1965, many researchers began to study machine scheduling problems by fuzzy set theory. Prade [28] first used fuzzy set theory to deal with a real scheduling problem in 1979. Later, Ishibuchi et al. [8] proposed two fuzzy flowshop scheduling problems with fuzzy due dates and provided hybrid genetic algorithms and neighborhood search algorithms. Peng and Liu [24] presented three types of parallel machine scheduling models with fuzzy processing times in order to satisfy the different decision requirements, and used a revised genetic algorithm to solve the models in 2004. Petrovic and Fayad [25] described a fuzzy shifting bottleneck procedure hybridised with genetic algorithm for a real-world job shop scheduling problem where fuzzy sets were used to model uncertain processing times of jobs and their release dates and due dates. Gharehgozli et al. [5] presented a new mixed-integer goal programming model for a parallel-machine scheduling problem with sequence-dependent setup times and release dates. Two objectives were considered in the model to minimize the total weighted flow time and the total weighted tardiness simultaneously in 2009.

As we know, in reality, there are cases that we lack observed data and all available are only belief degrees that are given by experts to describe the distributions of processing times. For example, when processing new types of products, there are no historical data of the processing times and the distributions of them can only be given by domain experts’ evaluations expressed by belief degrees. Kehneman and Tversky [10] found that too much weight was given to the chance of unlikely events. A lot of surveys showed that human beings usually estimate a much wider range of values than the object actually takes (Liu [17]). For this reason, the belief degree is inappropriate to be treated as random variable or fuzzy variable. In order to deal with the belief degree mathematically, an uncertainty theory was founded by Liu [13] in 2007 and refined by Liu [16] in 2010 based on normality axiom, duality axiom, subadditivity axiom and product axiom.

Within the framework of uncertainty theory, a concept of uncertain variable was defined by Liu [13] as a measurable function on an uncertainty space. Meanwhile, a series of concepts such as uncertainty distribution, independence, expected value, variance and entropy, etc, were also proposed to describe an uncertain variable. And now, uncertainty theory has been deeply developed in many fields such as uncertain programming [18, 31, 33], uncertain finance [4, 15] and uncertain differential equation [30, 34], etc.

Uncertain programming, as a type of mathematical programming involving uncertain variables, was first proposed by Liu [14] in 2009. Machine scheduling problem with uncertain processing times was also proposed as an example. An uncertain machine scheduling model [16] was built, of which the objective is to minimize the expected makespan. Since then uncertain multi-objective programming and uncertain goal programming were presented by Liu and Chen [18], and uncertain multilevel programming was proposed by Liu and Yao [19]. In 2013, Zhang and Meng [35] proposed an expected-variance-entropy model for uncertain parallel machine scheduling where the processing times are regarded as uncertain variables with known uncertainty distributions. Li and Liu [20] built an uncertain goal programming model for the machine scheduling problem and an intelligent algorithm was introduced to solve the equivalence based on a revised genetic algorithm.

Using uncertainty theory to solve machine scheduling problem, less effort has been done for studying the case where the release date of each job is indeterminate. In reality, the release dates of jobs are not determinate. So in many literatures, release dates are considered as random variables [1, 26] or fuzzy variables [5, 25]. However, for example, when there does not exist sample data for the release date of a new job, it is advisable to regard the release date as an uncertain variable. The domain experts are invited to estimate the distributions of the uncertain variables so as to be accordant with the practical situation. And it is well-known that any machine has different processing ability which is taken into account in this paper. So in this paper, the highlights is that we regard processing times and release dates as uncertain variables, meanwhile, we consider the machines with different processing capacity. The objective is to minimize the expected makespan and the tardiness time of the scheduling under the processing ability constraint.

In this paper, we further study machine scheduling problem, and build a multi-objective programming model for machine scheduling problem, of which the objectives are to minimize the makespan and the maximum tardiness time under the constraint of the capacity of a certain machine. The rest of the paper is organized as follows. In Sect. 2, some basic concepts and theorems about uncertain variables are introduced. Section 3 describes the uncertain machine scheduling problem with uncertain processing times, uncertain release dates and a common determinate due date. In Sect. 4, we will build an uncertain multi-objective machine scheduling model, and transform it into a crisp programming model. After that, we will introduce an intelligent algorithm to solve the crisp programming model in Sect. 5, and illustrate the algorithm via some numerical experiments in Sect. 6. At last, some remarks are made in Sect. 7.

2 Preliminary

In this section, some basic concepts and theorems in uncertainty theory are introduced, which are used throughout this paper.

Definition 2.1

(Liu [13]) Let \(\mathcal {L}\) be a \(\sigma\)-algebra on a nonempty set \(\Gamma\). A set function \(\mathcal {M}\) is called an uncertain measure if it satisfies the following axioms:

Axiom 1. (Normality Axiom) \(\mathcal {M}\{\Gamma \}=1\);

Axiom 2. (Duality Axiom) \(\mathcal {M}\{\Lambda \}+\mathcal {M}\{\Lambda ^{c}\}=1\) for any \(\Lambda \in \mathcal {L}\);

Axiom 3. (Subadditivity Axiom) For every countable sequence of \(\{\Lambda _i\}\in \mathcal {L}\), we have

$$\begin{aligned} \displaystyle \mathcal {M}\left\{ \bigcup _{i=1}^{\infty }\Lambda _i\right\} \le \sum _{i=1}^{\infty }\mathcal {M}\{\Lambda _i\}. \end{aligned}$$

The triplet \((\Gamma ,\mathcal {L},\mathcal {M})\) is called an uncertainty space, and each element \(\Lambda\) in \(\mathcal {L}\) is called an event. In addition, in order to obtain an uncertain measure of compound event, a product uncertain measure is defined by Liu [15] via the following product axiom:

Axiom 4. (Product Axiom) Let \((\Gamma _k,\mathcal {L}_k,\mathcal {M}_k)\) be uncertainty spaces for \(k=1,2,\ldots\). The product uncertain measure \(\mathcal {M}\) is an uncertain measure satisfying

$$\begin{aligned} \mathcal {M}\left\{ \prod _{k=1}^{\infty }\Lambda _k\right\} =\bigwedge _{k=1}^{\infty }\mathcal {M}_k\{\Lambda _k\} \end{aligned}$$

where \(\Lambda _k\) are arbitrarily chosen events from \(\mathcal {L}_k\) for \(k=1,2,\ldots\), respectively.

Definition 2.2

(Liu [13]) An uncertain variable \(\xi\) is a measurable function from an uncertainty space \((\Gamma ,\mathcal {L},\mathcal {M})\) to the set of real numbers, i.e., for any Borel set B of real numbers, the set

$$\begin{aligned} \{\xi \in B\}=\{\gamma \in \Gamma |\xi (\gamma )\in B\} \end{aligned}$$

is an event.

Definition 2.3

(Liu [13]) The uncertainty distribution \(\Phi\) of an uncertain variable \(\xi\) is defined by

$$\begin{aligned} \Phi (x)=\mathcal {M}\left\{ \xi \le x\right\} ,\quad \forall x\in \mathfrak {R}. \end{aligned}$$

Definition 2.4

(Liu [16]) An uncertainty distribution \(\Phi (x)\) is said to be regular if it is a continuous and strictly increasing function with respect to x at which \(0 < \Phi (x) < 1\), and

$$\begin{aligned} \lim _{x\rightarrow -\infty } \Phi (x)=0,\quad \lim _{x\rightarrow +\infty } \Phi (x)=1. \end{aligned}$$

In addition, the inverse function \(\Phi ^{-1}(\alpha )\) is called the inverse uncertainty distribution of \(\xi\).

An uncertain variable \(\xi\) is said to be linear if it has a linear uncertainty distribution

$$\begin{aligned} \Phi (x)=\left\{ \begin{array}{ll} 0,&{}\text{ if } x < a\\ (x-a)/(b-a),&{}\text{ if } a \le x\le b \\ 1,&{}\text{ if } x > b \end{array}\right. \end{aligned}$$

which is denoted by \(\xi \sim \mathcal {L}(a, b)\). Apparently, the linear uncertain variable \(\xi\) is regular, and has an inverse uncertainty distribution

$$\begin{aligned} \Phi ^{-1}(\alpha )=\alpha (b-a)+a. \end{aligned}$$

An uncertain variable \(\xi\) is said to be normal if it has a normal uncertainty distribution

$$\begin{aligned} \Phi (x)=\left( 1+\text{ exp }\left( \frac{\pi (e-x)}{\sqrt{3}\sigma }\right) \right) ^{-1},\quad x\in \mathfrak {R}\end{aligned}$$

denoted by \(\xi \sim \mathcal {N}(e,\sigma )\) where e and \(\sigma\) are real numbers with \(\sigma >0\). The normal uncertain variable is regular, and the inverse uncertainty distribution is

$$\begin{aligned} \Phi ^{-1}(\alpha )=e+\frac{\sigma \sqrt{3}}{\pi }\text{ ln }\frac{\alpha }{1-\alpha }. \end{aligned}$$

Definition 2.5

(Liu [15]) The uncertain variables \(\xi _1,\xi _2,\ldots ,\xi _n\) are said to be independent if

$$\begin{aligned} \mathcal {M}\left\{ \bigcap _{i=1}^{n}(\xi _i\in B_i)\right\} =\bigwedge _{i=1}^n\mathcal {M}\left\{ \xi _i\in B_i\right\} \end{aligned}$$

for any Borel sets \(B_1,B_2,\ldots ,B_n\) of real numbers.

Definition 2.6

(Liu [13]) Let \(\xi\) be an uncertain variable. The expected value of \(\xi\) is defined by

$$\begin{aligned} E[\xi ]=\int _{0}^{+\infty }\mathcal {M}\{\xi \ge r\}\mathrm{d}r-\int _{-\infty }^{0}\mathcal {M}\{\xi \le r\}\mathrm{d}r \end{aligned}$$

provided that at least one of the above two integrals is finite.

For an uncertain variable \(\xi\) with an uncertainty distribution \(\Phi\), we have

$$\begin{aligned} E[\xi ]=\int _{0}^{+\infty }\left( 1-\Phi (r)\right) \mathrm{d}r-\int _{-\infty }^{0}\Phi (r)\mathrm{d}r. \end{aligned}$$

If the inverse uncertainty distribution \(\Phi ^{-1}\) exists, then

$$\begin{aligned} E[\xi ]=\int _{0}^{1}\Phi ^{-1}(\alpha )\mathrm{d}\alpha . \end{aligned}$$

Theorem 2.1

(Liu [16]) Assume \(\xi _1,\xi _2,\ldots ,\xi _n\) are independent uncertain variables with regular uncertainty distributions \(\Phi _1,\Phi _2,\ldots ,\Phi _n\), respectively. If the function \(f(x_1,x_2,\ldots ,x_n)\) is strictly increasing with respect to \(x_1,x_2,\ldots\), \(x_m\) and strictly decreasing with respect to \(x_{m+1},x_{m+2},\ldots ,x_n\), then \(\xi =f(\xi _1,\xi _2,\ldots ,\xi _n)\) has an inverse uncertainty distribution

$$\begin{aligned} \Psi ^{-1}(\alpha )=f\left( \Phi _1^{-1}(\alpha ),\ldots , \Phi _m^{-1}(\alpha ),\Phi _{m+1}^{-1}(1-\alpha ),\ldots ,\Phi _n^{-1}(1-\alpha )\right) . \end{aligned}$$

In addition, Liu and Ha [21] proved that the uncertain variable \(\xi\) has an expected value

$$\begin{aligned} E[\xi ]=\int _{0}^{1}f\left( \Phi _1^{-1}(\alpha ),\ldots , \Phi _m^{-1}(\alpha ),\Phi _{m+1}^{-1}(1-\alpha ),\ldots ,\Phi _n^{-1}(1-\alpha )\right) \mathrm{d}\alpha . \end{aligned}$$

Theorem 2.2

(Liu [17]) Let \(\xi _1,\xi _2,\ldots ,\xi _n\) be independent uncertain variables with regular uncertainty distributions \(\Phi _1,\Phi _2,\ldots ,\Phi _n\), respectively. If the function \(g(\xi _1,\xi _2,\ldots ,\xi _n)\) is strictly increasing with respect to \(\xi _1,\xi _2,\ldots\), \(\xi _m\) and strictly decreasing with respect to \(\xi _{m+1},\xi _{m+2},\ldots ,\xi _n\), then \(\mathcal {M}\{g(\xi _1,\xi _2,\ldots ,\xi _n)\le 0 \}\ge \alpha\) holds if and only if

$$\begin{aligned} g(\Phi _1^{-1}(\alpha ),\ldots , \Phi _m^{-1}(\alpha ),\Phi _{m+1}^{-1}(1-\alpha ),\ldots ,\Phi _n^{-1}(1-\alpha ) )\le 0. \end{aligned}$$

3 Uncertain parallel machine scheduling problem

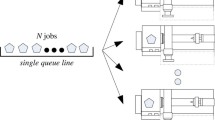
Parallel machine scheduling is used to schedule jobs processed on a series of same-function machines, with optimized objective. For example, in surgery scheduling, we regard surgery patients as jobs, and regard the doctor, anesthesiologist, nurse and surgical equipment taken as a whole as a machine. If we regard the hospital operating rooms as parallel machines, a surgery is regarded as a job which need some machines to carry on at the same time. Then surgery scheduling is the parallel machine scheduling problem. Assigning the doctors and the surgery who will perform to the operating room in order to make the latest operation as early as possible which lead to all the procedure done as soon as possible. Obviously, in this surgery scheduling, the processing times and release dates of jobs are indeterminate and it is more reasonable for doctors to estimate the processing times and release dates.

In a parallel machine scheduling problem suppose that n independent jobs have to be processed on m machines. In addition, the following hypotheses are considered.

  • \(H_1\) There is only one operation for each job and this operation can be processed on any one of the machines without interruption.

  • \(H_2\) Uncertain release dates or ready times, and a common determinate due date D may be considered for jobs.

  • \(H_3\) Each machine can process only one job at a time.

  • \(H_4\) The processing times are uncertain variables with known uncertainty distributions.

  • \(H_5\) The release dates are uncertain variables with known uncertainty distributions.

We utilize the representation method proposed by Liu ([16]) via two decision vectors \(\varvec{x}\) and \(\varvec{y}\), where

\(\varvec{x}\) \(=(x_1,x_2,\ldots , x_n)\): integer decision vector representing n jobs with \(1\le x_i\le n\) and \(x_i\ne x_j\) for all \(i\ne j\), \(i,j=1,2,\ldots , n\). That is, the sequence \(\{x_1,x_2,\ldots , x_n\}\) is a rearrangement of \(\{1,2,\ldots , n\}\);

\(\varvec{y}\) \(=(y_1,y_2,\ldots , y_{m-1})\): integer decision vector with \(y_0\equiv 0\le y_1\le y_2\le \cdots \le y_{m-1}\le n\equiv y_m\).

Note that the schedule is fully determined by the decision vectors \(\varvec{x}\) and \(\varvec{y}\) in the following way. For each \(k (1\le k\le m)\), if \(y_k=y_{k-1}\), then the machine k is not used, and if \(y_k>y_{k-1}\), then machine k is used and processes jobs \(x_{y_{k-1}+1}\), \(x_{y_{k-1}+2}\), \(\ldots ,x_{y_k}\) in turn. In other words, the schedule of all machines are as follows:

$$\begin{aligned}&\text{ Machine } \text{1 }: x_{{y_0}+1}\rightarrow x_{{y_0}+2}\rightarrow \cdots \rightarrow x_{y_1};\\&\text{ Machine } \text{2 }: x_{{y_1}+1}\rightarrow x_{{y_1}+2}\rightarrow \cdots \rightarrow x_{y_2};\\&\ \ \cdots \\&\text{ Machine } \text{ m }: x_{y_{m-1}+1}\rightarrow x_{y_{m-1}+2}\rightarrow \cdots \rightarrow x_{y_m}. \end{aligned}$$

Let \(\eta _{i}\) denote the uncertain release dates of jobs i, \(\xi _{i,k}\) denote the uncertain processing times of jobs i on machines k and \(C_i({\varvec{x}},{\varvec{y}},{\varvec{\xi }})\) denote the completion times of jobs i , \(i=1,2,\ldots ,n\), respectively. For each k with \(1\le k\le m\), if the machine k is used, (i.e., \(y_k>y_{k-1}\)), we can obtain

$$\begin{aligned} C_{x_{y_{k-1}+1}}({\varvec{x}},{\varvec{y}},{\varvec{\xi }})=\eta _{x_{y_{k-1}+1}}+\xi _{x_{y_{k-1}+1,k}} \end{aligned}$$

and

$$\begin{aligned} C_{x_{y_{k-1}+j}}({\varvec{x}},{\varvec{y}},{\varvec{\xi }})=C_{x_{y_{k-1}+j-1}}({\varvec{x}},{\varvec{y}},{\varvec{\xi }}) \vee \eta _{x_{y_{k-1}+j}} + \xi _{x_{y_{k-1}+j,k}} \end{aligned}$$

for all \(2\le j\le y_k -y_{k-1}\). From the recursive formula, we can derive the value \(C_{x_{y_k}}({\varvec{x}},{\varvec{y}},{\varvec{\xi }})\) which is the time that the machine k finishes all the jobs assigned to it. Thus the makespan of the schedule of \(({\varvec{x}},{\varvec{y}})\) is determined by

$$\begin{aligned} f({\varvec{x}},{\varvec{y}},\varvec{\xi })=\max _{1\le k\le m}C_{x_{y_k}}({\varvec{x}},{\varvec{y}},\varvec{\xi }). \end{aligned}$$

Thus the tardiness time of the scheduling is \((f({\varvec{x}},{\varvec{y}},\varvec{\xi })-D)^{+}\) where D is the common determinate due date of the scheduling.

4 Uncertain multi-objective machine scheduling model

There is a common situation in real applications where there are parallel machines with different capabilities. For simplicity, assume that the machine \(k_0\) is supposed to stop working before time \(T_0\) with a confidence level \(\alpha _0\). Then we have the constraint

$$\begin{aligned} \mathcal {M}\{ C_{x_{y_{k_0}}}({\varvec{x}},{\varvec{y}},{\varvec{\xi }})\le T_0\}\ge \alpha _{0}. \end{aligned}$$

In order to minimize the expected makespan and the tardiness time of the scheduling under the above constraint, we construct the following uncertain multi-objective machine scheduling model,

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{\varvec{x,y}}, \left( E[f({\varvec{x}},{\varvec{y}}, {\varvec{\xi }})],E[(f({\varvec{x}},{\varvec{y}},{\varvec{\xi }})-D)^{+}]\right) \\ \displaystyle subject \ \ to:\\ \quad \mathcal {M}\{ C_{x_{y_{k_0}}}({\varvec{x}},{\varvec{y}},{\varvec{\xi }})\le T_0\}\ge \alpha _0\\ \quad 1\le x_i\le n, x_i\ne y_j, i\ne j, i,j=1,2,\ldots ,n\\ \quad 0\le y_1\le y_2\le \cdots \le y_{m-1}\le n\\ \quad x_i, y_j, \ i=1,2,\ldots ,n, \ j=1,2,\ldots ,m-1,\ integers \end{array}\right. \end{aligned}$$
(1)

where \({\alpha _0}\in [0,1]\) is a predetermined confidence level.

Let \(\Phi _{i,k}\) denote the uncertainty distribution of \(\xi _{i,k}\) and \(\Psi _{i}\) denote the uncertainty distribution of \(\eta _{i}\). In the premise of using the machine k, (i.e., \(y_k>y_{k-1}\)), \(C_{x_{y_{k-1}+1}}({\varvec{x}},{\varvec{y}},{\varvec{\xi }})=\eta _{x_{y_{k-1}+1}}+\xi _{x_{y_{k-1}+1,k}}\) which is the completion time of job \(x_{y_{k-1}+1}\), is an increasing function with respect to \(\eta _{x_{y_{k-1}+1}}\) and \(\xi _{x_{y_{k-1}+1,k}}\). By Theorem 2.1, it has an inverse uncertainty distribution \(\Theta ^{-1}_{x_{y_{k-1}+1}}({\varvec{x}},{\varvec{y}},\alpha )\) via

$$\begin{aligned} \Theta ^{-1}_{x_{y_{k-1}+1}}({\varvec{x}},{\varvec{y}},\alpha )=\Psi ^{-1}_{x_{y_{k-1}+1}}({\varvec{x}},{\varvec{y}},\alpha ) +\Phi ^{-1}_{x_{y_{k-1}+1},k}({\varvec{x}},{\varvec{y}},\alpha ). \end{aligned}$$

Similarly, \(C_{x_{y_{k-1}+j}}({\varvec{x}},{\varvec{y}},\varvec{\xi })=C_{x_{y_{k-1}+j-1}}({\varvec{x}},{\varvec{y}},\varvec{\xi }) \vee \eta _{x_{y_{k-1}+j}} + \xi _{x_{y_{k-1}+j,k}}\), the completion time of job \({x_{y_{k-1}+j}}\), has an inverse uncertainty distribution

$$\begin{aligned} \Theta ^{-1}_{x_{y_{k-1}+j}}({\varvec{x}},{\varvec{y}},\alpha )=\Theta ^{-1}_{x_{y_{k-1}+j-1}}({\varvec{x}},{\varvec{y}},\alpha )\vee \Psi ^{-1}_{x_{y_{k-1}+j}}({\varvec{x}},{\varvec{y}},\alpha )+\Phi ^{-1}_{x_{y_{k-1}+j},k}({\varvec{x}},{\varvec{y}},\alpha ) \end{aligned}$$

for all \(2\le j\le y_k -y_{k-1}\). In fact, we can derive the inverse uncertainty distribution \(\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )\) of the makespan \(f({\varvec{x}},{\varvec{y}},\varvec{\xi })\) via

$$\begin{aligned} \Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )= \max _{1\le k\le m}\Theta ^{-1}_{x_{y_{k}}}({\varvec{x}},{\varvec{y}},\alpha ). \end{aligned}$$

It follows from Liu and Ha [21] that

$$\begin{aligned} E[f({\varvec{x}},{\varvec{y}},\varvec{\xi })]= \int _{0}^{1}\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )\mathrm{d}\alpha \end{aligned}$$

and

$$\begin{aligned} E[(f({\varvec{x}},{\varvec{y}},\varvec{\xi })-D)^{+}]=\int _{0}^{1}[\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )-D]^{+}\mathrm{d}\alpha . \end{aligned}$$

Besides, by Theorem 2.2, the constraint \(\mathcal {M}\{ C_{x_{y_{k_0}}}({\varvec{x}},{\varvec{y}},\varvec{\xi })\le T_0\}\ge \alpha _0\) is equivalent to

$$\begin{aligned} \Theta ^{-1}_{x_{y_{k_0}}}({\varvec{x}},{\varvec{y}},\alpha _0)\le T_0. \end{aligned}$$

So the uncertain multi-objective machine scheduling model (1) is equivalent to

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{{\varvec{x}},{\varvec{y}}}\left( \int _{0}^{1}\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )\mathrm{d}\alpha , \int _{0}^{1}[\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )-D]^{+}\mathrm{d}\alpha \right) \\ \displaystyle subject \ \ to:\\ \quad \Theta ^{-1}_{x_{y_{k_0}}}({\varvec{x}},{\varvec{y}},\alpha _0)\le T_0 \\ \quad 1\le x_i\le n, x_i\ne y_j, i\ne j, i,j=1,2,\ldots ,n\\ \quad 0\le y_1\le y_2\le \cdots \le y_{m-1}\le n\\ \quad x_i, y_j, \ i=1,2,\ldots ,n, \ j=1,2,\ldots ,m-1,\ integers. \end{array}\right. \end{aligned}$$
(2)

In order to solve the crisp model (2), we employ the weighted sum method, and solve the following programming model

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{{\varvec{x}},{\varvec{y}}}\left( \omega _1 \int _{0}^{1}\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )\mathrm{d}\alpha +\omega _2 \int _{0}^{1}[\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )-D]^{+}\mathrm{d}\alpha \right) \\ \displaystyle subject \ \ to:\\ \quad \Theta ^{-1}_{x_{y_{k_0}}}({\varvec{x}},{\varvec{y}},\alpha _0)\le T_0 \\ \quad 1\le x_i\le n, x_i\ne y_j, i\ne j, i,j=1,2,\ldots ,n\\ \quad 0\le y_1\le y_2\le \cdots \le y_{m-1}\le n\\ \quad x_i, y_j, \ i=1,2,\ldots ,n, \ j=1,2,\ldots ,m-1,\ integers \end{array}\right. \end{aligned}$$
(3)

where \(\omega _1\) and \(\omega _2\) are the weights of the first and second objectives, respectively.

5 Hybrid intelligent algorithm

In this section, we employ a genetic algorithm to solve the crisp programming model (3), which is performed in the following steps.

Step 1: Representation

In an uncertain machine scheduling problem, we use a vector \(V =({\varvec{x,y}})=(x_{1}, x_{2},\ldots , x_{n}, y_{1}, y_{2}, \ldots , y_{m-1})\) as a chromosome to represent a solution, where \({\varvec{x}}=(x_{1}, x_{2},\ldots , x_{n})\), representing n jobs, is a rearrangement of \(\{1,2, \ldots , n\}\), and \({\varvec{y}}=(y_{1}, y_{2}, \ldots , y_{m-1})\) satisfying \(0\le y_{1}\le y_{2}\le \cdots \le y_{m-1}\le n\) represents an assignment of n jobs on m machines.

Step 2: Initialization

Give the population size of one generation \(pop\_size\) and the confidence level \(\alpha _0\) in advance. Generate \(({\varvec{x,y}})\) randomly, and obtain a vector \(({\varvec{x}},{\varvec{y}})=(x_{1}, x_{2},\ldots , x_{n}, y_{1}, y_{2}, \ldots , y_{m-1})\). Calculate \(\Theta ^{-1}_{x_{y_{k_0}}}({\varvec{x}},{\varvec{y}},\alpha _0)\) and verify whether it is less than \(T_0\) or not. If so, the vector \(({\varvec{x}},{\varvec{y}})\) is feasible, and we get a chromosome. Otherwise, regenerate another vector \(({\varvec{x}},{\varvec{y}})\). Repeat this process for \({pop\_size}\) times, and we get \({pop\_size}\) chromosomes \(({\varvec{x}}_{1},{\varvec{y}}_{1}), ({\varvec{x}}_{2},{\varvec{y}}_{2}),\cdots , ({\varvec{x}}_{pop\_size},{\varvec{y}}_{pop\_size})\).

Step 3: Evaluation

Give the weights \(\omega _1\) and \(\omega _2\) in advance. For each chromosome \(({\varvec{x,y}})\), calculate the objective values

$$\begin{aligned} \omega _1 \int _{0}^{1}\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )\mathrm{d}\alpha +\omega _2 \int _{0}^{1}[\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )-D]^{+}\mathrm{d}\alpha . \end{aligned}$$

Rearrange \(({\varvec{x}}_{1},{\varvec{y}}_{1}), ({\varvec{x}}_{2},{\varvec{y}}_{2}),\ldots , ({\varvec{x}}_{pop\_size},{\varvec{y}}_{pop\_size})\) according to their objective values in an ascending order, and denote them by \(({\varvec{x}}_{1}',{\varvec{y}}_{1}'), ({\varvec{x}}_{2}',{\varvec{y}}_{2}'),\ldots , ({\varvec{x}}_{pop\_size}',{\varvec{y}}_{pop\_size}')\). Then the fitness of the chromosome \(({\varvec{x}}_{i}',{\varvec{y}}_{i}')\) is \(f_i=a(1-a)^{i-1}\) for \(i=1,2,\ldots ,pop\_size\), where \(a \in [0,1]\) is a given parameter. Calculate the total fitness \(F=\sum \nolimits _{i=1}^{pop\_size}f_i\) and further the evaluation function is \(Eval({\varvec{x}}_{i}',{\varvec{y}}_{i}')=\frac{f_i}{F}\).

Step 4: Selection

Calculate the cumulative probability \(q_{k}\) for the kth chromosomes \(({\varvec{x}}_{k}',{\varvec{y}}_{k}')\) by \(q_{k}=\sum \nolimits _{i=1}^{k}Eval({\varvec{x}}_{i}',{\varvec{y}}_{i}'), \ \ k=1,2,\ldots ,pop\_size,\) and set \(q_{0}=0\). Generate a random number \(u\in (0,1]\) and select the chromosome \(({\varvec{x}}_{k}',{\varvec{y}}_{k}')\) if \(q_{k-1}<u \le q_{k}\). Repeat the process for \({pop\_size}\) times to get a new generation of the chromosomes.

Step 5: Crossover

Give a crossover probability \(P_{c}\) in advance. For each chromosome \(({\varvec{x}}_{i},{\varvec{y}}_{i})\), generate a random number \(u_{i}\in [0,1],i=1,2, \ldots ,pop\_size\). If \(u_{i}\le P_{c}\), then \(({\varvec{x}}_{i},{\varvec{y}}_{i})\) is selected as a parent for crossover operation. Divide all the selected chromosomes into some groups such that each group contains only two chromosomes and perform crossover operations on these groups. Without loss of generality, suppose two chromosomes \(V_{1}=({\varvec{x}}_{1},{\varvec{y}}_{1})\) and \(V_{2}=({\varvec{x}}_{2},{\varvec{y}}_{2})\). And their children chromosomes are \(V_{1}^{'}=({\varvec{x}}_{1},{\varvec{y}}_{2})\) and \(V_{2}^{'}=({\varvec{x}}_{2},{\varvec{y}}_{1})\). If these two children are feasible, then we replace the parents with them. Otherwise, we use the original chromosomes \(V_{1}=({\varvec{x}}_{1},{\varvec{y}}_{1})\) and \(V_{2}=({\varvec{x}}_{2},{\varvec{y}}_{2})\).

Step 6: Mutation

Give a mutation probability \(P_{m}\) in advance. For each chromosome \(({\varvec{x}}_{i},{\varvec{y}}_{i})\), generate a random number \(u_{i}\in [0,1]\), \(i=1,2,\ldots ,pop\_size\). If \(u_{i}\le P_{m}\), then (\({\varvec{x}}_{i},{\varvec{y}}_{i})\) is selected for mutation operation. For a chosen chromosome \(V=({\varvec{x}},{\varvec{y}})\), as for the gene \({\varvec{x}}\), generate two different integers \(n_{1}\) and \(n_{2}\) between 0 and n randomly. Replace \(n_{1}\) and \(n_{2}\) and obtain a new gene. As for the gene \({\varvec{y}}\), generate two integers \(k_{1}\) and \(k_{2}\) between 1 and \(m-1\) randomly, Without loss of generality, suppose \(k_{1} < k_{2}\). Generate randomly \(k_{2}-k_{1}+1\) integers, sort the sequence in ascending order, get \(y'_{k_1}, y'_{k_1+1},\ldots , y'_{k_2}\) replacing \(y_{k_1}, y_{k_1+1},\ldots , y_{k_2}\) and obtain a new gene. If it is feasible, then replace the chromosome with the new one. Otherwise, regenerate \(n_{1}\), \(n_{2}\), \(k_{1}\) and \(k_{2}\) until the new one is feasible.

Step 7: Repetition

Repeat Steps 3–6 for a number of cycles, and select the best chromosome as the optimal solution for model (3).

6 Experimental illustration

A numerical example is covered in this section to illustrate the feasibility and effectiveness of the designed hybrid algorithm. The numerical experiments are performed on a personal computer, and the parameters of genetic algorithm include the population size \(pop\_size\), the probability of crossover \(P_c\), the probability of mutation \(P_m\) and the parameter a in the evaluation function. Assume 12 jobs will be processed on 4 machines with corresponding parameters of the programming model (3) are shown in Table 1.

Table 1 Jobs, uncertain processing times and uncertain release dates
Full size table

In addition, assume machine \(k_0=2\) tends to stop working before \(T_0=20\) with a confidence level \(\alpha _0=0.9\). The common determinate due date is \(D=30\) and the weights of the objectives are \(\omega _1=1\), \(\omega _2=100\) which indicate that more attention is paid to minimize the tardiness time. Then the crisp model (3) is

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{{\varvec{x}},{\varvec{y}}}\left( \int _{0}^{1}\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )\mathrm{d}\alpha +100 \int _{0}^{1}[\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )-30]^{+}\mathrm{d}\alpha \right) \\ \displaystyle subject \ \ to:\\ \quad \Theta ^{-1}_{x_{y_2}}({\varvec{x}},{\varvec{y}},0.9)\le 20 \\ \quad 1\le x_i\le n, x_i\ne y_j, i\ne j, i,j=1,2,\ldots ,n\\ \quad 0\le y_1\le y_2\le \cdots \le y_{m-1}\le n\\ \quad x_i, y_j, \ i=1,2,\ldots ,n, \ j=1,2,\ldots ,m-1,\ integers. \end{array}\right. \end{aligned}$$
(4)

In view of identification of parameters’s influence on solution quality, we compare solution by careful variation of parameters of genetic algorithm with the same generation as a stopping rule. The computational results are collected in Table 2, where the parameters of genetic algorithm are given in table from the first column to the fourth column. ‘gen’ in fifth column is the generation in genetic algorithm, and ‘objective schedule’, ‘objective value’ are provided in the sixth column and seventh column respectively. In addition, the parameter ‘relative error’ in the last column is defined as

$$\begin{aligned} {\text{(objective } \text{ value }} - {\text{ optimal } \text{ value) }}/{\text{ optimal } \text{ value }} \times 100\,\% \end{aligned}$$

where the optimal value is the least one of the six objective values in the seventh column.

Table 2 Compare solutions
Full size table

From Table 2, we can see that the relative error does not exceed 4.15 % when various parameters of genetic algorithm are selected, which implies the hybrid algorithm is effective to solve model (4). We can obtain the optimal value in the fifth line of Table 2, and optimal schedule is displayed in Table 3.

Table 3 Optimal schedule
Full size table

Since there are two parameters \(\omega _1\), \(\omega _2\) in objective function in model (3), we had better analysis the relationship between the objective value and the two parameters. In the following, we fix \(pop\_size=40\), \(P_c=0.4\), \(P_m=0.2\) and \(a=0.05\). We consider one case as under different weights and fix other parameters as in the model (4) and the result of the objective value is displayed in Table 4. It can be seen from Table 4 that different weights affect the objective values. In the experimental environment, the objective values are not monotone.

Table 4 The objective values under different weights
Full size table

In real life, once attention is paid only to reduce the losses caused by tardiness, we assume \(\omega _1=0\) and \(\omega _2=1\). Then the model (3) is changed into

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \min _{{\varvec{x}},{\varvec{y}}} \int _{0}^{1}[\Upsilon ^{-1}({\varvec{x}},{\varvec{y}},\alpha )-D]^{+}\mathrm{d}\alpha \\ \displaystyle subject \ \ to:\\ \quad \Theta ^{-1}_{x_{y_{k_0}}}({\varvec{x}},{\varvec{y}},\alpha _0)\le T_0 \\ \quad 1\le x_i\le n, x_i\ne y_j, i\ne j, i,j=1,2,\ldots ,n\\ \quad 0\le y_1\le y_2\le \cdots \le y_{m-1}\le n\\ \quad x_i, y_j, \ i=1,2,\ldots ,n, \ j=1,2,\ldots ,m-1,\ integers. \end{array}\right. \end{aligned}$$
(5)

In the model (5), we still employ the processing times and release dates showed in Table 1 and set \(k_0=2\), \(T_0=20\), and \(D=30\). Examine the sensitivity of confidence level \(\alpha _0\) in the constraint \(\Theta ^{-1}_{x_{y_{2}}}({\varvec{x}},{\varvec{y}},\alpha _0)\le 20\) and the result is displayed in Table 5. As is seen from Table 5, the objective values are increasing with respect to the confidence level \(\alpha _0\).

Table 5 The objective values under different \(\alpha _0\) in model (5)
Full size table

7 Conclusions

This paper proposed an uncertain machine scheduling problem, of which the release dates and processing times were described as uncertain variables with known uncertainty distributions. An uncertain multi-objective programming model was built for the problem, where the objectives are to minimize the makespan and the tardiness time of the scheduling simultaneously. The proposed uncertain machine scheduling model was transformed into a crisp equivalence by assigning different weights. An intelligent algorithm was designed to solve the crisp equivalence, and was illustrated via some numerical experiments.