1 Introduction

Support vector machine (SVM) [1–3] finds the maximal margin between two classes [4] by solving a quadratic programming problem (QPP) in the dual space based on the structural risk minimization principle. Within a few years after its introduction SVM not only has a serious of improvements [5, 6], but also has already outperformed most other systems in a wide variety of applications [7–9]. However, classical SVM not only has the large computational cost, but also usually pays more attention to the separation between classes than the prior structural information within classes. In fact, for different real-world problems, different classes may have different underlying data structures.

Recently, a class of nonparallel hyperplane classifiers have been developed. For instance, TWSVM [10] aims at generating a pair of nonparallel planes such that each plane is as close as possible to the corresponding class and is at least one far from the other class. To this end, it solves a pair of smaller-sized QPPs, instead of a large one in SVM, making the learning speed of TWSVM be approximately four times faster than that of SVM in theory [10]. Some extensions to TWSVM include the least squares TWSVM (LSTWSVM) [11], nonparallel-plane proximal classifier (NPPC) [12], \(\nu\)-TWSVM [13], twin parametric-margin SVM (TPMSVM) [14], projection twin support vector machine (PTSVM) [15], nonparallel hyperplane SVM (NHSVM) [16], twin support vector regression (TSVR) [17], and twin parametric insensitive support vector regression (TPISVR) [18].

Different from TWSVM which seeks a hyperplane for each class using a SVM-type formulation, Peng and Xu [19] proposed a twin-hypersphere support vector machine (THSVM) classifier for binary classification, which aims at generating two hyperspheres in the feature space such that each hypersphere contains as many as possible samples in one class and is as far as possible from the other one. The THSVM not only has a faster learning speed than classical SVM since it solves two smaller sized QPPs instead of a large QPP as in classical SVM, but also successfully avoids the shortcomings in TWSVM [19], such as the matrix inversion problem. In this paper, we mainly focus on this THSVM.

As the relation between the structural information of data and SVM, it is desirable that an SVM classifier be adaptable to the discriminant boundaries to fit the structures in the data, especially for increasing the generalization capacities of the classifier. Fortunately, some algorithms have been developed to focus more attention on the structural information than SVM recently. They provide a novel view in which to design a classifier, that is, a classifier should be sensitive to the structure of data distribution [20]. These algorithms can be mainly divided into two kinds of approaches. The first one is manifold assumption-based, which assumes that the data actually lie on a sub-manifold in the input space. A typical model is Laplacian SVM (LapSVM) [21, 22]. LapSVM constructs a Laplacian graph for each class on top of the local neighborhood of each point to form the corresponding Laplacian (matrix) to reflect the manifold structure of individual-class data. They are then embedded into the traditional framework of SVM as additional manifold regularization terms. The second approach is cluster assumption-based [23], which assumes that the data contains clusters. For instance, structured large margin machine (SLMM) [20], ellipsoidal kernel machine (EKM) [24], minimax probability machine (MPM) [25], and maxi-min margin machine (\(\text {M}^4\)) [26]. However, the computational cost of these approaches is larger than classical SVM. More recently, Xue et al. [27] proposed a structural regularized SVM (SRSVM). This SRSVM embeds a cluster granularity into the regularization term to capture the data structure, Peng et al. [28] proposed a structural regularized PTSVM (SRPTSVM) for data classification in the spirit of this SRSVM.

THSVM only considers the relationship between two classes, i.e., it finds two hyperspheres to respectively cover the classes of points. In other words, it embeds the class granularity-based structural information [27] into the optimization problems, but not the covariance matrices of two classes. However, this structural information is too rough for real-world problems, which makes THSVM can not find the reasonable projection for each class, then reduce the generalization performance. To overcome this shortcoming, we present an improvement version for THSVM in this paper, called the structural-information-based THSVM (STHSVM) classifier. This STHSVM respectively embeds the data structures of two classes into the optimization problems based on the cluster granularity [27]. That is, in the pair of optimization problems of STHSVM, it considers the cluster-based structural-information constraints for each class, i.e., it introduces a series of hyperspheres but not a single hypersphere to respectively cover the corresponding class of points. Further, for each point in the opposite class, this STHSVM wishes it be as far as possible from the centers of all hypersphres under the given probability values. This STHSVM only needs to solve a series of much smaller sized QPPs compared with THSVM, indicating it has a much faster learning speed than THSVM for solving their QPPs. The experiment results show that this STHSVM obtains the better generalization than THSVM and the other classifiers.

The rest of this paper is organized as follows: Sect. 2 briefly introduces the structural granularities of data and THSVM. Section 3 presents the proposed STHSVM. Experimental results both on the toy and real-world problems are given in Sect. 4. Some conclusions and possible further work are drawn in Sect. 5.

2 Background

In this paper, the training samples are denoted by a set \({\mathcal {D}}=\{( {x}_i,y_i)\}_{i=1}^l\), where \({x}_i\in {\mathcal {X}}\subset {\mathcal {R}}^m\) and \(y_i\in \{+1,-1\}\), \(i=1,\ldots ,l\). For simplicity, we use \({\mathcal {I}}_{\pm }\) to denote the sets of index \(i\) such as \(y_i=\pm\), \(k=1,2\), use the set \({\mathcal {I}}\) to denote all point indices, i.e., \({\mathcal {I}}= \mathcal {I}_+\cup {\mathcal {I}}_-\), and use the matrices \({C}\in {\mathcal {R}}^{m\times {l}}\), \({C}_+\in {\mathcal {R}}^{m\times {l_+}}\) and \({C}_-\in {\mathcal {R}}^{m\times {l_-}}\) to represent all training points, and points belonging to classes \(\pm 1\), respectively, where \(l_\pm =|{\mathcal {I}}_\pm |\).

2.1 Structural granularity

Let \({\mathcal {S}}_1,\ldots,{\mathcal {S}}_t\) be a partition of \({\mathcal {D}}\) according to some relation measure, where the partition characterizes the whole data in the form of some structures such as cluster, and \({\mathcal {S}}_1\cup \ldots \cup {\mathcal {S}}_t= {\mathcal {D}}\). Here \({\mathcal {S}}_i\), \(i=1,\ldots ,t\) is called structural granularity [27]. In general, four granularity layers can be differentiated:

Global granularity The granularity refers to the dataset \({\mathcal {D}}\). With this granularity, the whole data are characterized or enclosed by a single ellipsoid with center \(\mu\) and covariance matrix \(\Sigma\) obtained by minimizing its volume [24]:

$$\begin{aligned} \min _{\mu ,\,\Sigma }&\,\,\ln \left|\Sigma \right| \nonumber \\ \text {s.t.}&\,\,\left|\left|(x_i-\mu )^{-1}\Sigma ^{-1}(x_i-\mu )\right|\right|\le 1,\,\forall i,\nonumber \\&\,\,\Sigma \ge 0. \end{aligned}$$
(1)

The corresponding classifier, such as EKM [24], aims to utilize such global data structure, or more precisely, global data scatter in its design.

Class granularity The granularities are the class partitioned data subsets. Single ellipsoid can be used to describe an individual class to form the so called class structure. The covariance matrices of two classes are defined as

$$\begin{aligned} \Sigma _\pm =\frac{1}{l_\pm }\sum _{i\in \mathcal {I}_\pm }\left[ {x_i}-\mu _\pm \right] \left[ {x_i}-\mu _\pm \right] ^T= {C}_{\pm }{J}_\pm {J}_\pm ^T {C}_{\pm }^T, \end{aligned}$$
(2)

where \({J}_\pm =\frac{1}{\sqrt{l_\pm }} \left( {I}-\frac{1}{l_\pm }{e}{e}^T\right)\), \(\mu _\pm =\frac{1}{l_\pm } \sum _{i\in \mathcal {I}_\pm }x_i\) are the means of two classes, \({e}\) is the vector of ones with appropriate dimensions, and \({I}\) is the identity matrix with appropriate dimension. For example, PTSVM [15], respectively embeds the class granularities into the two optimization problems.

Cluster granularity The granularities are the data subsets within each class. The data structures within each class are depicted by a certain amount ellipsoids that are obtained by some clustering techniques. The corresponding covariance matrix in cluster \(i\) is: \(\Sigma _{{\mathcal {C}}_i}= {C}_{{\mathcal {C}}_i}{J}_{{\mathcal {C}}_i} {J}_{{\mathcal {C}}_i}^T {C}_{{\mathcal {C}}_i}^T\), where \({\mathcal {C}}_i\) is the index set of cluster \(i\) and \({J}_{{\mathcal {C}}_i}=\frac{1}{\sqrt{|{\mathcal {C}}_i|}}\left( {I}-\frac{1}{|{\mathcal {C}}_i|}{ee}^T\right)\). For example, SLMM [20] considers the cluster assumption about the data.

Point granularity The granularities are the neighborhoods \(ne( {x}_i)\) of each point \({x}_i\), which are described by overlapped local ellipsoids surrounding the data in each class, whose covariance matrix can be viewed as a kind of local generalized covariance \(\Sigma _i=\sum _{j\in {ne({x}_i)}}s_{ij}({x}_i- {x}_j)( {x}_i-{x}_j)^T\), where \(s_{ij}=\exp (-\gamma || {x}_i- {x}_j||^2)\), \(\gamma >0\). One of the most successful classifier under this granularity is LapSVM [21], which is successfully applied into semi-supervised problems.

2.2 Twin-hypersphere support vector machine

For binary pattern recognition, the THSVM uses a pair of hyperspheres, one for each class, to describe the samples in two classes, and classifies points according to which hypersphere a given point is relatively closest to. To this end, it obtains two optimization problems, and each one has an SVM-type formulation. Specifically, the THSVM is obtained by solving the following pair of optimization problems:

$$\begin{aligned} \min&\,\,\,\,R_+^2-\frac{\nu _+}{l^-}\sum _{j\in \mathcal {I}^-}\left| \left| \varphi ({x}_j)-{c}_+\right| \right| ^2+ \frac{\gamma _+}{l^+}\sum _{i\in \mathcal {I}^+}\xi _i\nonumber \\ \text {s.t.}&\,\,\,\,\left| \left| \varphi ({x}_i)-{c}_+\right| \right| ^2\le R_+^2+\xi _i,\nonumber \\&\,\,\,\,R_+^2\ge 0,\,\xi _i\ge 0,\,i\in \mathcal {I}_+, \end{aligned}$$
(3)
$$\begin{aligned} \min&\,\,\,\,R_-^2-\frac{\nu _-}{l^+}\sum _{i\in \mathcal {I}^+}\left| \left| \varphi ({x}_i)-{c}_+\right| \right| ^2+ \frac{\gamma _-}{l^-}\sum _{j\in \mathcal {I}^-}\xi _j\nonumber \\ \text {s.t.}&\,\,\,\,\left| \left| \varphi ({x}_j)-{c}_-\right| \right| ^2\le R_-^2+\xi _j,\nonumber \\&\,\,\,\,R_-^2\ge 0,\,\xi _j\ge 0,\,j\in \mathcal {I}_-, \end{aligned}$$
(4)

where \(\gamma _\pm >0\) and \(\nu _\pm >0\) are pre-specified penalty factors, and \({c}_\pm \in \mathcal {H}\) and \(R_\pm\) are the centers and radiuses of the hyperspheres, respectively.

Clearly, the first term of (3) or (4) minimizes the squares radius of the hypersphere to keep the hypersphere as compact as possible. The second term in the objective function of (3) or (4) maximizes the sum of squared distances from the center of hypersphere to the points of the opposite class, which leads to keep the center of this hypersphere far from the samples of the opposite class. The constraints require that the samples of the corresponding class be covered by this hypersphere. Otherwise, a set of error variables is used to measure the errors wherever these points are not covered by this hypersphere. The last term of (3) or (4) minimizes the sum of error variables, thus attempting to minimize misclassification due to points belonging to the opposite class.

Introducing the Lagrangian functions for the problems (3) and (4) and considering the Karush–Kuhn–Tucker (KKT) necessary and sufficient optimality conditions, we obtain their dual problems

$$\begin{aligned} \max&\,\,\sum _{i\in \mathcal {I}_+}\alpha _{i}\Big [\frac{2\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}k({x}_{j},{x}_{i}) +(1-\nu _+)k({x}_{i},{x}_{i})\Big ]-\sum _{i_{1},i_{2}\in \mathcal {I}_+}\alpha _{i_1}\alpha _{i_2}k({x}_{i_1},{x}_{i_2}) \nonumber \\ \text {s.t.}&\,\,\sum _{i\in \mathcal {I}_+}\alpha _{i}=1,\,0\le \alpha _i\le \frac{\gamma _+}{l_+}, \quad i\in \mathcal {I}_+. \end{aligned}$$
(5)
$$\begin{aligned} \max&\,\,\sum _{j\in \mathcal {I}_-}\alpha _{j}\Big [\frac{2\nu _-}{l_+}\sum _{i\in \mathcal {I}_+}k({x}_{i},{x}_{j}) +(1-\nu _-)k({x}_{j},{x}_{j})\Big ]-\sum _{j_1,j_2\in {\mathcal {I}_-}}\alpha _{j_1}\alpha _{j_2}k({x}_{j_1},{x}_{j_2}) \nonumber \\ \mathrm {s.t.}&\,\,\sum _{j\in \mathcal {I}_-}\alpha _{j}=1,\,0\le \beta _j\le \frac{\gamma _-}{l_-}, \quad j\in \mathcal {I}_-, \end{aligned}$$
(6)

where \(\alpha _i\)’s are the nonnegative Lagrangian multipliers, and \(k(u,v)\) is a kernel function: \(k(u,v)=u^Tv\) for the linear case, and \(k(u,v)=\varphi (u)^T\varphi (v)\) for the nonlinear case, such as the Gauss kernel \(k(u,v)=\exp \{-\sigma ||u-v||^2\},\sigma >0\).

After solving (5) and (6), we will obtain the two hyperspheres \(\left| \left| \varphi ({x})-{c}_\pm \right| \right| ^2\le R^2_\pm\), where the \(c_\pm\) and \(R^2_\pm\) values are computed by the KKT necessary and sufficient optimality conditions, which are:

$$\begin{aligned} {c}_\pm =\frac{1}{1-\nu _\pm }\bigg (\sum _{i\in \mathcal {I}_\pm }\alpha _i\varphi ({x}_i)-\frac{\nu _\pm }{l_\mp }\sum _{j\in \mathcal {I}_\mp }\varphi ({x}_j)\bigg ), \end{aligned}$$
(7)
$$\begin{aligned} R^2_\pm =\frac{1}{|\mathcal {I^\prime}_\pm |}\sum _{i\in \mathcal {I^\prime}_\pm }\left| \left| \varphi ({x}_i)-{c}_\pm \right| \right| ^2, \end{aligned}$$
(8)

where the index sets \(\mathcal {I^\prime}_\pm =\bigg \{i\Big |0<\alpha _i<\frac{c_\pm }{l_\pm },\,i\in \mathcal {I}_\pm \bigg \}\).

Then, a new test sample \({x}\) is assigned to the class \(+\) or \(-\), depending on which of the two hyperspheres it lies relatively closest to, i.e.:

$$\begin{aligned} f({x})=\text {arg}\min \limits _{+,-}\left\{ \frac{\left| \left| \varphi ({x})-{c}_+\right| \right| ^2}{R^2_+},\frac{\left| \left| \varphi ({x})-{c}_-\right| \right| ^2}{R^2_-}\right\} . \end{aligned}$$
(9)

3 Structural information-based twin-hypersphere support vector machine

Following the line of the cluster granularity model, the structural information-based twin-hypersphere support vector machine (STHSVM) classifier has two steps: clustering and learning. STHSVM first adopts some clustering techniques to capture the data distribution within classes, then respectively embeds the minimization of the compactness between the estimated clusters into the objective functions. In the following subsections, we will discuss these steps concretely.

3.1 Clustering

In this step, many clustering methods, such as \(k\)-means [29], nearest neighbor clustering [30], and fuzzy clustering [31], can be employed. The aim of clustering is to investigate the underlying data distribution within classes in SRPTSVM. After clustering, the structural information is introduced into the optimization problem by the covariance matrices of the clusters. So the clusters should be compact and spherical for the computation. Following this objective, we consider the following Wards linkage clustering (WLC) technique [32]. Here we only show the linear case, while this clustering method can also be applicable in the kernel space.

Concretely, if \(\mathcal {C}_1\) and \(\mathcal {C}_2\) are two clusters, also are the index sets of the points in the two clusters, then their Wards linkage \(W(\mathcal {C}_1, \mathcal {C}_2)\) can be calculated as

$$\begin{aligned} W({\mathcal {C}}_1,{\mathcal {C}}_2)=\frac{|{\mathcal {C}}_1|\cdot |{\mathcal {C}}_2|\cdot || {\mu }_{{\mathcal {C}}_1} - {\mu }_{{\mathcal {C}}_2}||^2}{|{\mathcal {C}}_1|+|{\mathcal {C}}_2|}, \end{aligned}$$
(10)

where \({\mu }_{\mathcal {C}_1}\) and \({\mu }_{\mathcal {C}_2}\) are the means of the two clusters, respectively.

Initially, each sample is a cluster in the clustering algorithm. The Wards linkage of two samples \({x}_i\) and \({x}_j\) is defined as \(W( {x}_i, {x}_j)=|| {x}_i- {x}_j||^2/2\). During clustering, the two clusters with the smallest Wards linkage value are merged. When two clusters \(\mathcal {C}_1\) and \(\mathcal {C}_2\) are being merged to a new cluster \(\mathcal {C^\prime}\), the linkage \(W(\mathcal {C^\prime},\mathcal {C})\) of \(\mathcal {C^\prime}\) and other cluster \(\mathcal {C}\) can be conveniently derived from \(W(\mathcal {C}_1,\mathcal {C})\), \(W(\mathcal {C}_2,\mathcal {C})\), and \(W(\mathcal {C}_1,\mathcal {C}_2)\) by

$$\begin{aligned} W(\mathcal {C^\prime},\mathcal {C})=\frac{(|\mathcal {C}_1|+|\mathcal {C}|)W(\mathcal {C}_1,\mathcal {C})+ (|\mathcal {C}_2|+|\mathcal {C}|)W(\mathcal {C}_2,\mathcal {C})- |\mathcal {C}|W(\mathcal {C}_1,\mathcal {C}_2)}{|\mathcal {C}_1|+|\mathcal {C}_2|+|\mathcal {C}|}. \end{aligned}$$
(11)

To simply determine the cluster number, this WLC uses kernels to measure the similarity between clusters. Salvador and Chan [33] provided a method to automatically determine the number of clusters that selects the number corresponding to the knee point, i.e., the point of maximum curvature, on the curve.

3.2 STHSVM classifier

Without loss of generality, we denote the clusters in two classes as \(\mathcal {P}_1,\ldots , \mathcal {P}_{c_1}\) and \(\mathcal {N}_1,\ldots ,\mathcal {N}_{c_2}\), respectively. To find the hyperspheres for each class, which show the compactness within classes, i.e., the clusters that cover the different structural information in different classes, the STHSVM classifier optimizes the following two optimization problems:

$$\begin{aligned} \min&\,\,\sum _{s=1}^{c_1}\frac{l_{+,s}}{l_+}R^2_{+,s}-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-} \sum _{s=1}^{c_1}p_{j,s}\left| \left| \varphi (x_j)-c_{+,s}\right| \right| ^2 +\frac{\gamma _+}{l_+}\sum _{i\in \mathcal {I}_+}\xi _i\nonumber \\ \text {s.t.}&\,\,||\varphi (x_i)-c_{+,s}||^2\le R^2_{+,s}+\xi _i,\,\,\text {if}\,\,i\in \mathcal {P}_s,\\&\,\,\xi _i\ge 0,\,R^2_{+,s}\ge 0,\,i\in \mathcal {I}_+,\quad s=1,\ldots ,c_1,\nonumber \end{aligned}$$
(12)
$$\begin{aligned} \min&\,\,\sum _{t=1}^{c_2}\frac{l_{-,t}}{l_-}R^2_{-,t}-\frac{\nu _-}{l_+}\sum _{i\in \mathcal {I}_+} \sum _{t=1}^{c_2}p_{i,t}\left| \left| \varphi (x_i)-c_{-,t}\right| \right| ^2 +\frac{\gamma _-}{l_-}\sum _{j\in \mathcal {I}_-}\xi _j\nonumber \\ \text {s.t.}&\,\,||\varphi (x_j)-c_{-,t}||^2\le R^2_{-,t}+\xi _j,\,\,\text {if}\,\,j\in \mathcal {N}_t,\\&\,\,\xi _j\ge 0,\,R^2_{-,t}\ge 0,\,j\in \mathcal {I}_-,\quad t=1,\ldots ,c_2,\nonumber \end{aligned}$$
(13)

where \(\gamma _\pm ,\nu _\pm\), \(k=1,2\) are penalty factors given by users, \(l_{+,s}=|\mathcal {P}_s|\), \(s=1,\ldots ,c_1\) and \(l_{-,t}=|\mathcal {N}_t|\), \(t=1,\ldots ,c_2\) denote the sizes of the clusters \(\mathcal {P}_s\) and \(\mathcal {N}_t\), \(l_+=\sum _{s=1}^{c_1}l_{+,s}\), \(l_-=\sum _{t=1}^{c_2}l_{-,t}\), \(c_{+,s}, R_{+,s}\), \(s=1,\ldots ,c_1\) and \(c_{-,t},R_{-,t}\), \(t=1,\ldots ,c_2\), are the centers and radiuses of clusters \(\mathcal {P}_s\) and \(\mathcal {N}_t\), respectively. In addition, \(p_{j,s}\), \(s=1,\ldots ,c_1\), \(j\in \mathcal {I}_-\) are the probabilities of \(x_j\) belonging to clusters \(\mathcal {P}_s\), and \(p_{i,t}\), \(t=1,\ldots ,c_2\), \(i\in \mathcal {I}_+\) are the probabilities of \(x_i\) belonging to clusters \(\mathcal {N}_t\). In this work, we define them as

$$\begin{aligned} p_{i,t}=\frac{\kappa \Big (||x_i-\mu _{-,t}|| \Big )}{\sum _{t^\prime=1}^{c_2}\kappa \Big (||x_i-\mu _{-,t^\prime}|| \Big )},\quad i\in \mathcal {I}_+, \quad t=1,\ldots ,c_2, \end{aligned}$$
(14)

and

$$\begin{aligned} p_{j,s}=\frac{\kappa \Big (||x_j-\mu _{+,s}||\Big )}{\sum _{s^\prime=1}^{c_1}\kappa \Big (||x_j-\mu _{+,s^\prime}||\Big )}, \quad j\in \mathcal {I}_-, \quad s=1,\ldots ,c_1, \end{aligned}$$
(15)

where \(\kappa (u)=\exp (-\tau {u^2})\), \(\tau >0\), \(\mu _{+,s}\), \(s=1,\ldots ,c_1\) and \(\mu _{-,t}\), \(t=1,\ldots ,c_2\) are the means of clusters \(\mathcal {P}_s\) and \(\mathcal {N}_t\), respectively. We have \(\sum _{t=1}^{c_2}p_{i,t}=1\) for all \(i\in \mathcal {I}_+\) and \(\sum _{s=1}^{c_1}p_{j,s}=1\) for all \(j\in \mathcal {I}_-\). Obviously, for any point \(x_i\), \(i\in \mathcal {I}_+\), we have a larger value \(p_{i,t}\) if \(x_i\), \(i\in \mathcal {I}_+\) is nearer to cluster \(t\) than the other clusters in Class \(-\).

First of all, we consider the illustrations of the optimization problems (12) and (13) before optimizing them. First, the constraints require that the samples in a cluster of the corresponding class be covered by one hypersphere. Otherwise, a set of error variables \(\{\xi _i,i\in \mathcal {I}_+\}\) or \(\{\xi _j,j\in \mathcal {I}_-\}\) is used to measure the errors wherever these points are not covered by this hypersphere. Compared with the corresponding term of THSVM, this term makes STHSVM pay more attention to the cluster granularity-based structure information, which are more reasonable for real-world problems. Clearly, for many real-world problems, it is not suitable to use one hypersphere to only cover the points in one class. The last term of the objective function of (12) or (13) minimizes the sum of error variables, thus attempting to minimize misclassification due to points belonging to the opposite class. Second, the first term in the objective function of (12) or (13) minimizes the squares radiuses of the hyperspheres. Hence, minimizing them tends to keep these hyperspheres as compact as possible, i.e., makes these hyperspheres be as small as possible. Note that this term gives the different weights for these hyperspheres according to the sizes of clusters. This definition for weights is reasonable since the clusters with larger sizes should have larger influence than those with smaller sizes. Last, the second term in the objective function of (12) or (13) maximizes the sum of squared distances from the centers of hyperspheres to the points of the opposite class, which leads to keep the centers of this hyperspheres far from the samples of the opposite class. However, by considering the cluster granularity-based structure information, this term introduces the different weights \(p_{j,s}\) or \(p_{i,t}\). In fact, if one point in Class \(-\) is nearer to a cluster of Class \(+\), we will hope it is as far as possible from the corresponding hyperphere’s center of this cluster than the other centers. In this STHSVM, we use (14) or (15) to depict this end, which can describe the above design.

We now consider to optimize the primal optimization problems (12) and (13). The corresponding Lagrangian function of the problem (12) is

$$\begin{aligned} \mathcal {L}(c_{+,s},R^2_{+,s},\xi _i,\alpha _i,\beta _i,\lambda _s)=&\sum _{s=1}^{c_1}\frac{l_{+,s}}{l_+}R^2_{+,s} -\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-} \sum _{s=1}^{c_1}p_{j,s}\left| \left| \varphi (x_j)-c_{+,s}\right| \right| ^2\nonumber \\ +&\frac{\gamma _+}{l_+}\sum _{i\in \mathcal {I}_+}\xi _i- \sum _{i\in \mathcal {I}_+}\beta _i\xi _i-\sum _{s=1}^{c_1}\lambda _sR^2_{+,s}\nonumber \\ +&\sum _{s=1}^{c_1}\sum _{i\in \mathcal {P}_s}\alpha _i\left( ||\varphi (x_i)-c_{+,s}||^2-R^2_{+,s}-\xi _i\right) , \end{aligned}$$
(16)

where \(\lambda _s\ge 0\), \(s=1,\ldots ,c_1\), \(\alpha _i\ge 0,\,\beta _i\ge 0,\,i\in {\mathcal {I}}_+\) are the Lagrangian multipliers. Differentiating the Lagrangian function () with respect to \({c}_{+,s},\,R^2_{+,s}\), and \(\xi _i,\,i\in \mathcal {I}_+\) yields the following Karush–Kuhn–Tucker (KKT) necessary and sufficient optimality conditions:

$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial {c}_{+,s}}=&-\frac{2\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s} \left( c_{+,s}-\varphi (x_j)\right) +2\sum _{i\in \mathcal {P}_s}\alpha _i\left( c_{+,s}-\varphi (x_i)\right) =0\nonumber \\ \Rightarrow&c_{+,s}=\frac{1}{\sum _{i\in \mathcal {P}_s}\alpha _i-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s}} \left(\sum _{i\in \mathcal {P}_s}\alpha _i\varphi (x_i)-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s}\varphi (x_j)\right) \nonumber \\&\quad s=1,\ldots ,c_1, \end{aligned}$$
(17)
$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial {R^2_{+,s}}}=\frac{l_{+,s}}{l_+}-\sum _{i\in \mathcal {P}_s}\alpha _i-\lambda _s=0\Rightarrow \sum _{i\in \mathcal {P}_s}\alpha _i\le \frac{l_{+,s}}{l_+}, \quad s=1,\ldots ,c_1, \end{aligned}$$
(18)
$$\begin{aligned} \frac{\partial \mathcal {L}}{\partial \xi _i}=\frac{\gamma _+}{l_+}-\alpha _i-\beta _i=0\Rightarrow 0 \le \alpha _i\le \frac{\gamma _+}{l_+}, \quad i\in \mathcal {I}_+, \end{aligned}$$
(19)
$$\begin{aligned} \left| \left| \varphi ({x}_i)-{c}_{+,s}\right| \right| ^2\le {R^2_{+,s}}+\xi _i, \quad i\in \mathcal {P}_s, \end{aligned}$$
(20)
$$\begin{aligned} \alpha _i\left( ||\varphi (x_i)-c_{+,s}||^2-R^2_{+,s}-\xi _i\right) =0, \quad \alpha _i\ge 0, \quad i\in \mathcal {P}_s, \quad s=1,\ldots ,c_1, \end{aligned}$$
(21)
$$\begin{aligned} \beta _i\xi _i=0, \quad \xi _i\ge 0, \quad \beta _i\ge 0, \quad i\in \mathcal {I}_+, \end{aligned}$$
(22)
$$\begin{aligned} \lambda _sR^2_{+,s}=0, \quad R^2_{+,s}\ge 0, \quad \lambda _s\ge 0. \end{aligned}$$
(23)

Note that \(R_{+,s}^2>0\) will hold in the optimality result of problem (12) if the suitable parameters \(\nu _+\) and \(\gamma _+\) are given. Then, we have \(\sum _{i\in \mathcal {P}_s}\alpha _i=\frac{l_{+,s}}{l_+}\), \(s=1,\ldots ,c_1,\) according to the KKT conditions (18) and (23), and

$$\begin{aligned} c_{+,s}=\frac{1}{\frac{l_{+,s}}{l_+}-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s}} \bigg (\sum _{i\in \mathcal {P}_s}\alpha _i\varphi (x_i)-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s}\varphi (x_j)\bigg ), \quad s=1,\ldots ,c_1. \end{aligned}$$
(24)

Substituting (18), (19) and (24) into (16), we obtain the dual optimization problem of (12) as following:

$$\begin{aligned} \max \,\,&-\sum _{s=1}^{c_1}\Bigg [\frac{1}{\frac{l_{+,s}}{l_+}-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s}} \sum _{i_1\in \mathcal {P}_s}\sum _{i_2\in \mathcal {P}_s}\alpha _{i_1}\alpha _{i_2}k(x_{i_1},x_{i_2})\nonumber \\&-2\frac{1}{\frac{l_{+,s}}{l_+}-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s}}\sum _{i\in \mathcal {P}_s}\alpha _i\sum _{j\in \mathcal {I}_-} \frac{\nu _+}{l_-}p_{j,s}k(x_i,x_j)-\sum _{i\in \mathcal {P}_s}\alpha _ik(x_i,x_i)\Bigg ]\nonumber \\&+\text {constant}\nonumber \\ \text {s.t.}\,\,&\sum _{i\in \mathcal {P}_s}\alpha _{i}=\frac{l_{+,s}}{l_+},\,0\le \alpha _i\le \frac{\gamma _+}{l_+}, \,i\in \mathcal {P}_s, \quad s=1,\ldots ,c_1, \end{aligned}$$
(25)

where the constant term does not influence the solution of this optimization problem. Hence we can omit this term in the optimization process.

This optimization problem can be broken down into a series of small-sized optimization problems by multiplying the objective functions by \(\left( {\frac{l_{+,s}}{l_+}-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s}}\right)\) for \(s=1,\ldots ,c_1\):

$$\begin{aligned} \min \,\,\,\,\,\,&\sum _{i_1\in \mathcal {P}_s}\sum _{i_2\in \mathcal {P}_s}\alpha _{i_1}\alpha _{i_2}k(x_{i_1},x_{i_2})\nonumber \\ -&\sum _{i\in \mathcal {P}_s}\alpha _i\Bigg [\sum _{j\in \mathcal {I}_-}\frac{2\nu _+}{l_-}p_{j,s}k(x_i,x_j)+ \left (\frac{l_{+,s}}{l_+}-\frac{\nu _+}{l_-}\sum _{j\in \mathcal {I}_-}p_{j,s}\right )k(x_i,x_i)\Bigg ]\nonumber \\ \text {s.t.}\,\,&\sum _{i\in \mathcal {P}_s}\alpha _{i}=\frac{l_{+,s}}{l_+}, \quad 0\le \alpha _i\le \frac{\gamma _+}{l_+}, \quad i\in \mathcal {P}_s, \quad s=1,\ldots ,c_1. \end{aligned}$$
(26)

Next, notice that \(\left| \left| \varphi ({x}_i)-{c}_{+,s}\right| \right| ^2=R_{+,s}^2\) if \(0<\alpha _i<\frac{\gamma _+}{l_+},i\in \mathcal {P}_s\) according to the KKT conditions (19)–(23). Thus, we compute the square radiuses \(R_{+,s}^2\), \(s=1,\ldots ,c_1\) by the following formula:

$$\begin{aligned} R^2_{+,s}=\frac{1}{|\mathcal {I}_{+,s}^{R}|}\sum _{i\in \mathcal {I}_{+,s}^{R}} \left| \left| \varphi ({x}_i)-{c}_{+,s}\right| \right| ^2, \quad s=1,\ldots ,c_1, \end{aligned}$$
(27)

where the index sets \(\mathcal {I}_{+,s}^{R}=\left\{ i\bigg |0<\alpha _i<\frac{\gamma _+}{l_+},\,i\in \mathcal {P}_s\right\}\), \(s=1,\ldots ,c_1\).

Similarly, we obtain the \(c_2\) simplified dual of problems (13) as following:

$$\begin{aligned} \min \,\,\,\,\,\,&\sum _{j_1\in \mathcal {N}_t}\sum _{j_2\in \mathcal {N}_t}\alpha _{j_1}\alpha _{j_2}k(x_{j_1},x_{j_2})\nonumber \\ -&\sum _{j\in \mathcal {N}_t}\alpha _j\bigg [\sum _{i\in \mathcal {I}_+}\frac{2\nu _-}{l_+}p_{i,t}k(x_j,x_i)+ \bigg (\frac{l_{-,t}}{l_-}-\frac{\nu _-}{l_+}\sum _{i\in \mathcal {I}_+}p_{i,t}\bigg )k(x_j,x_j)\bigg ]\nonumber \\ \text {s.t.}\,\,&\sum _{j\in \mathcal {N}_t}\alpha _{j}=\frac{l_{-,t}}{l_-}, \quad 0\le \alpha _j\le \frac{\gamma _-}{l_-}, \quad j\in \mathcal {N}_t, \quad t=1,\ldots ,c_2, \end{aligned}$$
(28)

where \(\alpha _j,\,j\in \mathcal {I}_-\) are the nonnegative Lagrangian multipliers, and the centers \({c}_{-,t}\), \(t=1,\ldots ,c_2\) are

$$\begin{aligned} c_{-,t}=\frac{1}{\frac{l_{-,t}}{l_-}-\frac{\nu _-}{l_+}\sum _{i\in \mathcal {I}_+}p_{i,t}} \bigg (\sum _{j\in \mathcal {N}_t}\alpha _j\varphi (x_j)-\frac{\nu _-}{l_+}\sum _{i\in \mathcal {I}_+}p_{i,t}\varphi (x_i)\bigg ), \quad t=1,\ldots ,c_2. \end{aligned}$$
(29)

Also, the square radiuses \(R_{-,t}^2\), \(t=1,\ldots ,c_2\) are

$$\begin{aligned} R^2_{-,t}=\frac{1}{|\mathcal {I}_{-,t}^{R}|}\sum _{j\in \mathcal {I}_{-,t}^{R}} \left| \left| \varphi ({x}_j)-{c}_{-,t}\right| \right| ^2, \quad t=1,\ldots ,c_2, \end{aligned}$$
(30)

where the index sets \(\mathcal {I}_{-,t}^{R}\), \(t=1,\ldots ,c_2\) are

$$\begin{aligned} \mathcal {I}_{-,t}^{R}=\left\{ j\bigg |0<\alpha _j<\frac{\gamma _-}{l_-},\,j\in \mathcal {N}_t\right\} , \quad t=1,\ldots ,c_2. \end{aligned}$$

Once the elements \(({c}_{+,s}, R^2_{+,s})\), \(s=1,\ldots ,c_1\) and \(({c}_{-,t},R^2_{-,t})\), \(t=1,\ldots ,c_2\) are calculated by (24), (27), (29) and (30), a series of hyperspheres

$$\begin{aligned}&\left| \left| \varphi ({x})-{c}_{+,s}\right| \right| ^2\le R^2_{+,s}, \quad s=1,\ldots ,c_1,\nonumber \\&\left| \left| \varphi ({x})-{c}_{-,t}\right| \right| ^2\le R^2_{-,t}, \quad t=1,\ldots ,c_2 \end{aligned}$$
(31)

are obtained. A new test sample \({x}\) is assigned to the class \(+\) or \(-\), depending on which of these hyperspheres given by (31) it lies relatively closest to, i.e.,

$$\begin{aligned} f({x})=\text {arg}\min \limits _{+,-}\left\{ \min _{s=1,\ldots ,c_1}\bigg [\frac{\left| \left| \varphi ({x})-{c}_{+,s}\right| \right| ^2}{\frac{l_{+,s}}{l_+}R^2_{+,s}}\bigg ], \min _{t=1,\ldots ,c_2}\bigg [\frac{\left| \left| \varphi ({x})-{c}_{-,t}\right| \right| ^2}{\frac{l_{-,t}}{l_-}R^2_{-,t}}\bigg ]\right\} . \end{aligned}$$
(32)

In summary, our STHSVM algorithm for pattern recognition is listed as follows:

Algorithm 1

The STHSVM algorithm

  1. 1.

    Set the parameters \(\nu _\pm\), \(\gamma _\pm\), and kernel function;

  2. 2.

    Determine the clusters \(\mathcal {P}_1,\ldots ,\mathcal {P}_{c_1}\) for Class \(+\) and the clusters \(\mathcal {N}_1,\ldots ,\mathcal {N}_{c_2}\) for Class \(-\) according to some clustering technique;

  3. 3.

    Optimize the optimization problems (26) and (28) by some optimization technique;

  4. 4.

    Compute \(({c}_{+,s}, R^2_{+,s})\), \(s=1,\ldots ,c_1\) and \(({c}_{-,t},R^2_{-,t})\), \(t=1,\ldots ,c_2\) by (24), (27), (29) and (30);

  5. 5.

    Predict the label for a new point \(x\) by (32).

4 Experiments

In this section, we run a series of experiments systematically on both toy and real-world classification problems to evaluate the proposed STHSVM algorithm. First, we present two synthetic datasets, i.e., the XOR and Hex datasets, to intuitively compare STHSVM with THSVM. On real-world problems, several datasets in the UCI database are used to evaluate the classification accuracies derived from STHSVM in comparison to some other algorithms, including the TWSVM [10], TPMSVM [14], SRSVM [27], SRPTSVM [28], and THSVM [19]. Remark that the regularization terms are introduced in the TPMSVM, which is helpful to the generalization performance. Here only Gaussian kernel is employed for nonlinear problems. For these classifiers, the kernel widths and the regularization parameters are selected from the set \(\{2^{-9},\ldots ,2^{10}\}\) by cross-validation. While the \(\nu /c\) values in TPMSVM are selected from the set \(\{0.05,0.1,\ldots ,0.95\}\). All methods are implemented in MATLABFootnote 1 on Windows XP running on a PC.

4.1 Toy datasets

In this part we compare our method with THSVM on the 2-D XOR and Hex problems, in which the points are randomly generated under Gaussian distributions in each class. Table 1 describes the corresponding attributes of the XOR and Hex problems. It can be easily seen that, for the two problems, the two classes are composed of some clusters and these clusters have totally different distributions. Thus, in these cases, the structural information within the classes may be more important than the discriminative information between the classes. For each cluster of the two problems, we randomly generate 100 training points and 500 test points, respectively.

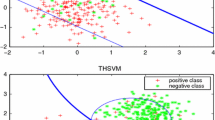
Table 1 Attributes of the toy XOR and Hex datasets
Full size table

For the XOR and Hex problems, we use the linear and kernel STHSVM and kernel THSVM classifiers to find the decision bounds. Remark that the linear THSVM can not successfully obtain the suitable separating bound for this problem, Figs. 1 and 2 show the one-run training results obtained by the linear and kernel STHSVM and kernel THSVM on these two problems. Due to the formal neglect of the structural information within the classes, kernel THSVM cannot differentiate the different data occurrence trends, i.e., the clusters in each class. Then, the derived hyperspheres for two classes only as possibly as cover the points in the corresponding classes. Specifically, it can be found from Figs. 1a and 2a that the obtained hyperspheres cover the same area, i.e., they can not successfully depict the data, since the structural information under cluster granularity is ignored. Different to the THSVM classifier, STHSVM embeds the structure information within the classes into the optimization problems. Then, STHSVM should get more reasonable discriminant boundaries than THSVM which basically accord with the data occurrence trend, and thus has the best classification performance than the other classifiers in theory. Figures 1b, c and 2b, c confirm this conclusion, in which the results show that it obtains a better separating bound than THSVM. To further explain the conclusion, we make ten independent runs on the XOR and Hex problems and compare with the results of the two classifiers, listed in Table 2. It can be found that our linear and kernel STHSVM obtains the better performance than the kernel THSVM classifier.

Fig. 1
figure 1

Training results of kernel THSVM (a), linear STHSVM (b), and kernel STHSVM (c) on the XOR problem. The two classes of points are marked by “\(\times\)” and “\(+\)”, the decision bounds of these classifiers are marked by solid curves in black, and the hyperspheres of these classifiers marked by solid curves in blue and red, respectively

Full size image
Fig. 2
figure 2

Training results of kernel THSVM (a), linear STHSVM (b), and kernel STHSVM (c) on the Hex problem. The two classes of points are marked by “\(\times\)” and “\(+\)”, the decision bounds of these classifiers are marked by solid curves in black, and the hyperspheres of these classifiers marked by solid curves in blue and red, respectively

Full size image
Table 2 Results of linear/kernel STHSVM and kernel THSVM on XOR and Hex datasets
Full size table

To further explain the performance of the proposed STHSVM classifier, in Figs. 3 and 4, we depict the two-dimensional scatter plots for kernel THSVM and linear/nonlinear STHSVM on the XOR and Hex problem with \(100+100\) and \(150+150\) test points, respectively. The plots are obtained by plotting test points with coordinates \((d_1, d_2)\). Here, \(d^i_+\) and \(d^i_-\) are the relative ‘distances’ of a test point \({x}_i\) to the centers of the positive and negative hyperspheres for the THSVM, i.e., \(d^i_\pm = ||{\varphi }({x}_i)-{c}_\pm || /R_\pm\) for the THSVM. While \(d^i_+\) and \(d^i_-\) are the minimum relative ‘distances’ of a test point \({x}_i\) to the centers of the positive and negative hyperspheres for the STHSVM, i.e., \(d^i_+=\min _{s}\left[ {\sqrt{l_+}||\varphi ({x}_i)-{c}_{+,s}||}/{\sqrt{l_{+,s}}R_{+,s}}\right]\) and \(d^i_-=\min _{t}\left[ {\sqrt{l_-}||\varphi ({x}_i)-{c}_{-,t}||}/{\sqrt{l_{-,t}}R_{-,t}}\right]\) for the STHSVM. In short, the point \({x}_i\) is assigned to class \(+1\) if the value of \(d_+^i\) is less than \(d_-^i\) and vice versa. In Figs. 3 and 4, each point is marked as “\(\circ\)” if its class label is \(+1\) and “\(\Box\)” otherwise. Obviously, the two-dimensional projections for test points indicate how well the classification criterion is able to discriminate between the two classes. It can be seen that for the kernel THSVM, most points are covered by the corresponding hyperspheres and are far from the opposite hyperspheres, i.e., the corresponding \(d_+^i\)’s or \(d_-^i\)’s are not larger than one. This indicates the hyperspheres in the THSVM can effectively depict the data characteristic of classes. However, for the linear and kernel STHSVM, it not only can be found that most points are covered by the corresponding hyperspheres and are far from the opposite hyperspheres, but also is more robust than the THSVM. In fact, this is because the STHSVM embeds the structure information within the classes into the optimization problems.

Fig. 3
figure 3

Two-dimensional projections for test points from the XOR dataset with the kernel THSVM (a), linear STHSVM (b), and kernel STHSVM (c)

Full size image
Fig. 4
figure 4

Two-dimensional projections for test points from the Hex dataset with the kernel THSVM (a), linear STHSVM (b), and kernel STHSVM (c)

Full size image

4.2 Benchmark datasets

In this section, we compare with the performance of TWSVM, TPMSVM, SRSVM, SRPTSVM, THSVM, and STHSVM on the 13 benchmark datasets [34] in that order: Banana (B), Breast Cancer (BC), Diabetes (D), Flare (F), German (G), Heart (H), Image (I), Ringnorm (R), Splice (S), Thyroid (Th), Titanic (T), Twonorm (Tw), and Waveform (W). In particular, we use in each problem the train-test splits given in that reference (100 for each dataset except for Image and Splice, where only 20 splits are given).

In Table 3, we report the training time of one-run and the average test accuracies of linear TWSVM, TPMSVM, SRSVM, SRPTSVM, THSVM, and STHSVM on these benchmark datasets. For the linear SRPTSVM classifier, we adopt the recursive strategy to find the best prediction performance. Table 4 lists the training time of one-run and the average test accuracies of nonlinear TWSVM, TPMSVM, SRSVM, SRPTSVM, THSVM, and STHSVM with Gaussian kernels. From these results, we can find that STHSVM obtains the best learning results than THSVM and other classifiers for most datasets. In fact, this is because STHSVM embeds the structural information of each class under cluster granularity into its two optimization problems, which is more helpful to further improve the learning performance. In addition, it can be found that compared with the other methods, SRSVM and SRPTSVM obtain better generalization performance than TWSVM and TPMSVM for many datasets. This is also because the two methods successfully embed the data structural information into their optimization problems. However, the results in Tables 3 and 4 show that our method outperforms SRSVM and SRPTSVM for many datasets. A possible reason is that it uses a more reasonable strategy to depict the data structure than the latter. In order to find out whether STHSVM is significantly better than the other algorithms, we perform the \(t\) test on the classification results to calculate the statistical significance of STHSVM. The null hypothesis \(H_0\) demonstrates that there is no significant difference between the mean numbers of patterns correctly classified by STHSVM and the other algorithms. If the hypothesis \(H_0\) of each dataset is rejected at the 5 % significance level, i.e., the \(t\) test value is more than 1.734, the corresponding results in Tables 3 and 4 is denoted “*”. Consequently, as shown in Tables 3 and 4, it can be clearly found that STHSVM possesses significantly superior classification performance compared with the other classifiers on the most datasets. This just accords with our conclusions. As for the learning time of these methods, remark that it need find the cluster-based structural information through some clustering technique, which leads to some extra learning time compared with THSVM. However, it can be seen that, for most datasets, the proposed STHSVM with different kernels has a comparable speed with THSVM. In fact, this is because this proposed STHSVM only needs to optimize a series of smaller-sized optimization problems compared with THSVM, which leads it to have a much faster speed than THSVM. Tables 3 and 4 also confirm this conclusion. In fact, the time for clustering in this STHSVM is listed in tables indicates this method is much efficient. In summary, these simulation results show that our STHSVM not only obtains a better generalization performance than these related methods, but also has a fast learning speed.

Table 3 Prediction accuracies and learning time (in s) of linear TWSVM, TPMSVM, SRPTSVM, SRSVM, THSVM, and STHSVM on benchmark datasets
Full size table
Table 4 Prediction accuracies and learning time of nonlinear TWSVM, TPMSVM, SRPTSVM, SRSVM, THSVM, and STHSVM on benchmark datasets
Full size table

5 Conclusions

The twin-hypersphere support vector machine (THSVM) [19] for binary classification seeks two hypersphres by solving two SVM-type problems, one for each class, to make the points in each class are covered as many as possibly by one hyperphere. Then, it classifies a new point according to which hypersphere is relatively closest to. However, it only considers the global structure information of each class, which leads to hardly extend to real-world problems.

In this paper, under the structural granularity [27], which characterizes a series of data structures involved in the various classifier design ideas, we have introduced an improved THSVM named the structural information-based THSVM (STHSVM) classifier. In each optimization problem of STHSVM, a data structural-information derived from the cluster granularity [27] is absorbed into the learning process. Further, STHSVM introduces a different probability sum of projected center for each point to depict the cluster granularity-based structural information. The experiments have confirmed that this STHSVM successfully embeds into the cluster granularity-based structural information and obtains the good performance. The idea in this method can be easily extended to some other TWSVM classifiers. There still exists some future work. For example, we only apply our method into the middle-scale classification problems since it has a large cost to cluster large-scale datasets. In addition, another problem is to discuss the relationship between the performance and the cluster number. Also, the parameter-selection problem is an important further problem.