1 Introduction

The applications of the magneto-hydro-dynamic with controlling heat and mass transfer over a continuously extending sheet, reactors for nuclear, generators of power, understating plasma, and extracting the energy of geothermal grab the eyeballs of many researchers. The involvement of magneto-hydro-dynamic flow of convective induced the Hall current in the magnetic and electric field from the normal direction. The impact of Hall current cannot be ignored due to the strong magnetic field or/and low density of the ionized gasses. The flow of convective utilizing magneto-hydro-dynamic was analyzed in [1,2,3,4,5,6,7,8,9,10,11], having a strong magnetic field passing over a vertical flat plate which is semi-infinite. There is some researcher who discussed this with vertical plate [12,13,14,15,16,17] with other parameters.

Due to the broader applications in the jet motors, mass spectrometry, computer floppy drive, domain of nutrition processing, turbine systems, generation of electric power, and rotational fluids are gaining the attention of researchers. Some researchers [18,19,20,21,22,23,24,25,26] studied the rotational body with the Hall current, considering the presence of a magnetic field very high. While [27] discussed the impact of Hall current combined with a strong magnetic field, with the free stream flow over a horizontally moving plate, and [28] studied the flow of rotational fluid of secondary grade for heat transfer with Hall current passing over a porous media. Several scenarios of the rotating disk concept have been studied by researchers, including the use of ferrofluid [29], Darcy-Forchheimer fluid [30], Stefan Blowing on Rener-Rivlin flow [31], and MHD flow with radiative heat [32]. Additionally, some authors have considered entropy optimization on a rotating disk [33, 34]. Several authors [35,36,37] have analyzed the effects of different parameters on micropolar fluids.

To emphasize the energy system by thermal conductivity, researchers used several methods in the heat mass transmission, and then microorganisms incorporated in bio-convection nanofluids grabbed their attention. The movements of these microorganisms in the nanofluid modernize as the bio-convection nanofluid, which is in higher dimension. Many researchers have been working on controlling heat, momentum, and mass transmission rates of nanofluids and microbial microorganisms [37,38,39,40,41]. Analysis of mass and heat transmission for convective borderline circumstances is significant for reactors of atoms and turbines of gasses, accompanied by exchangers of heat into the industries. Nanofluids are integrated into bio-medical disciplines due to their solicitation in the labeling of cancerous tissues, cancer therapeutics, magnetic resonance imaging (MRI), and magnetic resonance, nano-drug delivery, nano-cryosurgery, localized therapy, and bacteriostatic activity, which was investigated in [42]. The impact of viscous dissipation for convection nanofluid flow via vertical surface was observed by many researchers. The nanofluid flow of mixed convection with the presence of different parameters is numerically instigated in [43,44,45,46].

The application of the Lorentz force, a magnetic field, has led to numerous modern applications such as plastic material assembly, glass fiber production, fluid engineering, and disease treatment. Several researchers have discussed the use of the Lorentz force in various domains [47,48,49,50]. For instance, the Coriolis force has been studied in geophysics, astrophysics problems, and centrifugal reactors of bio [48], while its impact on the stretching surface of the nanofluid of Prandtl was analyzed by another researcher [49].

In scientific studies, different types of rotating nanofluids have been analyzed for their properties. One study in [50] looked at the microorganism in rotating nanofluid on the Riga plate using non-Fourier flux of heat and binary chemical reaction. Another study in [51] investigated the importance of Lorentz and Coriolis forces on rotating Boger nanofluid. While [52] researched the rotational nanofluid of Carreau-Yasuda with the Coriolis force, including gyrotactic microorganisms, while [53] analyzed the impact of these forces on the Maxwell nanofluid.

The bivariate spectral quasi-linearization method is very useful for explaining the nonlinear differential equations having two variables. Due to its accuracy and time-consuming nature, researchers are using this for different studies [54, 55].

The above literature assessment shows that very few researchers have studied the combination of microorganisms with Lorentz and Coriolis forces on a vertically placed plate in rotating fluid with the effect of Hall current. This article examined the influence of rotational nanofluid flows with Coriolis and Lorentz force on microorganisms and viscous dissipation on a motile, semi-infinite vertical plate. To solve the governing partial differential equations along with the boundary conditions, we used suitable similarity constraints to transform them into ordinary differential equations. We utilize the Bivariate Spectral Quasi Linearization Method (BSQLM) to solve the improved boundary equations along the momentum, energy, solute, and microbial equations. Moreover, we also analyzed the impact of some other constraints on the assumed model.

2 Mathematical Analysis

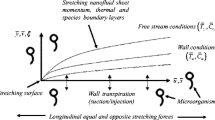
A rotational viscous dissipative nanofluid flow on a vertically placed mobile plate accompanied by the magnetic field and motile microorganism is considered in this investigation. The Coriolis and Lorentz forces generated by applying the strong magnetic field on the vertically placed semi-infinite plate, from the buoyancy forces engendered from the concept of coupled occurrence of heat and species-concentration, into an incompressible, steady, and electrically conducting magneto-hydro-dynamic bio-convective rotational nanofluid.

Figure 1 reflects the physical demonstration of our assumed model; the rectangular coordinates are x, y, and z, while the flow constituents are u, v, and w to the corresponding orders. A semi-infinite vertically placed flat plate is considered for our model at the plane x-z, which traces z by velocity U1 into an electrically conducted, viscous dissipative rotational nanofluid stream, spinning with the uniform angular velocity Ω0 in the y-axis direction incorporated with the oxytaxis microbes. While the persistent flow of free stream U2 is assumed comparable in the z-axis direction, and the strong force field B0 is considered on the plate normally beside the y-axis, and thus, the impact of Hall currents is quite influential since the Reynolds numerals of the magnetic field are tiny, i.e., \({\mu}_0\overline{V}\overline{L}<<1;\) here characteristic length is \(\overline{L}\), characteristic flow is \(\overline{V}\), and magnetic permeability is μ0, as referenced in [27, 56]. The mathematical formulation of our model can be written as follows:

Fig. 1
figure 1

Graphical demonstration of the model

Full size image

The continuity equation

$$\nabla .V=0.$$
(1)

The equation of momentum

$$\left(\mathrm{V}.\nabla \right)V+2{\Omega}_0\times V+\frac{1}{\uprho}\nabla p-\upnu {\nabla}^2V-\frac{1}{\uprho}\left(J\times B\right)-\overline{{\mathrm{g}}_{\mathrm{t}}}\ \upbeta \left(1-{\mathrm{C}}_{\infty}\right)\ \left(\mathrm{T}-{\mathrm{T}}_{\infty}\right)+\frac{\left({\uprho}_{\mathrm{p}}-{\uprho}_{\mathrm{f}}\right)}{\uprho_{\mathrm{f}}}\ \overline{{\mathrm{g}}_{\mathrm{t}}}\ \left(\mathrm{C}-{\mathrm{C}}_{\infty}\right)+\frac{\upgamma\ \overline{{\mathrm{g}}_{\mathrm{t}}}\ \left({\uprho}_{\mathrm{p}}-{\uprho}_{\mathrm{f}}\right)}{\uprho_{\mathrm{f}}}\left(\mathrm{n}-{\mathrm{n}}_{\infty}\right)=0.$$
(2)

The equation of energy

$$\left(\mathrm{V}.\nabla \right)T-{\alpha}_m{\nabla}^2T-\tau \left[{D}_B\nabla \mathrm{T}\nabla \mathrm{C}+\frac{D_T}{T_{\infty }}\nabla \mathrm{T}.\nabla \mathrm{T}+{D}_n\nabla \mathrm{T}\nabla \mathrm{n}\right]-\frac{\nu }{c_p}\left[{\left(\nabla V\right)}^2\right]-\frac{1}{\uprho}\left(J\times B\right)\left({V}^2\right)=0$$
(3)

The equation of mass concentration

$$\left(\mathrm{V}.\nabla \right)C-{D}_B{\nabla}^2C-\frac{{\mathrm{D}}_{\mathrm{T}}}{{\mathrm{T}}_{\infty }}{\nabla}^2T=0$$
(4)

The equation of microorganism concentration

$$\left(\mathrm{V}.\nabla \right)n-\nabla .\left(\frac{\mathrm{b}{\mathrm{w}}_{\mathrm{c}}}{\Delta \mathrm{C}}\left(n\nabla \mathrm{C}\right)\right)-{D}_n{\nabla}^2n-\frac{{\mathrm{D}}_{\mathrm{T}}}{{\mathrm{T}}_{\infty }}{\nabla}^2T=0$$
(5)

Here, the fluids flow vector is represented by V(u, v, w), while the magnetic field implemented on the plate is denoted by B(0, B0, 0).

The induced Hall current is given by a generalized Ohm’s law, as referenced in [17, 27, 47],

$$\mathrm{J}=\frac{\upsigma}{1+{\left(\frac{\upomega}{\upnu_{\mathrm{e}}}\right)}^2}\left[\mathrm{E}+\left(\mathrm{V}\times \mathrm{B}\right)-\frac{\mathrm{J}\times B}{\mathrm{e}{\mathrm{n}}_{\mathrm{e}}}\right]$$
(6)

The stimulating current vector J = (Jx, Jy, Jz), velocity vector V, and ferocity of tense field E, B magnetic-induction, 1/ne Hall factor, N = ω/νe Hall parameter, ne electron number density, νe frequency of electron-atom collision, and ω electron cyclotron. The very large ω/νe affects the electromagnetic field, which affects ions and electrons both for relative drift between these with the neutrals; this is known as ion slip; in addition, it is usually insignificant for highly ionized gasses.

Moreover, the equivalence of Maxwell’s with the Hartmann numeral

$$\nabla \times \mathrm{H}=\mathrm{J};\kern0.5em \nabla \times \mathrm{E}=0;\nabla .\mathrm{B}=0.$$
(7)

Since the electrical field from outside is not included and can be assumed as zero; thus, Eq. (6) can be rewritten as follows, as referenced in [17, 47]:

$$J=\frac{\sigma }{1+{\left(\frac{\omega }{\nu_e}\right)}^2}\left[\left(V\times B\right)-\frac{J\times B}{e{n}_e}\right].$$
(8)

In this investigation, we assumed that the ion slip and pressure of thermo-electric are insignificant with electrical and viscous dissipation of the fluid. The cross flow induced in the z-direction is generated by the Coriolis force. Moreover, there are no changes in the flow, mass, and heat transmission on the assumed semi-infinite vertically placed plate in this direction:

$${J}_x=\frac{\sigma {\mathrm{B}}_0}{1+{\mathrm{N}}^2}\left[\mathrm{Nu}-\mathrm{w}\right];{J}_y=0;\mathrm{and}\ {J}_z=\frac{\sigma {\mathrm{B}}_0}{1+{\mathrm{N}}^2}\left[\mathrm{u}+\mathrm{Nw}\right]\ .$$
(9)

The flow heat, solute, and microbes are considered as persistent on the wall and denoted as Tw, Cw, and nw, and from the wall, which is the free stream, they are denoted as T∞, C∞, and n∞ correspondingly. The Hall currents and Coriolis energy enhance a force toward the y-axis by generating the cross flow in the z-axis. The electromagnetic equations of Maxwell with the spinning flow of our assumed model, as referenced in [24, 47], are transcribed as

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$
(10)
$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+2\Omega_0w=-\frac1\rho\frac{\partial p}{\partial x}+\nu\frac{\partial^2u}{{\partial y}^2}-\frac{\sigma B_0^2}{\rho\left(1+N^2\right)}\left(u+Nw\right)+g_t\;\beta\left(1-C_\infty\right)\left(T-T_\infty\right)-\frac{\left(\rho_{p-}\rho_f\right)}{\rho_f}g_t\left(C-C_\infty\right)-\frac{\gamma\;g_t\left(\rho_p-\rho_f\right)}{\rho_f}\left(n-n_\infty\right).$$
(11)
$$\mathrm{u}\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}-2\Omega u=-\frac{1\ \partial p}{\rho\ \partial z}+v\frac{\partial^2w}{{\partial y}^2}-\frac{\sigma {B}_0^2}{\rho \left(1+{N}^2\right)}\left(w- Nu\right)$$
(12)
$$u\frac{\partial T}{\partial x}+{v}\frac{{\partial T}}{{\partial y}}={\alpha}_m\frac{\partial^2T}{\partial {y}^2}+\tau \left[{D}_B\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial y}\right)}^2+{D}_n\frac{\partial T}{\partial y}\frac{\partial n}{\partial y}\right]+\frac{\nu }{c_p}\left[{\left(\frac{\partial u}{\partial y}\right)}^2+{\left(\frac{\partial w}{\partial y}\right)}^2\right]+\frac{\sigma {\mathrm{B}}_0^2}{\rho \left(1+{\mathrm{N}}^2\right)}\left({u}^2+{w}^2\right)$$
(13)
$${u}\frac{{\partial C}}{{\partial x}}+{w}\frac{{\partial C}}{{\partial z}}={{D}}_{{B}}\frac{\partial^2{C}}{\partial {{z}}^2}+\frac{{{D}}_{{T}}}{{{T}}_{\infty }}\frac{\partial^2{T}}{\partial {{z}}^2},$$
(14)
$${u}\frac{{\partial n}}{{\partial x}}+{w}\frac{{\partial n}}{{\partial z}}+\frac{{b}{{W}}_{{c}}}{\Delta {C}}\frac{\partial }{{\partial z}}\left({n}\frac{{\partial n}}{{\partial z}}\right)={{D}}_{{n}}\frac{\partial^2{n}}{\partial {{z}}^2},$$
(15)

The Coriolis and Lorentz forces are considered for balancing the pressure in the fluid toward the y and x axes, −ρ−1ρz and −ρ−1ρx, respectively, and are written as

$$-\frac{1}{\rho}\frac{\partial p}{\partial x}=2{\varOmega}_0{U}_2+\frac{\sigma {B}_0^2}{\rho \left(1+{N}^2\right)}N{U}_2,-\frac{1}{\rho}\frac{\partial p}{\partial z}=\frac{\sigma {B}_0^2}{\rho \left(1+{N}^2\right)}{U}_2$$
(16)

The borderline conditions for Eqs. (10)–(15) are given as

$$u\left(x,0\right)=0,v\left(x,0\right)=0,w\left(x,0\right)={U}_1,$$

T = Tw, C = Cw,   n = nw at y = 0,

$$w=U_2,u,v=0,T=T_\infty,C=C_\infty,n=n_\infty,as\quad y\rightarrow\infty.$$
(17)

Here, base fluid density is denoted by ρ, kinematic viscosity is υ, fluid’s electrical conductivity is σ, the gravitational acceleration by gt, Hall parameter is N, expansion of volumetric coefficient by β, the nanoparticles density is ρp and nanofluid density is ρf, microbes density is ρm, microbes average volume by γ, microbes thermal diffusivity by αm, τ is the heat capacitance for nanoparticles to the base fluid ratio, the thermophoretic diffusion by DT, solutal Brownian diffusion quantity is DB, microorganism Brownian diffusion by Dn, the extreme cell spinning rapidity (bWc is considered to be uniform) by wc, and chemotaxis constant by b.

3 Transformation of Equations

To transform the assumed system of equations of our model specified in Eqs. (10)–(15), subsequent similarity transformations are considered:

$$\eta =y\sqrt{\frac{U_0}{\upsilon x}},\psi =\sqrt{U_0\upsilon x}f\left(\xi, \eta \right),\xi =\frac{\varOmega x}{U_0},$$
$$w={U}_0g\left(\xi, \eta \right),{U}_0={U}_1+{U}_2,\kern0.75em S=\frac{U_1}{U_0},$$
$$\theta \left(\xi, \eta \right)=\frac{T-{T}_{\infty }}{T_w-{T}_{\infty }},\phi \left(\xi, \eta \right)=\frac{C-{C}_{\infty }}{C_w-{C}_{\infty }},\chi \left(\xi, \eta \right)=\frac{n-{n}_{\infty }}{n_w-{n}_{\infty }}$$
(18)

The flow constituents \(u=\frac{\partial \psi }{\partial z}\) and \(w=-\frac{\partial \psi }{\partial x}\) and \(v=-\frac{\partial \psi }{\partial x}\) are given as

$$u={U}_0{f}^{\prime}\left(\xi, \eta \right),v=-\sqrt{\frac{\upsilon \varOmega}{\xi }}\left[\xi \frac{\partial f}{\partial \xi }+f-\frac{1}{2}{\eta f}^{\prime}\right],$$
(19)

Equations (11)–(15), with the help of Eqs. (16), (18)–(19), considering borderline conditions from Eq. (17), are renovated into the subsequent boundary value problem:

$${f}^{\prime \prime \prime }+f{f}^{\prime \prime }-{f^{\prime}}^2-2\xi g+2\xi \left(1-S\right)-\frac{M}{1+{N}^2}\xi \left({f}^{\prime }-N+ NS+ Ng\right)+\frac{Gr}{{\mathit{\operatorname{Re}}}^2}\xi \left(\theta - Nr\varphi - Rb\chi \right)-\xi \left({f}^{\prime}\frac{\partial {f}^{\prime }}{\partial \xi }-{f}^{\prime \prime}\frac{\partial f}{\partial \xi}\right)=0.$$
(20)
$${g}^{\prime \prime }+f{g}^{\prime }-g{f}^{\prime }+2\xi {f}^{\prime }-\frac{M}{1+{N}^2}\xi \left[g+S-N{f}^{\prime }-1\right]-\xi \left({f}^{\prime}\frac{\partial g}{\partial \xi }-{g}^{\prime}\frac{\partial f}{\partial \xi}\right)=0$$
(21)
$$\theta''+Pr\;f\;\theta'+Pr\left(Nb\theta'\varphi'+Nt\theta'^2+Nt\theta'\chi'\right)+PrEc\left(f''^2+g'^2\right)+\frac M{1+N^2}PrEc\xi\left(f'^2+g^2\right)-Pr\;\xi\left(f'\frac{\partial\theta}{\partial\xi}-\theta'\frac{\partial f}{\partial\xi}\right)=0$$
(22)
$$\varphi''+Scf\;\varphi'+\frac{Nt}{Nb}\theta''-Sc\xi\left(f'\frac{\partial\varphi}{\partial\xi}-\varphi'\frac{\partial f}{\partial\xi}\right)=0$$
(23)
$$\chi''+Sbf\;\chi'-Pb\left[\chi'\varphi'+\left(\tau_0+\chi\right)\varphi''\right]+\frac{Nt}{Np}\theta''-Sb\xi\left(f'\frac{\partial\chi}{\partial\xi}-\chi'\frac{\partial f}{\partial\xi}\right)=0$$
(24)

Here, the primes are the differentiation w. r. to η. The transformed boundary conditions of the corresponding borderline situations (7) are

$$\begin{array}{cc}f'\left(\xi,\infty\right)\rightarrow0,\;f'\left(\xi,0\right)=0,&f\left(\xi,0\right)=0,\\g\left(\xi,0\right)=S,&g\left(\xi,\infty\right)=1-S,\\\theta\left(\xi,\infty\right)\rightarrow0,&\theta\left(\xi,0\right)=1,\\\varphi\left(\xi,\infty\right)\rightarrow0,&\varphi\left(\xi,0\right)=1,\\\chi\left(\xi,\infty\right)\rightarrow0,&\chi\left(\xi,0\right)=1.\end{array}$$
(25)

The parameters defined in the associated equations with borderline conditions are as follows.

Here, the modified Hartmann number \(M=\frac{\sigma {B}_0^2}{\rho \varOmega}\), the Grashof number \(Gr=\frac{\left(1-{C}_{\infty}\right){\mathrm{g}}_{\mathrm{t}}\beta \left({T}_w-{T}_{\infty}\right)}{U_0\varOmega }\), \(\mathit{\operatorname{Re}}=\frac{{\mathrm{U}}_0\ \mathrm{x}}{\upupsilon}\), Reynolds number, ξ is the rotational parameter, the buoyancy ratio parameter \(Nr=\frac{\left({\rho}_p-{\rho}_f\right)\left({C}_w-{C}_{\infty}\right)}{\left(1-{C}_{\infty}\right)\rho \beta \left({T}_w-{T}_{\infty}\right)}\), the bio-convection Rayleigh number\(Rb=\frac{\gamma \left({\rho}_m-{\rho}_f\right)\left({n}_w-{n}_{\infty}\right)}{\beta {\rho}_f\rho {f}_{\infty}\left(1-{C}_{\infty}\right)\left({T}_w-{T}_{\infty}\right)}\), the Schmidt number \(Sc=\frac{\upsilon }{D_B}\), the Brownian motion parameter \(Nb=\frac{\tau {D}_B\left({C}_w-{C}_{\infty}\right)}{\nu }\), the Prandtl number\(\mathit{\Pr}=\frac{\upsilon }{\alpha }\), the bio-convection Brownian motion parameter \(Np=\frac{\tau {D}_n\left({n}_w-{n}_{\infty}\right)}{\nu }\), the thermophoresis parameter \(Nt=\frac{\tau {D}_T\left({T}_w-{T}_{\infty}\right)}{\nu {T}_{\infty }}\), the bio-convection Schmidt number \(Sb=\frac{\upsilon }{D_n}\), the constant microorganisms concentration difference parameter is \({\tau}_0=\frac{n_{\infty }}{n_w-{n}_{\infty }}\), the Reynolds number \({\mathit{\operatorname{Re}}}_x=\frac{U_0x}{\upsilon }\), and the velocity ratio \(S=\frac{U_1}{U_0}\), bio-convection Peclet number \(Pb=\frac{b{w}_c}{D_n}\).

4 Coefficients of Heat Mass and Momentum

The coefficients of local skin friction toward the horizontal and free stream directions are

$$ {C}_{fx}=\frac{\tau_{wx}}{\frac{1}{2}\rho {U_0}^2}=2{\left({\mathit{\operatorname{Re}}}_x\right)}^{-\frac{1}{2}}{f}^{\prime \prime}\left(\xi, 0\right),\kern0.75em \textrm{where}\ {\tau}_{wx}=\mu {\left.\frac{\partial u}{\partial y}\right|}_{y=0}\ \textrm{and}\ {C}_{fy}=\frac{\tau_{wy}}{\frac{1}{2}\rho {U}_0^2}=2{\left({\mathit{\operatorname{Re}}}_y\right)}^{-\frac{1}{2}}{g}^{\prime}\left(\xi, 0\right),\kern0.5em \textrm{where}\ {\tau}_{wz}=\mu {\left.\frac{\partial w}{\partial y}\right|}_{y=0} $$
(26)

The local Nusselt quantity, Sherwood quantity, and motile microbe’s density numeral are

$$N{u}_x=\frac{x{q}_w}{\kappa \left({T}_w-{T}_{\infty}\right)}=-{\mathit{\operatorname{Re}}}_x^{\frac{1}{2}}{\theta}^{\prime}\left(\xi, 0\right),\mathrm{where}\ {q}_w=-\kappa {\left.\frac{\partial T}{\partial y}\right|}_{y=0},$$
(27)
$$S{h}_x=\frac{x{q}_w}{D_B\left({C}_w-{C}_{\infty}\right)}=-{\mathit{\operatorname{Re}}}_x^{\frac{1}{2}}{\varphi}^{\prime}\left(\xi, 0\right),\mathrm{where}\ {q}_m=-{D}_B{\left.\frac{\partial C}{\partial y}\right|}_{y=0},$$
(28)
$$N{n}_x=\frac{x{q}_n}{D_n\left({n}_w-{n}_{\infty}\right)}=-{\mathit{\operatorname{Re}}}_x^{\frac{1}{2}}{\chi}^{\prime}\left(\xi, 0\right),\mathrm{where}\ {q}_n=-{D}_n{\left.\frac{\partial n}{\partial y}\right|}_{y=0}.$$
(29)

5 Method of Solution

The Bivariate Spectral Quasi Linearization scheme (BSQLM) was deployed to resolve our assumed modeled nonlinear boundary value problem of two variables specified in Eqs. (20)–(24) and borderline Eq. (25). This method minimizes the computational time and maximizes the results’ accuracy compared to the methods discussed in [45, 46]). The domain of the stream and phases taken by ξ ∈ [0, Lt] and η ϵ [0, Lx] was renovated to t ∈ [−1, 1] and x ϵ [−1, 1] consuming the linear conversions η ϵ Lx(x + 1)/2 and ξ ϵ Lt(x + 1)/2, respectively.

The polynomial of the Lagrange interpolation was used to approximate the solution:

$$\mathrm{u}\left(\mathrm{x},\mathrm{t}\right)=\sum\nolimits_{\mathrm{i}=0}^{{\mathrm{N}}_{\mathrm{x}}}\sum\nolimits_{\mathrm{j}=0}^{{\mathrm{N}}_{\mathrm{t}}}\hat{\mathrm{u}}\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{t}}_{\mathrm{j}}\right){\mathrm{L}}_{\mathrm{i}}\left(\mathrm{x}\right){\mathrm{L}}_{\mathrm{j}}\left(\mathrm{t}\right),.$$
(30)

Here, toward the x and t lines, we interpolated u(x,t) in particular grid points, which are

$$\left\{{\mathrm{x}}_{\mathrm{i}}\right\}={\left\{\cos \left(\frac{\uppi \mathrm{i}}{{\mathrm{N}}_{\mathrm{x}}}\right)\right\}}_0^{{\mathrm{N}}_{\mathrm{x}}},\left\{{\mathrm{t}}_{\mathrm{j}}\right\}={\left\{\cos \left(\frac{\uppi \mathrm{j}}{{\mathrm{N}}_{\mathrm{t}}}\right)\right\}}_0^{{\mathrm{N}}_{\mathrm{t}}}.$$
(31)

The polynomials of Lagrange cardinal functions Li(x) are

$${\mathrm{L}}_{\mathrm{i}}\left(\mathrm{x}\right)=\prod\nolimits_{\mathrm{i}=0,\mathrm{i}\ne \mathrm{j}}^{{\mathrm{N}}_{\mathrm{x}}}\frac{\mathrm{x}-{\mathrm{x}}_{\mathrm{k}}}{{\mathrm{x}}_{\mathrm{i}}-{\mathrm{x}}_{\mathrm{k}}},$$
(32)

where

$${\mathrm{L}}_{\mathrm{i}}\left(\mathrm{x}\right)={\updelta}_{\mathrm{i}\mathrm{k}}=\left\{\begin{array}{c}0,\mathrm{if x}\ne \mathrm{k}\\ {}1,\mathrm{if x}=\mathrm{k}.\end{array}\right..$$
(33)

6 Convergence Analysis

The accuracy of the assumed model was confirmed by the graphical representation of the error graph. The convergence and accuracy were numerically analyzed and reflected by the graph. The graph consists of the residual errors norm on the y-axis and the number of iterations on the x-axis. For the flow velocity of primary and secondary variables, the residual error norms are under 10−11 after 8 repetitions, while the other variables like thermal, solute, and microbial are less than 10−10 after 8 iterations.

The error graph results show that for solving the borderline value problem, BSQLM is an appropriate scheme. Figure 2 demonstrates the residual error norm for existing variables of the model at a diverse number of repetitions.

Fig. 2
figure 2

Residual norm iterations on variation

Full size image

The collocation points of our model are represented in Fig. 3 for the principal and subordinate flow, heat, solute, and microorganism outlines.

Fig. 3
figure 3

Collocation points of (a) principal velocity, (b) subordinate velocity, (c) heat profile, (d) concentration profile, and (e) microbial contour

Full size image

7 Discussion for the Results

This segment explains the details of our assumed model and the comparison with the related model. This numerically solved set of ODEs derived from the energy, momentum, solutal, accompanied microbial Eqs. (20)–(24), and subjected to the borderline conditions Eq. (25) were analyzed by bivariate quasi-linearization function using MATLAB. We analyzed the results using a bivariate quasi-linearization technique and obtained graphs that show the flow velocity, temperature, concentration, and microbial behavior under various conditions. The outcomes are presented in graphical form for easy understanding.

7.1 Impact of Velocity Fraction Parameter (S)

Here, in Fig 4, we can see that for different values of S, the principal flow and subordinate flow accompanied by temperature profile decrease. The concentration profile of the microbial profile decreases for the growing values of the velocity fraction parameter. The buoyancy forces affect the fluid velocity at the boundary layer. The principal flow is rapidity decreases for higher S, while the subordinate flow was initially enhanced in the range of 0 ≤ η ≤ 0.5, but then the subordinate swiftness decreases for the range of η ≥ 0.5. Thermal buoyancy affects temperature, and concentration buoyancy affects solute and microbial profiles.

Fig. 4
figure 4

Influence of S on (a) principal velocity and (b) subordinate velocity. Repercussion of S on (c) heat profile, (d) concentration profile, and (e) microbial contour

Full size image

7.2 Impact of Hartmann Number (M)

The impact of the Hartmann number was graphically analyzed in Fig. 5 for different profiles. The dimensionless parameter Hartmann number is the quotient of viscous strength to electromagnetic force. For the growing Hartmann parameter, the primary flow decreases initially for the range of 0 ≤ η ≤ 3 while an increase at the boundary layer for the range of η ≥ 3 of the fluid.

Fig. 5
figure 5

Influence of M on (a) principal flow and (b) subordinate flow. Impact of Hartmann number on (c) heat profile and (b) solute profile. (e) Influence of Hartmann number on microorganisms profile

Full size image

The subordinate flow increases initially for the range of 0 ≤ η ≤ 2 but declines at the borderline layer for the growing Hartmann number layer for the range of η ≥ 2 of the fluid. The enhanced Lorentz force reverses the stream in a frictional drag. The increasing values of the Hartmann number increase the heat profile, while the reverse impact was analyzed for the solute and microbial profile by decreasing.

7.3 Impact of Hall Current (N)

The impact of Hall current affected by the electromagnetic field reflected on various profiles consists in Fig. 6. The increasing values of Hall current N increase the principal flow in the range of 0 ≤ η ≤ 3 and then decrease at the boundary layer for the range of η ≥ 3 of the fluid, while the subordinate flow initially decreases flow in the range of 0 ≤ η ≤ 1 after that start increases at the boundary layer for the range of η ≥ 1 of the fluid. However, the heat profile decreases, while the concentration in addition to the microbial concentration profile increases for the greater Hall current parameter.

Fig. 6
figure 6

Influence of Hall current on (a) principal flow, (b) subordinate flow, (c) heat profile, (d) solute profile, and (e) microorganisms profile

Full size image

7.4 Impact of Grashof Number (Gr)

The impacts of the Grashof number on the principal and subordinate flow, followed by other profiles, are graphically represented in Fig. 7. The Grashof number represents the ratio of buoyant forces to viscous forces. It is used to determine the flow regime of fluid boundary layers. The enhancement of the Gr parameter enhances the principal flow, subordinate flow, solute, and microorganism concentration of the nanofluid while discriminating the temperature outline of the nanofluid.

Fig. 7
figure 7

Influence of Gr on (a) principal flow, (b) subordinate flow, (c) heat profile, (d) solute profile, and (e) microorganisms profile

Full size image

7.5 Impact of Eckert Number (Ec)

The impact of Eckert quantity Ec on the temperature, solutal, and microbial outlines is graphically represented in Fig. 8. The Eckert number causes the (viscous) dissipation of energy in low-speed flow when combined with the Prandtl number. The enhancement of the parameter discriminates the concentration and microorganism concentration outline of the nanofluid while improving the temperature profile.

Fig. 8
figure 8

Influence of Eckert number on (a) heat profile, (b) solute profile, and (c) microbial profile

Full size image

7.6 Impact of Buoyancy Ratio Parameter (Nr)

The repercussion of the buoyancy ratio parameter Nr is graphically studied in Fig. 9. The influence of forced and free convection was measured by the buoyancy ratio parameter. When an external operation is used to maintain or generate the flow, it is known as forced convection, while when the flow is generated because of its internal gradients, like temperature, then it is known as free convection. The enhancement of the parameter increases the principal and subordinate flows accompanied by concentration as well as the microbial concentration of the nanofluid while declining the temperature outline.

Fig. 9
figure 9

Influence of Nr on (a) principal flow, (b) subordinate flow, (c) temperature profile, (d) concentration profile, and (e) microorganisms concentration

Full size image

7.7 Impact of Microorganism Brownian Motion Parameter (Np)

The impression of microorganism Brownian motion parameter Np on heat, concentration, and microorganism concentrations was graphically represented in Fig. 10. The Brownian motion parameter with the swimming microorganism affects the usual flow of the fluid. For greater values of Np, it discriminates the heat profile while the concentration and microorganism concentration of the profile are enhanced.

Fig. 10
figure 10

Influence of Np on (a) temperature profile, (b) solute profile, and (c) microbial profile

Full size image

7.8 Impact of Schmidt Number (Sc)

The impressions of Sc Schmidt quantity for the concentration as well as the microbial concentration of the fluid are graphically represented in Fig. 11. This is the ratio of kinematic viscosity (momentum diffusivity) to mass diffusivity, used to characterize fluid flows involving simultaneous momentum, mass diffusion, and convection processes. The improvement of the constraint declines the concentration with microbial concentration profile.

Fig. 11
figure 11

Influence of Sc on (a) solute profile and (b) microbial profile

Full size image

7.9 Impact of Bio-convection Peclet Number (Pb)

The significance of the bio-convection Peclet quantity Pb on the outline of microorganism concentration of the liquefied was graphically represented in Fig. 12. This is a dimensionless quantity used to indicate the relative significance of convection and diffusion in a flow system. It is defined as the ratio of diffusive transport to convective transport (advection). Considering the motion of microbes and their diffusion ratio, the bio-convection Peclet number is determined. The escalation of the parameter discriminates the microbe concentration of the fluid.

Fig. 12
figure 12

Influence of Pb on microbial profile

Full size image

7.10 Impact of Bio-convection Schmidt Number (Sb)

The impression of the bio-convection Schmidt quantity Sb on the outline of microorganism concentration of the liquefied was graphically represented in Fig. 13. The parameter increase decreases thermal borderline thickness, increasing Nusselt number and fluid heat profile. The escalation of the parameter discriminates the microbe concentration of the fluid.

Fig. 13
figure 13

Influence of Sb on microbial profile

Full size image

7.11 Impact of Prandtl Number (Pr)

The impressions of the Prandtl number Pr on heat, concentration, and microorganism concentrations were graphically represented in Fig. 14. An increase in the Prandtl number results in a reduction of the thermal boundary layer thickness. The Prandtl number represents the ratio of momentum diffusivity to thermal diffusivity. In heat transfer problems, the Prandtl number governs the relative thickening of the momentum and thermal boundary layers. For greater values of Pr, it enhances the heat profile while concentration and microorganism concentration of the profile discriminate.

Fig. 14
figure 14

Influence of Pr on (a) temperature profile, (b) solute profile, and (c) microbial profile

Full size image

7.12 Impact of Reynolds Number (Re)

Figure 15 reflects that the increasing values of Reynolds numeral Re increase the principal and subordinate flow accompanied by solute as well as microbial outline; however, the heat outline decreases. The high concentration of nanoparticles in nanofluids results in a decrease in velocity and temperature profiles. However, as the fluids come closer to the boundary layer, the increase in Reynolds number leads to an increase in the intermittency of the turbulent fluids, which, in turn, increases the solute and microbial profiles of the fluid.

Fig. 15
figure 15

Influence of Re on (a) principal flow, (b) subordinate flow, (c) heat profile, (d) solute profile, and (e) microorganisms profile

Full size image

7.13 Comparison of Graph/Table

The graphical comparison between our model and the reference paper is shown in Fig. 16, confirming our model’s validity.

Fig. 16
figure 16

Comparison graph for the principal velocity profile

Full size image

Table 1 presents numerical representative values of the skin friction coefficient, Sherwood number, and microbial density number for variations in different engineering parameters’ rotational viscous dissipation. Skin friction drag represents the force per unit area acting tangentially to the solid surface. In this case, the skin friction drag increases for different values of engineering parameters. We observed overall increases in the Sherwood number and microbial density at the boundary layer thickness for different parameters.

Table 1 Numerical values of the Nusselt number, Sherwood number, and microbial for different values of engineering parameters
Full size table

8 Conclusion

This rotational viscous dissipative nanofluid flow on a vertically placed mobile plate accompanied by the magnetic field and motile microorganism was considered for this study. The Coriolis and Lorentz forces generated by applying the strong magnetic field on the vertically placed semi-infinite plate, from the buoyancy forces engendered from the concept of coupled occurrence of heat and species-concentration, into an incompressible, steady, and electrically conducting magneto-hydro-dynamic bio-convective rotational nanofluid. The significance of the diverse constraints for the primary and subordinate flow, temperature, solute, and microbe profiles is examined explicitly plus reflected in the encouraging outcomes. The consequences we established in our investigation are summarized as follows.

  • The higher value of the wall velocity discriminates the flows in both directions.

  • The rise in the Reynolds numbers enhances the heat and discriminates the others.

  • Enhancement of the bio-convection Schmidt quantity decreases the microbial outline of the liquefied.

  • Enhancement of the bio-convection Peclet numeral decreases the microorganism concentration of the fluid.

  • Enrichment of the buoyancy ratio constraint enhances the microbial outline of the fluid.

  • Enrichment of the bio-convection Brownian motion constraint decreases the microbe outline of the fluid.

  • Advancement of the Schmidt numeral accompanied by the Eckert numeral decreases the concentration of the fluid, while Eckert quantity improves the temperature outline.

  • The uptrend of the Hall quantity enhances the concentration as well as microorganism concentration while decreasing the temperature outline of the fluid.

Funding Statement

None.