Introduction

During the late 20th Century, due to augmentation of anthropogenic activities, there is a gradual surge of greenhouse gas emission (Sachindra et al. 2016). It is a common understanding that global warming and greenhouse gas emission will act as a catalyst to facilitate frequent occurrence of extreme climatic events (Crowley 2000; Sachindra et al. 2016). Intergovernmental Panel on Climate Change (IPCC) (IPCC 2012) reported that increased greenhouse gases in the atmosphere has contributed to change the patterns of rainfall. Large scale-climate drivers, initial weather conditions, regional effects and stochastic process further aggravate the processes of extreme events (Sillmann et al. 2017). Consequently, several studies (Mekanik et al. 2013; Yilmaz et al. 2014; Hossain et al. 2018a, b, 2020a) carried out analysis to identify climate change effects on rainfall using linear (multiple linear regression) and non-linear (artificial neural network, non-linear regression) models. Seasonal rainfall forecasting techniques using the influential climatic variables, e.g. ENSO, IOD were the focus of the above stated studies. Nevertheless, it was identified that linear and non-linear modelling approaches are not effectual to forecast the actual behaviour of the extreme rainfall (Hossain et al. 2020a, b). On the other hand, it is well established that the frequency and occurrence of extreme climatic events are changing globally (Fischer and Knutti 2015; Pereira et al. 2018).

Due to widespread global warming scenarios throughout the world in recent years, the changes in the extreme climatic events are evident in different parts of Australia followed by their changed frequency and occurrence. For example, Melbourne observed an incessant eleven-year drought period with cumulative rainfall continuing to be significantly below average (Khastagir and Jayasuriya 2010). Due to the continuous accumulation of carbon di-oxide in the environment, the pace of climate change is aggravated (Cox et al. 2000). As a result, considerable changes in the frequency and occurrence of extreme rainfall are expected to increase in near future (Bryson Bates 2015).

In Australian context, extreme rainfall is more common in the island state Tasmania. Although the average rainfall in some cities of Tasmania is 775 mm, the minimum rainfall could be only 31 mm per month in the summer months. Increased flood risk associated with extreme rainfall event is causing substantial losses in properties and human lives in different parts of Tasmania. Therefore, it is intrinsic to accurately predict the frequency and magnitude of extreme rainfall to prepare our future society.

The climatic system in the earth is made up of regions where the response to energy balance is different. The dynamics of each region are controlled by the local physical–chemical boundary conditions. Therefore, regional physical–chemical-biological process dictate the intrinsic patterns of climatic variability (Loubere 2012). Consequently, several climatic modes have significant influence on the variability of extreme climatic events, e.g., extreme rainfall. Nevertheless, the uneven distribution of worldwide rainfall has already been observed in many parts of the world. For example, Kumar et al. (2020) noted that there will be significant variation in the distribution of projected extreme rainfall in Bihar, India. As a result, the productivity of crops in the arid and semi-arid regions have declined inferring increased uncertainty. Ghorbani et al. (2021) observed declining rainfall trend in the central part and increasing rainfall trend in northern and southern part of Algeria. Lai and Dzombak (2019) observed significantly different extreme rainfall in the US cities. They further noted investigated that cities within the same climatic region has the potential to encounter substantially different extreme rainfall. Therefore, the importance of regional analysis is underlined by many research studies around the world in extreme climatic event study.

Extreme rainfall is generally analysed to determine flood magnitude of specified return periods for the scarce record of gauged streamflow data regions (Cannon and Innocenti 2019). Although, it is intricate to predict the historical increase in extreme rainfall due to natural variability, uncertainties in the measurement and long-term records, the observation from the large regions and climatic model’s simulation are consistent with thermodynamically driven increased extreme rainfall in near future (Min et al. 2011; Westra et al. 2012; Pfahl et al. 2017). Therefore, study on the extreme rainfall analysis and forecasting is a matter of great concern throughout the world (Ávila et al. 2019). For the prediction of flood values from extreme rainfall, extreme value statistics are generally interest to the hydrologists and water resources engineers (Towler et al. 2010). The extreme value statistics projects the occurrence of future extreme rainfall through frequency analysis of the previous data (El Adlouni et al. 2007).

Frequency analysis is carried out for a series of previous observations to fit statistical probability distributions (Khaliq and Ouarda 2007). As for example, Log Pearson Type III (LPIII) distribution is recommended as a suitable general distribution for extreme value analysis as detailed in flood (McMahon and Srikanthan 1981) and fire (Khastagir 2018) frequency analyses in Australia. Although, several probability distribution functions can be used for the frequency analysis of extreme rainfall, the generalised extreme value (GEV) distribution is commonly used in extreme rainfall analysis. The GEV is statistical distribution of three parameters (location, scale, and shape). Although different methods of the GEV parameters estimation techniques are available in literature, no specific guideline was found to adopt suitable technique. However, selection of parameters estimation technique can significantly influence the return levels estimation of extreme rainfall (Lazoglou et al. 2019; Hossain et al. 2021a; Khastagir et al. 2021).

In this study, evaluation of different parameters estimation techniques of the GEV distribution was performed. Frequency analysis of Tasmanian extreme rainfall (monthly maximum from daily rainfall) were used to estimate the parameters of the GEV distribution. As higher number of GEV models that may arise from non-stationary consideration has the potential to decrease the performance of GEV selection criteria (Xavier et al. 2019), the analysis of this paper was performed considering that the rainfall pattern is stationary. The main objective of this study was to identify the most appropriate parameter estimation technique for GEV statistics. The results obtained from this study will significantly contribute to identify the most appropriate parameter estimation technique of the GEV distribution, which is commonly used for extreme rainfall analysis.

Data collection and study area

Tasmania is the island state of Australia, which is located around 240 km south from the mainland state Victoria. Average elevation of the state 104 m above the mean sea level. The climate of the state varies greatly comparing with the other parts of Australia. There is rainfall in all season in Tasmania with mild to warm summer and mild winter because of southerly marine air masses. The annual rainfall around the state is highly variable ranges from 510 to 2500 mm. There is also remarkable variation in the summer rainfall from year to year.

Wide geographic and terrestrial variation in biodiversity make Tasmania a unique heritage region in the world. However, the climate change trends of the state are coherent with the worldwide trend leading to extreme climatic events (such as extreme rainfall, drought, bushfire) (DPI 2010). Like other parts of the world, several large-scale climatic modes are significantly affecting the Tasmanian extreme rainfall (Hill et al. 2009). Therefore, study on Tasmanian extreme rainfall has the potential to reflect the global context.

From 1996 to 2009, much of the south Australian region including Tasmania experienced a persistent dry period. The long-term average rainfall declined significantly with more severity in the densely populated area, especially in all the southern cropping zone of Australia. However, significant amount of rainwater is required to maintain balance growth of Australian crops (Hossain et al. 2021b). The periodic dry episode is considered as the millennium drought in Australia.

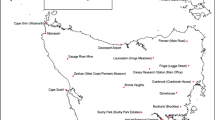
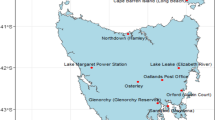
In this study, daily rainfall data from selected 20 rainfall stations spearing all around Tasmania were collected and analysed. Figure 1 delineates the locations of the rainguage stations considered in this study. The daily rainfall data for the selected 20 rainfall stations from 1965 to 2018 was collected using SILO database, which is the Queensland Government database. Missing data filling was carried out using the data from Bureau of Meteorology (BoM) and incorporated in the SILO database.

Fig. 1
figure 1

Location of rainguage stations considered in this study

Full size image

Detailed information of the rainfall stations is shown in Table 1. The selection of rainguage stations is based on the following criteria:

  • Adequate distribution of stations across Tasmania to represent all climatic conditions.

  • Availability of rainfall data at a station.

  • Number of years of data available.

Table 1 Details of the meteorological stations used to estimation the GEV parameters
Full size table

Methodology

As mentioned earlier, historical daily rainfall data from SILO database were analysed using the extreme value theory. Monthly maximum rainfall was extracted from the collected daily data. As the removal of outliers have the potential to change the variance and the analysis may produce biased result, it is important to note that outliers of the rainfall data were not removed in this analysis. However, assessment of the variation in the extreme data sets, homogeneity was performed using the Buishand’s range test. The adjusted partial sum in the Buishand range test can be represented according to Eq. 1 (Buishand 1982).

$${S}_{k}^{*}=\sum_{i=1}^{n}\left({Y}_{i}-\overline{Y }\right)$$
(1)

where \({Y}_{i}\) is the extremely rainfall for the \(i{\text{th}}\) time step, \(\overline{Y }\) is the average of extreme rainfall data series and is the number of observations. The re-scaled adjusted range (R) factor is then measured to estimate \(R/\sqrt{n}\) to compare with critical values Of Buishand (Buishand 1982). The magnitude of R is estimated from the difference between the maximum and minimum value of \({S}_{k}^{*}\).

Asymptotic extreme value models are generally fitted to identify the extremal behaviour of the climatic events especially for short series of data. It was evidenced from the observations that the daily extreme rainfall follows extreme value distribution with heavy upper tail (Papalexiou and Koutsoyiannis 2013). Therefore, three parameters GEV distribution has been widely applied to describe the characteristics of extreme climatic events, e.g. rainfall, floods, wind speed, snow depth, wave heights and other maxima. The mathematical application of the GEV distribution is also very attractive in extreme events characterisation (Hosking 1990).

Extreme value distribution

In this study, the GEV distribution was used for the frequency analysis of Tasmanian extreme rainfall. The GEV distribution is suggested for the extreme data generated using the block-maxima approach (Park et al. 2011). Since our extreme rainfall data were generated using block-maxima approach (monthly maximum from daily record), the GEV distribution was used in this study. The cumulative distribution function of the GEV distribution can be found in most of the recently conducted extreme data analysis research. The function has been re-written here according to Eq. 2:

$$G\left(Y;\theta \right)=exp\left\{-{\left[1+\xi \left(\frac{Y-\mu }{\sigma }\right)\right]}^{-1/\xi }\right\}$$
(2)

where Y represents the extreme rainfall data (in this case monthly maximum daily rainfall) and \(\theta \left(\mu , \sigma , \xi \right)\) represents the parameters of the GEV distribution.

The physical origin of the extreme events suggests that their distribution follow in any of the three extreme value types (types I, II and III) (Martins and Stedinger 2000). The GEV distribution has three types of parameters: location \(\left(\mu \right)\), scale \(\left(\sigma \right)\) and shape \(\left(\xi \right)\). Depending on the values of the parameters, the distribution can follow either Gumbel, or Fréchet or Weibull type GEV (Park et al. 2011). For the shape parameter ξ = 0, the distribution becomes Gumbel (type I) class of normal, log-normal, gamma or exponential distribution. The positive shape parameter \(\left(\xi >0\right)\) produces Fréchet (type II) distribution and negative shape parameter \(\left(\xi <0\right)\) produce Weibull (type III) distribution.

Parameters estimation

The common problem in the application of statistical distribution is the estimation of the unknown parameters (Hosking 1990). The support of the GEV distribution shown in Eq. 1 depends on the appropriate estimation of its parameters. There are different techniques available to estimate of the parameters of the GEV distribution. Stationary vs non-stationary rainfall is still debatable. For example, Yilmaz et al. (2014), Yilmaz and Perera (2014) could not detect the presence of non-stationarity in the extreme rainfall analysis in Melbourne. Therefore, this study was performed considering the stationary behaviour of extreme rainfall data. However, the parameters of the GEV statistics can be modified to incorporate the non-stationarity of rainfall data (Coles 2001; Towler et al. 2010). In this research, the parameters of the GEV distribution were estimated using four different methods: MLE, GMLE, Bayesian and L-moments.

The maximum likelihood estimation (MLE) method

The maximum likelihood estimation (MLE) is a powerful approach to estimate the parameters of the GEV distribution where data length are relatively short (Coles and Dixon 1999). Therefore, the method has been used in several studies (Towler et al. 2010) in estimating the parameters of the non-stationary GEV models. The values of the parameters \(\left(\mu , \sigma , \xi \right)\) that maximises the likelihood function are the estimated parameters. In practice, the MLE is expressed as the log likelihood \(\left(L\right)\) function of the GEV distribution as shown in Eq. 3.

$$L\left( \theta ;{y}_{i}\right)=\sum_{i=1}^{N}log\left\{G\left(\theta ;{y}_{i}\right)\right\}$$
(3)

The log likelihood function of the Eq. 2 can be expanded according to Eq. 4 as follows (Yoon et al. 2010).

$$log\left[L\left(\theta ;{y}_{i}\right)\right]=-N\times log\left(\sigma \right)-\left(1+\frac{1}{\xi }\right)\sum_{i=1}^{N}log\left({x}_{i}\right)-\sum_{i=1}^{N}{\left({x}_{i}\right)}^{-1/\xi }$$
(4)

where \(\theta =\left(\mu , \sigma , \xi \right)\) and \({x}_{i}=\left[1+\xi \left(\frac{{y}_{i}-\mu }{\sigma }\right)\right]\).

The partial derivatives of the log-likelihood functions can be solved to estimate the parameters of the GEV distribution. The negative log likelihood function also can be minimised to find out the parameters using MLE method (Katz 2013). The negative log likelihood functions are minimised with respect to three parameters: location, scale, and shape parameters. However, the method is computationally intensive (Nakajima et al. 2012). Moreover, the method underestimates the negative value of the shape parameter for small or moderate sample size (Park 2005).

The generalised maximum likelihood estimation (GMLE) method

To overcome the limitation of the MLE method for small or moderate sample size, the generalised maximum likelihood (GMLE) method was developed (Park 2005). The method has been developed based on the MLE method. The method included an additional constraint of the shape parameters to eliminate the invalid results that may be produced in MLE method. The method uses a prior distribution of the shape parameter to avoid the value of the parameters being large negative (Park 2005; Yoon et al. 2010).

$$GL\left( {y}_{i};\mu ,\sigma ,\xi \right)=L\left( {y}_{i};\mu ,\sigma ,\xi \right)\pi \left(\xi \right)$$
(5)

Consequently, the generalised log-likelihood of Eq. 4 can be expanded as Eq. 6.

$$log\left[L\left(\theta ;{y}_{i}\right)\right]=-N\times log\left(\sigma \right)-\left(1+\frac{1}{\xi }\right)\sum_{i=1}^{N}log\left({x}_{i}\right)-\sum_{i=1}^{N}{\left({x}_{i}\right)}^{-1/\xi }++ln\left\{\pi \left(\xi \right)\right\}$$
(6)

To maximize this function for the estimation of the GEV parameters, Newton Raphson can be used (Yoon et al. 2010).

The Bayesian method

Like the GMLE method, the Bayesian method was also developed to overcome the limitation of small sample size of the extreme time-series data. The fundamental of Bayesian method require the prior distribution of the GEV parameters \(\theta =\left(\mu , \sigma , \xi \right)\). Therefore, the essential of Bayesian method is a prior distribution \(f\left(\theta \right)\) and a likelihood \(f\left(Y\mathrm{\rm I}\theta \right)\) (Coles and Tawn 2005). Bayes theorem balances these two sources produces the posterior distribution \(f\left(\theta \mathrm{\rm I}Y\right)\), such that:

$$f\left(\theta \mathrm{\rm I}Y\right)\alpha f\left(\theta \right)f\left(Y\mathrm{\rm I}\theta \right)$$
(7)

where Y is the historical data set and \(\theta =\left(\mu , \sigma , \xi \right)\) is the location, scale and shape parameter of the GEV distribution.

The posterior probability density of the GEV parameters \(p\left(\theta \mathrm{\rm I}Y\right)\) can be obtained by the well-known Bayes theorem as follows:

$$p\left(\theta \mathrm{\rm I}Y\right)=\frac{f\left(Y\mathrm{\rm I}\theta \right)\pi \left(\theta \right)}{\int f\left(Y\mathrm{\rm I}\theta \right)\pi \left(\theta \right)d\theta }$$
(8)

where \(p\left(\theta \mathrm{\rm I}Y\right)\) is the posterior probability density of the GEV parameters, Y is the observations, \(f\left(Y\mathrm{\rm I}\theta \right)\) is the likelihood of the observations and \(\pi \left(\theta \right)\) is prior probability density of the GEV parameters.

Since analytical determination of the posterior distribution is difficult, Markov Chain Monte Carlo algorithm can be used to derive the parameters \(\pi \left(\theta \right)\). Details of the method can be found in Gilks et al. (1995).

L-moments method

The L-moments is based on the probability weighted moments which describe the shape of probability distributions. The method can be defined as the linear combination of probability weighted moments (Hosking 1990). The method estimates the parameters of the statistical distribution by equating the first p-sample L-moments to the corresponding population sample. The L-moment method is less affected from data variability and outliers. Moreover, the method is comparatively unbiased for the small number of samples. Details of the L-moment method can be found in Hosking (1990).

The GEV distribution parameters according to the L-moments method can be described as follows (Hosking and Wallis 1993; Huard et al. 2010).

$$\mu ={l}_{1}+\frac{\sigma \left[\Gamma \left(1+\xi \right)-1\right]}{k}$$
(9)
$$\sigma =\frac{\xi {l}_{2}}{\Gamma \left(1+\xi \right)\left(1-{2}^{-\xi }\right)}$$
(10)
$$\xi =7.8590z+2.9554{z}^{2}$$
(11)

where \(\mu ,\sigma {\text{ and }}\xi\) are the location, scale and shape parameters respectively; \({l}_{1}, {l}_{2}\,{\text{and}}\,{l}_{3}\) are the L-moments and

$$z=\frac{2{l}_{2}}{{l}_{3}+3{l}_{2}}-\frac{ln\left(2\right)}{ln\left(3\right)}$$
(12)

Results and discussions

This section presents the outcomes of analysis performed in this research, including subsequent discussions. The application of homogeneity test, three parameters (location, scale and shape) of the GEV technique were obtained using the computer programming language R and RStudio.

The extent of the variability amongst the time-series extreme rainfall were determined using the statistical tests skewness and coefficient of variation. Estimated values of the skewness and coefficient of variance are shown in Table 2. From Table 2, it was observed that estimated values of the skewness were positive for all the rainfall stations implying that the right tail of the distribution is longer. It was also detected that estimated coefficient of variance was less than one for all the selected meteorological stations indicating that the variation of monthly maximum rainfall is considerably low.

Table 2 Buishand range homogeneity test result for the selected rainfall station in Tasmania from 1965 to 2018
Full size table

Homogeneity of time series observations reflects the variability of data sets. Location, instruments or recording time may cause non-homogeneity of observed data sets (Wijngaard et al. 2003). Nevertheless, assumption of homogeneity is essential for the statistical hypothesis testing on meteorological observation. In this research, Buishand Range homogeneity test was performed to identify whether the time series is homogeneous. The test was applied for 5% significant level. The outcomes of the homogeneity analysis for the selected 20 rainfall stations are shown in Table 2. The critical value of the test statistics was determined as 1.75 from Buishand (1982). The result of the Buishand Range homogeneity test indicated that the test statistic is lower than the critical value for all the rainfall stations except two as shown in Table 2. The possible reason for the non-homogeneity of two stations may be due to the changes in the surrounding environment or instrumentation inaccuracy or changes in the calculation procedure for the missing value (Wijngaard et al. 2003; Domonkos 2015). Since extreme rainfall data for 90% of the selected meteorological stations are homogeneous, statistical hypothesis can be applied with confidence.

After determining the homogeneity of the extreme rainfall data, the GEV distribution was fitted using the four different parameters estimation techniques. The parameters of the GEV distribution were estimated for four different time-series using four different parameters estimation techniques. Due to the page limitation, only the one time-series analysis (whole study period) has been provided in this article. The estimated GEV parameters of the analysis for the whole analysis period (1965–2018) are shown in Tables 3, 4, 5, 6 for the MLE, GMLE, Bayesian and L-moments techniques.

Table 3 Estimated GEV parameters using MLE technique rainfall data from 1965 to 2018
Full size table
Table 4 Estimated GEV parameters using GMLE technique rainfall data from 1965 to 2018
Full size table
Table 5 Estimated GEV parameters using Bayesian technique rainfall data from 1965 to 2018
Full size table
Table 6 Estimated GEV parameters using L-moments technique rainfall data from 1965 to 2018
Full size table

It has been noted that the shape parameter \(\left(\xi \right)\) of the GEV distribution is positive for all the considered rainfall stations except station 97047. The statement is true for any of the methods considered in this study as evidenced from Tables 3, 4, 5, 6 for the whole study period. This implies that the GEV is Fréchet (type II) distribution (except station #97047) for the data series from 1965 to 2018. The outcomes of Table 3 suggest that the type of the GEV distribution to be used in extreme climatic modelling did not depend on the parameter estimation technique. The observed negative shape parameter can be attributed by the influence of climate indices or elevation above mean sea level (Ragulina and Reitan 2017; Tyralis et al. 2019). However, all the stations located in the high altitude did not produce negative shape parameter due to the non-linear dependency of the shape parameter on elevation. In addition, influence of climate indices on shape parameter was not considered in this research as the analysis was performed considered the rainfall as stationary.

The parameters of the GEV distribution were also estimated for three other time-series: before millennium drought (1965–1996), during millennium drought (1997–2009) and after millennium drought (2010–2018). Due to the space limitation, they were not shown in this paper. Like the whole study period time-series analysis, positive shape parameter was observed for all the selected rainfall stations except two (stations 91072 and 97047) before millennium drought, two stations (stations 97047 and 97054) during millennium drought and two stations (stations 97047 and 91011) after millennium drought. Therefore, the Fréchet (type II) distribution GEV distribution is suitable for modelling monthly maximum of daily rainfall in Tasmania.

All the parameter estimation techniques adopted in this research are showing the same outcomes. Therefore, the GEV parameters estimation technique has negligible impact on the extreme rainfall modelling. Any of the methods can be applied in modelling daily extreme rainfall. However, the length of the data series used for the analysis has some impacts on the parameters values as evidenced from Tables 3, 4, 5, 6. Nevertheless, large samples should be adopted to identify the true behaviour of extreme rainfall (Papalexiou and Koutsoyiannis 2013). Therefore, the distribution that was identified considering the whole study period (1965–2018) is the appropriate distribution for a particular meteorological station.

The analysis of the study was further extended by estimating the return levels of the monthly maximum of the daily rainfall. The return levels were estimated for 2, 5, 10, 20, 50 and 100 years average recurrence interval (ARI). The estimated return levels are shown in Tables 7, 8, 9, 10 for MLE, GMLE, Bayesian and L-moments parameter estimation techniques for the whole study period, i.e. 1965–2018.

Table 7 Estimated return level of the monthly maximum daily rainfall (in mm) for difference ARI using the MLE parameter estimation technique
Full size table
Table 8 Estimated return level of the monthly maximum of daily rainfall for difference ARI using the GMLE parameter estimation technique
Full size table
Table 9 Estimated return level of the monthly maximum of daily rainfall for difference ARI using the Bayesian parameter estimation technique
Full size table
Table 10 Estimated return level of the monthly maximum of daily rainfall for difference ARI using the L-moments parameter estimation technique
Full size table

Similar to the estimated parameters, there is not much variation of the return levels of the monthly maximum of the daily rainfall for different ARI events. Using different GEV parameters estimation technique, similar return level was observed for the same ARI events for a particular station. The outcomes of the return levels estimation are evidenced from Tables 7, 8, 9, 10 for the whole study period. The same outcomes were observed for the other time-series data before millennium drought, during millennium drought and after millennium drought. To keep the length of the paper minimum, they are not shown here. Therefore, any of the GEV parameters estimation technique could be used to estimate the future daily extreme rainfall.

The visual comparison of the return levels estimation on the adopted parameters estimation techniques are also provided in this research. The plotted results of the return levels are shown from Figs. 2, 3, 4, 5 for the whole study period, before millennium drought, during millennium drought and after millennium drought respectively. The outcomes of four selected rainfall stations (stations 91011, 92012, 96002 and 99005) for different parameter estimation techniques (MLE, GMLE, Bayesian and L-moments) are shown in this paper. All of the figures clearly indicated that the influence of parameter estimation techniques on the return levels for different ARI events are minor.

Fig. 2
figure 2

Comparison of the maximum daily rainfall prediction for different average recurrence interval (ARI) using different GEV parameters estimation techniques for the whole study period (1965–2018)

Full size image
Fig. 3
figure 3

Comparison of the maximum daily rainfall prediction for different average recurrence interval (ARI) using different GEV parameters estimation techniques before millennium drought (1965–1996)

Full size image
Fig. 4
figure 4

Comparison of the maximum daily rainfall prediction for different average recurrence interval (ARI) using different GEV parameters estimation techniques during millennium drought (1997–2009)

Full size image
Fig. 5
figure 5

Comparison of the maximum daily rainfall prediction for different average recurrence interval (ARI) using different GEV parameters estimation techniques after millennium drought (2010–2018)

Full size image

To identify the discrepancy between the observations and the predicted values, goodness of fit test was performed. The example plots of the goodness of fit test for Cape Grim (91011) station is shown in Fig. 6 in terms of probability plot (PP), quantile plot (QQ), density and return level plot. The graphical plot (Fig. 6) of the goodness of fit test suggested that the daily extreme rainfall data set were successfully fitted with the stationary GEV models.

Fig. 6
figure 6

Probability plot (PP), quantile plot (QQ), density and return level plot for Cape Grim (91011) station

Full size image

The evaluation of the parameters estimation techniques of the GEV distribution were performed based on Mean Square Error (MSE) and Mean Absolute Error (MAE). The outputs of the error analysis are shown in Table 11. The results of the MSE analysis suggest that GMLE technique has is less error for most of the meteorological stations in the quantile estimation. However, the MAE analysis produced less error for the L-moment parameters estimation method. Nevertheless, there are four rainfall stations (stations #92006, #92008, #92012, #92047) with very high MSE. The presence of higher MSE for these rainfall stations may be due to the presence of outliers. It should be noted that outliers were not removed from the original data sets. Although MLE, GMLE and Bayesian methods produced very large MSE for these stations, the L-moments have the least MSE. The MAE of these stations are reasonable as evidence in Table 11. Therefore, we recommend the L-moments method to be adopted for the estimation of parameters for the GEV distribution.

Table 11 Estimated errors of the GEV models for the selected rainfall stations
Full size table

Conclusions and recommendations

In this study, monthly maximum of daily rainfall from 1965 to 2018 were used to estimate the parameters of the generalised extreme value (GEV) distribution using several parameters estimation techniques. Four different GEV parameters estimation techniques used in this study was MLE, GMLE, Bayesian and L-moments. The study was conducted to recommend appropriate parameters selection method for the application of the GEV technique in modelling extreme rainfall. Since the three parameters GEV distribution has been widely applied for describing the extreme climatic events, the method was adopted in this research. The available parameters estimation methods of the GEV distribution were applied on Tasmanian extreme rainfall. The parameters were estimated for four different time-scale data: the whole study period (1965–2018), before millennium drought (1965–1996), during millennium drought (1997–2009) and after millennium drought (2010–2018).

The outcomes of the errors (MSE and MAE) analysis in quantile estimation suggests that L-moments is the best method in estimating the parameters of the GEV distribution, especially when there is presence of outliers in the data series. Therefore, the L-moments method should be adopted for the estimation of the GEV parameters for rainfall analysis in Tasmania. This research provides a primary indication for the selection of appropriate GEV parameters estimation techniques in extreme rainfall modelling in Tasmania. Nevertheless, further researches in Tasmania and other regions are required for a generic conclusion. Moreover, the length of the data series has considerable implications on the magnitude of the estimated GEV parameters. The Fréchet (type II) GEV distribution is suitable for most of the rainfall stations for extreme rainfall modelling.

It should be noted that the spatial analysis of the stations and the GEV distribution parameters were considered in this research. This research can be extended to determine the degree of spatial persistence using the covariance between two random variables (Campling and Gobin 2001). That will allow to determine the potential parameter values of the GEV distribution at unsampled locations. As such, GIS based ordinary kriging which is the weighted moving average interpolation technique using covariance models can be applied.