Introduction

The gravity method is considered one of the geophysical methods because it is non-invasive, less expensive, and gives support information about the subsurface geologic structures. This method defines the density contrasts between sediments sequences and the basement rock, helps to understand and study the shallow and deep basins including their faults to demonstrate the dynamic behavior (Telford et al. 1990; Deng et al. 2016; Kabirzadeh et al. 2020). Gravity data interpretation is valuable in discovering areas that have anomalies below the surface and has numerous applications in hydrocarbon exploration, minerals exploration, environmental and engineering applications, geothermal studies, archeological investigations (Abdelfettah et al. 2014; Biswas et al. 2017; Jacob et al. 2018; Essa and Géraud 2020; Zhao et al. 2020). Gravity data interpretation suffers from ill-pose and non-uniqueness like all potential data. To minimize these problems, we discovered the appropriate geometry for the subsurface structure with a recognized density followed by the inversion process (Asfahani and Tlas 2012; Martyshko et al. 2018).

The present study aims identify the fault geometry parameters, in other words, the assessment of the amplitude coefficient that is a function of density and fault thickness, the depths of two-sides, the inclined angle, and the location of fault origin are very important in evaluating the importance of the buried fault-like geologic structures and evaluate its hazards.

Numerous scientists presented different methods for the interpretation problem and forward modeling calculation due to this source (e.g., Geldart et al. 1966; Paul et al. 1966; Green 1976; Gupta and Pokhriyal 1990). However, these methods depend on definite points and curves and the subjectivity of humans in determining the parameters of the structures (Essa 2013). So, it is still essential for finding a more stable interpretation way, and provides approximate geometric parameters. Furthermore, the precision of assessing the fault parameters depends on how to get the residual field from the Bouguer gravity data.

Chakravarthi and Sundararajan (2004) established an inversion approach using the iterative ridge-regression formula to assess the parameters for fault structures, in addition to the influence of regional field through an analytical formula for gravity anomalies of an inclined fault based on the parabolic relationship between the depth and density contrast. However, the fault structures frequently have finite strike lengths with the fault planes listric in nature. Based on the window curves method, Abdelrahman et al. (2013) developed a minimization algorithm to estimate the depth and the inclined angle of the fault structure from the moving average residual gravity anomalies. The limitation of applying the windowed curves method is the chance of being trapped in a local minimum. In other words, the windowed curves intersect in various places (solutions) and sometimes do not converge. Toushmalani (2013) developed a method that applied particle swarm optimization to estimate the fault parameters from the residual gravity anomalies. Abdelrahman and Essa (2015) established three successive least-squares minimization method as follows: first least-squares minimization is to solve a nonlinear form in-depth, then after estimated the depth, another nonlinear least-squares approach to evaluate the dip angle, lastly after the depth and dip angle estimation, a linear least-squares formula to estimate the amplitude factor of a buried inclined fault applying the first moving average operator to confiscate a regional background up to 1st-order. This approach relies on describing the anomaly at the origin and zero-distance for each residual moving average gravity anomaly. Kusumot (2017) proposed an approach to estimate the dip of the fault structures, which is dependent on applying the eigenvector of the observed or calculated gravity gradient tensor on a profile and exploring its properties through numerical simulations because the fault dip is a predominantly significant parameter in understanding the amount of hazard and disaster can be created. However, to get more accurate results about the dip, it needs more a priori geologic information. Ekinci et al. (2019) used naturally inspired metaheuristic optimization algorithms (DE and PSO) to estimate the deep-seated fault parameters from gravity and magnetic anomalies data. Anderson et al. (2020) used particle swarm optimization for interpreted only 2D vertical fault structure using horizontal gradient anomalies. Uzun et al. (2020) proposed a method to estimate the dip angle, location, and density of the dip-slip fault structure using a gravitational gradient derived from recently constructed EGM2008 and available seismic data. Essa et al. (2021) proposed a method to interpret a two-sided fault structure using the second horizontal derivative method to eliminate only a 1st-order regional background.

Thus, gravity anomaly profiles generated by different types of faults structure were studied to infer the parameters (the amplitude coefficient, the depth of the shallow side, the depth of the deeper side, and the origin position) and these data were including different levels of noise (0%, 5%, and 10%) to evaluate the robustness of the suggested method. This method is tested by a field example from Egypt.

Methodology

The Bouguer gravity anomaly is expressed by the form:

$$B_{{{\text{ouguer}}}} = R_{{{\text{esidual}}}} + R_{{{\text{egional}}}} ,$$
(1)

where \({B}_{\mathrm{ouger}}\) represents the measured Bouguer gravity data, \({R}_{\mathrm{esidual}}\) represents the residual gravity anomaly, and \({R}_{\mathrm{egional}}\) is the regional gravity anomaly (Obasi et al. 2016). The present study focused on interpreting the gravity anomaly due to fault-like geologic structures. The fault structures here can be classified into two types as follows:

Two-sided fault forward model formula

Gravity anomaly profile generated by the two-sided semi-infinite horizontal thin sheet, which represents the normal and reverse faults with inclined angle (θ) (Telford et al. 1990; Hinze et al. 2013) along the profile is:

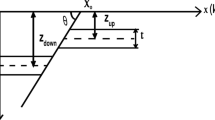
$$R_{{{\text{esidual}}}} \left( {x_{j} ,h_{1} ,h_{2} ,\theta } \right) = K\left\{ {1 + \frac{1}{\pi }\tan^{ - 1} \left[ {\frac{{\left( {x_{j} - c} \right)}}{{h_{1} }} + \cot \theta } \right] - \frac{1}{\pi }\tan^{ - 1} \left[ {\frac{{\left( {x_{j} - c} \right)}}{{h_{2} }} + \cot \theta } \right]} \right\}$$
(2)

where \({h}_{1}\) is the depth to the shallow side (km), \({h}_{2}\) is the depth to the deeper side (km), \(K= 2\pi G\Delta \sigma t\) is the amplitude coefficient (mGal) and is a function of density contrast and thickness of the fault and Δσ is the density contrast between the fault and the surrounding (g/cc), G is the gravitational constant, and t is the thickness (km), θ is the angle of inclination, xj is the measured points position (km), c is origin location of the anomaly (km).

In case of θ = 90°, the term \(\mathrm{cot}\theta =0.\) So, this inclined fault reduced to the vertical and the gravity anomaly is:

$$R_{{{\text{esidual}}}} \left( {x_{j} ,h_{1} ,h_{2} } \right) = K\left\{ {1 + \frac{1}{\pi }\tan^{ - 1} \left[ {\frac{{\left( {x_{j} - c} \right)}}{{h_{1} }}} \right] - \frac{1}{\pi }\tan^{ - 1} \left[ {\frac{{\left( {x_{j} - c} \right)}}{{h_{2} }}} \right]} \right\}$$
(3)

Figure 1 shows a sketch for the three different types of the fault structure and all parameters are demonstrated.

Fig. 1
figure 1

A sketch diagram for the different fault-types: a normal fault, b reverse fault, and c vertical fault and all parameters are demonstrated

Full size image

Moving average method

The first-order moving average technique is considered as one of several methods in separating the regional gravity anomaly that was signified by a first-order polynomial (Griffin 1949). The first moving average residual anomaly along the measured profile is:

$$R_{1} \left( {x_{j} ,h_{1} ,h_{2} ,\theta } \right) = \frac{{2B_{{{\text{ouguer}}}} \left( {x_{j} } \right) - B_{{{\text{ouguer}}}} \left( {x_{j} + s} \right) - B_{{{\text{ouguer}}}} \left( {x_{j} - s} \right)}}{2} ,$$
(4)

where s is the window length.

Particle swarm

A particle swarm was established and presented during the last years to explain various geophysical problems (Singh and Biswas 2016; Roshan and Singh 2017; Essa and Munschy 2019; Loni and Mehramuz 2020; Moura et al. 2020). The particle swarm optimization is a stochastic algorithm modeled on social performances detected in flocking birds looking for foods. Entire the particle swarm search space is crowded with particles, where each particle in the swarm includes the parameter information of the models. Also, each model has a position and velocity. Moreover, the particle swarm adapts the particles to reach the model parameters at which the objective function is minimal. In each step of iterations, each model modernizes its velocity and place utilizing the next formulas:

$$V_{j}^{k + 1} = c_{3} V_{j}^{k} + c_{1} {\text{rand}}\left( {T_{{{\text{best}}}} - x_{j}^{k + 1} } \right) + c_{2} {\text{rand}}\left[ {\left( {J_{{{\text{best}}}} - x_{j}^{k + 1} } \right)} \right] ,$$
(5)
$$x_{j}^{k + 1} = x_{j}^{k} + v_{j}^{k + 1} ,$$
(6)

where \({v}_{j}^{k}\) is the velocity of the jth particle, \({x}_{j}^{k}\) is the present place, rand is a non-uniform random number, \({c}_{1}\) and \({c}_{2}\) are the control parameters for the swarm, which are equal 2 (Parsopoulos and Vrahatis 2002), c3 is the inertial parameter, which equals 0.8. The motivation of the particle swarm utilization is to reach a global solution of the subsurface targets from interpreting gravity data quickly and point out the prominence of employing this approach among various conventional, non-conventional, and optimization techniques. Moreover, synthetic and real data examined below are confirmed the motivation of exploitation of the particle swarm at any time within the future.

Fault parameters calculation

In this present study, the main objective is to find the optimized solution for the two-sided fault structure from gravity anomaly. The beginning model fault parameters (K, h1, h2, θ, and c) are improved and update during the process of iteration until reaching the best-fit model between the measured and calculated gravity anomalies using the following objective function \(\left(\psi \right)\):

$$\psi = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left[ {\Delta B_{{{\text{ouguer}}\,j}}^{o} \left( {x_{j} } \right) - \Delta B_{{{\text{ouguer}}\,j}}^{c} \left( {x_{j} } \right)} \right]^{2} } ,$$
(7)

where N is the observed points, \(\Delta {{B}_{\mathrm{ouguer}}}_{j}^{o}\) is the Bouguer gravity anomaly and \(\Delta {{B}_{\mathrm{ouguer}}}_{j}^{c}\) is the calculated gravity anomaly at the point xj.

Finally, Fig. 2 demonstrates the flow chart of the parameters estimation of the suggested method.

Fig. 2
figure 2

A flow-chart for fault parameters estimation through particle swarm

Full size image

Particle swarm optimization tuned study

The influence of the parameters \({c}_{1}\), \({c}_{2}\) and \({c}_{3}\) on the rate of particle swarm convergence rate was investigated (Fig. 3). Figure 3 demonstrates the impact of each set of the \(({c}_{1}\), \({c}_{2}\) and \({c}_{3})\) parameters on the convergence rate as well as the convergence behavior. Also, Fig. 3 recommends that the optimum set is that of \(({c}_{1}={c}_{2}=2.0\) and \({c}_{3}=0.8)\), which has a minimum standard deviation (0.05) than other sets and gives a fast convergence to the optimum solution.

Fig. 3
figure 3

The impact of the different sets of the parameters c1, c2 and c3 on the convergence rate

Full size image

Validation of the suggested method

The suggested method was used for examining the Bouguer gravity anomalies due to a two-sided fault-like geologic structure and a field example from Egypt to study the robustance and constancy of the method.

Synthetic model

Synthetic finite two-sided fault model of parameters with K = 100 mGal, h1 = 5 km, h2 = 8 km, θ = 35°, c = 5 km, and profile length = 100 km and a first-order regional anomaly has been used to examine the accuracy of the present approach and created from the following equation:

$$\Delta B_{{{\text{ouguer}}}} \left( {x_{j} } \right) = 100\left\{ {1 + \frac{1}{\pi }\tan^{ - 1} \left[ {\frac{{\left( {x_{j} - 5} \right)}}{5} + \cot 35} \right] - \frac{1}{\pi }\tan^{ - 1} \left[ {\frac{{\left( {x_{j} - 5} \right)}}{8} + \cot 35} \right]} \right\} + 2x_{j} + 40 .$$
(8)

and subjected to different noise levels (0%, 5%, and 10%). This anomaly interpreted using the particle swarm. The optimal model parameters were gotten after 200 iterations and the parameter values range are in Table 1. Table 1 presents all parameters ranges and their assessed results at each window lengths (s-values). Furthermore, it expresses the average value (ϕavg-value), uncertainty and percentage of error (E-value) and the ψ-value that points out the misfit among the Bouguer and calculated anomalies. This examination is done to get the actual two-sided inclined fault model parameters as follows:

Table 1 Numerical results for applying the particle swarm to interpret moving average anomalies using several s-values for a two-sided inclined fault model generated Eq. (8) without and with various noise levels
Full size table

First, gravity anomaly with 0% noise level (noise-free) of a fault model (Fig. 4a) is exposed to moving average method to eliminate the regional anomaly exploiting numerous window lengths (s = 3, 4, 5, 6, 7, and 8 km) (Fig. 4b). After that, the fault parameters (K, h1, h2, θ, and c) are achieved by particle swarm (Table 1). Table 1 expresses the parameters ranges as; the amplitude coefficient (K) is between 50 and 500 mGal, depth of shallow side (h1) is between 1 and 20 km, depth of the deeper side (h2) is between 1 and 20 km, the inclined angle (θ) is 10°–180°, and the position of the origin (c) is between 1 and 20 km. Also, Table 1 displays the parameters results at each s-value, the average value (ϕavg-value), uncertainty, percentage error (E-value), and the root mean squared value (ψ-value), which represents the misfit. The E-values and ψ-value equal zero (Table 1).

Fig. 4
figure 4

a Synthetic gravity anomaly generated applying Eq. (8). b Moving average anomalies for anomaly in Fig. 4a. c Noisy anomaly (5% noise added). d Moving average anomalies for anomaly in Fig. 4c. e Noisy anomaly (10% noise added). f Moving average anomalies for anomaly in Fig. 4e

Full size image

The proposed method’s performance was studied after imposing different level of noise (L.N.) on the above composite gravity anomaly (Fig. 4a) using the following form:

$$\Delta B_{{{\text{ouguer}}}}^{{{\text{rand}}}} \left( {x_{j} } \right) = \Delta B_{{{\text{ouguer}}}} \left( {x_{j} } \right) \times \left[ {1 + {\text{L.N.}} \times \left( {{\text{RAND}}\left( j \right) - 0.5} \right)} \right],$$
(9)

where \({\Delta B}_{\mathrm{ouguer}}^{\mathrm{rand}}\left({x}_{j}\right)\) is the theoretical model including noise level, \(\Delta {B}_{\mathrm{ouguer}}\left({x}_{j}\right)\) is original theoretical model, L.N. is level of noise, and RAND(i) is a non-uniform and pseudo-random number whose range is [0, 1].

The composite anomaly (Δ\({B}_{\mathrm{ouguer}})\) was corrupted with a 5% noise level using Eq. (9) (Fig. 4c). For the same window lengths values (s = 3, 4, 5, 6, 7, and 8 km), the residual moving average anomalies is displayed in Fig. 4d. These anomalies were interpreted by the particle swarm to achieve the optimal fit results (Table 1). In Table 1, the ϕavg-values for K, h1, h2, θ, and c are 100.89 ± 3.6 mGal, 4.99 ± 0.11 km, 8.07 ± 0.15 km, 35.73° ± 1.61°, and 5.07 ± 0.13, the E-values are 0.89%, 0.10%, 0.98%, 2.07%, and 1.47%, respectively, and the ψ-value is 10.45 ± 10.36 mGal and the misfit was shown in Fig. 4c.

Furthermore, the noise level was increased to be 10% added (Fig. 4e). The residual moving average anomalies were revealed in Fig. 4f and the optimal fit results were shown in Table 1. From Table 1, the estimated ϕavg-values for K, h1, h2, θ, and c are 107.99 ± 17 mGal, 5.14 ± 0.34 km, 8.18 ± 1 km, 37.49° ± 5.36°, and 4.73 ± 0.11 km, the E-values are 7.99%, 2.87%, 2.29%, 7.1%, and 5.47%, respectively. The relationship between the Bouguer and the calculated was assessed (the ψ-value is 21.41 ± 20.19 mGal) and the difference (residual) among them was presented in Fig. 4e.

Finally, the optimal fit results for different noise cases for the two-sided fault model explain that the developed method can estimate the fault model parameters precisely.

Field model

The Gazal fault is located in the west of Lake Nasser and south of the Kalabsha fault. This fault is trending nearly N–S and extends for about 35 km refer to Fig. 5a. The area that has this fault is characterized by the Nubia Sandstone with a flat-lying, relatively under-formed, and gently dipping westward while it ranges in thickness from 200 to 400 m (WCC 1985) (Fig. 5a). The depth to the basement is 200 m (drilling information; Evans et al. 1991). This area is very important in evaluation because it is near Aswan Lake and High Dam. Moreover, it is characterized by high active seismicity due to more fault-controlled area.

Fig. 5
figure 5

a Geological map of the Lake Nasser region, South Aswan modified by the WCC (1985), which 1 is the latest Cretaceous sandstones and shale of Nubia Formation, 2 is the Precambrian metamorphic and plutonic rocks, 3 is the latest Cretaceous rocks, 4 is the Paleocene to Eocene age marine limestone, and 5 is the Quaternary deposits. b Bouguer gravity profile collected over the Gazal fault, Egypt. c Moving average anomalies for anomaly in Fig. 5b. d The relation between the misfit errors (Ψ-value) and the number of iterations (convergence rate) and impeded figure for demonstrating the change of errors in 20 independent runs

Full size image

Bouguer gravity profile collected over the Gazal fault, south Aswan, Egypt is interpreted to assess the fault parameter using the suggested method (Abdelrahman et al. 2013) (Fig. 5b). A 5-km profile length was digitized with an interval of 62.5 m. The developed method was applied to this profile to evaluate the fault model parameters (K, h1, h2, θ, and c) through the residual moving average anomalies. The optimal fit results were explained in Table 2. Figure 5c shows the moving average anomalies by utilizing numerous window lengths (s = 0.1875, 0.25, 0.3125, 0.375, 0.4375, 0.5, and 0.5625 km).

Table 2 Numerical results for applying the present approach to interpret Bouguer gravity anomaly for the Gazal fault example, Egypt
Full size table

The particle swarm optimization process is performed using the decided control parameters, 20 independent runs managed using a population number of 180 and 400 generations. The particle swarm was applied to these anomalies to conquer the parameters (Table 2). Table 2 illustrates the parameters ranges (K is 0.5–20 mGal, h1 is 0.1–2 km, h2 is 0.1–2 km, θ is 10°–180°, and c is – 1 to  + 1 km) and the result of each parameter at different s-value, the average value (ϕavg-value), uncertainty, and the ψ-value that exhibits the misfit among the Bouguer and the calculated anomalies. The optimal fit results are K = 3.35 mGal, h1 = 0.199 ± 0.03 km, h2 = 0.469 ± 0.04 km, θ = 54.33° ± 1.35°, and c = − 0.25 ± 0.01 km. The optimal error fit (ψ-value) is 1.07 ± 0.02 mGal (Fig. 5d). The forward model is calculated and a sketch diagram for the fault model is explained in Fig. 5b. The misfit between them (Fig. 5d) explained good agreement with the results obtained by several published methods (Table 3).

Table 3 Comparative results due to the interpretation of Bouguer gravity anomaly for the Gazal fault example, Egypt
Full size table

Finally, the present approach has successively interpreted the fault structures and delineates their parameters, which will be more informative for scientists in future studies.

Conclusions

The proposed global optimization is accomplished to assess the two-sided inclined fault structure parameters (the amplitude coefficient, the depth to the shallow side, the depth to the deep side, the inclined angle and, the location of buried fault structures) from the gravity anomaly. This method depends on assessing the first moving average residual anomalies exploiting numerous window lengths and then applying the particle swarm to evaluate the fault parameters. This method is less sensitive to noise and the regional background effect. Synthetic data (including noise) and field data were presented to reveal the efficacy in interpreting gravity data for the fault model. Thus, the estimated fault parameters were compared with other results attained from geologic and geophysical methods to reveal the efficiency of the suggested method.