Introduction

With the advancement and development of tunneling technology, the advanced methods such as the shield method (Wei et al. 2017) are applied to filed projects. However, for large-field projects such as mountain tunnels, open pits, and mine roadways (Zhang et al. 2020), the drilling and blasting method is still the construction method more favored by construction workers (Nateghi et al. 2009). During blasting construction, structural vibration caused by blasting construction is inevitable (Chen et al. 2017a, b). Therefore, effective control of the blasting vibration is of great engineering significance for the construction safety and the stability of surrounding structures. The peak particle vibration velocity is often used to evaluate the damage degree of blasting vibration. The peak particle vibration velocity is often used to evaluate the damage degree of blasting vibration. Therefore, it is particularly important to accurately predict and control the blast vibration velocity. Artificial neural networks, fuzzy mathematics, support vector machines and other artificial intelligence algorithms (Zhang et al. 2020) are increasingly applied in practice. Armaghani et al. (2019) combined three single-core functions and three multi-core functions, including two newly proposed multi-core functions, tenfold cross-validation, and hybrid particle swarm optimization (HPSOGWO) with gray wolf optimizer to improve the prediction performance of the RVM model. It is found that the improved intelligent prediction method has a good fitting effect on the peak blasting velocity. To accurately predict the vibration velocity of ground blasting, two intelligent models were proposed by hybridizing the relevance vector regression (RVR) with the gray wolf optimization (GWO) (which formed the RVR-GWO model) and with the bat-inspired algorithm (BA) (Fattahi and Hasanipanah 2020). Temeng et al. (2020) propose a new class of advanced artificial neural network known as brain-inspired emotional neural network (BI-ENN) to predict Air overpressure caused by blasting,which can get a good prediction effect. Zhou et al. (2020a) developed a Random Forest (RF) model and a Bayesian Network (BN) model predict the ground vibration due to quarry blasting. It is confirmed that the improved prediction model can be introduced as a new model in the field of blasting environmental issues. Armaghani et al. (2019) analyze results of vibration effect of blasting using a combination of predictive and probabilistic models (prediction and simulation phases).

In essence, the propagation of blasting vibration is the transmission and attenuation process of vibration energy. Therefore, the use of signal analysis method to study the law of blasting vibration fluctuation has important practical engineering significance. At present, the traditional time–frequency analysis methods of blast vibration velocity signals mainly include the Fourier transform (Chen et al. 2019), short-time Fourier transform (Tian et al. 2019), wavelet analysis (Chen et al. 2019) and wavelet packet analysis (Huang et al. 2019). The Fourier series transform is better for processing stationary signals, but it cannot accurately reflect the details of energy distribution in non-steady-state signals like blasting vibration. Although the wavelet and wavelet packet analysis are able to predict local characteristics (Zhong et al. 2012), the application of the two analysis methods is limited due to the Heisenberg uncertainty principle and the complexity of the optimal wavelet basis function determination (Xue et al. 2019), making it difficult to obtain the complete characteristic information of the blasting signal (Li et al. 2019).

The HHT analysis method is ideal for processing non-steady-state and non-linear signals, and it can extract the main feature information of the time–history curve from the original signal (Miao et al. 2018). Traditional HHT analysis mainly includes Empirical Mode Decomposition (EMD) and Hilbert transform (Shi et al. 2016). EMD can decompose the original signal into multiple intrinsic modal components (IMF) (Wang et al. 2015) of different time scales without any basis function, and most of the modal components have clear physical meanings. Therefore, the HHT analysis has good adaptability and high efficiency when processing blasting signals.

However, there are still a series of practical problems in the process of HHT analysis (Li et al. 2016): (1) modal aliasing often occurs during the EMD decomposition process, which affects the quality of signal processing; (2) there are some low-frequency components that are not highly correlated with the original signal in the modal components, which will adversely affect the accuracy of HHT subsequent analysis; (3) the main modal components of the original signal are often contaminated by some high-frequency noise, which will reduce the accuracy of analysis results (Shi et al. 2018). To make better use of the HHT analysis, this paper proposes an improved HHT analysis method that can be applied to the analysis of the tunnel-blasting vibration speed signals.

First, a CEEMDAN decomposition method is introduced to solve the modal aliasing problem in EMD decomposition. Second, the correlation coefficient, variance contribution rate and power spectrum analysis are used to eliminate the interference information in the original signal, and reconstruct the modal components containing the signal characteristics. The reconstructed components are further subjected to wavelet packet threshold de-noising to obtain the purified components which can reflect the original signal characteristic information. Finally, the HHT time–frequency analysis is performed on the purified components, and the energy spectrum of the measured signal is analyzed using the Hilbert transform (Li et al. 2017).

To effectively control the blasting effect of the tunnel, regression analysis on the measured blasting vibration signal is first conducted to obtain the model that can accurately reflect the blast vibration velocity and the maximum charge per delay. Then, the Hilbert transform is used to analyze the blast vibration velocity signal in time and frequency domain, and the division rule of blasting vibration energy is obtained. Finally, a prediction model that reflects the attenuation of blasting vibration energy is obtained for the case.

Project overview

Based on the engineering background of the newly built Caomaoshan Tunnel of Beijing–Zhangjiakou high-speed railway, this paper studies the distribution law of the blast vibration velocity based on the regression analysis and scientific numerical calculation. The newly built Caomaoshan Tunnel is located in Chenjiazhuang Village, Zhangjiakou City, Hebei Province. It has a total length of 7340 m and crosses the main mountain range of Caomaoshan (Fig. 1). The tunnel passes through the Quaternary Upper Pleistocene neo-loess, silty clay and other strata. The fully weathered tuff that passes through is highly expansive, which may cause accidents such as water inrush, mud burst, surrounding rock collapse, and large deformation. The geology can cause potential safety hazards due to construction blasting.

Fig. 1
figure 1

Caomaoshan Tunnel entrance area

Full size image

Blasting vibration monitoring and data processing

Monitoring program

The TC-4850N blasting vibration meter is applied to monitor vibration in this case. The blast vibration velocity in X, Y, and Z direction can be collected and a data processing software can be used to record the peak velocity and main frequency in the blast vibration velocity signal (Fig. 2).

Fig. 2
figure 2

TC-4850N blasting vibration meter and sensor

Full size image

Due to the small number of free surfaces during the blasting construction of the upper step of the tunnel and the massive use of surrounding rock clips, the blasting vibration generated by the upper step blasting is greater. Therefore, this paper mainly studies the adverse effects caused by the blasting vibration of the steps on the tunnel.

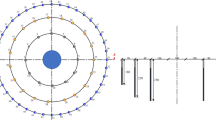
Before the tunnel-blasting construction, laser rangefinder and tape measure were applied to determine the location of the measuring points. The distance between the measuring point and the blast source is 15 m, 20 m, 25 m, and 30 m (Wang et al. 2018). The configured stainless-steel clips were used to fix the speed sensor on the initial lining of the tunnel. Sensors were close to the outer surface of the tunnel lining structure, with a distance of 2.5 m away from the tunnel ground. To protect the blasting vibration-measuring instrument, a self-made steel bar was used to cover the outer side of the vibration-measuring instrument to prevent damage by the stone throwing in the blasting process. During the field test, the X direction of the speed sensor was set toward the tunnel face, the Y direction was towards the tunnel line, and the Z direction was perpendicular to the XY plane. The specific measurement point arrangement is shown in Fig. 3.

Fig. 3
figure 3

Blast vibration measurement locations

Full size image

Selection of monitoring physical quantity

The blasting vibration amplitude strength has a harmful effect on the structure, and the impact of blasting shock wave can be divided into force effect and strain effect (Tolani et al. 2020; Yari et al. 2015). The force effect is mainly manifested in the change of internal pressure and tensile force of the structure caused by blasting vibration, while the strain effect refers to the change of internal stress caused by the blasting shock wave.

For a shock wave containing only one wave form, there seems to be a positive relationship between the limit stress of the structure and the propagation vibration speed. According to rock dynamics, the blasting vibration wave is the result of superposition of multiple vibration forms with different frequencies. With the propagation of the blasting vibration wave, there must exist a vibration strengthening area and a vibration attenuation area, and the structure in the vibration strengthening area is more likely to reach the limit stress state and fail. However, in the actual blasting construction process, the propagation direction of blasting vibration waves is ever-changing, and it is difficult to clearly define the vibration strengthening area and vibration attenuation area. Therefore, it is not appropriate to use the maximum value of the vibration velocity in a specific direction as the sole criterion to determine whether the structure is damaged (Hosseini et al. 2019).

In addition, the propagation direction of the blasting shock wave is relatively complicated, and the blasting vibration energy carried in each direction is different, which also confuses the choice of the direction of the blasting vibration velocity in practical research. According to the Mohr–Coulomb criterion, if the stress circle intersects or is tangent to the strength envelope, the structure will fail. The strength envelope for the hard rock in the mountain tunnel is approximately hyperbolic. On this basis, Liu and Wang (2004) considered the effect of intermediate stress and proposed a weighted double shear strength criterion, which is suitable for materials with similar differences in tensile and compressive strengths. The specific expression is as follows:

When \(\sigma_{2} \le \frac{{(\sigma_{1} + \alpha \sigma_{3} )}}{(1 + \alpha )}\), it gives

$$ F = \sigma_{1} - \frac{{(\sigma_{2} + 2\sigma_{3} )\alpha }}{3} = \sigma_{t} . $$
(1)

When \(\sigma_{2} \ge \frac{{(\sigma_{1} + \alpha \sigma_{3} )}}{(1 + \alpha )}\), it gives

$$ F = \frac{{(2\sigma_{1} + \sigma_{2} )}}{3} - \alpha \sigma_{3} = \sigma_{t} , $$
(2)

where \(\alpha = \frac{{\sigma_{{\text{t}}} }}{{\sigma_{{\text{c}}} }}\), \(\sigma_{{\text{t}}}\) is the tensile strength of the rock, \(\sigma_{{\text{c}}}\) is the compressive strength of the rock.

The rock failure process is complicated and related to the tensile and compressive strength of the rock and the principal stress directions. Therefore, it is not entirely reasonable to consider the stress change of the object caused by blasting vibration in a specific direction alone.

To sum up, this paper takes the vector synthetic blasting vibration speed in X, Y and Z directions as the control index for research. The calculation equation of the vector synthetic blast vibration velocity is as follows:

$$ V = \sqrt {\left( {V_{x}^{2} + V_{y}^{2} + V_{z}^{2} } \right)} . $$
(3)

Table 1 summarizes the monitoring data of the peak vibration velocity of the tunnel entrance section, and Fig. 4 shows the typical time-history curve of the on-site blasting monitoring results in the X, Y, Z directions and the synthetic vibration speed.

Table 1 Blast vibration velocity monitoring data at the entrance of Caomaoshan Tunnel
Full size table
Fig. 4
figure 4

Time–history curve of blasting vibration speed

Full size image

Regression analysis of blasting measured data

At present, the fitting analysis methods for blast vibration velocity mainly include traditional empirical formula fitting (Ongen et al. 2018; Deng et al. 2020; Qin and Zhang 2020) and artificial intelligence algorithm prediction (Mohamad et al. 2020; Armaghani et al. 2019; Yu et al 2020a; Ma et al. 2020; Huang et al. 2020; Zhou et al. 2020b; Yu et al. 2020b). Although artificial intelligence has strong advantages in forecasting the blast vibration velocity, the actual data measured in this article are limited, thus, not suitable for artificial intelligence forecasting research. Current empirical prediction formulas for blasting vibration strength prediction includes the United State Bureau of Mines model (USBM), Sadofsky prediction formula, Indian standard model, and Langefors and Kihlström model (Cardu et al. 2019; Jiang et al 2018; Yang et al 2019).

  1. 1.

    USBM model

    $$ V = K\left( {\frac{{Q^{\frac{1}{2}} }}{R}} \right)^{\alpha } $$
    (4)
  2. 2.

    Sadofsky prediction formula

    $$ V = K\left( {\frac{{Q^{\frac{1}{3}} }}{R}} \right)^{\alpha } $$
    (5)
  3. 3.

    Indian Standard

    $$ V = K\left( {\frac{Q}{{R^{\frac{2}{3}} }}} \right)^{\alpha } $$
    (6)
  4. 4.

    Langefors and Kihlström model

    $$ V = K\left( {\frac{{Q^{\frac{1}{2}} }}{{R^{\frac{3}{4}} }}} \right)^{\alpha } $$
    (7)

where V is the blast vibration velocity; Q is the maximum charge per delay; R is the distance from blast area; K and α are the relevant geological coefficients in the blasting project construction.

From the above, it can be seen that the blast vibration velocity is an exponential function of Q and R, the difference is only reflected in the different exponential ratio of Q and R. Therefore, on the basis of the above empirical formula, the correction formula of blasting vibration velocity in this paper is summarized as follows:

$$ V = kQ^{\alpha } R^{\beta } . $$
(8)

Based on the blasting vector synthetic vibration velocity data in Table 1, a non-linear regression analysis is performed on Eq. 8 via the least square method. The prediction equation of the blast vibration velocity used in this project is as follows:

$$ V = 0.0345Q^{2.788} R^{{{ - 1}{\text{.446}}}} . $$
(9)

The correlation coefficient square (r2) of the prediction equation obtained by regression is 0.963. At the same time, it can be seen from Table 1 that most of the formula calculation errors are below 15%. Therefore, it can be concluded that the fitted model equations can predict the blast vibration velocity of this project more accurately.

According to the “Safety Regulations for Blasting” (GB6722-2014), the blast vibration velocity of a traffic tunnel must not exceed 10 cm/s. According to the preliminary geological exploration results, the minimum burial depth of the Caomaoshan tunnel is 30 m. To minimize the impact of the tunnel-blasting construction on the surrounding buildings, the maximum charge per delay should be controlled. According to the obtained prediction equation, V = 10 cm/s and R = 30 m are input into Eq. 9 to obtain Q = 45.03 kg. Therefore, the maximum charge per delay of blasting construction in this section of tunnel should not exceed 45 kg.

Improved HHT algorithm

Traditional HHT algorithm

Compared with the time–frequency analysis methods such as Fourier transform and wavelet analysis, HHT algorithm is based on a brand-new time–frequency analysis technology and has strong adaptability. Unlike Fourier transform and wavelet transform, HHT analysis can decompose the original signal into multiple modal components without relying on any basis function (Jiang et al. 2017).

The traditional HHT method mainly includes the EMD and Hilbert transform. Through EMD, the collected blasting signal can be decomposed into multiple intrinsic modal components, IMF1, IMF2, IMF3 … IMFn−1, and the residual term rn, so that the original signal can be reconstructed into the following form:

$$ y(t) = \sum\limits_{i = 1}^{n - 1} {{\text{IMF}}_{i} + r_{n} } . $$
(10)

The Hilbert transform is then conducted on the obtained IMF component to obtain the instantaneous frequency, instantaneous phase and instantaneous amplitude of each component. The instantaneous frequency and instantaneous amplitude are both functions of time t, which also gives the instantaneous expression of the IMF component spectrum. Synthesizing the frequency spectrum of each component can produce the description method of the HHT time–frequency, namely Hilbert spectrum. The specific Hilbert transform steps are as follows:

The Hilbert transform for each IMFi(t) is

$$ H[i(t)] = \frac{1}{\pi }{\text{PV}}\int\limits_{\infty } {\frac{{i(t^{\prime})}}{{t - t^{\prime}}}} {\text{d}}t^{\prime}, $$
(11)

where PV represents the Cauchy principal value, and the analytical signal z(t) is constructed as follows:

$$ z(t) = i(t) + jH[i(t)] = a(t)e^{j\Phi (t)} , $$
(12)

where, \(a(t)\) is the amplitude function and \(\Phi (t)\) is the phase function:

$$ a(t) = \sqrt {c^{2} (t) + H^{2} [c(t)]} , $$
(13)
$$ \Phi (t) = \tan^{ - 1} \frac{H[i(t)]}{{i(t)}}. $$
(14)

So far, the Hilbert transform provides a unique function that defines the amplitude and phase, where Eq. 12 emphasizes the local characteristics of the Hilbert transform. Based on the above analysis, the instantaneous frequency is defined as follows:

$$ \omega (t) = \frac{{{\text{d}}\Phi (t)}}{{{\text{d}}t}}. $$
(15)

It can be seen from Eq. 15 that the instantaneous frequency is a function of time, which reveals a measure of the concentration of signal energy in the frequency at a certain moment. Simultaneously, the original signal y(t) is reconstructed as follows:

$$ y(t) = {\text{Re}} \sum\limits_{i = 1}^{n - 1} {a_{i} (t)e^{{j\Phi_{i} (t)}} } = {\text{Re}} \sum\limits_{i = 1}^{n - 1} {a_{i} (t)e^{{\int {\omega_{i} (t){\text{d}}t} }} } , $$
(16)

where Re is the real part, and the influence of residual terms is ignored in the calculation.

So far, the instantaneous frequency and instantaneous amplitude are both functions of time, and a three-dimensional spectrum can be constructed to represent the relationship between amplitude, frequency, and time, which is referred as the Hilbert spectrum.

Integrating \(H(\omega ,t)\) with time can get the Hilbert marginal spectrum (h(ω)), which expresses the accumulation degree of signal amplitude (energy) in each frequency range as:

$$ h(\omega ) = \int_{0}^{t} {H(\omega ,t){\text{d}}t} $$
(17)

The square of \(H(\omega ,t)\) is integrated with the frequency to obtain the Hilbert instantaneous energy spectrum, which expresses the distribution law of signal energy in time as follows:

$$ {\text{IE}}(t) = \int_{\omega } {H^{2} (\omega ,t){\text{d}}\omega } . $$
(18)

The instantaneous energy curve is integrated in time to obtain the total energy E carried by the signal:

$$ E = \int_{0}^{t} {{\text{IE}}(t){\text{d}}t} . $$
(19)

Improved HHT algorithm

Although HHT analysis shows strong adaptability in processing non-steady-state and non-linear signals, it also has several limits. For example, (1) EMD always results in aliasing of modal components, which affects the accuracy of subsequent analysis; (2) the low-frequency components obtained by EMD contain some components that are not highly correlated with the original signal, which should be eliminated in the actual analysis; (3) the main modal component (IMF) often contains a large amount of high-frequency and low-frequency interference information. Therefore, the signal must be de-noised before Hilbert transform (Zhen-xiong et al. 2016). To solve the above problems, this paper proposes an improved HHT algorithm based on CEEMDAN decomposition. The specific steps are as follows:

Step I: CEEMDAN decomposition of the original signal is conducted to obtain a finite number of modal components (IMF).

CEEMDAN decomposition is based on the Ensemble Empirical Mode Decomposition (EEMD) and Complete Ensemble Empirical Mode Decomposition (CEEMD) algorithms. Unlike the two decomposition methods, CEEMDAN decomposition adds pairs of positive and negative white noise signals to the original signal. The problem of noise residue is solved in two ways: (1) noise signal decomposed by the empirical mode decomposition (EMD) is added to the original signal instead of the Gaussian white noise signal; (2) different from EEMD and CEEMD decomposition, the modal components of the decomposition are averaged. The theory of CEEMDAN decomposition is to calculate the weighted average after the first-order IMF. Then, the above operations can be repeated for the signals of the IMF of each order in turn. Using CEEMDAN decomposition can solve the problem of modal component aliasing in EMD decomposition. In addition, it also eliminates the additional white noise and has a strong applicability in processing unsteady signal.

Step II: Correlation analysis should be conducted for each modal component obtained by CEEMDAN decomposition in Step I with the original signal. The corresponding threshold is set based on the correlation coefficient (ri). If ri of IMFi is greater than the threshold, the corresponding modal component is retained. Conversely, if the ri is less than the threshold, it will be deleted in subsequent analysis. In addition, variance contribution rate and spectrum analysis will be used to verify the feasibility of the selected results.

Step III: Reconstruction operation on the modal components retained in Step II is performed, and the high-frequency noise information contained in the signal is deleted.

Step IV: Based on the reconstructed signal obtained in Step III, the HHT transform is performed to obtain the Hilbert spectrum, marginal spectrum, instantaneous energy spectrum and signal energy.

Analysis of HHT blasting vibration signal based on CEEMDAN decomposition

Taking the Y direction blasting signal, which indicates the strongest vibration in the measuring point 1–2, as an example, the above-mentioned HHT analysis method is used for the time–frequency analysis. The time course of the original blasting signal is shown in Fig. 5.

Fig. 5
figure 5

Time–history curve of blasting vibration speed in Y direction at measuring point 1–2

Full size image

First, CEEMDAN is used to decompose the original blasting signal empirically. In this paper, the parameters of CEEMDAN decomposition are set as follows: the positive and negative Gaussian white noise standard deviation is 0.2, the number of added noise signal is 200, and the maximum allowed number of filtering iterations is 3000. Through the decomposition, 14 components are obtained. Figure 6 shows the time–history curves of each modal component.

Fig. 6
figure 6

Time–history curves of each component

Full size image

Then, according to the definition of the linear correlation coefficient in Eq. 20, the correlation coefficient between each modal component and the original signal is calculated. The correlation coefficient is shown in Table 2:

$$ r = \frac{{\sum {(x - \overline{x})(y - \overline{y})} }}{{\sum {(x - \overline{x})^{2} \sum {(y - \overline{y})^{2} } } }}, $$
(20)
Table 2 Correlation coefficients of modal components (IMF)
Full size table

where x represents the component (IMF) signal of each modal, and y represents the original blast vibration velocity signal.

It can be seen from Table 2 that the correlation coefficients of each modal component and the original signal are quite different. Among them, the correlation coefficients of C6–C10 and the original signal in the modal components are all greater than 0.4. It can also be seen from the component time–history graph that the waveforms of C6–C10 have good similarity with the original blasting signal, while the correlation between C1–C5 and C11–C14 and the original signal is poor. Therefore, it is preliminarily determined that C1–C5 and C11–C14 modal components contain more interference information.

The fast Fourier analysis of the modal components is shown in Fig. 7. It can be seen from Fig. 7 that the main frequency of C1 is concentrated in 400 Hz ~ 500 Hz, the main frequency of C4–C3 component is concentrated in 250–300 Hz, the main frequency of C4 component is mainly around 150 Hz, and the main frequency of C5 component is around 100 Hz. Since the main frequency distribution range of the tunnel blast vibration velocity signal is mainly below 100 Hz (Lu et al. 2016), the C1–C5 components can be regarded as high-frequency secondary components in the signal. In addition, the magnitude of the power spectrum of the C1–C5 components does not exceed 10–2 at the maximum, which is not the main component of the original signal. The dominant frequency of the C6–C10 component is below 50 Hz. At the same time, it can be found that the amplitude of C6–C10 is the same as the original signal, and it contains the main characteristic information of the original signal. Although the vibration amplitudes of C11–C14 components are relatively large, their main frequency is close to 0 Hz, which is not in accordance with common sense. It is an interference trend item caused by instrument installation errors or temperature effects. In summary, from the perspective of the spectral distribution characteristics, the C1–C5 and C11–C14 components do contain some interference signals, while C6–C10 are the main components in the original signal, which is consistent with the selection result of the correlation coefficient.

Fig. 7
figure 7

The power spectrum of modal components

Full size image

The variance of the modal component (mse) is the difference between the arithmetic mean of the square of the modal component and the square of its mean. The feasibility of the above selection is checked by the variance contribution rate (mmse) of each modal component (Li et al. 2015). The variance and variance contribution rate of the modal components are calculated as follows:

$$ {\text{mse}}(j) = \frac{1}{n}\sum\limits_{i = 1}^{n} {{\text{IMF}}_{j} (i)^{2} } - \left[ {\frac{1}{n}\sum\limits_{i = 1}^{n} {{\text{IMF}}_{j} (i)} } \right]^{2} , $$
(21)
$$ {\text{mmse}}(j) = \frac{{{\text{mse}}(j)}}{{\sum\nolimits_{j = 1}^{N} {{\text{mse}}(j)} }} \times 100. $$
(22)

The calculated variance contribution rate of each modal component is shown in Table 3. It can be seen from Table 3 that the variance contribution rates of C6–C10 modal components all exceed 10, while the variance contribution rates of C1–C5 and C11–C14 are small, and the largest contribution rate of C11 is only 7.94. Therefore, it can be seen that the conclusion obtained from the variance contribution rate is consistent with the correlation coefficient screening and spectrum analysis results. In summary, it can be concluded that the two sets of components C1–C5 and C10–C14 contain interference information, while C6–C10 are the main components in the original signal.

Table 3 Variance contribution rate of modal component (IMF)
Full size table

Based on the above analysis, the dominant modal components C6–C10 should be reconstructed to obtain a reconstructed signal that removes interference information. Next, the wavelet packet decomposition method is used to perform adaptive threshold noise reduction on the reconstructed signal. The purified signal after de-noising is shown in Fig. 8. The processed signal basically retains the characteristic information of the original signal after eliminating the influence of external noise.

Fig. 8
figure 8

Signal time–history curve after reconstruction and de-noising

Full size image

Hilbert transform is performed on the reconstructed and de-noised signal according to Eqs. 11–16, and the Hilbert time spectrum, marginal spectrum and instantaneous energy spectrum are shown in Figs. 9, 10, and 11.

Fig. 9
figure 9

Three-dimensional time spectrum of blasting signal

Full size image
Fig. 10
figure 10

Marginal spectrum of blasting signal

Full size image
Fig. 11
figure 11

Instantaneous energy spectrum of blasting signal

Full size image

As can be seen from Figs. 9 and 10, the energy of the blasting signal is mainly concentrated in the low-frequency band, which presents the characteristics of multi-frequency band distribution. Among them, the signal energy distribution of 0–25 Hz is the most concentrated, which is the main frequency band. The proportion of vibration energy in each frequency band gradually decreases after 25 Hz and is almost 0 after exceeding 200 Hz. This shows that the energy of blasting vibration is mainly concentrated in the low-frequency band, while the energy in the high-frequency band is negligible.

It can be seen from Figs. 9 and 11 that the energy of blasting vibration is mainly distributed between 1.25–1.5 s and 1.5–1.8 s, which is basically consistent with the fluctuation law of the original blast vibration velocity signal.

The influence of the distance from blast area on the signal energy spectrum

To study the effect of distance from blast area on the energy carried by the signal, the main vibration frequency band (0–200 Hz) for Y direction in the measurement points 1–1 to 1–4 is taken as an example. Table 4 shows the energy distribution percentages of each frequency band from measuring point 1–1 to measuring point 1–4. Figure 12 is the distribution of energy proportion of measuring points 1–1 to 1–4.

Table 4 Percentage of energy measured at different burst distances
Full size table
Fig. 12
figure 12

Energy distribution of measuring points 1–1 to 1–4

Full size image

It can be seen from Table 4 that the low-frequency band energy ratio of each measurement point is relatively high, while the high-band energy ratio is relatively low. For example, the energy for point 1–4 in the 0–25 Hz band is 47.91%, which almost takes up 50% of the total energy, while the energy ratios in the 125–150 Hz, 150–175 Hz and 175–200 Hz bands are less than 1%. As can be seen from the above, the distance from blast area of measuring points 1–1 to 1–4 are 15 m, 20 m, 25 m and 30 m, respectively. It can be seen from Table 4 that with the increase of the distance from blast area, the energy in the high-frequency band is slightly attenuated, and the energy proportion in the low-frequency band increases rapidly. Taking the frequency band 0–25 Hz as an example, the occupancy ratio of this frequency band in the measurement point 1–1 is 21.50%, while the measurement point 1–4 at the distance from blast area of 30 m increases to 47.91%.

At the same time, it can be seen from Fig. 12 that with the increase of the distance from blast area, although the proportion of the mid-high frequency (75–200 Hz) energy band shows a downward trend as a whole, the decrease is not large, and there is fluctuation in some frequency bands. Compared with the middle and high-frequency bands, as the distance from blast area increases, the energy ratio of the low-frequency band, especially the 0–25 Hz frequency band increases significantly. Since the natural frequency of structures is mostly in the lower frequency band, it is very likely to cause resonance of surrounding buildings as the blasting vibration waves transmit.

The influence of the maximum charge per delay on the signal energy spectrum

From the above, the distance from blast area of the measuring points 1–3, 2–3, and 3–3 are all 25 m, and the maximum charges per delay are 21 kg, 24 kg, and 36 kg, respectively. Therefore, the blast vibration velocity signals in the Y direction at the measuring points 1–3, 2–3, and 3–3 are selected to study the effect of the maximum charge per delay on the signal energy distribution. The signal energy in each frequency bands for measuring points 1–3 to 3–3 has been shown in Table 5. Figure 13 shows the distribution of energy proportion of measuring points 1–3 to 3–3.

Table 5 Percentage of energy at each measuring point under different single-shot doses
Full size table
Fig. 13
figure 13

Energy distribution of measuring points 1–3 to 3–3

Full size image

It can be seen that the signal energy of each point is mainly concentrated in the low-frequency band (0–25 Hz and 25–50 Hz). As can be seen from the Table 5, with the increase of the maximum charge per delay the percentage of energy in the low-frequency band of blast vibration velocity signals increases monotonously. For example, the energy ratio of the 0–25 Hz frequency band increases from 38.16% for measuring point 1–3 to 48.64% for point 3–3. With the increase of the maximum charge per delay, the energy in the middle- and high-frequency bands shows moderate attenuation. Especially for measuring point 3–3 with the maximum charge per delay of 36 kg, the energy in the frequency band (75–200 Hz) shows a uniform distribution trend, which occupy 1–2% of the signal energy in each sub-band.

From the above analysis, it can be seen that increasing the charge will shift the dominant energy band of the blasting shock wave to the lower frequency band. This will increase the possibility of resonance for surrounding buildings, which is harmful to the safety of the tunnel and surrounding structures under construction. Therefore, during the blasting construction process, the maximum charge per delay and the total charge must be strictly controlled, and if necessary, reasonable explosion-control measures should be taken to prevent the occurrence of resonance phenomena.

Regression analysis of blasting vibration energy

The above only focus on the blasting vibration energy in the Y direction. However, in reality, blast vibration velocity energy will propagate in every direction. Therefore, it is necessary to comprehensively consider the impact of energy transmission in the three directions of X, Y, and Z and the influence of total energy of blasting vibration on the actual project. Table 5 shows the energy value and total energy value of the measuring point in each direction.

It can be seen from Table 6 that the signal energy distribution of each measuring point is different in X, Y, and Z direction, and no obvious rules can be found for the energy ratio in each direction. Therefore, the energy values in X, Y, and Z direction are superimposed to obtain the total energy of each measuring point.

Table 6 Energy values of measuring points
Full size table

The transmission of blasting vibration is essentially the transmission of blasting energy (Yang et al. 2020; Jayasinghe et al. 2019; Matidza et al. 2020). To further assess the predicted impact range of blasting vibration energy, this paper uses dimensional analysis to study the functional relationship between the total blasting energy and the distance from blast area R, the maximum charge per delay Q, the uniaxial compressive strength of surrounding rock mass σc, the propagation speed of blasting vibration wave in rock cp, the Poisson’s ratio of rocks μ and other influencing factors.

The functional relationship between the blasting energy E and various related physical quantities can be expressed as follows:

$$ E = \varphi (R,Q,\sigma_{{\text{c}}} ,c_{{\text{p}}} ,\mu ), $$
(23)

where R, Q, cp is set as the basic dimension. Equation 24 is the coefficient determinant, which is non-zero. Therefore, it is reasonable to choose the independent basic dimension.

$$ \left| {\begin{array}{*{20}c} {\alpha_{1} } & {\beta_{1} } & {\gamma_{1} } \\ {\alpha_{2} } & {\beta_{2} } & {\gamma_{2} } \\ {\alpha_{3} } & {\beta_{3} } & {\gamma_{3} } \\ \end{array} } \right| \ne 0 $$
(24)

According to the \(\pi\) value theorem, the six physical quantities mentioned in this article can be expressed using 3 dimensionless \(\pi\) values. According to the homogeneous theorem of dimension, the independent dimension coefficient corresponding to each physical quantity can be obtained, such as:

$$ \dim \sigma_{{\text{c}}} = ML^{ - 1} T^{ - 2} = QR^{ - 3} c_{{\text{p}}}^{{2}} . $$
(25)

Therefore, there are:

$$ \left\{ \begin{gathered} \pi_{1} = \frac{E}{{Qc_{{\text{p}}}^{2} }} \hfill \\ \pi_{2} = \frac{{R^{3} \sigma_{{\text{c}}} }}{{Qc_{{\text{p}}}^{{2}} }} \hfill \\ \pi_{3} = \mu \hfill \\ \end{gathered} \right.. $$
(26)

Therefore, the relationship between various physical quantities can be expressed as follows:

$$ f\left( {\frac{E}{{Qc_{{\text{p}}}^{{2}} }},\frac{{R^{3} \sigma_{{\text{c}}} }}{{Qc_{{\text{p}}}^{{2}} }},\mu } \right) = 0. $$
(27)

Since the product or power of different dimensionless numbers is a dimensionless number, \(\pi_{1} \pi_{3} = \frac{E}{{Qc_{{\text{p}}}^{{2}} }}\mu\) is still a dimensionless number. Therefore, there is \(\pi_{4} = \pi_{1} \pi_{3} = \frac{E}{{Qc_{{\text{p}}}^{{2}} }}\mu\).

Assuming \(\pi_{5} = \pi_{2}^{{ - \frac{1}{3}}} = \frac{{Q^{\frac{1}{3}} }}{R} \cdot \left( {\frac{{c_{{\text{p}}}^{{2}} }}{{\sigma_{{\text{c}}} }}} \right)^{\frac{1}{3}}\), then the Eq. 27 can be written as follows:

$$ f(\pi_{4} ,\pi_{5} ) = f\left( {\frac{E\mu }{{Qc_{{\text{p}}}^{{2}} }},\frac{{Q^{\frac{1}{3}} }}{R}\left( {\frac{{c_{{\text{p}}}^{{2}} }}{{\sigma_{{\text{c}}} }}} \right)} \right)^{\frac{1}{3}} = 0. $$
(28)

The above equation can be converted to

$$ \frac{E\mu }{{Qc_{{\text{p}}}^{2} }} = \mathop f\limits^{ \bullet } \left( {\frac{{Q^{\frac{1}{3}} }}{R}\left( {\frac{{c_{{\text{p}}}^{{2}} }}{{\sigma_{{\text{c}}} }}} \right)^{\frac{1}{3}} } \right). $$
(29)

Simplifying Eq. 29, to produce

$$ EQ{}^{ - 1} = K\phi \left( {\frac{{Q^{\frac{1}{3}} }}{R}} \right), $$
(30)

where K is the correlation coefficient related to the physical quantities such as the compressive strength and Poisson’s ratio of the surrounding rock mass of the tunnel.

Based on the equation form of the Sadofsky prediction model, the prediction model of the total blasting energy is approximately expressed as follows:

$$ EQ^{ - 1} = K_{1} \left( {\frac{{Q^{\frac{1}{3}} }}{R}} \right)^{\alpha } , $$
(31)

where, K1 and α are the correlation coefficient related to the mechanical properties of the surrounding rock mass of the tunnel.

Regression analysis is performed using the total blasting energy data E in Table 6, and the energy attenuation regression equation obtained is as follows:

$$ EQ^{ - 1} = 32.637\left( {\frac{{Q^{\frac{1}{3}} }}{R}} \right)^{1.759} . $$
(32)

The sum of the squared correlation coefficient of the regression equation curve (r2) and the actual data is 0.914, and the statistic value of F is 359.93. The obtained fitting curve is shown in Fig. 14.

Fig. 14
figure 14

Energy attenuation regression fitting equation

Full size image

The equation for calculating the total energy of blasting by collating Eq. 30 is as follows:

$$ E = 32.637\left( {\frac{{Q^{\frac{1}{3}} }}{R}} \right)^{1.759} Q. $$
(33)

It can be seen from Eq. 31 that the total energy of blasting increases with increasing maximum charge per delay but decreases with increasing distance from blast area. From the perspective of the equation, the impact index of the maximum charge per delay on the blasting energy is 1.586, and the impact index of the distance from blast area is − 1.759. Therefore, it can be concluded that the maximum charge per delay poses stronger influence on the vibration energy in the vicinity of blasting. However, in the far blasting area, the influence of the maximum charge per delay on the attenuation of the total blasting energy gradually weakens. In addition, as the propagation distance increases, the distance between the measuring point and the blast source gradually becomes the main factor affecting the blasting energy. Therefore, attention should also be paid to the damage range of the charge amount to the surrounding rock in the blasting area. For structures in the far zone of blasting, on the premise that the vibration speed does not exceed the standard, the occurrence of resonance due to blasting vibration waves should be prevented.

Conclusion

Based on the blasting construction of the new Beijing–Zhangjiakou high-speed railway Caomaoshan Tunnel, the maximum charge per delay at the tunnel entrance section has been estimated via the blast vibration velocity prediction equation, and an improved HHT method has been proposed for energy analysis of the measured blast vibration velocity signal. The main conclusions are summarized as follows:

  1. 1.

    Through the selection of modal components and the de-noising of wavelet packet threshold, the purified blasting vibration signal can be obtained. The proposed method eliminates the intrinsic modal components and high-frequency and low-frequency interference information that are not highly correlated with the original signal, and greatly improves the accuracy of the HHT analysis. Based on analysis of the measured signal using the improved HHT method, it can be concluded that with the increase of the distance from blast area and the maximum charge per delay, the dominant frequency band of blasting energy transfers to the lower frequency band (0–25 Hz). On the other hand, the high-frequency energy of the signal gradually weakens with changes.

  2. 2.

    The blasting energy prediction equation obtained by the principle of dimensional analysis can provide good fit to the measured data, and the influence indexes of the maximum charge per delay and distance from blast area on energy are 1.586 and − 1.759, respectively, which is instructive for the selection of the explosion-control measures and explosion-control technical parameters in similar cases.