Introduction

Block caving mining is a low-cost (Laubscher 1994), large-scale, and high-intensity (Rafiee et al. 2015a) underground mining method. This process refers to all mining operations in which the ore body caves naturally after undercutting and the caved ore is recovered at drawpoints (Laubscher 1994). However, block caving mining requires specific geological conditions and is difficult to implement. If block caving mining can no longer be applied in a mine, it is almost impossible to switch to another mining method under the preceding mining technology conditions, and the loss of the mine is permanent. Because this underground mining method is so specific, assessments of rock mass cavability are important.

The goal of cavability assessment is to determine the cavability level according to the influential factors for the given geological conditions and to determine whether the mine is suitable for block caving mining. To date, various approaches to cavability assessment have been presented in the literature, including numerical simulation analysis, geomechanical classification, and mathematical approaches.

Numerical simulations of cavability have been performed with the finite element method (Hassen et al. 1993) or the distinct element method (Hassen et al. 1993; Rafiee et al. 2018a). However, numerical models can only consider some of the factors that influence rock mass cavability, which is an important modelling limitation. Geomechanical classifications have been widely applied in rock mass cavability assessments (Chen et al. 2005). Geomechanical classifications and cavability assessment have been combined to describe the characteristics of rock masses (Chen et al. 2005). The methods of geomechanical classification include rock quality designation (RQD) (Kendrick 1970), rock mass rating (RMR) (Bieniawski 1973, 1993; Karaman et al. 2015), mining rock mass rating (MRMR) (Laubscher 1990, 1994), and rock mass quality Q-classification (Q) (Barton 2002; Barton et al. 1974). The geomechanical classifications of rock masses have been established according to empirical engineering, but these classifications and the choice of influential factors are both subjective, and the interrelationships among factors are often ignored. Mathematical approaches are also based on geomechanical classifications or empirical engineering, at least to some extent. In many cases, the influential factors and cavability levels are not clearly defined. Thus, it is common to combine mathematical methods and empirical engineering, and many scholars do the same.

Wang et al. (Wang et al. 2014) established a model of rock mass cavability in terms of complex fuzzy matter element analysis. He et al. (He et al. 2019) provided a fuzzy assessment approach according to the influencing factors and assessment approaches. These studies did not consider the interrelationships among factors related to cavability. Rafiee et al. (2014, 2015a, b, 2018b) applied the rock engineering system (RES) method to introduce a new cavability index, and fuzzy mathematics and probability theory were applied to establish the interaction matrix. They considered the interrelationships among the factors that influence rock mass cavability, but they did not use fuzzy mathematics to establish a comprehensive assessment model.

Cavability assessment is a multi-index and non-linear complex system engineering task (He et al. 2019), and three problems must be solved. First, due to the uncertainty in rock mass engineering, cavability assessment has certain subjectivity in determining the index value and the cavability level. That is, uncertainty exists in the assessment process. However, fuzzy mathematics is an effective way to solve uncertainty problems and minimize subjectivity. Fuzzy comprehensive assessment (FCA) can be applied to establish an assessment model. Second, another major problem in cavability assessment is appropriately considering the factors that influence cavability and their interrelationships. A RES can be used to study the interrelationships among various factors involved in cavability assessment. Third, the results of the cavability assessment are applicable to a partial rock mass due to the discontinuity of the cavability assessment index in space. If the spatial distribution of cavability is obtained, the results can provide a more comprehensive reference and basis for block caving mining. Geostatistics and block models can be used to study the cavability with randomness and structure in space and establish a regionalized model of rock mass cavability.

In this paper, we combine FCA with RES to assess cavability, and geostatistics and block models are adopted to establish a regionalized model of cavability. The FCA is used to establish the assessment model, which can minimize the subjectivity of human judgements in the assessment process. The RES is applied to determine the weights of the influential factor, and the interrelationships among factors are considered. The regionalized model is used to establish a three-dimensional spatial model that is convenient for assessing the spatial distribution characteristics of cavability.

Fuzzy comprehensive assessment (FCA)

The factors that influence cavability were the basic foundation for establishing cavability assessment models. These factors were determined based on geomechanical classification and empirical engineering.

Influential factors and assessment levels

Rock mass cavability was affected by many factors. These factors varied for different assessment methods. Uniaxial compressive strength (UCS) and point load strength (Is(50)) were indexes of rock strength. In the field, Is(50) was easier to measure than UCS (Ren et al. 2018). Many studies (Franklin 1985; Hobbs 1963; Mishra and Basu 2012; Singh et al. 2011) have shown that Is(50) can be used to calculate UCS. Thus the Is(50) was elected, and it was subdivided into five levels according to the RMR approach (Table 1).

Table 1 Cavability classification
Full size table

The other important influence was associated with joint properties. The indexes of joint properties included the RQD index, intactness index of the rock mass, volumetric joint count of the rock mass, joint spacing index, joint roughness index, joint orientation index, joint aperture index, and joint filling index. Many studies have shown that the RQD index can be determined based on the joint spacing, intactness index of the rock mass, or volumetric joint count index of the rock mass (Ministry of Water Resources of the People's Republic of China 2014; Palmstrom 2005; Priest and Hudson 1976; Şen 1993; Şen and Eissa 1992; Sen and Kazi 1984), and the RQD is the most common index of cavability because the required variables are easy to measure. Thus, these indexes, including the RQD index, joint roughness (Jr) index, joint aperture (Ja) index, joint filling (Jf) index, and joint orientation (Jo) index, were chosen to characterize joint properties; they were subdivided into five levels according to the RMR approach (Table 1).

The groundwater condition (Wc) was a qualitative index that affected the properties of a rock mass. In this study, this index was subdivided into five levels according to the RMR approach (Table 1).

Additionally, in-situ stress was also a key index related to cavability; it was usually associated with rock strength, which was a relative index. Rafiee et al. (2015b) adopted the ratio (UCS/in-situ stress) to characterize the influence of in-situ stress on cavability. This ratio (UCS/in-situ stress) could be converted to Is(50)/in-situ stress based on UCS = 22.8Is(50) (Ministry of Water Resources of the People's Republic of China 2014). The Is(50)/in-situ stress is abbreviated as Iss, and the conversion results are listed in Table 1.

The set of influential factor indexes was U = {u1, u2, u3, u4, u5, u6, u7, u8} = {Is(50), RQD, Jr, Ja, Jf, Jo, Wc, Iss}, and the set of assessment levels was V = {v1, v2, v3, v4, v5} = {I, II, III, IV, V}. It is convenient to assess cavability with the metrics in Table 1, where Qv is the quantitative value and Qr is the quantitative range of the assessment levels.

Fuzzy assessment matrix

The fuzzy assessment matrix was established based on the fuzzy mapping (membership degree) of each index. These indexes included qualitative indexes and quantitative indexes. The membership degree of qualitative indexes was obtained by statistics on the frequency of levels from surveyors. The membership degree of the quantitative index could be determined by the membership function.

To determine the membership degree of each quantitative index, first, the measured value was converted to a value within the quantitative range Qr. This conversion was beneficial for establishing the membership function in a unified way. The following linear conversion function is established:

$$f(u_{i} {) = }q_{i\min } { + }\frac{{q_{i\max } - q_{i\min } }}{{p_{i\max } - p_{i\min } }}(u_{i} - p_{i\min } )$$
(1)
$$f(u_{i} {) = }q_{{i{\text{m}} {\text{ax}}}} - \frac{{q_{i\max } - q_{i\min } }}{{p_{i\max } - p_{i\min } }}(u_{i} - p_{i\min } )$$
(2)

where ui is the measured value. In Eq. (1), the relation between cavability and the measured value has a negative correlation. In Eq. (2), cavability and the measured value have a positive correlation. pimax and pimin are the maximum and minimum values in the cavability classification range of the measured value ui. qimax and qimin are the maximum and minimum values in the cavability classification range of each quantitative range Qr.

After establishing the linear conversion function, the membership function was established. In fuzzy theory, the membership function of an index might contain some uncertainty, so membership was expressed as a degree associated with a set (Park et al. 2012). The membership functions given by different people might vary, even for the same fuzzy problem. However, Su et al. (2007) found that the results are generally consistent and used different membership functions in a fuzzy assessment of engineering rock masses. In fuzzy assessments of rock or rock mass engineering field (Aydin 2004; Finol et al. 2001; Jian et al. 2009; Khademi Hamidi et al. 2009; Liang et al. 2003; Park et al. 2012), triangular or trapezoidal membership functions are usually adopted.

In this paper, a membership function was established by the inference method. This method was mainly based on points with membership degrees of 0, 0.5, and 1. The intermediate type of membership function was usually applied (Aydin 2004; Finol et al. 2001; Jian et al. 2009; Khademi Hamidi et al. 2009; Liang et al. 2003; Park et al. 2012; Wang et al. 2014). In the middle area, the membership degree equalled 1. At the endpoint of each quantitative range Qr, the membership degree was equal to 0.5. Combining the above characteristics, the curve of the membership function is shown in Fig. 1.

Fig. 1
figure 1

The curve of membership function

Full size image

Eventually, the following membership function Aji = Aj(f(ui)) can be established:

$$A_{5} (f(u_{i} )) = \left\{ \begin{gathered} 1,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) \le 0.1{ + }\delta } \\ \end{array} \hfill \\ \frac{{f(u_{i} )}}{2\delta - 0.2} + \frac{\delta - 0.3}{{2\delta - 0.2}},\begin{array}{*{20}c} {} & {0.1{ + }\delta < f(u_{i} ) \le 0.3 - \delta } \\ \end{array} \hfill \\ 0,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) > 0.3 - \delta } \\ \end{array} \hfill \\ \end{gathered} \right.$$
(3)
$$A_{{4}} (f(u_{i} )) = \left\{ \begin{gathered} 0,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) \le 0.1{ + }\delta } \\ \end{array} \hfill \\ \frac{{f(u_{i} )}}{0.2 - 2\delta } - \frac{\delta + 0.1}{{0.2 - 2\delta }},\begin{array}{*{20}c} {} & {0.1{ + }\delta < f(u_{i} ) \le 0.3 - \delta } \\ \end{array} \hfill \\ 1,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {0.3 - \delta < f(u_{i} ) \le 0.3 + \delta } \\ \end{array} \hfill \\ \frac{{f(u_{i} )}}{2\delta - 0.2} + \frac{\delta - 0.5}{{2\delta - 0.2}},\begin{array}{*{20}c} {} & {0.3 + \delta < f(u_{i} ) \le 0.5 - \delta } \\ \end{array} \hfill \\ 0,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) > 0.5 - \delta } \\ \end{array} \hfill \\ \end{gathered} \right.$$
(4)
$$A_{3} (f(u_{i} )) = \left\{ \begin{gathered} 0,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) \le 0.3{ + }\delta } \\ \end{array} \hfill \\ \frac{{f(u_{i} )}}{0.2 - 2\delta } - \frac{\delta + 0.3}{{0.2 - 2\delta }},\begin{array}{*{20}c} {} & {0.3{ + }\delta < f(u_{i} ) \le 0.5 - \delta } \\ \end{array} \hfill \\ 1,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {0.5 - \delta < f(u_{i} ) \le 0.5 + \delta } \\ \end{array} \hfill \\ \frac{{f(u_{i} )}}{2\delta - 0.2} + \frac{\delta - 0.7}{{2\delta - 0.2}},\begin{array}{*{20}c} {} & {0.5 + \delta < f(u_{i} ) \le 0.7 - \delta } \\ \end{array} \hfill \\ 0,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) > 0.7 - \delta } \\ \end{array} \hfill \\ \end{gathered} \right.$$
(5)
$$A_{{2}} (f(u_{i} )) = \left\{ \begin{gathered} 0,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) \le 0.5{ + }\delta } \\ \end{array} \hfill \\ \frac{{f(u_{i} )}}{0.2 - 2\delta } - \frac{\delta + 0.5}{{0.2 - 2\delta }},\begin{array}{*{20}c} {} & {0.5{ + }\delta < f(u_{i} ) \le 0.7 - \delta } \\ \end{array} \hfill \\ 1,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {0.7 - \delta < f(u_{i} ) \le 0.7 + \delta } \\ \end{array} \hfill \\ \frac{{f(u_{i} )}}{2\delta - 0.2} + \frac{\delta - 0.9}{{2\delta - 0.2}},\begin{array}{*{20}c} {} & {0.7 + \delta < f(u_{i} ) \le 0.9 - \delta } \\ \end{array} \hfill \\ 0,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} } & {} & {} & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) > 0.9 - \delta } \\ \end{array} \hfill \\ \end{gathered} \right.$$
(6)
$$A_{{1}} (f(u_{i} )) = \left\{ \begin{gathered} 0,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {f(u_{i} ) \le 0.7{ + }\delta } \\ \end{array} \hfill \\ \frac{{f(u_{i} )}}{0.2 - 2\delta } - \frac{\delta + 0.7}{{0.2 - 2\delta }},\begin{array}{*{20}c} {} & {0.7{ + }\delta < f(u_{i} ) \le 0.9 - \delta } \\ \end{array} \hfill \\ 1,\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} \\ \end{array} \begin{array}{*{20}c} {} & {0.9 - \delta < f(u_{i} )} \\ \end{array} \hfill \\ \end{gathered} \right.$$
(7)

where δ is the range value and the membership degree is equal to 1 in this range.

By determining the membership degree of each index, the fuzzy assessment matrix can be established:

$$ \begin{gathered} \begin{array}{*{20}l} {\quad \quad \,\,\,\,{\text{I}}} \hfill & {\,\,\,\,{\text{II}}} \hfill & {\,\,\,{\text{III}}} \hfill & {\,\,\,{\text{IV}}} \hfill & {\,\,\,{\text{V}}} \hfill \\ \end{array} \hfill \\ R = \left[ {\begin{array}{*{20}l} {A_{{11}} } \hfill & {A_{{21}} } \hfill & {A_{{31}} } \hfill & {A_{{51}} } \hfill & {A_{{61}} } \hfill \\ {A_{{12}} } \hfill & {A_{{22}} } \hfill & {A_{{32}} } \hfill & {A_{{52}} } \hfill & {A_{{62}} } \hfill \\ {A_{{13}} } \hfill & {A_{{23}} } \hfill & {A_{{33}} } \hfill & {A_{{53}} } \hfill & {A_{{63}} } \hfill \\ {A_{{14}} } \hfill & {A_{{24}} } \hfill & {A_{{34}} } \hfill & {A_{{54}} } \hfill & {A_{{64}} } \hfill \\ {A_{{15}} } \hfill & {A_{{25}} } \hfill & {A_{{35}} } \hfill & {A_{{55}} } \hfill & {A_{{65}} } \hfill \\ {A_{{16}} } \hfill & {A_{{26}} } \hfill & {A_{{36}} } \hfill & {A_{{56}} } \hfill & {A_{{66}} } \hfill \\ {A_{{17}} } \hfill & {A_{{27}} } \hfill & {A_{{37}} } \hfill & {A_{{57}} } \hfill & {A_{{67}} } \hfill \\ {A_{{18}} } \hfill & {A_{{28}} } \hfill & {A_{{38}} } \hfill & {A_{{58}} } \hfill & {A_{{68}} } \hfill \\ \end{array} } \right]\begin{array}{*{20}l} {Is_{{(50)}} } \hfill \\ {RQD} \hfill \\ {J_{{\text{r}}} } \hfill \\ {J_{{\text{a}}} } \hfill \\ {J_{{\text{f}}} } \hfill \\ {J_{0} } \hfill \\ {W_{{\text{u}}} } \hfill \\ {Iss} \hfill \\ \end{array} \hfill \\ \end{gathered} $$
(8)

where Aji is the membership degree.

After establishing the fuzzy assessment matrix, a comprehensive fuzzy assessment could be performed considering the weight of each index.

Weights according to the rock engineering system (RES)

The weight of each index was different in the fuzzy assessment of cavability, and the interrelationships among these indexes varied. It was necessary to consider these interrelationships and determine the appropriate weights. A RES was an engineering technique introduced to study the interrelationships among various factors involved in an engineering project (Hudson 1992; Hudson and Harrison 1992). This approach has been applied in various fields related to rock engineering (Hasanipanah et al. 2016; Rafiee et al. 2015b; Rozos et al. 2008; Saeidi and Khalokakaie 2013; Yang and Zhang 1998; Zare Naghadehi et al. 2013; Zhang et al. 2004).

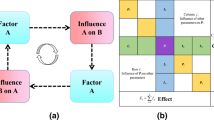
The basic idea of RES was to take all rock mechanics and engineering factors as a complete system. These factors were not fixed and isolated, and they were dynamic coexistent factors. In the RES in this study, the interaction matrix was used to represent the dynamic interactions among various factors. The basic principle of the interaction matrix is illustrated in Fig. 2 (Hudson and Harrison 1992). In the interaction matrix, all factors in the system are arranged along the leading diagonal (as shown by factor A and factor B in Fig. 2). The off-diagonal positions are used to describe the interaction mechanisms among factors. This approach indicates the direction of action according to the clockwise rotation rule.

Fig. 2
figure 2

The principle of the interaction matrix (Hudson and Harrison 1992)

Full size image

Another important task was to use a quantitative method to code the interaction matrix. The most common approach was the expert semi-quantitative method that was proposed by Hudson (Hudson 1992). Generally, the method divided the interaction mechanisms for various factors into five levels, from 0 to 4, corresponding to no interaction, weak interaction, medium interaction, strong interaction, and critical interaction.

After coding the matrix, the cause and effect coordinates are established (as shown in Fig. 3 (Hudson 1992)). The row of Pi represents the influence of Pi on all the other factors in the system, and the column of Pi reflects the influence of the other factors on parameter Pi. By summing the coding values in the row and column for each factor, ‘cause’ (Ci) and ‘effect’ (Ej) coordinates can be computed. The coordinates (Ci, Ej) represent the action mechanisms before and after construction. Then, the influence weight for each parameter can be calculated as a percentage of the sum of the system cause (Ci) and effect (Ej) for such parameters according to the following formula (Zare Naghadehi et al. 2013):

$$c_{{{\text{p}}i}} { = }\frac{{C_{i} { + }E_{i} }}{{\sum\limits_{j} {(C_{j} { + }E_{j} )} }} \times 100\%$$
(9)
Fig. 3
figure 3

Establish the cause and effect coordinates (Hudson 1992)

Full size image

In this paper, we determined the weights according to the RES. The first step was to determine the influential factors and analysis objectives. The set of influential factor indexes was U = {u1, u2, u3, u4, u5, u6, u7, u8} = {Is(50), RQD, Jr, Ja, Jf, Jo, Wc, Iss}, and the objective was assessing the cavability of the rock mass.

The second step was to build the interaction matrix of rock mass cavability. This model included the factors that influence cavability and their interaction relationships. There were nine factors on the leading diagonal: eight were the factor indexes, and one was the objective factor or potential for cavability. The objective factor gives the matrix practical significance. The interaction matrix of rock mass cavability is shown in Table 2.

Table 2 The interaction matrix of the rock mass cavability
Full size table

The third step was to code the matrix. It was impossible to directly determine the quantitative interactions among factors or between factors and cavability. The method of expert semi-quantitative was generally applied in such situations. Additionally, in the interaction matrix, one factor interacted with others, and each relation was encoded based on the results of the related rock engineering analysis. In this paper, the research results for rock mass cavability or rock engineering stability were used for coding. Rafiee et al. (2015a, b, 2018b) proposed a fuzzy expert semi-quantitative method to code the interaction matrix of cavability. The coding factors included uniaxial compressive strength, in-situ stress, joint spacing, joint orientation, joint aperture, joint roughness, filler, etc. (Yang and Zhang 1998) adopted neural networks to code the interaction matrix of rock engineering stability, and the coding factors included rock strength, discontinuity spacing, discontinuity type, discontinuity filling, discontinuity dip, RQD, groundwater conditions, etc. Kim et al. (2008) used the expert semi-quantitative to code an interaction matrix of rock behavior based on the opinions of 25 experts, the coding factors included uniaxial compressive strength, RQD, groundwater, stress, etc. Zare Naghadehi et al. (2013) used a back-propagation artificial neural network to code the interaction matrix of slope instability, and the coding factors included uniaxial compressive strength, RQD, groundwater condition, discontinuity persistence, discontinuity spacing, discontinuity orientation, etc. Moreover, the RMR (Bieniawski 1973, 1993) method used a scoring system for the influential factors, and this system was applied in coding. Based on the above approach, the coding results are shown in Table 2.

By substituting the results in Table 2 into formula (9), the weight vector cp for each influential factor index can be obtained as cp = [cp1, cp2, cp3, cp4, cp5, cp6, cp7, cp8] = [0.10, 0.12, 0.12, 0.14, 0.11, 0.10, 0.14, 0.16].

Fuzzy comprehensive assessment

The fuzzy subset can be obtained by the weighted average model:

$$B{ = }c_{{\text{p}}} \circ R = \begin{array}{*{20}c} {\begin{array}{*{20}l} {\text{ I}} \hfill & {\text{ II}} \hfill & {{\text{III}}} \hfill & {{\text{IV}}} \hfill & {\text{V}} \hfill \\ \end{array} } \\ {\left[ {\begin{array}{*{20}l} {b_{1} } \hfill & {b_{2} } \hfill & {b_{3} } \hfill & {b_{4} } \hfill & {b_{5} } \hfill \\ \end{array} } \right]} \\ \end{array}$$
(10)

where B is the fuzzy subset.

After determining the fuzzy subset B and combining it with the quantitative values Qvi, the quantitative value F of cavability can be calculated:

$$F{ = }\frac{{\sum\limits_{{i{ = 1}}}^{5} {b_{i} Q_{{{\text{v}}i}} } }}{{\sum\limits_{{i{ = 1}}}^{5} {b_{i} } }}$$
(11)

Practical application

The Luoboling copper-molybdenum mine belonged to a porphyry copper-molybdenum deposit. The spatial shape of the ore body was generally saddle-shaped and spread outward, and the ore body slope was gentle in the middle part and steep to the northwest and southeast. The distribution area of the ore body was large (approximately 2.14 km2), but the ore grade was low. In the feasibility stages, the mine owners selected block caving mining to achieve economic benefits. Therefore, it was important to assess the cavability.

In the current stage of mining, there was no rock excavation engineering, and the values of the influential factor indexes for cavability could not be measured directly. However, in the exploration stage, abundant borehole cores were preserved. Thus, we used these cores to determine the rock mass cavability. The positional relationship between the boreholes and the ore body is shown in Fig. 4.

Fig. 4
figure 4

The spatial position relationship between the measured boreholes and the ore body

Full size image

The FCA and RES methods were applied. The results of the cavability assessment are shown in Fig. 5. Based on Fig. 5 and Table 1, the levels of cavability vary from V to II, and the main levels are IV and III. The results show that mine is suitable for block caving mining.

Fig. 5
figure 5

The spatial position of F value in vertical direction of boreholes

Full size image

Regionalized model of cavability

The assessment results of cavability were for a partial rock mass due to the discontinuity of the cavability assessment index value in space. If a regionalized model of rock mass cavability was built based on these discrete results, it could provide a comprehensive reference and basis for assessments of block caving mining.

Rock mass cavability was a random function related to the spatial position in a mine, and cavability was used to describe the caving characteristic of the rock mass. Therefore, cavability was treated as a regionalized variable in this study. Geostatistics studies consider both randomness and structure in spatial distributions based on the relevant regionalized variables and variograms (Zheng and Lu 2018). Geostatistics can be used to make point predictions and estimates over large areas in two and three dimensions (Olive and Webster 2015). Therefore, a regionalized model of rock mass cavability was established based on geostatistics.

Basic geostatistics conditions

Before the regionalized model of cavability was established using geostatistics, it was necessary to test the cavability data and ensure that the basic conditions for applying geostatistics methods were met. That was, the data must obey a Gaussian distribution, and the experimental variogram must be valid.

As shown in Fig. 5, the cavability was estimated from borehole core. We combined the cavability with lithological and position information, and the core length was calculated for intervals with the same cavability levels in the vertical direction. Then, we identified the ore body according to the lithology and calculated the frequency of each level (Fig. 6). As shown in Fig. 6, the calculation results are fit with a Gaussian distribution function; the mean value μ is 0.461, the variance σ2 is 0.110, and the correlation coefficient R2 is 0.985. The results show that the cavability data obey a Gaussian distribution.

Fig. 6
figure 6

Distribution frequency histogram for the cavability assessment

Full size image

Accurate estimates of variograms were needed to obtain reliable predictions based on kriging and subsequent mapping and to optimize sampling schemes (Olive and Webster 2015). The corresponding equation is:

$$\gamma {(}h{) = }\frac{1}{2}\frac{1}{N(h)}\sum\limits_{i = 1}^{N(h)} {[Z(x_{i} ) - Z(x_{i} + h)} {]}^{2}$$
(12)

where Z(xi) is the observed value at xi, Z(xi + h) is the observed value at xi + h, and N(h) is the number of paired comparisons at lag h.

To establish the variogram, the sample data were analysed and counted in all directions. A variogram in all directions could reflect the total variation degree of cavability and judge whether the variogram could be obtained. The statistical range was 1000 m for the samples, and the lag distance h was 75 m.

As shown in Fig. 7, the variogram values are obtained in all directions. According to the characteristics of the data points in Fig. 7, the variogram adopts an exponential model. Specifically,

$$\gamma {(}h{) = }C_{0} + C_{1} \left( {1 - e^{\frac{h}{a}} } \right)$$
(13)
Fig. 7
figure 7

Scatter diagram of variogram in all directions

Full size image

where C0 is the nugget variance, C1 is the variance of the spatially correlated component and a is the distance parameter. C0 + C1 is the sill variance, and 3a is an effective range.

By fitting the data points in Fig. 7 according to formula (13), the results show that the variogram of cavability conforms to the exponential model, and the effective range of ore body 3a is 465.06 m. In general, for distances less than 465.06 m between any two points, the cavability of the two points is correlated; otherwise, the cavability of the two points may not be correlated. The effective range could be used as the range limit in subsequent interpolation. In summary, the cavability data obeyed a Gaussian distribution, and the experimental variogram was valid.

Anisotropic analysis

The variation in cavability might be anisotropic in different directions. Thus, an anisotropic analysis of the data was performed. The purpose of the anisotropic analysis was to provide necessary information about the regionalized variables for 3D spatial interpolation. The basic method of anisotropic analysis involved obtaining the variogram functions in three mutually perpendicular directions (spindle axis, secondary axis, and short axis). In this paper, the parameters of formula (13) were determined in three mutually perpendicular directions, and these parameters included the nugget variance C0, the variance of the spatially correlated component C1, and effective range 3a. The ratio of the effective range in the three directions was the proportion of central-axis anisotropy.

Based on the occurrence of the ore body, the variograms in 12 directions are statistically analysed (as shown in Fig. 8), and the spindle axis (DIR 01 in Fig. 8) is determined according to the best fit of the variogram curve. The effective range of the spindle axis was 794.04 m.

Fig. 8
figure 8

Scatter diagram of variogram in spindle direction

Full size image

The next 12 directions were generated perpendicular to the spindle axis (as shown in Fig. 9). The variograms in these 12 directions are statistically analysed, and the secondary axis (DIR 07 in Fig. 9) is determined according to the best fit of the variogram curve. The effective range of the secondary axis was 724.13 m.

Fig. 9
figure 9

Scatter diagram of variogram in secondary axis direction

Full size image

The short axis was perpendicular to the spindle axis and the secondary axis, and the short axis could be directly determined. The effective range of the short axis was 202.59 m.

Overall, the variogram functions in three directions were determined. The results show that the cavability at two points is correlated when the distance between the points is less than 794.04 m in the direction of the spindle axis. In the direction of the secondary axis, the distance of correlation is 724.13 m. In the direction of the short axis, the distance of correlation is 202.59 m. Otherwise, the cavability at two points may not be correlated in these three mutually perpendicular directions. The anisotropy of cavability was also assessed. The effective range of the spindle axis was 794.04 m. The ratio of the spindle axis to the secondary axis was 1.10, and the ratio of the spindle axis to the short axis was 3.92. Based on the results of the anisotropic analysis, a search ellipsoid of cavability is established, as shown in Fig. 10. The search ellipsoid was used as the range to search for sample points in the subsequent interpolation.

Fig. 10
figure 10

Search ellipsoid

Full size image

Geostatistics prediction method: kriging

Kriging is among the best unbiased linear prediction methods, and prediction error variances are minimized (Olive and Webster 2015). Based on the anisotropic information from the sampling data, the kriging prediction method used a weighted moving average approach in which the weights depended on the variogram and the configuration of the sample points within a given neighbourhood.

Kriging estimates can be made for points or blocks and are obtained by a linear combination of n effective sample values within the range of influence by:

$$Z_{v} (x) = \sum\limits_{i = 1}^{n} {\lambda_{i} Z} (x_{i} )$$
(14)

where, x is the position of any point in the target area, Z(xi) is a known value of cavability, and λi is a weight.

The cavability data met the basic geostatistic conditions, and mathematical expectation was not observed. Therefore, the ordinary kriging method was used for 3D interpolation. The ordinary kriging formulas are:

$$\left\{ {\begin{array}{*{20}c} {\sum\limits_{j = 1}^{n} {\lambda_{j} } \gamma {(}x_{i} ,x_{j} {) + }\mu = \gamma {(}x,x_{j} {)}} \\ {\sum\limits_{i = 1}^{n} {\lambda_{i} } { = 1}} \\ \end{array} } \right.$$
(15)

where μ is the Lagrange multiplier.

The estimation method is shown in Fig. 11. First, based on the position of the estimation point and the search ellipsoid, correlated points can be determined. Second, n effective sample values among the correlated points are determined according to the search distance from the estimation point. Third, by inputting the n effective samples and estimation point into formula (15), the weights λi can be determined. Then, the known value of cavability Z(xi) and λi are substituted into formula (14) to obtain the kriging estimate for the estimation point. By repeating the above process, the other unknown values of cavability in the space can be determined.

Fig. 11
figure 11

Estimation method

Full size image

Cross-validation

After the anisotropic analysis and kriging method were implemented, the correctness of the results was verified by cross-validation. The cross-validation method involved removing one value from the whole data set and using all the other values or those in the surrounding neighbourhood and the parameters of the given model to obtain kriging estimates. This process was repeated for each value in the data set.

The true values were compared with the kriging estimates, and the results are shown in Fig. 12. As illustrated, the range of residuals is − 0.05 to 0.05. The results suggest that the kriging method and anisotropic analysis can be used for 3D interpolations of cavability.

Fig. 12
figure 12

Ordinary kriging estimates and residual map

Full size image

Regionalized model

After anisotropic analysis and kriging, a spatial database was needed to store the data obtained from 3D interpolation, and for this purpose, a block model was created. The block model divided the ore body into several spatial blocks according to size. Each block had a centroid for data storage, and each centroid provided a spatial reference.

Based on the basic geostatistics conditions, anisotropic analysis, kriging, and cross-validation, a regionalized model of cavability was obtained by applying the block model and geostatistics interpolation. First, the ore body was divided into several blocks. The block size (20 m × 20 m × 20 m) was far less than the effective range.

Then, the cavability data were input, the anisotropic analysis parameters were used as the limit conditions for searching of sample points during the interpolation process, and the ordinary kriging method was used to complete the 3D spatial interpolation and assign the results to the corresponding block model. In the process of interpolation, the number of sample points was not less than 5, and considering the calculation speed, values of 5 to 15 were used. Finally, the regionalized model of ore body cavability was obtained (Fig. 13). As shown in Fig. 13, the spatial distribution information for cavability was obtained. This approach was beneficial for engineering design in block caving mining.

Fig. 13
figure 13

The regionalized model of ore body cavability

Full size image

Discussion

In underground mining, the existence of uncertainty associated with the physical and mechanical parameters leads cavability assessment to be impossible (Rafiee et al. 2018b). Cavability assessment is a multi-index and non-linear complex system engineering process (He et al. 2019), and the factors that influence cavability and their interrelationships need to be comprehensively considered. If the interrelationships among influential factors are ignored, the assessment results may deviate from the actual situation in mining engineering. Another problem in cavability assessment is that the results are valid for part of a rock mass because it is impossible to obtain continuous values of cavability assessment indexes in mining engineering.

To solve the above problems, this paper provided an assessment approach for rock mass cavability, and a regionalized model was established. The flow chart is shown in Fig. 14. For the assessment of rock mass cavability, first, we determined the influential factor indexes and classification levels for cavability. Second, we established the assessment model by obtaining conversion function, membership function, and fuzzy assessment matrix. Third, we determined the weights of the influential factors by establishing an interaction matrix according to the RES. Finally, we performed a fuzzy comprehensive assessment of cavability. This approach not only combined the influential factors, but also considered the interrelationships among factors, and it minimized the subjectivity of human judgement during the assessment process.

Fig. 14
figure 14

Flow chart of cavability assessment and regionalized model

Full size image

For the regionalized model of cavability, the basic geostatistics conditions were assessed and verified, and the anisotropy of cavability was analysed. The ordinary kriging method was applied, and the cross-validation was conducted. Based on these steps, geostatistics and block models were adopted to establish the regionalized model of cavability. This model estimated the spatial distribution of cavability. This approach was beneficial for engineering design in block caving mining.

It should be noted that cavability assessment should depend on engineering experience in some respects because of the complexity and uncertainty of rock mass engineering. Engineering experience may have a certain degree of subjectivity. In such situations, we can minimize subjectivity during the assessment process and combine mathematical methods with empirical engineering, as in this paper.

Conclusions

In this paper, a cavability assessment was performed for a rock mass in block caving mining, and a regionalized model was established. These were to minimize the subjectivity in the assessment process, integrate the factors that influence cavability and their interrelationships, and obtain the spatial distribution of cavability. First, the FCA and RES approaches were used, and a cavability assessment method was proposed. The results show that this approach unifies the cavability assessment process, integrates the factors that influence cavability and their interrelationships, and yields specific values of cavability. Second, geostatistics and block models were adopted to establish a regionalized model of rock mass cavability. The results show that this model is valid, and the spatial distribution of cavability is obtained. Finally, the rock mass cavability of the Luoboling copper-molybdenum mine was assessed, and a regionalized model of cavability was established. The results show that the levels of cavability vary from extremely easy caving V to difficult caving II, and the main levels are easy caving IV and fair caving III. The mine is suitable for block caving mining. However, the distribution of cavability is not uniform. Different engineering designs are needed for different cavability levels, and a zone mining strategy is recommended for block caving mining.