Introduction

The extraction of deep geothermal energy has become a worldwide hot topic in recent years prompting innovative research in the reduction of drilling costs and development of deep reservoir stimulation technologies (Tester et al. 2006). However, reliable assessment of geothermal resources at depth is very challenging because of the great uncertainties in the subsurface conditions (Fuchs and Balling 2016). Numerical simulations are quite a practical method to understand subsurface processes but require a solid theoretical background of physics and advanced computational capabilities (Vidal and Archer 2015). Taking the assessment of a specific deep geothermal reservoir, for example, in most cases, all numerical models of the subsurface fluid flow in a geothermal system will be strongly dependent on the knowledge about the geological structure, subsurface rock properties and so on. All these data are obtained from a multidisciplinary approach, including geology, geophysics, geochemistry, and drilling activities. The accuracy of a thermal model to estimate the spatial distribution of temperature at depth is directly related with the magnitude of the physio-chemical parameters (e.g., radiogenic elements concentration, thermal conductivity etc.) and their spatial distributions (Li and Heap 2014).

Parameterization of the variables from local points to spatial distribution is the key to a reliable assessment of geothermal resources. There are many methods for spatial interpolation of variables (such as radiogenic elements concentration and thermal conductivity) related with geothermal energy assessment which may be classified into three categories (Li and Heap 2008): (1) geostatistical; (2) non-geostatistical; and (3) a combination of both. Geostatistics can be regarded as a collection of numerical techniques that deal with the characterization of spatial attributes, primarily employing random models based on limited sample data points (Olea 1999). In geostatistics, semi-variogram analysis, kriging interpolation and stochastic simulation are often involved. Variogram-based models, also called the two-point statistical models, are widely applied in the simulation of groundwater flow, environmental pollution, distribution of mineral resources and geothermal resources (Yamamoto 2000; Yang et al. 2008). Among them, the kriging interpolation method is widely applied to estimate the mean value of a variable at un-sampled locations by calculating the weights of observation samples at un-sampled locations in a local region (Nshagali et al. 2015). Among the large series of kriging interpolation methods, ordinary kriging (OK) can provide an optimal unbiased estimation in a local region.

Another variogram-based model, stochastic simulation is a general means for generating multiple realizations of a specific variable, rather than a map of local best estimates produced by kriging (Goovaerts 1997a, b; Song et al. 2013). Unlike kriging, stochastic simulation approach takes into account both the spatial variation of original data at sampled locations and the variation of estimates at un-sampled locations (Delbari et al. 2009). The most widely used stochastic simulation method, Sequential Gaussian simulation (SGS), is based on the Monte Carlo method and overcomes the smoothing effect induced by the kriging interpolation method, is often applied in the description of the distribution of continuous variables (such as porosity, permeability, concentration of elements etc.), in the field of hydrogeology, ecology, pedology, mining, petroleum etc. (Dubrule 1989; Caers 2005; Doyen 2007). In comparison with the partial optimization of the estimator value in the kriging interpolation algorithm, geostatistical stochastic simulation is able to assess the spatial distribution of any desired variables while analysing its uncertainty (Soltani et al. 2013) and realizing the optimization of the estimator values in the whole region through multiple realizations based on the same input data (Zhao et al. 2010).

In addition to the high temperature hydrothermal system that are mainly related with the magmatic system, in the exploration for the production of deep geothermal energy potential sites are often located in the hot dry rocks, which are reservoirs with high concentrations of radiogenic elements, including uranium, thorium and potassium. A good example of this is the high-quality geothermal resource located in the Cooper Basin of Australia. Due to the presence of high heat generating granites in the range of 3.8–8.7 µW/m3, high temperature geothermal resources are attained (Meixner et al. 2012). Parameters involved in the calculation of radiogenic heat production include the concentration of uranium, thorium, potassium and rock density. However, because of the limited number of samples retrieved from the subsurface and the strong heterogeneity of the lithology associated with the geological formations, it is difficult to have a clear understanding on the spatial distribution of radiogenic heat produced over a large region.

The assessment of the geothermal potential in the western St. Lawrence Lowlands Basin located in the southwestern Québec requires a clear understanding of the characteristics of its crystalline basement, especially its radiogenic properties. However, because of the limited number of samples and the partial knowledge of the uncertainties associated with the prediction of the distribution of radiogenic elements in the western St. Lawrence Lowlands Basin, it is logic to investigate the radiogenic characteristics in the outcrops from the neighboring regions (e.g., Portneuf-Mauricie domain, Parc des Laurentides domain, Morin Terrane, etc.).

The main objective of this paper is to understand the radiogenic characteristics of the Grenvillian basement located in the northern part of the western St. Lawrence Lowlands Basin using geostatistical methods. Both the ordinary kriging (OK) and sequential Gaussian simulation (SGS) methods were applied to investigate the spatial distribution of the radiogenic elements to get their optimizations in the local and whole region, respectively. The spatial distribution of the radiogenic heat production is also studied statistically using the SGS to obtain optimal results at the regional scale.

Study area

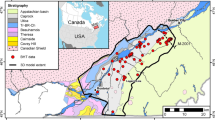
The study area lies in the Grenville Province (Fig. 1a), whose geology is composed of high-grade metamorphic terranes and stacks of thrust sheets along ductile shear zones (McLelland et al. 2010), equivalent to the roots of a Himalayan-type collisional orogeny (Rivers 1983, 2015; Davidson 1984; Dufréchou et al. 2014). The north–south strike of the Grenville structural belt extends from Canada southward into the subsurface of the Appalachian Foreland Basin (Shumaker and Wilson 1996), which belongs to part of the Appalachian orogeny that extends from Newfoundland to North Carolina (Fichter and Richard 1993; Hatcher et al. 2004). Rocks of Grenvillian age outcrop in the southwestern Québec in the lithotectonic domains of Morin Terrane, Portneuf-Mauricie and Parc des Laurentides.

Fig. 1
figure 1

(modified from Nadeau and Brouillette 1994, 1995; Sappin 2012)

a Location map of the southwestern Grenville Province and St. Lawrence Lowlands Basin (SLLB) in Québec Province. b Detailed geological map of the study area (composed of Grenville aged rocks) in the southwestern St. Lawrence Lowlands Basin and its neighboring regions including Portneuf-Mauricie (PM) domain, Shawinigan domain (SD) that is part of the Morin Terrane (MT) and Parc des Laurentides domain (PDLD)

Full size image

St. Lawrence Lowlands Basin, located in southwestern Québec, is comprised of Cambrian–Ordovician sedimentary rocks and a crystalline Grenvillian basement composed of rocks including granite, granitic gneiss, paragneiss, orthogneiss, gabbronorite, monzonite, and amphibolite (Tremblay et al. 2003; Lavoie et al. 2009; Pinti et al. 2011). Figure 1b shows simplified detailed geological map of the western part of the St. Lawrence Lowlands Basin and its neighboring regions in the Grenvillian province including the Portneuf-Mauricie (PM) domain, Morin Terrane (MT) and Parc des Laurentides domain (PDLD). The area bounded by the blue rectangle and covering the intrusions of Gagnon, Lapeyrere and Montauban group was selected in this paper. Figure 2 shows the sampling locations and concentrations of uranium, thorium and potassium in the study area.

Fig. 2
figure 2

Sampling locations and concentration of a uranium (ppm), b thorium (ppm) and c potassium (%) in the study area of the Grenville Province

Full size image

Methodology

Sampling and analysis methods

170 samples collected using RS-230 spectrometer together with data obtained from the Quebec Ministère des Ressources naturelles et de la Faune (SIGEOM database 2018) are prepared for the input data. From the SIGEOM database, samples for uranium concentration were analysed based on NAA-neutron activation method and samples for thorium concentration were analysed based on NAA and X-ray fluorescence, while those for potassium concentration were analysed based on X-ray fluorescence and plasma emission spectrometry. When a much larger region with longitudes ranging from 73°15′ to 71°45′ west of Greenwich and latitudes ranging from 46°04′ to 47°50′, see Fig. 1b, in the Grenville Province (covering Morin Terrane, Portneuf-Mauricie domain, Parc des Laurentides domain) is considered, a total number of 404 uranium, 357 thorium and 411 potassium samples were collected.

Ordinary kriging estimation method

Ordinary kriging estimation method on this paper aims to predict the value of a variable (e.g., concentration of radiogenic elements, rock density, thermal conductivity etc.) over any un-sampled location based on the values of the scattered measured data points available (Vidal and Archer 2015). As a popular tool of interpolation and extrapolation, kriging is a generic name adopted by geostatisticians for the family of generalized least-squares regression algorithms, which was developed by Matheron (1963) based on the pioneering work of Krige (1951).

The basic form of the kriging estimator can be written as (Goovaerts 1997a, b)

$${Z^*}({x_0}) - m({x_0})=\mathop \sum \limits_{{i=1}}^{n} {\lambda _i}[Z({x_i}) - m({x_i})],$$
(1)

where x0 and xi are location vectors at the estimation point and one of the neighboring data point, indexed i; n is the number of data points in local neighborhood used for estimation of Z*(x0); m(x0), m(xi) are the expected means of Z(x0) and Z(xi), respectively; \({\lambda _i}\) is the kriging weight assigned to datum Z(xi) at the estimation location point x0; note that the same datum may produce different weights at different estimation locations.

The number of data points involved in the estimation as well as their weights may change from one location to another. However, ordinary kriging (OK) allows one to account for the local variation of the mean by limiting the domain of stationarity of the mean to the local neighborhood centered at the location point x0 (Goovaerts 1997a, b).

The following generic equation can be used to describe the linear regression ordinary kriging estimator at a specific location:

$$Z_{{{\text{OK}}}}^{*}({x_0})=\mathop \sum \limits_{{i=1}}^{n} \lambda _{i}^{{{\text{OK}}}}Z({x_i}),$$
(2)

where \(Z_{{{\text{OK}}}}^{*}({x_0})\) is the ordinary kriging estimator at the location x0; x1,…, xn is a series of observation locations and Z(x1), …, Z(xn) are the corresponding measurement values at the observation or sampling locations; \(\lambda _{i}^{{{\text{OK}}}}\) is the vector of ordinary kriging weights for the surrounding data points and satisfy the relationship as follows:

$$\mathop \sum \limits_{{i=1}}^{n} \lambda _{i}^{{{\text{OK}}}}({x_0})=1.$$
(3)

Based on the unbiased condition and the relation that

$$C(h)=C(0) - \gamma (h),~$$
(4)

where C(0) is the sill value in the semi-variogram diagram \(\gamma (h)\).

The ordinary kriging system is expressed in terms of covariant (semi-variograms) as

$$\left\{ {\begin{array}{*{20}{l}} {\mathop \sum \limits_{{i=1}}^{n} C({x_i} - {x_j})\lambda _{i}^{{{\text{OK}}}}({x_0})+\mu =C({x_0} - {x_j}), \quad (j=1, \ldots ,n)\quad \quad (5)} \\ {\mathop \sum \limits_{{i=1}}^{n} \lambda _{i}^{{{\text{OK}}}}({x_0})=1,\qquad \quad\qquad \qquad\qquad \qquad\qquad \qquad\qquad \ \ (6)} \end{array}} \right.$$

where \(\mu\) is the Lagrangian parameter.

The ordinary kriging system can be written in the matrix form as

$${K_{{\text{OK}}}}{\lambda _{{\text{OK}}}}({x_0})={M_{{\text{OK}}}},$$
(7)

and the ordinary kriging weights can be described as [λOK] = [KOK]−1 [MOK]:

$$\left[ {\begin{array}{*{20}{c}} {{\lambda _1}} \\ {{\lambda _2}} \\ \ldots \\ {{\lambda _n}} \\ { - \mu } \end{array}} \right]={\left[ {\begin{array}{*{20}{c}} {{C_{11}}} \\ {{C_{21}}} \\ \ldots \\ {{C_{n1}}} \\ 1 \end{array}~~~~~\begin{array}{*{20}{c}} {{C_{12}}} \\ {{C_{22}}} \\ \ldots \\ {{C_{n2}}} \\ 1 \end{array}~~~~~\begin{array}{*{20}{c}} \ldots \\ \ldots \\ \ldots \\ \ldots \\ 1 \end{array}~~~~~\begin{array}{*{20}{c}} {{C_{1n}}} \\ {{C_{2n}}} \\ \ldots \\ {{C_{nn}}} \\ 1 \end{array}~~~~\begin{array}{*{20}{c}} 1 \\ 1 \\ \ldots \\ 1 \\ 0 \end{array}} \right]^{ - 1}}~\left[ {\begin{array}{*{20}{c}} {{C_{01}}} \\ {{C_{02}}} \\ \ldots \\ {{C_{0n}}} \\ 1 \end{array}} \right].$$
(8)

The solution of \({\lambda _i}\) depends on the solution of the covariance Cij between the point locations i, j. This requires the selection of a reasonable semi-variogram theoretical model (e.g., spherical, exponential, Gaussian model etc.) to fit the experimental data.

Sequential Gaussian simulation method

The sequential Gaussian simulation (SGS) requires a standard Gaussian data with mean of 0 and variance of 1. Therefore, the input data should be transformed into a normal (Gaussian) distribution through a quantile transform. In the SGS algorithm the mean and variance of the Gaussian distribution at any location point along the simulation path is estimated by the kriging estimate and the kriging variance (Vidal and Archer 2015). Rather than choosing the mean as the estimate at each grid node like in the kriging interpolation method, SGS uses a random deviate from the normal distribution. This random deviate is selected according to a uniform random number representing the probability level. The variable at each unknown grid node is simulated sequentially according to its normal conditional cumulative distribution function (ccdf). During multiple realizations, it uses not only the original data but also all the previously simulated values.

The detailed workflow of the conditional simulation of a continuous variable Z(xi) in a Gaussian space during one realization have already been investigated by many previous authors (e.g., Deutsch and Journel 1998; Remy et al. 2009; Soltani et al. 2013) thus not mentioned here. Randomization allows to perform multiple realizations including their mean values.

Calculation of radiogenic heat production

When the concentration of a radiogenic element (e.g., uranium, thorium or potassium) is known, together with the values of rock density at the sampled locations, radiogenic heat production can be calculated using the following empirical function (Mareschal and Jaupart 2004; Rybach 1976, 1988):

$$A={\rho _{\text{r}}}[9.52{C_{\text{u}}}+2.56{C_{{\text{Th}}}}+3.48{C_{\text{k}}}] \times {10^{ - 5}},$$
(9)

where \({\rho _{\text{r}}}\) is the dry density of rock (in kg/m3), Cu is the uranium content (in ppm), CTh is the thorium content (in ppm), and Ck is the potassium content (in %), A is the radiogenic heat production (measured in units of µW/m3).

Results and discussion

Concentration of radiogenic elements at sampled sites

In the study area (Fig. 1b), a region enclosed by longitudes in the range between 73°15′ and 71°45′ west of Greenwich and latitudes in the range between 46°04′ and 47°50′, a total of 404 uranium data, 357 thorium data and 411 potassium data were collected. Comparing the concentration of radiogenic elements for different rock types, including granitic gneiss, paragneiss, quartzite, amphibolite, granite, diorite, quartz monzonite and gabbro-gabbronorite that comprise the Precambrian Grenville Province (Fig. 3), it can be demonstrated that the distribution of radiogenic elements is very sparse in all types of rocks. In general, the concentration of uranium is in the range of 1–2 ppm for most samples (e.g., in granitic gneiss, amphibolite, granite, diorite and quartz monzonite), although a little higher in quartzite and lowest in gabbro-gabbronorite.

Fig. 3
figure 3

Boxplot of the concentration of radiogenic elements a uranium (ppm), b thorium (ppm) and c potassium (%) for different rock types sampled from outcrops in the Grenville Province including the Portneuf-Mauricie (PM) Domain, Morin Terrane (MT) and Parc des Laurentides Domain (PDLD). n the number of samples, Q1 the first quartile value, Q2 median value, Q3 the third quartile value, A1 = Q1 − 1.5 × (Q3 − Q1), is the smallest non-outlier value; A2 = Q3 + 1.5 × (Q3 − Q1), is the largest non-outlier value. The circular symbols represent extreme outlier values

Full size image

Similarly, the concentration of thorium for most rocks in the study area is in the range of 3–10 ppm, with gabbro-gabbronorite and quartz monzonite having the lowest and highest values, respectively.

The concentration of potassium ranges from 1 to 4% in most rock types investigated, with granite and quartz monzonite showing the highest values.

According to the boxplot the average concentration of uranium, thorium and potassium is 1.78 ppm, 6.01 ppm and 2.64%, with a standard deviation error of 3.57, 7.27 and 1.85, respectively. It can also be observed that 90% of the total samples have uranium concentration of less than 3 ppm, 64% of the samples have thorium concentration of less than 5 ppm, and 56% of the samples have potassium concentration of less than 3%.

The cumulative distribution frequency diagrams (in Fig. 4), it can be seen that only 3 and 4% of the samples from the Portneuf-Mauricie domain and Morin Terrane, respectively, have a uranium concentration of more than 6 ppm. As regards to thorium concentration, less than 2 and 12% of samples from the Portneuf-Mauricie domain and the Morin Terrane, respectively, have their concentrations higher than 15 ppm. This result demonstrates that radiogenic elements concentration for most samples in the research region is very low. Besides, the Portneuf-Mauricie domain is less radiogenic compared with the Morin Terrane.

Fig. 4
figure 4

Cumulative distribution curves for K2O, uranium (U) and thorium (Th) concentrations in the Portneuf-Mauricie domain and the Morin Terrane

Full size image

Kriging estimation of uranium concentration

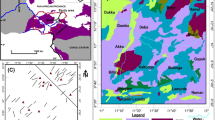
Results of the experimental semi-variance study and a spherical model fit to raw data for uranium concentration in the study area (of size 35 km × 80 km) are presented in Fig. 5. It can be observed that the omni-directional isotropic semi-variogram is identical to a spherical structural curve type, however, with a nugget effect of 0.4, and attains a sill of 0.8 (i.e., 1.2–0.4) at a range of 4500 m.

Fig. 5
figure 5

Omni-directional variogram for the concentration of uranium in the study area and the best fitting spherical model

Full size image

Using the spherical semi-variogram in Fig. 5 and a search ellipsoid range of 20 km for ordinary kriging estimation, Fig. 6a–c shows the variations in the concentration of radiogenic elements uranium, thorium and potassium, respectively, in the study area. When these results of Figs. 2 and 6 are compared, it can be seen that the ordinary kriging methods describe local estimates better. However, the overall distribution of the concentration is poorly illustrated because of sample limitation.

Fig. 6
figure 6

Spatial distribution of concentration of a uranium (ppm), b thorium (ppm) and c potassium (%) in the study area obtained through applying the ordinary kriging method (note: the sampling locations presented by rectangles and the main geological boundaries by contours)

Full size image

Spatial distribution of uranium, thorium and potassium based on SGS

Based on SGS modelling method and the omni-directional semi-variograms shown in Fig. 5, the spatial distribution of uranium (under 100 realizations) is generated in the study area of 35 × 80 km2, for a cell size of 175 m × 400 m using the geostatistics software—SGeMS.

Compared with the distribution of the uranium concentration using ordinary kriging interpolation method (Fig. 6) and the omni-directional variogram with a range of 3400 m for raw data after normal score transformation (as in Fig. 7a), SGS gives much more details for calculating the concentration of uranium by avoiding the smoothing effect (see Fig. 8a). In ordinary kriging method, the overall distribution of the uranium concentration cannot be described because of the limitation of the data set in the concentration of uranium. In contrast, the sequential Gaussian simulation method can better describe the structure of the database (e.g., uranium concentration, in Fig. 8a) using the probability distribution function. Table 1 presents the range of variations for measured uranium data, E-type from the SGS and the results from the ordinary kriging method. Results obtained from the E-type tallies well with those derived from the ordinary kriging method.

Fig. 7
figure 7

Omni-directional variograms for the concentration of uranium, thorium and potassium after the normal score transformation in the study area used for the sgs simulation

Full size image
Fig. 8
figure 8

Concentration of uranium (a), thorium (b) and potassium (c) using conditional SGS simulation based on 100 realizations applying the omni-directional variograms in Fig. 7

Full size image
Table 1 Basic statistics of uranium output data for different realizations, a comparison for raw data, E-type and kriged values
Full size table

In addition to the uranium concentration, the distribution of the thorium (Fig. 8b) and potassium (Fig. 8c) using SGS simulation method are also shown by applying the results of omni-directional variograms with the range of 7200 m and 6000 m, respectively (Fig. 7b, c). Minor differences occur in the E-type results derived from the two different realizations 30 and 100, demonstrating that the E-type based on the SGS simulation can still be further applied.

Spatial distribution of radiogenic heat production based on SGS

In the study area, not all data points that were measured the concentration of the radiogenic elements have the density values. Data points without density values were assigned values based on a data set from the neighboring regions according to the similar rock types. There is a large range of density for a specific rock over a large region, as shown in Fig. 1b, e.g., the density of gabbro ranges from 2600 to 3530 kg/m3, with a mean of 2995 kg/m3, granite ranges from 2620 to 2760 kg/m3, with a mean of 2670 kg/m3, granitic gneiss ranges from 2530 to 3160 kg/m3, with a mean of 2650 kg/m3, granodiorite ranges from 2730 to 2970 kg/m3, with a mean of 2840 kg/m3 etc. Therefore, radiogenic heat production can only be calculated using the empirical function Eq. 9 when the concentration of uranium, thorium, potassium and their density values are known. Accordingly, three types of radiogenic heat production can be calculated based on the range of the rock density values (i.e., minimum, average and maximum). Afterwards, the spatial distribution of the heat production can be simulated by applying the SGS method (Fig. 9). Result shows that using average densities, the heat production is in the range of 0.01–3.4 µW/m3. The difference between calculated radiogenic heat production using the minimum and maximum density values can reach to an extent of 30%, see Fig. 8a, c for comparison.

Fig. 9
figure 9

Spatial distribution of the radiogenic heat production (unit: µW/m3) using the average (a), minimum (b) and maximum (c) density values for specific rocks at the sample points through applying the conditional SGS with 100 realizations

Full size image

Conclusions

Knowledge of the radiogenic characteristics of the crystalline basement of the western St. Lawrence Lowlands Basin is essential to evaluate the potential of geothermal resources at depth. Since data are typically sparse and expensive to acquire, the radiogenic characteristics of the outcrops in the neighboring Grenville Province may provide a good reference in understanding the heterogeneity of the basement buried by sedimentary rocks in the western St. Lawrence Lowlands Basin. Both the ordinary kriging and the sequential Gaussian simulation methods were applied to analyse the spatial distribution of radiogenic element concentration in a selected region of size 35 km × 80 km to calculate the spatial distribution of radiogenic heat production.

Some main conclusions can be drawn as follows: (1) for most rocks from the study region that may represent the granitic basement of the western St. Lawrence Lowlands Basin, the concentration of uranium, thorium and potassium is in the range of 1–2 ppm, 3–10 ppm and 1–4%, respectively; (2) a strong anisotropy exists in the distribution of the radiogenic elements concentration data; (3) compared with the ordinary kriging method, which is better in describing the estimates at a local scale, SGS gives much more details for calculating the concentration of radiogenic elements in the overall region when data are very sparse; (4) the spatial distribution of radiogenic heat production in the study area is highly dependent on the value of rock density, and concentrations of the radiogenic elements uranium, thorium and potassium; and (5) using the sequential Gaussian simulation method the difference between the minimum and the maximum radiogenic heat production values is 30%, considering the differences in radiogenic element concentration values and different rock density values.