Introduction

Many landslides exhibit long-lasting, small-scale movements under gravity loads that are affected by the creep property of slope materials (Desai et al. 1995). Recent fatalities and economic damages have amplified interest in slowly creeping landslides (Crosta et al. 2014; Jarman et al. 2014; Klimeš et al. 2016; Wartman et al. 2016). Much progress has been made using available models to back-analyze and predict creep in landslides, e.g., the Kelvin model (Feng et al. 2003; Gasc-Barbier et al. 2004; Mitchell 2008; Tang and Wang 2008; Rutter and Green 2011), Burgers model (Jian et al. 2009; Bizjak and Zupancic 2009; Bozzano et al. 2012), Voellmy model (Manzella and Labiouse 2009; Welkner et al. 2010; Pirulli et al. 2011) and Bingham model (Gauer et al. 2005; Geertsema et al. 2006; Ulusay et al. 2007; Di Maio et al. 2013). Considerable effort has also been made to correlate creep with external triggers such as underground erosion (Furuya et al. 1999; Bhuiyan et al. 2016; Yu et al. 2016), rainfall and groundwater (Sasaki et al. 2000; D’Odorico and Fagherazzi 2003; Qi et al. 2006; Peng et al. 2009), reservoir level (Deng et al. 2000; Qi et al. 2006), temperature (Ladanyi 2006; Vlcko et al. 2009; Darrow et al. 2012; Krautblatter et al. 2013).

Previous studies have applied pre-existing constitute models to analyze the creep behavior of homogeneous soil or rock, sometimes involving the testing of small-scale rock or homogeneous soil samples (Yang et al. 2004; Petley et al. 2005; Ham et al. 2006; Ham 2006; Wang 2008). In contrast, few studies of the creep behavior of landslide materials containing coarse particles, as large-scale experiments, are required. However, the creep properties of geological materials containing coarse particles, especially soil in the slip zone, play a crucial role in the evolution of slopes. In particular, many studies have shown that rock fragments have a significant effect on the mechanical properties of soils (Bagherzadeh-Khalkhali and Mirghasemi 2009; Ham et al. 2010; Ishikawa and Miura 2011; Venkatarama Reddy and Latha 2013). It is therefore necessary to execute large-scale creep tests and model quantitative expressions of relevant materials with large clasts.

This paper reports a series of compression experiments carried out on large-scale clayey gravel samples obtained from the slip zone of the Majiagou landslide, which is an unstable slowly creeping natural slope(200 mm/a on average). The slip zone contains abundant coarse particles which necessitate the use of a large triaxial apparatus for determining sample strength and other relevant properties. These test results were used to analyze the creep characteristics of the slip zone, employing a new empirical creep equation to describe the time-dependent behavior of coarse granular soils.

Nature of investigated landslide

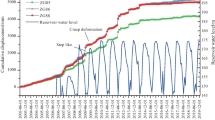
The Majiagou landslide is located on the left bank of the Zhaxi River which forms a tributary of the Yangtze River (Fig. 1). The landslide is composed of slide mass #1 and #2 (Fig. 2). Investigated here is slide mass #1, where slow and continuous deformation has been observed by GPS monitoring since 2009. The tongue-shaped mass is approximately 538 m long, 180 m wide and 13 m thick, indicating a volume of about 1.3 × 106 m3. The crown has formed at an elevation of 280 m above sea level (a.s.l), and the toe is 135 m.a.s.l. Slope angles in the landslide vary from 30° at the crown to 10° near to the toe. The landslide mass is comprised of clayey and silty gravel lying above flysch layers of argillaceous siltstones and silty mudstones of the Jurassic Suining Formation (J3s), which have a dip of about 25°–30° in the direction of 280°–290° (Zhang and Tan. 2013).

Fig. 1
figure 1

Location map of Majiagou landslide

Full size image
Fig. 2
figure 2

Photograph of Majiagou landslide, looking NE

Full size image

A monitoring network was established in October 2014 to improve understanding of the mechanism and deformation characteristics of this landslide. In order to install the monitoring instruments, two 40-m-deep trial wells (TW-A and TW-B) were excavated at the middle part of the landslide (see Fig. 2). During excavations, samples were collected from a profile across the slip zone exposed in TW-A (Fig. 3).

Fig. 3
figure 3

Close-up of the slip zone exposed in TW-A

Full size image

The triaxial creep experiments

Test equipment

An initial series of drained triaxial compression tests were conducted by a static strain-controlled triaxial machine (Fig. 4) to obtain the peak strengths. The maximum vertical force of the static testing system is 300 kN, and the maximum confining pressure is 1.5 MPa.

Fig. 4
figure 4

SY250 strain-controlled machine

Full size image

The triaxial creep tests were performed by a self-developed stress-controlled apparatus (Fig. 5). This creep testing device consists of a loading frame, a triaxial cell, an electronic signal conditioning and control system, and a data acquisition and display system. Specially, it is equipped with a power container to supply stable pressure during loading. The maximum vertical force of the testing system is 100 kN, and the maximum confining pressure is 1.5 MPa. The testing time, the testing load (including the confining pressure and axial force), the axial and volume deformations of each specimen are automatically recorded.

Fig. 5
figure 5

YLSZ150-3 stress-controlled machine

Full size image

Samples preparation and test scheme

Physical properties for the slip zone materials are listed in Table 1. The diameter (D) and height (H) of the cylindrical specimens were measured after preparation, and they averaged 149.8 and 300.5 cm, corresponding to H/D = 2.01. Figures 6 and 7 show the stress–strain and volume–axial strain curve of the static triaxial compression tests, respectively. The peak deviatoric stress was 206.76, 376.41, 686.57, 982.17 for confining stresses of 0.1, 0.2, 0.4, 0.6 MPa, respectively.

Table 1 Physical properties of the specimen sets
Full size table
Fig. 6
figure 6

Axial stress–axial strain curve of drained compression tests

Full size image
Fig. 7
figure 7

Volume strain–axial strain curve of drained compression tests

Full size image

The time-dependent behavior of the soil was observed for a variety of drained conditions. Drained creep triaxial tests were conducted at four confining stresses (CS = 0.1, 0.2, 0.4, and 0.6 MPa) and four stress levels (SL = 0.30, 0.45, 0.60 and 0.75). Stress level (SL) was defined as the ratio of the creep stress with respect to the strength at a corresponding confining stress. A multiple-step loading scheme was used for this test, and the Boltzmann linear superposition law (Tan et al. 1989) was used to process the data obtained from the stepped loading. The stress level was defined to be the ratio of axial stress in the creep test to the peak stress in the drained triaxial compression tests under corresponding confining pressure. According to a large amount of test data, the axial deformation always becomes stable later than the volume deformation (Gao et al. 2012). Therefore, the axial deformation was chosen to be the criterion of the experiments. The load was maintained until the axial creep deformation became larger than 0.15. The interval for each deviatoric stress increment was 21–22 days in this study. To maintain a constant temperature inside the triaxial cell, the temperature in the laboratory was continuously maintained at 20 ± 0.5 °C. The total test arrangement is shown in Table 2.

Table 2 Loading scheme of triaxial creep test
Full size table

Creep tests of clayey gravel

Creep axial and volume deformation–time relationship curves of clayey soil under different confining pressures and increasing axial stresses are shown in Figs. 8 and 9, respectively. According to the Boltzmann superposition law, the strain–time relationship can be plotted as Fig. 10. From these figures, the deformation characteristics of the slip zone soil are as follows:

Fig. 8
figure 8

Axial strain–time relationship curves

Full size image
Fig. 9
figure 9

Volumetric strain–time relationship curves

Full size image
Fig. 10
figure 10

Axial strain–time relationship curves according to Boltzmann superposition law. a σ 3 = 0.1, b σ 3 = 0.2, c σ 3 = 0.4, d σ 3 = 0.6

Full size image
  1. 1.

    The slip zone soil experienced two creep stages, i.e., the decay creep stage (primary stage) and constant speed creep stage (secondary stage), and none of the soil specimen got into an accelerated deformation stage during the experiments. Following each loading step, the soil specimen entered the decay creep stage after immediate strain and deformation increased persistently as creep time increased. The figures also indicate that time effects were more pronounced at higher deviatoric stresses. The relation between strain rate of the second creep stage and SL is shown in Fig. 11. It can be seen that the average creep rate of the secondary creep stage increased linearly with the increase of SL.

    Fig. 11
    figure 11

    Strain rate–stress level relationship

    Full size image
  2. 2.

    Experimental data allow us to identify the beginning of a constant rate creep stage because the creep curves clearly define the subsequent stage of decreasing strain rate. The start of the constant creep rate was taken as 36 h on average from the beginning of each loading step. The general relation is that the duration of the decayed creep stage increased linearly with the increase of deviatoric stress. Studies have suggested that soil grains may keep their position until breakage due to static fatigue of a number of particles located in the force chain during creep (Karimpour and Lade 2010, 2013; Karimpour 2012). Because the stresses on the boundaries are constant, rearrangement and reorientation of the broken particles will culminate in formation of new force chains and creep deformation is observed (Augustesen et al. 2004; Liingaard et al. 2004; Karimpour and Lade 2013). As particles fracture and fit into available voids, the coordination numbers increase and the critical forces passing through the particles decrease with time (Lade et al. 1998, Lade and Liu 1998; Karimpour and Lade 2010; Karimpour 2012). Therefore, the rates of particle breakage and creep deformations decrease with time. Once the stable packing structure and force chains have developed after a period of time, the same creep deformation rate is obtained (Lade 2007; Lade et al. 2009; Lade and Karimpour 2010). The observed creep behavior can be related to the mechanism presented above. When the SL increased, there were more particles to fracture in the specimen and it took more time for the specimen to form a stable structure, so the interval required for the strain rate to remain constant increased with SL in all tests.

  3. 3.

    Taking the axial strain and deviatoric stress values from Fig. 10 at a given time (such as t = 2, 4 h and so on), the isochronous stress–strain curves can be obtained, as shown in Fig. 12. These isochronous stress–strain curves of clayey gravel appear to be piecewise curves. For low values of loading stress, the relationship between stress and strain was approximately linear. As the deviatoric stress level increased, the deformation modulus of the soil decreased and the curve evolved into a hyperbola. The long-term strength of the clayey gravel, which is defined as the inflection point in the isochronous stress–strain curve (Yan et al. 2008), can be estimated to range from 0.60 to 0.75 of the instant strength. Moreover, we can conclude that the long-term strength decreased sharply as the creep time increased when the creep time is less than 136 h (Fig. 12).

    Fig. 12
    figure 12

    Isochronous stress–strain curves under different confining stress. a CS = 0.1 MPa, b CS = 0.2 MPa, c CS = 0.4 MPa, d CS = 0.6 MPa

    Full size image

Creep constitutive equation of clayey gravel

According to the characteristics of the creep curves, two well established creep models, the Burgers model and Singh–Mitchell model, were used to describe the time-dependent behavior of the clayey gravel soil.

Comparisons of test data with established models

The Burgers model is composed of a Maxwell element and a Kelvin element (Fig. 13). The Maxwell element can be used to simulate the instantaneous and stationary creep strains, and the decreasing creep strain can be simulated by the Kelvin element (Barnes 2000).

Fig. 13
figure 13

Elements of a Burger’s model

Full size image

The creep equation of the Burgers model is given as:

$$\varepsilon (t) = \frac{\sigma }{{\eta_{2} }}t + \left[\frac{1}{{E_{1} }} + \frac{1}{{E_{2} }}(1 - e^{{ - \frac{{E_{2} }}{{\eta_{1} }}t}} )\right]\sigma$$
(1)

where σ and ε are stress and strain; η 1 and E 1 are viscosity and modulus of the dashpot and spring elements in serial; and η 2 and E 2 are the viscosity and modulus of the dashpot and spring elements in parallel. The dashpot element can describe the linear relationship between creep stress and strain rate, while the spring element can describe the linear relationship between creep stress and strain.

The Singh–Mitchell model is an empirical equation with three parameters based on many drained and undrained tests (Singh and Mitchell 1969). It is valid for a variety of soils with stress levels in the range of 30–90 %. The Singh–Mitchell model combines exponential stress–strain rate and power strain rate–time relationships, which is expressed as:

$$\dot{\varepsilon } = \frac{d\varepsilon }{dt} = Ae^{\alpha D} \left(\frac{{t_{1} }}{t}\right)^{m}$$
(2)

where ε is axial strain, t the creep time, and D the deviatoric stress level; and t 1 is the elapsed time at which A is defined. Moreover, A is the intercept on a plot of ln(dε/dt) versus D when t = t 1; m is the absolute value of slope of ln(dε/dt) versus lnt, and α is the absolute value of the slope of ln(dε/dt) versus lnD.

Equation (2) is integrated to obtain strain. If the lower limit of integral is taken as t 1, the simplified form can be written as:

$$\mathop \varepsilon \limits^{{}} = B_{1} e^{\beta D} \left(\frac{\text{t}}{{{\text{t}}_{1} }}\right)^{\lambda }$$
(3)
$$B_{1} = \frac{{A_{1} t_{1} }}{1 - m},\quad \beta = \alpha ,\quad \lambda = 1 - m$$
(4)

where λ is the slope of lnε against ln t at any fixed value of D and β is the slope of ln t against D, at any fixed time. B 1 is the intercept of lnε against D at t = t 1.

The Singh–Mitchell and the Burgers models were used to fit the creep data (Fig. 14). The Burgers model can fit the initial sharp rising strain and the decayed strain better than the Singh–Mitchell model, but it cannot predict the trend of the second creep stage as well as the Singh–Mitchell model. Figure 14 reveals that both models can capture some aspects of the soil long-term behavior, but neither model accurately describes the long-term behavior of the soil. Because they were developed by fitting the creep curves, these empirical models may not be general enough and their applicability tends to be limited to specific boundary and loading conditions, as pointed out by Liingaard et al. (2004).

Fig. 14
figure 14

Creep model fitting for confining pressure = 0.1 MPa

Full size image

A new empirical model

The above comparisons show that both models can describe certain time-dependent behaviors, but that discrepancies remain between the fits and the experimental data. Therefore, a new semiempirical creep formulation was developed based on the experimental studies. The details of function selection and parameters estimates are provided below.

Morgan–Mercer–Flodin function

Decaying exponential, hyperbolic and power functions are widely used to describe the time-dependent response of soils (Singh and Mitchell 1969; Semple 1973; Mesri et al. 1981), but they might not be the most appropriate. When the deformation is predicted by a power or exponential law, the value of creep is generally too high in the early creep stages and too low in the later stages. The opposite occurs for creep deformation modeled by a hyperbolic formula (Fig. 15). Abundant data indicate that the shape of creep curves with two creep stages is often convex with an approach to an upper asymptote (Mesri et al. 1981). Therefore, a function with these characteristics can be a candidate for modeling test data.

Fig. 15
figure 15

Fitting results of different functions

Full size image

Growth models have been widely used to describe time-dependent responses (Tjørve 2003; Pandey and Chand 2004; Phoon et al. 2007; Kondraivendhan et al. 2013; Organtini and Russo 2013). It is reasonable to apply a nonlinear growth model to the creep strain of soil. The MMF model proposed by Morgan et al. (1975) has been used to describe a wide variety of nutrient–response relationships in higher organisms; this is an asymmetrical sigmoidal function with four parameters (Morgan et al. 1975; Seber and Wild 2003). The general form of the MMF function is:

$$y = \frac{{ab + ct^{\delta } }}{{b + t^{\delta } }}$$
(5)

The initial value of Eq. (5) is:

$$\mathop {\lim }\limits_{t \to 0} \frac{{ab + ct^{\delta } }}{{b + t^{\delta } }} = a$$
(6)

And the ultimate value of Eq. (5) is:

$$\mathop {\lim }\limits_{t \to \infty } \frac{{ab + ct^{\delta } }}{{b + t^{\delta } }} = c$$
(7)

In order to interpret the parameters physically, Eq. (5) is recast:

$$\varepsilon = \varepsilon_{\infty } - \frac{{\varepsilon_{\infty } - \varepsilon_{0} }}{{1 + (kt)^{\delta } }}$$
(8)

The creep strain, which subtracts the instant strain from the total strain, can be expressed as:

$$\varepsilon_{c} = (\varepsilon_{\infty } - \varepsilon_{0} ) - \frac{{(\varepsilon_{\infty } - \varepsilon_{0} )}}{{1 + (kt)^{\delta } }}$$
(9)

Defining ε ∞  − ε 0 as ε f , we get Eq. (10):

$$\varepsilon_{c} = \varepsilon_{f} - \frac{{\varepsilon_{f} }}{{1 + (kt)^{\delta } }}$$
(10)

where ε c is creep strain at a fixed time t; ε 0 = a the strain at t = 0; ε ∞  = c the upper asymptote; k = (1/b) 1/δ affects the creep rate and the duration of the first creep stage; and δ a parameter that controls the point of inflection. The point of inflection is located at: t = [(δ − 1)/(δ + 1)]δ, and ε t  = (δ − 2)/2δ. Figure 16 shows example plots of the MMF curves for different values of δ. There is no point of inflection for δ < 1, and then the curve degenerates to a convex shape.

Fig. 16
figure 16

MMF curves for different values of δ

Full size image

Determination of the parameters

For each creep curve, the four parameters were estimated using least squares (Newton–Gauss also known as Marquardt method). The following constraints apply to the fit coefficients:

$$\varepsilon_{\infty } > 0,\varepsilon_{0}^{{}} > 0,k > 0,\delta > 0,\varepsilon_{\infty } > \varepsilon_{0}$$

The fitting curves (Fig. 17) and associated parameters were determined for the MMF model (Table 3). Table 3 shows that ε f depends on both the confining stress and the stress level, while k and δ only depend on the stress level.

Fig. 17
figure 17

MMF model fitting for different confining stresses. a Confining stress = 0.1 MPa, b confining stress = 0.2 MPa, c confining stress = 0.4 MPa, d confining stress = 0.6 MPa

Full size image
Table 3 Parameters and coefficients of determination R 2 derived from MMF model
Full size table

The parameter ε f , which is defined as (ε ∞  − ε 0), increases with the confining stress. When ε f is plotted versus confining stress, as shown in Fig. 18, a linear relationship can be established as:

$$\varepsilon_{f} = \alpha \cdot \sigma_{3} + \beta$$
(11)

where α and β are the slope and intercept of the straight line, respectively. From Fig. 18, β = −0.0072, −0.0171, −0.0238, −0.0308 for σ 3 = 0.1, 0.2, 0.4, 0.6 MPa, respectively. Compared to the strain obtained in the test, the value of β is much smaller and it is reasonable to ignore the value of β to simplify the model.

Fig. 18
figure 18

Relationship between ε f and confining stress

Full size image

The relationship between α and stress level is shown in Fig. 19. The expression of α can be obtained by formula (3):

$$\alpha = \gamma \cdot S_{L} + \eta$$
(12)

where γ = 11.50 and η = −2.67 fitted from Fig. 19.

Fig. 19
figure 19

Relationship between α and stress level

Full size image

By substituting Eq. (12) into Eq. (11), the expression of ε f can be obtained as:

$$\varepsilon_{f} = (\gamma \cdot {\text{SL}} + \eta ) \cdot \sigma_{3}$$
(13)

Table 3 indicates that k and δ appear to be independent of confining stress. Thus, the average values of k and δ in Eq. (10) for different confining stresses can be plotted against shear stress level SL, as shown in Fig. 20 and Fig. 21. The fitting curve suggests the relation between k and SL is

$$k = \frac{\text{SL}}{{\theta_{1} \cdot {\text{SL}} + \theta_{2} }}$$
(14)

and that between δ and SL is

Fig. 20
figure 20

Relationship between k and stress level

Full size image
Fig. 21
figure 21

Relationship between k and stress level

Full size image
$$\delta = \lambda \cdot {\text{SL}} + \mu$$
(15)

By combining Eqs. (13), (14) and (15) with Eq. (10), the empirical creep model can be established as

$$\varepsilon_{t} = (\gamma \cdot {\text{SL}} + \eta ) \cdot \sigma_{3} - \frac{{(\gamma \cdot {\text{SL}} + \eta ) \cdot \sigma_{3} }}{{1 + (\frac{\text{SL}}{{\theta_{1} \cdot {\text{SL}} + \theta_{2} }} \cdot t)^{{(\lambda \cdot {\text{SL}} + \mu )}} }}$$
(16)

Values of the six parameters in Eq. (16) are provided in Table 4. The comparisons between the proposed model and test data for different confining pressures are shown in Fig. 17. As can be graphically seen in Fig. 17, the model correlates relatively well with the test data. Quantitatively, the average absolute difference was 0.1 in item of the strains. We conclude that MMF models can quantify the time-dependent response of gravel soils.

Table 4 Values of parameters in the model
Full size table

Conclusion and discussion

The creep behavior of gravel clay in the slip zone of the Majiagou landslide was investigated. A series of triaxial drained creep tests were conducted on the slip zone soil at different confining and deviatoric stresses. The test results indicate that the slip zone soil had two creep stages, namely the decay creep stage and the constant speed creep stage. We conclude that the average creep rate of the secondary creep stage and the duration of the decayed creep stage increase with the stress level. The tests also show that the long-term strength of the slip soil is about 60–75 % of the instant strength.

The empirical Burgers and Singh–Mitchell models were used to simulate the creep strain of the slip zone soil. The Burgers method can model the initial sharp rising strain and the decayed strain better than the Singh–Mitchell method, but it cannot predict the trend of the second creep stage as closely as the latter. Overall, large discrepancies exist between the strain predicted by these models and that obtained from the tests.

As a consequence a new empirical creep model has been developed to describe the drained creep behavior of the soil tested under triaxial conditions. Based on the creep characteristics of the soil, the MMF growth model was chosen to predict the time-dependent strains. The values of four parameters in the model were obtained through curve fitting. These four parameters were then expressed as functions of confining stress and stress level. The proposed creep model was compared with test data, revealing that a better prediction of the creep strain was achieved.

The primary purpose of this study was to establish that the MMF model assists in displacement prediction of the Majiagou landslide, and can help analyze the interactions between anti-slide piles and the sliding mass; our purpose was not to establish the general applicability of this model. Although the empirical models developed in this paper may not be general enough, this is acceptable in view of the role of the model in this study. Hereafter, the empirical model will be added to numerical simulations. Comparison of simulation results and field data will be performed to further verify this model after a period of monitoring.