Introduction

Numerous foundation pits were planned, designed, and constructed in China in the course of urbanization. The foundation pit accidents caused by confined groundwater have recently been increasing in China. Several water inrush accidents have been reported: (1) In October 1998, water inrush occurred in a two-story underground foundation pit that was 24 m wide, 52 m long, and 8 m deep. When a part of the pit was excavated to about 8 m below the ground, water inrush occurred at the bottom. Although the groundwater was pumped rapidly, the inrush of sand and slurry became serious. The ground surrounding the pit began to subside, cracks appeared in a four-story building in the west, the water supply pipe broke, and water leaked. Within a few days, dozens of cracks formed throughout the four floors of the building, and their widths reached 30 cm. The cement road cracked and deformed, and a number of subsidence cones emerged. The cones had diameters of 2–3 m and depths of several meters. Two other buildings were also endangered (Zhang et al. 1999). (2) On March 20, 2009, water inrush occurred in the pit bottom of a swirling pool excavated to 35.5 m below the ground. Although the emergency treatment of bagged cement blocking was adopted, the water inrush and piping could not be controlled effectively. A large volume of groundwater burst out. To avoid further soil erosion and large-scale subsidence of the surrounding buildings, pumping was stopped and the foundation pit was recharged with water. Water inrush was not stopped until the water level was recharged to an elevation of 15 m below ground to reach a new balance (Zou and Zhang 2009). (3) A water inrush accident was reported in a foundation pit in Hangzhou. One day, at 5 o’clock pm, water inrush occurred in the southwest corner of the pit when it was excavated to the depth of 12 m. Backfill earthwork was performed immediately, and hanging steel mesh and shotcrete block measures were adopted. However, due to the high water pressure, the block work failed. A large volume of groundwater rushed in until 8 o’clock that night, and the pit water level increased rapidly. At 9 o’clock am the next day, the water inflow rate reached 288 m3/h. The depth of water in the pit reached 8 m, endangering the safety of the pit and the nearby Shanghai–Hangzhou Railway (Peng and Li 2004). Therefore, understanding the course and mechanism of water inrush is very important.

Water inrush was generally considered as an engineering problem. Limit equilibrium theory was often adopted in dewatering designs. In traditional calculation methods, only the gravity of the aquitard was considered as an anti-inrushing force; the shear strength and suffusion erosion of different soil types were not fully considered. Water inrush induced by water pressure has been studied in soil erosion, including quicksand and piping (Bryan and Jones 1997; Tomlinson and Vaid 2000; Ojha et al. 2003; Fontana 2008; Kompani-Zare et al. 2009; Richards and Reddy 2010, 2012; Kadau et al. 2011; Koyama et al. 2011; Verachtert et al. 2011; Benaissa et al. 2012; Bruthans et al. 2012; Delgado-Ramos et al. 2012; Behrooz-Koohenjani et al. 2013; Lomine et al. 2013; Fleshman and Rice 2014; Fox et al. 2014; Chen et al. 2014). Ding et al. (2014) analyzed the influence of a foundation pit’s size on the plastic deformation failure of soil during water inrush. Li and Zhang (2011) used a back-propagation neural network to determine the source of mine water inrush. Sun and Wang (2013) used centrifugal model tests to prove the main failure modes of impermeable layers in Shanghai. However, the water inrush course cannot be fully explained just by quicksand and piping for the aquitard, such as clay or silty clay, which is often not a granular material.

In the paper, the aquitards in Shanghai (clay ⑤1 and silty clay ⑤3) were adopted as aquitard materials. A model test device was designed, and eight model tests of water inrush were performed to study the occurrence of water inrush in a local deep pit in a foundation pit.

Materials and methods

Conceptual model

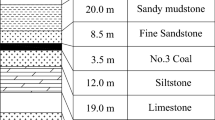
The model tests were conducted to observe water inrush phenomena, analyze water inrush mechanism, and verify predication criteria. The conceptual model was the aquitard of a foundation pit that had been excavated to the thickness in limit equilibrium state under the confined water pressure, any further excavation or water pressure increase may induce water inrush in a local deep pit excavated in foundation pit bottom. As shown in Fig. 1, the study area was marked with a rectangle. A study unit including the aquitard and local deep pit was summarized as the prototype of the model test. The similitude was selected as 1.0, i.e., the model tests were performed in a limited original scale. In order to avoid water inrush in a foundation pit, dewatering is often performed to lower the water pressure of pit bottom. The pore water pressure distribution and even water flow direction are influenced by not only the diaphragm wall but also pumping wells. In the perspective of whole foundation pit, diaphragm walls (curtains) influence the water flow nearby the pit during dewatering. However, for a local place with limited volume, the variation of water flow is limited when the volume is small enough. The water flow variation was ignored in the model test. The influence of diaphragm wall was treated as constant. So the diaphragm wall was not considered in the model tests.

Fig. 1
figure 1

Conceptual model of water inrush during foundation pit excavation

Full size image

Model test soils

The remolded aquitard soils were sampled from the clay ⑤1 and silty clay ⑤3 in a metro foundation pit of subway line 14, Shanghai. Their physical and mechanical parameters are shown in Table 1.

Table 1 Soil parameters of model tests
Full size table

Model test device

A model test device was designed (Fig. 2). The test box was 50 cm wide, 70 cm long and 75 cm high. Constant water pressure was provided at the bottom of the test box via an external water tank.

Fig. 2
figure 2

Sketch map of the model test device. a In plane, b in section

Full size image

Working conditions

Eight working conditions were designed (Table 2) to study the deformation and failure characteristics of the aquitards under confined water pressures.

Table 2 Scheme of model tests
Full size table

Model test operation

To maintain a constant water pressure, four filter layers were installed at the bottom of the aquitard: (1) a filter plate with 5 mm apertures, (2) a filter screen with 2 mm apertures, (3) 30–50 mm gravel, and (4) 1 mm quartz sand and silty sand of the confined aquifer.

Given that the sidewall of the test box was made of tempered glass, the friction between the sidewall and the test soil may produce a boundary effect, and water may permeate along the contact surface. Three impermeable layer films were installed to solve the problem. The films were made of plastic wrap and were 80 mm wide. For one film, 30 mm was pasted on the sidewall, while 45 mm was used as a tile on the test soil. To prevent the constraint of soil deformation, a 5-mm margin was reserved at the pasting site. Meanwhile, petroleum jelly was smeared on the sidewall for water blocking.

The model test soil was filled by a layered tamp, and the test sensors were embedded. The aggregate thickness of the test soil was 50 cm, which was divided into ten layers. To ensure the uniform property of each layer, the weight, water content, and shear strength were measured after the soil was tamped.

After soil filling, water pressure was applied to consolidate the soil until the deformation was less than 0.01 mm/h. Then, the valve of the water supply tank was turned off. A 30-cm-long, 20-cm-wide, and 45-cm-deep rectangular pit was excavated to simulate the excavation.

To eliminate the border effects of the model test, the distance between the sidewall of the test box and the sidewall of the local deep pit fulfilled the following formula:

$$ d \ge h \cdot \tan \left( {45^\circ - \frac{\varphi }{2}} \right) $$
(1)

where d is the distance between the sidewall of the test box and the sidewall of the pit (m), h is the depth of the local deep pit (m), and φ is the internal friction angle of the test soil (°).

Hierarchical displacement meters and pore water pressure gauges were used to observe deformation and pore pressure, respectively. Nine hierarchical displacement observation poles (B1–B9) were installed at the center and both sides of three layers of the pit (Fig. 2a). The depths of observation points were 0, 2, and 4 cm below the bottom of pit. The displacement variation of the pit bottom soil at different depths could be obtained. Three pore water pressure sensors (A1–A3) were laid on the center of the pit in three layers (Fig. 2b), and the depth of which was 2, 4, and 6 cm under the pit bottom. The thickness of the aquitard was 5 cm, so the lowest pore water pressure sensor was laid in the confined aquifer.

Results

Water pressure

In the loading course, water pressure of external water tank was set in advance and applied to the bottom of aquitard instantaneously. When water pressure under the aquitard reached 6 kPa and water inrush did not occur, the water pressure was released. Then, the water pressure was increased at an increment of 0.5 kPa in external water tank and applied to the bottom of aquitard instantaneously in the next step. The water pressure was released and increased until water inrush occurred. The load curve (applied water pressure) is shown in Fig. 3.

Fig. 3
figure 3

Load curve (applied water pressure)

Full size image

Water inrush occurred in the clay when water pressure was between 7.5 and 8.5 kPa, while it occurred in the silty clay when the water pressure was between 6.5 and 7.5 kPa. Water inrush occurred under a larger water pressure in the clay than in the silty clay.

Phenomena

For the clay, the failure and water inrush generally appeared in the location 3–5 cm away from the edge of the local deep pit. Local uplift and cracks appeared in the surface before failure (Fig. 4a, c). The penetration area appeared inside the aquitard owing to the continuous development of cracks. Next, water gushed into the cracks following the release of gas, and confined water rushed in with sand (Fig. 4b, d).

Fig. 4
figure 4

Inrush phenomena of the tests. a Phenomenon before failure in the clay \( \left( {\gamma = 16.9\,{\text{kN/m}}^{3} } \right) \), b phenomenon after failure in the clay \( \left( {\gamma = 16.9\,{\text{kN/m}}^{3} } \right) \), c phenomenon before failure in the clay \( \left( {\gamma = 17.9\,{\text{kN/m}}^{3} } \right) \), d phenomenon after failure in the clay \( \left( {\gamma = 17.9\,{\text{kN/m}}^{3} } \right) \), e failure phenomenon of the silty clay \( \left( {\gamma = 16.7\,{\text{kN/m}}^{3} } \right) \), f failure phenomenon of the silty clay \( \left( {\gamma = 17.2\,{\text{kN/m}}^{3} } \right) \)

Full size image

For the silty clay, the failure and water inrush generally appeared in the corner of the local deep pit. Local uplift appeared on the surface of the aquitard before failure, and then water inrush occurred in a short time without obvious cracks in the corner following the release of gas. Confined water then rushed in with sand. After the water inrush, the residual holes were significantly larger than those in the clay, and a large amount of sand rushed in with water from the confined aquifer (Fig. 4e, f).

Deformation and water inrush stage

The displacement–time curves of working Conditions 1, 3, 5, and 7 are shown in Fig. 5. For the confined aquifer with insufficient water pressure, only a specific amount of uplift deformation was observed in the aquitard, and water inrush did not occur. The process can be divided into three stages based on the deformation rate and experimental phenomena:

Fig. 5
figure 5

Displacement–time curves of working Conditions 1, 3, 5, and 7. a Clay \( \left( {\gamma = 16.9\,{\text{kN/m}}^{3} } \right) \), b clay \( \left( {\gamma = 17.9\,{\text{kN/m}}^{3} } \right) \), c silty clay \( \left( {\gamma = 16.7\,{\text{kN/m}}^{3} } \right) \), d silty clay \( \left( {\gamma = 17.2\,{\text{kN/m}}^{3} } \right) \)

Full size image
  1. 1.

    Continuous deformation stage under the water pressure of the confined aquifer, the pores of the aquitard were compressed, which caused continuous deformation. For water pressure was constant during the test, the creep contributed most of the deformation in the stage.

  2. 2.

    Progressive deformation stage the aquitard was continually compacted, which caused progressive deformation. For water pressure was constant during the test, the creep and development of micro-cracks contributed most of the deformation in the stage.

  3. 3.

    Equilibrium stage when the micro-cracks were extended to the maximum, the shear stress caused by the confined water was still not large enough to cause failure in the overlying soil at the bottom of the local deep pit. The deformation of the aquitard reached equilibrium and no longer increased.

The displacement–time curves of working Conditions 2, 4, 6, and 8 are shown in Fig. 6. For the confined aquifer with sufficient water pressure, a greater uplift deformation was formed until water inrush occurred in the aquitard. The process can be divided into four stages:

Fig. 6
figure 6

Displacement–time curves of working Conditions 2, 4, 6, and 8. a Clay \( \left( {\gamma = 16.9\,{\text{kN/m}}^{3} } \right) \), b clay \( \left( {\gamma = 17.9\,{\text{kN/m}}^{3} } \right) \), c silty clay \( \left( {\gamma = 16.7\,{\text{kN/m}}^{3} } \right) \), d silty clay \( \left( {\gamma = 17.2\,{\text{kN/m}}^{3} } \right) \)

Full size image
  1. 1.

    Continuous deformation stage (Fig. 7a) under the water pressure of the confined aquifer, the pore of the aquitard soil was compressed, which caused continuous deformation. The aquitard under the local deep pit was uplifted under the water pressure.

    Fig. 7
    figure 7

    Water inrush mechanism and stages. a Continuous deformation, b progressive deformation, c shear failure, d water inrush and sinking

    Full size image
  2. 2.

    Progressive deformation stage (Fig. 7b) shear deformation increased under the water pressure of the confined aquifer and under the constraint of the surrounding soil. Micro-cracks continuously developed around the edge inside the aquitard. Meanwhile, the confined water gradually infiltrated the local pit.

  3. 3.

    Shear failure stage (Fig. 7c) for the clay, the shear stress of the aquitard approached its maximum shear strength owing to the development of micro-cracks and the confined water infiltration. A tensile fracture appeared in the surface along the free direction, and ultimately, failure appeared in the weak parts. Afterward, water inrush occurred. For the silty clay, a suffusion erosion hole was formed inside the soil under the infiltration of confined water. Finally, failure and water inrush occurred under the seepage pressure.

  4. 4.

    Water inrush and sinking stage (Fig. 7d) gas release from the breakthrough points and confined water rushed in with sand. Water pressure under the aquitard was released, and deformation gradually sprang back.

Spatial deformation

When water inrush did not occur in the length orientation of the model box (Fig. 8a), the location of the maximum deformation appeared in the center of the local deep pit. On the other hand, if water inrush occurred (Fig. 8b), the location of the maximum deformation would appear around the edge of the local deep pit.

Fig. 8
figure 8

Displacement–time curves of silty clay \( \left( {\gamma = 17.2\,{\text{kN/m}}^{3} } \right) \) in the horizontal orientation. a Without water inrush, b water inrush

Full size image

Under the pressure of confined water, compression deformation was observed in the vertical orientation (Fig. 9); thus, the deformation also increased with the increasing depth.

Fig. 9
figure 9

Displacement–time curves of silty clay \( \left( {\gamma = 17.2\,{\text{kN/m}}^{3} } \right) \) in the vertical orientation. a Without water inrush, b water inrush

Full size image

Pore water pressure

The analysis was based on the pore water pressure–time curves of working Conditions 2 and 4 (Fig. 10a, b). The poor permeability of clay resulted in the poor transference of pore water pressure. When the cracks appeared, developed, and connected with the underlying aquifer, the pore pressure increased rapidly. For the pore water pressure sensors were installed in the middle of the local deep pit, the observed pore water pressure did not relate with corner displacement closely.

Fig. 10
figure 10

Pore water pressure–time curves of working Conditions 2, 4, 6, and 8. a Clay \( \left( {\gamma = 16.9\,{\text{kN/m}}^{3} } \right) \), b clay \( \left( {\gamma = 17.9\,{\text{kN/m}}^{3} } \right) \), c silty clay \( \left( {\gamma = 16.7\,{\text{kN/m}}^{3} } \right) \), d silty clay \( \left( {\gamma = 17.2\,{\text{kN/m}}^{3} } \right) \)

Full size image

The pore water pressure–time curves of working Conditions 6 and 8 (Fig. 10c, d) indicate that the pore water pressure was increasing continually in the soil for the permeability of the silty clay was larger than that of the clay. The increase in pore water pressure was stable, and the rate increased closely related with observed displacement. It varied quickly when the difference between the pore water pressure and the lower confined water pressure was large. The variation of pore water pressure on the top of confined aquifer is shown as the red curve in Fig. 10.

Discussion

Responding pore water pressure and deformation in aquitard

The pore water pressure observed was the response of aquitard during its failure and water inrush course. The observed pore water pressure and displacement increased with the time, and a sharp drop down was observed when the water inrush occurred.

Groundwater did not infiltrate clay easily because of its low permeability. Small amount of groundwater infiltration occurred due to the instantaneous applied water pressure on the model bottom boundary. Hydraulic gradient was observed at the bottom of the aquitard and stabilized soon. For silty clay, due to the doping of sand particles, its permeability was relatively larger. Groundwater infiltrated it easily and needed a longer time to reach stabilization.

Under the confined water pressure, uplift deformation of aquitards in foundation pit bottom occurred and micro-cracks were produced. For clay, it is hard to generate upward water flow and seepage failure before the cracks penetrated the whole clay although the micro-cracks were filled with water. However, it is relatively easier for silty clay.

Figure 10 shows that pore water pressures in clay quickly stabilize and maintain at a lower level with the increasing displacement. However, the increasing trend of pore water pressure in silty clay was basically consistent with the displacement. The pore water pressure was one of the key factors inducing water inrush for silty clay, but not for clay.

When water inrush occurred, groundwater channels in the aquitard were formed and water pressures under the aquitard were released. Subsidence occurred in aquitard bottom. As the sand in the confined aquifer rushed out gradually with inrush groundwater flow, secondary subsidence occurred. Water inrush resulted in not only inrush groundwater, but also land subsidence and even collapse of aquitard and aquifer in and out of pit.

Aquitard creep before failure and water inrush

In Figs. 5 and 6, the boundary water pressure below the excavated aquitard was constant. However, the deformation of the aquitard increased continually before water inrush. The displacement–time curves are quite similar to the creep deformation–time curves of creep experiments. The aquitard failure did not instantaneously occurred corresponding to the constant water pressure. It included a creep deformation and micro-cracks development course (Fig. 7b, c) before failure. It was not an instantaneous phenomenon corresponding to excavation but a time-depending course. The precursor observed in the tests can be used to predict the possible water inrush for the real deep excavations.

In order to distinguish the potential creep deformation, a three-element rheological model (two dash-pots and one spring, Fig. 11) was introduced:

$$ \varepsilon = \frac{{\sigma_{0} }}{{\eta_{m} }}t + \frac{{\sigma_{0} }}{{E_{k} }}\left[ {1 - {\text{e}}^{{ - \frac{{E_{k} }}{{\eta_{k} }}t}} } \right] $$
(2)

where ɛ is strain (%); σ 0 is constant stress (kPa); η m and η k are viscosity coefficient (kPa s); E k is elastic modulus (kPa); t is time (s).

Fig. 11
figure 11

Rheological solid standard three-element model

Full size image

Singh–Mitchell model (Singh and Mitchell 1968) was also introduced to fit the surface displacement–time curves

$$ \varepsilon = B\exp \left( {\alpha \bar{D}} \right)\left( {\frac{t}{{t_{1} }}} \right)^{n} $$
(3)

where B, α, and n are arguments; t 1 is unit time increment (s); and \( \bar{D} \) is stress level, \( \bar{D} = D/D_{\hbox{max} } = \left( {\sigma_{1} - \sigma_{3} } \right)/\left( {\sigma_{1} - \sigma_{3} } \right)_{f} \).

The two models were used to fit the displacement–time curves of stages I and II (Fig. 6). The fitting arguments are shown in Table 3. Simulated results match well with experiments (Fig. 12). For working Conditions 4 and 6, the creep deformation lasted for a longer time under the relatively stable pore water pressure. Several tiny ladders in displacement–time curves match well with the ladders of pore water pressure–time curves (Fig. 10), which can be explained by the contribution of the developing micro-cracks. For working Condition 8, the pore water pressure increased with time, the deformation included not only the creep deformation but also the development of producing and pore water pressure.

Table 3 Fitting arguments
Full size table
Fig. 12
figure 12

Fitting effect of working Conditions 4, 6, and 8. a Clay \( \left( {\gamma = 17.9\,{\text{kN/m}}^{3} } \right) \), b silty clay \( \left( {\gamma = 16.7\,{\text{kN/m}}^{3} } \right) \), c silty clay \( \left( {\gamma = 17.2\,{\text{kN/m}}^{3} } \right) \)

Full size image

Application in verifying theoretical water inrush calculation methods

Several methods were suggested to determine the water inrush conditions for foundation pit dewatering. They were verified by the model tests.

  1. 1.

    Limit equilibrium method

Limit equilibrium method assumes that water inrush does not occur when the gravity of the overlying soil is larger than the water pressure under a coefficient, i.e.,

$$ h_{\text{cr}} = \frac{{\gamma_{\text{w}} H_{\text{w}} }}{\gamma } $$
(4)

where \( h_{\text{cr}} \) is the critical thickness of the aquitard layer under the bottom of the local deep pit (m), H w is the height of the confined water level above the roof of the confined aquifer, γ is the unit weight of soil (kN/m3), and γ w is the unit weight of water (kN/m3).

  1. 2.

    Homogeneous continuous-beam method

The aquitard under the pit bottom can be simplified as a homogeneous continuous beam under lateral shear stress (Q), bending moment (M) on both ends of the beam, and water pressure of the confined aquifer on the bottom (Fig. 13). The excavation critical thickness is as follows (Liang 1996):

$$ h_{\text{cr}} = \frac{{H_{\text{w}} }}{{\frac{\gamma }{{\gamma_{W} }} + \frac{2c}{{\gamma_{\text{w}} B}}}} $$
(5)

where c is the undrained cohesion of bottom soil (kPa), and B is the width of the local deep pit (m).

Fig. 13
figure 13

Conceptual model of the homogeneous continuous beam

Full size image

Excavation critical thickness can be derived through the rigidity requirements as follows:

$$ h_{\text{cr}} = \frac{{H_{\text{w}} }}{{\frac{\gamma }{{\gamma_{\text{w}} }} + \frac{32}{{m_{s} }}\left( {\frac{H}{B}} \right)^{2} \frac{E}{{\gamma_{\text{w}} B}}}} $$
(6)

where m s is the deflection coefficient, E is the elastic modulus of soil (kPa), and H is the thickness of the aquitard under the bottom of the local deep pit (m).

If \( b/h \le \left( {4/\sqrt {m_{s} } } \right)\sqrt {E/c} \), then the excavation critical thickness is controlled by the shear strength; otherwise, it is controlled by the rigidity requirements.

  1. 3.

    Prestressed homogeneous continuous-beam method

The aquitard under the pit bottom is simplified as a homogeneous continuous beam. Axial compression (N) and bending moment (M) of the lateral earth pressure are exerted on both ends of the beam, and water pressure of the confined aquifer is exerted at the bottom (Fig. 14). Excavation critical thickness controlled by the shear strength is listed as follows (Du 1998):

$$ h_{\text{cr}} = \frac{{BH_{\text{w}} \gamma_{\text{w}} - 2\alpha k_{0} \gamma D}}{{2c + \gamma \left( {B + \alpha k_{0} } \right)}} $$
(7)

where α is the shear coefficient of extrusion effect, the recommended value is 0.07, k 0 is the lateral earth pressure coefficient, and D is the depth of excavation (m).

Fig. 14
figure 14

Conceptual model of the prestressed homogeneous continuous beam

Full size image

The test results and calculations are listed in Table 4. The result of Eq. (4) using the traditional limit equilibrium method, mostly used in foundation pit dewatering, was significantly larger than the others. The best prediction of excavation critical thickness was calculated by Eq. (7), which simplified the aquitard as a prestressed homogeneous continuous beam.

Table 4 Verification of water inrush calculation method using model tests
Full size table

Conclusion

A model test device was designed to observe the water inrush phenomenon. Eight model tests were performed to verify the inrushing course. The water inrush modes in a foundation pit bottom were analyzed for the main aquitard clay of layer ⑤1 and silty clay of layer ⑤3 in Shanghai, China. The deformation and failure characteristics under different water pressures were obtained. The deformation course without water inrush was divided into three stages: continuous deformation, progressive deformation, and equilibrium stages. The deformation course with water inrush included four stages: continuous deformation, progressive deformation, shear failure, and water inrush and sinking. The aquitard failure included creep deformation and micro-cracks development course before failure. It was a time-depending course. The displacement–time curves under constant pore water pressure were fitted well using three elements model and Singh–Mitchell model. The small ladders of the displacement–time curves were induced by the development of micro-cracks and pore water pressure. The water inrush formulas were verified and tested using the model test results. The limit equilibrium method had larger safe reserves. The prestressed homogeneous continuous-beam method could calculate the excavation critical thickness relatively accurately.