Analyzing streamflow extremes in the upper Ürümqi River with the generalized Pareto distribution

Abstract

The generalized Pareto distribution (GPD), as one of the most important distributions in statistical theory of extreme value, is often used to explain the probability of extreme events in nature, through setting up a model with the observation points exceeding the threshold. This paper uses GPD model to fit the distributions of the relatively large and small monthly average discharge of Ürümqi River in Northwest China and gives the detailed steps of this method. Firstly, the Mean Excess, shape parameter and modified scale parameter plots are applied to determine the thresholds; then the parameters of GPD are estimated by the maximum likelihood method; next the models are diagnosed by the probability and quantile plots; finally the return levels and the corresponding 95 % confidence intervals of the discharge are calculated by the maximum likelihood and profile likelihood methods, respectively. The results show that the return levels of the maximum monthly average discharge with the return periods 10, 25, 50 and 100 years are 35.4, 39.9, 43.2 and 46.3 m³ s⁻¹, respectively, and the return levels of the minimum monthly average discharge with the return periods 10, 25, 50 and 100 years are 0.60, 0.43, 0.30 and 0.18 m³ s⁻¹, respectively. Some comparisons are also made between the generalized extreme value (GEV) and GPD models. The results of these two models are close to each other while the GPD model should be more reliable because it can make use of more information than the GEV model. This paper proposes a complete framework for modeling hydrological data by GPD model.

Introduction

Research shows that the frequency and magnitude of extreme climate and hydrology events are on the rise significantly (IPCC 2013). The extreme events in climate and hydrology drive the application of extreme value statistics in hydrology (Wang 1991; Rasmussen 2001; Katz et al. 2002; Towler et al. 2010; Liu et al. 2012; Saidi et al. 2014). A large body of literature exists that correlates extreme hydrological events with flood events. For example, the generalized extreme value (GEV) distribution has been widely used in describing flood characteristics (Lettenmaier et al. 1987; Hosking and Wallis 1988; Morrison and Smith 2002; Najib et al. 2008; Gilroy and McCuen 2012; Xia et al. 2012). Recently, Liu et al. (2013a, b) applied the GEV model in groundwater area to model the minimum discharge of Niangziguan Springs and predicted the probability of drying up in the future. However, the GEV model is only based on block maxima, and it is a wasteful approach to extreme value analysis (Coles 2001). Comparing with GEV model, the generalized Pareto distribution (GPD) can make full use of the scarce observed data by determining a proper threshold, and simulate the distribution of extreme values more reliably in hydrology, meteorology and other fields (Holmes and Moriarty 1999; Macdonald et al. 2006; Zagorski and Wnek 2007; Burke et al. 2010; Lucio et al. 2010; Grigg and Tawn 2012; Fan et al. 2013).

Glacier-fed inland river is one of important sources of inland rivers in arid Central Asia, maintaining the ecological functions, the life of people and the economic development of the local areas (Kutuzov and Shahgedanova 2009; Duan et al. 2012; Kong and Pang 2012; Wang et al. 2012; Hagg et al. 2013; Gao et al. 2013; Wu et al. 2013; Wang et al. 2013a, b). Thus the research on the hydrological extreme events of glacier-fed inland rivers is of great significance (Chen et al. 2012; Deng et al. 2012). To study this problem, this paper chooses the Ürümqi River upstream basin, which is a typical inland river basin as the study area, applies the GPD models to analyze the extreme values of monthly average discharge in the mountain areas of Ürümqi River and provides the detailed calculations at each step. Some comparisons are also made between the results obtained by GPD and GEV models, respectively. The Ürümqi River from 1958 to 2006 was barely interfered by human or climate changes and its discharge data present steady characteristics without any long-term trends, and thus can be modeled by GPD and GEV models directly. The results of this paper provide some basis for decision making in Ürümqi city water regulation and meanwhile gives a complete framework of applying the GPD model to analyze the hydrological extreme events.

Data and methods

Research area

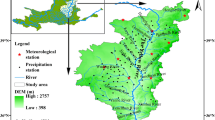
Located in the hinterland of Eurasia, the Ürümqi River is a typical inland mountainous river fed by the glacier melt and rainfalls. It originates from the Glacier No. 1 with an elevation of 3900 m above mean sea level (AMSL) on the northern flank of Tianger Peak II (4479 m AMSL) in the middle Tianshan Mountains in northwest China (Métivier et al. 2004; Liu et al. 2008), and goes northwards from Urabo Reservoir, then passes through the downtown Ürümqi and vanishes north of Miquan County. It runs as long as 214.3 km (Liu et al. 2011). The watershed of Ürümqi River ranges from 86°45′E to 87°56′E and 43°00′N to 44°07′N, with a drainage area of 4684 km² (Lan et al. 2010; Kong and Pang 2012).

Our research area was constricted to the upstream area of the Ürümqi River. The length of the upper above the mountain pass is about 63 km with a drainage area of 924 km² and an average altitude of 3083 m Liu et al. (2013, 2015) (Fig. 1). Yingxiongqiao Hydrological Station (YHS), the unique control station of the upstream of the Ürümqi River, is near the mountain pass. Daxigou Meteorological Station (DMS) is located at about 2 km downstream of the Glacier No.1. The information of the two stations is listed in the Table 1.

Fig. 1

DEM map and hydro-meteorological observation sites in the upstream of Ürümqi River basin

Table 1 The parameters of the two stations

The Ürümqi River is mainly fed by the precipitation and glacier melt water (Zhang 2010). According to the meteorological data observed from 1958 to 2006 at DMS and YHS, the annual average precipitation in the upstream of Ürümqi River is 454 mm. Rainfalls in the upstream area occur most frequently from June to August, and they account for 60–80 % of the total precipitation in a year (Liu et al. 2015). The annual average runoff is 2.43 × 10⁸ m³ in the upstream mountainous region by YHS, with glacier melt water accounting for nearly 12 %, snow melt water accounting for 37 %, rainfalls accounting for 36 % and underground water accounting for 15 %.

Data acquisition

YHS has an abundant long sequence of the streamflow observations of Ürümqi River from the year of 1958 until now. Since the Daxigou Reservoir was constructed 5 km upstream of YHS for flood control and irrigation in 2007, the streamflow is intervened artificially hereafter. In order to analyze monthly average discharge extremes of the Ürümqi River under natural hydrological conditions, this paper selects the monthly average discharge data from January 1958 to December 2006. The monthly discharge data are shown in Fig. 2 as blue points. In Fig. 2 almost all of the points are above 10 m³ s⁻¹ during flood periods (June to August), and below 5 m³ s⁻¹ during dry periods (December to February of the next year).

Fig. 2

Scatter diagram of the monthly average discharge from 1958 to 2006

Research method

The theory of GPD is as follows:

Suppose $X_{1} ,X_{2} , \ldots , X_{N}$ is a sequence of independent random variables with common distribution function $F$, let $M_{N} = \hbox{max} \{ X_{1} , \ldots ,X_{N} \}$ and denote an arbitrary term in the $X_{\text{t}}$ sequence by $X$. If $M_{N}$ satisfies $\mathop {\lim }\limits_{N \to \infty } \Pr (M_{N} \le z) = G(z)$, where $G(z)$ is the distribution function of a nondegenerate distribution, then $G(z)$ must be the distribution function of a generalized extreme value (GEV) distribution i.e.,

$$G\left( z \right){ = }\exp \left\{ { - \left[ {1 + \xi \left( {\frac{z - \mu }{\omega }} \right)} \right]^{{ - \frac{1}{\xi }}} } \right\} , {\text{ defined on }}\left\{ {z:1 + \xi \left( {z - \mu } \right)/\omega > 0} \right\}$$

(1)

and what is more, for a large enough threshold $u$, the distribution function of $(X - u)$, conditional on $X > u$, approximately obeys a GPD, i.e.:

$$\Pr (X - u \le x|X > u) \approx H(x) ,$$

(2)

where,

$$H(x) = 1 - (1 + \frac{\xi x}{\sigma })^{ - 1/\xi },\,defined \, on\, \{ x:x > 0,(1 + \frac{\xi x}{\sigma }) > 0\}$$

(3)

and

$$\sigma = \omega + \xi (u - \mu )$$

(4)

Equation 1 is the distribution function of GEV distribution with parameters $\mu$, $\omega$ and $\xi$. $H(x)$ defined in Eq. 3 is called two parameters GPD who only has scale and shape parameters $\sigma$ and $\xi$. The $\mu$ in Eqs. 1 and 4 are identical. In Eqs. 2 and 4, $u$ represents a specified threshold and in this paper, it represents a specified discharge; GEV distribution in Eq. 1 and GPD in Eq. 3 share the same shape parameter $\xi$ and their scale parameters $\omega$ and $\sigma$ also have some relation which is revealed in Eq. 4. (Coles 2001).

The above theory implies that for an independent random variables sequence $X_{1} ,X_{2} , \ldots, X_{N}$ with common distribution $F$, if their maximum $M_{N}$ nearly follows a nondegenerate distribution, then $M_{N}$ will nearly follow a GEV distribution, and the threshold excesses $(X - u)$, under the condition of $X > u$, will nearly follow a GPD, regardless of what form the distribution function $F$ has.

In fact most $M_{N}$ always converges to a nondegenerate distribution in the reality, and this paper assumes that the maxima of the monthly average discharge in each year nearly follow GEV distribution, and thus the threshold excesses of the monthly average discharges, for a proper threshold, approximately follow a GPD, under the condition that the monthly average discharge exceeds the threshold. Whether the data follow the GEV and GPD distributions can be further diagnosed via probability and quantile plots.

The aforementioned GPD model can only study the varying pattern of the observation values that exceed threshold, namely, can only model relatively large values. In order to model the relatively small observations, this paper takes the opposite number of these observations and then repeats the above theory to set up a GPD model with the threshold excesses of these negative values. Finally, this paper takes the opposite of the output results so that the results can be back to positive numbers.

Calculation procedure

Determination of threshold

Two methods are usually used to determine a reasonable threshold.

One is observing the trend of the mean excess function $e(u)$, which is defined as:

$$e(u) = E(X - u|X > u)$$

If $u_{0}$ is an appropriate threshold, which means the distribution of the random variable $X - u_{0}$ under the condition $X > u_{0}$ really obeys a GPD, then for any $u > u_{0}$, the mean excess function:

$$e(u) = E(X - u|X > u) = \frac{{\sigma_{u} }}{1 - \xi } = \frac{\omega + \xi (u - \mu )}{1 - \xi }$$

(5)

is a linear function of $u$, where $\sigma_{u}$ denotes the scale parameter of the GPD model with the threshold $u$, $\mu$ and $\omega$ are the location and scale parameters of the GEV model in Eq. 1, which can be thinked as constants here. For a given $u$, the $e(u)$ can be estimated by $e_{\text{m}} (u)$ defined in the following:

$$e_{\text{m}} (u) = \frac{1}{{N_{\text{u}} }}\sum\limits_{i = 1}^{{N_{u} }} {(x_{(i)} - u)}$$

(6)

where $N_{\text{u}}$ is the number of observations which exceed $u$, and $x_{(1)} , \ldots ,x_{{(N_{u} )}}$ are just these $N_{\text{u}}$ observations. For a reasonable threshold $u_{0}$, the scatter plot of $\{ (u,e_{m} (u))|u > u_{0} \}$ i.e., $\{ (u,\frac{1}{{N_{u} }}\sum\nolimits_{i = 1}^{{N_{u} }} {(x_{(i)} - u)} )|u > u_{0} \}$ should fluctuate around a straight line.

Generally, the plot of $\{ u,\frac{1}{{N_{u} }}\sum\nolimits_{i = 1}^{{N_{u} }} {(x_{(i)} - u)} \}$ is called Mean Excess plot (Coles 2001). Thus $u_{0}$ can be an appropriate threshold if the Mean Excess plot presents the linear trend against $u$ on the right of $u_{0}$, i.e., when $u > u_{0}$, the Mean Excess plot vibrates around a straight line. Most literatures select the smallest $u_{0}$ which satisfies the above condition so that more data can be introduced into the model and therefore more information can be used.

The other method to select the threshold is to estimate the model at a range of thresholds. If $u_{0}$ is a reasonable threshold, then for any threshold $u$ larger than $u_{0}$, the shape parameter $\xi$ of the distribution of threshold excess $X - u$ under the condition $X > u$ should be invariant, and the modified scale parameter $\sigma^{ *}$ should also be a constant, where

$$\sigma^{ *} { = }\,\sigma_{\text{u}} - \xi u = \omega - \xi \mu$$

(7)

Thus, if the estimates of $\xi$ and $\sigma^{ *}$, i.e., $\hat{\xi }$ and $\hat{\sigma }^{ *}$, exhibit vibrations around two certain constants respectively when $u > u_{0}$, then it can be inferred that $u_{0}$ is an appropriate threshold. Similarly, most literatures generally choose the smallest point satisfying the above condition as $u_{0}$, namely, on the right of this $u_{0}$, $\hat{\xi }$ and $\hat{\sigma }^{ *}$ vibrate around two constants.

After the threshold is determined, this paper uses the corresponding excesses of the threshold, i.e. $x_{(1)} - u_{0} , \ldots ,x_{{(N_{{u_{0} }} )}} - u_{0}$ to set up the GPD model.

Parameter estimation

The parameters $\sigma$ and $\xi$ in the GPD can be estimated via the maximum likelihood method. Suppose that the values $y_{1} , \ldots ,y_{k}$ are the $k$ excesses of the threshold. For $\xi \ne 0$, the likelihood function can be written as:

$$\ell (\sigma ,\xi ) = - k\log \sigma - (1 + \frac{1}{\xi })\sum\limits_{i = 1}^{k} {\log (1 + \frac{{\xi y_{i} }}{\sigma }} )$$

(8)

where $(1 + \xi \frac{y}{\sigma }) > 0$, for $i = 1, \ldots ,k$. Some numerical techniques are used to search the maximum likelihood estimated values $\hat{\xi }$ and $\hat{\sigma }$ which make the likelihood function $\ell (\sigma ,\xi )$ reach its maximum.

The calculation of return level

The $N$-year return level, denoted by $z_{N}$, can be estimated via the following formula:

$$\hat{z}_{N} = u + \frac{{\hat{\sigma }}}{{\hat{\xi }}}[(Nn\hat{\varsigma }_{u} )^{{\hat{\xi }}} - 1]$$

(9)

where $\hat{z}_{N}$ is the estimate of $z_{N}$; $u$ is the specified threshold; $n$ represents the number of observations each year, and in this paper $n = 12$; $\zeta_{\text{u}}$ is the probability of the random variable $X$ exceeding threshold $u$, i.e., $\zeta_{\text{u}} = {\text{P}}_{\text{r}} (X > u)$ and the symbol $\hat{\varsigma }_{\text{u}}$, calculated via the sample proportion of points exceeding $u$, is the estimate of $\zeta_{u}$. The $\hat{\sigma }$ and $\hat{\xi }$, calculated by the maximum likelihood method, are the estimates of the scale and shape parameters $\sigma$ and $\xi$ in the GPD model respectively. In addition, $z_{N}$ can be interpreted as the extreme event that occurs once in $N$ years on average. After determining the parameters estimated values $\hat{\sigma }$, $\hat{\xi }$ and $\hat{\varsigma }_{\text{u}}$, then for any given return period $N$-year, Eq. 9 can provide the corresponding estimation of the return level $\hat{z}_{N}$.

Results and discussion

Figure 2 shows the monthly average discharge data of the upstream of Ürümqi River recorded at YHS from 1958 to 2006 (totally 49 years, 588 observations), whose maximum and minimum are analyzed via GPD models in this paper.

Maximal monthly average discharge

Before establishing a proper GPD model, a reasonable threshold $u_{0}$ should be determined first. Two methods are used to select an appropriate $u_{0}$.

The first method involves mean excess function. The Mean Excess plot is drawn in Fig. 3 which shows that: when the threshold $u$ is in the interval [10, 25], the curve presents approximately linear decreasing trend; when $u < 10$, the curve exhibits a quadratic trend; when $u > 25$, the vibration becomes severe, for which the number of observations exceeding 25 is so small that the curve vibrates severely. Too small sample size will result in an unstable model and thus $u > 25$ will not be considered. This plot implies that the reasonable threshold should be between 10 and 25, but it is not very obvious that from which point the curve becomes linearly decreasing in Fig. 3. Thus the second method should be used to find out the accurate $u_{0}$.

Fig. 3

Mean Excess plot of the monthly average discharge in the upstream of Ürümqi River

According to the second method, the plots of modified scale parameter $\sigma^{*}$ and shape parameter $\xi$ against threshold $u$ are drawn in Fig. 4, which show that when $u$ is in [19.92, 22.71], the modified scale parameter $\sigma^{*}$ is fluctuating around the constant 6.630, and the shape parameter $\xi$ is vibrating centering on the constant −0.0426. In short, the estimations of $\sigma^{*}$ and $\xi$ present constant trends starting from 19.92, thus the reasonable threshold should be near 19.92. Here this paper chooses 20 as the threshold for convenience.

Fig. 4

Modified scale σ* (a) and shape ξ (b) against threshold $u$ in the case of the maximum average discharge

The return level plot of GPD model can be used to further analyze whether the chosen $u_{0} = 20$ is a reasonable threshold. This paper selects equidistant 11 points in the interval [19, 23], then lets each of them be the threshold and builds the corresponding GPD models. The return level plots show that only when $u_{0} = 20$, almost all of the observation points fall in the 95 % confidence interval of the return level (not shown in this paper). Thus $u_{0} = 20$ is a proper threshold.

After $u_{0}$ is determinated, the shape and scale parameters $\xi$ and $\sigma$ of GPD are estimated through the maximum likelihood method. The estimations are $\hat{\sigma } = 5.99$, $\hat{\xi } = - 0.06$, and the standard errors of $\hat{\sigma }$ and $\hat{\xi }$ are 0.814 and 0.077, respectively. Then the corresponding GPD model is:

$$\Pr (X - 20 \le x|X > 20) \approx H(x) ,$$

(10)

where

$$H(x) = 1 - (1 - \frac{0.06x}{5.99})^{1/0.06} ,defined \, on\{ x:x > 0,(1 - \frac{0.06x}{5.99}) > 0\}$$

(11)

Finally, the model diagnosis plots including probability, quantile, return level and density plots are shown in Fig. 5. Both probability and quantile plots show that all the points scatter around the straight line with slope 1, which means that the data and model coincide well. In the return level plot, almost all of the observation points fall within the 95 % confidence interval of the GPD model, and in the density plot, the sample histogram is consistent with the density curve of GPD. The four diagram plots consistently indicate that the fitted GPD model is reasonable.

Fig. 5

Diagnostic plots of the GPD model for the threshold excess in the case of maximum monthly average discharge [Probability plot (a), Quantile plot (b), Return level plot (c) and Density plot (d)]

Compared with the maximum likelihood method, the profile likelihood method is also used to estimate the return levels and the corresponding 95 % confidence intervals. Table 2 lists the return level estimates of the maximal monthly average discharge corresponding to the return periods 10, 25, 50 and 100 years, respectively. In the last column of Table 2, the ratio is shown. The symbols $x_{\text{MU}}$, $x_{\text{ML}}$ represent the upper and lower bounds of the 95 % confidence interval of maximum likelihood estimation, while $x_{\text{PU}}$, $x_{\text{PL}}$ denote the bounds of the 95 % confidence interval of profile likelihood estimation. The ratio is written as following:

$${\text{ratio}} = \frac{{x_{\text{MU}} - x_{\text{ML}} }}{{x_{\text{PU}} - x_{\text{PL}} }}$$

Table 2 Return level estimations of the maximum monthly average discharge in different return periods by maximum and profile likelihood methods respectively

It represents the ratio of the confidence interval lengths obtained by the two methods. It is apparent that in the last column of Table 2, all the ratio is less than 1, i.e., the confidence intervals deduced by maximum likelihood are shorter than those obtained by profile likelihood. But it does not mean that the maximum likelihood is more accurate. It is worth noting that the maximum discharge of Ürümqi River is 55.2 m³ s⁻¹ during the 49 years (much less than 100 years) from 1958 to 2006; however, the 95 % confidence interval of 100-year return level based on maximum likelihood is [38.8, 53.9] which does not include 55.2, while the corresponding confidence interval obtained by profile likelihood is [41.2, 61.1], covering the point 55.2. Actually, the confidence interval of profile likelihood is virtually always broader and more reliable than maximum likelihood.

Figure 6 shows the return level’s estimates and 95 % confidence intervals based on profile likelihood corresponding to the return periods 10, 25, 50 and 100 years, respectively. As we expected, the estimate of return level is increasing when the return period is extending in Fig. 6. And the confidence interval becomes broader when return period is larger, which means the estimations will get less accurate along with the extension of return period.

Fig. 6

P Profile likelihood estimates of the return levels of maximum monthly average discharge with the return periods 10, 25, 50 and 100 years, respectively (a is the lower bound of the 95 % confidence interval, b is the point estimate, and c is the upper bound of the 95 % confidence interval)

This paper also sets up the GEV model with the maxima of monthly average discharge in each year, and the result of the maximum estimations of the GEV and GPD models are listed in the Table 3, where the number 5.2183 is calculated via Eq. 4, i.e., 5.04 − 0.0424 × (20 − 24.205) = 5.2183. According to Table 3, the shape parameter estimation $\hat{\xi }$ are both negative and have close values (−0.0424 and −0.06), and the two $\hat{\sigma }$s also have similar values (5.2183 and 5.99). The similar results of the two models further verify that the models in this paper are proper and can reflect the reality correctly. The GPD model should be more accurate because it uses 79 points, which involve more information than the 49 points in GEV model; thus this paper uses the GPD model to analyze the discharge.

Table 3 The estimation results from the GEV and GPD models with the relatively large values

Minimal monthly average discharge

As one of the most important local water resources, the water in Ürümqi River accounts for around 40 % of the total surface water in the Ürümqi area. Considering the danger of drought, it is necessary to study the varying pattern of the minimum of the discharge.

The minimum discharge is also analyzed by the GPD model. Considering the discharge in the dry period is generally small, this paper defines the period when the discharge is lower than 2 m³ s⁻¹ as dry period. Take the opposite number of the discharge points less than 2 m³ s⁻¹, then the new sequence consisting of the negative values is shown in Fig. 7.

Fig. 7

Scatter diagram of the negative monthly average discharge during the dry period (<2 m³ s⁻¹) from 1958 to 2006

The negative sequence of the streamflow during the dry period is denoted by $Y_{\text{t}}$, where $Y_{\text{t}} = - X_{\text{t}}$.

To select a proper threshold $u_{0}$ for $Y_{\text{t}}$, the Mean Excess plot (Fig. 8) and the plots of $\hat{\sigma }^{*}$ and $\hat{\xi }$ (Fig. 9) against $u$ are drawn. In Fig. 8, when the threshold $u$ is in [−1.3, −1.11], the mean excess curve presents obviously linear trend, which implies that the value of $u_{0}$ should be in the interval [−1.3, −1.11]. Meanwhile, Fig. 9 indicates that when $u$ is in [−1.06, −0.63], $\hat{\sigma }^{*}$ is around the constant 0.22, and $\hat{\xi }$ is around 0. The number −1.06 seems to be a proper threshold because it is the start point after which the $\hat{\sigma }^{*}$ and $\hat{\xi }$ present constant trends. In addition, the −1.06 is in the range of [−1.3, −1.11], according to the theory introduced in the determination of threshold section, −1.06 should be a proper choice of $u_{0}$.

Fig. 8

Mean Excess plot of the negative monthly average discharge during the dry period

Fig. 9

Modified scale σ* (a) and shape ξ (b) against threshold $u$ for the opposite number of the minimum discharge during the dry period

This paper uses the return level plots with a range of thresholds to further verify that the threshold −1.06 is reasonable. First this paper chooses 23 equidistant points in the interval [−1.4, −0.96] as thresholds to build corresponding GPD models, respectively, and then output their diagnosed plots. The return level plots indicate that when $u_{0} = - 1.06$, most observation points fall into the 95 % confidence interval of the return level curve. Besides, the other three diagnostic plots also perform well as shown in Fig. 10. So $u_{0} = - 1.06$ is a reasonable choice and the distribution of threshold excess i.e., $Y_{\text{t}} - u_{0}$ under the condition $Y_{\text{t}} > u_{0}$, can be considered to follow GPD. The parameters estimations by maximum likelihood method are $\hat{\sigma } = 0.19$, $\hat{\xi } = - 0.01$, and their standard errors are 0.036 and 0.130, respectively. Then the final model is

$$\Pr (Y + 1.06 \le y|Y > - 1.06) \approx H(y)$$

(12)

where

$$H(y) = 1 - (1 - \frac{0.01y}{0.19})^{1/0.01},\, defined \ on\ \{ y:y > 0,(1 - \frac{0.01y}{0.19}) > 0\}$$

(13)

Fig. 10

Diagnostic plots of the GPD model for the threshold excess of the opposite number of the minimum monthly average discharge [probability plot (a), quantile plot (b), return level plot (c) and density plot (d)]

Similar with the case of the maximum discharge, the maximum likelihood and profile likelihood methods are used to estimate both $Y_{t}$’s return levels based on Eq. 13 and the 95 % confidence intervals corresponding to return periods 10, 25, 50 and 100 years, respectively. Figure 11 gives the results of the profile likelihood method. Take the opposite of these results to get the positive values. Table 4 lists all the results, which shows that the estimates of minimum return levels is around 0.60, 0.43, 0.30 and 0.18 m³ s⁻¹ corresponding to 10, 25, 50 and 100 years, respectively.

Fig. 11

Profile likelihood estimates of the return levels of the negative minimum monthly average discharge with the return periods 10, 25, 50 and 100 years, respectively (a is the lower bound of the 95 % confidence interval, b is the point estimate of profile likelihood, and c is the upper bound of the 95 % confidence interval)

Table 4 Return level estimations of the minimum monthly average discharge in different periods by the maximum and profile likelihood methods respectively

In Table 4, the last column also lists ratios of the confidence interval lengths deduced by maximum likelihood to those obtained by profile likelihood method. The ratio becomes smaller as return period $N$ increases, which suggests that return levels estimated by profile likelihood contain more uncertainty comparing with maximum likelihood when return period $N$ is increasing. In addition, the lower bound of the confidence interval obtained by profile likelihood corresponding to 50 years, and the lower bounds deduced by maximum likelihood and profile likelihood corresponding to 100 years are −0.295, −0.199, −0.746, respectively, all of which are below zero. The calculation result shows that the dry period (the discharge reaches zero) may happen before 2058.

This paper also applies the minimum of the monthly average discharge to set up the GEV model, and compares it with the GPD model, whose results are listed in the Table 5. From Table 5, the two $\hat{\xi }$ are both negative but their values are not so close (−0.285 and −0.01) and the two $\hat{\sigma }$ also have some difference (0.349 and 0.19). It is generally believed that the GPD model is more accurate because it has 55 points to build the model compared with the 49 points in GEV model.

Table 5 The estimation results from the GEV and GPD models with the relatively small values

Summary and conclusions

Taking the Ürümqi River as an example, this paper provides a method of modeling extreme discharge of a river by GPD model, and gives the detailed steps and the prediction of the future return levels. The analysis data are the monthly average discharge of the Ürümqi River from January 1958 to December 2006, which have not been interfered by human activities or climate changes, and thus can be seen as a stationary sequence. The GPD model performs well and can reflect the reality of the Ürümqi River accurately.

In the course of analyzing the maximum monthly average discharge, firstly, a proper threshold is chosen. After that, the maximum likelihood method is used to estimate the parameters in GPD model based on the threshold excesses. At last, the return levels and the 95 % confidence intervals of the monthly average discharge are given by the maximum likelihood and the profile likelihood methods, respectively. The results show that the return levels of the maximum monthly average discharge corresponding to 10, 25, 50 and 100-year return periods are 35.4, 39.9, 43.2 and 46.3 m³ s⁻¹, respectively.

In the course of the minimum monthly discharge, this paper first takes the opposite number of sequence, then repeats the above steps on the new sequence of negative values and finally takes the opposite of the output results again so that the results could be back to positive numbers. The results show that the return levels of the minimum monthly average discharge corresponding to 10, 25, 50 and 100 years are 0.60, 0.43, 0.30 and 0.18 m³ s⁻¹, respectively, and the dry period may appear before 2058.

In the last columns of Table 2 and Table 4, all the ratio is less than 1, i.e., the confidence intervals deduced by maximum likelihood are shorter than those obtained by profile likelihood. Besides, the 95 % confidence interval of 100-year return level based on maximum likelihood is [38.8, 53.9] which does not include 55.2, the maximum discharge of Ürümqi River from 1958 to 2006, while the corresponding confidence interval obtained by profile likelihood is [41.2, 61.1], covering the point 55.2. The above results suggest that the profile likelihood method is always more robust than the maximum likelihood at the cost of the boarder confidence interval. Besides, in the last column of Table 2, the ratio becomes smaller as return period $N$ increases, which suggests that the profile likelihood confidence intervals becomes wider and wider compared with the maximum likelihood when return period $N$ is increasing. In most literatures, the maximum likelihood are more frequently used than the profile likelihood.

Compared with other statistical models of extreme values such as the generalized extreme value (GEV) model, the GPD model is usually able to make full use of the observations. Thus, GPD model achieves higher accuracy and it performs better in the predictions of the future discharge. However, the uncertainty contained in estimations of return levels will increase with time, thus the confidence interval becomes wide when time is going. Complicated internal and external factors may also contribute to the uncertainty in the GPD model and impair the accuracy of the estimations, thus it is not suitable for the GPD model to make too long prediction in the future.