RETRACTED ARTICLE: Feature reduced blind steganalysis using DCT and spatial transform on JPEG images with and without cross validation using ensemble classifiers

Abstract

The paper discuss the outcome evaluation of JPEG images in both spatial and DCT transform and a comparative study is being done. There are four distinct steganographic algorithms—LSB matching, LSB replacement, pixel value differencing and F5 are used. The embedding performed on the images are 25% with text. The idea of cross validation is used to validate the classifier better and a comparative analysis is performed on results with and without cross validation. Features removed for investigation are the first order, second order, extended features and Markov features. Relevant features are chosen by feature reduction. This process is done using principal component analysis (PCA). This is done to eliminate redundant feature that can hamper the efficiency of classification. The classifiers used are support vector machine (SVM) and support vector machine with particle swarm optimisation (SVM-PSO). The classification is done based on six kernels like radial, dot, multiquadratic, epanechnikov and ANOVA and four sampling techniques like shuffled, linear, stratified and automatic sampling. The existing techniques had always used radial as kernel without sampling for a classification. The proposed system make use of this imperfection and has formulated the result.

1 Introduction

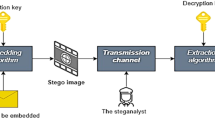
Steganography aims to give furtive information transmission. The goal line of steganography is to attach a message inside a carrier signal so that it has not been identified by unwanted receivers (Shih et al. 2011). Steganalysis is a technique for detecting the presence of concealed data (Das et al. 2011). Steganalysis discovers the hidden signals in supposed carriers or defines the media that possess the hidden signals/information. Steganography's primary problem is to define and apply a better identification methodology (Al-Kharobi et al. 2017). The method of steganography and steganalysis (Badr 2014) is better grasped through the picture depicted in Fig. 1.

Fig. 1

Diagram of the work flow of steganography and steganalysis

Although steganography throws light on information in any of the digital media, due to their recurrent use on the internet, electronic photographs/images are the most common as “carrier” (Altaay et al. 2012). Since the image file is large, it can contain enormous amounts of information. The human visual system cannot discriminate with secret information on the usual picture and the original picture. Furthermore, as there are large numbers of redundant bits in digital format pictures, they are mostly preferred as cover objects (Pal et al. 2017). This work therefore uses images as a cover file. The standard picture used for Image steganography is Joint Photographic Experts Group (JPEG), which make use of the concept of lossy compression while keeping up the nature of the picture (Liu et al. 2010).

The image steganography is commonly partitioned into spatial and transform domain (Kaur et al. 2014), which can be explained using the block diagram in Fig. 2

Fig. 2

Classification diagram of image steganography

The two fundamental kinds of steganalysis are targeted and blind steganalysis. Targeted steganalysis is proposed for a definite algorithm. This category is very tough since it deals with better accuracy of detection whereas blind steganalysis is not exposed to any distinct algorithm, thus eliminating the dependency of the same. Moreover, blind steganalysis works well with statistical data, hence also known as statistical steganalysis (Sabnis and Awale 2016). The various advances associated with steganalysis are feature selection, feature extraction and classification. Features that are pivotal to an image will be selected, extracted and send to the classifier. During feature extraction, there will also be features which is irrelevant and may adversely affect the efficacy of the classifier. Such features need to be removed, which can be done by a technique known as feature reduction (Jain and Singh 2018). In this research, principal component analysis is considered. Cross validation is a technique of validation a classifier to get a better efficiency. The data is divided into different folds and classified, hence known as k-fold classification. In this research we use tenfold classification for the research. The supervised learning techniques has previously given good results. The classifiers used in this research are support vector machine and its optimisation variant with particle swarm optimisation. The reason for the choice is that the SVM had been found to be very robust when working with high dimensionality inputs. Hence it is assumed that the optimisation variant may give a substantial result and is used here.

2 Related work

The effectiveness of steganalysis depend on how well the grouping of cover and stego images are done. With transformation and deciding on the optimum number of DCT coefficients, the embedding of data is done so that the images are not affected by visual attack (Zeng et al. 2017; Jiang et al. 2019). Transform domain approach can be integrated to achieve greater results with nominal modifications in the cover image (Attaby et al. 2018). Steganalysis is likewise completed in the spatial area, where the implanting happens straightforwardly into the picture's pixel intensity (Tuithung et al. 2015). Rabee et al. (2018) suggested a novel way of effectively revealing the presence of a concealed message in a JPEG image. discrete cosine transform (DCT) is generally incorporated in statistical steganalysis for JPEG picture format, which would help reduce the cost of memory and time of computation. After the classification, various features that will be statistically prominent in both spatial and transform domain, will be extracted. This is because the features are the best objects to describe an image (Ker et al. 2013). The combination of both spatial and transform domain yield better results in previous literature (Fridrich et al. 2012; Kodovsky et al. 2010). Large feature set would imply a big dimensionality which could adversely influence the efficiency of the classifier. Previous literature (Cadima et al. 2016) states that principal component analysis (PCA) is better suited to decrease the dimension when huge unrelated data is involved (Han et al. 2012; Lever et al. 2017). Cross validation is a technique used in machine learning which is used during classification to avoid the problem of overfitting, hence used as an optimal model (Liu et al. 2019). Thus the concept of cross validation is widely used to survey the generability of an algorithm (Bergmeir et al. 2018). The classifiers then decide whether the image is a stego or cover. SVM classifiers are the most popular ones for classification (Farid et al. 2003). Hence the application of SVMs are diverse, since it can be applied to graphs, sequences and even relational data and thereby designing the corresponding kernels for each (Ebrahimi et al. 2017). Particle swarm optimisation (PSO) has been of great significance due to its flexibility and low computation (Liliya Demidova et al. 2016). PSO helps in optimisation thus improving the performance when linked with SVM (Garcia Nieto et al. 2016). The same research is also done with calibrated images (Shankar and Azhakath 2020). Different embedding percentage and optimization variant of classifier had also been considered (Azhakath et al. 2019). Classification in low embedding percentage with SVM as classifier is considered for research (Shankar and Upadhyay 2020)

3 Problem statement

This research is intended to perform a blind steganalysis for an embedding of 25%. The images used are in JPEG format which is changed using discrete cosine transform. The dimensionality reduction of features is completed using principal component analysis. The steganographic algorithms used for embedding are LSB replacement, LSB matching, Pixel Value Differencing and F5. SVM and SVM PSO are the classifiers incorporated for the comparative study. Six various kernels and four diverse sampling methods are taken into consideration. The kernels are multiquadric, radial, dot, polynomial, Epanechnikov and ANOVA. The different sampling methods are linear, shuffled, stratified and automatic. The outline of implementation is given in Fig. 3.

Fig. 3

Implementation block diagram

4 Methodology

This part deals with the methodology of the research using JPEG image format. This is because the previous literature (Bedi et al. 2013) states that such a system is simple to store and transmit data over the internet. A low scale embedding percentage of 25 is used for the research. The raw images are converted to transform domain and the appropriate characters are being mined. The image attributes are normalised to promote the effectiveness of the steganographic algorithm.

4.1 Dataset

The presentation of any framework relies upon the nature of dataset utilized for it. This research considers a set of 2300 images from two different standard datasets. Out of them 1500 images from UCID image dataset (Schaefer et al. 2004) is used as the training set and 800 images from INRIA image database (Jegou et al. 2008) is used as the test dataset. The image is transformed as needed and the features are selected, extracted and classified. The selection and extraction is done on features that are profound to any changes in embedding.

4.2 Feature vector extraction

Four types of features namely first order features, second order features, extended DCT features and Markov features are considered for extraction. The functionalities of the features are as shown in Table 1.

Table 1 Table of extracted features

The regular features of DCT (Fridrich 2004) will contain 23 functions, which can be made comprehensive to get extended features of DCT. 193 such functions can be extended (Pevny et al. 2007). Another feature set used is the Markovian features. The dimensionality is high for this and hence the features are condensed to get only 81 vital features using PCA. The DCT features have inter block dependencies whereas Markov features have intrablock dependencies. The DCT features have been mined and it is calculated as per the following steps:

• Calculate the difference of cover and stego images

• Consider the absolute value

• Find the L1 Norm

• The result is the DCT feature.

However, some of the pertinent features that are required for the investigation would be missed during the process of DCT extraction. Therefore, some functional with projected differences have been used in DCT, which are the features of extended DCT.

The Markovian features have been mined and it is computed as per the following steps:

• Find the absolute values of adjacent DCT constants

• Calculate the difference

The functional of Markovian itself counts to 324 features. All these features, if applied as such, would make dimensionality issues. Hence, it is converted to 4 set of dimensionality of 81. Since, the Markovian and DCT features sets are combined for the reasons stated above; the resultant combined set will carry just 274 features. A stego picture is characterized by DCT coefficient cluster d_p (i, j), where i and j are coefficients and p is the block (Fridrich et al. 2004). The global histogram is symbolised by Gr where r = P, Q where P = min_p,i,j (d_P(i,j)), Q = max_P,i,j(d_P(i,j)).The dual histogram, which gives an impression of the dispersal of the numbers, is characterised by

$$ g_{ij}^{d} = \sum\limits_{p = 1}^{n} {x(d,d_{p(i,j)} } ) $$

(1)

where g is the aggregate number of blocks and d is a fixed coefficient rate. The variance (Pevny et al. 2007; Shankar et al. 2011, 2012) can be denoted by

$$ V = \frac{{\sum\limits_{i,j = 1}^{8} {\sum\limits_{p = 1}^{|Ir| - 1} {|d_{Ir(p)(i,j) - } d_{Ir(p + 1)(i,j)} |} + \sum\limits_{i,j = 1}^{8} {\sum\limits_{p = 1}^{|Ic| - 1} {|d_{Ic(p)(i,j) - } d_{Ic(p + 1)(i,j)} |} } } }}{{|I_{r} | + |I_{c} |}} $$

(2)

where Ir and Ic are vectors of block indices when scanned by rows and columns. Blockiness can be signified as

$$ B_{\alpha } = \frac{{\sum\limits_{i = 1}^{|(A - 1)/8|} {\sum\limits_{j = 1}^{B} {|x_{(8i,j) - } x_{(8i + 1,j)} |}^{n} + \sum\limits_{i = 1}^{|(B - 1)/8|} {\sum\limits_{j = 1}^{A} {|x_{(8i,j) - } x_{(8i + 1,j)} |} } } }}{B[(A - 1)/8] + A[(B - 1)/8]} $$

(3)

where A and B are the dimensions of the image. The probability dispersal of adjoining DCT coefficient pairs is known as co-occurrence. It is signified as

$$ C_{st} = \frac{{\sum\limits_{p = 1}^{{|I_{r} | - 1}} {\sum\limits_{j = 1}^{8} {\delta (s,d_{i,p} (i,j)\delta (t,d_{i,(p + 1)} (i,j) + \sum\limits_{p = 1}^{{|I_{r} | - 1}} {\sum\limits_{j = 1}^{8} {\delta (s,d_{i,p} (i,j)\delta (t,d_{i,(p + 1)} (i,j)} } } } }}{{|I_{r} | + |I_{c} |}} $$

(4)

The Markov feature set model the distinction between the absolute values of nearby DCT coefficients as a Markov procedure. Four different arrays are calculated along four directions—horizontal, vertical and two diagonals. With this features, four transition probability matrices are calculated. The original Markovian features will mount up to 324. This increases the dimensionality. To reduce it, the average of four 81 dimensionality features is taken.

4.3 Cross validation

Generally, an image database is divided into training and testing set. This is done by random assignment of the image, which avoids any bias. There is no standard that the training image set and testing image set should be equivalent. The training set in an actual scenario is much less than the available content on the internet to be tested. This creates a solid presentation variation. So the training and test dataset check are performed multiple times. This is known as k-fold validation. This method assesses the stability of the scheme assessing the statistical output of the detection scheme. The cross-validation used in this study has a value of k = 10.

4.4 Classification

The classification phase follows the extraction of the features. This is used to decide whether the obtained picture is a stego or a cover. There are two learning strategies—supervisory and nonsupervisory. In the supervisory system, the input values are mapped with the output values and the training is monitored. In the unsupervisory method, the input values are not shifted to the output values. In this study, we use the supervisory learning method and therefore use support vector machine (SVM) and support vector machine with particle swarm optimisation (SVM-PSO).

4.4.1 Support vector machine

Given a set of data for training, SVM demonstrates an optimal hyper plane which would clearly categorize the data. In two dimension, the separability is by means of a line, in higher dimensions, the separation is by means of hyper plane. Support vectors are datasets which lies closest to the hyperplane. These points are very difficult to classify. Hence they are able to change the position of the hyper plane. The support vectors can be a subsets of training datasets.

The hyper plane can be so decided to give the biggest least distance, called margin to the support vectors. If the classification hyper plane is too close to a sample feature, it will be noisy and the classification will not be proper. Hence the hyper plane should be so selected in a way that the line should be far from all the points and also should classify. Such a hyper plane is called optimal hyper plane.

Consider the hyper plane of the form

$$ w^{T} x + b $$

(5)

where w is the weight vector which is normal to the hyper plane and b is the bias

Let yi =  + 1, − 1 be the classes for the training dataset (Fletcher 2008). The margin can be signified as

$$ w^{T} x + b = 0 $$

(6)

The classification of the training dataset can be so done if the support vector for each classes can be represented by planes H1 and H2, so that

$$ w^{T} x_{1} + b = 1\;{\text{for}}\;{\text{H1}} $$

(7)

$$ w^{T} x_{2} + b = - 1\;\;{\text{for H2}} $$

(8)

The margin needs to be equidistant from H1 and H2. To place the margin as far as possible, from the support vectors, the SVM margin needs to be maximized. The margin can be represented in many ways by surmounting the values of w and b. The distance between a point x and the hyper plane (w, b) can be

$$ {\text{Distance }} = \frac{{|w^{T} x + b|}}{||w||} $$

(9)

For canonical hyperplane, the numerator is 1, hence the distance is

$$ {\text{Distance }} = \frac{1}{||w||} $$

(10)

Since the margin is twice the distance to the closest support vectors, the margin M can be denoted as

$$ {\text{M }} = \frac{2}{||w||} $$

(11)

Since there are constraints for minimization of M due to

y_i (x_i∙w + b)− 1 ≥ 0 for all I.

4.4.2 Support vector machine with particle swarm optimisation

If a computer learning model has to be developed with a collection of information, it needs to be divided into training dataset and test dataset. The model is being taught through the training set which would assist to authenticate the exam data (Margaritis et al. 2018). 80% of the information is usually held as a training set and the other 20% is used as sample information. The images are categorized into distinct groups according to the features (Hou et al. 2017).

The particle swarm optimization (PSO) algorithm is a search algorithm centered on population dependent on bird flocking simulation. PSO also uses the model of personal data exchange, similar to other developmental computing algorithms (Eberhart et al. 2001). The suggested approach evolves with each iteration in SVM-PSO and thus works towards the ideal approach. In each iteration, a fresh population is acquired in the algorithm by the location change of the previous iteration. The PSO initializes the system with a population of discrete solutions and aims optimal solutions where the particles themselves behave as solutions. The objective is to optimize the particles and achieve optimum alternative (Huang and Dun et al. 2008; Du et al. 2017). In PSO, the bird cluster called particle shapes a population in a D-dimensional feature space. If the vector space Xi = (xi1, xi2, xi3,…xiD) is represented as the ith particle, where i = 1, 2…m, Xi is the position of the ith particle which acts as a solution. The velocity and the position will be iterated to form the equation

$$ v_{id}^{t + 1} = \omega .v_{id}^{t} + c_{1} r_{1} .(p_{id} - x_{id}^{t} ) + c_{2} r_{2} .(p_{gd} - x_{gd}^{t} ) $$

(12)

$$ x_{id}^{t + 1} = x_{id}^{t} + v_{id}^{t + 1} $$

(13)

where Vi = (vi1, vi2, vi3….viD) is the velocity of the ith particle, Pi = (pi1, pi2, pi3….piD) is the optimal position of this particle. The optimum swarm position is Pg = (pg1, pg2, pg3….pgD). When the ith particle is at the tth iteration, xtid and ytid are the dth location and velocity. c1, c2, r1 and r2 are random numbers which may acquire a value ranging from 0 to 1. These values are the inertial weight of the PSO algorithm. The PSO algorithm helps to optimize features, thereby improving efficiency when paired up with SVM.

4.5 Principal component analysis

The notion of principal component analysis (PCA) is used for reduce the dimensionality (He et al. 2013). The principal components received will either be the same as the original components or less than them. principal component analysis works well with normalized data (Miranda et al. 2008). The implementation of principal component analysis is done as follows. The dataset is first normalized. Normalization is prepared by subtracting the corresponding means from the numbers in the corresponding column. Thus a dataset is created whose means is zero. The image is pixel based. After transformation, the matrix is arranged in terms of frequency (Bao et al. 2019). Since the matrix is multidimensional, the covariance will also be multidimensional.

Consider a 2 × 2 Matrix. This will result in a 2 × 2 covariance matrix.

$$ \begin{aligned} & {\text{Covariance }} = \left[ \begin{gathered} {\text{var}} \left[ {x1} \right] \, {\text{cov}} \left[ {x1, \, x2} \right] \, \hfill \\ {\text{cov}} \left[ {x2, \, x1} \right] \, {\text{var}} \left[ {x2} \right] \, \hfill \\ \end{gathered} \right] \\ & {\text{var}}\left[ {{\text{x1}}} \right] \, = {\text{ cov}}\left[ {{\text{x1}},{\text{ x1}}} \right]{\text{ and var}}\left[ {{\text{x2}}} \right] \, = {\text{ cov}}\left[ {{\text{x2}},{\text{ x2}}} \right] \\ \end{aligned} $$

(14)

Once the covariance matrix is calculated, the Eigen value and Eigen vector needs to be found. λ can be considered as the Eigen value for a matrix A if determinant (λI − A) = 0, where I is an identity matrix and it has to be the same dimensionality as matrix A. For each Eigen value λ, a corresponding Eigen vector v, can be calculate using the formula

$$ (\lambda {\text{I}} - {\text{A}}){\text{ v }} = \, 0 $$

(15)

Once the Eigen values are calculated, it is arranged in the descending order so that the significant components are ordered first. Hence the highest Eigen value will be the principal component of the particular dataset. To reduce the dimension, we choose the first few Eigen values and the rest are ignored. If the ignored Eigen values are small, not much data is lost. Thus a feature vector is created using the Eigen values. A matrix of the principal component can be created with a multiplication of the transpose of the Eigen vector that is chosen and the transpose of the scaled version of the original data.

$$ {\text{Final result }} = \, \left( {\text{feature value}} \right){\text{ T }} \times \, \left( {\text{scaled original value}} \right){\text{ T}} $$

The final data would form the principal component.

4.6 Kernels

Kernels are used to calculate large-dimensional function identification. The paper uses six kernel types such as linear, polynomial, dot, multiquadric, radial, and ANOVA. The kernel of the radial base function is as given in Eq. (16).

$$ {\text{k}}\left( {{\text{a}},{\text{b}}} \right) \, = {\exp}\left( { - {\text{g}}\left| {\left| {{\text{a}} - {\text{b}}} \right|} \right|^{{2}} } \right) $$

(16)

where g is the gamma parameter of the kernel. The greater price of g produces a big variance, whereas the reduced price produces a smoother border with a minimum variance.

The polynomial kernel is denoted mathematically by

$$ {\text{k}}\left( {{\text{a}},{\text{b}}} \right) = \left( {{\text{a}}*{\text{b}} + {1}} \right)^{{\text{p}}} $$

(17)

where the exponent p is the polynomial degree.

The dot kernel is described as

$$ {\text{k}}\left( {{\text{a}},{\text{b}}} \right) = {\text{a}}*{\text{b}} $$

(18)

The dot kernel is the product of inner variables a and b.

The multiquadratic kernel is defined by

$$ {\text{k}}\left( {{\text{a}},{\text{b}}} \right) = \left( {\left| {\left| {{\text{a}} - {\text{b}}} \right|} \right|^{{2}} + {\text{c}}^{{2}} } \right)0.{5} $$

(19)

where c is a constant.

The ANOVA kernel, whose performance is prominent in multidimensional problems, is defined as

$$ k(a,b) = \sum\limits_{k = 1}^{n} {\exp \left( { - \sigma \left( {a^{k} - b^{k} } \right)^{2} } \right)} $$

(20)

where σ can be derived from gamma, g; g = 1/(2σ²).

The Epanechnikov kernel, which is parabolic, is defined with the following equation,

$$ k(u) = \frac{3}{4}(1 - u^{2} )\;\;for\,|u|\; \le 1 $$

(21)

5 Results of experimentation

5.1 Results with no cross-validation

The following tables show the results with no cross validation.

The details of SVM and PCA on LSB Replacement is as shown in Table 2.

Table 2 Details with SVM and PCA on LSB replacement

As per Table 2, Radial kernel and Epanechnikov kernel give a low result with all sampling methods for LSB replacement in spatial domain. A better classification result is given by the dot kernel in stratified sampling method.

The details of SVM and PCA on LSB Matching is as shown in Table 3.

Table 3 Details with SVM and PCA on LSB matching

In Table 3, all kernels give closely to similar classification rate with linear sampling method.

The radial and epanechnikov has given low classification results. However, the dot kernel with stratified and automatic sampling methods give a better classification rate.

The details of SVM and PCA on PVD is as shown in Table 4.

Table 4 Details with SVM and PCA on PVD

As in Tables 2 and 3, the radial and epanechnikov kernels give a comparatively low classification rate. But the dot has maintained as good classification rate when stratified sampling methods are applied.

The details of SVM and PCA on F5 is shown in Table 5.

Table 5 Details with SVM and PCA on F5

As per the table, the radial kernel and Epanechnikov kernel give the same low embedding percentage over various sampling methods. But lower rates are displayed by dot kernel and multiquadric kernel with shuffled sampling. Dot kernel give better rates in linear sampling methods. However the best classification rates are shown by ANOVA with stratified sampling method.

Detail with SVM-PSO and PCA on LSB replacement is as shown in Table 6

Table 6 Details with SVM-PSO and PCA on LSB replacement

As per the table, radial kernel give a low classification rate with linear sampling and stratified sampling methods, but give a fairly better result with stratified sampling. Epanechnikov give a better classification with linear sampling. The dot kernel give a better classification rate.

Detail with SVM-PSO and PCA on LSB Matching is as shown in Table 7.

Table 7 Details with SVM-PSO and PCA on LSB matching

As per the table, the better classification rate is achieved by multiquadratic kernel with linear sampling method. The polynomial kernel is next in line with shuffled sampling. Radial kernel and Epanechnikov give a low classification percentage.

Detail with SVM-PSO and PCA on PVD is as shown in Table 8.

Table 8 Details with SVM-PSO and PCA on PVD

As the table suggest, multiquadratic kernel with linear sampling give a good rate of classification followed by polynomial kernel with shuffled sampling. Radial kernel gives less classification percentage on shuffle and stratified kernels. The lease classification percentage is demonstrated by dot kernel with linear sampling.

Detail with SVM-PSO and PCA on F5 is as shown in Table 9.

Table 9 Details with SVM-PSO and PCA on F5

As per the given table and results, the dot kernel give a good classification rate all through the sampling methods. However, the ANOVA kernel gives a better rate than dot kernel for shuffled, stratified and automatic sampling. The least classification is done with radial kernel on linear sampling.

5.2 Results with cross-validation

The results from Tables 10, 11, 12, 13, 14, 15, 16 and Table 17 give the details with cross validation, SVM and PCA. Table 10 provide the result on LSB Replacement.

Table 10 Details with cross validation, SVM and PCA on LSB replacement

Table 11 Details with cross validation, SVM and PCA on LSB matching

Table 12 Details with cross validation, SVM and PCA on F5

Table 13 Details with cross validation, SVM and PCA on PVD

Table 14 Details with cross validation, SVM-PSO and PCA on LSB replacement

Table 15 Details with cross validation, SVM-PSO and PCA on LSB matching

Table 16 Details with cross validation, SVM-PSO and PCA on PVD

Table 17 nDetails with cross validation, SVM-PSO and PCA on F5

After the cross validation, the result percentage has risen and Dot kernel give a decent outcome with stratified sampling. This is followed by ANOVA kernel on shuffled sampling. The lowest classification is given now by radial kernel in linear sampling method.

Table 11 gives the details with cross validation, SVM and PCA on LSB Matching.

The dot kernel for shuffled, stratified sampling method and automatic sampling method give a good classification rate. This is followed by the polynomial kernel. However, the radial, multiquadratic and epanechnikov give a very low classification rate.

Table 12 gives the details with cross validation, SVM and PCA on F5.

As per the table, the dot kernel and polynomial kernel gives good results all through the sampling methods. Better results are given by ANOVA Linear sampling gives very low classification rate for radial, multiquadric and Epanechnikov kernels.

Table 13 provides the details with cross validation, SVM and PCA on PVD.

The classification rate is good with stratified sampling and ANOVA kernel. Multiquadratic in stratified sampling give the next better rate for classification.

Table 14 provides the details of cross validation SVM-PSO and PCA on LSB replacement.

The highest classification rate is given by dot kernel in stratified and automatic sampling. The next higher classification percentage is exhibited by dot kernel in shuffled sampling. ANOVA follows it with the next classification rate of 83.84%.

Table 15 gives the results of cross-validation SVM-PSO and PCA on LSB matching.

The dot kernel and the ANOVA kernel gives good results at par with the other kernels.

Table 16 highlights the results of cross validation, SVM-PSO and PCA on PVD.

ANOVA kernel gives the superior classification rate with shuffled, stratified and automatic kernels. The next better classification is projected by the multiquadric kernel with linear, shuffle, stratified and automatic sampling.

Table 17 list the results of cross validation, SVM-PSO and PCA on F5.

The table give an overall good result than the previous tables. ANOVA results are exemplary in shuffle and stratified sampling. The dot kernel in stratified and automatic follow ANOVA with better results than before.

6 Conclusions

A feature based steganalysis had been performed using DCT, extended DCT and Markovian features. The impact of features had been studied and unwanted features are eliminated using PCA. Cross validation is employed due to the real time applicability of the research and a comparative study is done using data retrieved without cross validation. The extracted features are put into two different classifiers-SVM and SVM PSO. The majority of result states that radial kernel does not give a good result with the features and different types of sampling. A good classification rate is generally produced by dot kernel in spatial transformation. For DCT transformation, ANOVA generally give a good result. Hence the research states that the radial kernel with linear sampling that is generally used for classification gives low classification rate. As the SVM used optimization with removal of redundant data and cross validation, the results had improved.