1 Introduction

Multi attribute decision making (MADM) which is an important part of decision science is to find an optimal alternative, which are characterized in terms of multiple attribute, from alternative sets. In some real applications, the decision makers may be not capable to find exactly the values of the MADM problems due to uncertain and asymmetric information between decision maker. Multi-attribute decision making is the process to select an optimal alternative from the gathering feasible alternatives based on the number of attributes. But due to uncertainty and incompleteness decision making information, decision making process is not so easy to select the alternative from the set of feasible alternatives. As the result, output of the ranking order of alternatives is not accurate always. It is helpful for some sets, which deal with uncertainty, incomplete information such as fuzzy set, intuitionistic fuzzy set, neutrosophic set.

Some recent useful applications of fuzzy decision making are stated (Kacprzak 2019; Yazdani et al. 2019). Bellman and Zadeh (1970) gave first a decision making concept in fuzzy set environment. After that, Atanassov (1986) introduced intuitionistic fuzzy set (IFS) defining non-membership functions at first as independent component to reveal the uncertainty in different way. Recently, Jiang et al. (2018) defined new power aggregation operator on IFS and applied it to software selection problem. Liu et al. (2018) introduced intuitionistic fuzzy Dombi Bonferroni mean (IFDBM) operator depend on the Dombi operations and Bonferroni mean operator. Garg (2016) presented generalized intuitionistic fuzzy aggregation operators under the intuitionistic multiplicative preference relation instead of intuitionistic fuzzy preference relations. Some other important applications of intuitionistic fuzzy set in decision making (Jiang et al. 2019; Rashid et al. 2018). Joshi and Kumar (2018) defined a new accuracy functions under interval-valued intuitionistic fuzzy sets (IVIFSs), namely improved accuracy function to compare all comparable IVIFSs correctly. Using proposed accuracy function, they developed a multi-attribute group decision making (MAGDM) method with partially known attributes’ weight. Garg and Arora (2018) developed some new Bonferroni mean (BM) and weighted BM averaging operator for aggregating the different preferences of the decision-maker in intuitionistic fuzzy soft set environment. Recently, Garg (2017) introduced a series of averaging aggregation operators in the intuitionistic fuzzy environment by considering the degrees of hesitation between the membership functions and non-membership functions. Based on these averaging aggregation operators, he has been proposed a multi-criteria decision making method. Li (2014) gave a ranking method of intuitionistic fuzzy numbers and application to multi-attribute decision making problems in which attribute ratings are expressed with intuitionistic fuzzy numbers in management problem.

However, the theories of FS and IFS are incapable of managing the uncertainties such as indeterminate and inconsistent information. To get rid of such uncertainties, a new theory of neutrosophic sets (NSs) was introduced by Smarandache (1999), which is a branch of philosophy, studies the nature and scope of neutralities. The neutrosophic set (NS) as the generalization mathematical structure of FS and IFS by defining the three independent component. Truth, indeterminacy and falsity membership degree are the three independent components of NS. Later on, Wang et al. (2010) defined a special form of NS for realistic applications is called single valued neutrosophic set (SVNS). Liu and Wang (2018b) has been established interval neutrosophic prioritized owa operator and its application to multiple attribute decision making problems. Garg and Nancy (2018) was proposed the tinguistic single valued neutrosophic prioritized aggregation operators and their applications to multiple attribute group decision making problems. Liu and Wang (2018a) presented a multiple attribute decision-making method based on single-valued neutrosophic normalized weighted bonferroni mean. Some important study on SVN-sets which have been great impact on decision making (Sodenkamp et al. 2018; Wei and Wei 2018; Ren 2017).

Due to existence of uncertainty in real application data, Zadeh (1965) first introduced fuzzy set to deal with uncertainty in real and scientific problems. Possibility theory is one of the current uncertainty theories devoted to the handling of incomplete information, more precisely it is the simplest one, mathematically. To a large extent, it is similar to probability theory because it is based on set-functions. The possibility theory of fuzzy set was proposed by Zadeh (1978) and developed by many researchers, e.g., Dubois and Prade (1988), Yager (1992), Klir (1999) and others. Its academic meaning is in building a theoretical appearance of real applications for fuzzy sets. The possibility mean is the significant mathematical prominence of fuzzy numbers. Carlsson and Fuller (2001) introduced the notations of lower and upper possibilistic mean values and the inter valued possibilistic mean. They also proposed the notations of crisp possibilistic mean value and crisp possibilistic variance of continuous possibility distributions. Fuller and Majlender (2003) considered the notation of weighted interval-valued possibilistic mean value of fuzzy numbers and investigate its relationship to the interval-valued probabilistic mean. Wan et al. (2013) introduced the possibility mean, variance and covariance of triangular intuitionistic fuzzy numbers. Recently, the concept of the possibility mean, variance and covariance of generalized intuitionistic fuzzy number proposed by Garai et al. (2018).

In multiple difficult decision making problems, the decision information provided by a decision maker is often imprecise or uncertain due to time pressure, lack of data, or the decision maker’s limited attention and information processing capabilities. Therefore, introducing the possibility mean and variance into the nutrosophic the multi-attribute decision making (MADM) is of a great importance for scientific researches and real applications. However, there was no investigation on the possibility mean of nutrosophic number and application to MADM problems. The aim of this paper is defined a new ranking method based on possibility mean. Instead of this the proposed method has been applied for solving MADM problems under nutrosophic numbers.

In spite of the above mentioned developments, following additions can also be made in the possibility mean of single valued nutrosophic numbers and its application to multi-attribute decision making problem.

\(\bullet \):

Possibility mean of single valued nutrosophic numbers.

\(\bullet \):

The weighted possibility mean of single valued nutrosophic numbers.

\(\bullet \):

Formulation of some valuable theorems with possibility of single valued nutrosophic numbers.

\(\bullet \):

First time a rigorous ranking methodology to solve multi-attribute decision making problem.

The rest of the paper is organized as follows: In Sect.  2, we present some basic knowledge of SVN-numbers, In Sect.  3, we formulate the possibility mean of SVN-numbers and its valuable theorems. In Sect.  4, we introduce a multi-attribute decision making method based on possibility mean with SVN-numbers. The numerical examples with comparative studies are given in Sect.  5. Finally, the conclusion and scope of future work plan affair in Sect.  6.

2 Basic preliminaries

Definition 2.1

Let X be universe set. An intuitionistic fuzzy set (Deli and Broumi 2015) K over X is defined by \(K=\{\langle x, \mu _{K} (x), \nu _{K} (x) \rangle : x \in X\}\), where \(\mu _{K}: X\rightarrow [0, 1]\) and \(\nu _{K} : X \rightarrow [0, 1]\) such that \(0 \le \mu _{K} (x)+ \nu _{K} (x) \le 1\) for any \(x \in X\). For each \(x \in X\), the values \(\mu _{K} (x)\) and \(\nu _{K} (x)\) are the degree of membership and non-membership of x, respectively.

Definition 2.2

Let X be a universe. A nutrosophic sates (Deli and Broumi 2015) A over X is defined by \(A=\{\langle x, (T_{A} (x), I_{A} (x)\), \( F_{A} (x)) \rangle : x \in X\}\), where \(T_{A} (x), I_{A} (x)\) and \(F_{A} (x)\) are called truth membership function, indeterminacy-membership function and falsity membership function, respectively. They are respectively defined by

$$\begin{aligned} T_{A}: X\rightarrow ]^{-} 0, 1^{+}[, ~~ I_{A}: X\rightarrow ]^{-} 0, 1^{+}[, ~~ F_{A}: X\rightarrow ]^{-} 0, 1^{+}[ \end{aligned}$$

such that \(0^{-}\le T_{A} (x)+ I_{A} (x)+ F_{A} (x) \le 3^{+}\)

Definition 2.3

Let X be a universe (Deli and Broumi 2015). An single valued neutrosophic set (SVN-set) over X is a neutroophic set over X, but the truth-membership function, indeterminacy-membership function and falsity-membership function are respectively defined by

$$\begin{aligned} T_{A}: X\rightarrow [ 0, 1], ~~ I_{A}: X\rightarrow [ 0, 1], ~~ F_{A}: X\rightarrow [0, 1] \end{aligned}$$

such that \(0 \le T_{A} (x)+ I_{A} (x)+ F_{A} (x) \le 3\).

Definition 2.4

Let \(w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \in [0, 1]\) be any real numbers, \(a_{j}^{t}, a_{j}^{i}, a_{j}^{f} \in {\mathbb {R}} ~~ (j=1, 2, 3, 4)\) and \(a_{1} \le a_{2} \le a_{3} \le a_{4}\). Then a single valued neutrosophic number (Deli and Broumi 2015) (SVN-number) \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t);\) \(w_{\tilde{a}}), ( (a_{1}^i, a_{2}^i, a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) is a special netrosophic set on the set of real numbers \({\mathbb {R}}\), whose truth-membership function \(\mu _{\tilde{a}} : {\mathbb {R}}\rightarrow [0, 1]\), indeterminacy membership function \(\nu _{\tilde{a}} : {\mathbb {R}}\rightarrow [0, 1]\) and falsity membership function \(\lambda _{\tilde{a}} : {\mathbb {R}}\rightarrow [0, 1]\) are respectively defined by

$$\begin{aligned} \mu _{\tilde{a}} (x)=\left\{ \begin{array}{ll}f_{\mu }^{l} (x), &{}\quad \text{ if } a_{1}^t\le x<{a_{2}^t}\\ w_{\tilde{a}}, &{}\quad \text{ if } a_{2}^t\le x \le a_{3}^t\\ f_{\mu }^{r} (x), &{}\quad \text{ if } a_{3}^t< x\le a_{4}^t\\ 0 &{}\quad \text{ otherwise } \end{array}\right. \\ \nu _{\tilde{a}} (x)=\left\{ \begin{array}{ll}f_{\nu }^{l} (x), &{}\quad \text{ if } a_{1}^i\le x<{a_{2}^i}\\ u_{\tilde{a}}, &{} \quad \text{ if } a_{2}^i\le x \le a_{3}^i\\ f_{\nu }^{r} (x), &{} \quad \text{ if } a_{3}^i< x\le a_{4}^i\\ 0 &{} \quad \text{ otherwise } \end{array}\right. \\ \lambda _{\tilde{a}} (x)=\left\{ \begin{array}{ll}f_{\lambda }^{l} (x), &{}\quad \text{ if } a_{1}^f\le x<{a_{2}^f}\\ y_{\tilde{a}}, &{}\quad \text{ if } a_{2}^f\le x \le a_{3}^f\\ f_{\lambda }^{r} (x), &{}\quad \text{ if } a_{3}^f< x\le a_{4}^f\\ 0 &{}\quad \text{ otherwise } \end{array}\right. \end{aligned}$$

where the function \(f_{\mu }^{l}: [a_{1}^{t}, a_{2}^{t}]\rightarrow [0, w_{\tilde{a}}]\), \(f_{\nu }^{l}: [a_{3}^{i}, a_{4}^{i}]\rightarrow [u_{\tilde{a}}]\) and \(f_{\lambda }^{l}: [a_{3}^{f}, a_{4}^{f}]\rightarrow [y_{\tilde{a}}, 1]\) are continuous and non increasing, and satisfy the conditions: \(f_{\mu }^{l} (a_{1}^t)=0, f_{\mu }^{l} (a_{2}^t)=w_{\tilde{a}}\), \(f_{\nu }^{r} (a_{4}^i)=u_{\tilde{a}}, f_{\nu }^{r} (a_{4}^i)=1\), \(f_{\lambda }^{r} (a_{3}^f)=y_{\tilde{a}}, f_{\lambda }^{r} (a_{4}^f)=1\); the functions \(f_{\mu }^{r}: [a_{3}^{t}, a_{4}^{t}]\rightarrow [0, w_{\tilde{a}}]\), \(f_{\nu }^{r}: [a_{1}^{i}, a_{2}^{i}]\rightarrow [u_{\tilde{a}}]\) and \(f_{\lambda }^{r}: [a_{1}^{f}, a_{2}^{f}]\rightarrow [y_{\tilde{a}}, 1]\) are continuous and increasing, and satisfy the conditions: \(f_{\mu }^{r} (a_{3}^t)=0, f_{\mu }^{r} (a_{4}^t)=w_{\tilde{a}}\), \(f_{\nu }^{l} (a_{1}^i)=u_{\tilde{a}}, f_{\nu }^{l} (a_{2}^i)=1\), \(f_{\lambda }^{l} (a_{1}^f)=y_{\tilde{a}}, f_{\lambda }^{l} (a_{2}^f)=1\). \([a_{2}^t, a_{3}^t]\), \(a_{1}^t, a_{4}^t\) are called the mean interval and lower and upper limits of the general neutrosophic number \(\tilde{a}\) for truth-membership function, respectively. \([a_{2}^i, a_{3}^i]\), \(a_{1}^i, a_{4}^i\) are called the mean interval and lower and upper limits of the general neutrosophic number \(\tilde{a}\) for indeterminacy-membership function, respectively. \([a_{2}^f, a_{3}^f]\), \(a_{1}^f, a_{4}^f\) are called the mean interval and lower and upper limits of the general neutrosophic number \(\tilde{a}\) for falsity-membership function, respectively. \(w_{\tilde{a}}, u_{\tilde{a}}\) and \(y_{\tilde{a}}\) are called the maximum truth membership degree, minimum indeterminacy-membership degree and minimum falsity membership degree, respectively.

Example 1

Assume that \(\tilde{a}=\langle ( (1, 3, 5, 8), 0.9), ( (1, 2, 6, 8), 0.3), ( (1, 3, 5, 8), 0.5)\rangle \) be a SVN-number. Then, the meanings of \(\tilde{a}\) is interpreted as follows: For example the truth-membership degree of the element \(3 \in {\mathbb {R}}\) belonging to \(\tilde{a}\) is 0.9 whereas the indeterminacy membership degree is 0.1 and falsity-membership degree is \(\mu _{\tilde{a}} (3)=0.9, \nu _{\tilde{a}} (3)=0.3\) and \(\lambda _{\tilde{a}} (3)=0.5\) (cf. Fig. 1).

Fig. 1
figure 1

\(\alpha \)-cut set of truth-membership, \(\beta \)-cut set of indeterminacy-membership, and \(\gamma \)-cut set of falsity-membership functions for SVN-numbers (\(\tilde{a}\))

Full size image

Definition 2.5

A single valued trapezoidal neutrosophic number (SVTN-number) \(\tilde{a}=\langle (a_{1}, a_{2}, a_{3}, a_{4})\); \(w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle \) is a special neutrosophic set (Deli and Broumi 2015) on the real number set \({\mathbb {R}}\), whose truth-membership, indeterminacy membership and falsity membership functions are given as follows:

$$\begin{aligned} \mu _{\tilde{a}} (x)= &\, {} \left\{ \begin{array}{ll}\dfrac{x-a_{1}}{a_{2}-a_{1}}w_{\tilde{a}}, &{}\quad \text{ if } a_{1}\le x<{a_{2}}\\ w_{\tilde{a}}, &{}\quad \text{ if } a_{2}\le x \le a_{3}\\ \dfrac{a_{4}-x}{a_{4}-a_{3}}w_{\tilde{a}}, &{}\quad \text{ if } a_{3}< x\le a_{4}\\ 0 &{}\quad \text{ otherwise } \end{array}\right. \\ \nu _{\tilde{a}} (x)= &\, {} \left\{ \begin{array}{ll}\dfrac{ (a_{2}-x)+ (x-a_{1})u_{\tilde{a}}}{a_{2}-a_{1}}, &{}\quad \text{ if } a_{1}\le x<{a_{2}}\\ u_{\tilde{a}}, &{}\quad \text{ if } a_{2}\le x \le a_{3}\\ \dfrac{ (x-a_{3})+ (a_{4}-x)u_{\tilde{a}}}{a_{4}-a_{3}}, &{}\quad \text{ if } a_{3}< x\le a_{4}\\ 0 &{}\quad \text{ otherwise } \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \lambda _{\tilde{a}} (x)=\left\{ \begin{array}{ll}\dfrac{ (a_{2}-x)+ (x-a_{1})y_{\tilde{a}}}{a_{2}-a_{1}}, &{}\quad \text{ if } a_{1}\le x<{a_{2}}\\ y_{\tilde{a}}, &{}\quad \text{ if } a_{2}\le x \le a_{3}\\ \dfrac{ (x-a_{3})+ (a_{4}-x)y_{\tilde{a}}}{a_{4}-a_{3}}, &{}\quad \text{ if } a_{3}< x\le a_{4}\\ 0 &{}\quad \text{ otherwise } \end{array}\right. \end{aligned}$$

respectively.

Definition 2.6

A single valued triangular neutrosophic number (SVTrN) \(\tilde{a}=\langle (a_{1}, a_{2}, a_{3}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle \) is a special neutrosophic set (Deli and Broumi 2015) on the real number set \({\mathbb {R}}\), whose truth-membership, indeterminacy membership and falsity membership functions are given as follows:

$$\begin{aligned} \mu _{\tilde{a}} (x)= &\, {} \left\{ \begin{array}{ll}\dfrac{x-a_{1}}{a_{2}-a_{1}}w_{\tilde{a}}, &{}\quad \text{ if } a_{1}\le x<{a_{2}}\\ w_{\tilde{a}}, &{}\quad \text{ if } x=a_{2}\\ \dfrac{a_{3}-x}{a_{3}-a_{2}}w_{\tilde{a}}, &{}\quad \text{ if } a_{2}< x\le a_{3}\\ 0 &{}\quad \text{ otherwise } \end{array}\right. \\ \nu _{\tilde{a}} (x)= &\, {} \left\{ \begin{array}{ll}\dfrac{ (a_{2}-x)+ (x-a_{1})u_{\tilde{a}}}{a_{2}-a_{1}}, &{}\quad \text{ if } a_{1}\le x<{a_{2}}\\ u_{\tilde{a}}, &{}\quad \text{ if } x=a_{2}\\ \dfrac{ (x-a_{2})+ (a_{3}-x)u_{\tilde{a}}}{a_{3}-a_{2}}, &{}\quad \text{ if } a_{2}< x\le a_{3}\\ 0 &{}\quad \text{ otherwise } \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \lambda _{\tilde{a}} (x)=\left\{ \begin{array}{ll}\dfrac{ (a_{2}-x)+ (x-a_{1})y_{\tilde{a}}}{a_{2}-a_{1}}, &{}\quad \text{ if } a_{1}\le x<{a_{2}}\\ y_{\tilde{a}}, &{}\quad \text{ if } x=a_{2}\\ \dfrac{ (x-a_{2})+ (a_{3}-x)y_{\tilde{a}}}{a_{3}-a_{2}}, &{}\quad \text{ if } a_{2}< x\le a_{3}\\ 0 &{}\quad \text{ otherwise } \end{array}\right. \end{aligned}$$

respectively.

If \(a_{1}>0\) \( (a_{1} \le a_{2} \le a_{3})\) and at least \(a_{3}>0\) then \(\tilde{a} = \langle (a_{1}, a_{2}, a_{3}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}}\rangle \) is called a positive SVTrN, denoted by \(\tilde{a}\). Likewise, if \(a_{3}\le 0\) \( (a_{1} \le a_{2} \le a_{3})\) and at least \(a_{1}<0\), then \(\tilde{a} = \langle (a_{1}, a_{2}, a_{3}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}}\rangle \) is called a negative SVTrN, denoted by \(\tilde{a}<0\). A SVTrN \(\tilde{a}\) may be express an \(\tilde{a} = \langle (a_{1}, a_{2}, a_{3}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}}\rangle \).

Definition 2.7

Let \(\tilde{a} = \langle (a_{1}, a_{2}, a_{3}, a_{4}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}}\rangle \) and \(\tilde{b} = \langle (b_{1}, b_{2}, b_{3}, b_{4}); w_{\tilde{b}}, u_{\tilde{b}}, y_{\tilde{b}}\rangle \) be a SVTN-numbers and \(k\ne 0\) be any number and \(\wedge =min\), \(\vee =max\). Then

  1. (i)

    \(\tilde{a} + \tilde{b}= \langle (a_{1}+b_{1}, a_{2}+b_{2}, a_{3}+b_{3}, a_{4}+b_{4}); w_{\tilde{a}}\wedge w_{\tilde{b}}, u_{\tilde{a}}\vee u_{\tilde{b}}, y_{\tilde{a}}\vee y_{\tilde{b}} \rangle \)

  2. (ii)

    \(\tilde{a}\tilde{b}=\left\{ \begin{array}{ll} \langle (a_{1}b_{1}, a_{2}b_{2}, a_{3}b_{3}, a_{4}b_{4}); w_{\tilde{a}}\wedge w_{\tilde{b}}, u_{\tilde{a}}\vee u_{\tilde{b}}, y_{\tilde{a}}\vee y_{\tilde{b}} \rangle &{} a_{4}> 0, b_{4}>0\\ \langle (a_{1}b_{4}, a_{2}b_{3}, a_{3}b_{2}, a_{4}b_{1}); w_{\tilde{a}}\wedge w_{\tilde{b}}, u_{\tilde{a}}\vee u_{\tilde{b}}, y_{\tilde{a}}\vee y_{\tilde{b}} \rangle &{} a_{4}<0, b_{4}>0\\ \langle (a_{4}b_{4}, a_{3}b_{3}, a_{2}b_{2}, a_{1}b_{1}); w_{\tilde{a}}\wedge w_{\tilde{b}}, u_{\tilde{a}}\vee u_{\tilde{b}}, y_{\tilde{a}}\vee y_{\tilde{b}} \rangle &{} a_{4}<0, b_{4}<0 \end{array}\right. \)

  3. (iii)

    \(\gamma \tilde{a}=\left\{ \begin{array}{ll} \langle (\gamma a_{1}, \gamma a_{2}, \gamma a_{3}, \gamma a_{4}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle &{} \gamma > 0\\ \langle (\gamma a_{4}, \gamma a_{3}, \gamma a_{2}, \gamma a_{1}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle &{} \gamma <0\\ \end{array}\right. \)

3 Concept of possibility mean for SVN-numbers

In this section, we first define the concept of cut sets, possibility mean values, weighted possibility mean values of SVN-numbers and give some desired properties. Also we have developed a new ranking method of SVN-numbers. In the following definitions and operations on generalized intuitionistic numbers, defined (Garai et al. 2018), we extend these definitions and operations to single valued neutrosophic numbers.

Definition 3.1

Let \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t); w_{\tilde{a}})\); \( ( (a_{1}^i, a_{2}^i, a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) be a SVN-number. Then \(\langle \alpha , \beta , \gamma \rangle \)-cut of the SVN-number \(\tilde{a}\), denoted by \(\tilde{a}_{\alpha , \beta , \gamma }\), is defined as:

$$\begin{aligned} \tilde{a}_{\langle \alpha , \beta , \gamma \rangle } =\{x: \mu _{\tilde{a}} (x) \ge \alpha , \nu _{\tilde{a}} (x) \le \beta , \lambda _{\tilde{a}} (x) \le \gamma , x \in {\mathbb {R}}\} \end{aligned}$$

which satisfies the conditions as follows: \(0 \le \alpha \le w_{\tilde{a}}\), \(u_{\tilde{a}} \le \beta \le 1\), \(y_{\tilde{a}} \le \beta \le 1\) and \(0 \le \alpha + \beta +\gamma \le 3\).

Clearly, any \(\langle \alpha , \beta , \gamma \rangle \)-cut set \(\tilde{a}_{\langle \alpha , \beta , \gamma \rangle }\) of a SVN-number \(\tilde{a}\) is a crisp subset of the real number set \({\mathbb {R}}.\)

Definition 3.2

Let \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t); w_{\tilde{a}})\); \( ( (a_{1}^i, a_{2}^i, a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) be a SVN-number. Then \(\alpha \)-cut set of the SVN-number \(\tilde{a}\), denoted by \(\tilde{a}_{\alpha }\) is defined as: \(\tilde{a}_{\alpha }=\{x: \mu _{\tilde{a}} (x)\ge \alpha , x \in {\mathbb {R}}\}\), where \(\alpha \in [0, w_{\tilde{a}}]\).

Clearly, any \(\alpha \)-cut set of a SVN-number \(\tilde{a}\) is a crisp subset of the real number set \({\mathbb {R}}\).

In here, any \(\alpha \)-cut set of a SVN-number \(\tilde{a}\) for falsity membership function is closed interval, denoted by \(\tilde{a}_{\alpha }=[a_{\alpha }^{l}, a_{\alpha }^{r}]\).

Definition 3.3

Let \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t); w_{\tilde{a}})\); \( ( (a_{1}^i, a_{2}^i, a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) be a SVN-number. Then \(\beta \)-cut set of the SVN-number \(\tilde{a}\), denoted by \(\tilde{a}_{\beta }\) is defined as: \(\tilde{a}_{\beta }=\{x: \nu _{\tilde{a}} (x)\le \beta , x \in {\mathbb {R}}\}\), where \(\beta \in [u_{\tilde{a}}, 1]\).

Clearly, any \(\beta \)-cut set of a SVN-number \(\tilde{a}\) is a crisp subset of the real number set \({\mathbb {R}}\).

In here, any \(\beta \)-cut set of a SVN-number \(\tilde{a}\) for indeterminacy membership function is closed interval, denoted by \(\tilde{a}_{\beta }=[a_{\beta }^{l}, a_{\beta }^{r}]\).

Definition 3.4

Let \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t); w_{\tilde{a}})\); \( ( (a_{1}^i, a_{2}^i, a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) be a SVN-number. Then \(\gamma \)-cut set of the SVN-number \(\tilde{a}\), denoted by \(\tilde{a}_{\gamma }\) is defined as: \(\tilde{a}_{\gamma }=\{x: y_{\tilde{a}} (x)\le \gamma , x \in {\mathbb {R}}\}\), where \(\gamma \in [u_{\tilde{a}}, 1]\).

Clearly, any \(\gamma \)-cut set of a SVN-number \(\tilde{a}\) is a crisp subset of the real number set \({\mathbb {R}}\).

In here, any \(\gamma \)-cut set of a SVN-number \(\tilde{a}\) for falsity membership function is closed interval, denoted by \(\tilde{a}_{\gamma }=[a_{\gamma }^{l}, a_{\gamma }^{r}]\).

Definition 3.5

Let \(\tilde{a}_{\alpha }=[a_{\alpha }^{l}, a_{\alpha }^{r}]\) be the \(\alpha \)-cut set of a SVN-number \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t); w_{\tilde{a}})\), \( ( (a_{1}^i, a_{2}^i, a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) with \(0 \le \alpha \le w_{\tilde{a}}\). The f lower and upper possibility (Pos) means of truth membership function (Wan et al. 2013) for the SVN-number \(\tilde{a}\) are respectively defined as follows:

$$\begin{aligned} \underline{M}_{\mu } (\tilde{a})= &\, {} \int _{0}^{w_{\tilde{a}}}f (Pos[\tilde{a} \le a_{\alpha }^{l}])a_{\alpha }^{l}d\alpha =\int _{0}^{w_{\tilde{a}}}f (\alpha )a_{\alpha }^{l}d\alpha \nonumber \\ \overline{M}_{\mu } (\tilde{a})= &\, {} \int _{0}^{w_{\tilde{a}}}f (Pos[\tilde{a} \ge a_{\alpha }^{r}])a_{\alpha }^{r}d\alpha =\int _{0}^{w_{\tilde{a}}}f (\alpha )a_{\alpha }^{r}d\alpha \end{aligned}$$
(1)

where, \(f: [0, w_{\tilde{a}}] \rightarrow {\mathbb {R}}\) is a increasing and non-negative weighted function satisfying that \(\int _{0}^{w_{\tilde{a}}}f (\alpha )d\alpha =w_{\tilde{a}}\) and \(f (0)=0\), and

$$\begin{aligned} Pos[\tilde{a} \le a_{\alpha }^{l}]=\sup _{x \le a_{\alpha }^{l}}\{\mu _{\tilde{a}} (x)\}=\alpha ~~~ Pos[\tilde{a} \ge a_{\alpha }^{r}]=\sup _{x \ge a_{\alpha }^{r}}\{\mu _{\tilde{a}} (x)\}=\alpha \end{aligned}$$
(2)

If \(\underline{M}_{\mu } (\tilde{a})\) and \(\overline{M}_{\mu } (\tilde{a})\) are the lower and upper possibility mean for truth-membership function of a SVN-number \(\tilde{a}\), then possibility mean for truth-membership function defined as :

$$\begin{aligned} M_{\mu } (\tilde{a})= &\, {} \dfrac{\underline{M}_{\mu } (\tilde{a})+\overline{M}_{\mu } (\tilde{a})}{2}\nonumber \\= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{a}}}f (\alpha )\left( a_{\alpha }^{l} + a_{\alpha }^{r} \right) d\alpha \end{aligned}$$
(3)

Definition 3.6

Let \(\tilde{a}_{\beta }=[a_{\beta }^{l}, a_{\beta }^{r}]\) be the \(\beta \)-cut set of a SVN-number \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t); w_{\tilde{a}}), ( (a_{1}^i, a_{2}^i,\) \( a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) with \(u_{\tilde{a}}\le \beta \le 1\). The lower and upper possibility (Pos) means of indeterminacy membership function for the SVN-number \(\tilde{a}\) are respectively defined as follows:

$$\begin{aligned} \underline{M}_{\nu } (\tilde{a})= &\, {} \int _{u_{\tilde{a}}}^{1}g (Pos[\tilde{a} \le a_{\beta }^{l}])a_{\beta }^{l}d\beta =\int _{u_{\tilde{a}}}^{1}g (\beta )a_{\beta }^{l}d\beta \end{aligned}$$
(4)
$$\begin{aligned} \overline{M}_{\nu } (\tilde{a})= &\, {} \int _{u_{\tilde{a}}}^{1}g (Pos[\tilde{a} \ge a_{\beta }^{r}])a_{\beta }^{r}d\beta =\int _{u_{\tilde{a}}}^{1}g (\beta )a_{\beta }^{r}d\beta \end{aligned}$$
(5)

where, \(g: [u_{\tilde{a}}, 1] \rightarrow {\mathbb {R}}\) is a non-increasing and non-negative weighted function satisfying that \(\int _{u_{\tilde{a}}}^{1}g (\beta )d\beta =1-u_{\tilde{a}}\) and \(g (1)=0\), and

$$\begin{aligned} Pos[\tilde{a} \le a_{\beta }^{l}]=\sup\nolimits _{x \le a_{\beta }^{l}}\{\nu _{\tilde{a}} (x)\}=\beta ~~~ Pos[\tilde{a} \ge a_{\beta }^{r}]=\sup\nolimits _{x \ge a_{\beta }^{r}}\{\nu _{\tilde{a}} (x)\}=\beta \end{aligned}$$

If \(\underline{M}_{\nu } (\tilde{a})\) and \(\overline{M}_{\nu } (\tilde{a})\) are the lower and upper possibility mean for indeterminacy-membership function of a SVN-number \(\tilde{a}\), then possibility mean for indeterminacy-membership function defined as :

$$\begin{aligned} M_{\nu } (\tilde{a})= &\, {} \dfrac{\underline{M}_{\nu } (\tilde{a})+\overline{M}_{\nu } (\tilde{a})}{2} \nonumber \\= &\, {} \frac{1}{2}\int _{u_{\tilde{a}}}^{1}g (\beta )\left( a_{\beta }^{l} + a_{\beta }^{r} \right) d\beta \end{aligned}$$
(6)

Definition 3.7

Let \(\tilde{a}_{\gamma }=[a_{\gamma }^{l}, a_{\gamma }^{r}]\) be the \(\gamma \)-cut set of a SVN-number \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t); w_{\tilde{a}}) ( (a_{1}^i, a_{2}^i,\) \( a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) with \(y_{\tilde{a}}\le \gamma \le 1\). The lower and upper possibility (Pos) means of falsity membership function (Wan et al. 2013) for the SVN-number \(\tilde{a}\) are respectively defined as follows:

$$\begin{aligned} \underline{M}_{\lambda } (\tilde{a})= &\, {} \int _{y_{\tilde{a}}}^{1}h\left( Pos\left[ \tilde{a} \le a_{\gamma }^{l}\right] \right) a_{\gamma }^{l}d\gamma =\int _{y_{\tilde{a}}}^{1}h (\gamma )a_{\gamma }^{l}d\gamma \end{aligned}$$
(7)
$$\begin{aligned} \overline{M}_{\lambda } (\tilde{a})= &\, {} \int _{y_{\tilde{a}}}^{1}h\left( Pos\left[ \tilde{a} \ge a_{\gamma }^{r}\right] \right) a_{\gamma }^{r}d\gamma =\int _{u_{\tilde{a}}}^{1}h (\gamma )a_{\gamma }^{r}d\gamma \end{aligned}$$
(8)

where, \(h: [y_{\tilde{a}}, 1] \rightarrow {\mathbb {R}}\) is a non-increasing and non-negative weighted function satisfying that \(\int _{y_{\tilde{a}}}^{1}h (\beta )d\gamma =1-y_{\tilde{a}}\) and \(h (1)=0\), and

$$\begin{aligned} Pos[\tilde{a} \le a_{\gamma }^{l}]=\sup _{x \le a_{\gamma }^{l}}\{\lambda _{\tilde{a}} (x)\}=\gamma ~~~ Pos[\tilde{a} \ge a_{\gamma }^{r}]=\sup _{x \ge a_{\gamma }^{r}}\{\lambda _{\tilde{a}} (x)\}=\gamma \end{aligned}$$

If \(\underline{M}_{\lambda } (\tilde{a})\) and \(\overline{M}_{\lambda } (\tilde{a})\) are the lower and upper possibility mean for falsity-membership function of a SVN-number \(\tilde{a}\), then possibility mean for falsity-membership function defined as :

$$\begin{aligned} M_{\lambda } (\tilde{a})= &\, {} \dfrac{\underline{M}_{\lambda } (\tilde{a})+\overline{M}_{\lambda } (\tilde{a})}{2} \nonumber \\= &\, {} \frac{1}{2}\int _{y_{\tilde{a}}}^{1}h (\gamma )\left( a_{\gamma }^{l} + a_{\gamma }^{r} \right) d\gamma \end{aligned}$$
(9)

Corollary 1

Let \(\tilde{a}=\langle (a_{1}, a_{2}, a_{3}, a_{4}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle \) be a SVTN-number. Then

  1. 1.

    \(\alpha \)-cut set of the SVTN-number \(\tilde{a}\) for truth-membership function is calculated as

    $$\begin{aligned} \tilde{a}_{\alpha }=\left[ a_{\alpha }^{l}, a_{\alpha }^{r}\right] =\left[ a_{1}+\dfrac{\alpha (a_{2}-a_{1})}{w_{\tilde{a}}}, a_{4}-\dfrac{\alpha (a_{4}-a_{3})}{w_{\tilde{a}}}\right] \end{aligned}$$

    where \(\alpha \in [0, w_{\tilde{a}}]\). If \(f (\alpha )=2 \alpha \), we can obtain the possibility mean of a SVTN-number \(\tilde{a}\) for truth-membership function as follows:

    $$\begin{aligned} M_{\mu } (\tilde{a})= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{a}}}f (\alpha )\left( a_{\alpha }^{l} + a_{\alpha }^{r} \right) d\alpha \\= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{a}}}\\&\times \left( 2\alpha \right) \left[ (a_{1}+a_{4}) + \dfrac{ (a_{2}+a_{3}-a_{1}-a_{4})\alpha }{w_{\tilde{a}}} \right] d\alpha \\= &\, {} \dfrac{ (a_{1}+2a_{2}+2a_{3}+a_{4})}{6}w_{\tilde{a}}^{2} \end{aligned}$$
  2. 2.

    \(\beta \)-cut set of the SVTN-number \(\tilde{a}\) for indeterminacy-membership function is calculated as

    $$\begin{aligned} \tilde{a}_{\beta }= &\, {} \left[ a_{\beta }^{l}, a_{\beta }^{r}\right] =\left[ a_{1}+\dfrac{ (1-\beta ) (a_{2}-a_{1})}{1-u_{\tilde{a}}},\right. \\&\left. a_{4}-\dfrac{ (1-\beta ) (a_{4}-a_{3})}{1-u_{\tilde{a}}}\right] \end{aligned}$$

    where \(\beta \in [u_{\tilde{a}}, 1]\). If \(g (\beta )=2 (1-\beta )\), we can obtain the possibility mean of a SVTN-number \(\tilde{a}\) for indeterminacy-membership function as follows:

    $$\begin{aligned} M_{\nu } (\tilde{a})= &\, {} \frac{1}{2}\int _{u_{\tilde{a}}}^{1}g (\beta )\left( a_{\beta }^{l} + a_{\beta }^{r} \right) d\beta \\= &\, {} \frac{1}{2}\int _{u_{\tilde{a}}}^{1}2 (1-\beta )\\&\times \left[ (a_{1}+a_{4})+\dfrac{ (a_{2}+a_{3}-a_{1}-a_{4}) (1-\beta )}{1-u_{\tilde{a}}}\right] \\= &\, {} \dfrac{ (a_{1}+2a_{2}+2a_{3}+a_{4})}{6} (1-u_{\tilde{a}})^{2} \end{aligned}$$
  3. 3.

    \(\gamma \)-cut set of the SVTN-number \(\tilde{a}\) for indeterminacy-membership function is calculated as

    $$\begin{aligned} \tilde{a}_{\gamma }= &\, {} \left[ a_{\gamma }^{l}, a_{\gamma }^{r}\right] =\left[ a_{1}+\dfrac{ (1-\gamma ) (a_{2}-a_{1})}{1-y_{\tilde{a}}},\right. \\&\left. a_{4}-\dfrac{ (1-\gamma ) (a_{4}-a_{3})}{1-y_{\tilde{a}}}\right] \end{aligned}$$

    where \(\gamma \in [y_{\tilde{a}}, 1]\). If \(g (\gamma )=2 (1-\gamma )\), we can obtain the possibility mean of a SVTN-number \(\tilde{a}\) for indeterminacy-membership function as follows:

    $$\begin{aligned} M_{\lambda } (\tilde{a})= &\, {} \frac{1}{2}\int _{y_{\tilde{a}}}^{1}h (\gamma )\left( a_{\gamma }^{l} + a_{\gamma }^{r} \right) d\gamma \\= &\, {} \frac{1}{2}\int _{y_{\tilde{a}}}^{1}2 (1 - \gamma )\\&\times \left[ (a_{1}+a_{4})+\dfrac{ (a_{2}+a_{3}-a_{1}-a_{4}) (1-\gamma )}{1-y_{\tilde{a}}}\right] \\= &\, {} \dfrac{ (a_{1}+2a_{2}+2a_{3}+a_{4})}{6} (1-y_{\tilde{a}})^{2} \end{aligned}$$

Corollary 2

Let \(\tilde{a}=\langle (a_{1}, a_{2}, a_{3}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle \) be a SVTrN-number. Then

  1. 1.

    \(\alpha \)-cut set of the SVTrN-number \(\tilde{a}\) for truth-membership function is calculated as

    $$\begin{aligned} \tilde{a}_{\alpha }=\left[ a_{\alpha }^{l}, a_{\alpha }^{r}\right] =\left[ a_{1}+\dfrac{\alpha (a_{2}-a_{1})}{w_{\tilde{a}}}, a_{3}-\dfrac{\alpha (a_{3}-a_{2})}{w_{\tilde{a}}}\right] \end{aligned}$$

    where \(\alpha \in [0, w_{\tilde{a}}]\). If \(f (\alpha )=2 \alpha \), we can obtain the possibility mean of a SVTrN-number \(\tilde{a}\) for truth-membership function as follows:

    $$\begin{aligned} M_{\mu } (\tilde{a})= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{a}}}f (\alpha )\left( a_{\alpha }^{l} + a_{\alpha }^{r} \right) d\alpha \\= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{a}}}\left( 2\alpha \right) \left[\vphantom{\left. + \dfrac{ (4a_{2}-a_{1}-a_{3})\alpha }{w_{\tilde{a}}} \right] } (a_{1}+a_{3})\right. \\&\left. + \dfrac{ (4a_{2}-a_{1}-a_{3})\alpha }{w_{\tilde{a}}} \right] d\alpha \\= &\, {} \dfrac{ (a_{1}+4a_{2}+a_{3})}{6}w_{\tilde{a}}^2 \end{aligned}$$
  2. 2.

    \(\beta \)-cut set of the SVTrN-number \(\tilde{a}\) for indeterminacy-membership function is calculated as

    $$\begin{aligned} \tilde{a}_{\beta }= &\, {} \left[ a_{\beta }^{l}, a_{\beta }^{r}\right] =\left[ a_{1}+\dfrac{ (1-\beta ) (a_{2}-a_{1})}{1-u_{\tilde{a}}},\right. \\&\left. a_{3}-\dfrac{ (1-\beta ) (a_{3}-a_{2})}{1-u_{\tilde{a}}}\right] \end{aligned}$$

    where \(\beta \in [u_{\tilde{a}}, 1]\). If \(g (\beta )=2 (1-\beta )\), we can obtain the possibility mean of a SVTrN-number \(\tilde{a}\) for indeterminacy-membership function as follows:

    $$\begin{aligned} M_{\nu } (\tilde{a})= &\, {} \frac{1}{2}\int _{u_{\tilde{a}}}^{1}g (\beta )\left( a_{\beta }^{l} + a_{\beta }^{r} \right) d\beta \\= &\, {} \frac{1}{2}\int _{u_{\tilde{a}}}^{1}2 (1- \beta )\left[ \vphantom {\left. +\dfrac{ (2a_{2}-a_{1}-a_{3}) (1-\beta )}{1-u_{\tilde{a}}}\right] } (a_{1}+a_{3})\right. \\&\left. +\dfrac{ (2a_{2}-a_{1}-a_{3}) (1-\beta )}{1-u_{\tilde{a}}}\right] \\= &\, {} \dfrac{ (a_{1}+4a_{2}+a_{3})}{6} (1-u_{\tilde{a}})^2 \end{aligned}$$
  3. 3.

    \(\gamma \)-cut set of the SVTrN-number \(\tilde{a}\) for falsity-membership function is calculated as

    $$\begin{aligned} \tilde{a}_{\gamma }= &\, {} \left[ a_{\gamma }^{l}, a_{\gamma }^{r}\right] =\left[ a_{1}+\dfrac{ (1-\gamma ) (a_{2}-a_{1})}{1-y_{\tilde{a}}},\right. \\&\left. a_{3}-\dfrac{ (1-\gamma ) (a_{3}-a_{2})}{1-y_{\tilde{a}}}\right] \end{aligned}$$

    where \(\gamma \in [y_{\tilde{a}}, 1]\). If \(g (\gamma )=2 (1-\gamma )\), we can obtain the possibility mean of a SVTrN-number \(\tilde{a}\) for indeterminacy-membership function as follows:

    $$\begin{aligned} M_{\lambda } (\tilde{a})= &\, {} \frac{1}{2}\int _{y_{\tilde{a}}}^{1}h (\gamma )\left( a_{\gamma }^{l} + a_{\gamma }^{r} \right) d\gamma \\= &\, {} \frac{1}{2}\int _{y_{\tilde{a}}}^{1}2 (1 - \gamma )\left[ \vphantom {\left. +\dfrac{ (2a_{2}-a_{1}-a_{3}) (1-\gamma )}{1-y_{\tilde{a}}}\right] } (a_{1}+a_{3})\right. \\&\left. +\dfrac{ (2a_{2}-a_{1}-a_{3}) (1-\gamma )}{1-y_{\tilde{a}}}\right] \\= &\, {} \dfrac{ (a_{1}+4a_{2}+a_{3})}{6} (1-y_{\tilde{a}})^2 \end{aligned}$$

Definition 3.8

Let \(\tilde{a}=\langle ( (a_{1}^t, a_{2}^t, a_{3}^t, a_{4}^t); w_{\tilde{a}})\); \( ( (a_{1}^i, a_{2}^i, a_{3}^i, a_{4}^i), u_{a}), ( (a_{1}^f, a_{2}^f, a_{3}^f, a_{4}^f); y_{\tilde{a}})\rangle \) be a SVN-number. Then for \(\vartheta \in [0, 1]\), the weighted possibility mean value of the SVN-number \(\tilde{a}\) are defined as:

$$\begin{aligned} M_{\vartheta } (\tilde{a})=\vartheta M_{\mu } (\tilde{a})+ (1-\vartheta )M_{\nu } (\tilde{a})+ (1-\vartheta )M_{\lambda } (\tilde{a}) \end{aligned}$$

Corollary 3

Let \(\tilde{a}=\langle (a_{1}, a_{2}, a_{3}, a_{4}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle \) is an arbitrary SVTN-number. Then the weighted possibility mean value is calculated as

$$\begin{aligned} M_{\vartheta } (\tilde{a})= &\, {} \dfrac{a_{1}+2a_{2}+2a_{3}+a_{4}}{6}\left[ \vartheta w_{\tilde{a}}^2\right. \\&+\left. (1-\vartheta ) (1- u_{\tilde{a}})^2 + (1- \vartheta ) (1-y_{ \tilde{a}})^2\right] \end{aligned}$$

Corollary 4

Let \(\tilde{a}=\langle (a_{1}, a_{2}, a_{3}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle \) is an arbitrary SVTrN-number. Then the weighted possibility mean value is calculated as

$$\begin{aligned} M_{\vartheta } (\tilde{a})=\dfrac{a_{1}+4a_{2}+a_{3}}{6}\left[ \vartheta w_{\tilde{a}}^2+ (1-\vartheta ) (1- u_{\tilde{a}})^2 + (1- \vartheta ) (1-y_{ \tilde{a}})^2\right] \end{aligned}$$

Now we give a new ranking method of SVN-numbers based on the weighted possibility mean value can be considered as follows:

Definition 3.9

Let \(\tilde{a}\) and \(\tilde{b}\) be two SVN-number and \(\vartheta \in [0, 1]\). For weighted possibility values of the SVN-numbers \(\tilde{a}\) and \(\tilde{b}\), the ranking order of \(\tilde{a}\) and \(\tilde{b}\) is defined as

  1. (i)

    If \(M_{\vartheta } (\tilde{a}) > M_{\vartheta } (\tilde{b})\), then \(\tilde{a}\) is bigger than \(\tilde{b}\), denoted by \(\tilde{a} \succ \tilde{b}\);

  2. (ii)

    If \(M_{\vartheta } (\tilde{a}) < M_{\vartheta } (\tilde{b})\), then \(\tilde{a}\) is smaller than \(\tilde{b}\), denoted by \(\tilde{a} \prec \tilde{b}\);

  3. (iii)

    If \(M_{\vartheta } (\tilde{a}) = M_{\vartheta } (\tilde{b})\), then

    1. (a)

      if \(M_{\mu } (\tilde{a}) > M_{\mu } (\tilde{b})\) then \(\tilde{a} > \tilde{b}\);

    2. (b)

      when \(M_{\mu } (\tilde{a}) = M_{\mu } (\tilde{b})\), if \(M_{\lambda } (\tilde{a}) > M_{\lambda } (\tilde{b})\) , then \(\tilde{a} < \tilde{b}\);

    3. (c)

      when \(M_{\mu } (\tilde{a}) = M_{\mu } (\tilde{b})\) and \(M_{\lambda } (\tilde{a}) = M_{\lambda } (\tilde{b})\), if \(M_{\nu } (\tilde{a}) > M_{\nu } (\tilde{b})\), then \(\tilde{a} < \tilde{b}\);

  4. (iv)

    If \(M_{\vartheta } (\tilde{a}) = M_{\vartheta } (\tilde{b})\), \(M_{\mu } (\tilde{a}) = M_{\mu } (\tilde{b})\), \(M_{\nu } (\tilde{a}) = M_{\nu } (\tilde{b})\), and \(M_{\lambda } (\tilde{a}) = M_{\lambda } (\tilde{b})\), then \(\tilde{a} = \tilde{b}\), i.e., two SVN-number are equal.

Example 2

Let \(\tilde{a}=\langle (3, 5, 7); 0.7, 0.6, 0.4\rangle \) and \(\tilde{b}=\langle (2, 5, 6); 0.4, 0.6, 0.5\rangle \) be two SVTrN-numbers. Then, we can compare the two SVTrN-numbers \(\tilde{a}\) and \(\tilde{b}\).

Sol: We can calculate the possibility mean value of the SVTrN-number \(\tilde{a}\) as:

$$\begin{aligned} M_{\vartheta } (\tilde{a})= &\, {} \dfrac{3 + 4\times 5 + 7}{6}\\&\times \left[ \vartheta (0.7)^2\right. \\&\left. + (1-\vartheta ) (1-0.6)^2 + (1-\vartheta ) (1-0.4)^2\right] \\= &\, {} 5 (0.52 - 0.03 \vartheta )\\= &\, {} 2.6 - 0.15 \vartheta \\ M_{\vartheta } (\tilde{b})= &\, {} \dfrac{2 + 4\times 5 + 6}{6}\\&\times \left[ \vartheta (0.4)^2 + (1-\vartheta ) (1-0.6)^2 \right. \\&+\left. (1-\vartheta ) (1-0.5)^2\right] \\= &\, {} \frac{28}{6} (0.41 - 0.25 \vartheta )\\= &\, {} 1.91 - 1.16 \vartheta \end{aligned}$$

Then we have

$$\begin{aligned} M_{\vartheta } (\tilde{a}) - M_{\vartheta } (\tilde{b})= &\, {} (2.6 - 0.15 \vartheta ) - (1.91 - 0.04 \vartheta )\\= &\, {} 0.69 - 0.11 \vartheta \end{aligned}$$

Therefore, it is clearly that \(0.57 \le 0.69 - 0.11 \vartheta \le 0.69\), (for \(0 \le \vartheta \le 1\)) which implies that \(M_{\vartheta } (\tilde{a}) > M_{\vartheta } (\tilde{b})\) for any \(\vartheta \in [0, 1]\). Hence, it easily the ranking order of the SVTrN-number \(\tilde{a}\) and \(\tilde{b}\) is \(\tilde{a} \succ \tilde{b}\).

Theorem 1

Let \(\tilde{a}=\langle (a_{1}, a_{2}, a_{3}, a_{4}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle \) and \(\tilde{b}=\langle (b_{1}, b_{2}, b_{3}, b_{4}); w_{\tilde{b}}, u_{\tilde{b}}, y_{\tilde{b}} \rangle \) be two SVTN-numbers with \(w_{\tilde{a}}=w_{\tilde{b}}\), \(u_{ \tilde{a}}=u_{\tilde{b}}\) and \(y_{\tilde{a}}=y_{\tilde{b}}\). Then for any \(\epsilon _{1}, \epsilon _{2} \in {\mathbb {R}}\), the following equalities are valid:

$$\begin{aligned} M_{\mu } (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})=\epsilon _{1} M_{\mu } (\tilde{a})+\epsilon _{2}M_{\mu } (\tilde{b}) \end{aligned}$$
(10)
$$\begin{aligned} M_{\nu } (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})=\epsilon _{1} M_{\nu } (\tilde{a})+\epsilon _{2}M_{\nu } (\tilde{b}) \end{aligned}$$
(11)
$$\begin{aligned} M_{\lambda } (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})=\epsilon _{1} M_{\lambda } (\tilde{a})+\epsilon _{2}M_{\lambda } (\tilde{b}) \end{aligned}$$
(12)

Proof

Let us assume \(\epsilon _{1}, \epsilon _{2} >0\). From the definition 3.2, we get that the \(\alpha \)-cut set of a SVTN-number \(\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b}\) is \( (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})_{\alpha }=[\epsilon _{1}a_{\alpha }^{l}+ \epsilon _{2}b_{\alpha }^{l}, \epsilon _{1}a_{\alpha }^{r}+\epsilon _{2}b_{\alpha }^{r}]\). Using Eq. 10, we obtain

$$\begin{aligned} M_{\mu } (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})= &\, {} \dfrac{1}{2}\int _{0}^{w_{\tilde{a}}\wedge w_{\tilde{b}}}\Big (\epsilon _{1}a_{\alpha }^{l}+\\&\times \epsilon _{2}b_{\alpha }^{l}+\epsilon _{1}a_{\alpha }^{r}+\epsilon _{2}b_{\alpha }^{r}\Big )f (\alpha )d\alpha \\= &\, {} \dfrac{1}{2}\int _{0}^{w_{\tilde{a}}}\left( \epsilon _{1}a_{\alpha }^{l}+ \epsilon _{1}a_{\alpha }^{r}\right) f (\alpha )d\alpha \\&+\dfrac{1}{2}\int _{0}^{w_{\tilde{b}}}\left( \epsilon _{2}b_{\alpha }^{l}+\epsilon _{2}b_{\alpha }^{r}\right) f (\alpha )d\alpha \\= &\, {} \epsilon _{1} M_{\mu } (\tilde{a})+\epsilon _{2}M_{\mu } (\tilde{b}) \end{aligned}$$

From the Definition 3.3, we get that the \(\beta \)-cut set of a SVTN-number \(\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b}\) is \( (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})_{\beta }=[\epsilon _{1}a_{\beta }^{l}+ \epsilon _{2}b_{\beta }^{l}, \epsilon _{1}a_{\beta }^{r}+\epsilon _{2}b_{\beta }^{r}]\). Using Eq.  (11), we have

$$\begin{aligned} M_{\nu } (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})= &\, {} \dfrac{1}{2}\int _{u_{\tilde{a}}\vee u_{\tilde{b}}}^{1}\left( \epsilon _{1}a_{\beta }^{l}+ \epsilon _{2}b_{\beta }^{l}+\epsilon _{1}a_{\beta }^{r}+\epsilon _{2}b_{\beta }^{r}\right) g (\beta )d\beta \\= &\, {} \dfrac{1}{2}\int _{u_{\tilde{a}}}^{1}\left( \epsilon _{1}a_{\beta }^{l}+ \epsilon _{1}a_{\beta }^{r})g (\beta )d\beta +\dfrac{1}{2}\int _{u_{\tilde{b}}}^{1} (\epsilon _{2}b_{\beta }^{l}+\epsilon _{2}b_{\beta }^{r}\right) g (\beta )d\beta \\= &\, {} \epsilon _{1} M_{\nu } (\tilde{a})+\epsilon _{2}M_{\nu } (\tilde{b}) \end{aligned}$$

Further, from the Definition 3.4, we get that the \(\gamma \)-cut set of a SVTN-number \(\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b}\) is \( (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})_{\gamma }=[\epsilon _{1}a_{\gamma }^{l}+ \epsilon _{2}b_{\gamma }^{l}, \epsilon _{1}a_{\gamma }^{r}+\epsilon _{2}b_{\gamma }^{r}]\). Using Eq. 12, we have

$$\begin{aligned} M_{\lambda } (\epsilon _{1}\tilde{a}+\epsilon _{2}\tilde{b})= &\, {} \dfrac{1}{2}\int _{u_{\tilde{a}}\vee u_{\tilde{b}}}^{1}\Big (\epsilon _{1}a_{\gamma }^{l}+\\&\times \epsilon _{2}b_{\gamma }^{l}+\epsilon _{1}a_{\gamma }^{r}+\epsilon _{2}b_{\gamma }^{r}\Big )g (\gamma )d\gamma \\= &\, {} \dfrac{1}{2}\int _{u_{\tilde{a}}}^{1} (\epsilon _{1}a_{\gamma }^{l}+ \epsilon _{1}a_{\gamma }^{r})g (\gamma )d\gamma \\&+\dfrac{1}{2}\int _{u_{\tilde{b}}}^{1}\left( \epsilon _{2}b_{\gamma }^{l}+\epsilon _{2}b_{\gamma }^{r}\right) g (\gamma )d\gamma \\= &\, {} \epsilon _{1} M_{\lambda } (\tilde{a})+\epsilon _{2}M_{\lambda } (\tilde{b}^{I}) \end{aligned}$$

Using the Eqs. (10), (11) and (12). We can also verify that for \(\epsilon _{1}>0, \epsilon _{2}<0\); \(\epsilon _{1}<0, \epsilon _{2}>0\); \(\epsilon _{1}<0, \epsilon _{2}<0\).

This completes the proof. \(\square \)

Theorem 2

Let \(\tilde{a}=\langle (a_{1}, a_{2}, a_{3}, a_{4}); w_{\tilde{a}}, u_{\tilde{a}}, y_{\tilde{a}} \rangle \) and \(\tilde{b}=\langle (b_{1}, b_{2}, b_{3}, b_{4}); w_{\tilde{b}}, u_{\tilde{b}}, y_{\tilde{b}} \rangle \) be two SVTN-numbers with \(w_{\tilde{a}}=w_{\tilde{b}}\), \(u_{ \tilde{a}}=u_{\tilde{b}}\) and \(y_{\tilde{a}}=y_{\tilde{b}}\). If \(a_{1} > b_{4}\), then \(\tilde{a} \succ \tilde{b}\)

Proof

It is easily derived from Eq. (3) that

$$\begin{aligned} M_{\mu } (\tilde{a})= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{a}}}\left( a_{\alpha }^{l} + a_{\alpha }^{r}\right) f (\alpha )d\alpha \\\ge & {} \int _{0}^{w_{\tilde{a}}} a_{1} f (\alpha )d\alpha \\= &\, {} a_{1} \int _{0}^{w_{\tilde{a}}} f (\alpha )d\alpha \end{aligned}$$

and

$$\begin{aligned} M_{\mu } (\tilde{b})= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{b}}}\left( b_{\alpha }^{l} + b_{\alpha }^{r}\right) f (\alpha )d\alpha \\\ge & {} \int _{0}^{w_{\tilde{b}}} b_{4} f (\alpha )d\alpha \\= &\, {} b_{4} \int _{0}^{w_{\tilde{b}}} f (\alpha )d\alpha \end{aligned}$$

Since \(w_{\tilde{a}}=w_{\tilde{b}}\), we have \(\int _{0}^{w_{\tilde{a}}} f (\alpha )d\alpha = \int _{0}^{w_{\tilde{b}}} f (\alpha )d\alpha \). So, Combining both conditions \(w_{\tilde{a}}=w_{\tilde{b}}\) and \(a_{1} > b_{4}\), we have \(M_{\mu } (\tilde{a}) > M_{\mu } (\tilde{b})\).

It easily derived from Eq. (6) that

$$\begin{aligned} M_{\nu } (\tilde{a})= &\, {} \frac{1}{2}\int _{u_{\tilde{a}}}^{1}\left( a_{\beta }^{l} + a_{\beta }^{r}\right) g (\beta )d\beta \\\ge & {} \int _{u_{\tilde{a}}}^{1} a_{1} g (\beta )d\beta \\= &\, {} a_{1} \int _{u_{\tilde{a}}}^{1} g (\beta )d\beta \end{aligned}$$

and

$$\begin{aligned} M_{\nu } (\tilde{b})= &\, {} \frac{1}{2}\int _{u_{\tilde{b}}}^{1}\left( a_{\beta }^{l} + a_{\beta }^{r}\right) g (\beta )d\beta \\\ge & {} \int _{u_{\tilde{b}}}^{1} b_{4} g (\beta )d\beta \\= &\, {} b_{4} \int _{u_{\tilde{b}}}^{1} g (\beta )d\beta \end{aligned}$$

For the condition \(u_{\tilde{a}}=u_{\tilde{b}}\), we have \(\int _{u_{\tilde{a}}}^{1}g (\beta )d\beta =\int _{u_{\tilde{b}}}^{1} g (\beta )d\beta \). Combining the assume conditions: \(u_{\tilde{a}}=u_{\tilde{b}}\) and \(a_{1}> b_{4}\), we have \(M_{\nu } (\tilde{a}) > M_{\nu } (\tilde{b})\).

Similarly, it easily follows from Eq. (9) that

$$\begin{aligned} M_{\lambda } (\tilde{a})= &\, {} \frac{1}{2}\int _{y_{\tilde{a}}}^{1}\left( a_{\gamma }^{l} + a_{\gamma }^{r}\right) h (\gamma )d\gamma \\\ge & {} \int _{y_{\tilde{a}}}^{1} a_{1} h (\gamma )d\gamma \\= &\, {} a_{1} \int _{y_{\tilde{a}}}^{1} h (\gamma )d\gamma \end{aligned}$$

and

$$\begin{aligned} M_{\lambda } (\tilde{b})= &\, {} \frac{1}{2}\int _{y_{\tilde{b}}}^{1}\left( a_{\gamma }^{l} + a_{\gamma }^{r}\right) h (\gamma )d\gamma \\\ge & {} \int _{y_{\tilde{b}}}^{1} b_{4} h (\gamma )d\gamma \\= &\, {} b_{4} \int _{y_{\tilde{b}}}^{1} h (\gamma )d\gamma \end{aligned}$$

For the assume condition: \(y_{\tilde{a}}=y_{\tilde{b}}\), we have \(\int _{y_{\tilde{a}}}^{1}h (\gamma )d\gamma =\int _{y_{\tilde{b}}}^{1} h (\gamma )d\gamma \). Combining the both assume conditions: \(y_{\tilde{a}}=y_{\tilde{b}}\) and \(a_{1} > b_{4}\), we have \(M_{\lambda } (\tilde{a}) > M_{\lambda } (\tilde{b})\).

For any \(\vartheta \in [0, 1]\), according to Definition 3.8, we have

$$\begin{aligned}&\vartheta M_{\mu } (\tilde{a}) + (1- \vartheta )M_{\nu } (\tilde{a})+ (1- \vartheta ) \\&\quad \times M_{\lambda } (\tilde{a}) > \vartheta M_{\mu } (\tilde{b}) + (1- \vartheta )M_{\nu } (\tilde{b})+ (1- \vartheta ) M_{\lambda } (\tilde{b}) \end{aligned}$$

i.e., \(M_{\vartheta } (\tilde{a}) > M_{\vartheta } (\tilde{b})\). Therefore, it directly follows from the case Definition 3.9 that \(\tilde{a} > \tilde{b}\). \(\square \)

Theorem 3

Let \(\tilde{a}\), \(\tilde{b}\) and \(\tilde{c}\) be two SVTN-numbers with \(w_{\tilde{a}}=w_{\tilde{b}}\), \(u_{ \tilde{a}}=u_{\tilde{b}}\) and \(y_{\tilde{a}}=y_{\tilde{b}}\). If \(\tilde{a} > \tilde{b}\), then \(\tilde{a}+ \tilde{c} > \tilde{b} + \tilde{c}\).

Proof

It is easily derived from Eq. (3) that

$$\begin{aligned} M_{\mu } (\tilde{a} + \tilde{c})= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{a}}\wedge w_{\tilde{c}}}\left[ \left( a_{\alpha }^{l} + a_{\alpha }^{r}\right) + \left( c_{\alpha }^{l} + c_{\alpha }^{r}\right) \right] f (\alpha )d\alpha \\= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{a}}\wedge w_{\tilde{c}}}\left( a_{\alpha }^{l} + a_{\alpha }^{r}\right) f (\alpha )d\alpha \\&+\frac{1}{2}\int _{0}^{w_{\tilde{a}}\wedge w_{\tilde{c}}}\left( c_{\alpha }^{l} + c_{\alpha }^{r}\right) f (\alpha )d\alpha \end{aligned}$$

and

$$\begin{aligned} M_{\mu } (\tilde{b} + \tilde{c})= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{b}}\wedge w_{\tilde{c}}}\left[ \left( b_{\alpha }^{l} + a_{\alpha }^{r}\right) + \left( c_{\alpha }^{l} + c_{\alpha }^{r}\right) \right] f (\alpha )d\alpha \\= &\, {} \frac{1}{2}\int _{0}^{w_{\tilde{b}}\wedge w_{\tilde{c}}}\left( b_{\alpha }^{l} + b_{\alpha }^{r}\right) f (\alpha )d\alpha + \frac{1}{2}\int _{0}^{w_{\tilde{b}}\wedge w_{\tilde{c}}}\\&\times \left( c_{\alpha }^{l} + c_{\alpha }^{r}\right) f (\alpha )d\alpha \end{aligned}$$

Where \(w_{\tilde{c}}\) is the truth-membership of the SVN-number \(\tilde{c}\). For the assume conditions: \(\tilde{a} > \tilde{b}\) and \(w_{\tilde{a}}=w_{\tilde{b}}\), we have

$$\begin{aligned} \frac{1}{2}\int _{0}^{w_{\tilde{a}}\wedge w_{\tilde{c}}}\left( a_{\alpha }^{l} + a_{\alpha }^{r}\right) f (\alpha )d\alpha > \frac{1}{2}\int _{0}^{w_{\tilde{b}}\wedge w_{\tilde{c}}}\left( b_{\alpha }^{l} + b_{\alpha }^{r}\right) f (\alpha )d\alpha \end{aligned}$$

So,

$$\begin{aligned} M_{\mu } (\tilde{a} +\tilde{c}) > M_{\mu } (\tilde{b} + \tilde{c}) \end{aligned}$$
(13)

Likewise, it is derived from Eq. (6) that

$$\begin{aligned} M_{\nu } (\tilde{a} + \tilde{c})= &\, {} \frac{1}{2}\int _{u_{\tilde{a}}\vee u_{\tilde{c}}}^{1}\left[ \left( a_{\beta }^{l} + a_{\beta }^{r}\right) + \left( c_{\beta }^{l} + c_{\beta }^{r}\right) \right] g (\beta )d\beta \\= &\, {} \frac{1}{2}\int _{u_{\tilde{a}}\vee u_{\tilde{c}}}^{1} (a_{\beta }^{l} + a_{\alpha }^{r})g (\beta )d\beta \\&+\frac{1}{2}\int _{u_{\tilde{a}}\vee u_{\tilde{c}}}^{1}\left( c_{\beta }^{l} + c_{\beta }^{r}\right) g (\beta )d\beta \end{aligned}$$

and

$$\begin{aligned} M_{\nu } (\tilde{b} + \tilde{c})= &\, {} \frac{1}{2}\int _{u_{\tilde{b}}\vee u_{\tilde{c}}}^{1}\left[ \left( b_{\beta }^{l} + a_{\beta }^{r}\right) + \left( c_{\beta }^{l} + c_{\beta }^{r}\right) \right] g (\beta )d\beta \\= &\, {} \frac{1}{2}\int _{u_{\tilde{b}}\vee u_{\tilde{c}}}^{1}\left( b_{\beta }^{l} + b_{\beta }^{r}\right) g (\beta )d\beta +\\&\frac{1}{2}\int _{u_{\tilde{b}}\vee u_{\tilde{c}}}^{1}\left( c_{\beta }^{l} + c_{\beta }^{r}\right) g (\beta )d\beta \end{aligned}$$

where \(u_{\tilde{c}}\) is the indeterminacy-membership of the SVN-number \(\tilde{c}\). For the assumption conditions: \(\tilde{a} > \tilde{b}\) and \(u_{\tilde{a}}=u_{\tilde{b}}\), we have

$$\begin{aligned} \frac{1}{2}\int _{u_{\tilde{a}}\vee u_{\tilde{c}}}^{1}\left( a_{\beta }^{l} + a_{\beta }^{r}\right) g (\beta )d\beta > \frac{1}{2}\int _{u_{\tilde{b}}\vee u_{\tilde{c}}}^{1}\left( b_{\beta }^{l} + b_{\beta }^{r}\right) g (\beta )d\beta \end{aligned}$$

Therefore, we have

$$\begin{aligned} M_{\nu } (\tilde{a} +\tilde{c}) > M_{\nu } (\tilde{b} + \tilde{c}) \end{aligned}$$
(14)

Similarly, it is derived from Eq. (9) that

$$\begin{aligned} M_{\lambda } (\tilde{a} + \tilde{c})= &\, {} \frac{1}{2}\int _{y_{\tilde{a}}\vee y_{\tilde{c}}}^{1}\left[ \left( a_{\gamma }^{l} + a_{\gamma }^{r}\right) + \left( c_{\gamma }^{l} + c_{\gamma }^{r}\right) \right] h (\gamma )d\gamma \\= &\, {} \frac{1}{2}\int _{y_{\tilde{a}}\vee y_{\tilde{c}}}^{1}\left( a_{\gamma }^{l} + a_{\gamma }^{r}\right) h (\gamma )d\gamma \\&+\frac{1}{2}\int _{y_{\tilde{a}}\vee y_{\tilde{c}}}^{1}\left( c_{\gamma }^{l} + c_{\gamma }^{r}\right) h (\gamma )d\gamma \end{aligned}$$

and

$$\begin{aligned} M_{\lambda } (\tilde{b} + \tilde{c})= &\, {} \frac{1}{2}\int _{y_{\tilde{b}}\vee y_{\tilde{c}}}^{1}\left[ \left( b_{\gamma }^{l} + a_{\gamma }^{r}\right) + \left( c_{\gamma }^{l} + c_{\gamma }^{r}\right) \right] h (\gamma )d\gamma \\= &\, {} \frac{1}{2}\int _{y_{\tilde{b}}\vee y_{\tilde{c}}}^{1}\left( b_{\gamma }^{l} + b_{\gamma }^{r}\right) h (\gamma )d\gamma \\&+ \frac{1}{2}\int _{y_{\tilde{b}}\vee y_{\tilde{c}}}^{1}\left( c_{\gamma }^{l} + c_{\gamma }^{r}\right) h (\gamma )d\gamma \end{aligned}$$

we have

$$\begin{aligned} M_{\lambda } (\tilde{a} +\tilde{c}) > M_{\lambda } (\tilde{b} + \tilde{c}) \end{aligned}$$
(15)

According to Definition 3.8, and combining with Eqs.  (13), (14) and (15) the following inequality is always valid for any \(\vartheta \in [0, 1]\)

$$\begin{aligned}&\vartheta M_{\mu } (\tilde{a}+\tilde{c}) + (1- \vartheta )M_{\nu } (\tilde{a}+\tilde{c})+ (1- \vartheta ) M_{\lambda } (\tilde{a}+\tilde{c})\\&\quad > \vartheta M_{\mu } (\tilde{b}+\tilde{c}) + (1- \vartheta )M_{\nu } (\tilde{b}+\tilde{c})+ (1- \vartheta ) M_{\lambda } (\tilde{b}+\tilde{c}) \end{aligned}$$

\(M_{\vartheta } (\tilde{a}+\tilde{c})>M_{\vartheta } (\tilde{b} + \tilde{c})\)

So, we have to seen that from the case (1) of the definition 3.9 that \(\tilde{a}+\tilde{c}> \tilde{b}+\tilde{c}\). \(\square \)

4 A multi-attribute decision making method based on possibility mean with single valued neutrosophic numbers

In this section we develop a novel MADM method based on possibility mean of single valued neutrosophic numbers.

Let \(A=\{A_1,A_2,...,A_m\}\) and \(G=\{G_1,G_2,...,G_n\}\) be the discrete set of alternatives and attributes respectively. Let \(W=\{w_1,w_2,...,w_n\}\) be the normalized weight vector of attributes \(G_j\) (j = 1, 2, 3, ..., n), where \(w_j\ge 0\) and \(\sum _{j=1}^{n}w_j=1\).

Now, we describe the following steps for the proposed method, and flow chart of this method given in Fig. 2.

Step 1: Formulate the decision matrix For MADM with SVN-number information, the rating values of the alternative \(A_i (i=1,2,...,m)\) on the basis of attribute \(G_j (j=1,2,...,n)\) can be expressed in SVN-number as \(a_{ij}\) where (i = 1, 2, 3, ..., m; j = 1, 2, 3, ..., n).

The decision matrix is represented as follows:

$$\begin{aligned} M= \begin{pmatrix} &{}G_{1} &{} G_{2} &{}.&{}.&{}.&{} G_{n}\\ A_{1}&{}a_{11} &{}a_{12}&{}.&{}.&{}.&{} a_{1n} \\ A_{2}&{}a_{21} &{}a_{22}&{}.&{}.&{}.&{} a_{2n} \\ &{}\vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{}\vdots \\ A_{m}&{}a_{m1} &{}a_{22}&{}.&{}.&{}.&{} a_{mn} \\ \end{pmatrix} \end{aligned}$$
(16)

Step 2: Formulate the normalized decision matrix. To make normalized decision matrix we use the following formula: for benefit type attribute \(a_{ij}^{*}=\dfrac{a_{ij}}{\max \{a_{ij}\}}\) and for cost type attribute \(a_{ij}^{*}=1-\dfrac{a_{ij}}{\max \{a_{ij}\}}.\)

The normalized decision matrix is represented as follows:

$$\begin{aligned} M^{*}= \begin{pmatrix} &{}G_{1} &{} G_{2} &{}.&{}.&{}.&{} G_{n}\\ A_{1}&{}a_{11}^{*} &{}a_{12}^{*}&{}.&{}.&{}.&{} a_{1n}^{*} \\ A_{2}&{}a_{21}^{*} &{}a_{22}^{*}&{}.&{}.&{}.&{} a_{2n}^{*} \\ &{}\vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{}\vdots \\ A_{m}&{}a_{m1}^{*} &{}a_{22}^{*}&{}.&{}.&{}.&{} a_{mn}^{*} \\ \end{pmatrix} \end{aligned}$$
(17)

Step 3: Calculate weighted aggregated values. We calculate weighted aggregate values of all attributes for each alternative using the equation

$$\begin{aligned} \tilde{a_{i}}=\sum _{j=1}^{n}a_{ij}^{*}w_j \end{aligned}$$
(18)

Therefore, the aggregated decision matrix is defined as follows:

$$\begin{aligned} \tilde{M} = \begin{pmatrix} A_{1}&{}\quad \tilde{a}_{1}\\ A_{2}&{}\quad \tilde{a}_{2}\\ \vdots &{}\quad \vdots \\ A_{m}&{}\quad \tilde{a}_{m}\\ \end{pmatrix} \end{aligned}$$
(19)

Step 4: Calculate the possibility mean values of alternatives Using the Corollary 3.4, we calculate the possibility mean values of these alternatives.

Step 5: Rank the alternatives We rank the alternatives \(A_{i} (i=1,2,...,m)\) according to the decreasing values of possibility mean value.

4.1 Working rule of the proposed algorithm

In this section, a decision making method is proposed to deal with decision making problems in the single-valued neutrosophic environment. Therefore, the decision making proposed algorithm is stated below Firstly, we define a multi attribute decision making problem in the neutrosophic set environment. Then, we apply our proposed algorithm as follows:

Rule 1  Formulate the decision matrix From the decision making problem we formulate the decision matrix based on the attribute of alternatives (see the decision matrix in Eq.  (16)).

Rule 2  Formulate the normalized decision matrix To make dimension less quantity of rating values of alternative provided by decision maker we use the formula are stated in Sect.  4 step 2 and proposed normalized decision matrix is in the Eq.  (17).

Rule 3  Calculate weighted aggregated values We calculate weighted aggregate rating values of alternatives using Eq.  (18).

Rule 4  Calculate the possibility mean values of alternatives Using Corollary 3.4, we calculate the possibility mean values for ranking of alternatives.

Rule 5  Rank the alternatives We rank the alternatives according to our proposed method.

Fig. 2
figure 2

Flow chart of proposed ranking method

Full size image

5 Numerical example

Let us assume that a software company required a system analyst. After screening test, candidates \( A_{1}, A_{2}\) and \(A_{3}\) are remain for further evaluation. The MADM problem is adopted from Li (2014) and Li et al. (2014). The software company wants to select a best alternative (Candidate) among the set of three alternatives. The best alternative is selected based on the following attributes:

  1. 1.

    Emotional steadiness \(\{G_{1}\}\).

  2. 2.

    Oral communication skill \(\{G_{2}\}\).

  3. 3.

    Personality \(\{G_{3}\}\).

  4. 4.

    Past experience \(\{G_{4}\}\).

  5. 5.

    Self-confidence \(\{G_{5}\}\).

The weight vector of five attributes is \(\{0.15, 0.25, 0.20, 0.25, 0.15\}\). Here, possible candidates are to evaluated under the above five attributes which considering by SVTrN-numbers. The steps of the decision making procedure to select the best alternative based on the proposed method are presented in the following:

Step 1. Formulate the decision matrix The rating values of the alternatives \(A_{1}, A_{2}\) and \( A_{3}\) on the basis of attribute \(G_{1}, G_{2},G_{3},G_{4}\) and \(G_{5}\) can be expressed in SVTrN-number and represented as follows:

$$\begin{aligned} \tiny {M= \begin{pmatrix} &{} G_{1} &{} G_{2}&{} G_{3} &{} G_{4} &{} G_{5}\\ A_{1} &{} \langle (4.7, 5.4, 8.5); 0.4, 0.6, 0.2\rangle &{} \langle (5.7, 6.8, 8.7); 0.6, 0.3, 0.3\rangle &{} \langle (5.3, 6.6, 9.8); 0.3, 0.6, 0.2\rangle &{} \langle (4.4, 5.8, 7.3); 0.7, 0.3, 0.3\rangle &{} \langle (6.4, 6.8, 8.6); 0.6, 0.7, 0.1\rangle \\ A_{2} &{}\langle (6.2, 7.5, 8.3); 0.4, 0.2, 0.3\rangle &{} \langle (7.2, 7.6, 8.2); 0.5, 0.3, 0.4\rangle &{} \langle (6.2, 8.8, 9.0); 0.6, 0.4, 0.5\rangle &{} \langle (6.3, 7.4, 8.8); 0.7, 0.5, 0.6\rangle &{} \langle (7.5, 7.8, 8.5); 0.8, 0.4, 0.4\rangle \\ A_{3} &{} \langle (5.5, 6.3, 7.3); 0.8, 0.2, 0.2\rangle &{} \langle (4.7, 6.8, 8.5); 0.7, 0.3, 0.6\rangle &{} \langle (7.1, 8.6, 8.9); 0.5, 0.3, 0.7\rangle &{} \langle (6.6, 8.7, 10); 0.6, 0.3, 0.2\rangle &{} \langle (5.3, 7.4, 8.7); 0.7, 0.3, 0.7\rangle \\ \\ \end{pmatrix}} \end{aligned}$$
(20)

Step 2: Formulate the normalized decision matrix Since all attributes are benefit type attribute so we use \(a_{ij}^{*}=\dfrac{a_{ij}}{\max \{a_{ij}\}}\) for normalized the decision matrix M and the normalized decision matrix is

$$\begin{aligned} M^{*}= \tiny {\begin{pmatrix} &{} G_{1} &{} G_{2}&{} G_{3} &{} G_{4} &{} G_{5}\\ A_{1} &{} \langle (.47, .54, .85); 0.4, 0.6, 0.2\rangle &{} \langle (.57, .68, .87); 0.6, 0.3, 0.3\rangle &{} \langle (.53, .66, .98); 0.3, 0.6, 0.2\rangle &{} \langle (.44, .58, .73); 0.7, 0.3, 0.3\rangle &{} \langle (.64, .68, .86); 0.6, 0.7, 0.1\rangle \\ A_{2} &{} \langle (.62, .75, .83); 0.4, 0.2, 0.3\rangle &{} \langle (.72, .76, .82); 0.5, 0.3, 0.4\rangle &{} \langle (.62, .88, .9); 0.6, 0.4, 0.5\rangle &{} \langle (.63, .74, .88); 0.7, 0.5, 0.6\rangle &{} \langle (.75, .78, .85); 0.8, 0.4, 0.4\rangle \\ A_{3} &{} \langle (.55, .63, .73); 0.8, 0.2, 0.2\rangle &{} \langle (.47, .68, .085); 0.7, 0.3, 0.6\rangle &{} \langle (.71, .86, .89); 0.5, 0.3, 0.7\rangle &{} \langle (.66, .87, 1); 0.6, 0.3, 0.2\rangle &{} \langle (.53, .74, .87); 0.7, 0.3, 0.7\rangle \\ \\ \end{pmatrix}} \end{aligned}$$
(21)

Step 3: Calculate weighted aggregated values We calculate weighted aggregate rating values of alternatives using Eq.  (18).The weighted aggregate values of all attributes for each alternative as follows:

$$\begin{aligned} \tilde{M} = \left\{ \begin{array}{ll} A_{1}=\langle (0.53, 0.65, 0.85); 0.3, 0.8, 0.3\rangle \\ A_{2}=\langle (0.65, 0.80, 0.88 ); 0.4, 0.5, 0.6\rangle \\ A_{3}=\langle (0.59, 0.76, 0.88); 0.5, 0.3, 0.8\rangle \\ \end{array} \right. \end{aligned}$$
(22)

Step 4: Calculate the possibility mean values of alternatives Using Corollary 3.4, we calculate the possibility mean values for ranking of alternatives. The possibility mean values of three alternatives are represented as follows:

$$\begin{aligned} M_{\vartheta } (A_{1})= &\, {} 0.65[0.89 - 0.64 \vartheta ] \end{aligned}$$
$$\begin{aligned} M_{\vartheta } (A_{2})= &\, {} 0.78[0.72 - 0.36 \vartheta ] \end{aligned}$$
$$\begin{aligned} M_{\vartheta } (A_{3})= &\, {} 0.75[0.74 - 0.38 \vartheta ] \end{aligned}$$
Fig. 3
figure 3

Ranking results based on proposed method

Full size image

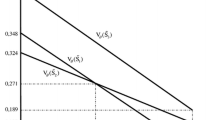
From the Fig. 3 clearly depict that the ranking order of alternatives based on the weighted possibility mean divided in three region.

Step 5: Rank the alternatives Form Fig. 3, we can conclude that, \(A_{1}>A_{2}>A_{3}\), when \(\vartheta \in [0, 0.14]\) and the best alternative is \(A_{1}\). \(A_{2}>A_{1}>A_{3}\), when \(\vartheta \in (0.14, 0.17)\) and the best alternative is \(A_{2}\). \(A_{2}>A_{3}>A_{1}\), when \(\vartheta \in [0.17, 1]\) the best alternative is \(A_{2}\).

5.1 Comparative study

In order to show the validity of the proposed ranking method, a comparative study with other methods was constructed. The proposed method compared to the methods that were outlined in Refs. Deli and şubaş (2017) and Aal et al. (2018) using SVTrN numbers. The weighted and ambiguities operators are developed in order to aggregate the SVTrN numbers which is used in Deli and şubaş (2017), and the arithmetic and geometric aggregation operators were introduced in order aggregate the SVTrN numbers which used in Aal et al. (2018). The results from the different methods used to resolve the proposed MADM problem are shown in Table 1.

From the result presented in Table 1, the best alternative is \(A_{3}\) and worst one is \(A_{1}\) in all methods. In Refs. Deli and şubaş (2017) and Aal et al. (2018) used the weighted and ambiguities operators, arithmetic and geometric aggregation operators, which are very difficult for decision makers to confirm their judgement when using operators and measures that have same characteristics. But, the proposed method in this paper pays more attention to the impact that uncertainty has on the alternatives and also takes into weighted possibility mean of SVN-numbers by using the concept of possibility measures. By comparison, the proposed method in this paper focuses on the weighted possibility mean of the SVN-numbers, the ranking procedure of the proposed method is different from other method. Thus, proposed method gives the more reasonable results (viz. Table 1) than the existing methods.

Table 1 Comparative study with existing methods
Full size table

6 Conclusion

The concept of single valued neutrosophic number (SVN) number is of importance of quantifying an ill-known quantity and the ranking of SVN-numbers are a very labored in the MADM problems. The main focus of this paper is to present possibility mean of SVN-numbers. Using the concept of possibility mean we have ranked the SVN-numbers. Then, a new ranking method is introduced for the ordering of SVN-numbers and applied to solve MADM problems with SVN-numbers. It is easily seen that the proposed ranking method can be extended to rank more general SVN-numbers in a straightforward manner. Finally, we illustrated a numerical example to demonstrate the proposed decision making method. Here, we illustrate not only the usefulness of the ranking method is given also. The comparison studies show that the proposed ranking method in this paper has some remarkable advantages over existing methods (cf. Table 1).

Our proposed method is the first method in which fuzzy neutrosophic possibility mean is applied for ranking the alternatives. This is the main difference of our proposed method with respect to the other existing previously fuzzy neutrosophic set decision making methods. The proposed possibility mean is more important than other existing mean exist in an uncertain environment because it contain truth membership part, indeterminacy part and falsity part of an element. We hope that this decision making method may be used in the fields of others decision making area such as: teacher selection (Mondal and Pramanik 2014), logistics location selection problem (Pramanik et al. 2016), etc.