1 Introduction

The least mean square (LMS) algorithm is one of the most popular adaptive algorithms used in a wide range of applications. The desirable characteristics of simplicity in terms of computational complexity, robustness, ease of implementation and good tracking capability are the main advantages of the LMS algorithm. The main drawback of this algorithm is that the misadjustment factor is directly proportional to the adaptation step size (Haykin 1991). A small value of the step size ensures the robustness of the LMS algorithm as well as a low misadjustment. However, it also results in a high time-constant for the learning rate and consequently, a low rate of convergence for the LMS algorithm (Haykin 1991). In short, the value-selection of the adaptation step imposes a compromise between the efficiency of the LMS algorithm in terms of its steady-state error and the speed of convergence. In fact, this design trade-off is governed by the adaptation step in the affine projection (AP) algorithm, the regularization parameter in the normalized LMS (NLMS) algorithm and by the forgetting factor in the recursive least squares (RLS) algorithm.

One possible solution to the above mentioned problem is the application of the least mean fourth (LMF) algorithm (Walach and Widrow 1984). As compared to the LMS algorithm, the LMF algorithm minimizes the fourth power of the residual error and achieves a faster convergence for values of the absolute error greater than unity. However, to ensure stability of the LMF filter, a stricter constraint is imposed on the maximum value of the step size parameter. A combination of LMS and LMF, that takes advantage of the speed of the LMF algorithm and the stability as well as the efficiency of the LMS algorithm, was proposed in (Chambers et al. 1994; Pazaitis and Constantinides 1995). Alternatively, VSS algorithms may also be used to tackle the compromise between the rate of convergence and the steady-state error. Instead of a single step size parameter, the algorithm presented in Harris et al. (1986) proposes the use of a diagonal matrix consisting of step sizes for each coefficient of the adaptive filter. These step size values can vary within a fixed maxima and minima; they are decreased by dividing them by a constant when the gradient of the mean square error (MSE) alternates in sign and increased by multiplying with the same constant if the error sign remains constant along a number of successive samples. Having a different step size for each filter tap is beneficial when the autocorrelation matrix of the input process has a high eigen-value spread or when some of the filter taps remain constant during changes in the environment to be identified (Arenas-Garcia et al. 2003). However, the use of error signs makes the algorithm susceptible to the pernicious effect of noise and non-monotonic convergence (Martinez-Ramon et al. 2002). A group of more popular VSS algorithms use a single but adaptive step size parameter for all the adaptive filter weights. The step size value is small when the adaptive filter is in the vicinity of its optimum value and large, otherwise. However, more efforts are still being directed towards developing a more robust criterion, such as a function of quadratic error (Liu et al. 2009) and that of the correlation between two consecutive samples of the error signal (Aboulnasr and Mayyas 1997), for managing the step size value. Although the recent VSS algorithms are computationally efficient and obtain good results, they introduce some new parameters which must be initialized apriori. The selection of these values itself presents a compromise between the precision of the adaptive filter and its convergence capability, while its optimum value depends upon the characteristics of the environment for a particular application (Arenas-Garcia et al. 2006).

The work in (Arenas-Garcia et al. 2003, 2006; Singer and Feder 1999; Kozat and Singer 2000) proposes to combine a number of filters of different tap lengths to make the design robust to the selection of a fixed adaptive filter order for plant identification. Mostly, VSS algorithms are considered for the application of acoustic feedback cancellation. This is because the use of the LMS algorithm and its variants or even an adaptive combination-configuration of filters suffers from the detrimental effects of introduction of bias in the estimate of the feedback path. Owing to the closed-loop correlation between the incoming signal and the loudspeaker output, a biased identification of the feedback path degrades the feedback cancellation performance and efficiency (Guo 2012; Anand et al. 2017). The linear prediction-based feedback canceller with probe noise presented in Anand et al. (2017) uses the NLMS algorithm to attenuate bias in the high-frequency region, which is vulnerable to feedback whistling as well as howling, and also in the low-frequency region. However, a small step size value sacrifices the speed of convergence of the adaptive filter in favour of obtaining a good estimate of the feedback path. Therefore, it is desired to update the adaptive filter using an algorithm that converges faster to the estimate and without incurring a large steady-state error.

In this paper, we propose to use a convex combination of two independent LMS algorithm-based adaptive filters, with different step size parameters, for feedback cancellation. The ‘fast’ filter (high step size) and the ‘slow’ filter (small step size) are combined using a combination parameter for a faster convergence and a smaller stationary misalignment. The single adaptive filter in the linear prediction-based adaptive feedback canceller with probe noise is replaced by the aforementioned two-filter scheme to suppress the bias introduced in the feedback-path estimate as well as to mitigate the compromise between convergence rate and tracking ability. We also employ an acceleration procedure to improve the practical performance of the affine filter-combination to further increase the convergence speed of the adaptive estimator. To further improve the tracking of the time-varying feedback path, we analyze the application of different combination parameters for different adaptive filter taps in the above-mentioned two-filter scheme. Moreover, the convex combination approach and the VSS approach are combined, resulting in a more sophisticated three-filter configuration, which controls the overall step size of the estimation filter to maintain an efficient tracking ability and fast convergence. Finally, we compare the performances of all the proposed feedback cancellation schemes with that of the VSS algorithm. Simulation results show that the combination algorithms perform better than the single-adaptive-filter-based VSS algorithm.

The following notation is adopted throughout the paper; \({\left[ . \right] ^T}\) for the transpose operation, \(\mathrm{{sgm}}\left( . \right)\) for the sigmoid function, \({\left\| {.} \right\| _2}\) for the \({l_2}\) norm of a vector, n for discrete-time index, k for discrete-time delay operator such that \({k^{ - 1}}\,m\left( n \right) = m\left( {n - 1} \right),\) bold-faced upper-case letters for the matrices and bold-faced lower-case letters for the column vectors. A discrete-time filter \(F\left( k \right)\) of length L is represented as a polynomial in terms of \({k^{ - 1}}\) as \(F\left( k \right) = {f_0} + {f_1}\,{k^{ - 1}} + \cdots + {f_{L - 1}}\,\,{k^{ - L + 1}}\) or by its coefficient vector \(\mathbf{{f}} = {\left[ {{f_0},{f_1},...,{f_{L - 1}}} \right] ^T}\). The signal \(m\left( n\right)\) is filtered by \(F\left( k\right)\) as \(F\left( k \right) m\left( n \right) = {\mathbf{{f}}^T}\left( n \right) \mathbf{{m}}\left( n \right)\), with \(\mathbf{{m}}\left( n \right) = {\left[ {m\left( n \right) ,m\left( {n - 1} \right) ,...,m\left( {n - L + 1} \right) } \right] ^T}\).

2 Brief system description

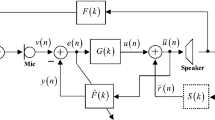
In this section, we present a summary of the linear prediction-based feedback canceller with probe noise which has been proposed in Anand et al. (2017). Figure 1 presents the block diagram of the aforementioned AFC scheme. The acoustic environment of the user, i.e. the feedback route from the loudspeaker to the microphone, is represented by an FIR filter \(F\left( k\right)\) of length \(L_{f}\) and its coefficient vector defined as \(\mathbf{{f}}\left( n \right) = {\left[ {{f_0},{f_1},...,{f_{{L_f} - 1}}} \right] ^T}\). The adaptive estimation filter to identify \(F\left( k\right)\) is also an FIR filter \(\hat{F}\left( k\right)\) of length \(L_{\hat{f}}\) and a coefficient vector defined as \({\hat{\mathbf {f}}}\left( n \right) = {\left[ {{{\hat{f}}_0},{{\hat{f}}_1},...,{{\hat{f}}_{{L_{\hat{f}}} - 1}}} \right] ^T}\). The incoming signal \(x\left( n\right)\) is assumed to be wide sense stationary stochastic process (Anand et al. 2017). The output of the system microphone

$$\begin{aligned} y\left( n \right) = x\left( n \right) + {f_\mathrm{{b}}}\left( n \right) , \end{aligned}$$
(1)

where the feedback signal

$$\begin{aligned} {f_\mathrm{{b}}}\left( n \right) = F\left( k \right) {q_r}\left( n \right) , \end{aligned}$$
(2)

and

$$\begin{aligned} {q_r}\left( n \right) = q\left( n \right) + r\left( n \right) \end{aligned}$$
(3)

is the loudspeaker output, \(q\left( n\right)\) is the input to the loudspeaker and \(r\left( n\right)\) is the probe noise signal, and their respective vector definitions being \(\mathbf{{q}}_r\left( n \right) = \Big [ {q_r}\left( n \right) , {q_r}\left( {n - 1} \right) ,...,{q_r}\left( {n - {L_{\hat{f}}} + 1} \right) \Big ]^T\), \(\mathbf{{q}}\left( n \right) = {\left[ {q\left( n \right) ,q\left( {n - 1} \right) ,...,q\left( {n - {L_{\hat{f}}} + 1} \right) } \right] ^T}\) and \(\mathbf{{r}}\left( n \right) = {\left[ {r\left( n \right) ,r\left( {n - 1} \right) ,...,r\left( {n - {L_{\hat{f}}} + 1} \right) } \right] ^T}\). The loudspeaker input \(q\left( n \right) = {u_{\mathrm{{syn\_hp}}}}\left( n \right) + {u_{\mathrm{{lp}}}}\left( n \right)\) can be expressed in vector form as

$$\begin{aligned} \mathbf{{q}}\left( n \right) = {\mathbf{{u}}_{\mathrm{{syn\_hp}}}}\left( n \right) + {\mathbf{{u}}_{\mathrm{{lp}}}}\left( n \right) , \end{aligned}$$
(4)

where \({u_{\mathrm{{syn\_hp}}}}\left( n \right)\) and \({u_{\mathrm{{lp}}}}\left( n \right)\) are, respectively, the high and low-frequency components of the synthetic version \({u_{\mathrm{{syn}}}}\left( n \right)\) of the reinforced signal \(u\left( n \right)\) (Ma et al. 2011).

Fig. 1
figure 1

Linear prediction-based feedback canceller with probe noise (Anand et al. 2017)

Full size image

In order to attenuate the occurrence of feedback whistling and alleviate the problem of signal correlation between the system input and the loudspeaker output, the authors in Ma et al. (2011) proposed the idea of replacing the high-frequency component of \(u\left( n\right)\) by \({u_{\mathrm{{syn}}}}\left( n \right)\), which is generated by passing a zero-mean white noise signal \(w\left( n\right)\) through a linear-prediction filter \(\hat{H}\left( k \right)\). The reinforced signal is basically the error signal amplified for the listening-convenience of the hearing-aid user. The vector definitions \({\mathbf{{u}}_{\mathrm{{syn\_hp}}}}\left( n \right)\) and \({\mathbf{{u}}_{\mathrm{{lp}}}}\left( n \right)\) are similar to that of \(\mathbf{{q}}\left( n \right)\). The complimentary filter pair of the high-pass filter \({H_\mathrm{{p}}}\left( k \right)\) and the low-pass filter \({L_\mathrm{{p}}}\left( k \right)\) have a cut-off frequency of 2 kHz (Anand et al. 2017; Ma et al. 2011). The filter output

$$\begin{aligned} v\left( n \right) = \hat{F}\left( k \right) r\left( n \right) \end{aligned}$$
(5)

is an estimate of \(f_\mathrm{{b}}\left( n\right)\) and is subtracted from it to obtain the error signal

$$\begin{aligned} e\left( n \right) = y\left( n \right) - v\left( n \right) \end{aligned}$$
(6)

such that \(e\left( n\right)\) is a good estimate of the incoming signal \(x\left( n\right).\) The basic closed-loop AFC system is prone to a biased estimation of the feedback path. The feedback canceller in Ma et al. (2011) suppressed the high-frequency bias, but the low-frequency bias still affected the identification of the feedback path in situations of large low-frequency noise. In Anand et al. (2017), the authors proposed the use of probe noise in the linear prediction-based feedback canceller and based the adaptive estimation process of \(F\left( k\right)\) on it. It can be observed from (Guo 2012; Anand et al. 2017) that due to the probe signal being uncorrelated with the system input as well as the loudspeaker output, the closed-loop signal correlation between them no longer influences the estimation process. Thus, the linear prediction-based feedback canceller with probe noise attenuates the low-frequency as well as the high-frequency feedback and leads to an unbiased estimate of the feedback path (Anand et al. 2017).

In (Guo 2012; Anand et al. 2017), the efficient performance of the feedback canceller came at the cost of low convergence speed due to a small adaptation step size. In the next section, we replace the single-adaptive-filter configuration of the linear prediction-based feedback canceller with probe noise (Anand et al. 2017) with that of an affine combination of two adaptive filters for increasing the speed of convergence of the adaptive algorithm while efficiently tracking the changes in the feedback path.

Fig. 2
figure 2

Linear prediction-based feedback canceller with probe noise using C-LMS algorithm (equivalent CLMS filter represented by dashed enclosure)

Full size image

3 Proposed affine combination for adaptive feedback cancellation

3.1 C-LMS algorithm

In this section, we propose to replace the LMS adaptive filter in the linear prediction-based AFC system with probe noise in Fig. 1 by an adaptive combination of two filters, as shown in Fig. 2. Thus, instead of \(\hat{F}\left( k\right)\) being a single adaptive filter as in Anand et al. (2017), we now have \(\hat{F}\left( k\right)\) as a convex combination of two LMS algorithm-based adaptive filters viz. \(\hat{F}_1\left( k\right)\) and \(\hat{F}_2\left( k\right)\), with coefficient vectors \({{\hat{\mathbf {f}}}_1}\left( n \right) = {\left[ {{{\hat{f}}_1}\left( 0 \right) ,{{\hat{f}}_1}\left( 1 \right) ,...,{{\hat{f}}_1}\left( {{L_{\hat{f}}} - 1} \right) } \right] ^T}\) and \({{\hat{\mathbf {f}}}_2}\left( n \right) = \Big [ {{\hat{f}}_2}\left( 0 \right) ,{{\hat{f}}_2}\left( 1 \right) ,..., {{\hat{f}}_2}\left( {{L_{\hat{f}}} - 1} \right) \Big ]^T\), respectively (Arenas-Garcia et al. 2003, 2006; Singer and Feder 1999; Kozat and Singer 2000). The operation of both the combination filters \(\hat{F}_1\left( k\right)\) and \(\hat{F}_2\left( k\right)\) is decoupled completely such that their respective filter coefficients undergo adaptation using the LMS algorithm to minimize the square of their respective errors \(e_1\left( n\right)\) and \(e_2\left( n\right)\) (Arenas-Garcia et al., 2006). The equivalent combined LMS (C-LMS) filter \(\hat{F}(k)\) has been depicted in Fig. 2 in the dashed enclosure. The expression for the combination-filter coefficient update can be written as

$$\begin{aligned} {{\hat{\mathbf {f}}}_i}\left( {n + 1} \right) = {{\hat{\mathbf {f}}}_i}\left( n \right) + {\mu _i}\,{e_i}\left( n \right) \mathbf{{r}}\left( n \right) ,\quad i = 1,2, \end{aligned}$$
(7)

where \({e_\textit{i}}\left( n \right)\) are the corresponding combination-filter error signals expressed as

$$\begin{aligned} {e_i}\left( n \right) = y\left( n \right) - {v_i}\left( n \right) , \end{aligned}$$
(8)

where \({v_i}\left( n\right)\) are the corresponding outputs of the combination-filters expressed as

$$\begin{aligned} {v_i}\left( n \right) = {{\hat{\mathbf {f}}}_i}^T\left( n \right) \mathbf{{r}}\left( n \right) , \end{aligned}$$
(9)

and \({\mu _1}\) and \({\mu _2}\) are the step sizes for \({\hat{F}_1}\left( k \right)\) and \({\hat{F}_2}\left( k \right)\), respectively. Between the two combination-filters, \({\hat{F}_1}\left( k \right)\) undergoes fast adaptation to facilitate a high rate of convergence during periods of rapidly-occurring variations in the feedback path, and \({\hat{F}_2}\left( k \right)\) converges slower to facilitate a lower steady-state error during slowly-occurring variations or a stationary feedback path. To support this, \({\mu _1} \ge {\mu _2}\) (Martinez-Ramon et al. 2002). Finally, the coefficients of the equivalent C-LMS filter \(\hat{F}\left( k\right)\) are updated via a convex combination scheme as

$$\begin{aligned} {\hat{\mathbf {f}}}\left( n \right) = \psi \left( n \right) {{\hat{\mathbf {f}}}_1}\left( n \right) + \left[ {1 - \psi \left( n \right) } \right] {{\hat{\mathbf {f}}}_2}\left( n \right) , \end{aligned}$$
(10)

where \(\psi \left( n \right)\) is the combination parameter expressed using a sigmoid function as

$$\begin{aligned} \psi \left( n \right)&= \mathrm{{sgm}}\left[ {\alpha \left( n \right) } \right] \nonumber \\&= \frac{1}{{1 + {e^{ - \alpha \left( n \right) }}}}. \end{aligned}$$
(11)

The error of the C-LMS filter can be expressed as the convex combination of combination-filter errors as

$$\begin{aligned} e\left( n \right)&= y\left( n \right) - v\left( n \right) \nonumber \\&= \psi \left( n \right) {e_1}\left( n \right) + \left[ {1 - \psi \left( n \right) } \right] {e_2}\left( n \right) , \end{aligned}$$
(12)

where the output of the C-LMS filter

$$\begin{aligned} v\left( n \right)&= {{{\hat{\mathbf {f}}}}^T}\left( n \right) \mathbf{{r}}\left( n \right) \nonumber \\&= \psi \left( n \right) {v_1}\left( n \right) + \left[ {1 - \psi \left( n \right) } \right] {v_2}\left( n \right) \end{aligned}$$
(13)

The values of \(\psi \left( n \right)\) are restricted within the interval \(\left[ {0,1} \right]\) by using a sigmoid function in (11) to define it (Arenas-Garcia et al. 2003). For the adaptation of \(\psi \left( n \right)\), \(\alpha \left( n \right)\) is updated for each iteration with step size \({\mu _\alpha }\), using the stochastic gradient (SG) algorithm (Haykin 1991) to minimize the square of the error \(e\left( n\right)\) of \(\hat{F}\left( k \right)\), as

$$\begin{aligned} \alpha \left( {n + 1} \right)&= \alpha \left( n \right) - \frac{{{\mu _\alpha }}}{2}\frac{{\partial {e^2}\left( n \right) }}{{\partial \alpha \left( n \right) }}\nonumber \\&= \alpha \left( n \right) + {\mu _\alpha }\,e\left( n \right) \left\{ {\psi \left( n \right) \left[ {1 - \psi \left( n \right) } \right] } \right\} {\left[ {{{{\hat{\mathbf {f}}}}_1}\left( n \right) - {{{\hat{\mathbf {f}}}}_2}\left( n \right) } \right] ^T}{} \mathbf{{r}}\left( n \right) . \end{aligned}$$
(14)

Using (9) in (14), we have

$$\begin{aligned} \alpha \left( {n + 1} \right) = \alpha \left( n \right) + {\mu _\alpha }\,e\left( n \right) \left[ {{v_1}\left( n \right) - {v_2}\left( n \right) } \right] \psi \left( n \right) \left[ {1 - \psi \left( n \right) } \right] . \end{aligned}$$
(15)

When rapid time-variations occur in \(F\left( k\right)\), the tracking capability of the fast filter \({\hat{F}_1}\left( k \right)\) must be used to achieve a lower squared misadjustment. The learning rule in (15) will force \(\psi \left( n \right)\) to approach unity by increasing the value of \(\alpha \left( n \right)\) and consequently, \(\hat{F}\left( k \right) \approx {\hat{F}_1}\left( k \right)\) and \({\mu _1}\) is the step size for the combined filter. However, the slow filter \({\hat{F}_2}\left( k \right)\) is capable of performing more precisely during a stationary or nearly stationary feedback path. In such a case, (15) forces \(\psi \left( n \right)\) to approach zero by decreasing the value of \(\alpha \left( n \right)\), and, thus, \(\hat{F}\left( k \right) \approx {\hat{F}_2}\left( k \right)\) with \({\mu _2}\) as the step size. During intermediate situations, \(\psi \left( n \right)\) attains intermediate values and \(\hat{F}\left( k\right)\) is a mixture of both the combination-filters. To enable faster operation of the C-LMS filter as compared to the fastest combination-filter, \({\mu _\alpha }\) value is selected to be higher than \({\mu _1}.\) Hence, at each time instant n, the C-LMS filter \(\hat{F}\left( k\right)\) performs as the best filter in the combination (Arenas-Garcia et al. 2005). The stability of the C-LMS filter is guaranteed only when each of the combination-filters is individually stable.

In (14), the importance of the factor \(\psi \left( n \right) \left[ {1 - \psi \left( n \right) } \right]\), which is the derivative of the sigmoid function in (11), is three-fold (Arenas-Garcia et al. 2006):

  1. 1.

    It locks the combination of \(\hat{F}_1\left( k\right)\) and \(\hat{F}_2\left( k\right)\) to that particular combination-filter, which is performing more efficiently than the other one for a given situation.

  2. 2.

    It decreases the adaptation speed and the gradient noise in the vicinity of the end points 0 and 1, where the C-LMS filter must perform as the ‘slow’ and ‘fast’ filter, respectively.

  3. 3.

    It facilitates soft-switching between \(\hat{F}_1\left( k\right)\) and \(\hat{F}_2\left( k\right)\).

It must be noted that unless there are extremely abrupt (very fast or very slow) changes in the feedback path, switching from one combination-filter to another at each instant is prevented in the C-LMS algorithm.

3.2 Increasing the convergence-rate of the slow filter

We know that in the C-LMS algorithm, both \(\hat{F}_1\left( k\right)\) and \(\hat{F}_2\left( k\right)\) are decoupled completely. When an abrupt change occurs in the original feedback path, both \(\hat{F}_1\left( k\right)\) and \(\hat{F}_2\left( k\right)\) independently try to achieve convergence. To track this abrupt variation efficiently, \(\hat{F}\left( k\right)\) is equivalent to the fast filter \(\hat{F}_1\left( k\right)\) until the steady state is reached and now the slow filter \(\hat{F}_2\left( k\right)\) presents a smaller squared misadjustment. Then, at that instant, the C-LMS filter will become equivalent to \(\hat{F}_2\left( k\right),\) thereby forcing the overall convergence rate of \(\hat{F}\left( k\right)\) to be as slow as that of \(\hat{F}_2\left( k\right)\) when the combination-filters are updated using the SG algorithm. Therefore, to efficiently tackle the abrupt changes in the acoustic environment of the hearing-aid user, the convergence of the slow filter must be accelerated (Arenas-Garcia et al. 2003, 2006).

The increase in convergence-rate of \(\hat{F}_2\left( k\right)\) and consequently, the improvement in the performance of the C-LMS filter during occurrence of abrupt changes can be obtained by using the information from \(\hat{F}_1\left( k\right)\). A part of the coefficient vector \({{\hat{\mathbf {f}}}_1}\left( n \right)\) is transferred to \({{\hat{\mathbf {f}}}_2}\left( n \right)\) in a step-wise manner and \(\hat{F}_2\left( k\right)\) is

$$\begin{aligned} {{\hat{\mathbf {f}}}_2}\left( {n + 1} \right) = \phi \left[ {{{{\hat{\mathbf {f}}}}_2}\left( n \right) + {\mu _2}\,{e_2}\left( n \right) \mathbf{{r}}\left( n \right) } \right] + \left( {1 - \phi } \right) {{\hat{\mathbf {f}}}_1}\left( {n + 1} \right) , \end{aligned}$$
(16)

where the parameter \(\phi\) is close to 1. The above equation is basically a coefficient-transfer scheme for the acceleration of convergence rate of \(\hat{F}_2\left( k\right)\).Thus, as seen from (16), even though \(\hat{F}_2\left( k\right)\) is still updated using the SG algorithm, the convergence-rate of \(\hat{F}_2\left( k\right)\) will increase after numerous consecutive iterations of (16). Therefore, the C-LMS filter \(\hat{F}\left( k\right)\) will reach the final steady-state error of \(\hat{F}_2\left( k\right)\) sooner, as compared to \(\hat{F}_2\left( k\right)\) operating by itself for AFC process.

However, the weight update of \(\hat{F}_2\left( k\right)\) in (16) suffers from another drawback in that the final misadjustment of \(\hat{F}_2\left( k\right)\) increases as a result of the coefficient-transfer from \(\hat{F}_1\left( k\right)\). To prevent this, the update procedure of (16) must be activated only when (Arenas-Garcia et al. 2003):

  1. 1.

    \(\hat{F}_1\left( k\right)\) is performing more efficiently and effectively than \(\hat{F}_2\left( k\right)\) in tracking the variations of the acoustic environment, i.e. \(\psi \left( n \right)\) must be close to unity. The aforementioned condition can be verified when

    $$\begin{aligned} \psi \left( n \right)> \lambda , \end{aligned}$$
    (17)

    where \(\lambda\) is a threshold value which is close to the maximum possible value of \(\psi \left( n \right)\).

  2. 2.

    \({{\hat{\mathbf {f}}}_1}\left( n \right)\) and \({{\hat{\mathbf {f}}}_2}\left( n \right)\) must be different from one another. This condition can be verified if the components \({{\hat{\mathbf {f}}}_{2\, \bot }}\left( n \right)\) and \({{\hat{\mathbf {f}}}_{2\,\parallel }}\left( n \right)\) of \({{\hat{\mathbf {f}}}_2}\left( n \right)\) satisfy the condition that

    $$\begin{aligned} \dfrac{{{{\left\| {{{{\hat{\mathbf {f}}}}_{2\, \bot }}\left( n \right) } \right\| }_2}}}{{{{\left\| {{{{\hat{\mathbf {f}}}}_{2\,\parallel }}\left( n \right) } \right\| }_2}}}> \eta , \end{aligned}$$
    (18)

    where \({{\hat{\mathbf {f}}}_{2\, \bot }}\left( n \right)\) is perpendicular to, and \({{\hat{\mathbf {f}}}_{2\,\parallel }}\left( n \right)\) is parallel to, the coefficient vector of the fast filter \({{\hat{\mathbf {f}}}_1}\left( n \right)\), and \(\eta\) is a constant.

Thus, using the procedure in (16) subject to the above mentioned conditions, the convergence of \(\hat{F}_2\left( k\right)\) can be accelerated while keeping the final error lower, and the performance of the C-LMS filter can be further improved upon.

In the subsequent section, we explore the idea of trading a single common combination parameter in favour of \(L_{\hat{f}}\) combination parameters, corresponding to each adaptive filter weight, to bring improvement in performance of the C-LMS algorithm for time-varying feedback paths.

4 Decoupled-CLMS algorithm

The C-LMS algorithm uses a global combination-parameter \(\psi \left( n \right)\) for all the coefficients of the combination-filters. However, while identifying varying acoustic environments, some of the estimation-filter coefficients may remain unaltered. In such situations, having a different combination-parameter for each coefficient of the adaptive combination-filters, i.e. multiplication with a high combination-parameter for some coefficients and with a low-combination parameter for the rest, would be advantageous. The decoupled C-LMS (D-CLMS) algorithm is such an extension of the C-LMS algorithm (Arenas-Garcia et al. 2003). Thus, the coefficients of the D-CLMS filter can be updated using a convex combination scheme similar to (10) as

$$\begin{aligned} {\hat{\mathbf {f}}}\left( n \right) = \mathbf{{\Gamma }}\left( n \right) {{\hat{\mathbf {f}}}_1}\left( n \right) + \left[ {\mathbf{{I}} - \mathbf{{\Gamma }}\left( n \right) } \right] {{\hat{\mathbf {f}}}_2}\left( n \right) , \end{aligned}$$
(19)

where \(\mathbf{{\Gamma }}\left( n \right)\) is a diagonal matrix whose entries consist of the combination-parameters \({\psi _j}\left( n \right) ,\,j = 1,2,...,{L_{\hat{f}}}\) as

$$\begin{aligned} \mathbf{{\Gamma }}\left( n \right) = \left[ {\begin{array}{*{20}{c}} {{\psi _1}\left( n \right) }&{}0&{} \cdots &{}0\\ 0&{}{{\psi _2}\left( n \right) }&{} \cdots &{}0\\ \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0&{}0&{} \cdots &{}{{\psi _{{\mathrm{{L}}_{\hat{f}}}}}\left( n \right) } \end{array}} \right] . \end{aligned}$$
(20)

The different combination-parameters \({\psi _j}\left( n \right)\) can be defined using the sigmoidal form by rewriting (11) as

$$\begin{aligned} {\psi _j}\left( n \right)&= \mathrm{{sgm}}\left[ {{\alpha _j}\left( n \right) } \right] ,\,j = 1,2,...,{L_{\hat{f}}}\nonumber \\&= \frac{1}{{1 + {e^{ - {\alpha _j}\left( n \right) }}}}, \end{aligned}$$
(21)

where the parameters \({\alpha _j}\left( n \right)\) are updated using the expression obtained by rewriting (14) as

$$\begin{aligned} {\alpha _j}\left( {n + 1} \right) = {\alpha _j}\left( n \right) + {\mu _\alpha }\,e\left( n \right) \left\{ {{\psi _j}\left( n \right) \left[ {1 - {\psi _j}\left( n \right) } \right] } \right\} \left[ {{{\hat{f}}_{1j}}\left( n \right) - {{\hat{f}}_{2j}}\left( n \right) } \right] {r_j}\left( n \right) , \end{aligned}$$
(22)

where \(j = 1,2,...,{L_{\hat{f}}}\), and \({\hat{f}_{1j}}\left( n \right)\), \({\hat{f}_{2j}}\left( n \right)\) and \({r_j}\left( n \right)\) are the \({j{\mathrm{{th}}}}\) components of vectors \({{\hat{\mathbf {f}}}_1}\left( n \right)\), \({{\hat{\mathbf {f}}}_2}\left( n \right)\) and \(\mathbf{{r}}\left( n \right)\), respectively.

Since the D-CLMS algorithms is an extension of the C-LMS algorithm, it also suffers from the problem of low convergence-rate of the slow filter \(\hat{F}_2\left( k\right)\). To alleviate this problem, the coefficient-transfer strategy of the C-LMS algorithm may be used (Arenas-Garcia et al. 2003). However, it transfers the entire coefficient vector from the fast filter to the slow filter, leading to an inefficient equivalent filter performance due to a large final misadjustment, as discussed in the previous section. A simple procedure, similar to (16) for the C-LMS algorithm, can be used to improve D-CLMS algorithms performance only in certain conditions. In this new coefficient-transfer scheme, only those coefficients from the D-CLMS filter having an associated \({\psi _j}\left( n \right)\) close to unity are transferred to the slow filter according to the expression

$$\begin{aligned} {{\hat{\mathbf {f}}}_2}\left( {n + 1} \right) = \phi \left[ {{{{\hat{\mathbf {f}}}}_2}\left( n \right) + {\mu _2}\,{e_2}\left( n \right) \mathbf{{r}}\left( n \right) } \right] + \left( {1 - \phi } \right) {\hat{\mathbf {f}}}\left( {n + 1} \right) , \end{aligned}$$
(23)

where \(\phi\) is same as defined in the previous section. The coefficient-transfer strategy of (23) must be applied subject to the following conditions (Arenas-Garcia et al. 2003):

  1. 1.

    The fast filter \(\hat{F}_1\left( k\right)\) is performing significantly better than \(\hat{F}_2\left( k\right)\) and is incurring a lower misadjustment in tracking the variations in the acoustic feedback path. The aforementioned condition can be verified for \({\psi _j}\left( n \right)> \lambda\), for any \(j = 1,2,...,{L_{\hat{f}}}\).

  2. 2.

    The coefficient vectors of \(\hat{F}_2\left( k\right)\) and \(\hat{F}\left( k\right)\) must differ from each other significantly. The aforementioned condition is verified when the components \({{\tilde{\mathbf {f}}}_{2\, \bot }}\left( n \right)\) and \({{\tilde{\mathbf {f}}}_{2\,\parallel }}\left( n \right)\) of \({{\hat{\mathbf {f}}}_2}\left( n \right)\) satisfy the condition that

    $$\begin{aligned} \frac{{{{\left\| {{{{\tilde{\mathbf {f}}}}_{2\, \bot }}\left( n \right) } \right\| }_2}}}{{{{\left\| {{{{\tilde{\mathbf {f}}}}_{2\,\parallel }}\left( n \right) } \right\| }_2}}}> \eta , \end{aligned}$$
    (24)

    where \({{\tilde{\mathbf {f}}}_{2\, \bot }}\left( n \right)\) is perpendicular to, and \({{\tilde{\mathbf {f}}}_{2\,\parallel }}\left( n \right)\) is parallel to, the C-LMS filter coefficient vector \({\hat{\mathbf {f}}}\left( n \right)\).

5 Double-nested C-LMS algorithm

In this section, we propose three-filter version of the C-LMS algorithm called the double-nested C-LMS (DN-CLMS) algorithm (Arenas-Garcia et al. 2006), which can be used for updating the adaptive filter to estimate the original feedback path. The three-filter configuration has an advantage of not requiring the weight-transfer strategy, which increases the computational complexity of the algorithm. Instead, the step sizes \({\mu _1}\) and \({\mu _2}\) of the combination-filters are managed using the global combination-parameter \(\psi \left( n \right)\) to increase the convergence speed of the slow component-filter. In this way, an efficient and effective tracking performance is obtained along with fast convergence of the adaptive algorithm.

The filter \(\hat{F}_1\left( k\right)\) possesses a fast-tracking capability and hence it is not much advantageous to manage \({\mu _1}\). On the other hand, \({\mu _2}\) can be managed by expressing \(\hat{F}_2\left( k\right)\) as a convex combination of C-LMS filters \({\hat{F}_{21}}\left( k \right)\) and \({\hat{F}_{22}}\left( k \right)\) with step sizes \({\mu _{21}}\) and \({\mu _{22}}\), respectively, such that

$$\begin{aligned} {\mu _1}> {\mu _{21}}> {\mu _{22}}. \end{aligned}$$
(25)

Thus, the coefficients of this nested C-LMS filter \(\hat{F}_2\left( k\right)\) can now be expressed similar to (10) as

$$\begin{aligned} {{\hat{\mathbf {f}}}_2}\left( n \right) = {\psi _2}\left( n \right) {{\hat{\mathbf {f}}}_{21}}\left( n \right) + \left[ {1 - {\psi _2}\left( n \right) } \right] {{\hat{\mathbf {f}}}_{22}}\left( n \right) , \end{aligned}$$
(26)

where \(\psi _2\left( k\right)\) is the combination parameter of the nested-C-LMS filter and is defined as

$$\begin{aligned} {\psi _2}\left( n \right) = \mathrm{{sgm}}\left[ {{\alpha _2}\left( n \right) } \right] . \end{aligned}$$
(27)

In order to minimize the quadratic error

$$\begin{aligned} e_2^{2}\left( n \right) = {\left[ {y\left( n \right) - {{{\hat{\mathbf {f}}}}_2}^T\left( n \right) \mathbf{{r}}\left( n \right) } \right] ^2} \end{aligned}$$
(28)

of \(\hat{F}_2\left( k\right)\), the update of \(\psi _2\left( n\right)\) is performed similar to that in (15) as

$$\begin{aligned} {\alpha _2}\left( {n + 1} \right) = {\alpha _2}\left( n \right) + {\mu _{{\alpha _{_\mathrm{{2}}}}}}{e_2}\left( n \right) \left\{ {{\psi _2}\left( n \right) \left[ {1 - {\psi _2}\left( n \right) } \right] } \right\} \left[ {{e_{21}}\left( n \right) - {e_{22}}\left( n \right) } \right] . \end{aligned}$$
(29)

It must be noted that during the procedure for estimating \(F\left( k\right)\), the AFC system of Fig. 2 switches between the two-filter scheme of the basic C-LMS algorithm and the three-filter scheme of the double-nested extension of C-LMS algorithm, i.e. the DN-CLMS algorithm, subject to the value of \(\psi \left( n\right)\) as (Arenas-Garcia et al. 2006)

  1. 1.

    Initially, the operation begins with the two-filter scheme of the basic C-LMS algorithm. The step sizes under consideration are \(\mu _1\) and \(\mu _2\), and \({\alpha _2}\left( n \right)\) is set to its maximum value

  2. 2.

    If \({\psi _2}\left( n \right)\) attains a value less than \(\lambda\) as the feedback cancellation progresses, the switch-over is made to the three-filter scheme of DN-CLMS algorithm. The slow filter \({{\hat{\mathbf {f}}}_2}\left( n \right)\) is now composed of \({{\hat{\mathbf {f}}}_{21}}\left( n \right)\) and \({{\hat{\mathbf {f}}}_{22}}\left( n \right)\). The parameter \({\alpha _2}\left( n \right)\) for updating \({\psi _2}\left( n \right)\) is set to zero and the step sizes under consideration are now \({\mu _{21}}\) and \({\mu _{22}}\), which are set to the values \({\mu _2}\) and \(\frac{{{\mu _2}}}{\tau },\tau\) being a positive constant greater than unity, respectively.

  3. 3.

    Finally, when the condition in (17) is satisfied, the AFC system returns to the two-filter scheme in accordance with the present value attained by \({{\hat{\mathbf {f}}}_2}\left( n \right)\).

Since

$$\begin{aligned} \left| {{e_{21}}\left( n \right) - {e_{22}}\left( n \right) } \right| < \left| {{e_1}\left( n \right) - {e_2}\left( n \right) } \right| , \end{aligned}$$
(30)

the learning rate \({\mu _{{\alpha _{_\mathrm{{2}}}}}}\) must be higher than \({\mu _\alpha }\)(typically 10 times) (Arenas-Garcia et al. 2006). Thus, the DN-CLMS retains the simplicity of the C-LMS algorithm, along with the highly desirable characteristics of precision in adaptive estimation and speedy convergence of the adaptive algorithm.

In the next section, C-LMS, D-CLMS and the DN-CLMS algorithms are compared in terms of their computational complexities.

6 Computational complexity

In this section, we analyse the computational complexity of the proposed combination techniques in terms of the required number of real multiplications per iteration, for the application of acoustic feedback cancellation. We only consider the number of real multiplications for the proposed algorithms as the number of additions is comparable to that of multiplications. A look-up table can be used to efficiently evaluate the sigmoid function.

6.1 C-LMS algorithm

For an adaptive filter of length \(L_{\hat{f}}\), the LMS procedure requires \(2 L_{\hat{f}}+1\) number of multiplications. The C-LMS algorithm consists of a combination of two LMS adaptive algorithm-based filters and, therefore, the filter update in (7) for both the combination-filters require total number of \(4L_{\hat{f}}+2\) multiplications. Moreover, a total of 6 multiplications are required to compute (13) for the adaptive filter output and (14) for updating \(\alpha \left( n\right)\). The coefficient-transfer strategy, applied when \(\psi \left( n \right)> \lambda\), increases the computational burden of the adaptive filters by as it requires computation of an additional \(2L_{\hat{f}}\) number of multiplications to speed-up the convergence of the slow combination-filter. For computing the coefficients of the C-LMS filter using (10), the number of extra multiplications required is \(2L_{\hat{f}}\).

6.2 D-CLMS algorithm

Similar to the C-LMS algorithm, the filter update for both the combination-filters in D-CLMS algorithm also requires \(4L_{\hat{f}}+2\) multiplications. Also, the number of multiplications required for computing the adaptive filter output and that for the \(\alpha \left( n\right)\) update is 6, for a particular value of j in (22). The coefficient-transfer strategy in (23) requires \(2L_{\hat{f}}\) number of multiplications, while \(2L_{\hat{f}}\) multiplications are required for computing the D-CLMS coefficients in (19) for a particular value of j.

6.3 DN-CLMS algorithm

The computational complexity of the DN-CLMS algorithm is calculated for both the cases of \(\psi \left( n \right)> \lambda\) and \(\psi \left( n \right) < \lambda\). Initially, when \(\psi \left( n\right)\) is greater than \(\lambda\), the system operates in the two-filter configuration of the C-LMS scheme and the computational complexity is the same as that of the C-LMS algorithm. During the AFC operation, when \(\psi _2\left( n\right)\) attains a value less than \(\beta\), the three-filter configuration of the DN-CLMS algorithm is applied and update of combination-filters requires a total of number of \(6L_{\hat{f}}+3\) multiplications. Moreover, computation of the DN-CLMS filter output using (1), and updating \(\alpha \left( n\right)\) by (14) and \(\alpha _2\left( n\right)\) by (29) requires a sum of 12 additional multiplications. For computing the coefficients of the DN-CLMS filter using (26), \(3L_{\hat{f}}+2\) further multiplications are required.

Table 1 summarizes the computational complexity of the proposed algorithms. It can be seen from Table 1 that the complexity of all of the proposed algorithms is \(O\big ({L_{\hat{f}}}\big )\), i.e. the complexity increases linearly with the number of coefficients of the adaptive filter. Also, the computational complexity of the proposed algorithms is twice that of the LMS algorithm, with the ‘coefficient-transfer’ strategy adding to the computational burden. The coefficient-transfer strategy is, however, used only when we want to increase the convergence rate of the ‘slow’ combination-filter.

Table 1 Summary of computational complexity of the proposed algorithms
Full size table
Fig. 3
figure 3

Frequency response of the true feedback path

Full size image
Fig. 4
figure 4

Frequency response of the complimentary filter pair

Full size image

7 Simulation and results

In this section, we compare the performance of the linear prediction-based feedback canceller with probe noise for adaptive estimation of the feedback path by using the C-LMS, D-CLMS and the DN-CLMS algorithms. The simulations are performed on a common platform of MATLAB using 16 kHz as the sampling frequency, and the results are compared over an average of 200 simulation runs of \(10^4\) number of iterations, in terms of misalignment between the coefficients of the true feedback path and the estimated feedback path as

$$\begin{aligned} \mathrm{{MSD}}\left( n \right) \mathrm{{ = }}\frac{{\left\| {\mathbf{{f}}\left( n \right) - {\hat{\mathbf {f}}}\left( n \right) } \right\| _2^2}}{{\left\| {\mathbf{{f}}\left( n \right) } \right\| _2^2}}. \end{aligned}$$
(31)
Fig. 5
figure 5

Impulse response of the 1st order AR random process for generating speech-shaped signal

Full size image
Fig. 6
figure 6

Time waveform of female speech input

Full size image

The true feedback path is represented by an FIR filter of order 50. Figure 3 shows the frequency response of the feedback path obtained using a behind-the-ear assistive listening device (Anand et al. 2017). It can be observed in Fig. 2 that the magnitude of the feedback path is high in the high-frequency range of 2 to 7 kHz and gain applied in this frequency range will make the system prone to feedback oscillations. The variations in the feedback path are represented using the random walk model as \(\mathbf{{f}}\left( {n + 1} \right) = \mathbf{{f}}\left( n \right) + {{\varvec{\theta } }}\left( n \right)\), where \({{\varvec{\theta } }}\left( n \right)\) is a zero-mean Gaussian stochastic sequence of variance \(10^{-3}\). The adaptive combination filters are also FIR filters, each of order 50. The forward path consists of a constant reinforcement gain of 5 and a delay of 55 samples. The frequency response of the complimentary filter pair \({{H_\mathrm{{p}}}\left( k \right) ,{L_\mathrm{{p}}}\left( k \right) }\) with cut-off frequency of 2 kHz is shown in Fig. 4 (Anand et al. 2017). The probe noise signal is a Gaussian sequence of zero mean and unit variance. Two types of input signals are used viz., a stationary speech-shaped signal generated by passing a white Gaussian noise signal through an Auto-regressive (AR) process of first order expressed as

$$\begin{aligned} Q\left( k \right) = \frac{{\sqrt{1 - {\gamma ^2}} }}{{1 - \gamma \,{k^{ - 1}}}}, \end{aligned}$$
(32)

where \(\gamma\) is set to 0.8, and a speech signal consisting of female speech, depicted in Fig. 6. The impulse response of \(Q\left( k\right)\) is depicted in Fig. 5. For the fast combination-filter, the step size is set to 0.007 for good tracking of the abruptly occurring changes in the feedback path, while that for the slow filter is set to a small value of 0.0009 for obtaining a lower steady-state error; bearing in mind the individual stability of the two filters for a stable equivalent filter. The adaptation step for the equivalent filter is set to a positive constant value of unity for the C-LMS algorithm and 50 for the D-CLMS algorithm so that the affine combination of the combination-filters can adapt faster than the fastest combination-filter. Typically, the step size for the D-CLMS algorithm must be set to a value \(L_{\hat{f}}\) times that for the C-LMS algorithm (Arenas-Garcia et al. 2003). For the DN-CLMS algorithm, \({\mu _{{\alpha _{_\mathrm{{2}}}}}}\) is fixed at 10. The acceleration procedure parameters \(\phi\) and \(\lambda\) are set to 0.9 and 0.98, respectively (Arenas-Garcia et al. 2003). The constant \(\eta\) for weight-update condition of (18) and (24) is set to 0.03. The value of constant \(\tau\) is set to 2 for the DN-CLMS algorithm. The value of \(\alpha \left( n\right)\) for updating the combination parameter \(\psi \left( n \right)\) and the coefficients of the combination-filters are initialized to zero. To prevent stagnation when \(\psi \left( n \right) = 0\,\mathrm{{or}}\,\mathrm{{1}}\), \(\alpha \left( n\right)\) is restricted within the interval \(\left[ { - \varpi ,\varpi } \right]\), \(\varpi\) being a positive constant. This restriction of values of \(\alpha \left( n\right)\) limits \(\psi \left( n \right)\) within the range \(\left[ {1 - \psi ,\,\,\psi } \right]\), \(\psi\) being a positive constant. The value of \(\psi\) is set to 4 such that \(\psi \left( n \right) \in \left[ {0.018,\,0.982} \right]\), thereby preventing the algorithm from ceasing its operation due to either \(\psi \left( n \right)\) or \(1 - \psi \left( n \right)\) being nearly zero. For the VSS algorithm (Mathews and Xie 1993), the value of step-size adaptation-control parameter is set to 0.0008 and the step size is initialized at 0.0001.

Fig. 7
figure 7

Misalignment evolution for stationary speech-shaped input

Full size image
Fig. 8
figure 8

Misalignment evolution for female-speech input

Full size image

Figures 7 and 8 depict the MSD evolution of the C-LMS, D-CLMS, DN-CLMS and the single-filter VSS algorithm for the stationary speech-shaped signal and the female speech signal, respectively. It can be observed from both the figures that D-CLMS offers a lower misalignment at steady state than C-LMS. However, since the \(\alpha \left( n\right)\) update for C-LMS is easier than that of D-CLMS containing 50 mixing parameters, D-CLMS converges slightly slower than C-LMS. It can also be seen from the figures that the performance of the single-filter VSS algorithm is worse than that of C-LMS or D-CLMS during the stationary period as well as when abrupt changes occur. Moreover, it can be seen that the DN-CLMS algorithm outperforms the VSS, C-LMS and D-CLMS algorithms in terms of achieving a lower MSD during the stationary intervals in the acoustic environment as well as in tracking abrupt variations in the feedback path for both types of chosen inputs.

8 Conclusion

In this paper, we have proposed a convex combination of two independent LMS filters for achieving a high convergence rate and a low steady-state misalignment in the application of adaptive feedback cancellation. The linear prediction-based adaptive feedback canceller with probe noise was used to suppress the bias introduced in the feedback-path estimate, while the single-adaptive-filter was replaced by a convex combination of adaptive filters to mitigate the compromise between convergence rate and tracking ability. The fast filter, having a larger step size for a faster convergence, and the slow filter, having a smaller step size for a smaller stationary misalignment, were combined using a single combination parameter. We used an acceleration procedure to further improve upon the convergence rate of the affine filter-combination for feedback estimation. Also, we proposed the application of different combination parameters for different adaptive filter weights in the affine-combination scheme to improve the tracking performance of the adaptive filter for the time-varying feedback path. Moreover, a more sophisticated three-filter configuration, which combines the convex-combination and the idea of a varying step size, was applied for feedback cancellation to manage the overall step size of the adaptive estimation filter while simultaneously maintaining an efficient tracking ability and speedy convergence. We computed the complexity of the proposed algorithms for feedback cancellation and found that, as compared to the LMS algorithm, the proposed algorithms require more number of multiplications per iteration. Further, we compared the performances of the proposed algorithms with that of the VSS algorithm in terms of normalized misalignment. Simulation results showed that while the adaptive-combination algorithms performed better than the single-adaptive-filter-based VSS algorithm, the DN-CLMS algorithm outperformed the D-CLMS and C-LMS algorithms for the stationary speech-shaped input as well as the speech input signal.

In future, we wish to explore further nesting of the three-filter configuration in the DN-CLMS algorithm to enhance the tracking ability of the adaptive filter in time-varying and high-noise environments, at the same time achieving speed-up its convergence.