Analyzing two-dimensional cellular detonation flows from numerical simulations with proper orthogonal decomposition and Lagrangian descriptors

Abstract

In this study, the data analysis technique of proper orthogonal decomposition (POD) is applied to the numerical simulation solutions of two-dimensional unsteady cellular detonation. As a first stage to introduce the idea, the analysis is performed on the simulation results obtained numerically with the reactive Euler equations with a one-step Arrhenius kinetic model. Cases with different activation energies $E_{{\rm{a}}}$ are considered, yielding different degrees of cellular instability of the detonation frontal structure. The POD modes are obtained by performing a singular value decomposition (SVD) of the full ensemble matrix whose columns are the snapshots of time-dependent pressure fields from the stored numerical solutions. The dominant spatial flow features behind the detonation front with varying $E_{{\rm{a}}}$ are revealed by the resulting POD modes that represent flow structures with decreasing flow energy content. The accuracy of the pressure flow field reconstructed using different levels of POD basis modes for reduced-order modeling is demonstrated. The coherent structures and increasing complexity of the flow fields with higher $E_{{\rm{a}}}$ are elucidated with the use of Lagrangian descriptors (LD). The potential of the methods described in this work is discussed.

Graphical abstract

1 Introduction

Detonation is a self-sustained, supersonic, combustion-driven compressible wave, characterized by significant increases in pressure and temperature (Lee 2008). Traditionally, detonation research has also been largely driven by its broad range of safety engineering applications and industrial processes in the chemical and energy sectors, and energy conversion in internal combustion engines experiencing severe knock. Recently, the detonation phenomenon has also emerged as a viable option for the development of advanced power systems which harness the conditions generated by this combustion mode. For instance, detonation is used as a combustion mode for hypersonic propulsion systems, leading to the development of pulsed or continuous detonation engines (Wolanski 2013). Additionally, the detonation wave possesses numerous reproducible dynamic features that can be analyzed to understand the interplay between fluid dynamics and chemical reactions. Therefore, applying modern analytical tools to conduct fundamental studies aimed at enhancing our understanding of detonation dynamics could have a wide-reaching impact. This includes improving measures for mitigating accidental detonative combustion and exploring alternative applications of detonation waves in various industrial sectors, such as defense, aerospace, and mining.

In a homogeneous explosive mixture without losses, a detonation propagates in a tube at a steady, unique velocity known as the Chapman–Jouguet (CJ) velocity (Fickett and Davis 2000). This unique velocity can be determined from thermodynamic equilibrium analysis using a control volume approach, given by the solution of the one-dimensional (1-D) conservation equations and the sonic condition, i.e., the Chapman–Jouguet (CJ) criterion. Equivalently, the latter requires the Rayleigh line to be tangent to the equilibrium Hugoniot curve. However, to model the dynamics of the detonation wave propagation, i.e., initiation and failure limit, a description of the wave structure and its propagation mechanism are required. The idealized 1-D steady detonation structure was obtained through the Zel’dovich–von Neumann–Döring (ZND) model, where the structure consists of an inert shock followed by a reaction zone of which the end corresponds to the CJ state. The ZND model also provides a wave propagation mechanism caused by shock ignition and a characteristic length scale which takes into account the influence of chemical reaction kinetics. However, real detonation fronts are inherently unstable, shown both experimentally and numerically, exhibiting different behaviors such as longitudinal oscillation and cellular instability development. The flow field is complex with an ensemble of waves sweeping across the front and compressible turbulence behind the structure, see Fig. 1. The unstable structure results in the cellular pattern as observed experimentally using the smoked foil technique or numerically from the time-integrated maximum pressure contour. Experimentally, high-speed flow visualization using Schlieren and laser diagnostic techniques such as planar laser-induced fluorescence (PLIF) (Austin et al. 2005) may shed light on the complex detonation structure, but resolving quantitatively the complete flow field behind the detonation front is not yet possible. Nowadays, using high-resolution numerical simulations, the detailed flow fields behind a detonation front can be obtained (Ng and Zhang 2012). As detonation itself is a coupled fluid and chemical reaction phenomenon, its computational data output is high, and thus, it is necessary to find ways to interpret the results to further elucidate the flow dynamics and possibly develop the reduced model by performing data compression.

Fig. 1

a Numerical temperature flow field and b numerical and c experimental Schlieren pictures of a propagating methane-oxygen detonation (Kiyanda et al. 2015)

Recent research trends state the importance of data science as a tool to sort and study a large amount of data. Besides direct visualization, it is desirable to further “dissect” the flow data for further reduced-order modeling using modern analysis techniques. With the recent increase in interest in data science, modal decomposition techniques are increasingly becoming a useful tool for pattern detection in fluid phenomena and are being used as a data science tool to assess and predict data in its energy properties (Kutz et al. 2016). In this study, we employ a well-established modal decomposition technique, namely, proper orthogonal decomposition (POD) to re-analyze and compress the raw numerical simulation data for further modeling the flow structure of a detonation. The POD was originally developed by Pearson (1901) about 100 years ago for graphical analyses. The method was further developed by Hotelling (1933), Karhunen (1946), and Loève (1955). This modal decomposition approach considers a linear statistical method that was introduced subsequently by Lumley (1967) to the field of hydrodynamics. Since then, POD has been applied to study turbulent flow in a pipe, turbulent jets, shallow water flows, cardiovascular flows, and combustion fields. The main interpretation of POD is that it sorts time-dependent data of the full transient flow field into linear combinations of a set of fixed basic orthogonal modes along with temporal coefficients so that the coherent structure embedded in the time-changing data can be revealed. The POD method also determines the amount of energy contribution of each spatially orthogonal mode in the whole dataset. By identifying crucial POD modes with dominant energy contents, a reduced-order model can be constructed by the superposition of these modes in its temporal dynamics representing the original full flow field with relatively low error to an acceptable level. In other words, the data reduction using POD minimizes the error in the reconstruction of the dataset by considering sufficient modes ranked according to their energy content. Reducing the amount of information required to capture the essential dynamics of the detonation structure to a minimum thus provides an alternate way to interpret the flow nature and its instabilities. To assess the complexity of the compressible flow and reveal any signature such as embedded Lagrangian coherent structures (LCS) behind the propagating detonation front, we extend the analyses using Lagrangian-based techniques (Allshouse and Peacock 2015). Specifically for computational efficiency, the technique of Lagrangian descriptors (LD) is employed in this study. LD evaluates the finite-time Euclidean arc length of Lagrangian trajectories and the abrupt changes in their vicinity to detect LCS, and it can be used as a scalar trajectory-based diagnostic tool based on fluid parcel trajectories (Mancho et al. 2013; Mendoza and Mancho 2010; Darwish et al. 2021). Functions obtained from particle trajectories evolve advected by fluid flows according to a dynamical system.

2 Numerical simulations

High-resolution, numerical simulations of cellular detonation waves are achieved by solving numerically the two-dimensional (2-D) reactive Euler equations with a one-step Arrhenius kinetic model (Ng and Zhang 2012). The governing equations for this process are as follows:

$$\begin{aligned} \frac{\partial {{\textbf {U}}} }{\partial t} +\frac{\partial {{\textbf {F}}} }{\partial x} +\frac{\partial {{\textbf {G}}} }{\partial y} ={{\textbf {S}}} \end{aligned}$$

(1)

$$\begin{aligned} {{\textbf {U}}}=\begin{bmatrix} \rho \\ \rho u\\ \rho v\\ \rho e\\ \rho \lambda \\ \end{bmatrix}, {{\textbf {F}}}=\begin{bmatrix} \rho u\\ \rho u^2+p\\ \rho uv\\ \rho u(e+p) \\ \rho u\lambda \\ \end{bmatrix}, {{\textbf {G}}}=\begin{bmatrix} \rho v\\ \rho uv\\ \rho v^2+p\\ \rho v(e+p) \\ \rho v\lambda \\ \end{bmatrix}, {{\textbf {S}}}=\begin{bmatrix} 0\\ 0\\ 0\\ 0 \\ \rho {\dot{\omega }}\\ \end{bmatrix} \end{aligned}$$

with

$$\begin{aligned} e=\frac{p}{(\gamma -1)\rho }+\frac{1}{2}(u^2+v^2)+\lambda Q\; \; \rm{and} \; p=\rho T \end{aligned}$$

(2)

$$\begin{aligned} {\dot{\omega }}=- k \lambda {\exp } (\frac{-E_a}{T}) \end{aligned}$$

(3)

All the flow variables have been made dimensionless in reference to the upstream quiescent state, i.e.,

$$\begin{aligned}{} & {} \rho =\frac{\tilde{\rho }}{\tilde{\rho }_0}, p=\frac{\tilde{p}}{\tilde{p}_0}, T=\frac{\tilde{T}}{\tilde{T}_0}, {c}_0=\sqrt{\gamma \tilde{T}_0}, u=\frac{\tilde{u}}{{c}_0},\nonumber \\{} & {} \quad Q=\frac{\tilde{Q}}{R\tilde{T}_0}, E_a=\frac{\tilde{E_a}}{R\tilde{T}_0}, x=\frac{\tilde{x}}{l_{1/2}} \end{aligned}$$

(4)

The pre-exponential factor k in the rate law is adjusted such that the reference length scale, i.e., the half-reaction zone length scale $l_{1/2}$ (when the reaction process $\lambda$ = 1/2) of the steady ZND detonation structure is unity. Using typical canonical values, the normalized heat release Q is equal to 50 and the isentropic exponent $\gamma$ = 1.2. The corresponding post-shock state and CJ detonation properties are: $T_s$ = 4.814; $p_s$ = 42.063; $T_{{\rm{CJ}}}$ = 11.998; $p_{{\rm{CJ}}}$ = 21.531; and the CJ detonation velocity $D_{{\rm{CJ}}} = \tilde{D_{{\rm{CJ}}}}/{{c}_0}$ = 6.8095. The activation energy is varied to change the mixture sensitivity, and four activation energies are considered here, i.e., $E_{{\rm{a}}}$ = 5, 10, 20, and 25. Numerical simulations are performed using an in-house code implemented in Nvidia’s CUDA programming language and on a Nvidia Tesla K40 GPU computing processor (Kiyanda et al. 2015; Mi et al. 2017, 2018; Yan et al. 2019). The governing equations are solved numerically using the MUSCL-Hancock scheme with the van Leer non-smooth slope limiter and a Harten–Lax–van Leer contact (HLLC) approximate solver for the Riemann problem. The top and the bottom boundary conditions are periodic, and the right and left are transmissive boundary conditions. A typical grid resolution of 20 $l_\mathrm {1/2}$ is used, and the complete simulation domain grid is 4000 $\times$ 2000. The detonation is initiated using a high-pressure zone, and cellular instability is promoted by slightly curving the interface. To reduce the simulation run-time, once the detonation front reaches the end (right boundary) of the computational domain, the detonation structure is patched back at the left boundary, allowing the detonation to propagate continuously to the right. A converged resulting cellular pattern was depicted after the simulation run long enough for the instability to manifest (t > 500).

3 Analysis methodology

3.1 Proper orthogonal decomposition (POD) analysis

In this study, the focus will be on the pressure field, and each instantaneous flow field is defined as a snapshot. For a two-dimensional instantaneous flow field, each snapshot is represented by an x $\times$ y matrix, containing grid points in the x and y directions, respectively. For each grid point, a value of pressure is contained. Then, the pressure field for each snapshot is mapped into a single column vector U = (p), the size of which is M = x $\times$ y, matching the position vector x = (x, y). In numerical simulation, each snapshot represents the flow field in the corresponding time point. Now a matrix X is introduced to contain all data points in all instantaneous flow fields, where each column represents the column vector U, which contains all the pressure values in a snapshot, and each row represents pressure values in a specified spatial position at different time points. The size of the matrix X is M $\times$ N, where N is the total number of snapshots. The matrix X is as follows:

$$\begin{aligned} {{\textbf {X}}} = \begin{bmatrix} p_1^1&{} p_1^2 &{}\cdots &{}p_1^N\\ p_2^1&{} p_2^2 &{}\cdots &{}p_2^N\\ \vdots &{} \vdots &{}\ddots &{}\vdots \\ p_M^1&{} p_M^2 &{}\cdots &{}p_M^N \end{bmatrix}, \end{aligned}$$

(5)

$$\begin{aligned} {{\textbf {X}}} = \begin{bmatrix} {{\textbf {U}}}_1&{{\textbf {U}}}_2&\cdots&{{\textbf {U}}}_N \end{bmatrix}, \end{aligned}$$

(6)

where ${\textbf{U}}_{k}$ is a vector containing all pressure values at the time point k = 1,..., N. In order to describe the correlation between the instantaneous pressure fields, we compute the temporal correlation symmetric matrix C as follows:

$$\begin{aligned} {{\textbf {C}}} = {{\textbf {X}}}^{\rm{T}}{{\textbf {X}}}, \end{aligned}$$

(7)

where T denotes the transpose of matrix X, and the size of C is N $\times$ N. Now, the eigenvectors A and eigenvalues $\mathbf {\Lambda }$ of the correlation matrix C can be computed using the eigen decomposition:

$$\begin{aligned} {{\textbf {C}}}{{\textbf {A}}} = {{\textbf {A}}}\mathbf {\Lambda }, \end{aligned}$$

(8)

where A contains the eigenvectors in its columns (${\textbf{A}}_{k}$), while $\mathbf {\Lambda }$ is a diagonal matrix of the positive eigenvalues ($\lambda _{k}$). By sorting the eigenvalues $\lambda _{k}$ in descending order, the columns of A are arranged by the corresponding eigenvectors (${\textbf{A}}_{k}$) accordingly. Now the POD modes can be evaluated by projecting the flow matrix X on the eigenvectors A as follows:

$$\begin{aligned} \mathbf {\Phi } ={{\textbf {X}}}{{\textbf {A}}}\mathbf {\Lambda }^{-1/2}, \end{aligned}$$

(9)

where $\mathbf {\Phi }$ is the POD modes with a size of 2 M $\times$ N, and each column $\mathbf {\Phi }_{k}$ represents a $k{{\rm{th}}}$ POD mode of the decomposed flow X. And then, we can compute the temporal coefficients ${\textbf{B}}_{k}$ of each POD mode from:

$$\begin{aligned} {{\textbf {X}}}=\mathbf {\Phi }{\textbf{B}}, \end{aligned}$$

(10)

$$\begin{aligned} {\textbf{B}} = \mathbf {\Phi }^{\rm{T}}{{\textbf {X}}}, \end{aligned}$$

(11)

where each row ${\textbf{B}}_{k}$ represents the temporal coefficient of corresponding POD mode $\mathbf {\Phi }_{k}$. In this work, the POD was performed using the snapshot algorithm defined by Sirovich (1987), and then Sirovich and Kirby (1987).

From the decomposition, we can extract coherent flow features by inspecting the POD modes. The $1{{\rm{st}}}$ mode is generally very similar to the time-averaged flow while the subsequent modes capture dynamically relevant structures that contribute to the instantaneous flow features. Following the above procedure, POD analysis is performed on pressure fields from the numerical simulations representing the detonation wave structure. A total of 500 transient flow field snapshots around the cellular detonation frontal structure are considered. A window frame of 20 $\times$ 100 $l_{1/2}$ enclosing the flow field in the proximity of the detonation front is considered.

3.2 Global entropy

The Shannon’s or global entropy (Aubry 1991), introduced to POD, is used to: (1) characterize the energy based on the pressure distribution among the modes of the investigated flow and (2) indicate the compactness of the reduced-order model (ROM) size. Specially, the energy used in this paper refers to the contribution of each mode to the total variance or dynamics captured by the dataset. For instance, if POD decomposition is performed with the 1st eigenvalue only equals nonzero, in such case, the entropy H will be zero for this decomposition. This simply means that the first mode encapsulates all the energy of the investigated system. On the contrary, if a POD decomposition produces equal nonzero eigenvalues for all modes, one can say that the energy is equally distributed among all the modes and the global entropy H = 1. By reflecting on the complexity of flow structures, one can anticipate that higher activation energy will lead to more complex flow structures causing the energy to be distributed over a wider range of scales in space and time, and therefore, this will be reflected in the eigenvalues of the POD modes. The global entropy (H) is computed as follows:

$$\begin{aligned} H = - \frac{1}{\ln {N}}\sum _{j = 1}^{N}\frac{\lambda _j}{tr(\mathbf {\Lambda })}\ln {( \frac{\lambda _j}{tr(\mathbf {\Lambda })})}, \end{aligned}$$

(12)

where N is the number of snapshots, $\lambda _j$ is the eigenvalue corresponding to mode j, and $\mathbf {\Lambda }$ is the diagonal matrix of all eigenvalues. POD analysis also demonstrated that the entropy level could provide a quantitative measure of the flow complexity. The mean entropy is higher in the unstable flow group than in the stable flow group (Byrne et al. 2014; Kefayati and Poepping 2013).

3.3 Lagrangian descriptors (LD)

The methodology of LD represents a trajectory-based technique to diagnose the geometric flow structures and any distinct dynamical behavior that could govern reactivity and mixing. This methodology is acknowledged for its enhanced efficiency, circumventing the extensive computational demands typical of other geometric techniques, thereby facilitating a more streamlined visualization of LCS (Mendoza et al. 2010, 2014). In essence, a function is proposed as a global LD, evaluating the finite-time Euclidean arc length of Lagrangian trajectories originating from predetermined initial positions within the flow and the abrupt changes of these lengths in their vicinity to detect attracting and repelling LCS (Mendoza and Mancho 2010). Additionally, the scope of the LD technique has been expanded to encompass the finite-time integration of scalar attributes (either geometrical or physical) along these trajectories (Hadjighasem et al. 2017; Lopesino et al. 2015, 2017).

Starting with a time-dependent velocity field u(x,t), a set of uniformly spaced passive particles is uniformly seeded across a grid at a specified initial time $t_0$. Subsequently, the Lagrangian trajectories are traced by advecting the particles in time utilizing a fourth-order Runge–Kutta scheme. This scheme is complemented by a bicubic spatial interpolation of the velocity fields, a method that, as expounded by Mendoza et al. (2014), guarantees both the efficiency and precision in the computation of the trajectories.

For a specific Lagrangian trajectory that intersects a position $\rm{x}_0$ at time $t_0$, the Euclidean arc length of this trajectory over a designated time interval $\tau$ is utilized to determine the value of the Lagrangian descriptors through a function ${{\textbf {M}}}(\rm{x}_0,t_0,\tau )$ (Madrid and Mancho 2009). Following Darwish et al. (2021), the discrete form of ${{\textbf {M}}}$ (denoted hereafter as ${\textbf {DM}}$), where the Lagrangian trajectory is defined over 2N + 1 time steps, with $N \in {\mathbb {N}}$, is used (Lopesino et al. 2015). The Lagrangian descriptors for a trajectory i is completely represented by Eq. (13), by summing Eqs. (14) and (15), i.e.,

$$\begin{aligned} {\textbf {DM}}_{i}= {\textbf {DM}}_{i}^{F}+{\textbf {DM}}_{i}^{B} = \sum _{n=-N_B}^{N_F}{\sqrt{(x_{i}^{n+1} - x_{i}^{n})^2 + (y_{i}^{n+1} - y_{i}^{n})^2}} \end{aligned}$$

(13)

$$\begin{aligned} {\textbf {DM}}_{i}^{F} = \sum _{n=0}^{N_F}{\sqrt{(x_{i}^{n+1} - x_{i}^{n})^2 + (y_{i}^{n+1} - y_{i}^{n})^2}} \end{aligned}$$

(14)

$$\begin{aligned} {\textbf {DM}}_{i}^{B} = \sum _{n=-N_B}^{0}{\sqrt{(x_{i}^{n+1} - x_{i}^{n})^2 + (y_{i}^{n+1} - y_{i}^{n})^2}} \end{aligned}$$

(15)

Equation (14) represents the forward ${\textbf {DM}}$ (${\textbf {DM}}^F$) of the Lagrangian descriptors for a trajectory i by computing for the trajectory ending at $x_0$ and from $t_0$ to $t_0+\tau _F$, while Eq. (15) gives the backward ${\textbf {DM}}$ (${\textbf {DM}}^B$) evaluated for a trajectory i ending at $x_0$ and from $t_0 - \tau _B$ to $t_0$. If $\Delta {t}$ represents the time step between the investigated velocity fields, the time interval can be defined as $\tau = N\Delta {t}$.

As the attracting and repelling LCS partition the fluid into regions with different dynamics, these can thus be captured by finding locations with sharp gradients in the ${\textbf {DM}}$ contours. In other words, in the vicinity of LCS (i.e., separating flow regions with different dynamics), the trajectory coinciding with these structures will witness an abrupt change in its ${\textbf {DM}}$ value relative to other nearby trajectories. The locations of the sharp color gradient are referred to as singular features of the Lagrangian descriptors and are aligned with the attracting LCS (in ${\textbf {DM}}^B$). To improve the accuracy of detecting the singular features of the ${\textbf {DM}}$ map, a Sobel filter can be used, which serves to identify the edges at locations where the gradient of ${\textbf {DM}}$ is maximum (García-Garrido 2020). The detected edges are stored in a new two-dimensional field called ${\textbf {EDM}}$ “indicating the edge of the ${\textbf {DM}}$ field” (Darwish et al. 2021).

4 Results and discussion

Fig. 2

Pressure flow fields showing the cellular detonation structure for the four different activation energies $E_{{\rm{a}}}$: a 5; b 10; c 20; and d 25

4.1 CFD raw data

Sample pressure flow fields at different time instants after a long-term evolution of the detonation wave front from the initiation transient for the three different activation energies $E_{{\rm{a}}}$ cases are shown in Fig. 2. Cellular detonation waves were depicted with the appearance of triple shock points (i.e., the point of interaction of the incident, Mach, and transverse waves). In cases with lower activation energies $E_{{\rm{a}}}$ = 5 and 10, the cellular detonation is relatively stable with regular frontal structure. The transverse waves are also weak and move essentially in a regular periodic fashion across the front. As $E_{{\rm{a}}}$ increases, much more irregular wave behavior can be seen. The transverse waves are stronger with localized explosion-like features within the detonation structure and intermittent generation of triple points along the front. Corresponding numerical smoked foils showing the time-integrated maximum pressure contour are given in Fig. 3. Equivalently, for low activation energy cases, the cellular detonation structure is moderately stable, and the cellular pattern remains very regular. In contrast, as the activation energy increases, the cellular patterns become chaotic showing various waves interacting with each other. The instabilities associated with high reaction sensitivities lead to unstable detonation behavior with highly irregular cells. The unstable cellular detonation dynamics with increasing $E_{{\rm{a}}}$ have been well-observed and reported in the literature, e.g., Gamezo et al. (1999).

Fig. 3

Numerical soot foils for the four different activation energies $E_{{\rm{a}}}$: a 5; b 10; c 20; and d 25

4.2 POD modes and reconstruction

Using the raw pressure field data from the computations, POD analysis is performed to deduce the spatial mode structures and their energy content. It is worth noting that in general, for fluid dynamics and turbulence study, POD is usually applied to velocity data. For detonation research, the transverse waves and cellular dynamics are more apparent from pressure data and, hence, used in this study. Figure 4 shows the first six POD modes for the stable detonation case with $E_{{\rm{a}}}$ = 5. In the POD analysis, each mode indicates some feature of the flow field. Modes are also ranked based on the energy contribution to the total flow. For instance, mode 1 represents the most energetic spatially orthogonal mode in the propagating detonation. From the spatial distribution, its pattern is close to the average state of the time-transient flow field, having a large contribution of 42.4% to the total eigenvalue sum. The mode 1 spatial distribution does not show many transverse features, and thus, mode 1 resembles approximately the average steady-state 1-D ZND detonation wave structure where the dynamics are dominated in the longitudinal direction. Figure 5a compares the corresponding steady ZND pressure profile and the POD mode 1 result along the middle, as well as the ensemble average pressure profile from the same dataset. The comparison shows a good agreement implying that for the highly stable case with low activation energy $E_{{\rm{a}}}$ = 5, the detonation structure, on average, remains piece-wise laminar and ZND profile-like. Inner features of the flow field are represented by higher POD modes. The cellular nature of the frontal surface begins to appear at mode 2. Predominantly, modes 2–4 represent the pressure fluctuations at the detonation front along the direction of the transverse waves. While modes 2–4 depict the larger wave structure that corresponds to the development of the cellular structure such as the periodic variations between the Mach stem and the incident shock, higher modes 5 and 6 provide more small-scale variations that occur at the front layer of the detonation front. These results depict the dominance of low-frequency modes, from the energy point-of-view, on the overall dynamics of the cellular detonation propagation.

Fig. 4

The first six POD modes of the cellular detonation with $E_{{\rm{a}}}$ = 5

Fig. 5

Comparison between the ideal ZND pressure profile with the POD mode 1 result along the middle domain and the ensemble average for a $E_{{\rm{a}}}$ = 5 and b $E_{{\rm{a}}}$ = 10

As $E_{{\rm{a}}}$ increases, a higher degree of cellular instabilities emerges within the detonation front. The POD spatial modes for $E_{{\rm{a}}}$ = 10 are plotted in Fig. 6. The mode 1 energy fraction reduced to 30.4%, i.e., the transverse features now contribute more to the flow, and the POD results show a clear development of cell-like structure. The mode 1 result deviates slightly from the ZND profile, see Fig. 5b. Globally, the POD mode 1 (and the averaged profile) from the CFD results follow well the ZND solution. For the weakly unstable detonation, one can notice for the average structure a slight extension near the tail of the profile. Due to an increasing front oscillation as $E_{{\rm{a}}}$ increases, the averaging result smears out the front shock. Mode 2 and mode 3 again depict the pressure fluctuations across the transverse wave direction at the downstream flow, their representing area similar to that modal decomposition of $E_{{\rm{a}}}$ = 5. However, higher POD Modes, i.e., modes 4–6 now show dominant spatial features immediately behind the front, see Fig. 6. Nevertheless, for $E_{{\rm{a}}}$ = 10, the spatial POD modes distribution can still be seen to be very regular, consistent with the raw data and smoked foil in Figs. 2 and 3. Similarly, low-frequency modes or larger structures are first emerged, followed by smaller-scaled, less energetic modes superimposed on those.

Fig. 6

The first six POD modes of the cellular detonation with $E_{{\rm{a}}}$ = 10

Figures 7 and 8 depict the POD results for the unstable cases $E_{{\rm{a}}}$ = 20 and 25, respectively. In these unstable cases, the energy content of the average flow field, i.e., mode 1, represents only 17.2% and 15.7%. As shown in Fig. 9, the difference between the averaging results and the ZND solution also becomes apparent. Not only does the smearing become more pronounced due to the increasing level of fluctuations at the shock front, which appears to destroy or suppress the main features of the detonation structure, but it is also due to these pressure fluctuations that the hydrodynamic thickness of the mean structure exceeds the ZND reaction zone length (Radulescu et al. 2007). For both cases, modes 1 and 2 show the average structure with a much larger thickness. The hydrodynamic thickness, which could be obtained easily from POD, in fact represents a useful characteristic length scale for assessing the degree of regularity of the detonation structure and also the scaling of data (Reynaud et al. 2020). Furthermore, the distinct features of the pressure peaks and troughs from the triple shock configuration become clear. The different shock-flame complexes composed of leading shock and transverse waves behind the front are revealed. Consistently from these results, the higher ranked modes (with higher energy fraction) appear to be dominant by large-scale features (from the emerging or decaying of large detonation cells). Weaker and smaller features closer to the detonation front begin to emerge at higher modes, corresponding to the presence of small cells. Some coherent structures from the lower spatial POD modes distributions can still be seen for the case of $E_{{\rm{a}}}$ = 20. However, as the degree of instability increases for increasing $E_{{\rm{a}}}$, the spatial regularity (or periodicity) of POD modes disappear. Overall, the detonation wave has a less orderly structure. Different combinations of all modes thus exhibit the complex dynamic process of the unstable cellular structure.

Fig. 7

The first twelve POD modes of the cellular detonation with $E_{{\rm{a}}}$ = 20

Fig. 8

The first twelve POD modes of the cellular detonation with $E_{{\rm{a}}}$ = 25

Performing POD on full spatial information from the original simulation data provides a prevailing method for isolating salient characteristic features and dominant modes, thus allowing the generation of low-dimensional models of complex flow systems. It provides a crucial tool for identifying the smallest possible set of basis functions that can be utilized to reconstruct each snapshot of the complete CFD solutions. The set of basis functions forms a series of POD modes, each carrying a percentage of the flow energy. To decide how many POD modes for the low-order model reconstruction of the flow field, Fig. 10 shows the cumulative energy content as a function of POD mode numbers for all four activation energy cases. It is clear from these plots that for higher activation energies, the number of modes needs to represent the majority of the total energy increases. For higher activation energy, the energy representation of the highest mode, mode 1 decreased due to the higher instability generated for higher activation energy. Hence, the spatially orthogonal modes, or patterns required to represent the flow, are in higher activation energy because of the irregular structure and a more complicated reaction zone behind the front.

Fig. 9

Comparison between the ideal ZND pressure profile with the POD mode 1 result along the middle domain and the ensemble average for a $E_{{\rm{a}}}$ = 20 and b $E_{{\rm{a}}}$ = 25

Fig. 10

a Accumulated fraction of total energy as a function of the number of modes used to reconstruct the original detonation flow field and b double-logarithmic plot of POD (N = 500) fractional energy spectrum as a function of the mode number

Fig. 11

Comparison between a full CFD simulation pressure field snapshot of the detonation frontal structure with the reduced models with different POD modes retained for $E_{{\rm{a}}}$ = 5

Fig. 12

Comparison between a full CFD simulation pressure field snapshot of the detonation frontal structure with the reduced models with different POD modes retained for $E_{{\rm{a}}}$ = 10

Fig. 13

Comparison between a full CFD simulation pressure field snapshot of the detonation frontal structure with the reduced models with different POD modes retained for a $E_{{\rm{a}}}$ = 20 and b $E_{{\rm{a}}}$ = 25

Figures 11, 12, and  13 show the full CFD solutions and the reduced-order solutions with different retained POD modes of the pressure field for the detonation waves with each activation energy $E_{{\rm{a}}}$. The comparison demonstrates well the feasibility and accuracy of the POD reduced-order model. Certainly, the flow field can be better resolved with increasing retained modes of reconstruction, especially for cases with higher activation energies of which the detonation dynamics are more involved with an increasingly larger number of unstable modes. Nevertheless, 300 modes retained, which capture more than 80% of the total energy, can be shown to recover accurately the leading frontal unstable surface and main downstream flow features as compared to the full CFD results. The percentage of modes required to reconstruct the flow field while capturing a defined threshold (TH) (80%) of the total energy is defined as follows:

$$\begin{aligned} \text {TH}[80\%] = \frac{\sum _{j=1}^{r}\lambda _{j}}{\sum _{j=1}^{N}\lambda _{j}} \end{aligned}$$

(16)

Table 1 Global entropy and required percentage of modes for 80% energy at different activation energy $E_{{\rm{a}}}$ out of 500 total snapshots

Table 1 gives the values of the global entropy H and the corresponding percentage of modes required to reconstruct 80% of the energy of the detonation flow field TH[80%] resulting from 500 snapshots at different activation energy $E_{{\rm{a}}}$. The relation between the global entropy H and the corresponding percentage of modes required to reconstruct 80% of the energy of the detonation flow field is given in Fig. 14. With the increase in activation energy $E_{{\rm{a}}}$ and the instability of the cellular detonation structure, the global entropy and the corresponding percentage of modes required to reconstruct 80% of the energy monotonously increase. With this agreement, the global entropy can be suggested as an alternate parameter, which is related to the complexity or mode spectrum characteristics of the flow field, to quantify the degree of regularity of the detonation structure. Table 2 gives the influence of the number of snapshots. With the increase in the total number of input snapshots, the global entropy increases, and TH[80%] decreases monotonously, approximately converging to a fixed value. Figure 15a gives an energy spectrum of how much energy fraction a single snapshot contributes at the activation energy of $E_{{\rm{a}}}$ = 20. Where n is the numbering of mode, and N is the total number of snapshots. Figure 15b provides a double-logarithmic plot of the fractional energy spectrum and the numbering of modes. As we can see from Fig. 15b, there is an approximately linear relation between log(n) and log(E) after the first several snapshots as specified in the plot, indicating that with the increase in N, the global entropy will continue increasing but approximately converges to a certain value as shown in Table 2.

Fig. 14

The global entropy H and the corresponding percentage of modes required to reconstruct 80% of the energy of the detonation flow field for different activation energy $E_{{\rm{a}}}$

Table 2 Global entropy and required percentage of modes for 80% energy at different number of total snapshots at $E_{{\rm{a}}}$ = 20

Fig. 15

Energy spectrum obtained by different numbers of total snapshots N at $E_{{\rm{a}}}$ = 20: a the fractional energy spectrum of each mode and b the linear relation in the double-logarithmic plot of the fractional energy spectrum and the numbering of modes

4.3 Lagrangian descriptors of cellular detonation

Fig. 16

Lagrangian descriptors of the cellular detonation flow field for different activation energy $E_{{\rm{a}}}$

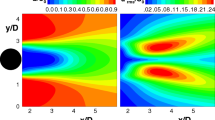
To systematically deduce any hidden LCS within the cellular detonation flow, Fig. 16 shows backward DM and EDM fields of the LD results of the cellular detonation flow field for different activation energy $E_{{\rm{a}}}$. The present results elucidate similar results where Lagrangian flow fields are solely obtained by introducing and storing the position of a passive scalar (Sow et al. 2021; Watanabe et al. 2023). In all cases, the vortical coherent structures can be seen. The clustering phenomena observed within the flow fields, as shown in the figures, serve as indicators of localized high-energy interactions and are critical to understanding the dynamics of detonation. These clusters represent areas where particles or fluid elements have been drawn together during the flow’s evolution, suggesting regions of converging dynamics within the broader flow field.

In the context of lower activation energies $E_{{\rm{a}}}$ = 5 and 10, discrete vortical structures not only persist but also advect entirely downstream. The clusters are relatively sparse and well-organized, indicating a flow field where the dynamics lead to regular, periodic patterns. These patterns can be associated with stable wave structures within the detonation, where the energy is sufficient to sustain the propagation of the detonation front but not to disrupt its orderly progression. Such clustering lends itself to predictability in the flow’s behavior over time. As the activation energy is increased to moderate levels $E_{{\rm{a}}}$ = 20, large-scale vortical structures still form but the clustering of particles occurs locally along the front, exhibiting a greater degree of complexity. For $E_{{\rm{a}}}$ above 25, the flow field becomes chaotic and dominated by convection mixing everywhere downstream.

5 Concluding remarks

Data analysis techniques such as modal decomposition are becoming standard post-processing methods in fluid dynamics to interpret either experimentally or numerical data in terms of the flow structures and characterize them spatially and temporally. These techniques reduce a large amount of flow data into a set of spatial modes for building reduced models aimed at better understanding complex flow evolution. In this study, we show using the high-resolution, two-dimensional, numerical simulation results obtained using the reactive Euler’s equations with one-step Arrhenius kinetics as an example, what POD can give to examine compressible flow instabilities and understand the underlying dominant characteristics of the dynamic of cellular detonation structures. CFD data computed using different activation energy $E_{{\rm{a}}}$ are analyzed. The results of such modal decomposition analysis help identify events that contribute the most to the energy of the flow and any dominant or coherent features, ultimately determining the hydrodynamic thickness of unstable cellular detonation based on the energy mode distribution. It provides an efficient way to isolate the mode spectrum characteristics. In the POD analysis, mode 1 corresponds to the mean velocity field in the detonation structure in close agreement with the ensemble average. The higher modal structures, emerging first from the larger oscillating modes (or cells), describe the vorticity component and different degrees of hydrodynamic instabilities embedded in the two-dimensional cellular detonation wave. The use of Shannon entropy provides also a more formal quantitative method to describe the complexity or irregularity of the detonation flow field. At last, the POD analysis provides a means to develop reduced flow models for detonation structures by possibly removing “redundant” information which does not contribute much energy to the flow reducing the complexity of the problem and its interpretation. Complemented with other modal decomposition methods such as dynamic mode decomposition (DMD) (Massa et al. 2012; Pavalavanni et al. 2023), it provides new insights on how detonation cells are formed and identifies dominant unstable modes governing the detonation propagation dynamics and structure.

Finally, this work introduces the applicability of the LD approach, computationally viable, to extract coherent structures in detonation flow. Applying this approach to construct scalar functions from particle trajectories, which evolve while being advected by fluid flows, could introduce innovative concepts to systematically detect critical combustion features, e.g., local ignition and explosion, within the detonation, and also for modeling the detonation structure as a dynamic system. The success of using such Lagrangian trajectory-based analysis could lead to more advanced topological studies such as braids theory (Allshouse and Peacock 2015) to describe the flow complexity, energy exchange, and mixing, as well as graph theory and network representation to reflect flow regions with strong coherence and connection forming the fundamental structure (Padberg-Gehle and Schneide 2017; Monnier et al. 2023). The LD could also be extended to include the finite-time integration of scalar properties along the trajectories and easily be expended to 3D flows (Abdallah et al. 2024).

In conclusion, the data analysis methods revisited in this paper open up new research direction to interpret and quantify the unstable detonation structure, provide further additional visualization tools to identify the topology or region of intense chemical activities, and isolate mode features which contribute to the dynamics of cellular detonation. This approach could be further extended by coupling it with machine learning in the future works to develop more thorough models to predict the detonation dynamics and scaling of data, e.g., Monnier et al. (2022) and Bakalis et al. (2023).