Statement of Novelty

Mathematical modeling can provide useful suggestions for the analysis, design and operations of fermentative processes. To the best of our knowledge, there is no studies using logistic models to predict substrate (cellulose) degradation as function of the time ferment, enzymatic activity (cellulase) as function of the substrate degradation and the cell growth as function of concentration dissolved oxygen in a stirred-tank bioreactor, containing Aspergillus niger and solids (sugarcane bagasse) in suspension.

Introduction

A large part of fuel ethanol produced in the world is sourced from starchy biomass or sucrose, especially cane juice [1]. Recently new technologies have been developed about alcohol's manufacture using non-food biomass, as sugar cane bagasse, rice straw, water hyacinth, and another [2, 3]. The use of non-food biomass reduces cost of “bio-ethanol” and, therefore, propels the large-scale production.

Theses lignocellulosic sources are mainly made up of cellulose, hemicellulose and lignin. The cellulose is the major component and can be enzymatically hydrolyzed to fermentable monomeric sugars [4, 5]. Cellulase enzyme secreted by filamentous fungus Trichoderma and Aspergillus have been showed great potential to hydrolyze the agricultural residues for lignocellulosic biofuel production. Theses fungus are highly specific and of high-cost commercial, but they have been presented high cellular activity [3, 6, 7].

The cultivation methods applied to produce enzymes can be conducted in either a liquid or solid medium. Solid-state fermentation is particularly advantageous for the growth of filamentous fungi, because it simulates the natural habitat of these microorganisms, resulting in higher enzyme productivity [8]. On the other hand, the application of solid-state fermentation in industrial processes has been delayed due to the difficulties involved in monitoring and controlling the various process parameters [9, 10]. For this reason, most large-scale industrial enzyme production processes currently use submerged fermentation [11, 12].

Several enzyme inducers have been studied and used to improve the synthesis of enzymes. Among them, the use of the substrates themselves as inducers stands out. The use of lignocellulosic raw materials as a source of nutrients, mainly carbon, for microorganisms in different types of fermentation processes reduce the costs of enzymatic production [13]. On the other hand, the use of lignocellulosic biomass provides an additional difficulty that is the cells quantification.

The quantification of cell biomass in fermentation media containing solids is complicated due to the difficulty involved in separating the microorganisms from the substrate and, often, require an indirect quantification methodology [14]. Different techniques for estimation of cell concentrations in the presence of suspended solids have been showed in biotechnological area [15].

Measurement of either oxygen consumed or carbon dioxide evolved are common methodologies used for estimating growth for cultivations carried out in bioreactors [16,17,18,19,20]. The use mass balance equations and kinetic expressions too have been employed [21,22,23,24]. Although theoretical models allow extrapolations most trusted, they are more complex, expensive and more time needed. These disadvantages favor the use of empirical models.

Mathematical models can explain quantitatively the behavior of a system and provide useful suggestions for the analysis, design and operation of a fermenter [25]. The present study focused in the use of non-linear empirical models to quantification of substrate degradation, enzyme activity, oxygen degradation, and cell growth in a submerged fermentation medium containing sugarcane bagasse and Aspergillus niger.

Materials and Methods

Carbon Source

Sugarcane bagasse (SB) was employed as main carbon source. The sugarcane bagasse was obtained from the Destilaria Itaúnas S/A, Espírito Santo, Brazil. The SB was dried in drying oven (EDUTEC) at 55 °C until constant. Then, the material was milled in a knife mill SL 32 (SOLAB) and sieved using the mesh with an upper opening of 0.500 mm and a lower opening of 0.355 mm.

Microorganisms

The filamentous fungus Aspergillus niger INCQS 40,018 was used in this study. The culture was obtained from the Oswaldo Cruz Foundation, Rio de Janeiro, Brazil. It was grown on potato dextrose agar (4.2% w/v) at 28 °C for 5 days and then used for inoculum preparation. Spores were harvested adding 10 mL of Tween-80 (0.1% v/v).

Operation Conditions in Bioreactor

Batch type of fermentation process was employed using the bioreactor 1.5 L TEC-BIO-7.5 V (TECNAL). The concentrations of 5, 10, 13, 15 and 20 g L−1 of pretreated sugarcane bagasse in 1.0 L of saline solution [26] was added in the bioreactor. The pH value was maintained constant (pH 5.0) and the bioreactor was autoclaved at 121 °C for 40 min. Then, 106 spore mL−1 were transferred into the bioreactor. Stirring was carried out using with 250 rpm Rushton type turbine and was maintained constant. The temperature (30 °C) and aeration rate (1 L min−1) too were maintained constants during fermentation’s time. The samples were collected at 0, 10, 24, 48 and 72 h for analysis of cellulose concentration, cells and enzymatic activity.

Analytical Procedures

Enzymatic activity of cellulases (CMCase) was determined using the methodology described by Ghose [27]. The quantification of cellulose concentration, total dry mass and cells were determined using the methodology described by Gelain et al. [24]. The analyses were carried out in quadruplicate. The data given here are the average of the measurements. The oxygen dissolved during the microbial fermentation was obtained real-time detected by the reactor’s sensor (METTLER TOLEDO).

Dimensionless Variables

Substrate degradation, dissolvide oxygen, enzyme activity and cells growth are variables that have different orders of magnitude. Therefore, comparisons between these data would be invalid because the measurement depends on the scale of the numbers used. As a general modeling procedure, it is convenient to redefine the problem variables in order to make them dimensionless, thus avoiding interpretation problems arising from the use of different units and allowing to group the parameters into a smaller set of parametric groups [28]. In this study, the standardization of variables was calculated as the difference in the trait values (substrate, oxygen, enzyme activity and cells growth) divided by the overall range for the trait, as follows:

$$ {z}_{\text{i};\text{S},\text{O}\text{D}}^{\text{e}}=1-\frac{{\text{y}}_{\text{i}}^{\text{e}}-{\text{y}}_{0}^{\text{e}}}{{\text{y}}_{\text{m}\text{a}\text{x}}^{\text{e}}-{\text{y}}_{\text{m}\text{i}\text{n}}^{\text{e}}} \left(1\right)$$
(1)
$$ z_{{{\text{i}};{\text{X}},{\text{E}}}}^{{\text{e}}} = \frac{{{\text{y}}_{0}^{{\text{e}}} - {\text{y}}_{{\text{i}}}^{{\text{e}}} }}{{{\text{y}}_{{{\text{min}}}}^{{\text{e}}} - {\text{y}}_{{{\text{max}}}}^{{\text{e}}} }} $$
(2)

where \({z}_{\mathrm{i}}^{\mathrm{e}}\) is the standardized variable; \({\mathrm{y}}_{\mathrm{i}}^{\mathrm{e}}\) and \({\mathrm{y}}_{0}^{\mathrm{e}}\) are the original values of variables at time ferment and \(\mathrm{t}\) time ferment initial, respectively; \({\mathrm{y}}_{\mathrm{max}}^{\mathrm{e}}\) and \({\mathrm{y}}_{\mathrm{min}}^{\mathrm{e}}\) are the maximal and minimum values of original variables, respectively. \(\mathrm{S}\), \(\mathrm{OD}\), \(\mathrm{X}\) and \(\mathrm{E}\) indices denote substrate degradation, oxygen dissolved, cells growth and enzyme activity, respectively. This method converts the original values to a new values on a scale of 0 to 1. This enables to analyze functional diversity at small and large scales. Furthermore, the use of standardized variables not requires the parameters's dimensional analysis.

Models for Substrate Degradation and Enzyme Activity

After inoculation, the culture shows a lag phase to adapt on the new conditions of reactor. Then, occurs an exponential growth suppose that microorganisms’ life maintenance need is covered by uptake of substrate [29]. The enzyme activity is susceptible to substrate inhibition problems, changes of temperature or pH [9, 10, 30]. The lack of substrate in fermentation medium results a decrease of biomass. However, the low enzyme production at high substrate concentrations may be attributed to production of toxic products which adversely affect the growth of the cells. It is reasonable to assume that consume of substrate and production of enzymes can be approximation by a sigmoidal function.

Sigmoidal function ("S" shaped curve) exhibits a small progression in initial stages, that accelerates and approaches a climax over time. These functions have horizontal asymptotes (t →  ± ∞), they don't have extreme points (relative maximum and minimum), but they have an inflection point that corresponds to the maximum rate of variation of the function [31]. The logistic model is an example of sigmoidal function studied in microorganism's growth [25, 32,33,34,35]. In this work, the evolution of substrate degradation (\(\mathrm{S}\)) was followed by the logistic equation:

$$ {\text{S}} = \frac{{{\text{S}}_{{\text{m}}} }}{{1 + {\text{exp}}\left[ { - {\upmu }\left( {{\text{t}} - {\text{C}}} \right)} \right]}}{ } $$
(3)

where \({\mathrm{S}}_{\mathrm{m}}\) is the minimal substrate degradation level (or upper asymptote of the sigmoid curve); \(t\) is the time ferment; \(\mathrm{C}\) is the time ferment at the midpoint of the sigmoid curve; \(\upmu \) is the maximum substrate degradation rate (or slope of the sigmoid curve). In the standardized form, \({\mathrm{S}}_{\mathrm{m}}\) values are established at the beginning of fermentation (\({\mathrm{S}}_{\mathrm{m}}=1\)). Thus, to determine substrate degradation using the Eq. (3) it is necessary to know the parameters \(\mathrm{C}\) and \(\upmu \).

During microorganism's growth to occurs consume of substrate and production of enzymes. Therefore, the substrate degradation and enzyme activity have an inversely relationship. In this work, the evolution of enzyme activity (\(\mathrm{E}\)) was followed by the logistic equation:

$$ {\text{E}} = \frac{{{\text{E}}_{{\text{m}}} }}{{1 + {\text{exp}}\left[ { - {\upmu }_{1} \left( {{\text{S}} - {\text{C}}_{1} } \right)} \right]}} $$
(4)

where \({\mathrm{E}}_{\mathrm{m}}\) is the minimal enzyme activity level (or upper asymptote of the sigmoid curve); \(\mathrm{S}\) is the evolution of substrate degradation; \({\mathrm{C}}_{1}\) is the time ferment at the midpoint of the sigmoid curve; \({\upmu }_{1}\) is the maximum enzyme activity rate (or slope of the sigmoid curve). In the standardized form, a good parameters estimation should give \({\mathrm{E}}_{\mathrm{m}}\) value nearby of 1.

Models for Cells Growth and Oxygen Degradation

During cells growth, microorganisms degrade the substrate to use as an energy source. In this respiration activity process occurs oxygen degradation and carbon dioxide production. There is a strong in oxygen degradation the beginning fermentation. After this period, the amount of oxygen increases in the bioreactor [16,17,18,19, 24]. Thus, it is reasonable to assume that sigmoidal form be able of fitting relationship between the cell growth (\(\mathrm{X}\)) and oxygen dissolved (\(\mathrm{OD}\)) as followed:

$$ \text{X}=\frac{1}{1+\text{e}\text{x}\text{p}\left[-{{\upmu }}_{2}\left(\text{O}\text{D}-{\text{C}}_{2}\right)\right]} \left(5\right)$$
(5)

where \({\mathrm{C}}_{2}\) is the time ferment at the midpoint of the sigmoid curve; \({\upmu }_{2}\) is the cell maturity rate (or upper asymptote of the sigmoid curve); \(\mathrm{OD}\) is the oxygen dissolved during the microbial fermentation.

Parameter Estimation

The estimation of kinetic parameters can be performed using non-linear least square fitting [36]. The least-squares assumes that the dependent variables can be calculated as function of the independent variables and of the model parameters. The least-squares function is usually inappropriate for multi-response models [37] and can be calculated as follows:

$$ F\left( {\uptheta } \right) = \mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{NE}}}} \left[ {{\text{y}}_{{\text{i}}}^{{\text{e}}} - {\text{y}}_{{\text{i}}}^{{\text{m}}} \left( {{\text{x}}_{{\text{i}}} ,{\uptheta }} \right)} \right]^{2} $$
(6)

where \(F\left(\uptheta \right)\) is the objective function to be minimized with respect to the parameter vector \(\uptheta \), \({\mathrm{y}}_{\mathrm{i}}^{\mathrm{e}}\) and \({\mathrm{y}}_{\mathrm{i}}^{\mathrm{m}}\) are the vector of experimental observations and model predictions of the dependent variables at experimental condition \(\mathrm{i}\) and \(\mathrm{NE}\) is the number of observations.

Due to existence of experimental errors, the results obtained after the parameters estimation are also uncertain. Thus, information concerning the sensitivity of the objective function to changes in a parameter is very important. That is, how much the objective function value changes when a parameter changes [37]. For some problems, a sensitivity analysis can be carried out analytically, but in others the sensitivity coefficients must be determined numerically [38]. This work, the relative sensitivity analysis consisted changed each parameter separately (one at a time) inside 95% confidence bounds (inferior and upper limits) and compute the values of models.

Statistical Analysis

The coefficient of determination (\({R}^{2}\)), reduced chi-square (\({\chi }^{2}\)), and standard residual deviation (\(SRD\)) were used in this study to evaluate the goodness of fit. Theses statistical values can be calculated as follows:

$$ R^{2} = 1 - \left[ {{{\sum\limits_{{{\text{i}} = 1}}^{{{\text{NE}}}} {\left( {{\text{y}}_{{\text{i}}}^{{\text{e}}} - {\text{y}}_{{\text{i}}}^{{\text{m}}} } \right)^{2} } } \mathord{\left/ {\vphantom {{\sum\limits_{{{\text{i}} = 1}}^{{{\text{NE}}}} {\left( {{\text{y}}_{{\text{i}}}^{{\text{e}}} - {\text{y}}_{{\text{i}}}^{{\text{m}}} } \right)^{2} } } {\sum\limits_{{{\text{i}} = 1}}^{{{\text{NE}}}} {\left( {{\text{y}}_{{\text{i}}}^{{\text{m}}} - \widehat{{\text{y}}}} \right)^{2} } }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{{{\text{i}} = 1}}^{{{\text{NE}}}} {\left( {{\text{y}}_{{\text{i}}}^{{\text{m}}} - \widehat{{\text{y}}}} \right)^{2} } }}} \right] $$
(7)
$$ \chi^{2} = \mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{NE}}}} \left( {{\text{y}}_{{\text{i}}}^{{\text{e}}} - {\text{y}}_{{\text{i}}}^{{\text{m}}} } \right)^{2} /\left( {{\text{NE}} - {\text{NP}}} \right) $$
(8)
$$ SRD = \frac{100}{{{\hat{\text{y}}}}} \cdot \sqrt {\mathop \sum \limits_{{{\text{i}} = 1}}^{{{\text{NE}}}} \left( {{\text{y}}_{{\text{i}}}^{{\text{m}}} - {\text{y}}_{{\text{i}}}^{{\text{e}}} } \right)^{2} } /{\text{NE }} $$
(9)

where NE is the number of observations, NP is the number of constants in model, \({\hat{\text{y}}}\) is the value about \({\text{y}}_{{\text{i}}}^{{\text{m}}}\) mean, \({\text{y}}_{{\text{i}}}^{{\text{e}}}\) and \({\text{y}}_{{\text{i}}}^{{\text{m}}}\) are the experimental and predicted moisture ratios, respectively. Higher values of \(R^{2}\) and lower values of \(\chi^{2}\) indicate better goodness of fit [39]. According to Atala et al. [40], values of \(SRD\) lower than 10% are acceptable for biotechnological process.

Results and Discussion

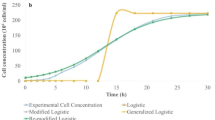
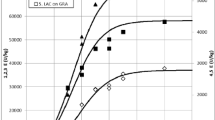
Tables 1, 2, 3 and 4 show the substrate degradation, enzyme activity, oxygen dissolved, and cells growth (all in dimensionless form) during the fermentation time. Sugarcane bagasse proved to be efficient as a carbon source for cellulases production with the fungus Aspergillus niger in stirred-tank bioreactor, requiring no other carbon sources. There seems to be some degree of inverse dependence between substrate degradation and enzyme activity and between dissolved oxygen and cells growth. In other words, fluctuations in substrate degradation (or dissolved oxygen) above average are accompanied by fluctuations in enzyme activity (or cell growth) below average, and vice versa. This degree of inverse dependence between variables can be seen in Figs. 1 and 2, where substrate degradation (and dissolved oxygen) is the independent variable and enzyme activity (and cell growth) is the dependent variable.

Table 1 Substrate degradation in dimensionless form
Full size table
Table 2 Enzyme activity in dimensionless form
Full size table
Table 3 Oxygen consumption in dimensionless form
Full size table
Table 4 Cells growth in dimensionless form
Full size table
Fig. 1
figure 1

Linear relationship in the inverse form between substrate degradation and enzyme activity

Full size image
Fig. 2
figure 2

Linear relationship in the inverse form between oxygen dissolved versus cells growth

Full size image

The kinetics of the process with four initials substrate concentration (5, 10, 13 and 20 g L−1 SB) was used simultaneously for parameters estimation. Table 5 shows the values of estimated parameters, using non-linear least square fitting in software Matlab R2015a. The assay using an initial concentration of 15 g L−1 SB was used to evaluate the model’s prediction capacity. Table 6 shows the estimated parameters for 15 g L−1 SB with 95% confidence bounds.

Table 5 Estimated model parameters for the concentrations of 5, 10, 13 and 20 g L−1 SB
Full size table
Table 6 Estimated model parameters for the concentrations of 15 g L−1 SB
Full size table

The estimated parameters values (except for μ, μ1 and μ2) showed that the likelihood confidence regions are narrow and do not contain zero values, which could indicated that the parameters were well estimated. Sm and Em parameters are an estimate of the minimal substrate degradation level and of the minimal enzyme activity level, therefore, they represent the upper asymptote of the sigmoid curve. In the standardized form, a good estimation these parameters should give values nearby of 1. The datas of Tables 5 and 6 show this proximity.

Table 7 shows the forecast quality statistics for the experimental data of 15 g L−1, using Eqs. (3), (4) and (5) with the parameters shown in Table 6. The \(R^{2}\) values were high, while the \(\chi^{2}\) and SRD had low values. The statistical values indicated a very good concordance with the experimental data. Thus, all models could reasonably describe biological process. In this particular case, the good agreement between model predictions and available experimental data, shown in Figs. 3, 4 and 5, supports the use of these models (Tables 8 and 9).

Table 7 Model prediction quality statistics for substrate
Full size table
Table 8 Model prediction quality statistics for activity
Full size table
Table 9 Model prediction quality statistics for cells
Full size table
Fig. 3
figure 3

Substrate degradation versus time ferment

Full size image
Fig. 4
figure 4

Enzyme activity versus substrate degradation

Full size image
Fig. 5
figure 5

Experimental data and model predictions for cell growth

Full size image

C, C1 and C2 parameters are an inference about the inflection point of the sigmoid curves, therefore, they indicates the value of the independent variable for which the function's concavity change occurs. These values can be seen directly in Figs. 3, 4 and 5. The inflection point is a relevant information from the point of view of process control and optimization.

Conclusion

The use of the agricultural waste make the fermentative production of cellulase enzyme more feasible. In this study, the sugarcane bagasse proved to be efficient as a carbon source for the production of cellulases with Aspergillus niger, requiring no other carbon sources in the bioreactor. The models proposed in this work allowed to predict the substrate degradation, as function of the fermentation time, enzymatic activity, as function of the substrate degradation, and cell growth, as function of dissolved oxygen concentration in the stirred-tank bioreactor. Combination of the non-linear empirical logistic models and the relative sensitivity analysis allowed for proper analysis of parameter estimates without introduction of unnecessary simplifications that may lead to erroneous conclusions when nonlinear models are considered. The use of these models could be encouraged to investigate submerged fermentation's characteristics in new experimental due to its mathematical simplicity and utility. Besides that, they provide relevant information from the point of view of process control and optimization, allowing to infer about the inflection point, which characterizes the maximum rate of variation of the function.