1 Introduction

The term nanofluid describes a suspension of nanoparticles in a regular (base) fluid [1]. Several applications in heat transfer benefit from the use of nanofluids, including nuclear reactors, hybrid-powered engines, pharmaceutical processes and fuel cells. Nanofluids possess necessary fortune that make it essentially useful for a wide variety of applications, such as acoustic properties. Their thermal conductivity and convective heat transfer coefficient are greatly enhanced in comparison with the base fluid [2]. Consequently, it is not surprising that nanofluids have been the subject of considerable research efforts. Jeffrey fluid conveying nanoparticle over a three-dimensional surface subject to convective boundary condition is discussed by Shehzad et al. [3]. Kumar et al. [4] studied the rotational effects of ferro-nanofluids convection past a bi-directional moving sheet via Joule and dissipation heat. Lawal et al. [5] examined the unsteady Eyring–Powell nanofluid flow by determining the effects of variable viscosity and thermal conductivity. The response of variable properties, viscous dissipation, dissipative heat, heat generation and chemical reaction were explored. Akolade and Tijani [6] studied the Casson and Williamson nanofluid along a penetrable stretched Riga plate and enumerated the features of thermophysical properties of the magnetohydrodynamics flow. The effects of double stratification, self-heating and electrical MHD were presented by Daniel et al. [7]. Hatami et al. [8] modeled a Cu–water nanofluid flow around a rotating cylinder turbulator in an oscillating non-convergent medium. The study identified that Reynolds number rise contributes efficiently heat transfer mechanism. Other related studies include: Ramzan et al. [9], Ramzan and Bilal [10], Hayat et al. [11], Lin et al. [12], Ogunseye et al. [13], Alotaibi and Rafique [14] on fluid flow with various nanofluid models over linear/nonlinear stretching surface.

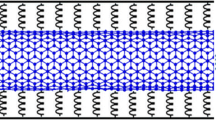
A carbon tube with a diameter commonly measured in nanometers is known as a carbon nanotube (CNT). The CNT can be modified or adjusted to increase the heat transfer of a fluid. An important change that may be made is to control the number of walls in each nanotube, series of it classifications were discussed (see Aqelet al. [15]). The nanostructure of these materials and the strength of their connections between carbon atoms make them to have an outstanding tensile strength, high electrical and thermal conductivity. They can also be chemically modified [15]. A wide range of technological applications benefit from these CNT features, including electronic devices, optics, composite materials and nanotechnology. The scientific/industrial importance of SWCNT and MWCNT has generated some research attention in fluid dynamics [16]. Ahmad et al. [16] probed the effect of a radiative SWCNT and MWCNT nanofluid flow along a rigid wedge with presence of magnetohydrodynamics (MHD). Hayat et al. [17] analyzed the importance of SWCNT and MWCNT in a mixed convective flow. They reported that the momentum boundary layer thickness increases with increasing magnetic field strength. Aladdin and Bachok [18] investigated the dual solutions of a hybrid nanofluid wrapped in SWCNT and MWCNT sheets using water as a base fluid. In their study, they found that while the first solution is preferable to the second, the hybrid nanofluid undergoes a reduction in heat transfer as the magnetic parameter increases. The MHD study of stagnation point flow of SWCNT and MWCNT over a stretching sheet with different shape effects was done by Shafiq et al. [19]. The behavior of the dual solution on flow and heat transfer using two different base (water and kerosene) fluids in a carbon nanotube was investigated by Norzawary et al. [20]. They found that the critical value for existence of a dual solution for \(f'(0) = \xi\) is when \(\xi = -0.5482\). Rezaee et al. [21] investigated the argon flow through elliptical carbon nanotube. The following research work will be of great interest to the reader for more study in this direction, see Xue [22] and Hayat [23].

Riga plate is an actuator constructed by arranging electrodes and magnets of equal sizes side by side. Putting the theory of the Riga surface into practice, Rafique et al. [24] analyzed the heat and mass transfer flow of a stratified micropolar nanofluid over a Riga plate. The study reported that the heat transfer on the surface decreases for the temperature stratification factor as mass transfer increases. Alotaibi and Rafique [25] probed the impact of micro-rotation on a nanofluid over a Riga plate. Their findings are that concentration distribution shows direct relation with thermophoretic impact. Additionally, increasing modified Hartmann numbers also increases energy and mass flux rates.

Reiner–Philippoff fluid investigation has been on researchers spotlight in recent time due to its highly nonlinear stress relation and its ability to behave both as a Newtonian and Non-Newtonian fluids in different regimes. Recently, the stability analysis of Reiner–Philippoff fluid flow subjected to radiation effect over a shrinking plate was presented by Waini et al. [26]. Tijani et al. [27] investigated the behavior of Reiner–Philippoff fluid flow using a stream function velocity that is not admissible to the similarity transformation technique. Their study reported that enhancing the radiation term, mass and thermal conductivity will lead to an increment in heat and mass transfer coefficient. Notable information in this direction can be found in the study of Yam et al. [28], Khan et al. [29], Ahmad et al. [30], Na [31] and Sajid et al. [32].

The spectral local linearization method pioneered by Motsa [39] is a numerical technique used to approximate solutions to nonlinear ordinary differential equations (ODEs) or systems of ODEs. This method combines elements of spectral methods and local linearization to achieve accurate and efficient solutions for linear/nonlinear dynamical systems. The spectral local linearization method offers several advantages. The method allows for the efficient representation of the solution using a small number of basis functions, resulting in reduced computational costs compared to some other numerical methods. SLLM can handle highly nonlinear systems with accuracy and stability, even when the nonlinearities are strong or the dynamical systems exhibiting chaotic behavior [5, 6, 13]. The spectral local linearization method has been shown to have a quadratic convergence [33].

The novelty of this research is that no other study has examined the Reiner–Philippoff hybrid nanofluid using SWCNT and MWCNT, at least not to the author’s knowledge. This current study aims at understanding the impacts of SWCNTs and MWCNTs nanoparticles on dissipative Reiner–Philippoff fluid with MHD effect and Darcy phenomenon through a two-dimensional stretched Riga plate subjected to the modified temperature gradient. The objectives of the study include: (i) the model of the 2D Reiner–Philippoff nanofluid over a Riga surface, (ii) transformation of the governing PDEs to systems of ODEs via an appropriate similarity variables, (iii) implementation of spectral local linearization method (SLLM) on the formulated problem, (iv) investigation of the behavior of the pertinent flow parameters via graphs and tables and (v) comparative analysis on the impact of SWCNT and MWCNT on the governing model.

2 Organization of the paper

Fig. 1
figure 1

Paper setup flowchart

Full size image

The paper setup is given in the following (see Fig. 1). Section 3 contains the model formulation analysis resulting in the dimensional governing flow equations, the thermophysical relation of the nanofluid and the similarity technique. The engineering quantities are presented in Sect. 4. In Sect. 5, we present the convergence analysis, numerical validation, and numerical solution via the spectral local linearization method (SLLM) implemented on a MATLAB R2015a. The importance of each emerging flow parameter is discussed in Sect. 6. Finally, the results and significance of the present study are elaborated in Sect. 7.

3 Model formulation analysis

3.1 Model governing assumptions

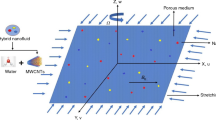
The two-dimensional flow with carbon nanotube over a magnetized sheet is the concern of this model. The flow equation in its generalized form is given as:

$$\begin{aligned}{} & {} \nabla \cdot \vec {q} = 0. \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \rho \big (\vec {q} \cdot \nabla \vec {q} \big ) = \nabla \cdot \uptau - \mu \dfrac{\vec {q}}{K}. \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \rho C_{p}\big (\vec {q} \cdot \nabla T \big ) = \kappa \nabla ^{2} T - \nabla q_{r} + \mu (\nabla \bar{q})^{2}. \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \big (\vec {q} \cdot \nabla C \big ) = D_{d} \nabla ^{2} C - \nabla q_{r} + D_{CT}\nabla ^{2} T. \end{aligned}$$
(4)

where \(\vec {q}\) is the fluid velocity vector.

Consider Reiner–Philippoff fluid exemplified by a nonlinear shear-stress deformation, which consists of shear-stress deformation of three-parameter model, namely pseudo-plastic, dilatant and Newtonian characteristic, well defined in Na [31] and expressed as

$$\begin{aligned} \dfrac{\partial u}{\partial y} = \dfrac{\uptau }{\mu _\infty + \dfrac{\mu _o - \mu _\infty }{1 + \big ( \frac{\uptau }{\uptau _s} \big )^{2}}}, \end{aligned}$$
(5)

where \(\uptau\) is the shear stress, \(\mu _\infty\) is the limiting viscosity, \(\uptau _s\) stands for reference shear stress and \(\mu _o\) is the zero shear viscosity. An incompressible, steady and 2D nanofluid of a dissipative Reiner–Philippoff fluid conveying SWCNT and MWCNT over a stretching surface is examined (see Fig. 2). Usual truncation of the higher-order terms is assumed to be arrived at the linear thermal radiative heat flux. The flow governing equations in regard to continuity, momentum, energy and concentration equations have a similar form as given in Na [31] and Sajid et al. [34],

Fig. 2
figure 2

Physical representation of the flow

Full size image
$$\begin{aligned}{} & {} \frac{\partial \bar{u}}{\partial \bar{x}} + \frac{\partial \bar{v}}{\partial \bar{y}}=0. \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \dfrac{\mu _{\rm{nf}}}{\rho _{\rm{nf}}}\dfrac{\partial \uptau }{\partial \bar{y}} + \frac{\pi j_0 M}{8 \rho _{\rm{nf}}} \exp \left( -\frac{\pi }{r_0}\bar{y}\right) - \frac{\mu _{\rm{nf}}}{{\rho _{\rm{nf}}}} \frac{\bar{u}}{K_p} = \bar{u}\frac{\partial \bar{u}}{\partial \bar{x}} + \bar{v}\frac{\partial \bar{u}}{\partial \bar{y}}. \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \frac{\mu _{\rm{nf}}}{(\rho c_{p})_{\rm{nf}}} \left( \frac{\partial \bar{u}}{\partial \bar{y}}\right) ^2 - \dfrac{1}{(\rho c_{p})_{\rm{nf}}} \dfrac{\partial q_{r}}{\partial \bar{y}} + \dfrac{\kappa _{\rm{nf}}}{(\rho c_{p})_{\rm{nf}}}\dfrac{\partial ^2 \bar{T}}{\partial \bar{y}^2} = \bar{u}\frac{\partial \bar{T}}{\partial \bar{x}} + \bar{v}\frac{\partial \bar{T}}{\partial \bar{y}}. \end{aligned}$$
(8)
$$\begin{aligned}{} & {} D_d \dfrac{\partial ^2 \bar{C}}{\partial \bar{y}^2} + D_{CT}\frac{\partial ^2 \bar{T}}{\partial \bar{y}^2} = \bar{u} \dfrac{\partial \bar{C}}{\partial \bar{x}} + \bar{v}\dfrac{\partial \bar{C}}{\partial \bar{y}}. \end{aligned}$$
(9)

The appropriate boundary conditions are,

$$\begin{aligned} \left. \begin{aligned}&\bar{u}(\bar{x},\bar{y}) = u_w , \quad \bar{v}(\bar{x},\bar{y}) = 0, \quad \bar{T}(\bar{x}, \bar{y}) = \bar{T}_w \quad \bar{C}(\bar{x}, \bar{y}) = \bar{C}_w \quad \rm {as} \quad \bar{y} = 0, \\&\bar{u}(\bar{x}, \bar{y}) \rightarrow 0,\quad \bar{T}(\bar{x}, \bar{y}) \rightarrow \bar{T}_\infty , \quad \bar{C}(\bar{x}, \bar{y}) \rightarrow \bar{C}_\infty , \quad \rm {as}\quad \bar{y} \rightarrow \infty . \end{aligned} \right\} \end{aligned}$$
(10)

The radiative heat flux resulting from the Rosseland approximation given that \(\bar{T}^{4} \approx 4\bar{T}^{3}_{\infty }\bar{T} - 3\bar{T}^{4}_{\infty }\) is defined as [35] and [36],

$$\begin{aligned} q_{r} = -\dfrac{4\sigma ^{*}}{3k_{1}}\dfrac{\partial \bar{T}^{4}}{\partial \bar{y}} = -\dfrac{16 \sigma ^{*} }{3k_{1}} \bigg [ \bar{T}^3_{\infty } \dfrac{\partial \bar{T}}{\partial \bar{y}} \bigg ]. \end{aligned}$$
(11)

Following the study of Magyari and Pantokratoras [37], Eq. (8) becomes

$$\begin{aligned} \frac{\mu _{\rm{nf}}}{(\rho c_{p})_{\rm{nf}}} \left( \frac{\partial \bar{u}}{\partial \bar{y}}\right) ^2 + \dfrac{\kappa _{{{\rm{nf}}_{\rm {eff}}}}(T)}{(\rho c_{p})_{\rm{nf}}} \dfrac{\partial ^2 \bar{T}}{\partial \bar{y}^2} = \bar{u}\frac{\partial \bar{T}}{\partial \bar{x}} + \bar{v}\frac{\partial \bar{T}}{\partial \bar{y}}. \end{aligned}$$
(12)

where \(\kappa _{{{\rm{nf}}_{\rm {eff}}}}(T) = \bigg (\dfrac{16 \sigma ^{*} \bar{T}^3_{w} }{3k_{1}} + \kappa _{\rm{nf}}\bigg )\) is the effective thermal conductivity of the hybrid nanofluid.

3.2 Thermophysical properties of the nanofluid

The mathematical expression of the nanofluid and the base fluid properties (i.e., viscosity, volumetric heat capacity, density and thermal conductivity) is given as follows (see Saeed et al. [38]):

Fluid viscosity:

$$\begin{aligned} \frac{\mu _{\rm{nf}}}{\mu _{\rm{f}}} = \Lambda _1 = \frac{1}{(1-\phi _1)^{2.5} (1-\phi _2)^{2.5}}. \end{aligned}$$
(13)

Specific heat capacity:

$$\begin{aligned} \frac{(\rho C_p)_{\rm{nf}}}{(\rho C_p)_{\rm{f}} } = \Lambda _2 = \phi _2\frac{(\rho C_p)_{\rm{SWCNT}}}{(\rho C_p)_{\rm{f}}}+(1-\phi _2)\left[ 1-\left( 1-\frac{(\rho C_p)_{\rm{MWCNT}}}{(\rho C_p)_{\rm{f}}}\right) \phi _1 \right] . \end{aligned}$$
(14)

Fluid density:

$$\begin{aligned} \frac{(\rho )_{\rm{nf}}}{(\rho )_{\rm{f}}} = \Lambda _3 = \phi _2\frac{(\rho )_{\rm{SWCNT}}}{(\rho )_{\rm{f}}}+(1-\phi _2)\left[ 1-\left( 1-\frac{(\rho )_{\rm{MWCNT}}}{(\rho )_{\rm{f}}}\right) \phi _1 \right] . \end{aligned}$$
(15)

Thermal conductivity:

$$\begin{aligned} \left. \begin{aligned}&\frac{\kappa _{\rm{nf}}}{\kappa _{\rm{bf}}} = \Lambda _4 = (1-\phi _2) + 2 \phi _2 \left( \frac{\kappa _{\rm{SWCNT}}}{\kappa _{\rm{SWCNT}} - \kappa _{\rm{bf}}}\right) \ln \left( \frac{\kappa _{\rm{SWCNT}}+\kappa _{\rm{bf}}}{2\kappa _{\rm{bf}}}\right) ,\\&\frac{\kappa _{\rm{bf}}}{\kappa _{\rm{f}}} = (1-\phi _1) + 2 \phi _1 \left( \frac{\kappa _{\rm{MWCNT}}}{\kappa _{\rm{MWCNT}} - \kappa _{\rm{f}}}\right) \ln \left( \frac{\kappa _{\rm{MWCNT}}+\kappa _{\rm{f}}}{2\kappa _{\rm{f}}}\right) . \end{aligned} \right. \end{aligned}$$
(16)

where \(\phi _1\) and \(\phi _2\) represent the nanoparticles of MWCNT and SWCNT, respectively. We have to mention that when \(\phi _1 = 0\) and \(\phi _2 = 0\), water is realized as the working fluid. The case of multi-wall carbon nanotube (MWCNT) nanofluid can be obtained by setting \(\phi _2 = 0\) and \(\phi _1 \ne 0\) and single-wall carbon nanotube (SWCNT) nanofluid when \(\phi _1 = 0\) and \(\phi _2 \ne 0\). Table 1 shows the numerical value of the thermophysical properties of the base fluid (H\(_{2}\)O), MWCNT and SWCNT.

Table 1 Thermophysical features of SWCNT, MWCNT nanoparticles and -H\(_2\)O, see [16]
Full size table

3.3 Similarity transformation

Introduce the following appropriate similarity transformation:

$$\begin{aligned}{} & {} \eta = \sqrt{\dfrac{a}{\nu }}\dfrac{\bar{y}}{\bar{x}^{\frac{1}{3}}}, \quad \psi = \sqrt{a \nu } \bar{x}^{\frac{2}{3}} f(\eta ), \quad \uptau = \rho \sqrt{a^3 \nu } g(\eta ), \nonumber \\{} & {} \theta (\eta ) =\dfrac{\bar{T} - \bar{T}_\infty }{\bar{T}_w - \bar{T}_\infty }, \quad \phi (\eta ) = \dfrac{ \bar{C} - \bar{C}_\infty }{\bar{C}_w -\bar{C}_\infty }. \end{aligned}$$
(17)

Implementing Eq. (17) on the governing Eqs. (6), (7), (9), (12) and the boundary conditions of Eq. (10), we obtain the following ordinary differential equations, given by

$$\begin{aligned}{} & {} \dfrac{g}{f''} = \dfrac{g^2 + \lambda \gamma ^2 }{g^2 + \gamma ^2 }, \end{aligned}$$
(18)
$$\begin{aligned}{} & {} g' - K^{*}_p \ f' + \frac{\rm {Z}}{\Lambda _1} \ \exp \left( -\rm {J} \eta \right) - \frac{\Lambda _3}{\Lambda _1} \left\{ \dfrac{1}{3}f'^{2} - \dfrac{2}{3}ff''\right\} = 0, \end{aligned}$$
(19)
$$\begin{aligned}{} & {} \frac{\Lambda _4}{\rm{P}{{{r_{\rm {eff}}}}}} \theta '' + \rm{Ec} \ \frac{\Lambda _1}{\Lambda _4} \ f''^{2} + \dfrac{2}{3} \frac{\Lambda _2}{\Lambda _4} \ f\theta ' = 0, \end{aligned}$$
(20)
$$\begin{aligned}{} & {} \phi '' + \dfrac{2}{3} \ S_{c}f\phi ' + S_{r}\theta '' = 0. \end{aligned}$$
(21)

Note that P\(_{r_{\rm {eff}}} = \rm{Pr}\bigg (\dfrac{\Lambda _4}{1 + \rm {R}\Lambda _4}\bigg )\) is the effective Prandtl number, see [37]. In addition, the dimensionless boundary conditions become:

$$\begin{aligned} \begin{aligned}&f'(\eta ) = 1,\quad f(\eta ) = 0, \quad \theta (\eta ) = 1, \quad \phi (\eta ) = 1, \quad \rm {as}\quad \eta = 0, \\&f'(\eta ) \rightarrow 0,\quad \theta (\eta ) \rightarrow 0, \quad \phi (\eta ) \rightarrow 0, \quad \rm {as}\quad \eta \rightarrow \infty . \end{aligned} \end{aligned}$$
(22)

With the resulting parameters

$$\begin{aligned} \left\{ \begin{aligned}&\rm {Z} = \dfrac{\pi j_0 M u_{w} }{8a^3 \rho _f}, \, \, \rm {J} = \frac{\pi }{r_0 a}\sqrt{\frac{\nu }{a}}u_{w} , \, \, \rm {R} = \dfrac{16\sigma ^{*} \bar{T}_{\infty }^{3}}{3k_{1}\kappa _{bf}}, \\&\quad \, \, \rm{Pr} = \dfrac{c_{p}\mu }{\kappa _0}, \, \, S_{c} = \dfrac{\nu }{D_{\infty }},\, \, \, K^{*}_p = \dfrac{\mu }{\rho a K_p},\\&\rm{Ec} = \dfrac{u_{w}^2}{c_{p}(\bar{T}_f - \bar{T}_{\infty })}, \quad \rm{Sr} = \frac{D_{CT} (\bar{T}_f - \bar{T}_\infty )}{D_d (\bar{C}_f - \bar{C}_\infty )}. \end{aligned} \right. \end{aligned}$$
(23)

4 Engineering physical quantity

The engineering physical significance of this study relates to the skin friction coefficient, Nusselt number and Sherwood number. The mathematical representation of these physical quantities is given as

$$\begin{aligned} \begin{aligned} \rm{C}_{f} = \dfrac{\uptau _w}{0.5 \rho _{\rm{f}} u^{2}_{w}}, \quad \rm{Nu}_x = \dfrac{\bar{x} q_w}{\kappa _{\rm{bf}} (\bar{T_{w}} - \bar{T_\infty })}, \quad \rm{Sh}_x = \dfrac{\bar{x} q_m}{D_{d} (\bar{C_{w}} - \bar{C_\infty })}, \end{aligned} \end{aligned}$$
(24)

where the shear stress, surface heat flux and mass flux are \(\uptau _w,\,q_w\), \(q_m\) , respectively, and are defined as

$$\begin{aligned} \uptau _w = \rho _{\rm{nf}} \sqrt{a^3 \nu } g(\eta ), \quad q_w = -\kappa _{\rm{nf}} \dfrac{\partial \bar{T}}{\partial \bar{y}} \bigg |_{\bar{y}=0} + q_r, \quad q_m = -D_{d} \dfrac{\partial \bar{C}}{\partial \bar{y}} \bigg |_{\bar{y}=0}. \end{aligned}$$
(25)

In dimensionless form, Eq. 24 using the definition defined in Eq. 25 becomes

$$\begin{aligned} \begin{aligned} \dfrac{1}{2}\rm{Re}^{\frac{1}{2}}_{\bar{x}} C_f = \Lambda _3 g(0), \quad Re^{-\frac{1}{2}}_{\bar{x}} \rm{Nu}_{\bar{x}} = - \big (\Lambda _4 + \rm {R} \big )\theta '(0), \\ Re^{-\frac{1}{2}}_{\bar{x}}\rm{Sh}_{\bar{x}} = - \phi '(0), \end{aligned} \end{aligned}$$
(26)

where \(\rm{Re}_{\bar{x}} = \dfrac{u_w\bar{x}}{\nu }\).

5 Numerical method

Equations (18)–(21) with their suitable conditions in Eq. (22) will be solved using the spectral approach. The spectral approach of interest here is the spectral local linearization method (SLLM), which is based on the work of Motsa [39]. The method works by locally linearizing our variables of interest before iteratively computing them. The local linearization technique is credited to Bellman and Kalaba [40], which can be seen as an extension of the Newton–Raphson approach. We refer the reader to the following work for more study of this method (Ogunseye et al. [41]). We start with the local linearization which takes the form:

$$\begin{aligned}{} & {} g_{(a+1)} = \dfrac{g^2_{(a+1)} + \lambda \gamma ^2 }{g^2_{(a+1)} + \gamma ^2 }f''_{(a+1)}. \end{aligned}$$
(27)
$$\begin{aligned}{} & {} \Omega _{1, a}f'''_{(a + 1)} + \Omega _{2, a}f''_{(a + 1)} + \Omega _{3, a}f'_{(a + 1)} + \Omega _{4, a}f_{(a + 1)} = R_{f_{1}}. \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \Omega _{5, a}\theta ''_{(a + 1)} + \Omega _{6, a}\theta '_{(a + 1)} = R_{f_{2}}. \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \Omega _{7, a}\phi ''_{(a + 1)} + \Omega _{8, a}\phi '_{(a + 1)} = R_{f_{3}}. \end{aligned}$$
(30)

as well as appropriate boundary conditions

$$\begin{aligned} \begin{aligned} f'_{(a+1)} = 1,\,f_{(a+1)} = 0,\,\theta _{(a+1)} = 1,\,\phi _{(a+1)} = 1 \,\,\,\rm {for}\,\,\eta = 0,\\ f'_{(a+1)} = 0,\,\theta _{(a+1)} = 0,\,\phi _{(a+1)} = 0 \,\,\,\rm {as}\,\,\eta \rightarrow \infty . \end{aligned} \end{aligned}$$
(31)

and the variable (coefficient) given as

$$\begin{aligned} \left\{ \begin{array}{ll} \Omega _{1, a} = \dfrac{g^2 + \lambda \gamma ^2 }{g^2 + \gamma ^2},\,\,\Omega _{2, a} = \dfrac{2}{3}\dfrac{\Lambda _3}{\Lambda _1} f + 2g\dfrac{g'\gamma ^2 (1 - \lambda ) }{(g^2 + \gamma ^2)^{2}},\,\,\Omega _{3, a} = -K^{*}_p - \dfrac{2}{3}\dfrac{\Lambda _3}{\Lambda _1}f', \,\, &{}\\ \Omega _{4, a} = \dfrac{2}{3}\dfrac{\Lambda _3}{\Lambda _1} f'',\,\,\Omega _{5, a} = \dfrac{\Lambda _4}{P_{r_{\rm {eff}}}},\,\,\Omega _{6, a} = \dfrac{2}{3}\dfrac{\Lambda _2}{\Lambda _4}f,\,\,\Omega _{6, a} = 1,\,\,\Omega _{7, a} = \dfrac{2}{3}S_{c}f. &{}\\ \end{array} \right. \end{aligned}$$
(32)

and residuals

$$\begin{aligned} \left\{ \begin{array}{ll} R_{f_{0}} = g_{(a)} - \dfrac{g^2_{(a)} + \lambda \gamma ^2 }{g^2_{(a+1)} + \gamma ^2 }f''_{(a)} - L_{0} &{}\\ R_{f_{1}} =\Omega _{1, a}f'''_{(a)} + \Omega _{2, a}f''_{(a)} + \Omega _{3, a}f'_{(a)} + \Omega _{4, a}f_{(a)} - L_1 &{}\\ R_{f_{2}} = \Omega _{5, a}\theta ''_{(a)} + \Omega _{6, a}\theta '_{(a)} - L_2 &{}\\ R_{f_{3}} = \Omega _{7, a}\phi ''_{(a)} + \Omega _{8, a}\phi '_{(a)} - L_3 &{} \end{array} \right. \end{aligned}$$
(33)

where \(L_{0}, L_1, L_2\) and \(L_3\) represent Eqs. (18), (19), (20) and (21), respectively. We kick start our iterative scheme by choosing a suitable guess function defined as:

$$\begin{aligned} f_{1(a)} = 1 - e^{-\eta },\,\,\theta _{2(a)} = e^{-\eta }\,\,\rm {and}\,\,\phi _{a} = e^{-\eta }. \end{aligned}$$
(34)

For brevity, the other numerical procedure can be found in references [5, 6, 41]. We provide the algorithm for the SLLM under the assumption that the well-known “cheb” function given by Trefethen [42] is utilized.

figure a

5.1 Numerical validation

In this section, the validation and accuracy of the numerical method using different metrics are reported. Convergence of the spectral method is displayed in Table 2 for Eqs.  (19), (20) and (21). The method shows rapid convergence by the fifth iteration. Validation of the spectral method is carried out in Tables 3 and 4. It is important to mention that due to the choice of effective Prandtl number P\(_{r_{\rm {eff}}}\) that we employed, the value of \(\rm {R} = \dfrac{4}{3}\) is equivalent to \(\rm {R} = 1\) chosen in references [43,44,45]. The numerical values of the temperature gradient and skin friction coefficient using the SLLM and for other previous results in literature are listed in Tables 3 and 4. The comparative results show good agreement with previously established results in the limiting cases.

Table 2 Convergence analysis of the spectral local linearization method (SLLM) with 50 collocation points using the following parameter values of \(\rm {Z} = 0.5,\,\,\rm {J} = 0.5,\,\,\rm {R} = 0.2\,\, \rm{Pr} = 7.2,\,\,\rm{Sc} = 2.0,\,\,K^{*}_p = 0.5,\,\,\rm{Ec} = 0.01,\,\,\rm{Sr} = 0.2\) and \(\phi _{1} = \phi _{2} = 0.0\)
Full size table
Table 3 Temperature gradient \(-\theta '(0)\) at the wall for the spectral local linearization method (SLLM) and results in [43,44,45] using the following parameter value of \({Z} = {J} = \rm{Sc} = K^{*}_p = \rm{Ec} = \rm{Sr} = \phi _{1} = \phi _{2} = 0.0\) and \(\rm{Pr} = 2.0\)
Full size table
Table 4 Comparative values of \(\rm{Re}_{x}^{-1/2}\rm{C}_{f}\) given the parameter value \({Z} = {J} = \rm{Sc} = K^{*}_p = \rm{Ec} = \rm{Sr} = \phi _{1} = \phi _{2} = 0.0\), \(\rm{Pr} = 10.0\) and \(\rm {R} = \dfrac{20}{3}\)  (equivalence to \({R} = 5.0\) chosen in [26])
Full size table

6 Results and discussion

This section graphically illustrates the response pertaining to parameter variations on the distribution profiles. Based on the assumption, this study utilizes a nanofluid containing either SWCNT or MWCNT, with MWCNT at \(\phi _1 = 0.05\) and SWCNT at volume fraction value \(\phi _2 = 0.05\).

Fig. 3
figure 3

Influence of \(\phi _{1}\) and \(\phi _{2}\) on the velocity profile (\(f'(\eta )\)) and temperature profile (\(\theta (\eta )\))

Full size image
Fig. 4
figure 4

Influence of \(\rm{Pr}_{\rm {eff}}\) on the temperature profile (\(\theta (\eta )\)) and concentration profile (\(\phi (\eta )\))

Full size image

If the presence of the nanoparticles is in excess of \(5\%\) in the nanofluid, it is important to note that the nanoparticles behaves like a non-Newtonian fluid. Consequently, we have taken nanoparticles volume fraction value of less than or equal to \(5\%\). In the numerical simulation, the non-dimensionalized parameters must be chosen properly and in agreement with the physics of the problem so that the required boundary conditions are satisfy correctly. Since the base fluid of this study is water, Prandtl number is fixed as 7.2 and the remaining physical parameters are taken as follows: \(K^{*}_p = 0.5,\,\rm {Z} = 1.0,\,\rm {J} = 0.8,\,\rm{Ec} = 0.01,\,\rm{Sc} = 2.0,\,\rm{Sr} = 0.2,\,\lambda = 1.0,\,\gamma = 1.0,\,\rm{Pr}_{\rm {eff}} = (\rm {i.e.}\,\rm{Pr} = 7.2,\,\rm {R} = 0.8)\) unless stated otherwise. Figures 3 and 4 show the influence of nanoparticle volume fraction on each nanofluid.

Fig. 5
figure 5

Influence of \(\rm {J}\) on the velocity profile (\(f'(\eta )\)) and temperature profile (\(\theta (\eta )\))

Full size image

The study shows that these volume fractions \(\phi _1\) and \(\phi _2\) had great effects on the temperature profile of SWCNT and MWCNT nanofluids, but less impact on the velocity profile. Figure 3b further establishes that the energy dissipation of the MWCNT-induced nanofluid is greatly influenced compared to the SWCNT-induced nanofluid.

The effective Prandtl parameter \(\rm{Pr_{{eff}}}\) has a diametrically opposed behavior on the temperature and velocity profiles. The parameter \(\rm{Pr_{{eff}}} \in [3.0, 6.0]\) greatly abates the heat dissipation of the MWCNT. Figure 5 shows that the material constant parameter \(\rm {J}\) indicates a negative motion of the momentum profile but supports the temperature profile. The concentration profile of the MWCNT has more influence compared to the SWCNT. Mathematically, the porosity parameter is directly proportional to the viscosity (resistance to movement at a given rate) of the hybrid nanofluid. This explains why an increase in the porosity parameter leads to a reduction in the velocity distribution, as shown in Fig. 6.

Fig. 6
figure 6

Influence of \(K^{*}_p\) on the velocity profile (\(f'(\eta )\)), temperature profile (\(\theta (\eta )\)) and concentration profile(\(\phi (\eta )\))

Full size image
Fig. 7
figure 7

Influence of \(\rm{Ec}\) on the temperature profile (\(\theta (\eta )\))

Full size image

The decrease in the velocity profile as we increase the porosity parameter results in more drag on the Riga plate, thereby increasing the temperature and concentration distributions. This is because molecules of the nanofluids collide more with the sheet, as shown in Fig. 6b and c. The SWCNT exhibits significantly more heat generation compared to the MWCNT, as shown in Fig. 6c. Figure 7 elucidates the importance of the Eckert dimensionless parameter on the temperature profile of the SWCNT and MWCNT Reiner–Philippoff nanofluid.

Fig. 8
figure 8

Influence of \(\rm{Sc}\) and \(\rm{Sr}\) on the concentration profile (\(\phi (\eta )\))

Full size image

Figure 7 illustrates how the Eckert parameter enhances heat transfer in the fluid. The Eckert parameter increases the advective transport of heat transfer dissipation rate. Moreover, the study shows a much larger percentage increase in MWCNT compared to SWCNT as we increase the Eckert parameter. Figure 8 depicts the influence of Schmidt and modified Soret numbers on the concentration profile. It is found that the concentration profile and its corresponding concentration boundary layer thickness are reduced for both SWCNT and MWCNT when the Schmidt number is increased. This is explained by the fact that increasing the Schmidt number impedes the molecular mass diffusion rate thereby reducing the concentration profile.

Fig. 9
figure 9

Influence of \(\rm {Z}\) on the velocity profile (\(f'(\eta )\)) and Temperature profile (\(\theta (\eta )\))

Full size image
Table 5 Numerical values of Nusselt and Sherwood numbers for SWCNT/H\(_2\)O and MWCNT/H\(_2\)O given the parameter value \(K^{*}_p = 0.5,\, {Z} = 1.0,\, {J} = 0.5,\,\rm{Ec} = 0.01,\,\rm{Sc} = 2.0,\,\rm{Sr} = 0.2\), \(\lambda = \gamma = 1.0\) and \(\rm{Pr_{{eff}}} = (\rm {i.e.}\,\rm{Pr} = 7.2,\,{R} = 0.8)\)
Full size table

The modified Soret number \(\rm{Sr}\) supports the growth of the concentration boundary layer thickness with increments in the dimensionless parameter while keeping other parameters constant (see Fig. 8b). Figure 9 shows that with an increase in the modified magnetic parameter \(\rm {Z}\) values, both SWCNT and MWCNT exhibit an increasing velocity profile. However, an opposing behavior, characterized by a reduction in heat dissipation, can be observed as the modified magnetic parameter is enhanced, as shown in Fig. 9b. The findings noted here for the modified magnetic parameter \(\rm {Z}\) is similar to the result of Ahmad et al. [16].

Table 6 Numerical values of skin friction coefficient \(\frac{1}{2}Re^{\frac{1}{2}}_x C_f\) and Nusselt number \(Re^{-\frac{1}{2}}_x \rm{Nu}_{x}\) for different values of \(\rm {Z},\,K^{*}_p,\,\rm{Ec}\) when P\(_{r_{\rm {eff}}} = (\rm {i.e.}\,\rm{Pr} = 7.2,\,\rm {R} = 0.8)\), \(\rm{Sc} = 2.0,\,\rm{Sr} = 0.2\) and \(\rm {J} = 1.0\) for different nanomaterials
Full size table

Table 5 shows the percentage increase from the SWCNT to the MWCNT nanofluids using the Nusselt number. The results indicate that as the nanoparticle volume fraction is enhanced, the Nusselt number for both SWCNT and MWCNT nanofluid decreases. The Sherwood number is an increasing function as the nanoparticle volume fraction increases for SWCNT but a decreasing function for MWCNT as nanoparticle volume fraction increases. The results of this study indicate that MWCNT exhibits a significantly more efficient convective process than SWCNT. Table 6 shows the comparative values of skin friction and Nusselt numbers for the base fluid, SWCNT and MWCNT. We found that increasing the porosity and Eckert parameters decreases the Nusselt number. Additionally, the modified magnetic parameter \(\rm {Z}\) is found to enhance both the skin friction coefficient and Nusselt number.

7 Conclusions

The study focuses on the comparative analysis between the Reiner–Philippoff nanofluid of SWCNT and MWCNT with water as working the fluid. The features of heat and mass transfer are carried out over a stretching sheet with the inclusion of magnetic effects, viscous dissipation and thermal radiation effects. The spectral-based numerical technique, specifically the spectral local linearization method (SLLM) implemented in MATLAB, was used to solve the coupled ordinary differential equations. The following are some of the key findings of this investigation:

  • The SWCNT can be used to increase the heat transfer dissipation of the base fluid the most.

  • The material constant \(\rm {J}\) decreased the velocity profile of both SWCNT and MWCNT nanofluid induced.

  • The concentration boundary layer thickness boosts for boosting the value of non-dimensional modified Soret number.

  • All dimensionless parameters except the modified magnetic term retard the velocity profile.

In our future study, the impact of Coriolis and centrifugal forces as well as the variations of the thermophysical properties will be explored.