1 Introduction

As is known, the influence of external factors (temperature, magnetic field, and pressure) on quantum-dimensional heterostructures leads to a change in the position of the energy levels of charge carriers and, consequently, to a shift of the magneto-optical absorption edge [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. The magneto-optical absorption spectrum of nanoscale semiconductors is determined by the energy distance between different minima of the sparse zone. Hence, the width of the forbidden zone of the quantum well can either decrease or increase due to external influences. Thus, the study of the magneto-optical absorption spectrum near the boundary of its absorption edge provides information about the structure of the energy spectrum of charge carriers near the lower edge of the conduction band and near the upper edge of the valence band of the quantum well, which is essential for determining the magnetic, optical, and electrical properties of nanoscale semiconductors.

The combined densities of quantum well states play an important role in the oscillation of interband magneto-optical absorption. Therefore, in many cases, the matrix element \(\left( {p_{c\upsilon } } \right)\) changes little within the Brillouin zone.

Consequently, the structure of the spectrum mainly determines the combined density of states in quantum-dimensional heterostructures. In works [1,2,3], a method was developed for calculating the oscillation of the combined density of states in a quantizing magnetic field with a non-quadratic law of dispersion under the influence of temperature and hydrostatic pressure. This method is used in the study of magnetic absorption in narrow-band semiconductors with a nonparabolic dispersion law. A fan diagram of the magnetic absorption spectrum in narrow-band semiconductors is constructed. However, these papers do not consider the temperature dependence of the two-dimensional combined density of states in the allowed zone of a quantum well with a parabolic law of dispersion. That is, the resulting method applies only to bulk semiconductor materials.

In addition, in works [4, 5], the spectrum of InGaN/AlGaN/GaN heterostructures with quantum wells is emitted by an LED and analyzed based on a two-dimensional combined density of states model. The considered model of approximation of the luminescence spectra of LEDs in these works was developed for complex heterostructures with multiple quantum wells. In work [6], a random walk in a two-dimensional space consisting of an energy parameter of the order and an energy correlation function was performed, and a two-dimensional combined density of quantum well states was obtained. The order parameter, susceptibility, and correlation function are calculated from the two-dimensional combined density of quantum well states. The numerical calculations of the author show that to determine the two–dimensional combined density of states in continuous models, the Wang–Landau transition matrix method can be considered an alternative to the pure Wang-Landau method. In work [7], an exact mathematical expression is proposed that directly combines the density functions of the states of the resolved zone of a quantum well to create a two-dimensional combined density of states for direct transitions. Using both expressions, the absorption coefficient of the quantum well and the superlattice was calculated, which led to a positive coincidence with the experimental data. In the above literature, the temperature dependence of the oscillation of the two-dimensional combined density of quantum well states in a quantizing magnetic field is not discussed. Also, the work determines the oscillations of the combined density of quantum well states at constant temperatures in the absence of a magnetic field.

The purpose of this work is to determine the effect of a strong magnetic field on the combined density of states in heterostructures with quantum wells.

2 Theoretical part

2.1 Calculation of the oscillation of the combined density of states in heterostructures with quantum wells in the presence of a magnetic field

In the absence of a magnetic field, the dependence of the density of the energy states of the conduction band and the valence band in the quantum well on the energy spectrum of charge carriers are step functions (Fig. 1a) [21]:

$$ \begin{gathered} g_{c} \left( E \right) = \frac{{m_{n}^{e} }}{{\hbar^{2} \pi }} \mathop \sum \limits_{n} \theta \left( {E - E_{n} } \right) \hfill \\ g_{v} \left( E \right) = \frac{{m_{n}^{h} }}{{\hbar^{2} \pi }} \mathop \sum \limits_{m} \theta \left( {E - E_{m} } \right) \hfill \\ \end{gathered} $$
(1)
Fig. 1
figure 1

The energy distribution of the density of electronic states in quantum-dimensional GeSi/Si structures [21]: (a) Quantum well, (b) Quantum dot

Full size image

Here, \(m_{n}^{e} \;{\text{and}}\;m_{n}^{h}\) are the effective masses of electrons and holes in the dimensional quantization subband in a quantum well numbered n and m. \(\theta (E)\)—Heaviside step function.

For direct interband transitions, the combined densities of states are a convolution in energy, which also has a step function in energy [21]:

$$ N_{jds}^{2d} \left( E \right) = \frac{{m_{mn}^{*} }}{{\hbar^{2} \pi }}\mathop \sum \limits_{m,n} \theta \left( {E - E_{mn} } \right) $$
(2)

Here, \(m_{mn}^{*}\) is the reduced effective mass of charge carriers for the subzones of dimensional quantization n and m, which is calculated by the ratio: \(\left( {m_{{{\text{mn}}}}^{*} } \right)^{ - 1} = \left( {m_{n}^{e} } \right)^{ - 1} + \left( {m_{m}^{h} } \right)^{ - 1}\).

If the electronic and hole states in GeSi structures turn out to be size-quantized in all three quasi-momentum components, that is, they represent a quantum dot for charge carriers, then in this case the combined density of states in the allowed band of such a structure is a Gaussian function (Fig. 1b). Then, in the allowed zone, there is a zero-dimensional combined density of states, which is a discrete non-decreasing function. In this case, the combined density of states is described using the so-called Dirac delta function \(\delta \left( E \right)\):

$$ N_{{{\text{jds}}}}^{0d} \left( E \right) = \mathop \sum \limits_{l,m,n} { }\delta \left( {E - E_{{{\text{lmn}}}} } \right) $$
(3)

The combined density of states is a collection of infinitely narrow and high peaks (Fig. 1b). All the results obtained above are valid for cases without the influence of quantization of the magnetic field, temperature, and pressure. Specific questions arise: How to determine the combined density of states in quantum-dimensional direct transitions of heterostructures in the presence of a strong magnetic field? How does the dynamics of temperature rise affect this process?

Let's calculate the dependence of the combined density of states on the quantizing magnetic field in two-dimensional semiconductor materials with direct allowed transitions. In a quantizing magnetic field, the combined density of states is defined as an integral over all states in the conduction band with energies EC and in the valence band with energies EV of the quantum well, which satisfies the law of conservation of energy during the magneto-optical transition. Let us analyze the simplest model of a band structure near the edge of the band gap of a straight-band heterostructure with a quantum well under the influence of a strong magnetic field. That is, the valence band of the quantum well is completely filled with charge carriers, and the conduction band is empty. Here, the filling functions of the corresponding states are equal to fV = 1, fC = 0. In addition, in this model, the dependence of impurity levels on the combined density of quantum well states with the parabolic law of dispersion can be neglected. The magnetic field inductions are directed across (along the Z axis) and will be perpendicular to the XY plane. This is called a transverse quantum magnetic field.

Hence, in the presence of a strong magnetic field, the laws of dispersion energy are used to calculate the combined density of quantum well states, which can be written as follows:

$$ \begin{aligned} & E_{c}^{2d} \left( {B,d,n_{cZ} } \right) = \left( {N_{L}^{c} + \frac{1}{2}} \right)\hbar \omega_{c}^{c} + \frac{{\hbar^{2} \pi^{2} }}{{2m_{c} d^{2} }}n_{eZ}^{2} + m_{s}^{c} g_{c} \mu_{B} H \\ & E_{v}^{2d} \left( {B,d,n_{vZ} } \right) = - \left( {N_{L}^{v} + \frac{1}{2}} \right)\hbar \omega_{c}^{v} - \frac{{\hbar^{2} \pi^{2} }}{{2m_{v} d^{2} }}n_{vZ}^{2} - m_{s}^{v} g_{v} \mu_{B} H - E_{g}^{2d} \left( 0 \right) \\ \end{aligned} $$
(4)

Here, \(N_{L}^{c} , N_{L}^{v}\) is the number of Landau levels of charge carriers in the allowed zone of the quantum well; \(\omega_{c}^{c} ,\omega_{c}^{v}\) is the cyclotron frequency of the magnetic field in the conduction band and valence band of the quantum well; d is the thickness of the quantum well; \(n_{eZ}^{2} , n_{vZ}^{2}\) is the number of the dimensional quantization subzone in the conduction band and the valence band of the quantum well; \(n_{eZ} ,n_{\nu Z}\) is the ordinal number of the quantization levels of electrons and holes along the Z axis, respectively.

Imagine that the electron and valence bands are symmetric, then the condition \(n_{eZ} = n_{\nu Z} = n_{Z} \) is fulfilled. \(m_{s}^{c} g_{c} \mu_{B} H,\; m_{s}^{v} g_{v} \mu_{B} H\) is the spin energy in the allowed zone; \(E_{g}^{2d} \left( 0 \right)\) is the width of the forbidden zone of the quantum well at absolute zero temperature; B is the induction of the magnetic field.

For \(E_{c}^{2d} \left( {B,d,n_{Z} } \right)\;{\text{and}}\;E_{v}^{2d} \left( {B,d,n_{Z} } \right)\), without taking into account spin, magneto-optical transitions will correspond to the law of conservation of energy

$$ \begin{aligned} & E_{cv}^{2d} \left( {B,d,n_{Z} } \right) = E_{c}^{2d} \left( {B,d,n_{Z} } \right) - E_{v}^{2d} \left( {B,d,n_{Z} } \right) \\ & E_{cv}^{2d} \left( {B,d,n_{Z} } \right) = E_{g}^{2d} \left( 0 \right) + \left( {N_{L}^{c} + \frac{1}{2}} \right)\hbar \omega_{c}^{c} + \left( {N_{L}^{v} + \frac{1}{2}} \right)\hbar \omega_{c}^{v} + \frac{{\hbar^{2} \pi^{2} }}{{2m_{cv}^{*} d^{2} }}n_{Z}^{2} \\ & h\nu \ge E_{cv}^{2d} \left( {B,d,n_{Z} } \right) \\ \end{aligned} $$
(5)

where \(h\nu\) is the absorbed photon energy, \(\nu\) is the frequency of light, \(\frac{1}{{m_{{{\text{cv}}}}^{*} }} = \frac{1}{{m_{c}^{*} }} + \frac{1}{{m_{v}^{*} }}\) is the combined (reduced) effective mass.

In the Z direction, a strong magnetic field does not change the relationship between the energy and the wave vector for the movement of charge carriers. However, for the movement of charge carriers in the direction of perpendicular magnetic induction (in the XY plane), the former quasi-continuous series of energy levels is replaced by a system of discrete Landau levels. Since the effective mass of electrons and holes is assumed to be constant, the distance between the Landau levels does not depend on the quantum number, which is \(\hbar \omega_{c}\). Hence, in the conduction band and the valence band of the quantum well, the movement of free electrons and holes in all three directions is limited. When exposed to a quantizing magnetic field, a quantum well becomes an analog of a quantum dot. And also, the energy spectrum of charge carriers will be entirely discrete. According to Eq. (3), when replacing E with \(\hbar \nu\) and \(E_{{{\text{lmn}}}}\) with \(E_{{{\text{cv}}}}^{2d} \left( {B,d,n_{Z} } \right)\) in the argument \(\delta \left( {E - E_{{{\text{lmn}}}} } \right)\), we have:

$$ N_{{{\text{jds}}}}^{2d} \left( {h\nu , E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{cv} ,n_{Z} } \right) } \right) = \frac{eB}{{\pi \hbar }}\mathop \sum \limits_{{N_{L}^{c} ,N_{L}^{v} ,n_{Z} }} { }\delta \left( {h\nu - E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{cv} ,n_{Z} } \right)} \right) $$
(6)

Thus, under the influence of a quantizing magnetic field, Eq. (6) can be used to determine the combined density of quantum well states. However, such equations do not take into account the influence of temperature and pressure on the discrete Landau levels of electrons and holes for straight-band quantum wells.

2.2 Effects of the quantizing magnetic field on the temperature dependence of the combined density of states in nanoscale straight-band heterostructures

The magneto-optical absorption spectrum is a key requirement for many volumetric and low-dimensional optoelectronic devices. The process of magneto-optical absorption in straight-band heterostructures with quantum wells and \(\alpha_{B}^{2d} \left( {\hbar \nu , B,d} \right)\) can be expressed as a function of the combined density of states. When exposed to a quantizing magnetic field, the combined density of states provides a measure of the number of allowed magneto-optical transitions between the electronic states of the filled valence band and the unoccupied electronic states of the conduction band separated by the photon energy \(\hbar \nu\). In well-known scientific literature, several attempts have been reported to relate the densities of the energy states of the permitted zone with the combined density of states in the absence and presence of a magnetic field. [4,5,6,7]. However, all the empirical and simplified expressions of the combined density of states obtained were limited by the absence of pressure and low temperatures.

From Eq. (6), it is clear that for \(h\nu > E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{cv} ,n_{Z} } \right) \), the form of the combined density of states as a function of energies reflects the nature of the deltoid. When exposed to a quantizing magnetic field, the two-dimensional combined density of states \(N_{{{\text{jds}}}}^{2d} \left( {h\nu , E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{cv} ,n_{Z} } \right)} \right)\) is determined by the energy spectrum of charge carriers in the allowed zone of the quantum well. Experiments show that the density of states of electrons and holes depends on temperature. The temperature dependence of the density of states of electrons and holes in a quantum well is explained by the thermal blurring of discrete Landau levels [22,23,24,25]. As shown in works [23, 24], the density of electron states in the conduction band of a quantum well at sufficiently high temperatures transforms from discrete Landau levels into a continuous energy spectrum. And at low temperatures, the quantizing magnetic field strongly affects the densities of states in the resolved zone of the quantum well, whereas the continuous energy spectrum decomposes into discrete Landau levels. In this case, as the temperature increases, collisions of charge carriers and thermal motions lubricate the discrete Landau levels, turning them into a continuous spectrum of the density of quantum well states. Hence, the temperature dependence of discrete Landau levels of charge carriers can be described by decomposing the combined density of quantum well states into a series of delta-shaped functions. The temperature dependence of the oscillation of the interband magneto-optical absorption in heterostructures with quantum wells was explained by a study using the delta-shaped functions of two-dimensional combined densities of states. The temperature dependence of the two-dimensional combined density of states is determined by the thermal broadening of discrete Landau levels of charge carriers in the allowed zone of the quantum well.

At T = 0, the Gaussian distribution function is delta-shaped and is defined by the following expression [26]:

$$ {\text{Gauss}}\left( {E,T} \right) = \frac{1}{{{\text{kT}}}} \cdot \exp \left( { - \frac{{\left( {E - E_{i} } \right)^{2} }}{{\left( {{\text{kT}}} \right)^{2} }}} \right) $$
(7)

In addition, to describe the interband magneto-optical absorption, it is usually assumed that each energy spectrum of a quantum well is blurred according to the Gaussian law with a blurring parameter. This approach can be described by the temperature dependence of the two-dimensional combined density of states in a quantum well. Hence, the deep filled discrete Landau levels of charge carriers in a quantum well depend exponentially on the two-dimensional combined density of states. To calculate the temperature dependence of the two-dimensional combined density of states \(N_{{{\text{jds}}}}^{2d} \left( {h\nu , E_{{{\text{cv}}}}^{2d} \left( {B,d,n_{Z} } \right) } \right)\) we assume that \(N_{{{\text{jds}}}}^{2d} \left( {\hbar \nu , E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{cv} ,n_{Z} } \right) } \right)\) for T = 0 equal to the known energy functions \( E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right)\). For a heterostructure with quantum wells, in a strong magnetic field, the two-dimensional combined density of states is calculated by Eq. (6). With increasing temperature, each combined density of states in the allowed zone of the quantum well with the energy of the conduction band and the valence band \( E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right)\) is eroded. Thermal blur \(N_{{{\text{jds}}}}^{2d} \left( {h\nu , E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right) } \right)\) with energy \( E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right)\) is calculated by the Shockley-Reed-Hall statistics [27]. Thus, under the influence of a quantizing magnetic field, in the permitted zone of the quantum well, the resulting two-dimensional combined density of states, taking into account the contribution of thermal blurring of all states, will be determined by the sum of all blurring. Hence, at a finite temperature T, this reduces to the decomposition into a series \(N_{{{\text{jds}}}}^{2d} \left( {h\nu , E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right) } \right)\) by Gaussian functions, for nanoscale semiconductor structures.

Equation (6) does not take into account thermal blurring of the two-dimensional combined density of states. If we decompose \(N_{{{\text{jds}}}}^{2d} \left( {h\nu , E_{{{\text{cv}}}}^{2d} \left( {B,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right) } \right)\) in a row according to Eqs. (7), then it is possible to take into account the temperature dependence of the two-dimensional combined density of states in the allowed zone of the quantum well. In a strong magnetic field, temperature blurring of the combined density of quantum well states leads to smoothing of discrete Landau levels of charge carriers and thermal blurring is calculated using Eq. (7). At T = 0, Eq. (7) turns into a delta-like function of the form:

$$ \mathop {{\text{Gauss}}\left( {E,E_{i} ,T} \right)}\limits_{T \to 0} \to \delta \left( {E - E_{i} } \right) $$
(8)

Thus, it follows from Eqs. (5), (6) and (7) that under the influence of a quantizing magnetic field, the temperature dependence of the combined density of quantum well states is reduced to the following analytical expression:

$$ \begin{aligned} & N_{{{\text{jds}}}}^{2d} \left( {h\nu , E_{{{\text{cv}}}}^{2d} \left( {B,T,d,N_{L}^{cv} ,n_{Z} } \right) } \right) = \frac{eB}{{\pi \hbar }} \cdot \frac{1}{kT} \cdot \\ & \mathop \sum \limits_{{N_{L}^{c} ,N_{L}^{v} ,n_{Z} }} \exp \left[ { - \frac{{\left( {h\nu - \left( {E_{g}^{2d} \left( 0 \right) + \left( {N_{L}^{c} + \frac{1}{2}} \right)\hbar \omega_{c}^{c} + \left( {N_{L}^{v} + \frac{1}{2}} \right)\hbar \omega_{c}^{v} + \frac{{\hbar^{2} \pi^{2} }}{{2m_{{{\text{cv}}}}^{*} d^{2} }}n_{Z}^{2} } \right)} \right)^{2} }}{{\left( {kT} \right)^{2} }}} \right] \\ \end{aligned} $$
(9)

where \(N_{{{\text{jds}}}}^{2d} \left( {\hbar \nu , E_{{{\text{cv}}}}^{2d} \left( {B,T,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right) } \right)\)—temperature dependence of the oscillation of the combined density of states in the allowed zone of the quantum well in the presence of a strong magnetic field. B is the induction of a transverse quantizing magnetic field.

This new analytical equation expresses the effect of the quantizing magnetic field on the temperature dependence of the two-dimensional combined density of states in heterostructures with quantum wells. The obtained expression is convenient for processing experimental data on the oscillation of interband magneto-optical absorption in quantum wells at various magnetic fields and temperatures. Thus, a mathematical model describing the effects of external factors (temperature and magnetic field) on the two-dimensional combined density of states in nanoscale semiconductor structures has been obtained.

3 Results and discussions

3.1 The results obtained on the new reduced model and its discussion

Now, for specific straight-band heterostructures based on quantum wells, we consider the temperature dependence of the two-dimensional combined density of states in a quantizing magnetic field. In work [28], a high-quality heterostructure with a GaAs/AlGaAs quantum well with a width of 14 nm with a small concentration of aluminum (3%) in the barrier layers was investigated. Heterostructures with a GaAs/AlGaAs quantum well were studied at a temperature of 4 K. In the absence of a magnetic field, the band gap of the GaAs quantum well is equal to 1.464 eV (Fig. 2). Figure 2 shows the dependence of the two-dimensional combined density of states on the absorbing photon energy for a GaAs quantum well d = 14 nm (nz = 1) at a temperature T = 4 K and a quantizing magnetic field B = 9 T. This graph was created by numerical calculation based on Eq. (9). In Fig. 2, the number of discrete Landau levels of charge carriers is fourteen. These peaks (discrete Landau levels of charge carriers (\(N_{L}^{{{\text{cv}}}}\) = 14)) are observed in the allowed band of the GaAs quantum well. It shows the two-dimensional combined density of states in a quantizing magnetic field \(\hbar \omega_{c} = 0.02\;{\text{eV}}\) at T = 4 K, kT = 4.10–4, \(\frac{{\hbar \omega_{c} }}{{{\text{kT}}}} = 50,\quad {\text{kT}} < < \hbar \omega_{c}\). In this case, the thermal smearing of the Landau levels of charge carriers is very weak and the two-dimensional combined density of states does not feel any deviation from the ideal shape. In this plot, the valence band and conduction band are chosen as symmetrical energy spectra. Then, from the first discrete Landau level of holes (NL(V) = 0) to NL(V) = 6, they are located higher from the beginning of the ceiling of the valence band of the quantum well. As well as other discrete Landau levels of electrons are located above the bottom of the conduction band of the quantum well.

Fig. 2
figure 2

Dependence of the two-dimensional combined density of states on the absorbing photon energy in direct-gap heterostructures with GaAs/AlGaAs quantum wells (d = 14 nm) at a temperature T = 4 K and a quantizing magnetic field B = 9 T

Full size image

Figure 3 shows the influence of temperature on the dependence of the two-dimensional combined density of states on the absorbing photon energy in direct-gap heterostructures with GaAs/AlGaAs quantum wells (d = 14 nm) under the action of a quantizing magnetic field. Here, the amount of induction of the quantizing magnetic field is 9 T and plots of \(N_{{{\text{jds}}}}^{2d} \left( {\hbar \nu , E_{{{\text{cv}}}}^{2d} \left( {B,T,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right) } \right) \) are created for temperatures of 4 K, 20 K, 40 K, 60 K, 77 K. It can be seen from Fig. 3 that with increasing temperature, the sharp peaks of the Landau levels begin to smooth out, and at sufficiently high temperatures the discrete energy densities of states turn into continuous energy spectra. These results were obtained for a constant quantum well thickness and magnetic field. With increasing temperature, the sharp peaks of the Landau levels of charge carriers begin to smooth out (Fig. 3) and at \({\text{kT}} \approx \hbar \omega_{c}^{{{\text{cv}}}}\) gradually disappear. And also, at sufficiently high temperatures \({\text{kT}} > \hbar \omega_{c}^{{{\text{cv}}}}\) \(N_{{{\text{jds}}}}^{2d} \left( {\hbar \nu , E_{{{\text{cv}}}}^{2d} \left( {B,T,d,N_{L}^{{{\text{cv}}}} ,n_{Z} } \right) } \right) \) they turn into a continuous combined density of states of the quantum well and there will be no feel the influence of a quantizing magnetic field. In addition, as the temperature increases, the sharp peaks in the Landau levels of charge carriers, due to the quantization of the energy levels of electrons and holes in the allowed quantum well gradually smooth out. This leads to the fact that at the temperature T = 40 K, kT = 3, 5·10–3, \({\text{kT}} \approx \hbar \omega_{c}^{{{\text{cv}}}}\) discrete Landau levels of quantum well charge carriers become invisible. At a temperature of 77 K, the discrete Landau levels in the allowed band of the GaAs/AlGaAs quantum well are almost invisible and coincide with the two-dimensional combined density of states in the absence of a magnetic field. Hence, the two-dimensional combined density of states in the conduction band and the valence band of the quantum well are observed at temperatures \({\text{kT}} < \hbar \omega_{c}^{{{\text{cv}}}}\). Starting from temperatures of the order of \(0.5\;{\text{kT}}\sim \hbar \omega_{c}^{{{\text{cv}}}}\), the two-dimensional combined densities of states due to Landau quantization in the allowed band of the quantum well are not observed.

Fig. 3
figure 3

Effects of temperature on the dependence of the two-dimensional combined density of states on the absorbing photon energy in direct-gap heterostructures with GaAs/AlGaAs quantum wells (d = 14 nm) under the influence of a quantizing magnetic field B = 9 T

Full size image

In this case, the measurements give a continuous spectrum of the two-dimensional combined density of states. Changing the cyclotron frequency of the magnetic field \(\omega_{c}^{{{\text{cv}}}}\) changes the energy distance between discrete Landau levels of charge carriers in the quantum well (Fig. 4). Figure 4 shows graphs of the two-dimensional combined density of states in direct-gap heterostructures with GaAs/AlGaAs quantum wells (d = 14 nm) at various magnetic fields B = 9 T and 12 T. As can be seen from these figures, with an increase in the induction of the quantizing magnetic field, we obtain a change in the discrete peaks of the Landau levels of charge carriers.

Fig. 4
figure 4

Influence of a quantizing magnetic field on the dependence of the two-dimensional combined density of states upon absorption of photon energy in direct-gap heterostructures with GaAs/AlGaAs (d = 14 nm) quantum wells at a temperature of T = 4 K

Full size image

3.2 Comparison of theory with experimental results in the absence and presence of a quantizing magnetic field

As is known from work [29], the influence of a quantizing magnetic field on two-dimensional electron systems will demonstrate very interesting physical properties arising from the quantum confinement of charge carriers in a quantum well. Because of this quantum constraint, the 2D combined density of states of charge carriers in a quantum well exhibits Van Hove singularities, whereas in the case of an ideal infinite zero-dimensional lattice (quantum dot), the combined density of states tends to infinity for well-defined energy values. Limiting a large number of 2D combined densities of states to a single energy value leads to striking physical properties such as extremely high magneto-optical absorption, increased thermoelectric power, quantized electronic conductivity, etc. Applications based on these properties could lead to important new nanotechnological and optoelectronic devices.

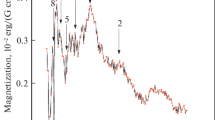
In particular, in work [30], two-dimensional combined densities of states of heterostructures based on an InGaN/GaN quantum well with different radiation wavelengths (violet, blue, and green) operating at different currents were studied. The results show that the blue shift of the emission with increasing current is associated with a change in the two-dimensional combined density of states. In this work, the dependence of the two-dimensional combined density of states of the InGaN/GaN quantum well on the absorbing photon energy in the absence of a magnetic field (B = 0) and at temperatures T = 300 K (Fig. 5) was obtained. Here, the band gap of the InGaN/GaN quantum well is Eg(0) = 3.2 eV, and the thickness of the quantum well is d = 10 nm.

Fig. 5
figure 5

Dependence of the two-dimensional combined density of states on the energy-absorbing photon in direct-gap heterostructures based on an InGaN/GaN quantum well in the presence of a magnetic field and at room temperature [30]

Full size image

Now, let's apply the proposed model to the InGaN/GaN material. Figure 6 shows the influence of the quantizing magnetic field on the dependence of the two-dimensional combined density of states of the InGaN/GaN quantum well on the energy-absorbing photon at different temperatures. Here, B = 10 T, T = 300 K, 77 K and 5 K. Figures 5 and 6 show similar results with and without a magnetic field at room temperature. At room temperature, the influence of the magnetic field is not felt when the photon energy of the two-dimensional combined density of states is absorbed, since \({\text{kT}} \gg \hbar \omega_{c}\). The combined density of states behaves as if there is no magnetic field.

Fig. 6
figure 6

Influence of temperature and quantizing magnetic field on the two-dimensional combined density of states in direct-gap heterostructures based on the InGaN/GaN quantum well. Calculated using the model

Full size image

It follows from this that the proposed model obeys certain laws, and this indicates the correctness of the model.

Using Eq. (9), one can observe oscillations of the two-dimensional combined density of states (6) at different low temperatures. Also, a new analytical expression (the proposed new model) allows one to obtain the results of changes in the thickness of the quantum well associated with the combined density of states. This leads to a theoretical analysis of some experimental data.

4 Conclusions

Based on the work carried out, the following conclusions can be drawn: An analytical expression is obtained for the oscillations of the two-dimensional combined density of states in the allowed band of a quantum well under the action of a quantizing magnetic field. A new model has been developed for calculating the effect of a quantizing magnetic field on the temperature dependence of the two-dimensional combined density of states in direct-gap heterostructures with quantum wells. The temperature dependence of the oscillations of the two-dimensional combined density of states of the quantum well is explained by the thermal smearing of the Gaussian distribution function in a strong magnetic field. Based on the proposed new models, the Landau levels of charge carriers in a direct-gap quantum well are determined in a wide temperature range. The experimental results were interpreted using the oscillations of the combined density of states of the quantum well in a quantizing magnetic field. The calculation results were compared with experimental results obtained for heterostructures based on an InGaN/GaN quantum well in a quantizing magnetic field at various temperatures.