1 Introduction

General relativity (GR) provides an acceptable explanation of numerous specifications of the universe that are based upon affirmed evidence and different theories. Currently, we need to focus on those research problems that are yet undetermined, such as the non-singularity in the standard Big-Bang cosmology. In order to overcome the problem of singularity, we require to develop a scientific framework, i.e., a model that should incorporate the known universe and can also provide an acceptable explanation for the universe as an oscillatory system. The idea of an oscillatory universe ensures that the present universe came into being after the disintegration of the previous universe [1]. Alternatively, an emerging idea of a bouncing universe was presented. The idea of a bouncing universe satisfactorily explains the Big-Bang cosmology and provides a relevant solution to the non-singularity problem in the field of Big-Bang cosmology [2, 3]. The idea that the universe experiences bouncing is widely appreciated, and other fields of cosmology, such as Brane cosmology [4] and vector field [5], have considered this idea to provide an explanation of different phenomena. Possibly, the bouncing in the universe can be explained as that due to the nonvanishing charge, bouncing can occur. This bouncing gives rise to a phase shift of the universe from a contracting phase to an expanding phase. During this phase shift, the Hubble parameter (H) changes in range from \(H<0\) (contracting phase) to \(H>0\) (expanding phase), and at \(H =0\)(bouncing phase), we get the point where bounce occurs [6,7,8,9].

Presently, with the availability of experimental data and different relevant theories that explain the expansion of the Universe, we have a comprehensive literature which establishes the accelerated phase expansion of the Universe. Firstly, the idea of accelerating expansion arose with the observations of Type Ia supernova [10], related to LSS (large-scale structure) [11] and cosmic microwave background [12]. It is observed that the universe is experiencing an expansion of an accelerated nature due to the presence of an unknown energy. This unknown energy is referred to as dark energy (DE). This so-called DE contributes almost \(70\%\) of the total universe’s energy. The universe is filled with a fluid of perfect nature that has negative pressure. This perfectly filled universe also obeys an EoS (equation of state), and the parameter of this EoS has a value of less than 1 (so-called phantom phase). There are different possibilities to explain the framework of DE, such as the cosmological constant [13], the scalar fields (that incorporate phantom, tachyon, quintom, quintessence, etc.) [14,15,16,17,18,19,20]. Some models, like holographic [21,22,23,24,25,26], modified [27,28,29], interacting [30,31,32,33,34,35], and Brane-world [36,37,38], also provide an acceptable explanation of DE.

Keeping in view the above-mentioned list of models, the appropriate choice is the modified theory of gravity. In comparison with other candidates, the modified theory of gravity has a significant edge over them because it avoids tedious computation of numerical solutions. Moreover, the modified theory of gravity is compatible with the latest experimental data related to DE and the late-time accelerating universe. In the literature, corresponding to the modified theory of gravity, different models have been developed using distinct techniques [39,40,41,42]. By transforming the Ricci scalar R to f(R) with a random function in the gravity action term, one such possible model is obtained. f(R) is the name of this model [43, 44]. When compared to traditional gravity models, the f(R) gravity is thought to be a better choice for justifying DE. The Einstein–Hilbert action, which was recently introduced, is defined by f(R) and the matter Lagrangian. This Einstein–Hilbert action produces Friedmann equations using the background of the FLRW (Friedmann–Lemaître–Robertson–Walker) metric.

In this paper, we use f(R) gravity calculations to solve the problem of the initial singularity in the Big-Bang theory. To achieve this goal, we will use distinct models within the framework of f(R) gravity, as well as bounce cosmology with f(R) gravity. We will establish that the phase shift is accelerated in nature. Initially, it accelerates from the contracting phase and then, by passing through a bouncing point, finally reaches the expanding phase. This specific problem is illustrated by using a scale factor (a(t)). The a(t) obeys the given conditions as follows: during the contracting phase, the derivative of the scale factor (\(\dot{a}<0\)) is negative; during the expanding phase, the \((\dot{a}>0\)) is positive; and at the bounce point, the \((\dot{a}=0\)). For the purpose of clarity and confirmation, these conditions are also illustrated by the relevant figures.

Moreover, we present a possible description of the idea that f(R) gravity is a source of DE. To support such a claim, we will reformulate f(R) gravity by incorporating the red-shift parameter. In accordance with the aforementioned concept, a parametrization for f(R) gravity will be investigated, which may provide acceptable arguments for the description of the universe’s accelerated expansion. Finally, we will use an arbitrary function (quantity of sound speed \(c_{s}^2\)) to test the stability of our proposed models.

This paper is classified as follows: In Sect. 2, we investigated f(R) gravity using four different models, and as a result, we solved field equations for the FLRW metric in a perfect fluid background. Then, in Sect. 3, we presented an analysis of the universe’s bouncing nature using H and a parameters, as well as different f(R) gravity models. We extended the reconstruction of the f(R) gravity using a new (red-shift) parameter in Sect. 4 of this article. We further used this red-shift parameter to redefine effective pressure, effective energy density, and the cosmological parameters. In Sect. 5, we checked the stability of the proposed models. In the last section of this article, we briefly described our obtained results and also presented a suitable conclusion.

2 f(R) gravitational theory

We can write the Einstein–Hilbert action (S) using the f(R) gravity background. The modified action (\(S_{f(R)}\) is as follows:

$$\begin{aligned} S_{f(R)}=\frac{1}{2\kappa }\int d^4x\sqrt{-g}f(R)+S_M, \end{aligned}$$
(1)

where the symbols used in \(S_f(R)\) are represented as follows: g is the tensor’s determinant, \(\kappa\) is the constant of the above-mentioned coupling, and \(S_M\) represents the action of the matter field. The main goal of this theory is to obtain a standard algebraic expression for the Ricci scalar rather than the cosmological constant (\(\Lambda\)) in the GR action term. Corresponding to Eq. (1), we can calculate the field equations of the f(R) gravity theory by varying \(S_ f(R)\) with respect to \(g_{\mu \nu }\) as follows:

$$\begin{aligned} R_{\alpha \beta }f_R-\frac{1}{2}f(R)g_{\alpha \beta }+\left( g_{\alpha \beta }{\Box } -\nabla _{\alpha }\nabla _{\beta }\right) f_R={\kappa }T_{\alpha \beta }. \end{aligned}$$
(2)

In Eq. (2), \(T_{\alpha \beta }\) represents the tensor of energy momentum in standard form, \(\nabla _{\beta }\) a derivative operator in covariant form, \(f_R\equiv \mathrm{{d}}f/\mathrm{{d}}R\), and \(\Box \equiv \nabla ^{\beta }\nabla _{\beta }\). The \(f_R\) term incorporates second corresponding derivatives of the metric variables, which is frequently named as scalaron, and propagates to a new scalar degree of freedom. By taking a trace of Eq. (2), we can specify the equation of motion (EoM) for scalaron as follows:

$$\begin{aligned} 3\Box {f_R}+{R}f_R-2f(R)={\kappa }T, \end{aligned}$$
(3)

where \(T\equiv T^\beta _{\beta }\). In \(f_R\), Eq. (3) appears to be a second-order differential equation. Equation (3) differs from GR in that the trace of the Einstein field equation yields \(R=-\kappa T\) in GR. This distinction demonstrates that the \(f_R\) term in f(R) gravity produces scalar degrees of freedom. It is not mandatory or implied by the condition \(T =0\) that the Ricci scalar R in dynamics disappears (or is set to a constant value). This makes Eq. (3) an important tool for the discussion of a number of unrevealed but fascinating cosmic fields, such as the Newtonian limit, and stability. The use of a constant Ricci scalar in conjunction with the condition \(T_{\alpha \beta }=0\) in Eq. (3) yields the following:

$$\begin{aligned} Rf_R-2f(R)=0. \end{aligned}$$
(4)

By making an appropriate choice of any feasible formulation of f(R) gravity, the above-mentioned equation is named the Ricci algebraic equation. In the case of obtaining constant roots of the above-mentioned equation, such as \(R=\Lambda\) (say), then Eq. (3) produces the following expression:

$$\begin{aligned} R_{\alpha \beta }=\frac{g_{\alpha \beta }\Lambda }{4}. \end{aligned}$$
(5)

Thus, it shows (anti) de Sitter as the maximally symmetric solution. The restructured form of Eq. (2) can be written as follows:

$$\begin{aligned} G_{\alpha \beta }=\frac{\kappa }{f_R}\left( \overset{(D)}{T_{\alpha \beta }}+T_{\alpha \beta }\right) \equiv {T_{\alpha \beta }^{\text {net}}}, \end{aligned}$$
(6)

where the symbol \(G_{\alpha \beta }\) denotes an Einstein tensor and \(\overset{(D)}{T_{\alpha \beta }}\) represents the energy-momentum tensor of effective form. The equivalent expression for \(\overset{(D)}{T_{\alpha \beta }}\) is as follows:

$$\begin{aligned} \overset{(D)}{T_{\alpha \beta }}=\frac{1}{\kappa }\left\{ \nabla _{\alpha }\nabla _{\beta }f_R-\Box f_Rg_{\alpha \beta }+\big (f-Rf_R\big )\frac{g_{\alpha \beta }}{2}\right\} . \end{aligned}$$

We used the FLRW background metric,

$$\begin{aligned} \mathrm{{d}}{s^2} = -\mathrm{{d}}{t^2}+ a^2\mathrm{{d}}{r^2}+{a^2}\left( {\mathrm{{d}}{\theta ^2} + {{r^2}{\sin }^2}\theta \mathrm{{d}}{\phi ^2}}\right) , \end{aligned}$$
(7)

In Eq. (7), a denotes a scale factor that is dependent on t. The Ricci scalar R associated with metric Eq. (7) is given by:

$$\begin{aligned} R = 6\dot{H(t)}+ 12 H(t)^2. \end{aligned}$$
(8)

Here, H(t) represents the Hubble parameter, which is \(H(t) = \frac{\dot{a(t)}}{a(t)}\), while \(\dot{H(t)}\) denotes the derivative of H(t) with respect to cosmic time (t).

By solving Eq. (6) for metric Eq. (7) results in the following:

$$\begin{aligned} 3H(t)^2&= \frac{1}{f_R}\left[ \kappa ^2 \rho _m+\frac{1}{2}\{R f_R-f\}-3 H(t) \dot{R} f_{RR}\right] , \end{aligned}$$
(9a)
$$\begin{aligned} -[2 \dot{H(t)}+ 3 H(t)^2]&= \frac{1}{f_R}\left[ \kappa ^2 P_m-\frac{1}{2}\{R f_R-f\}+\dot{R}^2 f_{RRR} \right. \\&\quad \left. +2 H(t) \dot{R} f_{RR}+\ddot{R} f_{RR}\right] . \end{aligned}$$
(9b)

In Eqs. (9a and 9b), the symbols \(\rho _m\) and \(P_m\) denote energy density and pressure, respectively. By considering the conservation equation, \(\nabla _\alpha T^{(m){\alpha \beta }} = 0\), as well as the EoS parameter, \(\omega _m= \frac{P_m}{\rho _m}\), the following equation can be obtained:

$$\begin{aligned} \dot{\rho }_m + 3 \rho _m(\omega _m + 1)H(t) = 0, \end{aligned}$$
(10)

the solution of the above equation gives,

$$\begin{aligned} \rho _m = \rho _{m_0} a^{-3(\omega _m + 1)}. \end{aligned}$$
(11)

Furthermore, by comparing standard Friedmann equations to the present approach,

$$\rho _{net} = \frac{3}{\kappa ^2} H(t)^2$$

and

$$\begin{aligned} P_\mathrm{{net}}= -\frac{1}{\kappa ^2} (3 H(t)^2+2 \dot{H(t)}), \end{aligned}$$

Additionally, by considering standard Friedmann equations and comparing with the present approach,

$$\begin{aligned} \rho _\mathrm{{net}} = \frac{3}{\kappa ^2} H(t)^2 \end{aligned}$$

and

$$\begin{aligned} P_\mathrm{{net}} = -\frac{1}{\kappa ^2} (3 H(t)^2+2 \dot{H(t)}), \end{aligned}$$

Equations () are reexpressed as follows:

$$\begin{aligned} \rho _\mathrm{{net}}&= \rho _m +\rho _{f(R)} = \kappa ^{-2} \left[ \kappa ^2 \rho _m+3 H(t)^2 (1-f_R)\right. \\&\quad \left. -\frac{1}{2}(f-R f_R)-3 H(t) \dot{R} f_{RR}\right] , \end{aligned}$$
(12a)
$$\begin{aligned} P_\mathrm{{net}}&= P_m + P_{f(R)} = \kappa ^{-2} \bigg [\kappa ^2 P_m-(3 H(t)^2+2 \dot{H(t)})(1-f_R) \\&\quad + \frac{1}{2}(f-R f_R)+\dot{R}^2 f_{RRR} \\&\quad +2 H(t) \dot{R} f_{RR}+\ddot{R} f_{RR}\bigg ], \end{aligned}$$
(12b)

where the symbols \(\rho _\mathrm{{net}}\) and \(P_\mathrm{{net}}\) denote net energy density and net pressure, respectively, while

$$\begin{aligned} \rho _{f(R)}&= \kappa ^{-2} \left[ 3 H(t)^2 (1-f_R)-\frac{1}{2}(f-R f_R)-3 H(t) \dot{R} f_{RR}\right] , \end{aligned}$$
(13a)
$$\begin{aligned} P_{f(R)}&= \kappa ^{-2} \left[ -(2 \dot{H(t)}+3 H(t)^2)(1-f_R)\right. \\&\quad \left. +\frac{1}{2}(f-R f_R)+\dot{R}^2 f_{RRR}+2 H \dot{R} f_{RR}+\ddot{R} f_{RR}\right] . \end{aligned}$$
(13b)

For net terms, we can reexpress the conservation equation using Eq. () as,

$$\begin{aligned} \dot{\rho }_\mathrm{{net}} + 3\rho _\mathrm{{net}} H(t) (1 + \omega _\mathrm{{net}}) = 0, \end{aligned}$$
(14)

here

$$\begin{aligned} \omega _\mathrm{{net}} = \frac{P_\mathrm{{net}}}{\rho _\mathrm{{net}}} = -\left( 1+\frac{2 \dot{H(t)}}{3 H(t)^2}\right) , \end{aligned}$$
(15)

denotes parameter that corresponds to effective EoS.

3 Reconstruction method for hybrid expansion law model

In this section, we are remodeling the present modified gravitational models. We use the methods presented in Refs. [45,46,47] for this remodeling, followed by the introduction of proper functions P and Q, which are functions of a scalar field (t), where t denotes the cosmic time. Provided that no matter what content is present, the action in Eq. (1) is expressed as follows:

$$\begin{aligned} I = \int {\mathrm{{d}}{x^4}\sqrt{ - g} \left[ {P R+ Q + {L_m}} \right] }. \end{aligned}$$
(16)

Now, by solving the above equation along with Eq. (9), we acquire,

$$\begin{aligned} Q = - 6{H^2}P' - 6P{H^2}, \end{aligned}$$
(17)

where prime denotes a derivative with respect to time, while the second equation reduces to the following,

$$\begin{aligned} P'' - HP' + 2PH'= 0. \end{aligned}$$
(18)

We obtain the solution of the above-mentioned differential equation for the case of hybrid expansion law. By manipulating the obtained solution, we express f(R) in general form as,

$$\begin{aligned} f(R)=P(R)R + Q(R). \end{aligned}$$
(19)

In order to derive exact solutions, we will consider the hybrid expansion law for the scale factor as written: [48]

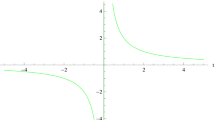
$$\begin{aligned} a(t)=t^n \mathrm{{e}}^{\beta t}, \end{aligned}$$
(20)

where n is an integer while \(\beta\) represents a constant. The bouncing behavior of such a type is demonstrated in Fig. 1.

Fig. 1
figure 1

Hubble parameter for hybrid expansion law

Full size image

By using the above-mentioned scale factor and probing for P and Q, we obtain the following,

$$\begin{aligned} p&= {t^{\frac{1}{2}\left( {{a_1} + n + 1} \right) }}\left[ {c_1}U\left( {\frac{1}{2}\left( {n + {a_1} + 1} \right) ,{a_1} + 1,t} \right) \right. \\&\quad \left. + {c_2}L_{\frac{1}{2}\left( { - {a_1} - n - 1} \right) }^{{a_1}}\left( t \right) \right] , \end{aligned}$$
(21)

and

$$\begin{aligned} Q&= 3{t^{\frac{1}{2}\left( {{a_1} + n - 3} \right) }}\left( {n + t} \right) \left[ {{c_1}\left\{ { - \left( {{a_1} + 3n + 2t + 1} \right) } \right\} } \right. U\left( {\frac{1}{2}\left( {n + {a_1} + 1} \right) ,{a_1} + 1,t} \right) \\&\quad + {c_1}t\left( {{a_1} + n + 1} \right) U\left( {\frac{1}{2}\left( {n + {a_1} + 3} \right) ,{a_1} + 2,t} \right) \\&\quad + {c_2}\left. {\left\{ {2tL_{\frac{1}{2}\left( { - {a_1} - n - 3} \right) }^{{a_1} + 1}\left( t \right) - \left( {{a_1} + 3n + 2t + 1} \right) L_{\frac{1}{2}\left( { - {a_1} - n - 1} \right) }^{{a_1}}\left( t \right) } \right\} } \right] , \end{aligned}$$
(22)

where,

$$\begin{aligned} {a_1} = \sqrt{{n^2} + 10n + 1}, \end{aligned}$$
(23)

and U(a, b, z) is hypergeometric function and \(L^{a}_{n}(x)\) is the generalized Laguerre polynomial.

Substituting these values into Eq. 19,

$$\begin{aligned} \begin{aligned} f&= {t^{\frac{1}{2}\left( {{a_1} + n - 3} \right) }}\left[ {R{t^2}} \right. \left\{ {{c_1}U\left( {\frac{1}{2}\left( {n + {a_1} + 1} \right) ,{a_1} + 1,t} \right) + {c_2}L_{\frac{1}{2}\left( { - {a_1} - n - 1} \right) }^{{a_1}}\left( t \right) } \right\} \\&\quad - 6{\left( {n + t} \right) ^2}\left\{ {{c_1}U\left( {\frac{1}{2}\left( {n + {a_1} + 1} \right) ,{a_1} + 1,t} \right) + {c_2}L_{\frac{1}{2}\left( { - {a_1} - n - 1} \right) }^{{a_1}}\left( t \right) } \right\} \\&\quad + 3\left( {n + t} \right) \left\{ {{c_1}\left( { - \left( {{a_1} + n + 1} \right) } \right) } \right. U\left( {\frac{1}{2}\left( {n + {a_1} + 1} \right) ,{a_1} + 1,t} \right) \\&\quad + {c_1}t\left( {{a_1} + n + 1} \right) U\left( {\frac{1}{2}\left( {n + {a_1} + 3} \right) ,{a_1} + 2,t} \right) \\&\quad + {c_2}\left. {\left. {\left( {2tL_{\frac{1}{2}\left( { - {a_1} - n - 3} \right) }^{{a_1} + 1}\left( t \right) - \left( {{a_1} + n + 1} \right) L_{\frac{1}{2}\left( { - {a_1} - n - 1} \right) }^{{a_1}}\left( t \right) } \right) } \right\} } \right] . \end{aligned} \end{aligned}$$
(24)

Furthermore, cosmic time has the following relationship to the Ricci scalar:

$$\begin{aligned} t_\pm = \frac{{12n \pm \sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } }}{{R - 12}}, \end{aligned}$$
(25)

where \(R\ne 12\) and by assuming \(t_+\), we get the reconstructed f(R) as follows:

$$\begin{aligned} \begin{aligned} {f_ + }(R)&= \frac{3}{{{{\left( {\sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } + 12n} \right) }^2}}}{\left( {\frac{{\sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } + 12n}}{{R - 12}}} \right) ^{\frac{1}{2}\left( {a_1 + n + 1} \right) }}\\&\qquad ({c_1}(n(3R\left( {4a_1 + \sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } + 16} \right) - \left( {a_1 + 3} \right) {R^2} + 12\sqrt{6} \\&\qquad \sqrt{n\left( {2nR - R + 12} \right) } - 144) - \sqrt{6} \left( {a_1 + 1} \right) \left( {R - 12} \right) \sqrt{n\left( {\left( {2n - 1} \right) R + 12} \right) } \\&\quad + {n^2}R\left( {R + 36} \right) )U\left( {\frac{1}{2}\left( {a_1 + n + 1} \right) ,a_1 + 1,\frac{{12n + \sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } }}{{R - 12}}} \right) \\&\quad + {c_1}n\left( {a_1 + n + 1} \right) (R\left( {\sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } + 24n - 6} \right) + 12\sqrt{6} \\&\qquad \sqrt{n\left( {2nR - R + 12} \right) } + 72)U\left( {\frac{1}{2}\left( {a_1 + n + 3} \right) ,a_1 + 2,\frac{{12n + \sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } }}{{R - 12}}} \right) + \\&\qquad {c_2}((n(3R(4a_1 + \sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } + 16) - \left( {a_1 + 3} \right) {R^2} + 12\sqrt{6} \\&\qquad \sqrt{n\left( {2nR - R + 12} \right) } - 144) - \sqrt{6} \left( {a_1 + 1} \right) \left( {R - 12} \right) \sqrt{n\left( {\left( {2n - 1} \right) R + 12} \right) } \\&\quad + {n^2}R\left( {R + 36} \right) )L_{\frac{1}{2}\left( { - a_1 - n - 1} \right) }^{a_1}\left( R \right) + 2n(R\left( {\sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } + 24n - 6} \right) \\&\quad + 12\sqrt{6} \sqrt{n\left( {2nR - R + 12} \right) } + 72)L_{\frac{1}{2}\left( { - a_1 - n - 3} \right) }^{a_1 + 1}\left( R \right) )). \end{aligned} \end{aligned}$$
(26)
Fig. 2
figure 2

The behavior of reconstructed function for different values of n

Full size image

The behavior of this reconstructed function can be seen in Fig. 2.

4 The bouncing behavior in modified gravitational theory

This section describes the universe’s bouncing behavior as well as bouncing conditions using the proposed models within the framework of the f(R) gravity theory. The occurrence of the bounce gives rise to fluctuations in the universe. The universe undergoes a phase shift by transferring fluctuations initially from a phase of contracting to a phase of expanding. Under the formulation of the Big-Bang cosmology theory, this phase shift provides a solution of non-singularity [6,7,8,9].

Consequently, for an effective bounce, the Hubble parameter runs through the range from \(H<0\)(contracting) to \(H>0\) (expanding) and satisfies \(H=0\) (bouncing) for the bounce point. Moreover, the problem of the bouncing universe can also be expressed by taking into account the scale factor a. The variance of the scale factor is related to the phase shift in the universe as follows: during the contracting phase, the scale factor decreases to \(\dot{a}<0\), while during the expanding phase, the scale factor increases to \(\dot{a}>0\). Additionally, at the point of bounce and around this pint, the scale factor obeys the variance conditions of \(\dot{a}=0\) and \(\ddot{a}>0\).

Considering the fact that for a bouncing universe, H ranges from the lower limit of \(H<0\) to the upper limit of \(H>0\) with respect to time evolution, additionally it puts a necessary condition on the Hubble parameter that at the bounce point when \(H =0\), then the derivative of the Hubble parameter must be greater than zero (\(\dot{H}_\mathrm{{bounce}}>0\)) at this point as:

$$\begin{aligned} \dot{H}_\mathrm{{bounce}}=-\frac{\kappa ^2}{2}(1+\omega _\mathrm{{net}}) \rho _\mathrm{{net}} > 0, \end{aligned}$$
(27)

the above-mentioned condition results in \(\rho _\mathrm{{net}}>0\) with \(\omega _\mathrm{{net}}<-1\).

At present, at the bounce point, the relevant bounce conditions for the model can be determined. As a result, in order to obtain the following expression for \(\dot{H}_\mathrm{{bounce}}\) using the condition in Eq. (27) along with Eq. (), it is necessary to have \(\dot{H}_\mathrm{{bounce}}>0\) and \(H_\mathrm{{bounce}}= 0\).

$$\begin{aligned} \dot{H}_\mathrm{{bounce}}=(2 f_R)^{-1}\left[ -\kappa ^2(\rho _m+P_m)+\dot{R}^2 f_{RRR}+\ddot{R} f_{RR}\right] >0. \end{aligned}$$
(28)

Now, using the proposed models in the framework of f(R) gravity, we will thoroughly investigate the universe’s bouncing behavior. Examining bouncing in the f(R) gravity framework is advantageous because it allows us to make specific choices for our investigation. Some of the suggested compatible forms of such models within the framework of f(R) gravity are denoted as [49]:

  • Model 1

    We consider the

    $$\begin{aligned} f(R)=R+\alpha _1 R^2 - \frac{\alpha _2}{R}, \end{aligned}$$
    (29)

    where \(\alpha _1\) and \(\alpha _2\) are the free parameters. The first term is a quadratic correction proposed by Starobinsky [50], while the last term is given in Ref. [51, 52].

  • Model 2

    We consider the

    $$\begin{aligned} f(R)=R + \beta _1 \ln \left[ \beta _2 R\right] , \end{aligned}$$
    (30)

    where \(\beta _1\) and \(\beta _2\) act as free parameters. The term proposed in Ref. [53] is proportional to \(\ln (R)\) or \(R^{-n}(\ln (R))^{m}\)

  • Model 3

    We consider the

    $$\begin{aligned} f(R)=R+\gamma _1 e^{\left( -\gamma _2 R\right) }, \end{aligned}$$
    (31)

    where \(\gamma _1\) and \(\gamma _2\) are the free parameters.

  • Model 4

    We consider the

    $$\begin{aligned} f(R)=R+\frac{\mu _1}{R}. \end{aligned}$$
    (32)

    where \(\mu _1\) is constant.

Fig. 3
figure 3

The scale factor, a(t), in terms of cosmic time

Full size image
Fig. 4
figure 4

The Hubble parameter(H(t)) in terms of cosmic time

Full size image

Moreover, by inserting models mentioned in Eqs. (29), (30), (31) and (32) in Eq. () separately and then by solving using numerical techniques, we obtain corresponding numerical solutions. Through plots of these numerical solutions, one can easily evaluate the cosmological parameters w.r.t. cosmic time as shown in Figs. 3 and 4.

The bouncing behavior in regime of distinct choices of f(R) is as following,

In case of model 1 mentioned in Eq. (29), we can see the bouncing behavior in the first part of Fig. 4, e.g., H runs from bounce point (\(H(t \sim -0.21562)=0\)) as \(H(t)<0\) to \(H(t)>0\), while the lowest scale factor is or \(\dot{a}(t \sim -0.21562)=0\).

In Fig. 4, the bouncing action can be noticed as \(H(t \sim -0.65023)=0\) , while \(H(t)<0\) to \(H(t)>0\). On the other hand, we notice that the minimal element for the scale is or \(\dot{a}(t \sim -0.65023)=0\) in case of model 2.

The same bouncing behavior is noticed in Fig. 4, which exhibit that from the bounce level, the Hubble parameter runs through \(H(t \sim -0.375342)=0\) as \(H(t)<0\) to \(H(t)>0\). Similarly, we can see how the minimal element for the scale or \(\dot{a}(t \sim -0.375342)=0\) in case of model 3.

Moreover, we are confident of the possibility of observing the bouncing behavior in Fig. 4. We can see in Fig. 4 that in the case of model 4, the Hubble parameter ranges from \(H(t \sim -0.260048)=0\) as \(H(t)<0\) to \(H(t)>0\), while the minimal element for the scale or \(\dot{a}(t \sim -0.260048)=0\).

Furthermore, Figs. 5 and 6 exhibit the variation of \(\rho _\mathrm{{net}}\) and \(P_\mathrm{{net}}\) in terms of cosmic time, respectively. It is noticed that \(\rho _\mathrm{{net}}>0\) and \(P_\mathrm{{net}}<0\) vary with respect to cosmic time, which provides an evidence for an accelerated universe. Figure 7 exhibits the variation of EoS in terms of cosmic-time. One can notice in Fig. 7 that there is a crossing occurring over divide line (phantom-divide line); this relates the problem with experimental data coming from late-time observations and crossing over phantom-divide line [54, 55].

In the next section, we will be reconstructing the above-mentioned model using red-shift parameter.

Fig. 5
figure 5

The energy density (\(\rho _\mathrm{{net}}\)) and pressure (\(P_\mathrm{{net}}\)) in terms of cosmic time under Models 1 and 2

Full size image
Fig. 6
figure 6

The energy density, \(\rho _\mathrm{{net}}\), and pressure, \(P_\mathrm{{net}}\), in terms of cosmic time under Models 3 and 4

Full size image
Fig. 7
figure 7

The variation of EoS parameter, \(\omega _\mathrm{{net}}\) w.r.t. cosmic time

Full size image

5 Reconstruction through red-shift

This section consists of the exploration of the described model using the red-shift parameter(z). This red-shift parameter can be written as \(z=\frac{a_\mathrm{{initial}}}{a(t)}-1\), where \(a_\mathrm{{initial}}\) represents the scale factor’s initial value. This \(a_\mathrm{{initial}}\) refers to the universe at present. The description of the red-shift parameter in this manner ensures that cosmic z is zero in late time. As a result, another dimensionless parameter, r(z), is defined as \(r(z)=\frac{H(z)^{2}}{H_\mathrm{{initial}}^{2}}\) in terms of the Hubble parameter. The \(H_\mathrm{{initial}}\) in the r(z) expression represents the initial value of the Hubble parameter for the current universe. To re-express the above-mentioned Friedmann equations involving the red-shift parameter z, we must first introduce a differential equation with the differentiation variable cosmic time t. Differential equation is of the following form:

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t}=-H(1+z)\frac{\mathrm{{d}}}{\mathrm{{d}}z}. \end{aligned}$$
(33)

The re-expressed form of Eqs. (8) and (12) involving the red-shift parameter z is now as follows:

$$\begin{aligned} R&=12H_{0}^{2}r-3H_{0}^{2}(1+z)\acute{r}, \end{aligned}$$
(34)
$$\begin{aligned} \rho _\mathrm{{net}}&=\frac{1}{\kappa ^{2}}\left[ \kappa ^{2}\rho _{m}+3H_{0}^{2}r(f_{R}(z)+1) -\frac{3}{2}H_{0}^{2}(1+z)\acute{r}f_{R}(z) \right. \\&\left. \quad +3H_{0}^{2}(1+z)rf_{R}'(z)-\frac{1}{2}f(z)\right] , \end{aligned}$$
(35)
$$\begin{aligned} P_\mathrm{{net}}&=\frac{1}{\kappa ^{2}}\left[ \kappa ^{2}P_{m}+\frac{1}{2}H_{0}^{2}(1+z) \acute{r}(f_{R}(z)+2)\right. \\&\left. \quad -3H_{0}^{2}r(f_{R}(z)+1)+\frac{1}{2}f(z) +H_{0}^{2}(1+z)^{2}rf_{R}''(z)\right. \\&\left. \quad +\frac{1}{2}H_{0}^{2}(1+z)^{2}\acute{r}f_{R}'(z)-H_{0}^{2}(1+z)rf_{R}'(z)\right] . \end{aligned}$$
(36)

The derivative w.r.t. z is represented by prime in Eqs. (35) and (36). The energy density of matter \(\rho _m\), the function f(R), and its derivative with respect to R are denoted as follows:

$$\begin{aligned} \rho _{m}=\rho _{m_{0}}\left( \frac{a_0}{1+z}\right) ^{-3(1+\omega _{m})}. \end{aligned}$$
(37)

For now, we will explain the origination of dark energy by redeveloping the model. For this specific purpose, we have introduced a function r(z). This function is fitted with the experimental data collected from the supernova [56, 57]. To achieve the best fit, the parametrization of r(z) involving the red-shift parameter is defined as a polynomial of third degree, as shown in [58, 59]:

$$\begin{aligned} r(z)=\Omega _{m_{0}}(1+z)^{3}+A_{0}+A_{1}(1+z)+A_{2}(1+z)^{2}. \end{aligned}$$
(38)

\(A_{0}=1-A_{1}-A_{2}-\Omega _{m_{0}}\). An important point to note here is that when \(A_{1}=A_{2}=0\), this parametrization agrees well with the \(\Lambda _{CDM}\) model as well as \(A_{0}=1-\Omega _{m_{0}}\). According to Ref. [54], the best fit parameters are \(\Omega _{m_{0}}=0.3\), \(A_{1}=-4.16\pm 2.53\) and \(A_{2}=1.67\pm 1.03\). In the present work, to achieve the best fit, parameters are adjusted as \(\Omega _{m_{0}}=0.3\), \(A_{0}=3.2\), \(A_{1}=-3.5\) and \(A_{2}=1\). It is worth mentioning here that these free parameters are of great importance for accomplishing this job. This selection of parameters is based upon positive and negative values of net energy density and net pressure, respectively, and also upon the overlapping of EoS over the phantom divide line.

After this, the cosmological parameters are acquired using Eq. (38) into Eqs. (35–36 ). The newly obtained cosmological parameters involve red-shift. As a result, we plot \(\rho _\mathrm{{net}}\), \(P_\mathrm{{net}}\), and \(\omega _\mathrm{{net}}\) with the red-shift parameter. These plots are shown in Figs. 8, 9 and 10.

For the assumption of choice 1, the net EoS variation shows that the value of EoS is approximately equal to \(-0.934827\) in late time (\(z=0\)). Similarly, in the case of option 2, the net EoS variation shows that the value of EoS in late time (\(z=0\)) is approximately equal to \(-1.08582\). The net EoS variation demonstrates that the value of EoS is approximately equal to \(-2.5\) in late time (\(z=0\)) for choice 3 and \(-2.50066\) in the case of choice 4.

This variation of EoS ensures that the expansion of the accelerated universe satisfies the condition \(\omega _\mathrm{{net}}<-1\). The acquired results agree with the results given in Ref. [60, 61] for the case of a flat universe.

Fig. 8
figure 8

The energy density, \(\rho _\mathrm{{net}}\), in terms of red-shift

Full size image
Fig. 9
figure 9

The pressure, \(P_\mathrm{{net}}\), in terms of red-shift

Full size image
Fig. 10
figure 10

The EoS parameter, \(\omega _\mathrm{{net}}\), in terms of red-shift

Full size image

In case of choice 3, the behavior is unusual and further we will check the stability of these models in the next section.

6 Stability

It is critical to argue the stability of the proposed models in f(R) gravity theory here. Keeping in view the fact that this universe is full of perfect fluid, one can treat it as a thermodynamical system. To accomplish this goal, an arbitrary function (quantity of sound speed (\(c_{s}^2\))) is introduced to explain the system composed of the perfect fluid. This arbitrary function can be written in terms of net energy density \(\rho _\mathrm{{net}}\) and net pressure \(P_\mathrm{{net}}\) of the universe as,

$$\begin{aligned} c_{s}^2= \frac{\mathrm{{d}}\rho _\mathrm{{net}}}{\mathrm{{d}}P_\mathrm{{net}}}. \end{aligned}$$

It is established that for a thermodynamical system the value of above function is greater than zero. Consequently, the conditions for stability can be checked when \(c_{s}^2>0\). A thermodynamic system can be explained perturbatively using adiabatic and non-adiabatic approaches. The possible perturbation quantities here can be net energy density, net pressure and entropy of the universe.

Now we define the above-mentioned system as \(P_\mathrm{{net}}=P_\mathrm{{net}}(S,\rho _\mathrm{{net}})\). This system is then solved perturbatively by applying perturbation w.r.t. \(P_\mathrm{{net}}\) as:

$$\begin{aligned} \delta P_\mathrm{{net}}&=\left( \frac{\partial P_\mathrm{{net}}}{\partial S}\right) _{\rho _\mathrm{{net}}}\delta S+\left( \frac{\partial P_\mathrm{{net}}}{\partial \rho _\mathrm{{net}}}\right) _{S}\delta \rho _\mathrm{{net}} \\&=\left( \frac{\partial P_\mathrm{{net}}}{\partial S}\right) _{\rho _\mathrm{{net}}} \delta S+c_{s}^{2}\delta \rho _\mathrm{{net}}, \end{aligned}$$
(39)

In the above equation, the first and second terms of the equation represent non-adiabatic and adiabatic processes, respectively, in the problem of cosmology. Because we are taking the perturbation as an adiabatic in cosmology, in the cosmological system, variations of entropy vanish to zero as \(\delta S=0\). As a result of the aforementioned argument, we only include adiabatically process in our research work.

Differentiating Eqs. (35) and (36) with respect to the red-shift parameter yields the arbitrary function \(c_{s}^2\). Now the calculated function \(c_{s}^2\) appears in terms of the red-shift parameter. By accruing such a function, we now further solve it using numerical techniques and plot it against the red-shift parameter, which is shown in Fig. 11. Considering Fig. 11, we can conclude that in late time (\(z =0\)), the value of \(c_{s}^2\) approaches approximately 2.49306 in the case of model 1 and 0.140505 in the case of model 4, and there are also some other regions where \(c_{s}^2>0\) and thus agrees with the condition \(c_{s}^2>0\). Similarly, in the case of model 2, \(c_{s}^2>0\) by \(z>0.6\). As a result, we see the unusual behavior of model 3, as shown in Fig. 11, in which \(c_{s}^2<0\), implying that model 3 is unstable and bouncing.

Fig. 11
figure 11

The speed of sound, \(c_s^2\), in terms of red-shift

Full size image

7 Conclusions

This research work has been carried out using the FLRW metric. We proposed four distinct viable models and then tested them in the context of f(R) gravity. The findings obtained by using the f(R) gravity in the context of wormhole modelling can also be discussed by mentioning the past works presented in Ref. [62,63,64,65,66,67,68]. We assumed that the fluid was perfect and hence obtained modified Friedmann equations using solutions of the field equations. Then, by modifying gravity, we separated the two functions (\(\rho _\mathrm{{net}}\) and \(P_\mathrm{{net}}\)) and acquired the corresponding useful EoS. Following that, we examined the bouncing behavior of our proposed models with respect to cosmic-time t to see whether they were viable in the f(R) gravity background. Keeping in view the bouncing behavior, we achieved a bounce state at the stage of bounce and demonstrated the corresponding cosmological parameters. Furthermore, using parametrization of the r(z) function, we reconstructed the gravitational constant f(R) in terms of the red-shift component and thus expressed corresponding cosmological parameters using red-shift z, specifically the Friedmann equations and the effective EoS. We then studied the nature of EoS along with effective energy density and pressure using red-shift, which resulted in: \(\rho _\mathrm{{net}}\) emerging as positive while \(P_\mathrm{{net}}\) emerged as negative. Additionally, the variance of \(\omega _\mathrm{{net}}\) showed that the EoS crosses over the phantom step. This important result agrees with the idea that the universe is expanding gradually and also corresponds to observational results [60, 61]. We observed that there is a key role for free parameters in drawing successive plots. These free parameters support those choices which depend upon values of net energy density and net pressure, respectively, as well as intersecting the \(\omega _\mathrm{{net}}\) over the phantom divide line. At the end, we examined the stability of the situation by computing an arbitrary function \(c_{s}^2\) (speed of the sound) in red-shift terms. For this, we drew a plot of \(c_{s}^2\) versus red-shift. Resultantly, we showed in Fig. 11 that late-time stability exists when \(c_{s}^2>0\) in the original time. The acquired results of our considered models in f(R) gravity also establish the results presented in Ref. [69, 70].