1 Introduction

In the last decades, the theory of optical solitons draws the attention of the researchers and scientific community, because it is an active area of research in the fields of telecommunication engineering and mathematical physics. Optical solitons are type of solitary waves which have the capability of propagation of waves without scattering over long distance, i.e., they maintain their shape for long period of time and distance. They are significant in optical fiber communication due to this feature. Optical solitons are the fundamental key of telecommunication society. Solitons models are extensively helpful in mechanism of solitary wave-based communications links, optical pulse compressors, fiber-optic amplifiers and several others. The propagation of optical soliton’s dynamics through nonlinear optical fibers governs next generation technology for data transfer across inter-continental distances. Solitonic solutions have become a popular topic among traveling wave solutions since they act as a bridge between physics and mathematics [1,2,3,4,5,6,7,8,9,10,11,12]. Lump solutions are constructed for KP hierarchy with higher-order dispersion relations [13]. A verity of lump and its interaction solutions are investigated in \((2+1)\) dimensions to linear PDE [14]. Soliton equations are computed in different fields, such as it is associated with bi-Hamiltonian structure [15]. Rational and exact solutions to JM equation are constructed, together with a Bäcklund transformation technique [16] and Cole–Hopf transformation [17]. Recently, different approaches are also considered for diverse lump solutions [18,19,20].

Furthermore, the nonlinear partial differential equations (NLPDEs) have remarkable importance because of its broad range usages and applications. Nonlinear phenomena have become one of the great impressive fields for the researchers in this modern era of science. NLPDEs are largely used in diverse scientific fields such as biology, physics, geochemistry, ocean engineering, fluid mechanics, solid-state physics, geophysics, optical fibers, plasma physics and many other fields to explain the physical behavior of natural phenomena and dynamical processes. NLPDEs are often used to explain the behavior of waves in diverse fields. In order to understand these intricate phenomena, it is key to extract more exact solutions of NLPDEs. By using the obtained exact solutions one can understand the complex structure of physical phenomena. It is notable that many NLPDEs in diverse fields like biology, physics and chemistry consist of unknown functions and parameters and the study of exact solutions provides the guidance to the researchers to maintain and design the experiments, by producing the suitable natural environment, to obtain the these unknown function and parameters.

One of the models that derived from the well-known nonlinear Schrodinger’s equation (NLSE) is CLL equation [21]. This is one of the three forms of derivative NLSE that are also generally investigated in nonlinear optics. Recently, different algorithms [22,23,24,25,26,27,28,29,30,31,32,33] have been implemented to extract the optical solitons in different forms to the CCL equation.

The propagation of optical pulses inside in a monomode fibers modeled by the CLL equation is given below:

$$\begin{aligned} i q_{t}+a q_{xx}+ib |q|^{2}q_{x}=0. \end{aligned}$$
(1)

When we take \(a = b = 1\), the above equation collapses to the regular CLL equation, see also [21]. The parameters a and b represent group velocity dispersion (GVD) and nonlinear dispersion coefficients, respectively [34].

However, Fan-extended sub equation method [35] is utilized as an integration approach to find out different kinds of solutions in monomode fibers modelde by CLL equation in this manuscript. This technique develop a significant relationships between NLPDEs and others simple NLODEs. It has been examined that with the aid of simple solutions and solvable ODEs, different kind of traveling wave solutions of some complicated NLPDEs can be easily constructed. This is the key concept of Fan’s technique. The main outcome of the proposed technique is that we have succeeded in a single move to get and organize various types of new solutions.

This piece of article is discussed as sequence: In Sect. 2, overview of the method. In Sect. 3, the CLL equation is studied. In Sect. 4, results and discussion and finally paper comes to end with conclusion in last Sect. 5.

2 Overview of the method

In this section, key points of the method are given. Suppose that a NLPDE of the form as

$$\begin{aligned} {\varGamma }( v, v_{t}, v_{ x}, v_{{ xt}}, \ldots )=0, \end{aligned}$$
(2)

where \(\varGamma\) is a polynomial in its arguments. For solving (2), we introduce traveling wave transformation as:

$$\begin{aligned} v= \varphi (\xi ),\quad \xi =\sum ^{l}_{i=0}\gamma _{i} x_{i}, \end{aligned}$$
(3)

where \(\gamma _{i}\) are all arbitrary constants. After replacing (3) into (2), we have NODE in the following form.

$$\begin{aligned} {\varUpsilon }\big (\varphi , \varphi ^{\prime }, \varphi ^{\prime \prime }, \varphi ^{\prime \prime \prime }, \ldots \big )=0, \end{aligned}$$
(4)

Furthermore, \(\varphi (\xi )\) and \(\varPhi (\xi )\) depicts the following polynomial relation

$$\begin{aligned} v=\varphi (\xi )=\sum ^{n}_{j=0}\delta _{j}\varphi ^{j}(\xi ), \end{aligned}$$
(5)

where the \(\delta _{j}\) are constants to be determined later, and \(\varphi (\xi )\) satisfying the following general elliptic equation:

$$\begin{aligned} \phi ^{'2}=\left( \frac{ {\mathrm{d}} \varphi }{{\mathrm{d}}\xi }\right) ^{2}= h_{0}+ {h_{1}}\phi + {h_{2}}\phi ^{2}+{h_{3}}\phi ^{3}+ {h_{4}}\phi ^{4}, \end{aligned}$$
(6)

where \(h_{0}\), \(h_{1}\), \(h_{2}\), \(h_{3}\), and \(h_{4}\) are constants. For detail see also [35, 36].

3 Extraction of solutions

For solving Eq. (1), we start with wave transformation \(q(x,t)=Q(\xi )e^{ i\psi }\), where \(\xi =x-\nu t\) and \(\psi = -\, k x + \omega t +\theta\). Here \(\theta ,\omega\) and k are parameters, which represent the phase constant, frequency and wave number, respectively. Substitute transformation into Eq. (1), we get imaginary and real components, respectively, one can get the following constraint condition.

$$\begin{aligned} \nu =-2 a k+ b Q^{2}. \end{aligned}$$
(7)

From imaginary part and the real part, one can obtain the following equation

$$\begin{aligned} a Q''+ b k Q^{3} - (\omega +a k^{2})Q =0. \end{aligned}$$
(8)

To find the various kinds of soliton solutions by using the above said method. The result can be written as,

$$\begin{aligned} \zeta _{1}Q''+\zeta _{2}Q^{3}+\zeta _{3}Q=0, \end{aligned}$$
(9)

where \(\zeta _1=a\), \(\zeta _2= b k\) and \(\zeta _3=-(\omega +a k^{2})\). Balance between the linear term \(Q^{\prime \prime }\) and the nonlinear term \(Q^{3}\) to determine the value of n by simple calculation, we get \(n=1\). So Eq. (9) has the following solution

$$\begin{aligned} Q(\xi )=\beta _{0}+\beta _{1}\phi (\xi ), \end{aligned}$$
(10)

where \(\beta _{0}\) and \(\beta _{1}\) will be calculated later and \(\phi (\xi )\) holds the generalized elliptic equation and adjusting Eq. (10) by the assistant of generalized elliptic Eq. (6) into Eq. (9), we have equations of an algebraic system for \(\beta _{0}\), \(\beta _{1}\), \(\zeta _{1}\), \(\zeta _{2}\) and \(\zeta _{3}\) as follow:

$$\begin{aligned}&\frac{\beta _{1}\zeta _{1}h_{1}}{2}+\beta ^{3}_{0}\zeta _{2}+\zeta _{3}\beta _{0}= 0, \end{aligned}$$
(11)
$$\begin{aligned}&\beta _{1}\zeta _{1}h_{2}+3\zeta _{2}\beta ^{2}_{0}\beta _{1}+\beta _{1}\zeta _{3}= 0,\end{aligned}$$
(12)
$$\begin{aligned}&\frac{3\beta _{1}\zeta _{1}h_{3}}{2}+3\beta _{0}\zeta _{2}\beta ^{2}_{1}= 0,\end{aligned}$$
(13)
$$\begin{aligned}&2\beta _{1}\zeta _{1}h_{4}+\zeta _{2}\beta ^{3}_{1}= 0. \end{aligned}$$
(14)

For getting the maximum of \(h_{i}\) \((i=0,1,2,3,4)\) arbitrary, it is necessary to select variables properly. Due to this, \(\beta _{0}\), \(\beta _{1}\), \(\zeta _{2}\) and \(\zeta _{3}\) are considered as variables. Solving (11)–(14), we have the solutions as follow:

$$\begin{aligned} \beta _{0}= & {} \bigg (\frac{-h_{3}\zeta _{1}}{2\zeta _{2}\beta _{1}}\bigg ),\end{aligned}$$
(15)
$$\begin{aligned} \beta _{1}= & {} \bigg (\pm \sqrt{\frac{-2\zeta _{1}h_{4}}{\zeta _{2}}}\bigg ),\quad \zeta _{1}h_{4}\zeta _{2}<0,\end{aligned}$$
(16)
$$\begin{aligned} \zeta _{2}= & {} \bigg (\frac{-\zeta _{1}\beta _{1}h_{1}}{2\beta ^{3}_{0}}-\frac{\zeta _{3}}{\beta ^{2}_{0}}\bigg ),\end{aligned}$$
(17)
$$\begin{aligned} \zeta _{3}= & {} \bigg (-\zeta _{1}h_{2}-3\beta ^{2}_{0}\zeta _{2}\bigg ). \end{aligned}$$
(18)

The new traveling wave solutions of Eq. (1) are determined, as

$$\begin{aligned} q(x,t)=Q(\xi )e^{i\psi }=[\beta _{0}+\beta _{1}\phi (\xi )]e^{i\psi }, \end{aligned}$$
(19)

where

$$\begin{aligned} \xi= & {} x-\nu t,\quad \psi = -\,k x + \omega t +\theta . \end{aligned}$$
(20)

It may also be noted that

$$\begin{aligned} \beta _{0}= & {} \frac{-\,a h_3}{2 b \beta _1 k},\end{aligned}$$
(21)
$$\begin{aligned} \beta _{1}= & {} \pm \, \sqrt{\frac{-2 a h_4}{b k}} ,\quad a b k h_{4}<0,\end{aligned}$$
(22)
$$\begin{aligned} \zeta _{2}= & {} \frac{a k^{2}+\omega }{\beta _0^{2}}-\frac{a \beta _1 h_1}{2 \beta _0^{3}},\end{aligned}$$
(23)
$$\begin{aligned} \zeta _{3}= & {} -\,3 b \beta _0^{2} k-a h_2. \end{aligned}$$
(24)

We can get different types of solutions by considering \(\zeta _{1}\), \(\zeta _{2}\), \(\zeta _{3}\), \(h_{0}\), \(h_{1}\), \(h_{2}\), \(h_{3}\) and \(h_{4}\) as arbitrary constants.

Case I \(\phi\) will be the one solution of the twenty four \(\phi ^{\mathrm{I}}_{l}\) \((l=1,2,3,\ldots ,24).\) When we take

$$\begin{aligned} h_{0}=r^{2},\; h_{1}=2rp,\; h_{2}=2rq+p^{2},\; h_{3}=2pq,\; h_{4}=q^{2}. \end{aligned}$$

In this case, we get more two types of solutions.

Type I \(\phi\) will be the one solution from \(\phi ^{\mathrm{I}}_{l}\) \((l=1,2,\ldots ,12)\). When we take

$$\begin{aligned} p^{2}-4qr>0 \;{\text {and}}\; pq\ne 0, qr\ne 0. \end{aligned}$$

For example, if by considering \(l=1, 2, 3, 4, 5, 9\) then we get following soliton solutions:


Dark soliton solution:

$$\begin{aligned} q_{1}(x,t)=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{- a}{2b k}}\right) } \times \left\{ p+G \tanh \bigg (\frac{G}{2}\xi \bigg )\right\} \bigg ] e^{i\psi }, \end{aligned}$$
(25)

Singular soliton solution:

$$\begin{aligned} q_{2}(x,t)=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{- a}{2b k}}\right) } \times \left\{ p+G \coth \bigg (\frac{G}{2}\xi \bigg )\right\} \bigg ] e^{i\psi }, \end{aligned}$$
(26)

The complex soliton solution:

$$\begin{aligned} q_{3}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{- a}{2b k}}\right) }\nonumber \\&\quad \times \left\{ p+G \bigg (\tanh \bigg (G\xi \bigg )\pm i{\mathrm{sech}}\bigg (G\xi \bigg )\bigg )\right\} \bigg ] e^{i\psi }, \end{aligned}$$
(27)

Combined singular soliton solution:

$$\begin{aligned} q_{4}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{- a}{2b k}}\right) }\nonumber \\&\quad \times \left\{ p+G \bigg (\coth \bigg (G\xi \bigg )\pm {\mathrm{csch}}\bigg (G\xi \bigg )\bigg )\right\} \bigg ] e^{i\psi }, \end{aligned}$$
(28)

Mixed dark-singular soliton solution:

$$\begin{aligned} q_{5}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{ -a}{8 b k}}\right) }\nonumber \\&\quad \times \left\{ 2p+G\bigg (\tanh \bigg (\frac{G}{4}\xi \bigg )+\coth \bigg (\frac{G}{4}\xi \bigg )\bigg )\right\} \bigg ] e^{i\psi }, \end{aligned}$$
(29)

Combined soliton solution:

$$\begin{aligned} q_{6}(x,t)&=\left[ \left( \frac{-a p q}{b \beta _1 k}\right) \pm q{\left( \sqrt{\frac{-2 a}{b k}}\right) }\right. \nonumber \\&\quad \left. \times \left\{ \frac{-2r\sinh \left( \frac{G}{2}\xi \right) }{p \sinh \left( \frac{G}{2}\xi \right) -G\cosh \left( \frac{G}{2}\xi \right) } \right\} \right] e^{i\psi }, \end{aligned}$$
(30)

where \(G=\sqrt{p^{2}-4qr}\).

Type II \(\phi\) has solution from \(\phi ^{\mathrm{I}}_{l}\) \((l=13,14,\ldots ,24)\).

By taking

$$\begin{aligned} p^{2}-4qr<0 \; {\text {and}}\; pq\ne 0, \; qr\ne 0. \end{aligned}$$

For example, the following trigonometric and combined trigonometric traveling wave solutions for \(l=13, 14, 16, 17, 20\) may be obtain:

$$\begin{aligned} q_{7}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\pm {\left( \sqrt{\frac{- a}{2b k}}\right) } \times \left\{ -p+H \tan \left( \frac{H}{2}\xi \right) \right\} \bigg ] e^{i\psi }, \end{aligned}$$
(31)
$$\begin{aligned} q_{8}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{- a}{2b k}}\right) } \times \left\{ p+H \cot \left( \frac{H}{2}\xi \right) \right\} \bigg ] e^{i\psi }, \end{aligned}$$
(32)
$$\begin{aligned} q_{9}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{- a}{2b k}}\right) }\nonumber \\&\quad \times \left\{ p+H\bigg ( \cot \bigg (H\xi \bigg )\pm \csc \bigg (H\xi \bigg )\bigg )\right\} \bigg ] e^{i\psi }, \end{aligned}$$
(33)
$$\begin{aligned} q_{10}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\pm {\left( \sqrt{\frac{- a}{8 b k}}\right) }\nonumber \\&\quad \times \left\{ -2p+H\bigg (\tan \bigg (\frac{H}{4}\xi \bigg )+\cot \bigg (\frac{H}{4}\xi \bigg )\bigg )\right\} \bigg ] e^{i\psi }, \end{aligned}$$
(34)
$$\begin{aligned} q_{11}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\pm q{\left( \sqrt{\frac{ -2 a}{b k}}\right) }\nonumber \\&\quad \times \left\{ -\frac{2r\cos \bigg (\frac{H}{2}\xi \bigg )}{H\sin \bigg (\frac{H}{2}\xi \bigg )+p\cos \bigg (\frac{H}{2}\xi \bigg )}\right\} \bigg ] e^{i\psi }, \end{aligned}$$
(35)

where \(H=\sqrt{4qr-p^2}\).

Here p, q and r are arbitrary constants. Moreover, the above solutions are valid for

$$\begin{aligned} (a)(b k)<0. \end{aligned}$$

and

$$\begin{aligned} \xi =x-\nu t,\quad \psi =-kx+\omega t+\theta . \end{aligned}$$

We cannot express each solution here due to the limit of length.

Case II \(\phi\) will be one of solution from \(\phi ^{\mathrm{II}}_{l}(l=1,2,3,\ldots ,12)\). When we take

$$\begin{aligned} h_{0}=r^{2},\; h_{1}=2rp,\; h_{2}=0,\; h_{3}=2pq,\; h_{4}=q^{2},\; p^{2}=-2rq. \end{aligned}$$

Only one type will be discussed in this case.


Type I

When

$$\begin{aligned} qr<0 \; {\text {and}}\; qr\ne 0. \end{aligned}$$

For instance, take \(l=1, 2, 3, 4, 9\) then we have the following soliton solutions:

Dark soliton solution:

$$\begin{aligned} q_{12}(x,t)&=\bigg [\bigg (\frac{-\,a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{-\, a}{2b k}}\right) }\nonumber \\&\quad \times \left\{ \pm \sqrt{-\,2qr}+\sqrt{-\,6qr} \tanh \left( \frac{\sqrt{-\,6qr}}{2}\xi \right) \right\} \bigg ]e^{i\psi }, \end{aligned}$$
(36)

Singular soliton solution:

$$\begin{aligned} q_{13}(x,t)&=\bigg [\bigg (\frac{-\,a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{-\, a}{2b k}}\right) }\nonumber \\&\quad \times \left\{ \pm \sqrt{-\,2qr}+\sqrt{-\,6qr} \coth \bigg (\frac{\sqrt{-\,6qr}}{2}\xi \bigg )\right\} \bigg ]e^{i\psi }, \end{aligned}$$
(37)

Bright-dark soliton solution:

$$\begin{aligned} q_{14}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{- a}{2b k}}\right) }\nonumber \\&\quad \times \left\{ \pm \sqrt{-2qr}+\sqrt{-6qr}\left( \tanh \left( \sqrt{-6qr}\xi \right) \pm i {\mathrm{sech}} \left( \sqrt{-6qr}\xi \right) \right) \right\} \bigg ]e^{i\psi }, \end{aligned}$$
(38)

The combined singular soliton solution:

$$\begin{aligned} q_{15}(x,t)&=\bigg [\bigg (\frac{-a p q}{b \beta _1 k}\bigg )\mp {\left( \sqrt{\frac{- a}{2b k}}\right) }\nonumber \\&\quad \times \left\{ \pm \sqrt{-2qr}+\sqrt{-6qr}\left( \coth \left( \sqrt{-6qr}\xi \right) \pm {\mathrm{csch}} \left( \sqrt{-6qr}\xi \right) \right) \right\} \bigg ]e^{i\psi }, \end{aligned}$$
(39)

Combined soliton solution:

$$\begin{aligned} q_{16}(x,t)&=\left[\left(\frac{-a p q}{b \beta _1 k}\right )\pm q{\left( \sqrt{\frac{-2 a}{b k}}\right) }\right. \nonumber \\&\quad \times \left. \left\{ \frac{-2r\sinh \left (\frac{\sqrt{-6qr}}{2}\xi \right )}{\pm \sqrt{-2qr} \sinh \left (\frac{\sqrt{-6qr}}{2}\xi \right )-\sqrt{-6qr}\cosh \left (\frac{\sqrt{-6qr}}{2}\xi \right)} \right\} \right ] e^{i\psi }, \end{aligned}$$
(40)

where p, q and r are arbitrary constants. Moreover, the above solutions are valid for

$$\begin{aligned} (a)(b k)<0. \end{aligned}$$

and

$$\begin{aligned} \xi =x-\nu t,\quad \psi =-kx+\omega t+\theta . \end{aligned}$$

Case III \(\phi\) has solution one of the ten \(\phi ^{\mathrm{III}}_{l}(l=1,2,3,\ldots ,10)\). If we take \(h_{0}=0\), \(h_{1}=0\) and \(h_{2}, h_{3}, h_{4}\) are arbitrary constants.

For instance, if we take \(l=1\), then

$$\begin{aligned} h_{2}=1, \; h_{3}=\frac{-2c}{a},\; h_{4}=\frac{c^{2}-b^{2}}{a^{2}}. \end{aligned}$$

The traveling wave solution will take the form as

$$\begin{aligned} q_{17}(x,t)=\left[ \left( \frac{c }{b \beta _1 k} \right) \pm \left( \sqrt{\frac{-2(c^{2}-b^{2})}{ab k}}\right) \left\{ \frac{a{\mathrm{sech}} \xi }{b+c{\mathrm{sech}}\xi }\right\} \right] e^{i\psi }, \end{aligned}$$
(41)

By taking \(l=2\), and

$$\begin{aligned} h_{2}=1, \; h_{3}=\frac{-2c}{a},\; h_{4}=\frac{c^{2}+b^{2}}{a^{2}}. \end{aligned}$$

We get soliton solution as

$$\begin{aligned} q_{18}(x,t)=\left[ \left (\frac{c }{b \beta _1 k} \right )\pm \left (\sqrt{\frac{-2(c^{2}+b^{2})}{a b k}}\right)\left\{ \frac{a{\mathrm{csch}} \xi }{b+c{\mathrm{csch}}\xi }\right\} \right] e^{i\psi }, \end{aligned}$$
(42)

where a, b and c are arbitrary constants. Moreover, above solutions are valid for

$$\begin{aligned}&(c^{2}-b^{2})(a)(b k)<0.\\&(c^{2}+b^{2})(a)(b k)<0. \end{aligned}$$

and

$$\begin{aligned} \xi =x-\nu t,\quad \psi =-kx+\omega t+\theta . \end{aligned}$$

Similarly for \(l=3\) and \(h_{2}=4,\; h_{3}=-\frac{4(2b+d)}{a}, \; h_{4}=\frac{c^{2}+4b^{2}+4bd}{a^{2}},\) then we have

$$\begin{aligned} q_{{19}} (x,t) & = \left( {\frac{{2(2b + d)}}{{b\beta _{1} k}}} \right) \pm \left( {\sqrt {\frac{{ - 2(c^{2} + 4b^{2} + 4bd)}}{{abk}}} } \right) \\ & \quad { \times \left\{ {\frac{{a{\text{sech}}^{2} \xi }}{{b{\text{sech}}^{2} \xi + c\tanh \xi + d}}} \right\}} e^{{i\psi }} . \\ \end{aligned}$$
(43)

Here a, b, c and d are arbitrary constants. Moreover, above solutions are valid for

$$\begin{aligned} (c^{2}+4b^{2}+4bd)(a)(b k)<0. \end{aligned}$$

and

$$\begin{aligned} \xi =x-\nu t,\quad \psi =-kx+\omega t+\theta . \end{aligned}$$

Case IV \(\phi\) has solution one of the sixteen \(\phi ^{\mathrm{IV}}_{l}(l=1,2,3,\ldots ,16)\). If we take \(h_{1}=0\), \(h_{3}=0\) and \(h_{0}\), \(h_{2}\), \(h_{4}\) as arbitrary constants.

Type 1 For instance, by choosing \(l=13\) and

$$\begin{aligned} h_{0}=\frac{1}{4},\; h_{2}=\frac{1-2m^{2}}{2},\; h_{4}=\frac{1}{4}. \end{aligned}$$

We get the wave solution as

$$\begin{aligned} q_{20}(x,t)=[\beta _{0}+\beta _{1}\left\{ {\mathrm{ns}}\xi \pm {\mathrm{cs}} \xi \right\} ] e^{i\psi }, \end{aligned}$$
(44)

In the limiting cases

Remark 1

if we take \(m\rightarrow 1\) and \({\mathrm{ns}}(\xi )={\mathrm{coth}}(\xi )\), \({\mathrm{cs}}(\xi )={\mathrm{csch}}(\xi )\) then Eq. (44) gains the form of Jacobi wave function degenerate as combined soliton like solutions as

$$\begin{aligned} q_{21}(x,t)=\pm {\left( \sqrt{\frac{- a}{2 b k}}\right) }[ \coth (\xi ) \pm {\mathrm{csch}}(\xi ) ] e^{i\psi }, \end{aligned}$$
(45)

From the above equation, one may obtain the singular and dark soliton solutions by using the identities \(\coth (\xi )+{\mathrm{csch}}(\xi )=\coth \xi /2, \coth (\xi )-{\mathrm{csch}}(\xi )=\tanh \xi /2\), respectively.

$$\begin{aligned} q_{21_{1}}(x,t)= & {} \pm {\left( \sqrt{\frac{- a}{2 b k}}\right) }\coth (\xi /2) e^{i\psi }, \end{aligned}$$
(46)
$$\begin{aligned} q_{21_{2}}(x,t)= & {} \pm {\left( \sqrt{\frac{ -a}{2 b k}}\right) }\tanh (\xi /2 ) e^{i\psi }, \end{aligned}$$
(47)

Remark 2

when \(m\rightarrow 0\) and \({\mathrm{ns}}(\xi )={\mathrm{csc}}(\xi )\), \({\mathrm{cs}}(\xi )={\mathrm{cot}}(\xi )\) in this case Eq. (44), takes the periodic singular solutions.

$$\begin{aligned} q_{22}(x,t)=\pm {\left( \sqrt{\frac{- a}{2 b k}}\right) }[ \csc (\xi ) \pm {\mathrm{cot}}(\xi ) ] e^{i\psi }, \end{aligned}$$
(48)

Type 2

If we take \(l=16\) and \(h_{0}=\frac{m^{2}}{4}\), \(h_{2}=\frac{m^{2}-2}{2}\) and \(h_{4}=\frac{m^{2}}{4}\) then we have the following solution as.

$$\begin{aligned} q_{23}(x,t)=[\beta _{0}+\beta _{1}\left\{ {\mathrm{sn}}\xi \pm {\mathrm{ics}} \xi \right\} ] e^{i\psi }, \end{aligned}$$
(49)

For limiting cases

Remark 1

when \(m\rightarrow 1\) and \({\mathrm{sn}}(\xi )={\mathrm{tanh}}(\xi )\), \({\mathrm{cs}}(\xi )={\mathrm{csch}}(\xi )\) then Eq. (49) gains the form of Jacobi wave function degenerate as combined soliton like solutions as

$$\begin{aligned} q_{24}(x,t)=\pm {\left( \sqrt{\frac{ -a}{2 b k}}\right) }[\left\{ \tanh (\xi ) \pm i{\mathrm{csch}}(\xi )\right\} ] e^{i\psi }, \end{aligned}$$
(50)

Remark 2

when \(m\rightarrow 0\) and \({\mathrm{sn}}(\xi )={\mathrm{sin}}(\xi )\), \({\mathrm{cs}}(\xi )={\mathrm{cot}}(\xi )\) then Eq. (49) has the periodic singular solution

$$\begin{aligned} q_{25}(x,t)=\pm {\left( \sqrt{\frac{- a}{2 b k}}\right) }[\left\{ {\mathrm{sin}}(\xi ) \pm i{\mathrm{cot}}(\xi )\right\} ] e^{i\psi }. \end{aligned}$$
(51)

Here a, b and c are arbitrary constants. Moreover, above solutions are valid for

$$\begin{aligned} (a)(b k)<0. \end{aligned}$$

and

$$\begin{aligned} \xi =x-\nu t,\quad \psi =-kx+\omega t+\theta . \end{aligned}$$

Case V

System does not admit a solution of this group if \(h_{2}=h_{4}=0\), \(h_{0},h_{1},h_{3}\), are arbitrary constants.

4 Results and discussion

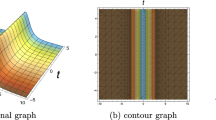
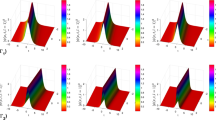
Based on the different values of the parameters, solutions are graphically depicted into distinct physical structures in the form of optical dark soliton, singular soliton, optical bright soliton and periodic singular wave function in the following section. The obtained solitonic wave solutions have different physical meanings. For example, hyperbolic functions such as, the hyperbolic tangent appears in the calculation and rapidity of special relativity while, the hyperbolic cotangent arises in the Langevin function for magnetic polarization. The physical movement of obtained solutions is shown by plotting 3D graphs, and 3D plotting for different value of parameters of the solutions given by Eqs. (25) and (27), in Fig. 1, by Eqs. (29) and (34) in Fig. 2, by (35) and (36) in Fig. 3, by (39) and (40) in Fig. 4, by Eqs. (41) and (42) in Fig. 5, in Eqs. (43) and (48) in Fig. 6, which helps to emphasize that all parameters have major influences for the solitary wave behavior. It is believed that the attained outcomes in our paper will be beneficial to explain the physical meaning of the studied model. The obtained results will be used thoroughly for the audience of optical solitons.

Fig. 1
figure 1

3D surfaces of Eqs. (25) and (27), respectively

Full size image
Fig. 2
figure 2

3D surfaces of Eqs. (29) and (34), respectively

Full size image
Fig. 3
figure 3

3D surfaces of Eqs. (35) and (36), respectively

Full size image
Fig. 4
figure 4

3D surfaces of Eqs. (37) and (40), respectively

Full size image
Fig. 5
figure 5

3D surfaces of Eqs. (41) and (42), respectively

Full size image
Fig. 6
figure 6

3D surfaces of Eqs. (43) and (48), respectively

Full size image

5 Conclusions

This paper retrieved the dynamics of optical solitons in optical monomode fibers which is modeled by CLL equation incorporating with group velocity dispersion. By using Fan extended sub equation method, we successfully recovered diverse solutions which are qualitative in nature. During the calculations, we found that our solutions take the form trigonometric and hyperbolic including known bright, dark, singular the some mixed form solutions. Furthermore, it is seen that for the limiting cases \(m\rightarrow 0, 1\), we get Jacobi elliptic functions degenerate into combined optical solitons and combined periodic singular solutions, respectively. We also plotted 3D sketches for better explanation of the attained solutions. The calculations also reveals us the importance of this method to find the analytically solutions in a more general way. The obtained solutions will be beneficial and helpful in the monomode fibers and nonlinear optics. It is claimed that this paper provides inspiration, motivation and encouragement for doing the research in future in the area of optical fibers, where these results are useful in telecommunication industry to enhance the performance and capacity of transmission systems.